误差函数公式及性质
误差函数表

误差函数表误差函数是数学中常见的一种函数,它在数学、物理、工程等领域中都有广泛的应用。
误差函数表是一份列出了误差函数在不同参数下取值的表格,它是一份重要的参考资料,可以帮助人们更好地理解误差函数的性质和应用。
本文将介绍误差函数的定义、性质和应用,并给出一份常用误差函数表,供读者参考。
一、误差函数的定义误差函数,又称为高斯函数,是一种特殊的积分函数。
它的定义如下:$$erf(x)=frac{2}{sqrt{pi}}int_{0}^{x}e^{-t^2}dt$$其中,$x$为自变量,$erf(x)$为函数值。
误差函数的图像呈现出一种钟形曲线,该曲线在$x=0$处取得最大值$1$,随着$x$的增大或减小,函数值逐渐减小,当$x$趋于正无穷或负无穷时,函数值趋于$1$或$-1$。
二、误差函数的性质1. 对称性误差函数具有对称性,即$erf(-x)=-erf(x)$。
这是因为误差函数的定义式中,$e^{-t^2}$为偶函数,因此积分区间$[0,x]$和$[0,-x]$的积分结果相同,只是符号相反。
2. 奇偶性误差函数具有奇偶性,即$erf(-x)=erf(x)$。
这是因为误差函数的定义式中,积分区间为$[0,x]$,而$e^{-t^2}$为偶函数,因此$erf(x)$为奇函数。
3. 渐进性当$x$趋于正无穷或负无穷时,误差函数的函数值趋于$1$或$-1$。
这是因为误差函数的定义式中,指数函数$e^{-t^2}$比分母中的$sqrt{pi}$增长得更快,因此当$x$趋于无穷时,分母可以忽略不计,误差函数的函数值趋近于$1$或$-1$。
4. 导数性质误差函数的导数具有简单的形式,即:$$frac{d}{dx}erf(x)=frac{2}{sqrt{pi}}e^{-x^2}$$这个导数的形式非常简单,但是它在误差函数的应用中起着重要的作用,比如在概率统计中经常用到的正态分布函数中,就涉及到误差函数的导数。
三、误差函数的应用误差函数在数学、物理、工程等领域中都有广泛的应用,以下列举几个例子:1. 概率统计误差函数在概率统计中应用广泛,特别是在正态分布函数中。
误差函数反常积分_概述说明以及解释

误差函数反常积分概述说明以及解释1. 引言1.1 概述本文将介绍误差函数反常积分的相关概念和特点,包括其定义、性质、计算方法以及在实际问题中的应用。
误差函数反常积分作为一种重要的数学工具,在物理学、工程学和经济学等领域中有广泛的应用。
通过深入研究误差函数反常积分,我们可以更好地理解其在实际问题求解中的作用和意义。
1.2 文章结构本文共分为五个部分。
首先是引言部分,对本文的背景和目标进行了简要介绍。
接着是第二部分,详细阐述了误差函数反常积分的定义与特点,包括对误差函数和反常积分基本概念的讲解,并探讨了误差函数反常积分的性质和特点。
第三部分介绍了计算误差函数反常积分的方法,包括数值逼近方法和解析求解方法,并对误差估计与收敛性进行了讨论。
第四部分通过物理学、工程学和经济学等领域的具体案例展示了误差函数反常积分在实际问题中的应用。
最后一部分是结论与展望,总结了本文的主要内容,并对未来的研究方向和应用前景进行了展望。
1.3 目的本文旨在全面介绍误差函数反常积分的概念、性质、计算方法以及应用,在读者中建立对误差函数反常积分重要性和关联领域的认识。
通过详细讲解,读者可以更好地理解和运用误差函数反常积分,在实际问题中获得准确性高、可靠性强的求解结果。
同时,本文也为未来相关研究提供了一个广阔的视野,希望能够激发更多学者对于误差函数反常积分的深入研究,挖掘其更多潜在应用场景。
2. 误差函数反常积分的定义与特点:2.1 误差函数的定义:误差函数(Error Function),又称为高斯积分函数,是数学中一种重要的特殊函数。
它以公式Erf(x)表示,定义如下:Erf(x) = (2/√π) ∫[0,x] e^(-t^2) dt其中,e代表自然对数的底数约等于2.71828,π为圆周率约等于3.14159。
误差函数在统计学、物理学、工程学和自然科学等领域中具有广泛的应用。
它常用于描述正态分布随机变量的累积分布函数,并在数据处理、信号处理和模型拟合等问题中发挥重要作用。
误差理论与数据处理知识总结

1.1.1 研究误差的意义为:1)正确认识误差的性质,分析误差产生的愿意,以消除或者减小误差2)正确处理测量和试验数据,合理计算所得结果,以便在一定条件下得到更接近于真值的数据3)正确组织实验过程,合理设计仪器或者选用仪器和测量方法,以便在最经济条件下,得到理想的结果。
1.2.1 误差的定义:误差是测得值与被测量的真值之间的差。
1.2.2 绝对误差:某量值的测得值之差。
1.2.3 相对误差:绝对误差与被测量的真值之比值。
1.2.4 引用误差:以仪器仪表某一刻度点的示值误差为份子,以测量范围上限值或者全量程为分母,所得比值为引用误差。
1.2.5 误差来源: 1)测量装置误差 2)环境误差 3)方法误差 4)人员误差1.2.6 误差分类:按照误差的特点,误差可分为系统误差、随机误差和粗大误差三类。
1.2.7 系统误差:在同一条件下,多次测量同一量值时,绝对值和符号保持不变,或者在条件改变时,按一定规律变化的误差为系统误差。
1.2.8 随机误差:在同一测量条件下,多次测量同一量值时,绝对值和符号以不可预定方式变化的误差称为随机误差。
1.2.9 粗大误差:超出在规定条件下预期的误差称为粗大误差。
1.3.1 精度:反映测量结果与真值接近程度的量,成为精度。
1.3.2 精度可分为:1)准确度:反映测量结果中系统误差的影响程度2)精密度:反映测量结果中随机误差的影响程度3) 精确度:反映测量结果中系统误差和随机误差综合的影响程度,其定量特征可用测量的不确定度来表示。
1.4.1 有效数字:含有误差的任何近似数,如果其绝对误差界是最末位数的半个单位,那末从这个近似数左方起的第一个非零的数字,称为第一位有效数字。
从第一位有效数字起到最末一位数字止的所有数字,不管是零或者非零的数字,都叫有效数字。
1.4.2 测量结果应保留的位数原则是:其最末一位数字是不可靠的,而倒数第二位数字应是可靠的。
1.4.3 数字舍入规则:保留的有效数字最末一位数字应按下面的舍入规则进行凑整:1)若舍去部份的数值,大于保留部份的末位的半个单位,则末位加一2)若舍去部份的数值,小于保留部份的末位的半个单位,则末位不变3)若舍去部份的数值,等于保留部份的末位的半个单位,则末位凑成偶数。
误差函数有如下的性质erf0
t1 t2 2 2 x1 x2
2 t1 x2 7 1.0 2 t2 2 28(h) 2 x1 0.5
思考题
已知Cu在Al中的扩散系数D, 在500℃和600℃时分别为 4.8×10-14 m2/s和5.3×10-13 m2/s。假如一个工件在600℃ 需要处理10小时,如果在500℃处理,要达到同样的效果 则需要多少小时? (Dt)500 = (Dt)600
§8.1.2 菲克第二定律
菲克第二定律是在菲克第一定律的基础上推导出来的。 其表达式为:
C 2C D 2 t x
c为扩散物质的体积浓度,原子数/m3或kg/m3;t为扩散时 间,s;x为距离,m。 上式给出了c=f(t,x)函数关系。由扩散的初始条件和边界 条件可求出通解。利用通解可解决包括非恒稳态扩散的具 体扩散问题。
§8.1.3 扩散方程在生产中的应用举例
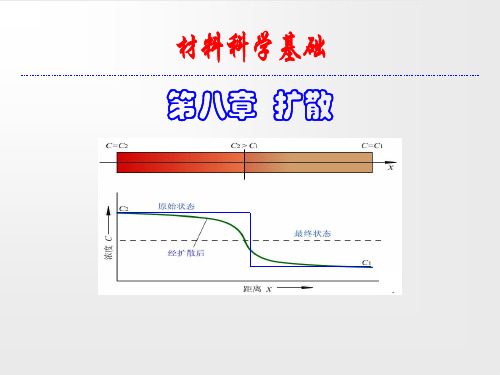
1.无限长扩散偶的扩散
图 无限长扩散偶中的溶质原子分布
将两根溶质原子浓度分别是C1和C2、横截面积和浓度均匀 的金属棒沿着长度方向焊接在一起,形成无限长扩散偶, 然后将扩散偶加热到一定温度保温,考察浓度沿长度方向 随时间的变化。 将焊接面作为坐标原点,扩散沿x轴方向,列出扩散问题 的初始条件和边界条件分别为 t=0时: x t≥0时:
x K Dt
直接应用菲克第二定律解决实际扩散问题,往往很复杂。 但是有两条由菲克第二定律推导出来的结论却十分简单、 有用: 对于钢铁材料渗碳处理时,扩散需要的时间t与扩散距离x 的平方成正比。 对于同一个扩散系统,扩散系数D与扩散时间t的乘积为一 常数。
思考题
假设对一个原始碳浓度为0.25wt %的钢件进行渗碳处理, 要求渗碳层厚度为0.5mm处的碳浓度为0.8wt %,渗碳气 体的碳浓度为1.2wt %,在950℃进行渗碳处理。应用菲克 第二定律计算可以知道,需要时间约7小时。如果将渗碳 层厚度由0.5mm提高到1.0mm,则需要多少时间?
误差基本知识

1.用真误差来确定中误差
在等精度观测条件下,对真值为X的某一量进行n 次观测,其观测值为L1,L2…Ln,相应的真误差为 1,2…n。取各真误差平方的平均值的平方根, 称为该量各观测值的中误差,以m表示,即:
Δi = X - L i
m =
2
i =1
n
n
2.用改正数来确定中误差
在实际工作中,未知量的真值往往不知道,真误差也无法 求得,所以常用最或是误差即改正数来确定中误差。
系统误差除可用改正数计算公式对观测 结果进行改正加以消除外,也可以用一 定的观测方法来消除其误差影响。
如经纬仪视准轴不垂直于横轴造成的误差,可以 用盘左、盘右观测角度,取其平均值的方法加以 消除;在水准测量中,采用前、后视距离相等来 消除水准仪的视准轴不平行于水准管轴造成的误 差。
由此可见,系统误差对观测结果影响较大,因此 必须采用各种方法加以消除或减少它的影响。比 如用改正数计算公式对丈量结果进行改正。
例四 某水准路线各测段高差的观测值中误差分别为h1 = 18.316 m ± 5 mm,h2 = 8.171 m ± 4 mm,h3 = 6.625 m ± 3 mm,试求总的高差及其中误差。 解:h = h1 + h2 + h3 = 15.316 + 8.171 6.625 = 16.862 (m)
1. 在一定的观测条件下,偶然误差的绝对值不 会超过一定的限值。 ………………….(有界性)
2. 绝对值小的误差比绝对值大的误差出现的机 会多。………………………………….(单峰性)
3.绝对值相等的正、负误差出现的机会基本相
等。 ………………………………次数的无限
容 = 2m 容 = 3m
误差计算公式

ess () ep () 1 K p
9
0型系统,N = 0,则位置稳态误差系数
m
Kk (Tis 1)
K p
lim
s0
i 1 n
Kk
(Tjs 1)
j 1
0型系统的位置稳态误差为
ep ()
1 1 Kp
1 1 Kk
0型以上系统,N≥1
m
KK (Tis 1)
K p
lim
s0
sN
i 1 nN
(Tjs 1)
(1)系统的控制目标:输出跟踪输入、对扰动具有抗干扰能力。 随动系统要求系统输出量以一定的精度跟随输入量的变化,
因而用给定稳态误差来衡量系统的稳态性能。系统的跟踪能力。 恒值系统需要分析输出量在扰动作用下所受到的影响,因
而用扰动稳态误差来衡量系统的稳态性能。系统的抗干扰能力。 (2)讨论系统稳态误差的前提:系统是稳定的。
E(s)
1 1 WK
s
X
r
(s)
用终值定理可求得稳态误差:
ess
lim sE(s)
s0
结论:系统稳态误差由开环传函和输入决定 。
东北大学《自动控制原理》课程组
7
3.6 稳 态 误 差
开环传递函数可以表示为时间常数(尾1)形式:
m
KK (Tis 1)
WK (s)
i 1 nN
sN (Tjs 1)
j 1
东北大学《自动控制原理》课程组
ep
()
1
1 K
p
0
10
3.6 稳 态 误 差
② 单位斜坡函数输入
xr t t
1 Xr (s) s2
1
ess
误差的基本性质与处理

1 0
f ( )
P[ ] 2(t )
2
得区间[ t , t ] 内的概率 P 2( t )
P
置信系数 置信概率 t 显著度 1 P 1 2( t )
14
四.不等精度测量的数据处理
为了得到更精确的测量结果或对比结果 而变更测量条件 不等精度测量 ① 测量次数
2.
3.
4.
系统误差的特殊性;
对系统误差的研究可以发现一些新事物。
19
定义: 在重复性条件下,对同一被测量进行 无限多次测量所得结果的平均值与被测量 的真值之差。 特征: 在同一测量条件下,多次测量同一量时, 误差的绝对值和符号保持恒定;或在条件改 变时,按某一确定的规律变化的误差。 产生原因: 测量装置的因素 测量方法的因素 测量环境的因素 测量人员的因素
Ⅱ:19.9990,20.0006,19.9995,20.0015,19.9994
均为 x 20.0000
标准差:
1 2 ... n
2 2
2
n
i 1
n
2 i
n
7
的物理意义:
大,数据分散,随机误差大,重复性差。
f ( )
小,小误差占优,数据集中,重复性好。
vi vi
使算术平均值增加或减小,对残差没 影响,只是引起误差分布曲线位置的平移, 而不影响分布曲线的形状。
23
2.
变值系统误差的影响 a. 对算术平均值的影响
x x
b. 对残差的影响
vi vi i
特点:1、具有确定规律性:测量过程中误差的大 小和符号固定不变,或按照确定的规律变化。 2、产生在测量开始之前:影响系统误差的因素在 测量开始之前就已经确定。 3、与测量次数无关:增加测量次数不能减小系统 误差对测量结果的影响。
误差函数 正态分布

误差函数正态分布一、引言在机器学习和统计学中,误差函数(error function)是用来衡量模型的预测值与真实值之间的差异的一种指标。
误差函数的选择对模型的训练和优化至关重要。
正态分布(normal distribution)又被称为高斯分布(Gaussian distribution),是一种常见的概率分布模型。
本文将深入探讨误差函数与正态分布的关系,以及它们之间的应用。
二、误差函数概述误差函数是用来度量预测值与真实值之间差异的函数。
在机器学习中,我们希望通过最小化误差函数来找到一个最佳的模型参数集合。
常见的误差函数包括均方误差(Mean Squared Error,简称MSE)、交叉熵(Cross Entropy)等。
2.1 均方误差均方误差是误差函数中最常用的一种,它衡量了模型预测值与真实值之间的平均差异的平方值。
均方误差的计算公式如下所示:MSE=1n∑(y i−y î)2ni=1其中,y i为真实值,y î为模型的预测值,n为样本数量。
均方误差广泛应用于回归问题的模型评估和参数优化。
2.2 交叉熵交叉熵常用于分类问题的模型评估和优化。
它衡量了模型预测值与真实类别之间的差异。
交叉熵的计算公式如下所示:CE=−∑y ini=1log(y î)其中,y i表示真实类别的概率分布,y î表示模型预测的类别概率分布,n表示类别数量。
交叉熵越小,模型的预测结果与真实结果越接近。
三、正态分布概述正态分布是一种连续型概率分布,它的概率密度函数呈钟形曲线。
正态分布的特点是其均值和方差完全决定了整个分布的形状。
正态分布的概率密度函数公式如下所示:f(x|μ,σ2)=1√2πσ2−(x−μ)22σ2其中,μ表示均值,σ2表示方差。
正态分布在统计学和概率论中广泛应用,因为许多自然现象都服从正态分布。
3.1 正态分布的特性正态分布有若干重要的特性,包括:1.对称性:正态分布的概率密度函数在均值处具有对称性,呈钟形曲线。
