状态反馈控制器设计习题
自动化专业06级《现代控制理论》试卷答案精选全文完整版

自动化专业06级《现代控制理论》试卷答案一、(10分,每小题1分)试判断以下结论的正确性,若结论是正确的,则在其左边的括号里打√,反之打×。
( √ )1. 相比于经典控制理论,现代控制理论的一个显著优点是可以用时域法直接进行系统的分析和设计。
( √ )2. 传递函数的状态空间实现不唯一的一个主要原因是状态变量选取不唯一。
( × )3. 状态变量是用于完全描述系统动态行为的一组变量,因此都是具有物理意义。
( × )4. 输出变量是状态变量的部分信息,因此一个系统状态能控意味着系统输出能控。
( √ )5. 等价的状态空间模型具有相同的传递函数。
( × )6. 互为对偶的状态空间模型具有相同的能控性。
( × )7. 一个系统的平衡状态可能有多个,因此系统的李雅普诺夫稳定性与系统受扰前所处的平衡位置无关。
( √ )8. 若一线性定常系统的平衡状态是渐近稳定的,则从系统的任意一个状态出发的状态轨迹随着时间的推移都将收敛到该平衡状态。
( × )9. 反馈控制可改变系统的稳定性、动态性能,但不改变系统的能控性和能观性。
( × )10. 如果一个系统的李雅普诺夫函数确实不存在,那么我们就可以断定该系统是不稳定的。
二、(15分)建立一个合理的系统模型是进行系统分析和设计的基础。
已知一单输入单输出线性定常系统的微分方程为:)(8)(6)()(3)(4)(t u t u t u t y t y t y++=++&&&&&& (1)采用串联分解方式,给出其状态空间模型,并画出对应的状态变量图;(7分+3分) (2)归纳总结上述的实现过程,试简述由一个系统的n 阶微分方程建立系统状态空间模型的思路。
(5分) 解:(1)方法一:由微分方程可得345213486)(222++++=++++=s s s s s s s s G令352113452)(21++⋅+=+++=s s s s s s s G 每一个环节的状态空间模型分别为:⎩⎨⎧=+−=1111x y u x x & 和 ⎩⎨⎧+−=+−=1212223u x y u x x&又因为11y u =, 所以⎩⎨⎧−=+−=212113x x x u x x&&, 212x x y −= 因此,采用串联分解方式可得系统的状态空间模型为:u x x x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡0131012121&& []u x x y +⎥⎦⎤⎢⎣⎡−=2112对应的状态变量图为:方法二: 由微分方程可得32143486)(22++⋅++=++++=s s s s s s s s s G 每一个环节的状态空间模型分别为:⎩⎨⎧+=+−=u x y u x x 11113& 和 ⎩⎨⎧+−=+−=121223u x y u x x&又因为11y u =, 所以⎩⎨⎧+−=+−=ux x x u x x2121133&&, u x x y +−=213 因此,采用串联分解方式可得系统的状态空间模型为:u x x x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡1133012121&& []u x x y +⎥⎦⎤⎢⎣⎡−=2113对应的状态变量图为(2)单输入单输出线性时不变系统传递函数的一般形式是1110111)(a s a sa sb s b s b s b s G n n nn n n n +++++++=−−−−L L若,则通过长除法,传递函数总可以转化成0≠n b )(s G d s a s c d a s a s a s c s c s c s G n n n n n +=++++++++=−−−−)()()(01110111L L 将传递函数c (s )/a (s )分解成若干低阶(1阶)传递函数的乘积,然后根据能控标准型或能观标准型写出这些低阶传递函数的状态空间实现,最后利用串联关系,写出原来系统的状态空间模型。
现代控制理论试卷答案3套

现代控制理论试卷 1一、(10分)判断以下结论,若是正确的,则在括号里打√,反之打×(1)用独立变量描述的系统状态向量的维数是唯一。
()(2)线性定常系统经过非奇异线性变换后,系统的能观性不变。
()(3)若一个系统是李雅普诺夫意义下稳定的,则该系统在任意平衡状态处都是稳定的。
()(4)状态反馈不改变被控系统的能控性和能观测性。
()(5)通过全维状态观测器引入状态反馈来任意配置系统的闭环极点时,要求系统必须同时能控和能观的。
()二、(12分)已知系统1001010,(0)00121x x x⎛⎫⎛⎫⎪ ⎪==⎪ ⎪⎪ ⎪⎝⎭⎝⎭,求()x t.三、(12分) 考虑由下式确定的系统:2s+2(s)=43Ws s++,求其状态空间实现的能控标准型和对角线标准型。
四、(9分)已知系统[]210020,011003x x y⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦,判定该系统是否完全能观?五、(17分) 判断下列系统的能控性、能观性;叙述李亚普诺夫稳定性的充要条件并分析下面系统的稳定性.[]xy u x x 11103211=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=六、(17分)已知子系统1∑ 111121011x x u -⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦,[]1110y x = 2∑ []22222110,01011x x u y x -⎡⎤⎡⎤=+=⎢⎥⎢⎥-⎣⎦⎣⎦求出串联后系统的状态模型和传递函数.七、(15分)确定使系统2001020240021a x x u b -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦为完全能控时,待定参数的取值范围。
八、(8分)已知非线性系统 ⎩⎨⎧--=+-=2112211sin 2x a x xx x x试求系统的平衡点,并确定出可以保证系统大范围渐近稳定的1a 的范围。
现代控制理论 试卷 1参考答案一、(10分)判断以下结论,若是正确的,则在括号里打√,反之打× (1) 用独立变量描述的系统状态向量的维数是唯一。
状态反馈和状态观测器习题与解答

第6章 “状态反馈和状态观测器”习题与解答6.1 判断下列系统能否用状态反馈任意地配置特征值。
1) 121310⎡⎤⎡⎤=+⎢⎥⎢⎥⎣⎦⎣⎦x x u2) 100100210100200⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦x x u解 1) []1103⎡⎤==⎢⎥⎣⎦c u b Ab ,秩2c u =,系统完全能控,所以可以用状态反馈任意配置特征值。
2) 2101010010204000000⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥⎣⎦c u bAbA b ,秩2c =u ,系统不完全能控,所以不能通过状态反馈任意配置特征值。
6.2 已知系统为122331233xx xx xx x x u ===---+试确定线性状态反馈控制律,使闭环极点都是3-,并画出闭环系统的结构图。
解 根据题意,理想特征多项式为*332()(3)92727s s s s s α=+=+++ 010*********u ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦x =x + 令[]123u k k k =-x ,并带入原系统的状态方程,可得123010001131313k k k ⎡⎤⎢⎥=⎢⎥⎢⎥------⎣⎦x x 其特征多项式为32321()(13)(13)(13)s s k s k s k α=++++++,通过比较系数得3139,k += 21327,k += 31327,k +=即,1263k =,2263k =,183k =,26268333u x ⎡⎤=-⎢⎥⎣⎦。
闭环系统的结构图:6.3 给定系统的传递函数为1()(4)(8)G s s s s =++ 试确定线性状态反馈律,使闭环极点为2 4 7---,,。
解 根据题意,理想特征多项式为*32()(2)(4)()1350567s s s s s s s α=+++=+++由传递函数 3211()(4)(8)1232g s s s s s s s==++++可写出原系统的能控标准形01000010032121u ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦x =x +令[]123u k k k =-x ,并带入原系统的状态方程,可得1230100013212k k k ⎡⎤⎢⎥=⎢⎥⎢⎥-----⎣⎦x x其特征多项式为32321()(12)(32)3s s k s k s k α=+++++通过比较系数得156,k =23250,k += 31213,k +=即 156,k =218,k =31k =。
现代控制理论实验五、状态反馈控制器设计河南工业大学

河南工业大学《现代控制理论》实验报告专业: 自动化 班级: F1203 姓名: 蔡申申 学号:201223910625完成日期:2015年1月9日 成绩评定:一、实验题目:状态反馈控制器设计二、实验目的1. 掌握状态反馈和输出反馈的概念及性质。
2. 掌握利用状态反馈进行极点配置的方法。
学会用MATLAB 求解状态反馈矩阵。
3. 掌握状态观测器的设计方法。
学会用MATLAB 设计状态观测器。
三、实验过程及结果1. 已知系统u x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=111100020003.[]x y 3333.02667.04.0= (1)求解系统的零点、极点和传递函数,并判断系统的能控性和能观测性。
A=[-3 0 0;0 2 0;0 0 -1];B=[1;1;1];C=[0.4 0.266 0.3333];[z p k]=ss2zp(A,B,C,0)系统的零极点:z =1.0017-1.9997p =-3-12k =0.9993[num den]=ss2tf(A,B,C,0)num =0 0.9993 0.9973 -2.0018den =1 2 -5 -6系统的传递函数:G1=tf(num,den)G1 =0.9993 s^2 + 0.9973 s - 2.002-----------------------------s^3 + 2 s^2 - 5 s - 6Continuous-time transfer function.Uc=ctrb(A,B); rank(Uc)ans =3满秩,系统是能控的。
Vo=obsv(A,C); rank(Vo)ans =3满秩,系统是能观的。
(2)分别选取K=[0 3 0],K=[1 3 2],K=[0 16 /3 –1/3](实验中只选取其中一个K为例)为状态反馈矩阵,求解闭环系统的零点、极点和传递函数,判断闭环系统的能控性和能观测性。
不确定切换中立时滞系统状态反馈控制器设计

摘 要 : 研 究 了具 有 两 类 不 确 定 性及 区 间 时 变 时 滞 切 换 中立 系 统 的 控 制 器 设 计 问 题 。 基 于 平 均 驻 留 时 间方 法 , 用 分 段 L a u o -Krsv ki 函 , 线 性 矩 阵 不 等 式 形 式 得 到 了依 赖 于 区 间 时 滞 的控 制 器 设 计 的 充 分 条 利 yp n v ao si泛 以
不 确 定 切 换 中立 时 滞 系统 状 态 反馈 控 制器 设 计
王 立敏 ,宋 岱 才 ,白 静
(. 宁石 油 化 工 大 学 理 学 院 , 宁 抚 顺 1 3 0 ; . 山火 炬 职 业 技 术 学 院 , 东 中 山 58 3 ) 1辽 辽 10 1 2 中 广 2 4 6
W ANG — m i ONG i c i,B ig Li n ,S Da— a AIJn
( . o lg f ce cs 1 C le eo S in e ,Lio ig S iu ie st a nn h h a Un v riy,Fu h nLio ig 1 3 0 ,P. Chn su ann 1 0 1 R. i a;
De i n o t t e b c n r l r f r Un e t i wic e sg fS a e Fe d a k Co t o l o c r an S t h d e Ne t a y t m sW ih Ti e Va y n l y u r lS s e t m — r i g Dea s
s tms ys e
S a i z t n Av r g wel tme De a tbl ai ; i o eae d l i ; l y— r n e— d p n e t Li e r ma rx i e u l is S t h d e ta ag e e d n ; n a t i n q ai e ; wi e n u r l t c
PID控制器与状态反馈控制器MATLAB教学实例设计

PID控制器与状态反馈控制器MATLAB教学实例设计作者:张栋来源:《教育教学论坛》2015年第04期摘要:为解决控制理论授课过程中PID控制器与状态反馈控制器设计的区别与联系,本文设计了一个MATLAB/SIMULINK仿真教学实例,便于学生深入理解与掌握教学过程中的基本理论与方法。
关键词:PID控制器;状态反馈;观测器;参数整定中图分类号:G642.1 文献标志码:A 文章编号:1674-9324(2015)04-0165-02一、引言PID控制器设计与状态反馈控制器两类控制器[1,2]相同之处为二者均属于反馈控制,因此在实际使用中,都需考虑闭环系统的稳定性;两类控制器最主要的相异之处为二者闭环系统极点的配置灵活性不同: PID控制器属于输出反馈,只能将闭环极点配置到闭环系统的根轨迹上;而状态反馈控制器在被控系统状态完全可控的条件下,可以将闭环极点任意配置。
本文利用MATLAB与SIMULINK仿真设计了一个实例,对同一个被控对象进行PID控制器设计与基于观测器的状态反馈控制器设计,将教学过程中较深刻的控制器设计理论用最直观的方式体现出来,利于学生的理解与掌握。
二、仿真实例设计选取被控对象微分方程数学模型如下:三种控制器下,单位阶跃响应曲线如图2所示。
在MATLAB中输入如下代码:G=tf([2.93*6 23.898*6 48.721*6],[1,6,41,7,0])%计算带有PID控制器的控制系统前向通道传递函数;rlocfind(G)%当K=1时,从根轨迹取相应闭环极点;rlocus(G)%绘制闭环系统根轨迹图;((a)闭环系统根轨迹图(根轨迹增益为1时的某一根);(b)PID控制器参数取某一数据时,闭环系统在根轨迹上的落点上。
)代码运行结果(图3)显示具有PID控制器的闭环系统闭环极点为-1.4771+6.3688i,-1.4771-6.3688i,-1.5229+2.1260i,-1.5229-2.1260i,一定落在该系统的根轨迹上。
状态反馈控制器设计
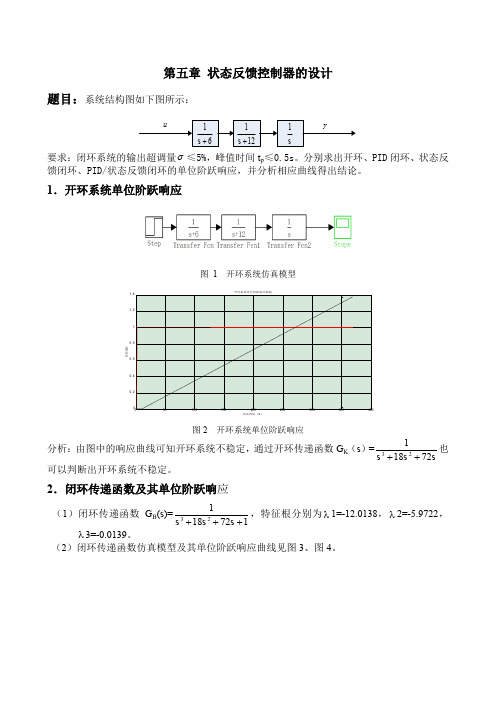
第五章 状态反馈控制器的设计题目:系统结构图如下图所示:要求:闭环系统的输出超调量σ≤5%,峰值时间t p ≤0.5s 。
分别求出开环、PID 闭环、状态反馈闭环、PID/状态反馈闭环的单位阶跃响应,并分析相应曲线得出结论。
1.开环系统单位阶跃响应图 1 开环系统仿真模型0.0.0.0.1.1.仿真时间(s )阶跃响应图2 开环系统单位阶跃响应分析:由图中的响应曲线可知开环系统不稳定,通过开环传递函数G K (s )=3211872s s s++也可以判断出开环系统不稳定。
2.闭环传递函数及其单位阶跃响应(1)闭环传递函数G B (s)=32118721s s s +++,特征根分别为λ1=-12.0138,λ2=-5.9722,λ3=-0.0139。
(2)闭环传递函数仿真模型及其单位阶跃响应曲线见图3、图4。
图3 闭环传递函数仿真模型图4 闭环传递函数单位阶跃响应分析:响应曲线表明,系统是稳定的,但是系统的响应时间太长,远达不到要求。
3.加入PID控制器,并进行参数整定后的单位阶跃响应图 5 PID控制仿真模型其中参数设置为:K p =256.8 ,K i =0.2,K d=23.2。
图6 PID 闭环控制输出波形图分析:通过Workspace 数据查询可知峰值时间tp=0.98686s ,最大输出值为1.0485,所以超调量为4.85%,满足要求,峰值时间达不到要求。
4.加入状态反馈控制器的单位阶跃响应图7 状态反馈控制仿真模型其中H1 到H3依次为10000、284.8、96.1。
0.0.0.0.1.-4t i m e(sec)O u t p u t图8 状态反馈控制单位阶跃响应分析:通过Workspace数据查询可知峰值时间tp=0.4492s,最大输出值为1.0449,所以超调量为4.49%,满足性能指标要求。
5.状态反馈/PID控制的单位阶跃响应图9 状态反馈/PID控制仿真模型其中PID参数设置为:K p =1.05 ,K i =0.01,K d=0;状态反馈控制H1 到H3依次为10000、284.8、96.1。
(完整版)状态反馈控制器的设计
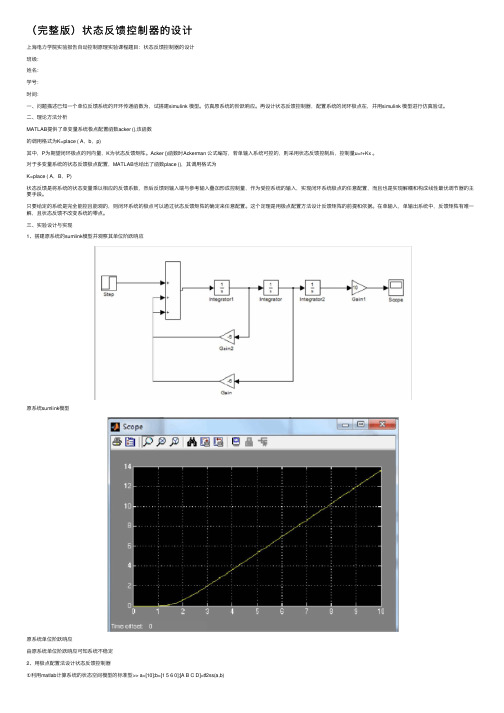
(完整版)状态反馈控制器的设计上海电⼒学院实验报告⾃动控制原理实验课程题⽬:状态反馈控制器的设计班级:姓名:学号:时间:⼀、问题描述已知⼀个单位反馈系统的开环传递函数为,试搭建simulink 模型。
仿真原系统的阶跃响应。
再设计状态反馈控制器,配置系统的闭环极点在,并⽤simulink 模型进⾏仿真验证。
⼆、理论⽅法分析MATLAB提供了单变量系统极点配置函数acker (),该函数的调⽤格式为K=place ( A,b,p)其中,P为期望闭环极点的列向量,K为状态反馈矩阵。
Acker ()函数时Ackerman 公式编写,若单输⼊系统可控的,则采⽤状态反馈控制后,控制量u=r+Kx 。
对于多变量系统的状态反馈极点配置,MATLAB也给出了函数place (),其调⽤格式为K=place ( A,B,P)状态反馈是将系统的状态变量乘以相应的反馈系数,然后反馈到输⼊端与参考输⼊叠加形成控制量,作为受控系统的输⼊,实现闭环系统极点的任意配置,⽽且也是实现解耦和构成线性最优调节器的主要⼿段。
只要给定的系统是完全能控且能观的,则闭环系统的极点可以通过状态反馈矩阵的确定来任意配置。
这个定理是⽤极点配置⽅法设计反馈矩阵的前提和依据。
在单输⼊,单输出系统中,反馈矩阵有唯⼀解,且状态反馈不改变系统的零点。
三、实验设计与实现1、搭建原系统的sumlink模型并观察其单位阶跃响应原系统sumlink模型原系统单位阶跃响应由原系统单位阶跃响应可知系统不稳定2、⽤极点配置法设计状态反馈控制器①利⽤matlab计算系统的状态空间模型的标准型>> a=[10];b=[1 5 6 0];[A B C D]=tf2ss(a,b)A = -5 -6 01 0 00 1 0B = 1C = 0 0 10③系统能控性矩阵>> uc=ctrb(A,B)uc = 1 -5 190 1 -50 0 1 >> rank(uc) ans = 3 所以系统完全能控③系统能观型矩阵>> vo=obsv(A,C) vo = 0 0 100 10 010 0 0 >> rank(vo) ans = 3 所以系统完全能观所以可以⽤极点配置法设计状态反馈控制器④求解系统反馈矩阵>> p=[-3 -0.5+j -0.5-j];k=acker(A,B,p)k = -1.0000 -1.7500 3.7500 加⼊反馈后的系统闭环极点为:>>sysnew=ss(A-B*k,B,C,D);pole(sysnew)ans = -3.0000-0.5000 + 1.0000i-0.5000 - 1.0000i⑤搭建加⼊反馈控制器后系统的sumlink模型⑥观察新系统的单位阶跃响应四、实验结果分析加⼊反馈控制器后系统的闭环极点在,符合题⽬要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter5 状态反馈控制器设计控制方式有“开环控制”、“闭环控制”。
“开环控制”就是把一个确定的信号(时间的函数)加到系统输入端,使系统具有某种期望的性能。
然而,由于建模中的不确定性或误差、系统运行过程中的扰动等因素使系统产生一些意想不到的情况,这就要求对这些偏差进行及时修正,这就是“反馈控制”。
在经典控制理论中,我们依据描述控制对象输入输出行为的传递函数模型来设计控制器,因此只能用系统输出作为反馈信号,而在现代控制理论中,则主要通过更为广泛的状态反馈对系统进行综合。
通过状态反馈来改变和控制系统的极点位置可使闭环系统具有所期望的动态特性。
利用状态反馈构成的调节器,可以实现各种目的,使闭环系统满足设计要求。
参见138P 例5.3.3,通过状态反馈的极点配置,使闭环系统的超调量%5≤p σ,峰值时间(超调时间)s t p 5.0≤,阻尼振荡频率10≤d ω。
5.1 线性反馈控制系统的结构与性质设系统),,(C B A S =为 Bu Ax x+= Cx y = (5-1)图5-1 经典控制-输出反馈闭环系统经典控制中采用输出(和输出导数)反馈(图5-1):v Fy u +-= F 为标量,v 为参考输入 (5-2)Bv x BFC A v Fy B Ax Bu Ax x+-=+-+=+=)()( 可见,在经典控制中,通过适当选择F ,可以利用输出反馈改善系统的动态性能。
现代控制中采用状态反馈(图5-1): v Kx u +-=,n m K ⨯~ (K 的行=u 的行,K 的列=x 的行)称为状态反馈增益矩阵。
状态反馈后的闭环系统),,(C B A S K K =的状态空间表达式为Bv x A Bv x BK A xK +=+-=)( Cx y = (5-3) 式中: BK A A K -≡ (5-4)图5-2 现代控制-状态反馈闭环系统若FC K =,“状态反馈”退化成“输出反馈”,表明“输出反馈”只是“状态反馈”的一种特例,因此,在经典控制理论中的“输出反馈”(比例控制P )和“输出导数反馈”(微分控制D )能实现的任务,状态反馈必能实现,反之则未必。
定理5-1(124P 定理5.1.1) 若n 阶系统),,(C B A S =是状态完全能控的,则经过状态反馈后的闭环系统),,(C B A S K K =仍然是状态完全能控的。
即状态反馈不改变系统的能控性。
但状态反馈不一定能保持原系统的能观性。
证明 对系统(5-1)的任意能控状态x ,根据能控性定义,在a t t ≤<0时间内,存在一个控制作用)(t u ,使得在该控制作用下0)()()0(=→=a t x t x x 。
对(5-1)加了状态反馈控制律v Kx u +-=后,需要证明x 仍然是闭环系统(5-3)的能控状态。
事实上,在时间段a t t ≤<0上,取 x K u v += (5-5)则由于 )()()]()([)()(t u B t x A t x K t u B t x BK A x+=++-= 所以,x 也是闭环系统(5-3)的能控状态。
由于x 的任意性,定理得证。
例5-1原系统为u x x x x ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛1013212121 ,⎪⎪⎭⎫⎝⎛=21)21(x x y ,状态反馈矩阵为 )13(--=K ,讨论系统经状态反馈前后的能控性和能观性。
解:n CA C n AB B==⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛==⎪⎪⎭⎫ ⎝⎛=24721Rank Rank 21120Rank )(Rank , 原系统能控且能观;经状态反馈后,⎪⎪⎭⎫⎝⎛=+=0021BK A A Kn B A BK ==⎪⎪⎭⎫⎝⎛=20120Rank )(Rank ,系统经状态反馈后能控性不变;但n CA C K <=⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛12121Rank Rank ,系统经状态反馈后不能保持原系统的能观性(状态反馈有可能改变输出端)。
定理5-2(126P 定理5.1.2)“输出反馈”不改变系统的能控性和能观性(证明略)。
定理5-3(126P 定理5.1.3)对能控的单输入、单输出系统,“状态反馈”不能移动系统的零点(证明见126P )。
证明:系统传递函数为 B A sI C s G 1)()(--=,由于系统的能控性,状态空间模型必能通过非奇异变换得到(等价于)能控标准型)~,~,~(C B A⎪⎪⎪⎪⎪⎭⎫⎝⎛---=-11...1...0000 (1)0~n a a a A,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=100~ B 由关系式 ⎪⎪⎪⎪⎪⎭⎫⎝⎛+++=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------0111111...001...1 (000)...11)~(a s a s s s a s a a s s s A sI n n n n n n)...(~011a s a s B n n n +++=--可得 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+++=-----101111...1~)~(n n n n s s a s a s B A sI由于等价的状态空间模型具有相同的传递函数,所以B A sIC a s a s c s c s c s s a s a s c c c B A sI C n n n n n n n n n n 1011011110111101)(...~~...~1...)~...~~(~)~(~-----------=++++++=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+++=- (1) 采用状态反馈v x K u +-=~~后,同理可得闭环系统的传递函数 )(...)(~~...~~)]~~~([~0011101111k a s k a s c s c s c B K B A sI C n n n n n n ++++++++=-------- (2) 其中 ]...[~110-=n k k k K 。
由(1)、(2)可知,状态反馈仅改变传递函数的分母多项式的系数(只改变系统的极点多项式),而不会改变分子多项式的系数。
此时,只要不发生零极点相消的现象,状态反馈就不能改变零点。
证毕。
5.2 稳定化状态反馈控制器的设计稳定是一个系统正常运行的首要条件。
若一个系统不稳定,则必须运用外部控制设法让其稳定。
如何确定增益矩阵K ,使下面闭环系统是渐近稳定的?Bv x A Bv x BK A xF +=+-=)( Cx y = (5-6) 根据Lyapunov 稳定性定理,系统(5-6)渐进稳定的充要条件是存在一个二次型的Lyapunov 函数Px x x V T =)(,其中P 是待定的对称正定矩阵。
可以通过使标量函数Px x x V T =)(的时间导数是负定的来确定P 和K 。
5.2.1 Riccati 矩阵方程处理方法这种方法可用来处理非线性系统、时滞系统等各类系统的镇定问题,也可用于鲁棒控制器的设计。
对标量函数Px x x V T =)(求时间导数:PBu x Px B u x PA P A x x P x Px x tx V T T T T T T T +++=+=)(d )(d (5-7) 应用P P =T 可知,后面两项“标量”相等PBu x Px B u T T T = (5-8) 于是PBu x x PA P A x tx V T T T 2)(d )(d ++= (5-9) 若选取控制u 具有以下结构形式Px kB u T -= 0>k (5-10)x P PBB kx PA P A x Px PBB kx x PA P A x tx V T T T T T T T T )2-(2-)(d )(d +=+= (5-11) 进一步,选取矩阵P P =T 使其满足(Riccati 矩阵方程)I P PBB kx PA P A T T T -=+2- (5-12) 则0d )(d <-=x x tx V T ,满足渐进稳定的充要条件。
从(5-12)解出正定对称矩阵P P =T ,代入(5-10)就可得到控制规律。
这种基于Riccati 矩阵方程(5-12)的稳定化控制器设计方法称为Riccati 矩阵方程处理方法。
若对给定的00>k ,Riccati 方程有一个正定对称解矩阵P ,则对任意的0k k ≥,x P PBB kx PA P A x tx V T T T T )2-(d )(d +=)2-(0<-=+≤x x x P PBB x k PA P A x T T T T T因此,对任意0k k ≥,Px kB u T -=都是系统的稳定化控制律。
这表明稳定化控制律Px kB u T -=具有正无穷大的稳定增益裕度,这在实际应用中是非常有用的,操作人员可以根据实际情况,在不破坏系统稳定性的前提下,调节控制器的增益参数,使系统满足其他性能要求。
例5-2 对双积分系统u x x x x ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛1001102121 设计稳定化状态反馈控制器。
解:已经讨论,系统不是一个渐近稳定的,取1=k ,Riccati 方程为⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-0110011032213221p p p p p p p p 01001)10(10232213221=⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-p p p p p p p p 可以求得: 23213233321=-==p p p ,, 容易验证⎪⎪⎭⎫⎝⎛3221p pp p 是正定的,因此,对任意的1≥k x kp p k x p pp p k Px kB u T )3231(2)()10(323221+--=-=⎪⎪⎭⎫⎝⎛-=-=都是所考虑系统的稳定化状态反馈控制器。
5.2.2 线性矩阵不等式处理方法根据线性时不变系统稳定性定理,闭环系统Bv x BK A x+-=)( 渐近稳定的充要条件是存在一个正定对称矩阵P ,使得0)()(<-+-BK A P P BK A T (5-13) 求解上述非线性矩阵方程十分困难,为此,作适当的变量代换0<--+PBK P B K P A PA T T T两边左、右×1-P 对称矩阵 01111<--+----)()(KP B B K P A P AP T T T记 110--=>=KP Y P X , (5-14) 0<--+BY B Y XA AX T T T (5-15) 不等式(5-15)是一个关于矩阵变量Y X 、的线性矩阵不等式。
如果能从(5-15)确定Y X 、(X 正定对称矩阵),则1-=KP Y 是系统(5-1)Bu Ax x+= 的一个稳定化状态反馈增益矩阵,01>=-P X 是Bv x BK A x+-=)( 相应闭环系统的一个Lyapunov 矩阵。
