现代控制理论大作业 北科
现代控制理论大作业
现代控制理论大作业一、位置控制系统----双电位器位置控制系统由系统分析可知，系统的开环传递函数：2233.3s =s s 2*0.07s*s 205353G（）（+1）*（++1）另：该系统改进后的传递函数：223.331s =s s 2*0.07s*s 3455353G （）（+1）*（++1）1、时域数学模型<1>稳定性>> s=tf('s');>> G=33.3/(s*(s/20+1)*(s^2/53^2+2*0.07*s/53+1)); >>sys=feedback(G,1); >> sysTransfer function:9.915e007 -----------------------------------------------------------53 s^4 + 1453 s^3 + 1.567e005 s^2 + 2.978e006 s + 9.915e007>> pzmap(sys)由零极点图可知，该系统有四个极点，没有零点，其中两个在左半s 开平面上，两个在s 平面的虚轴处，则，四个极点的坐标分别是：>> p=pole(sys)p =0.0453 +45.2232i0.0453 -45.2232i-13.7553 +26.9359i-13.7553 -26.9359i系统的特征方程有的根中有两个处于s的右半平面，系统处于不稳定状态<2>稳态误差分析稳态误差分析只对稳定的系统有意义，系统（G）处于不稳定状态，所以不做分析。
改进后系统（G1）如下，求其特征方程的极点：>> s=tf('s');>> G1=3.33/(s*(s/345+1)*(s^2/53^2+2*0.07*s/53+1));>> sys2=feedback(G1,1);>>p=pole(sys2);p =1.0e+002 *-3.4492-0.0206 + 0.5258i-0.0206 - 0.5258i-0.0338可以看出，改进后的传递函数G1的四个极点都在s平面的右半开平面上，则系统G1是稳定的，故对此系统做稳态误差分析：由系统G1的开环传递函数在原点处有一个极点，故属于1型系统。
《现代控制理论》课后习题全部答案(最完整打印版)
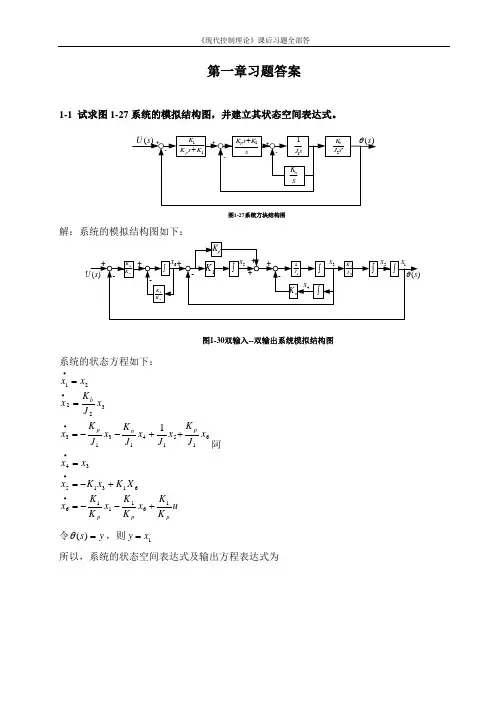
第一章习题答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解：系统的模拟结构图如下：)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
现代控制理论大作业课件
自适应控制设计需要建立合适的自适应算法和控制器结构。
详细描述
自适应控制设计需要建立合适的自适应算法和控制器结构， 以确保控制器能够实时地调整自身参数并保证系统的最优 性能。此外，还需要对算法和控制器结构进行充分的验证 和测试，以确保其在实际应用中的可靠性和有效性。
06
非线性系统理论
非线性系统的基本性质
齐次性
线性系统的输出与输入成正比，即当输入信 号乘以一个常数时，输出信号也乘以相同的 常数。
叠加性
对于线性系统的多个输入信号，其输出信号等于各 个输入信号单独作用于系统所产生的输出信号之和。
时不变性
线性系统的输出信号与输入信号在不同时刻 的比值保持恒定，即系统特性不随时间变化。
线性系统的状态空间表示
平衡点稳定性
分析非线性系统平衡点的稳定性，可以通过求 解系统的线性化方程来获得。
动态稳定性
动态稳定性是指非线性系统在受到扰动后恢复稳定的能力。
非线性系统的控制设计
状态反馈控制
通过测量系统的状态变量， 并使用状态反馈控制器来 控制非线性系统的输出。
滑模控制
滑模控制是一种变结构控 制方法，通过设计滑模面 和滑模控制器来实现对非
最优控制问题的描述
01
最优控制问题是在给定初始和终端状态约束下，寻找一个控制输 入，使得系统状态在满足约束条件下，某个性能指标达到最优。
02
性能指标通常包括系统状态和控制输入的能量、时间和成 本等。
03
约束条件可以是系统状态、控制输入或性能指标的限制。
极小值原理
极小值原理是求解最优控制问题的一种方法，它基于动态规划的思想，通 过求解一系列的子问题来找到最优解。
状态方程
描述系统内部状态变量随时间变化的数学方程，通常 表示为矩阵形式。
现代控制理论大作业
现代控制理论直流电动机模型的分析姓名：李志鑫班级：测控1003学号：20100203030921直流电动机的介绍1.1研究的意义直流电机是现今工业上应用最广的电机之一，直流电机具有良好的调速特性、较大的启动转矩、功率大及响应快等优点。
在伺服系统中应用的直流电机称为直流伺服电机，小功率的直流伺服电机往往应用在磁盘驱动器的驱动及打印机等计算机相关的设备中，大功率的伺服电机则往往应用在工业机器人系统和CNC铣床等大型工具上。
[1]1.2直流电动机的基本结构直流电动机具有良好的启动、制动和调速特性，可以方便地在宽范围内实现无级调速，故多采用在对电动机的调速性能要求较高的生产设备中。
直流伺服电机的电枢控制：直流伺服电机一般包含3个组成部分：-图1.1①磁极：电机的定子部分，由磁极N—S级组成，可以是永久磁铁（此类称为永磁式直流伺服电机），也可以是绕在磁极上的激励线圈构成。
②电枢：电机的转子部分，为表面上绕有线圈的圆形铁芯，线圈与换向片焊接在一起。
③电刷：电机定子的一部分，当电枢转动时，电刷交替地与换向片接触在一起。
直流电动机的启动电动机从静止状态过渡到稳速的过程叫启动过程。
电机的启动性能有以下几点要求：1）启动时电磁转矩要大，以利于克服启动时的阻转矩。
2）启动时电枢电流要尽可能的小。
3）电动机有较小的转动惯量和在加速过程中保持足够大的电磁转矩，以利于缩短启动时间。
直流电动机调速可以有：（1）改变电枢电源电压；（2）在电枢回路中串调节电阻；（3）改变磁通，即改变励磁回路的调节电阻Rf以改变励磁电流。
本文章所介绍的直流伺服电机，其中励磁电流保持常数，而有电枢电流进行控制。
这种利用电枢电流对直流伺服电机的输出速度的控制称为直流伺服电机的电枢控制。
如图1.2Bm电枢线路图1.2——定义为电枢电压（伏特）。
——定义为电枢电流（安培）。
——定义为电枢电阻（欧姆）。
——定义为电枢电感（亨利）。
——定义为反电动势（伏特）。
现代控制理论作业
现代控制理论作业Explorations and Practices on the Teaching Platform of Furuta Pendulum1. IntroductionThe Experimental Teaching is an important part of the computer control teaching. The teaching ofcontrol system needs physical objects to control, while the school of automation science school inBeihang university usually use aircraft as p坷sical object. It's difficult for senior undergraduate andgraduatestudents to learn. The control system is divided into process control and motion controlaccording to the response of the controlled variable speed. Motion control systems keep thephysical device as object, keep the controller as core and keep motor and power electronics, powerconversion device as an executive agency. Under the guidance of the automatic control theory, allabove compose the electrical transmission automatic control system. The flight control system is avery complex motion control system. Simplification and abstraction, the flight control system has been inverted pendulum control object. It is a multi-variable, higher order, front drive, the naturalinstable fast system [1], applied to the computer control systems and modern control theoryexperimentsInverted pendulum system includes linear inverted pendulum, planar inverted pendulum,pendubot. Inverted pendulum system is considered as typical experimental equipment in the moderncontrol theory [2]. It is a multi-variable, strong coupling, higher-order nonlinear natural unstablenon-minimum phase system. Only to take effective control method can make it stable. In thehardware experimental platform, much more research is focused on the linear inverted pendulumWhile this paper propose Fututa pendulum based on the linear inverted pendulum. Fututapendulum, also known as round rail inverted pendulum [3], consists of rotating arm and pendulum,shown in Figure 1, the rotating arm and the pendulum connect free. The rotating arm fixed to thebase driven by motor, do a circular motion around a rotation axis in a horizontal plane. With thecoupling effect, the sections of pendulum rotate free in the cylindrical inner and maintain itsstability. The angle sensors are respectively mounted on the junction of the pendulumand the shaft of rotating arm, for sensing the angle of rotating arm and pendulum. The schematic diagram isshown in Figure 2Fig. 1 Block Diagram of Furuta Pendulum As can be seen from that description, compared with the linear inverted pendulum, Fututapendulum has the advantage of small size, complexmechanical structure, difficulty to control etcWe can verithe control ability of many control methods for serious nonlinear and naturallyunstable system. Furuta pendulum covers a much smaller area. During the movement, the rotationof the rotating arm adds the role of the rotating fore to the system, so that the entire control processis close to the arm of the machine control, which increases the difficulty of control. It can be seen,the physical object of Furuta pendulum is much more suitable for the control experimentscurriculum teaching of undergraduates and graduate students2. InstanceAutomatic Control Theory Laboratory, part of Teaching Experiment Center of Automatic Controlin Beihang University, has applied the physical object of Furuta pendulum to experiment teachingUsing the control teaching platform, the authors develop a number of control experiment teaching,including graduated design. These developments can be used for experimental teaching directlyOwning to space constraints, this paper only shows one example of control system to illustrate theapplication of Furuta pendulum2.1 Control System of Two-link Furuta Pendulum.The two-link Furuta pendulum consists of two pendulums and a rotating arm. It has three degrees offreedom,、ich only the rotating arm controlled. The structure is shown in the following figure. Theconnections between rotating arm and pendulums can rotate free. The rotating arm fixed to the basedriven by motor, do a circular motion around a rotation axis in a horizontal plane. With the couplingeffect, the sections of pendulum rotate free in the cylindrical inner and maintainits stability. Thethree angle sensors are used to sense the angle of rotating arm andpendulums. Thesystem is drivenat the axis()and rotates around the axis. While the pendulums rotate around the axis Oland 02 freein the inertia. This inverted pendulum robot has natural instability, and iscontrolled very difficultlyHere we use the CPSO (Chaos Particle Swarm Optimization)control method [4] to make thesystem satisfy the control indicator. First, we establish the mathematical model of two-link FurutaWith the two-link Furuta pendulum shown in Figure 3, the centroid of rotating arm is cm higherthan the motor shaft, while the centroid of down pendulum is 2}cm higher and the centroid of uppendulum is jcm higher. Thus, the two-hnk Furuta pendulum is a highly naturalInvestigated the3. SummaryThis paper puts forth a teaching platform based on Furuta pendulum. The platform takes fulladvantage of the Furuta pendulum,、ich has small size, a complex structure and is difficult tocontrol. It can verify the control effects of the various moderncontrol algorithms. Practice showsthat with the application of Furuta pendulum, students can concentrate on the design andimplementation of control algorithms. The platform not only solves the traditional experimentalproblems, but also is applicable to a wide range and easy to teach. It increases students'understanding and interest in the control algorithm design. Teaching Center of Automatic Controlof Beihang University has put this teaching platform into the teaching ofmodern control andcomputer control, which praised by teachers and students, moreover obtained good teaching results References[1] Mori S Nishihara H. and Furuta K. Control of unstable mechanical system- control ofpendulum [J].Control 23.1976:673-692[2] Mori S Nishihara H and Furuta K. Control of unstable system[J]. Computer and Elec Eng1978,5(5):673-692[3] Meier H. Farwig Zu and Unbehauen H. Discrete computer control of a triple inverted pendulum[J]. Optimal Control Applications&Methods.VOL 11.1990: 151一171[4] PIAO H, WANG Z, ZHANG H. Cooperative-PSO-based new learning algorithm for PIDneural network and nonlinear control design【月The Mediterranean Journal of Measurementand Contro1,2009,5(2):60-70[5] S. Q. Yuan, F. Y. Xu, "Design of control system with limited feedback gain based on CPSOalgorithm," Control Conference (CCC), 2011 30th Chinese, pp. 3766-3771, 2011[6] Bnjamin Potsaid, John T. Wen. Optimal Mechanical Design of a Rotary Inverted PendulumProceedings of the 2002 IEEE/RSJ intl2002:2079-2084Conference onIntelligent Robots and Systems,。
现代控制理论大作业
现代控制理论大作业“现代控制理论”课本质上是一门工学理论基础课，它在电气工程领域众多研究工作中也有着广泛的应用，例如发电机励磁控制、发电机调速控制、电力电子装置控制等。
“现代控制理论”课立足于近年来控制理论与工程应用的最新进展，旨在实现以下两个目的：一是将控制与系统理论的前沿领域介绍给研究生，使之理解基本思想并掌握基本设计方法；二是在工程实践（主要是电力系统）与先进理论之间架设一座桥梁，使研究生能正确地运用有关理论和方法解决实际工程问题。
通过实现上述目标，本课程可拓宽研究生的专业基础知识，了解和掌握学科前沿动态，培养和提高研究生独立从事科研的能力。
课程内容本课程的教学理念是“用生动鲜活的例子诠释复杂的控制理论，用教师的研究经历点亮学生思考的火炬”。
“现代控制理论”立足于近年来控制理论与工程应用的最新进展，紧紧围绕鲁棒控制和非线性系统控制两个重点，主要讲述以下内容：①线性最优控制系统理论。
②非线性最优控制系统设计——微分几何方法。
③线性H∞控制设计原理。
④非线性控制系统H∞设计原理。
课程教学方式本课程采用教师讲授、学生课外阅读、习题练习和研究型大作业相结合的教学模式。
为加强理论联系实际，避免过分理论化，课程结合控制工程特别是电力系统工程实际，设置了下述专题研究：a. 汽轮机汽门开度系统非线性控制器设计b. 可控串联补偿鲁棒控制器设计c. 水轮机调速非线性鲁棒控制器设计d. 静止无功补偿器非线性控制器设计e. 直流输电系统非线性控制器设计f. 倒立摆控制器设计（购置2级和3级倒立摆各1台）g. 电力巡线机器人越障控制上述专题研究的目的是：在基本掌握现代控制理论主要设计方法的基础上，让研究生开展某一专题的研究，以培养学生的综合能力和素质。
这一部分内容可以代替课程的期末考试（笔试闭卷）。
教师事先就专题研究的要求、选题、难度等方面进行指导；专题研究一般由个人独立完成，内容较多的题目可以两个人作为一组来完成。
现代控制理论课程设计方案书(大作业)
现代控制理论课程设计报告题目打印机皮带驱动系统能控能观和稳定性分析项目成员史旭东童振梁沈晓楠专业班级自动化112指导教师何小其分院信息分院完成日期 2014-5-28目录1. 课程设计目的 (4)2.课程设计题目描述和要求 (4)3.课程设计报告内容 (4)3.1 原理图 (4)3.2 系统参数取值情况 (5)3.3 打印机皮带驱动系统的状态空间方程 (5)4. 系统分析 (8)4.1 能控性分析 (8)4.2 能观性分析 (8)4.3 稳定性分析 (9)5. 总结 (11)项目组成员具体分工打印机皮带驱动系统能控能观和稳定性分析课程设计的内容如下：1.课程设计目的综合运用自控现代理论分析皮带驱动系统的能控性、能观性以及稳定性，融会贯通并扩展有关方面的知识。
加强大家对专业理论知识的理解和实际运用。
培养学生熟练运用有关的仿真软件及分析，解决实际问题的能力，学会应用标准、手册、查阅有关技术资料。
加强了大家的自学能力，为大家以后做毕业设计做很好的铺垫。
2.课程设计题目描述和要求(1)环节项目名称：能控能观判据及稳定性判据(2)环节目的：①利用MATLAB分析线性定常系统的可控性和客观性。
②利用MATLAB进行线性定常系统的李雅普诺夫稳定性判据。
(3)环节形式：课后上机仿真(4)环节考核方式：根据提交的仿真结果及分析报告确定成绩。
(5)环节内容、方法：①给定系统状态空间方程，对系统进行可控性、可观性分析。
②已知系统状态空间方程，判断其稳定性，并绘制出时间响应曲线验证上述判断。
3.课程设计报告内容3.1 原理图在计算机外围设备中，常用的低价位喷墨式或针式打印机都配有皮带驱动器。
它用于驱动打印头沿打印页面横向移动。
图1给出了一个装有直流电机的皮带驱动式打印机的例子。
其光传感器用来测定打印头的位置，皮带张力的变化用于调节皮带的实际弹性状态。
图1 打印机皮带驱动系统3.2 系统参数取值情况表1打印装置的参数3.3 打印机皮带驱动系统的状态空间方程图2 打印机皮带驱动模型状态空间建模及系统参数选择。
现代控制理论作业
现代控制理论大作业要求：（1）自选一实际物理对象进行研究，建立实际物理系统的状态空间模型；（2）进行原系统的定性分析，包括稳定性、能控性、能观性分析；（3）根据系统提出的性能指标要求（如超调量、超调时间、调节时间等动态 性能指标以及稳态误差等稳态性能指标），进行原系统的仿真分析，和要求的性能指标做对比；（4）对不稳定系统且能镇定的系统，进行镇定控制；（5）对未达到性能指标要求的系统进行状态反馈控制设计，满足系统性能指 标要求；（6）设计状态观测器观测所有状态；（7）设计降阶状态观测器；（可选）（8）最优控制；（9）体会及对课程建议。
1实际物理模型：如图1所示，为一交接车前后连接振动简化模型。
设计一个调节器系统使得在无扰动的情况下，系统保持在零位置上（y1=0）。
其中m1=1，m2=2，k=36，b=0.62系统的描述方程：)()(m )()(m 212122121211y y b y y k yu y y b y y k y-+-=+-+-= 其空间状态模型为：设：。
,,,24132211y x yx y x y x ====[]⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡432121432143210001u 01003.03.018186.06.0-3636-10000100x x x x y y x x x x x x x x 3分析与求解过程：由根轨迹和特征根（a = -0.4500 + 7.3347i -0.4500 - 7.3347i -0.000 0 ）知虽实根都为负数但都靠近零轴，是李雅普诺夫定义下的稳定，但存在震荡，所以把希望闭环极点配置在10-s ,10-s ，32-2-s ，322-s ===+=和把最小阶观测器希望极点配置在16-s ,15-s ==来改善系统的性能。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
现代控制理论大作业分析对象：汽车悬架系统指导老师：周晓敏专业：机械工程姓名：白国星学号：S2*******1.建模悬架是车轮或车桥与汽车承载部分之间具有弹性的连接装置的总称，具有传递载荷、缓和冲击、衰减振动以及调节汽车行驶中的车身位置等作用。
传统汽车悬驾系统是被动悬驾，其参数不能改变，无法控制其对不同路面激励的响应，因此对不同路面的适应性较差。
为提高汽车的行驶平顺性、操纵稳定性和制动性等性能，人们开始用主动悬架系统来代替传统的被动悬架系统。
主动悬架系统能根据路面的情况通过一个动力装置改变悬挂架的参数，改善汽车的各方面性能。
对悬驾系统进行仿真计算首先要建立悬驾系统动力学模型，随后对所建立的模型进行仿真分析。
为了简化模型，取汽车的一个车轮的悬驾系统进行研究，该模型可简化为一维二自由度的弹簧阻尼质量系统，图1所示为该模型的模拟图。
图1 悬架系统模型的模拟图其中u为动力装置的作用力，w为路面位移，x1为车身位移，x2为悬驾位移，用车身位移来度量车身的振动情况，并视为系统的输出。
路面状况以w为尺度，并视为系统的一个干扰输入。
当汽车从平面落入坑时，w可用一个阶跃信号来模拟。
u 为主动悬架的作用力，它是系统的控制量。
进行受力分析，由牛顿第二规律可得车身悬架系统的动力学方程为:()()()()()1121212212122s s t m x K x x b x x u m x K x x b x x u K w x ⎧=-+-+⎪⎨=-+--+-⎪⎩&&&&&&&& 设系统状态变量为:[]1212x x x x x =&&则上面系统动力学方程可改写为状态空间表达式:xAx Bu y Cx Du=+⎧⎨=+⎩& 其中:()1111222200100001sss t s K K b b A m m m m K K K b b m m m m ⎡⎤⎢⎥⎢⎥⎢⎥--=⎢⎥⎢⎥-+⎢⎥-⎢⎥⎣⎦1220000101t B m K m m ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦[]1000C = []00D = u u w ⎡⎤=⎢⎥⎣⎦Matlab 系统模型程序代码：m1=800;m2=320;ks=10000;b=30000; kt=10*ks;a=[0 0 1 0;0 0 0 1;-ks/m1 ks/m1 -b/m1 b/m1; ks/m2 -(ks+kt)/m2 b/m2 -b/m2];b=[0 0;0 0;1/m1 0;-1/m2 kt/m2];c=[1 0 0 0];d=[0 0];G=ss(a,b,c,d)[num,den]=ss2tf(a,b,c,d,1);tfsys=tf(num,den)eig(a)figure(1)impulse(G)figure(2)step(G)系统状态空间模型：:系统传递函数：系统矩阵特征值：系统矩阵特征值都在左半平面，故系统稳定。
系统脉冲响应：系统阶跃响应：2.系统能控性与能观性分析Matlab系统能控性与能观性分析程序代码：m1=800;m2=320;ks=10000;b=30000;kt=10*ks;a=[0 0 1 0;0 0 0 1;-ks/m1 ks/m1 -b/m1 b/m1;ks/m2 -(ks+kt)/m2 b/m2 -b/m2];b=[0 0;0 0;1/m1 0;-1/m2 kt/m2];c=[1 0 0 0];d=[0 0];N=size(a);n=N(1)ud=ctrb(a,b);%能控矩阵%ob=obsv(a,c);%能观矩阵%if rank(ud)==n%判断能控性%disp('系统能控')elseif rank(ud)<ndisp('系统不能控')endif rank(ob)==n %判断能观性%disp('系统能观')elseif rank(ob)<ndisp('系统不能观')end运行结果：3.系统稳定性分析Matlab系统稳定性分析程序代码：m1=800;m2=320;ks=10000;b=30000;kt=10*ks;a=[0 0 1 0;0 0 0 1;-ks/m1 ks/m1 -b/m1 b/m1;ks/m2 -(ks+kt)/m2 b/m2 -b/m2];Q=eye(4,4);P=lyap(a,Q);%求解矩阵Pflag=0;n=length(a);for i=1:ndet(P(1:i,1:i))if(det(P(1:i,1:i))<=0)flag=1;endendif flag==1disp('系统不稳定');elsedisp('系统稳定');end运行结果：4.系统状态反馈控制器设计若系统期望性能指标为超调量小于5%，峰值时间小于0.5秒，即：()22exp 15051%.p n t w σξπξξ=--≤=≤-则：07079.n w ξ≥≥为计算方便取070710.n w ξ==则主导极点为：12707707..n w jw j λλξ==-±=-± 另两个极点应选择成使其和原点距离远大于主导极点和原点的距离，取：31411020λλλλ==则 34100200λλ=-=- 则期望特征多项式为：()()()()()()()22243220010022001001411003141243303120002000000..n n w w ∆λλλλξλλλλλλλλλ=++++=++++=++++Matlab 系统状态反馈控制器设计程序代码：m1=800;m2=320;ks=10000;b=30000;kt=10*ks;a=[0 0 1 0;0 0 0 1;-ks/m1 ks/m1 -b/m1 b/m1;ks/m2 -(ks+kt)/m2 b/m2 -b/m2];b=[0 0;0 0;1/m1 0;-1/m2 kt/m2];c=[1 0 0 0];d=[0 0];OG=ss(a,b,c,d);%原系统状态空间模型HPole=[-200 -100 -7.07+sqrt(-50) -7.07-sqrt(-50)];%期望极点K=acker(a,b*[1 0]',HPole)a0=a-b*[1 0]'*K;%极点配置后系统矩阵eig(a0)%显示极点配置后特征根NG=ss(a0,b,c,d)%状态反馈控制后系统状态空间模型figure(1)impulse(NG)hold onimpulse(OG)axis([0,10,-4,4]);gridfigure(2)step(NG)hold onstep(OG)axis([0,10,0,2]);grid状态反馈控制器增益矩阵：状态反馈控制后系统矩阵特征值：状态反馈控制后系统状态空间模型：系统脉冲响应对比：绿色线为原系统脉冲响应，蓝色线为状态反馈控制后系统脉冲响应。
系统阶跃响应对比：绿色线为原系统脉冲响应，蓝色线为状态反馈控制后系统脉冲响应。
5.系统状态观测器设计Matlab系统状态观测器设计程序代码：m1=800;m2=320;ks=10000;b=30000;kt=10*ks;a=[0 0 1 0;0 0 0 1;-ks/m1 ks/m1 -b/m1 b/m1;ks/m2 -(ks+kt)/m2 b/m2 -b/m2];b=[0 0;0 0;1/m1 0;-1/m2 kt/m2];c=[1 0 0 0];d=[0 0];HPole=[-200 -100 -7.07+sqrt(-50) -7.07-sqrt(-50)];K=acker(a,b*[1 0]',HPole);op=[-50 -50 -50 -50];L=(acker(a',c',op))'a1=[a -b*[1 0]'*K; L*c a-L*c-b*[1 0]'*K]e0=[1 2 0.1 -0.1 0 0 0 0];t=0:0.01:4;sys=ss(a1,eye(8),eye(8),eye(8));[y,t,e]=initial(sys,e0,t);subplot(2,2,1)plot(t,e(:,1))gridxlabel('time')ylabel('e1')subplot(2,2,2)plot(t,e(:,2))gridxlabel('time')ylabel('e2')subplot(2,2,3)plot(t,e(:,3))gridxlabel('time')ylabel('e3')subplot(2,2,4)plot(t,e(:,4))gridxlabel('time')ylabel('e4')状态观测器增益矩阵：状态估计误差曲线：6.系统最优控制Matlab系统最优控制程序代码：m1=800;m2=320;ks=10000;b=30000;kt=10*ks;a=[0 0 1 0;0 0 0 1;-ks/m1 ks/m1 -b/m1 b/m1;ks/m2 -(ks+kt)/m2 b/m2 -b/m2];b=[0 0;0 0;1/m1 0;-1/m2 kt/m2];c=[1 0 0 0];d=[0 0];Q=eye(4,4);R=1;[Kc,P]=lqr(a,b*[1,0]',Q,R)Ac=[(a-b*[1,0]'*Kc)]程序运行结果：7.体会和建议现代控制理论是许多新兴控制算法的基础，通过学习现代控制理论，对利用状态空间模型进行系统分析和设计有了一定了解，掌握了对系统的能控性、能观性和稳定性进行判断分析方法和对单输入单输出系统状态反馈控制器和状态观测器的设计方法，并逐步熟悉了应用MATLAB进行系统分析设计。
不过在后续的研究学习中，接触较多的是多输入多输出系统，而且多输入多输出系统的分析以及其控制器、观测器的设计更加复杂难懂，希望老师在以后的教学中能多涉及一些多输入多输出系统的内容。