Matlab作业 第5-7题
MATLAB作业5参考答案

MATLAB作业5参考答案1、 试求出下面线性微分方程的通解。
543225432()()()()()136415217680()[sin(2)cos(3)]3t d y t d y t d y t d y t dy t y t e t t dt dt dt dt dt π-+++++=++假设上述微分方程满足已知条件(0)1,(1)3,()2,(0)1,(1)2y y y y y π=====,试求出满足该条件的微分方程的解析解。
【求解】先定义t 为符号变量,求出等号右侧的函数,则可以由下面命令求出方程的解析 解,解的规模较大,经常能占数页。
>> syms texp(-2*t)*(sin(2*t+sym(pi)/3)+cos(3*t))ans =exp(-2*t)*(sin(2*t+1/3*pi)+cos(3*t))>> y=dsolve(['D5y+13*D4y+64*D3y+152*D2y+176*Dy+80*y=',...'exp(-2*t)*(sin(2*t+1/3*pi)+cos(3*t))'],'y(0)=1','y(1)=3','y(pi)=2',...'Dy(0)=1','Dy(1)=2')略:事实上,仔细阅读求出的解析解就会发现,其中大部分表达式是关于系数的,所以如果能对 系数进行近似则将大大减小解的复杂度。
>> vpa(y)ans =.20576131687242798353909465020576e-2*exp(-2.*t)*cos(3.*t)+.15538705805619602372728107411086e-1*exp(-2.*t)*sin(2.*t)+.76830587084294035590921611166287e-2*exp(-2.*t)*cos(2.*t)-106.24422608844727797303237726774*exp(-2.*t)*t^2+98.159206062620455331994871615083*exp(-2.*t)*t+59.405044899367325888329709780356*exp(-2.*t)*t^3-30.741892776456442808809983330755*exp(-2.*t)+.20576131687242798353909465020576e-2*exp(-2.*t)*sin(3.*t)+31.732152104579289125415500223136*exp(-5.*t)2、 试求解下面微分方程的通解以及满足(0)1,()2,(0)0x x y π===条件下的解析解。
Matlab优化设计作业答案

长江大学机械工程学院机械优化设计大作业班级2012年5月31-361、⎩⎨⎧=+-=++⋅+-++=22422min 321321321232221x x x x x x t s x x x x x x f解: function f=fun1(x)f=x(1)^2+2*x(2)^2+x(3)^2-2*x(1)*x(2)+x(3)clearclcx0=[1;1;1];A=[];b=[];Aeq=[1 1 1;2 -1 1];beq=[4;2];lb=[];ub=[];[x,fval,exitflag]=fmincon('fun1',x0,A,b,Aeq,beq,lb,ub)x =1.90911.95450.1364fval =3.9773exitflag =12、221212min ()2130f x x x x s t x =+-+⋅-≤解: function f=fun2(x)f=x(1)^2+x(2)^2-2*x(1)+1clearclcx0=[1;1];A=[0 -1];b=-3;Aeq=[];beq=[];lb=[];ub=[];[x,fval,exitflag]=fmincon('fun2',x0,A,b,Aeq,beq,lb,ub)x =13fval =9exitflag =13、 2212min ()(2)f X x x =-+112222312..()0()0()10s t g X x g X x g X x x =-≤=-≤=-+-≤解:function f=fun3(x)f=(x(1)-2)^2+x(2)^2function [g,ceq]=mycon3(x)g=[-x(1);-x(2);-x(1)^2+x(2)^2-1];ceq=[];clearclcx0=[0;0];A=[];b=[];Aeq=[];beq=[];lb=[];ub=[];[x,fval]=fmincon('fun3',x0,A,b,Aeq,beq,lb,ub,'mycon3')x =2.0000fval =2.2204e-0164、⎩⎨⎧≤--≤+--⋅++++=01005.1)12424(min 21212122122211x x x x x x t s x x x x x e f x解: function f=fun4(x)f=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);function [g,ceq]=mycon4(x)g(1)=1.5+x(1)*x(2)-x(1)-x(2);g(2)=-x(1)*x(2)-10;ceq=[];clearclcx0=[0;0];A=[];b=[];Aeq=[];beq=[];lb=[];ub=[];[x,fval]=fmincon('fun4',x0,A,b,Aeq,beq,lb,ub,'mycon4')x =1.1825-1.7398fval =3.06085 喜糖问题:需要购买甲乙两种喜糖,喜糖甲10元/斤,喜糖乙20元/斤。
MATLAB讲座5作业及答案(附程序)

C2=C2.^4
20
3、求 n! n1
Matlab 程序: clear all;clc;close all; n=20; sum=0; temp=1; for i=1:n
end end 2、已知 A=[2 13 23 5;7 4 12 9 ;10 17 4 5] ,B=eye (3),求 (1) A 中行的最大元素; (2) A 中列的最小元素; (3) 生成一个与 A 大小相等的单位阵; (4) C1=A’*B; (5) C2=A*B,C24 (6) C3=2A—3B Matlab 程序: clear all;clc;close all; A=[2 13 23 5;
matlab讲座5作业及答案附程序1将101125等25个数填入一个5行5列的表格中使每行每列及对角线的值和均为5652已知a213235
MATLAB 讲座 5 作业及答案(附程序) 1、将 101-125 等 25 个数填入一个 5 行 5 列的表格中,使每 行每列及对角线的值和均为 565 Matlab 程序: clear all;clc;close all; n=10000; for i=1:n
temp=temp*i; sum=sum+temp; end sum
4、求以下数列极限:
(1) lim x0
x2 1 x sin x
c os x
1
1
(2Байду номын сангаас lim x 1-
1
,
lim
MATLAB作业

MATLAB作业⼀、必答题:1. MATLAB系统由那些部分组成?答:MATLAB系统主要由开发环境、MATLAB语⾔、MATLAB数学函数库、图形功能和应⽤程序接⼝五个部分组成。
2. 如何启动M⽂件编辑/调试器?答:在操作界⾯上选择“建⽴新⽂件”或“打开⽂件”操作时,M⽂件编辑/调试器将被启动。
在命令窗⼝中键⼊“edit”命令也可以启动M⽂件编辑/调试器。
3. 存储在⼯作空间中的数组能编辑吗?如何操作?答:存储在⼯作空间的数组可以通过数组编辑器进⾏编辑:在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输⼊修改内容即可。
4. 在MATLAB中有⼏种获得帮助的途径?答:在MATLAB中有多种获得帮助的途径:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器;(2)help命令:在命令窗⼝键⼊“help” 命令可以列出帮助主题,键⼊“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗⼝键⼊“lookfor 关键词”可以搜索出⼀系列与给定关键词相关的命令和函数(4)模糊查询:输⼊命令的前⼏个字母,然后按Tab键,就可以列出所有以这⼏个字母开始的命令和函数。
5. 有⼏种建⽴矩阵的⽅法?各有什么优点?答:(1)以直接列出元素的形式输⼊;(2)通过语句和函数产⽣;(3).在m⽂件中创建矩阵;(4)从外部的数据⽂件中装⼊。
6. 命令⽂件与函数⽂件的主要区别是什么?答:命令⽂件: M⽂件中最简单的⼀种,不需输出输⼊参数,⽤M ⽂件可以控制⼯作空间的所有数据。
运⾏过程中产⽣的变量都是全局变量。
运⾏⼀个命令⽂件等价于从命令窗⼝中顺序运⾏⽂件⾥的命令,程序不需要预先定义,只要依次将命令编辑在命令⽂件中即可。
函数⽂件:如果M⽂件的第⼀个可执⾏⾏以function开始,便是函数⽂件,每⼀个函数⽂件定义⼀个函数。
数学建模作业题+答案

数学建模MATLAB 语言及应用上机作业11. 在matlab 中建立一个矩阵135792468101234501234A ⎡⎤⎢⎥⎢⎥=⎢⎥-----⎢⎥⎣⎦答案:A = [1,3,5,7,9;2,4,6,8,10;-1,-2,-3,-4,-5;0,1,2,3,4]2. 试着利用matlab 求解出下列方程的解(线性代数22页例14)123412423412342583692254760x x x x x x x x x x x x x x +-+=⎧⎪--=⎪⎨-+=-⎪⎪+-+=⎩ 答案:A=[2 ,1,-5,1;1,-3,0,-6;0,2,-1,2;1,4,-7,6]; B=[8;9;-5;0]; X=A\B 或A=[2,1,-5,1;1,-3,0,-6;0,2,-1,2;1,4,-7,6] b=[8,9,-5,0]' X=inv(A)*b3. 生成一个5阶服从标准正态分布的随机方阵,并计算出其行列式的值,逆矩阵以及转置矩阵。
答案:A=randn(5) det(A) inv(A) A'4. 利用matlab 求解出110430002A -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦的特征值和特征向量。
答案:A=[-1,1,0;-4,3,0;0,0,2] [V,D]=eig(A)5.画出衰减振荡曲线3sin3t y et -=在[0,4]π上的图像。
要求,画线颜色调整为黑色,画布底面为白色。
(在实际中,很多打印机时黑白的,因此大多数作图要考虑黑白打印机的效果。
) 给出恰当的x ,y 坐标轴标题,图像x 轴的最大值为4π。
6. 生成一个0-1分布的具有10个元素的随机向量,试着编写程序挑选出向量中大于0.5的元素。
数学建模和Matlab 上机作业2(2016-9-20)跟老师做(不用整合进作业中):上机演示讲解:函数,递归的两个例子的写法。
附:1. Fibonacci Sequence (斐波那契数列)在数学上,费波那西数列是以递归的方法来定义: F1= 1;F2= 1;F (n )=F (n-1)+F (n-2) 2. 阶乘举例:数学描述:n!=1×2×……×n ;计算机描述:n!=n*(n-1)!自己做(需要整合进作业中,提交到系统中):1. 写一个m 文件完成分值百分制到5分制的转换(即输入一个百分制,转换后输出一个5级对应的得分,联系条件控制语句)。
MATLAB实验练习题(计算机)-南邮-MATLAB-数学实验大作业答案
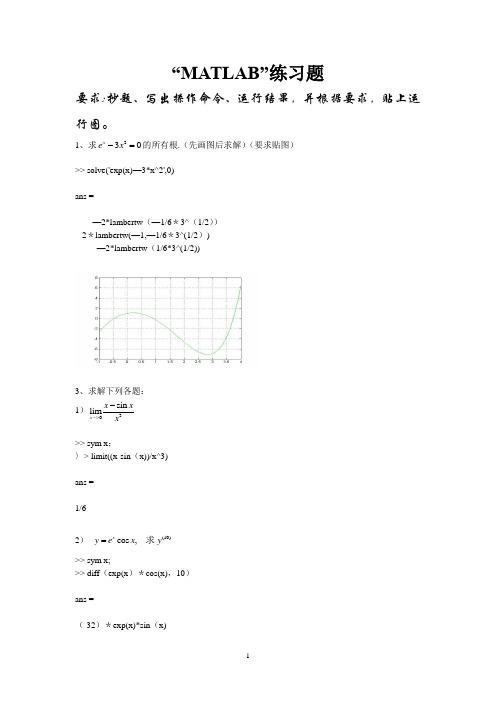
“MATLAB”练习题要求:抄题、写出操作命令、运行结果,并根据要求,贴上运行图。
1、求230x e x -=的所有根.(先画图后求解)(要求贴图)>> solve('exp(x)—3*x^2',0)ans =—2*lambertw (—1/6*3^(1/2))-2*lambertw(—1,—1/6*3^(1/2))—2*lambertw (1/6*3^(1/2))3、求解下列各题:1)30sin lim x x x x ->->> sym x ;〉> limit((x-sin (x))/x^3)ans =1/62) (10)cos ,x y e x y =求>> sym x;>> diff (exp(x )*cos(x),10)ans =(-32)*exp(x)*sin (x)3)21/20(17x e dx ⎰精确到位有效数字)〉〉 sym x;〉〉 vpa((int(exp(x^2),x,0,1/2)),17)ans =0.544987104183622224)42254x dx x+⎰〉> sym x ;>〉 int (x^4/(25+x^2),x)ans =125*atan (x/5) - 25*x + x^3/35)求由参数方程arctan x y t⎧⎪=⎨=⎪⎩dy dx 与二阶导数22d y dx 。
〉> sym t;>> x=log(sqrt (1+t^2));y=atan(t);〉> diff (y ,t )/diff (x ,t)ans =1/t6)设函数y =f (x )由方程xy +e y = e 所确定,求y ′(x ).>> syms x y ;f=x *y+exp(y )—exp (1);〉> -diff(f,x )/diff (f,y)ans =-y/(x + exp (y))7)0sin 2x e xdx +∞-⎰>〉 syms x ;>〉 y=exp(-x)*sin(2*x );〉> int(y ,0,inf )ans =2/58) 08x =展开(最高次幂为)〉> syms xf=sqrt(1+x);taylor(f,0,9)ans =— (429*x^8)/32768 + (33*x^7)/2048 — (21*x^6)/1024 +(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 19) 1sin (3)(2)x y e y =求〉> syms x y ;>〉 y=exp(sin (1/x));>〉 dy=subs (diff(y,3),x ,2)dy =—0.582610)求变上限函数2x x ⎰对变量x 的导数.>> syms a t ;>〉 diff (int(sqrt(a+t),t,x ,x^2))Warning: Explicit integral could not be found 。
MATLAB与控制系统仿真大作业

>> G1=tf(num,den);
>> G1=zpk(G1)
G1 =
5 (s+0.6) ----------------(s+3) (s+2) (s+1)
>> num=[2 1]; den=[1 2.9 1]; G2=tf(num,den); >> G2=zpk(G2)
G2 =
2 (s+0.5)
>> xlabel('x') ylabel('exp(-2.*x)')
三、simulink 建模(每题 10 分,共 20 分)
1、已知单位负反馈的开环传递函数为 G(s) =
2 s2 + 4s
,试利用
simulink
建立系在单位阶跃输入作用下的模型。
要求答案包括:(1)simulink 建模结构图;
(2)在同一个坐标中的阶跃信号和响应曲线图。
2、已知系统的开环传递函数为
G1(s)
=
2s2 + 5s + 6 s2 + 2s + 3
、G2 (s)
=
s2
s+6 + 7s +1
,H
(s)
=
5(s + 2) s +10
求:建立 Simulink 仿真模型,并求出其系统在单位阶跃响应;
要求答案包括:(1)simulink 建模结构图;
x=
-2.9709
0.5491
3.6000
0.0509
2. 已知下列矩阵
2 3 1
−1 3 5
A
=
matlab大作业

Matlab语言及应用周一晚作业廖育州07010559%第一组程序%绘制选用潍柴发动机WD615.50时汽车行驶性能曲线图,Ft--Ua图clear,clc;%清除内存变量,清屏%n为发动机的转速n=[1000,1100,1200,1300,1400,1500,1600,1700,1800,1900,2000,2100,2200];%Te为发动机在对应以上转速n下的外特性输出转矩Te=[1100,1125,1140,1145,1150,1180,1140,1125,1090,1060,1010,975,940];%ig为变速器不同档下的速比ig=[11.40;7.94;5.63;4.06;2.81;1.96;1.39;1.00];%nt为传动效率,是变速器、辅助变速器、传动轴、万向节、主减速器等四者的效率的乘积nt=0.849;Rr=0.5145; %Rr是车轮实际滚动半径i0=4.625; %i0是所选用的主减速器的速比ig1=1./(i0.*ig); %ig1只是为计算方便而设立的中间值,无物理意义Ua=0.377*Rr.*ig1*n; %Ua是在不同档位下,发动机不同扭矩下的车速Ft=ig*Te*i0*nt/(Rr*1000); %Ft是在不同档位下,发动机不同扭矩下的驱动力for n=1:8 % 8个档位对应八条曲线,八次循环p1=polyfit(Ua(n,:),Ft(n,:),5); %把先前计算所得的同一档位下的速度和驱动力拟合成曲线x2=Ua(n,1):0.1:Ua(n,13); % 设定曲线的X轴的取值范围和精度y1=polyval(p1,x2); % 计算曲线的Y轴的取值plot(x2,y1,'r-'); % 用红线绘制曲线hold on; % 把持当前的曲线,准备绘制下一条曲线end % 循环到此结束set(gca,'ygrid','on'); % 绘制水平线title('选用潍柴发动机WD615.50时汽车行驶性能曲线,Ft--Ua图'); %设定图片的标题名ylabel('Ft/(kN)'),xlabel('Ua/(km/h)'); %设定图片的x、y轴名称%******************************************************************************* %第二组程序绘制一个900*900的黑白格图片,并输出clear,clc;%清除内存中的变量,清屏B=ones(150,150); %定义一个150*150的一矩阵,作为白格C=zeros(150,150); %定义一个150*150的零矩阵,作为黑格A=[B,C,B;C,B,C;B,C,B]; %定义黑白格位置关系imshow(A)%******************************************************************************* %第三组程序计算曲线拟合系数clear,clc; %清除内存中的变量,清屏%n是发动机转速n=[1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100 2200];n1=n/(1000); %n1无物理意义,只是作为方便计算的中间变量%ge为与转速n对应的油耗ge=[202 200 195 194 192 194 196 199 202 207 212 217 223 ];p1=polyfit(n1,ge,5); %用5阶拟合n1和gep1 %输出p1,p1为比油耗特性拟合多项式的系数向量%Te为发动机在不同转速下的转矩Te=[1100 1125 1140 1145 1150 1180 1140 1125 1090 1060 1010 975 940];%转矩p2=polyfit(n1,Te,5); %用5阶拟合n1和Tep2 %输出p2,p2为转矩特性拟合多项式的系数向量%******************************************************************************* %第四组程序求符号表达式的和与差syms x fx gx %定义符号变量等于符号表达式fx=2*x^2+3*x-5; %定义fxgx=x^2+7; %定义gxfx+gx %求解fx+gx的符号表达式%******************************************************************************* %第五组程序绘制三维立体峰图[x,y]=meshgrid(-3:1/10:3,-3:1/10:3); %定义x,y的取值范围及网格划分精度z=peaks(x,y); %计算z值surfc(x,y,z); %绘图%******************************************************************************* %第六组程序计算导数clc,clear %清屏,清除内存中的变量syms a b t x y z; %定义a b t x y z等为变量符合f=sqrt(1+exp(x)); %定义原始式子fA=diff(f) %对f求一阶导数B=diff(f,x,3) %对f求三阶导数%****************************************************************************** %第七组程序求方程的所有解clear,clc;%清除内存中的变量,清屏p=[5,10,3,-71,9,13]; %定义方程x=roots(p) %求解方程的根%******************************************************************************* %第八组程序%找出一串奇数个数字串中的中间那个数字,或者偶数个数字串中的中间那两个数字的平均值clc , clear; %清屏,清除内存中的变量,A=input('请输入一串数据,并以回车键结束输入','s'); % 输入一串数字字符n=length(A); %计算字符串A的长度i=mod(n,2); %求余if i==1 %如果奇数个字符m=(n-1)/2+1; %找出中间那个数字middle=A(m) %输出中间那个数字else %如果是偶数个字符m=n/2;z=A(m)+A(m+1)-96; %把字符的ASCII码转换成数字s=z/2 %求出中间那两个数字的平均值end %程序到此结束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目五
题目
5:电器工程低通滤波电路
图3.8简单的低通滤波电路
上图是向大家展示的一个简单的低通滤波电路。
这个电路是由一个电阻和一个电容组成。
输出电压V0与输入电压V i的电压比为
V o V i =
1
1+j2πfRC
其中V i是在频率f下的正弦输入电压。
R代表电阻,单位为欧姆。
C代表电容,单位为法拉。
j为-1
假设R=16kΩ,电容C=1μF,请在同一个图形窗口下分别画出这个滤波器的幅频特性、相频特性曲线,要求幅频特性曲线坐标轴均采用对数坐标,相频特性曲线频率坐标用对数坐标。
代码:
clear all;
R=16000;
C=0.000001;
j=sqrt(-1);
f=1:1:10000;
A=1./(1+j*2.*pi.*f*R.*C);
X=angle(A);
subplot(2,1,1);
loglog(f,A);
title('幅频特性');
xlabel('f');ylabel('A');
grid on;
subplot(2,1,2);
semilogx(f,X);
title('相频特性曲线');
xlabel('f');ylabel('X');
grid on;
题目六
题目:工程师们经常用分贝或dB 来描述两功率之比.1dB 的定义如下
1
210
log 10P P dB =P 2是已测量的功率,P 1代表参考功率.
a.假设参考功率P 1为1mw,编写一个程序,接受一个输入功率P 2并把转化成为以1mw 为参考功率的dB.(它在工程上有一个特殊单位dBm).在编写程序时,注意培养好的编程习惯.
b.写一个程序,创建一个以W 为单位的功率的相对功率(单位为dBm)的图象.第一个图象的XY 轴都要用线性轴.而第二图象要用对数-线性xy 轴.
clear all
P2=input('请输入一个功率P2:');
P1=0.001;
dB=10*log10(P2/1000/P1);
fprintf('dB=%fdBm\n',dB);
P3=1:100;
dBm=10*log10(P3/1000/P1);
subplot(2,1,1);
plot(P3,dBm);
title('线性轴图');
xlabel('P3');ylabel('dBm');
grid on;
subplot(2,1,2);
semilogx(P3,dBm);
title('对数-线性轴图');
xlabel('P3');ylabel('dBm');
grid on;
结果:
R 题目七
题目:收音接收机.电阻上的电压可通过频率计算出来,公式如下
o
R V C
L R R V 2
2)1(ωω−
+=
ω=2πf ,以Hz 为单位的频率.假设L =0.1mH ,C =0.25nF ,R =50Ω,V 0=10mV.
a.画出以频率为自变量的电阻电压函数.在什么频率下,电阻上的电压最大?这时的电压为多少?这个频率叫做电路的固有频率.
b.如果这个频率比固有频率大百分之十,此时电阻上的电压为多少?
c.在什么频率下这个电阻上的电压会降到固有频率电压的一半?
代码:clear all
L=0.1*10^-3;C=0.25*10^-9;R=50;
V0=10*10^-3;f=1:(2*10^6);
VR=R./sqrt(R.^2+(2*pi*f*L-1./(2*pi*f*C)).^2)*V0;[Vm,Fm]=max(VR);
fprintf('在频率为%.4fMHz 时,电压最大,为%.3fmV ,这个频率叫做电路的固有频率。
\n\n',Fm/(10^6),Vm*10^3);plot(f,VR);hold on;
plot(Fm,Vm,'*r');grid;
F=1.1*Fm;
VR1=R./sqrt(R.^2+(2*pi*F*L-1./(2*pi*F*C)).^2)*V0;
fprintf('当频率比固有频率大百分之十时,电阻上的电压为%.3fmV\n\n',VR1*10^3);display('在下面两个频率下这个电阻上的电压会降到固有频率电压的一半')sym x;
x=solve('1/2*Vm=R*V0/sqrt(R^2+(2*pi*F1*L-1/(2*pi*F1*C))^2)','F1');y=eval(x);sym j;j=0;
for ii=1:length(y)
if y(ii)>0j=j+1;
fprintf('f%d=%.4fMHz\n',j,y(ii)/(10^6))end end
结果:
在频率为1.0066MHz时,电压最大,为10.000mV,这个频率叫做电路的固有频率。
当频率比固有频率大百分之十时,电阻上的电压为3.826mV
在下面两个频率下这个电阻上的电压会降到固有频率电压的一半
f1=1.0779MHz
f2=0.9400MHz。
