分析力学答案
分析力学参考答案

分析力学参考答案分析力学参考答案引言:分析力学是物理学的一个重要分支,研究物体在力的作用下的运动规律。
在学习分析力学的过程中,参考答案是一个非常重要的工具,可以帮助学生巩固知识,理解问题的解决方法。
本文将分析力学的一些典型问题,并给出参考答案,帮助读者更好地掌握分析力学的基本原理和解题技巧。
一、牛顿第二定律问题牛顿第二定律是分析力学的基础,描述了物体在力的作用下的加速度。
以下是一个典型的牛顿第二定律问题:问题:一个质量为m的物体在水平面上受到一个恒定的力F作用,求物体的加速度和受力大小的关系。
解答:根据牛顿第二定律的公式F=ma,我们可以得到物体的加速度a等于受力F除以物体的质量m,即a=F/m。
因此,物体的加速度与受力大小成反比。
二、动量守恒问题动量守恒是分析力学中的一个重要原理,描述了系统在没有外力作用下动量的守恒。
以下是一个典型的动量守恒问题:问题:两个质量分别为m1和m2的物体在水平面上碰撞,碰撞前物体1的速度为v1,物体2的速度为v2,碰撞后物体1的速度为v'1,物体2的速度为v'2,求碰撞前后两个物体的动量是否守恒。
解答:根据动量守恒定律,系统在没有外力作用下,动量守恒。
即m1v1 +m2v2 = m1v'1 + m2v'2。
因此,两个物体的动量在碰撞前后保持不变,动量守恒。
三、角动量问题角动量是分析力学中的一个重要概念,描述了物体绕某一点旋转的特性。
以下是一个典型的角动量问题:问题:一个质量为m的物体绕固定点O以角速度ω旋转,求物体的角动量L 与角速度ω的关系。
解答:根据角动量的定义L=Iω,其中I为物体对固定点O的转动惯量。
对于一个质量为m的物体,其转动惯量I等于mr^2,其中r为物体到固定点O的距离。
因此,物体的角动量L与角速度ω成正比,L=mr^2ω。
结论:通过以上的分析力学问题及其参考答案,我们可以看出分析力学的基本原理和解题技巧。
牛顿第二定律描述了物体在力的作用下的加速度,动量守恒原理描述了系统在没有外力作用下动量的守恒,角动量则描述了物体绕某一点旋转的特性。
分析力学基础答案非惯性系中的质点动力学答案

第一章分析力学基础答案1-1 图a自由度数为1;图b自由度数为2。
1-2广义力不都具有力的量纲,可以是力,也可以是力矩,还可以是其他量。
广义力与广义坐标的虚增量之积等于虚功。
1-3分别对图示系统写出其势能表达式,求一阶与二阶导数,由稳定性判别依据可得图a所示系统为不稳定平衡状态,图b所示系统为稳定平衡状态。
1-4只要内力作功就应该计入内力所作的功。
1-5将摩擦力看作为“主动力”,即可应用动力学普遍方程或拉格朗日方程。
1-6刚体平面运动有3个自由度,选质心坐标和转角为广义坐标,写出系统的动能,刚体所受力系向质心简化,此即为3个广义力,代入拉格朗日方程运算即可。
1-7在证明拉格朗日两个恒等式时,在推导以广义坐标表示的动力学普遍方程时。
第二章非惯性系中的质点动力学答案2-1找不到作用处;不成立。
2-2略。
2-3A对。
2-4向右面;(2)向左面;(3)与南、北半球情况相同。
2-5 略。
第三章碰撞答案3-1按恢复因数定义结合动量守恒定理求解。
时,基本按原速返回,基本不动;时,停止运动,以速度前进;时,以速度继续前进,以速度2前进。
3-2一般情况下,难以积分;碰撞过程中,可看为常量,容易积分。
3-3弹性碰撞时变形不能全部恢复,机械能损耗难以计算,不适宜用动能定理;恢复因数e=1时,是完全弹性碰撞,无机械能损失,可以用动能定理。
3-4恢复因数定义为碰撞后与碰撞前物体接触点处法向速度的比值;补充动力学方程以解决机械能损耗难以计算的困难。
3-5棒球击于球棒的撞击中心且与球棒垂直时,不震手;反之,手握棒处有碰撞冲量,有碰撞力,震手。
3-6用撞击中心的概念解释;撞击中心趋于无穷远处,无意义。
3-7均可用动量定理和对质心的动量矩定理求解。
作用于距质心l/6长度处。
第四章机械振动基础答案4-1 弹簧固有频率与弹簧松紧程度无关;不可以。
4-2不同,水平放置重力不是恢复力,铅直放置重力为恢复力。
如果在无重力场,固有频率与放置方式无关。
高一物理力学分析习题及答案

图2-1-7图2-2-2高一物理力学受力分析1如图2-1-7所示,甲、乙球通过弹簧连接后用绳悬挂于天花板,丙、丁球通过细绳连接后也用绳悬挂天花板.若都在A 处剪断细绳,在剪断瞬间,关于球的受力情况,下面说法中正确的是( )A .甲球只受重力作用B .乙球只受重力作用C .丙球受重力和绳的拉力作用D .丁球只受重力作用分析:当在A 处剪断时两球看作一个整体,整体加速度为g ,此时弹簧中的力不变,对A B 球都会有力的作用故A B 错,绳在松弛状态不能提供力,假设绳中有拉力,则丁的加速度会大于g 而丙的加速度会小于g ,则两球会相互靠近,绳则松弛,假设不成立,故绳中无拉力2.如图2-2-8所示,物体a 、b 和c 叠放在水平桌面上,水平力F b =5N 、F c =10N 分别作用于物体b 、c 上,a 、b 和c 仍保持静止.以F 1、F 2、F 3分别表示a 与b 、b 与c 、cA .F 1=5N ,F 2=0,F 3=5NB .F 1=5N ,F 2=5N ,F3=0 C .F 1=0,F 2=5N ,F 3=5ND .F 1=0,F 2=10N ,F 3=5N 分析:(分析方法从简单到复杂)因为a 、b 、c 均保持静止,故加速度,合外力都为0。
先分析a 只受b 对a 的支持力,以及重力故F1=0,再分析b ,b 受到重力、a 对b 的压力、c 对b 的支持力、Fb 、以及c 对b 的摩擦力,c 对b 的摩擦力为水平方向,故需水平方向的力来平衡,故F2=Fb=5,方向向右。
同理在对c 分析3如图2-2-1所示,A 、B 两物体叠放在水平面上,水平力F 作用在A 上,使两者一起向右作匀速直线运动,下列判断正确的是( )A .A 、B 间无摩擦力 B .A 对B 的静摩擦力大小为F ,方向向右C .B 对地面的动摩擦力的大小为F ,方向向右D .B 受到了向右的静摩擦力和向左的滑动摩擦力分析:两者一起向右作匀速直线运动,则加速度都为0,处于平衡状态。
华中师大分析力学答案

2 2
( m M ) g sin
利用
d d d d dt d dt d
,即得
2 2 M m sin a d m a sin cos d ( m M ) g sin d
表示的表达式。 解:由 x r sin cos
z r cos r sin sin ) m(r sin cos r cos cos px mx
y r sin sin
r sin cos ) m(r sin sin r cos sin py my ) cos r sin m(r p mz
证明这一质点由 z 0 区域经过分界面进入 z 0 区域的运动轨迹 等同于光线从空气入射到折射率为 n 1 U0 / E 的介质所受到的折 E m12 / 2 是质点在 z 0 区域中的动能。 射。 其中, 证明:系统的能量守恒,则有
2U 0 U0 v 1 1 mv12 mv2 2 U 0 2 1 1 2 2 v1 mv12 E1 又系统具有水平面内的平移对称性,
a 0 cos ) MX m( X
再由能量守恒得到
1 2 1 2 cos ) 2 a sin mga cos mga cos 0 +0= MX + m ( X a 2 2
M m sin 2 2 a 2 ga cos cos 0 化简可得 m M
a
0
y
2 3 sin a xdm 0 r cos rdrd 3 2a sin xc a 2 a 3 rdrd dm
工程力学 受力分析练习 带答案

A
B
C
3、研究AB杆
4、研究整体
A
B
C
D
W
W
C
B
A
画受力图应注意的问题
除重力、电磁力外,物体之间只有通过接触才有相互机械作用力,要分清研究对象(受力体)都与周围哪些物体(施力体)相接触,接触处必有力,力的方向由约束类型而定。
2、不要多画力
要注意力是物体之间的相互机械作用。因此对于受力体所受的每一个力,都应能明确地指出它是哪一个施力体施加的。
1、不要漏画力
约束反力的方向必须严格地按照约束的类型来画,不能单凭直观或根据主动力的方向来简单推想。在分析两物体之间的作用力与反作用力时,要注意,作用力的方向一旦确定,反作用力的方向一定要与之相反,不要把箭头方向画错。
3、不要画错力的方向
即受力图一定要画在分离体上。
4、受力图上不能再带约束。
、正确判断二力构件。
整体受力图上只画外力,不画内力。 一个力,属于外力还是内力,因研究对象的不同,有可能不同。当物体系统拆开来分析时,原系统的部分内力,就成为新研究对象的外力。
、同一系统各研究对象的受力图必须整体与局部一致,相 互协调,不能相互矛盾。 对于某一处的约束反力的方向一旦设定,在整体、局部或单个物体的受力图上要与之保持一致。
解:(1)取管道O为研究对象.
O
(2)取斜杆BC为研究对象.
C
B
RC
RB
A
C
B
D
O
P
P
N
(3)取水平杆AB为研究对象.
A
B
D
RC
XA
YA
C
B
RB
例2 画出下列各构件的受力图。
力学参考答案解析

力学参考答案解析力学参考答案解析力学是物理学的一个重要分支,研究物体在受到外力作用下的运动和相互作用。
学习力学需要掌握一系列的基本概念和定律,并能够应用这些知识解决实际问题。
在学习过程中,参考答案解析是一个重要的辅助工具,它能够帮助我们理解问题的解题思路和方法。
首先,我们来看一个力学问题的例子:一个质量为m的物体以初速度v0沿着水平方向匀速运动,经过时间t后速度变为v。
求物体受到的合外力F。
解答这个问题的关键在于应用牛顿第二定律,即F=ma,其中F表示物体受到的合外力,m表示物体的质量,a表示物体的加速度。
根据题目中给出的条件,物体在时间t内的加速度为a=(v-v0)/t。
将这个加速度代入牛顿第二定律的公式中,可以得到F=m(v-v0)/t。
通过这个例子,我们可以看出参考答案解析的作用。
首先,它告诉我们解答这个问题的关键在于应用牛顿第二定律,这是我们解决力学问题的基本原理。
其次,它给出了具体的计算步骤和公式,帮助我们进行问题的求解。
最后,它给出了最终的答案,即物体受到的合外力为F=m(v-v0)/t。
在学习力学的过程中,参考答案解析不仅仅是为了得到正确的答案,更重要的是理解解题的思路和方法。
通过分析解答过程,我们可以看到问题的关键点和解题思路。
在解答问题的过程中,我们需要注意以下几点。
首先,要仔细阅读问题,理解问题的要求和条件。
在解答问题之前,我们需要明确问题的目标和所给的限制条件。
只有明确了问题的要求,我们才能有针对性地选择合适的解题方法和公式。
其次,要善于运用物理学的基本原理和定律。
力学是建立在牛顿力学定律基础上的,所以我们在解答力学问题时,需要熟练掌握牛顿力学的基本原理和定律。
只有掌握了这些基本概念和定律,我们才能够正确地应用它们解决实际问题。
再次,要注意问题的逻辑推理和计算过程。
在解答问题的过程中,我们需要进行逻辑推理和计算。
逻辑推理是为了找到问题的解题思路和方法,计算过程是为了得到最终的答案。
分析力学课件、答案 作业

(b)设 x(t1 ) a, x(t2 ) b,求 S0 ;并任意假定一种非真 实的运动方式,计算相应的作用量S1 ,验证 S1 S0 。 解:按真实情况运动时,自由质点作匀速直线运 动,速度为常数 。
S0 L( x, x, t )dt m 2 /2dt m 2 (t2 t1 ) / 2
那么
d L' L f q, t q q q dt
d d d L' L f q, t dt q dt q dt q
d 2 L f q, t q f q, t dt q tq q q
1 EM M ( X V ) 2 2
斜面的能量
1 2 EM MX 2
系统的总能量
E
1 m( X x cos ) 2 2 1 2 MX 2 mgx sin
E
1 m( X +x cos V ) 2 2 1 M ( X V )2 2 mgx sin
t1 t1 t2 t2
将 (x
2
x1 ) /(t2 t1 )
带入得到
m( x2 x1 )2 S0 2(t2 t1 )
将 (x
2
x1 ) /(t2 t1 )
带入得到
m( x2 x1 )2 S0 2(t2 t1 )
(b)假设自由质点不做匀速直线运动,则速 度为时间的函数 (t ) ,且满足:
a FT 0 sin 2l
3
杠对B的作用力向外 杠对B的作用力向内 杠对B无作用力
a FT 0 sin 2l
3
a FT 0 sin 2l
理论力学3分析力学基础课后答案
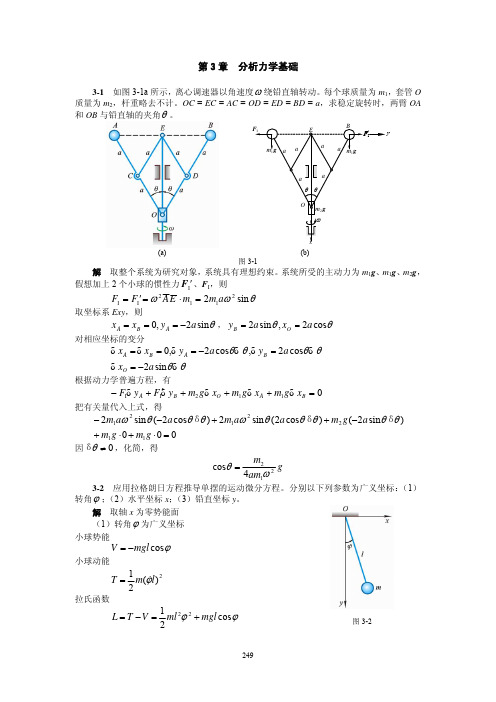
代入拉格朗日方程,得
则 3-3
[
]
质量为 m 的质点悬在 1 线上,线的另 1 端绕在 1 半径为 R 的固定圆柱体上,如图
250
3-3 所示。设在平衡位置时,线的下垂部分长度为 l,且不计线的 质量。求此摆的运动微分方程。 解 取 θ 为广义坐标,设小球的静平衡位置为其零势能点。 系统势能
V = mg [(l + R sin θ ) − (l + θR ) cosθ ]
A
A x
& & x
θ
C
θ
FN
ϕ
θ −ϕ
l & ϕ 2 y
θ
& & x
θ
x′ B
C mg B
(c)
l && ϕ 2 y
(a)
& (见图 3-7b) & 、ϕ 解 2 自由度,给广义坐标 x, ϕ ,则广义速度为 x
(b) 图 3-7
l & & − cos(θ − ϕ )ϕ vCx = x 2 l & sin(θ − ϕ ) vCy = ϕ 2
x A = x B = 0, y A = −2a sin θ , y B = 2a sin θ , xO = 2a cosθ
对相应坐标的变分
δ x A = δ x B = 0,δ y A = −2a cosθδ θ ,δ y B = 2a cosθδ θ δ xO = −2a sin θδ θ
根据动力学普遍方程,有
系统动能
势能
m 2 m 2 l2 2 m 1 m 2 & 2 = (x & + ϕ & − lx &ϕ & cos(θ − ϕ )) + l 2ϕ &2 (vCx + vCy ) + ⋅ l 2ϕ 2 2 12 2 4 24 m 2 m 2 2 m & + lϕ & − lx &ϕ & cos(θ − ϕ ) = x 2 6 2 l V = − mgx sin θ − mg cos ϕ (设初始 A 处势能为零) 2 T= ∂L m & cos(θ − ϕ ) & − lϕ = mx & ∂x 2 d ∂L m m && cos(θ − ϕ ) − lϕ & sin(θ − ϕ )ϕ & & − lϕ ( ) = m& x & dt ∂x 2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K FV
m 448浒 421122 - Ík 4- 4 行mg crank
代入⻮ 器 器 - 0中 可得
mki zmisinzeuttkicq 4.1 mg2Sin4 0 mEsin244 0 4 0 运动微分方程 miii miisiuqcose mg2siuqtkRi9-线 0
C2
0 时零解渐近稳定
1.8 试利用李雅普诺夫直接方法讨论系数在取不同值时判断
系统的零解稳定性
X X2
X十 a 3 加
解 选择正定李雅诺夫函数 比吅 二 水 水
计算 治 方程解曲线的全导数 V 荪义 器加二 zxixztzxzEXitlaih I
E 2 G 37 X22
则当 以 3时 V为负定 零解渐近稳定 a 3 时 V为零 零解稳定 a 3时 V为正定 零解不稳定
讨论是否存在初积分
i
䚡 取摇杆0A的转⻆为0 则系统的动能
T 士 加 以 04 Ìmi 旰士 Ìmhyo
二 Gmt Ém EG
取系统平衡位置为零势能 则运动时系统势能为
V kid 4 Ütmlglsin0
6 -sins
则L T V
且出售了一
是
tmtimtEG 二日 mini
zkdkcitmlgl sino tkdtimsglll cme
则 fm2以g外3tmlzmxitomtmiiiomy
f 去㗊㗊 a
i riiig 二his
3 8 质量为 m的均质摇杆0A 铰接 质量为 以的匀质圆盘A 在13 处联结刚度系数为人的弹簧 当系统平衡时 以处于水平位置 弹
簧处于铝垂位置如图所示 已知 非1.013 a 若圆盘沿固定圆弧形
轨道只滚不滑时 试用拉格朗日方法求系统的运动微分方程并
0 11 J
到 特征方程入 心 上0 XFO.it 不稳定
② 01 J
ID 特征方程仁入十4 0 入 it 不稳定
④ Cl 01 J
红 吕
特性方程 从 4二0 加 二 逃
不稳定
占 9 ⑤ H 07 J
特征方程 入 心 0 入二 入二 稳定
篚 ⑥ 匪 趁 J 慧
特征根 贴 ǖt
不稳定
碧 篮 ⑦ Cǖ Ǖl J
Win it 51-24 4 Étzz I 0
则 A 奸 2X B 奸列 E Et ZZ
哿 㼦 0 架 二是二0 叕 二奇 0
代入判别条件
A 叕 哥 13 毙一器 C 哿 一 哭 0
约束是可积的 为完整约束
1.4
试判断约束一义孤0十忙
涨
1红
0是否完整约束
解
对比可知 A sina BE Cost C
xitrq 0
xirq 0
1.2
- ⻓1的匀质杆支承在水平地板上 并靠在高山的墙上如图所示
取 心 以 加 则为杆位置坐标试列写约束方程
解
根据几何关系 可以得到约束方程为
火0
X xitcyry EE
兴以 一 责
解1
.3-
试判断约束xcx 整理约束方程 得
tzltzlxxtmitzi to 是否完整约束
EIWxx.lu tkuu 0
6 求出下列方程的平衡点 并用李雅普诺夫间接法分析每个平衡点 的稳定性
不二 火 Hx 一 们 加 二 X H X_x 7
解 乏方程左端等于点 得系统平衡点 0.01 0 1
十0 逛 逛 匪 逝
0,1 1,0
I 且 J
12 1十不必 似水 x
0,01 J
96
特征方程 心 0 加 二土 不稳定
0
T tv C
3.12 半径为12的光滑金属线弯成的圆环以匀⻆速度嘅 其铝直轴转 动 在圆环上套有质量为m的小圆环M 小圆环M用刚度加的弹簧 与大圆环上0点相联结 记弹簧未变形时⻓度为12 试用拉格朗 日方法建立小圆环M的运动微分方程 并写出初积分
解系统的动能
T Ìmlk年 44亥新年
取0为重力势能零点 则
4.3 图示用绳索联系的 二均质圆柱月和13的质量和半径分别为m
以 和 k kz 圆柱胢 绕定轴 0转动 圆柱13带动质量为M3的滑块 自由下落 以二国的转触 生为广义坐标 试写出哈密顿正则方程
并写出首次积分
解系统的动能
T msikitz in it Ìlzmi
生 以 秋 十发12212
加31歼 mpitznkiitfmz EE
又 在 二三 以年2 T 二三川游 许
V Ìki 4-4.12- mgkll
广义能量积分为
I It V mio zmiiiqtzkpiaqi mg Ruan C
3.18 多走路电路网络如图所示 试用拉格朗日方法建立系统的运
动微分方程
解 系统的动能
正 二 Ì Lie 4 Ìbieiei
系统的势能Veຫໍສະໝຸດ 特征根 加 式 二 土 厕后
不稳定
1.4利用劳斯- 赫尔维茨判据确定系数C 使得以下系统的零解稳定
为 X加
X ZX ZXz
xj cx sn
䚠
经 不伽 加 二
死心
⻔
特征方程 入3 1- 5入418 七八十4 -2C 0
a 0 1 1.23 且 HE a Grass
8-c 0.4 -2 C 0 518 - - 4-2 c
1.1 如图所示 质量为 M和 沿的两重珠用⻓1的不可伸⻓的轻绳联结
绳
子跨过半径加的定滑轮 假设绳子与滑轮之间无滑动 取火 加
和
4为坐标
试列写系统在铝垂面内运动时的约束方程
解
绳子不可伸⻓ 即
从十加十不 - 二 0
绳子与滑轮之间无滑动 有
it i 0
iri 0
综上 该系数的约束方程为
X 十加十大儿 0
tee it Èeil
系统的电磁耗散函数
De Reit Reit Bei 广义力 Qe 二 签 二上 Qez 0 Q e 0 4 Te Ve 么 eitihlei eii
且⻮ 器 器 - 器 Qek 可得 L ei ice e it 2ei u
fcei ei ticez eitRzei 0 Lz ej ei tEestR 3⻰ 0
l
代入判别条件
A 噐 一哥 13 表 器 一 C 器 器
- 81not since coso coso it since
1 -11Sino
约束不可积 为非完整约束
1
.5两个质点坐标分别为 心 以 到和 伽 上 名 用乱的不可伸⻓软
绳联结 并在空间运动 请写出该系统的约束方程
解
软绳不可伸⻓
发 以122Pa litmztmikh
MEEPa Íiitmztm 3
哈密顿函数H Èkti Pad 1在发一 L
ike 年1 2.4 发中不显金4 42
i Pi 㠭 录 二 n_n 812
章 辛 侯
-
二 2
2
Mzg122
首次积分 H C
5.2 请写出下列泛函对应的欧拉拉格朗日方程变显函数ucx y tl
的摩擦系数为 f 略去滑轮质量 系统开始时处于静止 求A 13
两物体的加速度
解系统有2个自由度 选取火火为广义坐标摩擦
这
力压 二Mzgf视为主动力 系统受理想约束 在
4烨
Ii 1 mi i
动力学普遍方程
mrixi is
hi
1
- Fftmilfxztlmg nilfxi Tci84 0
即 lzmg 3M it M is xz hngftczmztm im 义 我2 0
绕A点转动的⻆速度为 笇 4-
系统动能 T Ìmit 圢42 mt剨 侧242
器 广义力 Qq 二
M
代入拉格朗日方程⻮ 到 一二Qk 得
m 壳 12- 1 24 M
即X
Mr
Cmv4 IciCR以
2.8 质量为 m 半径加 的匀质圆柱体A上绕 一 细绳 细 绳的
一端跨过滑轮与质量为 以的物体13相连 已知物体 时水平面间
Fu
mj kca si 蕊 - 辰
又录 毙 人装 㼦 Q 即
Reit 箟 e E
Rè 十点e E
4.1 地球卫星系统可简化为如下模型 在某个平面上 质量为m的质
点 受到大小为吕的指向固定点0的引力 伪常数 内质点m到0
的距离 试求系统的哈密顿正则方程 以及首次积分
解 取放坐标 r 4 有
m
系统的动能 ㄒ二三m
系统的势能
V my a Ring 912 十发心
M3 - mdgRQ mgkh
li 下 V Ìmsttm 十三m RT tnRRzlitimREi
hPea
二
i
蛋
解得 4
CM3 -mzigR tmgRz ch
mstzmtmlRitmzR RU mzRB it ÍmRE发
212.年1 - 3122名1
ZMzkRF 3RFKGMHM tn
Eee it 站
3.20 设电容式话筒由弹性支承的电容器极板 电阻12和直流
电源E 组成 如图所示 电容极板的间隙加 作用于极板的
声波压力 Fit 使极板产生受迫振动并改变电容值 心 没动极
板的质量为 m 弹簧刚度系数为 k 弹簧不变形时的极板间隙
和电容值为人和 G 试用拉格朗日⻨克斯⻙方程建立系统的
二 F SESince_ 后8日Since 0
26 如图所示 转动力矩M作用在质量不计的曲柄上 带动半径为
下的⻮轮工在半径为12的定⻮轮丘内滚动 如⻮轮工的质量为m
对质心 的转动惯量为Ic 机构在水平面内运动 求曲柄的⻆加速度
解 系统受到理想约束 具有一个自由度 取
