数据结构 第5章
数据结构第五章

2.三角矩阵 (1)上三角矩阵 即矩阵上三角部分元素是随机的,而下三角部分元素全部 相同(为某常数C或全为0),具体形式见图5-2(a)。 (2)下三角矩阵 即矩阵的下三角部分元素是随机的,而上三角部分元素全 部相同(为某常数C或全为0),具体形式见图5-2(b)。
2012年11月1日
2012年11月1日
12
5.3.1 特殊矩阵
2 3 1 A= 5 4 2 4 6 3
图5-1 一个对称矩阵
1.对称矩阵 若一个n阶方阵A中元素满足下列条件: aij=aji 其中0≤i, j≤n-1,则称A为对称矩阵。 例如,如图5-1所示是一个3×3的对称矩阵。
0
1
2
3
4
5
6
7
……
n ( n +1 ) 2
-3
n ( n +1 ) 2
-2
n ( n +1 ) -1 2
a00 a01 a02 a03 a04 a05 a06 a07
……
an-2n-2
an-2n-1
an-1n-1
2012年11月1日
(b)上三角矩阵的压缩存储形式 图5-5 对称矩阵及用上三角压缩存储
第5章 多维数组和广义表
本章学习内容
5.1 多维数组
5.2 多维数组的存储结构
5.3 特殊矩阵及其压缩存储
5.4 稀疏矩阵
5.5 广义表
2012年11月1日 1
5.1 多维数组
5.1.1 多维数组的概念
1.一维数组
一维数组可以看成是一个线性表或一个向量(第2章中 已经介绍),它在计算机内是存放在一块连续的存储 单元中,适合于随机查找。
数据结构第五章 数组与广义表

压缩存储方法:只需要存储下三角 (含对角线)上的元素。可节省一 半空间。
可以使用一维数组Sa[n(n+1)/2]作为n阶对称矩阵A的存 储结构,且约定以行序为主序存储各个元素,则在Sa[k]和矩
阵元素aij之间存在一一对应关系: (下标变换公式)
i(i+1)/2 + j 当i≥j k = j(j+1)/2 + i 当i<j
q = cpot[col];
T.data[q].i = M.data[p].j; T.data[q].j = M.data[p].i; T.data[q].e = M.data[p].e; ++cpot[col]; }
分析算法FastTransposeSMatrix的时间 复杂度:
for (col=1; col<=M.nu; ++col) … … for (t=1; t<=M.tu; ++t) … … for (col=2; col<=M.nu; ++col) … … for (p=1; p<=M.tu; ++p) … …
//对当前行中每一个非零元
处
brow=M.data[p].j;
理
if (brow < N.nu ) t = N.rpos[brow+1];
M
else { t = N.tu+1 }
的
for (q=N.rpos[brow]; q< t; ++q) { ccol = N.data[q].j; // 乘积元素在Q中列号
一、三元组顺序表
对于稀疏矩阵,非零元可以用三元组表示, 整个稀疏矩阵可以表示为所有非零元的三元组所 构成的线性表。例如:
数据结构答案 第5章 串学习指导

第5章串5.1 知识点分析1.串的定义串(String)是由零个或多个任意字符组成的有限序列。
一般记作:s="a1 a2 …a i…a n"。
其中s 是串名,用双引号括起来的字符序列为串值,但引号本身并不属于串的内容。
a i(1<=i<=n)是一个任意字符,它称为串的元素,是构成串的基本单位,i是它在整个串中的序号;n为串的长度,表示串中所包含的字符个数。
2.几个术语(1)长度串中字符的个数,称为串的长度。
(2)空串长度为零的字符串称为空串。
(3)空格串由一个或多个连续空格组成的串称为空格串。
(4)串相等两个串相等,是指两个串的长度相等,且每个对应字符都相等。
(5)子串串中任意连续字符组成的子序列称为该串的子串。
(6)主串包含子串的串称为该子串的主串。
(7)模式匹配子串的定位运算又称为串的模式匹配,是一种求子串的第一个字符在主串中序号的运算。
被匹配的主串称为目标串,子串称为模式。
3.串的基本运算(1)求串长:LenStr(s)。
(2)串连接:ConcatStr(s1,s2) 。
(3)求子串:SubStr (s,i,len)。
(4)串比较:EqualStr (s1,s2)。
(5)子串查找:IndexStr (s,t),找子串t在主串s中首次出现的位置(也称模式匹配)。
(6)串插入:InsStr (s,t,i)。
(7)串删除:DelStr(s,i,len)。
4.串的存储(1)定长顺序存储。
(2)链接存储。
(3)串的堆分配存储。
5.2 典型习题分析【例1】下面关于串的的叙述中,哪一个是不正确的?()A.串是字符的有限序列B.空串是由空格构成的串C.模式匹配是串的一种重要运算D.串既可以采用顺序存储,也可以采用链式存储分析:空串是不含任何字符的串,即空串的长度是零。
空格串是由空格组成的串,其长度等于空格的个数。
答案为B。
【例2】两个串相等的充分必要条件是( )。
A.两个串长度相等B.两个串有相同字符C.两个串长度相等且有相同字符D.以上结论均不正确分析:根据串相等定义,两个串是相等是指两个串的长度相等且对应字符都相等,故A、B、C均不正确,答案为D。
数据结构 5数组和广义表A
1 Status Locate(Array A,va_list ap,int &off) 2{ 3 //若ap指示的各下标值合法,则求出该元素在A中,相对地
址off
4 off=0; 5 for(i=0;i<A.dim;++i) 6 { 7 ind=va_arg(ap,int); 8 if(ind<0||ind>A.bounds[i]) return OVERFLOW; 9 off+=A.constants[i] *ind; 10 } 11 return OK; 12 }
行数 总列数,即 第2维长度 元素个数
ij
补充:计算二维数组元素地址的通式
设一般的二维数组是A[c1..d1, c2..d2],这里c1,c2不一定是0。
单个元素 长度
二维数组列优先存储的通式为: LOC(aij)=LOC(ac1,c2)+[(j-c2)*(d1-c1+1)+i-c1)]*L
6
例1〖软考题〗:一个二维数组A[1..6, 0..7],每个数组元素
16
5.4
1、定义:
广义表的定义
广义表是线性表的推广,也称为列表(lists) 记为: LS = ( a1 , a2 , ……, an ) 广义表名 表头(Head) 表尾 (Tail) n是表长
在广义表中约定:
① 第一个元素是表头,而其余元素组成的表称为表尾; ② 用小写字母表示原子类型,用大写字母表示列表。
13
1 Status Value(Array A,ElemType &e,…){ 2 //A是n维数组,e为元素变量,随后是n个下标值,若各下
标不超界,则e赋值为所指定的A的元素值,即将指定元素值 读到e变量中。
数据结构(c语言版)第五章答案

第五章1、设二维数组A【8】【10】是一个按行优先顺序存储在内存中的数组,已知A【0】【0】的起始存储位置为1000,每个数组元素占用4个存储单元,求:(1)A【4】【5】的起始存储位置。
A【4】【5】的起始存储位置为1000+(10*4+5)*4=1180;(2)起始存储位置为1184的数组元素的下标。
起始存储位置为1184的数组元素的下标为4(行下标)、6(列下标)。
2、画出下列广义表D=((c),(e),(a,(b,c,d)))的图形表示和它们的存储表示。
略,参考第5·2节应用题第5题分析与解答。
3、已知A为稀疏矩阵,试从时间和空间角度比较采用两种不同的存储结构(二维数组和三元组表)实现求∑a(i,j)运算的优缺点。
稀疏矩阵A采用二维数组存储时,需要n*n个存储单元,完成求∑ii a(1≤i≤n)时,由于a【i】【i】随机存取,速度快。
但采用三元组表时,若非零元素个数为t,需3t+3个存储单元(t个分量存各非零元素的行值、列值、元素值),同时还需要三个存储单元存储存稀疏矩阵A的行数、列数和非零元素个数,比二维数组节省存储单元;但在求∑ii a(1≤i≤n)时,要扫描整个三元组表,以便找到行列值相等的非零元素求和,其时间性能比采用二维数组时差。
4、利用三元组存储任意稀疏数组时,在什么条件下才能节省存储空间?当m行n列稀疏矩阵中非零元素个数为t,当满足关系3*t<m*n时,利用三元组存储稀疏数组时,才能节省存储空间。
5、求下列各广义表的操作结果。
(1)GetHead((a,(b,c),d))GetHead((a,(b,c),d))=a(2)GetTail((a,(b,c),d))GetTail((a,(b,c),d))=((b,c),d)(3)GetHead(GetTail((a,(b,c),d)))GetHead(GetTail((a,(b,c),d)))=(b,c)(4)GetTail(GetHead((a,(b,c),d)))GetTail(GetHead((a,(b,c),d)))=()第六章1、已知一棵树边的集合为{(i,m),(i,n),(e,i),(b,e),(b,d),(a,b),(g,j),(g,k),(c,g),(c,f),(h,l),(c,h),(a,c)}用树形表示法画出此树,并回答下列问题:(1)哪个是根结点?(2)哪些是叶结点?(3)哪个是g的双亲?(4)哪些是g的祖先?(5)哪些是g的孩子?(6)哪些是e的子孙?(7)哪些是e的兄弟?哪些是f的兄弟?(8)结点b和n的层次号分别是什么?(9)树的深度是多少?(10)以结点c为根的子树的深度是多少?(11)树的度数是多少?略。
数据结构第五章考试题库(含答案)

第 5 章数组和广义表一、选择题为第一元素,其存储地址为1,1.设有一个10阶的对称矩阵A,采用压缩存储方式,以行序为主存储,a11的地址为()。
【燕山大学 2001 一、2 (2分)】每个元素占一个地址空间,则a85A. 13B. 33C. 18D. 402. 有一个二维数组A[1:6,0:7] 每个数组元素用相邻的6个字节存储,存储器按字节编址,那么这个数组的体积是(①)个字节。
假设存储数组元素A[1,0]的第一个字节的地址是0,则存储数组A的最后一个元素的第一个字节的地址是(②)。
若按行存储,则A[2,4]的第一个字节的地址是(③)。
若按列存储,则A[5,7]的第一个字节的地址是(④)。
就一般情况而言,当(⑤)时,按行存储的A[I,J]地址与按列存储的A[J,I]地址相等。
供选择的答案:【上海海运学院 1998 二、2 (5分)】①-④: A.12 B. 66 C. 72 D. 96 E. 114 F. 120G. 156 H. 234 I. 276 J. 282 K. 283 L. 288⑤: A.行与列的上界相同 B. 行与列的下界相同C. 行与列的上、下界都相同D. 行的元素个数与列的元素个数相同3. 设有数组A[i,j],数组的每个元素长度为3字节,i的值为1 到8 ,j的值为1 到10,数组从内存首地址BA开始顺序存放,当用以列为主存放时,元素A[5,8]的存储首地址为( )。
A. BA+141B. BA+180C. BA+222D. BA+225【南京理工大学 1997 一、8 (2分)】4. 假设以行序为主序存储二维数组A=array[1..100,1..100],设每个数据元素占2个存储单元,基地址为10,则LOC[5,5]=()。
【福州大学 1998 一、10 (2分)】A. 808B. 818C. 1010D. 10205. 数组A[0..5,0..6]的每个元素占五个字节,将其按列优先次序存储在起始地址为1000的内存单元中,则元素A[5,5]的地址是( )。
数据结构第5章课件 中国石油大学(华东)

二叉链表
leftChild
data rightChild
22
二叉树的链表表示(三叉链表)
每个结点增加一个指向双亲的指针parent,使 得查找双亲也很方便。
leftChild data parent rightChild
三叉链表
data
leftChild
27
BinTreeNode *LeftChild (BinTreeNode *current ) { return (current != NULL )? current->leftChild :NULL; } BinTreeNode *RightChild (BinTreeNode *current ) { return ( current!= NULL) ? current->rightChild : NULL; } int Height( ){return Height(root);} int Size( ){return Size(root);} BinTreeNode *GetRoot ( ) const { return root; } void preOrder( ) {preOrder(root);} //前序遍历 void inOrder( ) {inOrder(root);} //中序遍历 void postOrder( ) {postOrder(root);} //后序遍历 void levelOrder( ) ; // 不需要递归,所以直接对外接 口调用即可。层序遍历 28
b
f
c
d
g
6
e
a
b.嵌套集合表示法: b 根据树的集合定义,写出集合划分。 { a, {b,{e},{f}}, {c}, {d,{g}} } e c d
数据结构预算法 第5章习题解答
④
③
0 1 2 3 4 5
1 2 3 4 5 6 ^
3 0 3
^ 2 4 ^ 5 ^
0 1
1 4 ^
3 ^
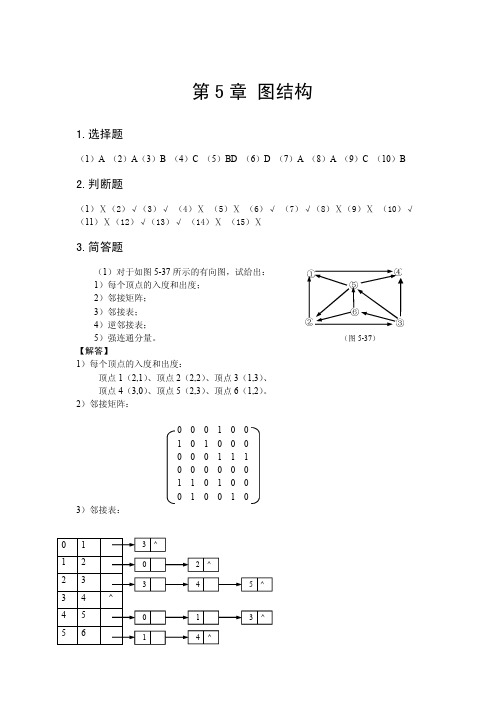
4)逆邻接表: 0 1 2 3 4 5 1 2 3 4 5 6 5)强连通分量:
1 4 1 0 2 2 ^ ^ 2 5 ^ 4 ^ 4 5 ^ ^
(2)设无向图 G 如图 5-38 所示,试给出: 1)该图的邻接矩阵; 2)该图的邻接表; 3)该图的多重邻接表; 4)从 V1 出发的“深度优先”遍历序列; 5)从 V1 出发的“广度优先”遍历序列。 【解答】 1) 该图的邻接矩阵: 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 0 1 1 0
{if(p!=s) p->next=s->next; else (G->adjlist[e->adjvex].firstedge=s->next;)} if(s) free(s); break; } } for(i=v;i<G->n;i++) /*删除顶点值*/ {G->adjlist[i].vertex=G->adjlist[i+1].vextex; G->adjlist[i].first[i].firstedge=G->adjlist[i+1].firstedge; } } void DeleteArc(AALGraph *G,int v,int w) /*在图 G 中删除序号为 v,w 的顶点之的边*/ {EdgeNode *s,*p; s=G->adjlist[v].firstedge; p=s; for(;s;s=s->next); /*在与 m 邻接的点中找 n*/ {if(s->adjvex==w) /*若找到邻接点 n,则将该边从边表中脱出*/ {if(p!=s) p->next=s->next; else G->adjlist[v].firstedge=s->next; } if(s) free(s); /*释放要删除的边结点*/ } s=G->adjlist[w].firstedge;p=s; for(;s;p=s,s=s->next) /*在与 n 邻接的点中找 m*/ {if(s->adjvex==v) /*若找到邻接点 m,则将该边从边表中脱出*/ {if(p!=s) p->next=s->next; else G->adjlist[w].firstedge=s->next; } if(s) free(s); /*释放要删除的边结点*/ } G->e--; } (3)试以十字链表为存储结构实现算法设计题(1)中所列图的基本操作。 算法略。 (4)试以邻接多重表为存储结构实现算法设计题(1)中所列图的基本操作。 算法略。 (5)对于含有 n 个顶点的有向图,编写算法由其邻接表构造相应的逆邻接表。 【解答】 Void InvertAdjList(ALGraph G, ALGraph *H) /*由有向图的邻接表 G 建立其逆邻接表 H*/ {for (i=1;i<=n;i++) /*设有向图有 n 个顶点,建逆邻接表的顶点向量*/ {H[i]->vertex=G.adjlist[i].vertex; H->firstedge=NULL;} for (i=0; i<n; i++) /*邻接表转为逆邻接表*/ {p= G.adjlist[i].firstedge; /*取指向邻接表的指针*/ while (p!=null) {j=p->adjvex;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本操作: (1) InitArray(A, n, bound1, …, boundn): 若维数n和各维 的长度合法,则构造相应的数组A,并返回TRUE。 (2) DestroyArray(A): 销毁数组A。 (3) GetValue(A,e, index1, …, indexn): 若下标合法, 则用e返回数组A中由index1, …, indexn所指定的元素的值。
图5.9 带状矩阵的压缩形式
2.确定非零元素在一维数组空间中的位置
Loc[i , j] = Loc[1, 1]+前i-1行非零元素个数+第i行中aij前非零元素个数;
前i-1行元素个数=3×(i-1)-1(因为第1行只有2个非零元素); 第i行中aij前非零元素个数=j-i+1,其中
-1 (j<i) j-i= 0 (j=i) 1 (j>i) 由此得到 Loc[i, j]=Loc[1, 1]+3(i-1)-1+j-i+1
Loc[ j1 , j2 ,, jn ] Loc[c1 , c2 ,cn ] ai ( ji ci )
i 1
n
其中
ai 1 (d k ck 1)
k i 1
n
(1≤i≤n)。
5.3 特殊矩阵的压缩存储
5.3.1 三角矩阵
三角矩阵大体分为三类:下三角矩阵、上三角矩阵和对称矩阵。对于
Loc[j1, j2, j3]=Loc[c1, c2, c3]+α1×(j1-c1)+α2×(j2-c2)+α3(j3-
c3)=Loc[c1, c2, c3]+∑αi×(ji-ci)(1 Nhomakorabeai≤3)
由公式可知Loc[j1, j2, j3]与j1, j2, j3呈线性关系。 对于n维数组A(c1∶d1, c2∶d2 ,…, cn∶dn),我们只要把 上式推广,就可以容易地得到n维数组中任意元素aj1j2…jn的 存储地址的计算公式:
a242,a342
以上的存放规则可推广到多维数组的情况。总之,知道了 多维数组的维数,以及每维的上下界,就可以方便地将多维数 组按顺序存储结构存放在计算机中了。同时,根据数组的下标, 可以计算出其在存储器中的位置。因此,数组的顺序存储是一 种随机存取的结构。
以二维数组Am×n 为例,假设每个元素只占一个存储单元,
教学重点与教学难点:
三角矩阵的压缩存储; 稀疏矩阵的压缩存储及其转置运算。
5.1 数组的定义和运算
图5.1 Am×n的二维数组
图5.2 矩阵Am×n看成n个列向量的线性表
图5.3 矩阵Am×n看成m个行向量的线性表
以上我们以二维数组为例介绍了数组的结构特性,实际 上数组是一组有固定个数的元素的集合。也就是说,一旦定
第5章 数组和广义表
5.1 数组的定义和运算
5.2 数组的顺序存储和实现
5.3 特殊矩阵的压缩存储
5.4 广义表
教学目的与要求: 掌握三角矩阵的概念及其在计算机中的存储方法; 掌握稀疏矩阵的概念及其在计算机中的存储方法; 掌握稀疏矩阵的运算,如转置等; 了解本章内容在数据结构中的作用,及其在数值分析 中的应用。
m
n
r
n m
k -1
图5.5 三维数组看成r个m×n的二维数组
j-1
假定每个元素占一个存储单元,采用以行为主序的方法存 放,即行下标r变化最慢, 纵下标n变化最快。 首元素a111的地
址为Loc[1, 1, 1],求任意元素aijk的地址。
显然 , ai11 的 地 址为 Loc[ i, 1, 1]=Loc[1, 1, 1]+(i1)×m×n, 因为在该元素之前, 有i-1个m×n的二维数组。 由ai11 的地址和二维数组的地址计算公式,不难得到三维数组 任意元素aijk的地址:
为主显然,二维数组Am×n以行为主的存储序列为:
a11, a12, …,a1n, a21, a22, …, a2n, …, am1, am2, …, amn
而以列为主的存储序列为:
a11, a21, …,am1,a12, a22, …, am2, …, a1n, a2n, …, amn
假设有一个3×4×2的三维数组A ,共有24个元素,其
Loc[i, j]=Loc[1, 1]+前i-1行非零元素个数+第i行中aij 前非零元素个数前。i-1行元素个数=1+2+3+4+…+(i-1)=i(i1)/2,第i行中aij前非零元素个数=j-1,所以有 Loc[i, j]=Loc[1, 1]+i(i-1)/2+j-1 同样,对于上三角矩阵,也可以将其压缩存储到一个大小 为n(n+1)/2的一维数组C中。其中元素aij(i<j)在数组C中的存储 位置为:
义了数组的维数和每一维的上下限,数组中元素的个数就固
定了。 例如二维数组A3×4,它有3行、4列,即由12个元素组 成。由于这个性质,使得对数组的操作不像对线性表的操作 那样可以在表中任意一个合法的位置插入或删除一个元素。 对于数组的操作一般只有两类:
(1) 获得特定位置的元素值;
(2) 修改特定位置的元素值。
根据计算公式,可以方便地求得aij的地址是Loc[i, j]。如果 每个元素占size个存储单元,则任意元素aij的地址计算公式为: Loc[i, j]=Loc[1, 1] + (n×(i-1)+j-1)×size 三维数组A(1..r , 1..m , 1..n)可以看成是r个m×n的二维数 组, 如图5.5所示。
A. i(i-l)/2+j
B. j(j-l)/2+i
C. j(j-l)/2+i-1
D. i(i-l)/2+j-1
2. A[N,N]是对称矩阵,将下面三角(包括对角线)以行序存储到一维数组 T[1..N(N+1)/2]中,则对任一上三角元素a[i][j]对应T[k]的下标k是( )。 A. i(i-1)/2+j B. j(j-1)/2+i C. i(j-i)/2+1 D. j(i-1)/2+1
第1行: 1个 第2行: 2个 第3行: 3个 … … 第n行: n个 1+2+3+4+5+…+n=n(n+1)/2
所以可压缩存储到一个大小为n(n+1)/2的一维数组C中,如图5.7 所示。
Loc(1,1)
Loc(i,j)
图5.7 三角矩阵的压缩形式
下三角矩阵中元素aij(i>j)在一维数组A中的位置为(设每个元素占一个字节):
0 0 12 9 0 0 0 0 3 0 0 0 M 0 0 24 0 0 18 0 0 15 0 0 7
0 0 0 0 0 14 0 0 0 0 0 0 0 0 0 0 67 0 0
6 1 1 3
1 2 3 4 5 6 7 8
Loc[i, j, k]=Loc[1, 1, 1]+(i-1)×m×n+(j-1)×n+(k-1)
其中1≤i≤r,1≤j≤m, 1≤k≤n。
如果将三维数组推广到一般情况,即:用j1 、j2 、j3 代替数
组下标i、j、k, 并且j1、j2、j3的下限为c1、c2、c3,上限分别 为d1、 d2、d3,每个元素占一个存储单元,则三维数组中任意
3. 假设一个15阶的上三角矩阵A按行优先顺序压缩存储在一维数组B中,则非零元
素A9,9在B中的存储位置k=_______。(注:矩阵元素下标从1开始)【北京工商大
学 2001 】
5.3.2 带状矩阵
图5.8 带状矩阵A 三对角带状矩阵有如下特点:
i=1, j=1, 2;
当 1<i<n, j=i-1, i, i+1; i=n, j=n-1, n;
时,aij非零,其它元素均为零。
1.确定存储该矩阵所需的一维向量空间的大小 在这里我们假设每个非零元素所占空间的大小为1个单元。 从图中观
察得知,三对角带状矩阵中,除了第一行和最后一行只有2个非零元素外,
其余各行均有3个非零元素。由此得到, 所需一维向量空间的大小为2+2+3 (n-2)=3n-2,如图5.9所示。
一个n阶矩阵A来说,若当i<j时,有aij=0,则称此矩阵为下三角矩阵;若 当i>j时,有aij=0,则称此矩阵为上三角矩阵;若矩阵中的所有元素均满足
aij=aji,则称此矩阵为对称矩阵。
图5.6 下三角矩阵A
对于下三角矩阵的压缩存储,只存储下三角的非零元素,对于零元素
则不存。我们按“行序为主序”进行存储,得到的序列是a11, a21, a22, a31, a32, a33, …, an1, an2, …, ann。由于下三角矩阵的元素个数为n(n+1)/2,即:
(下标从1开始)采用以行为主序的方法存放,即行下标变
化最慢,纵下标变化最快,则顺序为: a111,a112,a121,a122, …,a331,a332,a341,a342 采用以纵为主序的方法存放, 即纵下标变化最慢, 行下 标变化最快, 则顺序为:
a111 ,a211 ,a311 ,a121 ,a221 ,a321,…,a132,a232 ,a332 ,a142 ,
“以行为主”存放数组,下标从1开始,首元素a11 的地址为 Loc[1, 1],求任意元素aij的地址。aij是排在第i行,第j列, 并且前面的第i-1行有n×(i-1)个元素,第i行第j个元素前 面还有j-1个元素。由此得到如下地址计算公式: Loc[i, j]=Loc[1, 1]+n×(i-1)+(j-1)
3 4
