计算机基础二进制转换作业01
进制转换练习题带答案

进制转换练习题带答案一、十进制与二进制的转换(1) 25(2) 63(3) 102(4) 145(5) 189(1) 11011(2) 1010101(3) 11110000(4) 10011011(5) 11011101二、十进制与八进制的转换(1) 47(2) 123(3) 255(4) 365(5) 512(1) 57(2) 123(3) 456(4) 712(5) 754三、十进制与十六进制的转换(1) 79(2) 255(3) 439(4) 1023(5) 4095(1) 3F(2) FF(3) 1A3(4) AFE(5) FFF四、二进制与八进制的转换(1) 11011(2) 1010101(3) 11110000(4) 10011011(5) 11011101(1) 57(2) 123(3) 456(4) 712(5) 754五、二进制与十六进制的转换(1) 11011(2) 1010101(3) 11110000(4) 10011011(5) 11011101(1) 3F(2) FF(3) 1A3(4) AFE(5) FFF六、八进制与十六进制的转换(1) 57(2) 123(3) 456(4) 712(5) 754(1) 3F(2) FF(3) 1A3(4) AFE(5) FFF七、混合进制转换(1) 将八进制数 527 转换为十六进制数。
(2) 将二进制数 110101 转换为十进制数。
(3) 将十六进制数 2A 转换为二进制数。
(4) 将十进制数 198 转换为八进制数。
(5) 将二进制数 11110000 转换为十六进制数。
八、进制转换应用题(1) 如果一个十六进制数 1AB 表示的十进制数是多大?(2) 一个二进制数 1011 1110 转换为十进制后,再加上 25,结果是多少?(3) 将八进制数 765 转换为十进制数,然后除以 3,得到的商是多少?(4) 将十进制数 255 转换为二进制数,然后与二进制数11111111 进行按位与操作,结果是什么?(5) 将十进制数 100 转换为十六进制数,然后转换为二进制数,得到的二进制数是多少位?九、进制转换逻辑题(1) 十进制数 10 转换为二进制数是 1010。
进制转换练习题

进制转换练习题在计算机科学和数学中,进制转换是一种常见的运算,用于将一个数字从一种进制表示转换为另一种进制表示。
进制是用于表示数字的基数,通常使用的进制包括二进制,八进制,十进制和十六进制。
本文将提供一些进制转换的练习题,帮助读者加深对该概念的理解。
题目一:将二进制数1101100转换为十进制数。
解答:要将二进制数转换为十进制数,可以按照以下步骤进行计算:(1) 从二进制数的最右边一位开始,将每一位上的数字与2的相应次幂相乘。
(2) 将所有结果相加得到最终的十进制数。
根据上述步骤,我们可以计算出1101100的十进制表示:0*2^0 + 0*2^1 + 1*2^2 + 1*2^3 + 0*2^4 + 1*2^5 + 1*2^6 = 108。
因此,1101100的十进制表示为108。
题目二:将十进制数342转换为二进制数。
解答:(1) 用2整除该十进制数,并记录下余数。
(2) 将商继续用2整除,直到商为0为止。
将每次的余数按照从下到上的顺序排列即可得到二进制数。
根据上述步骤,我们可以计算出342的二进制表示:342 / 2 = 171 余 0171 / 2 = 85 余 185 / 2 = 42 余 142 / 2 = 21 余 021 / 2 = 10 余 110 / 2 = 5 余 05 / 2 = 2 余 12 / 2 = 1 余 01 /2 = 0 余 1将上述余数从下到上排列得到的二进制数为101010110。
题目三:将十进制数123转换为八进制数。
解答:(1) 用8整除该十进制数,并记录下余数。
(2) 将商继续用8整除,直到商为0为止。
将每次的余数按照从下到上的顺序排列即可得到八进制数。
根据上述步骤,我们可以计算出123的八进制表示:123 / 8 = 15 余 315 / 8 = 1 余 71 / 8 = 0 余 1将上述余数从下到上排列得到的八进制数为173。
题目四:将十进制数425转换为十六进制数。
进制转换 练习题

进制转换练习题1. 将二进制数110101转换为八进制和十六进制。
答:二进制数110101转换为八进制:65,转换为十六进制:35。
2. 将十进制数347转换为二进制和十六进制。
答:十进制数347转换为二进制:101011011,转换为十六进制:15B。
3. 将八进制数57转换为二进制和十进制。
答:八进制数57转换为二进制:101111,转换为十进制:47。
4. 将十六进制数CD3转换为二进制和十进制。
答:十六进制数CD3转换为二进制:11001101011,转换为十进制:3283。
5. 将二进制数101010101转换为八进制和十进制。
答:二进制数101010101转换为八进制:2525,转换为十进制:341。
6. 将十进制数123转换为二进制和十六进制。
答:十进制数123转换为二进制:1111011,转换为十六进制:7B。
7. 将八进制数672转换为二进制和十进制。
答:八进制数672转换为二进制:110110010,转换为十进制:442。
8. 将十六进制数ABC转换为二进制和十进制。
答:十六进制数ABC转换为二进制:101010111100,转换为十进制:2748。
9. 将二进制数1110001转换为八进制和十六进制。
答:二进制数1110001转换为八进制:161,转换为十六进制:71。
10. 将十进制数567转换为二进制和十六进制。
答:十进制数567转换为二进制:1000110111,转换为十六进制:237。
11. 将八进制数426转换为二进制和十进制。
答:八进制数426转换为二进制:100100110,转换为十进制:278。
12. 将十六进制数FE0转换为二进制和十进制。
答:十六进制数FE0转换为二进制:11111110000,转换为十进制:4064。
以上是一些进制转换的练习题,通过这些题目的练习,可以加深对不同进制间的转换方法的理解和掌握。
进制转换在计算机科学、数学等领域中非常重要,熟练掌握进制转换可以提高问题解决的效率和准确性。
二进制转十进制30道题目

二进制转十进制30道题目一、题目1. 将二进制数101转换为十进制数。
2. 把二进制数1101转换为十进制数。
3. 求二进制数1001对应的十进制数。
4. 二进制数111转换为十进制是多少?5. 将二进制数1010转换为十进制数。
6. 把二进制数11001转换为十进制数。
7. 求二进制数10001对应的十进制数。
8. 二进制数1111转换为十进制是多少?9. 将二进制数10110转换为十进制数。
10. 把二进制数11011转换为十进制数。
11. 求二进制数10011对应的十进制数。
12. 二进制数11101转换为十进制是多少?13. 将二进制数101010转换为十进制数。
14. 把二进制数110001转换为十进制数。
15. 求二进制数100001对应的十进制数。
16. 二进制数11111转换为十进制是多少?17. 将二进制数101110转换为十进制数。
18. 把二进制数110101转换为十进制数。
19. 求二进制数100101对应的十进制数。
20. 二进制数111001转换为十进制是多少?21. 将二进制数1010010转换为十进制数。
22. 把二进制数110011转换为十进制数。
23. 求二进制数100011对应的十进制数。
24. 二进制数111101转换为十进制是多少?25. 将二进制数1011110转换为十进制数。
26. 把二进制数110111转换为十进制数。
27. 求二进制数100111对应的十进制数。
28. 二进制数111011转换为十进制是多少?29. 将二进制数1010110转换为十进制数。
30. 把二进制数1100011转换为十进制数。
二、解析1. 对于二进制数101:- 按位权展开式为1×2^0+0×2^1+1×2^2- 计算得1×1 + 0×2+1×4 = 5。
2. 对于二进制数1101:- 按位权展开式为1×2^0+0×2^1+1×2^2+1×2^3 - 计算得1×1+0×2 + 1×4+1×8=13。
计算机基础01

.世界上第一台电子数字计算机ENIAC是()年在美国问世的。
.第三代计算机的主要元件是()。
.微型计算机诞生在()时期。
.未来计算机的应用发展趋势是继续以()的应用为核心,实现()的应用。
同时为了解决信息处理速度的问题,利用()增强计算机的网络功能和协同工作能力。
.个人计算机属于()。
.英文CAD的含义是()。
.用计算机管理科技情报资料,是计算机在()的应用。
.世界上公认的第一台计算机是(),诞生于(),所使用的逻辑元件是()。
.在计算机应用中,“计算机辅助设计”的英文缩写为()。
.现代微型机中采用的主要元件是()。
.办公自动化(OA)是计算机的一项应用,按计算机应用分类,它属于()。
.机器人研究、专家系统、模式识别、智能检索等是计算机在()方面的应用。
.目前,各企业在人事、财务、仓库等管理上广泛使用计算机,从计算机应用领域分类看,它们属于()。
.CAM是计算机主要应用领域之一,其中文含义是()。
.计算机最主要的工作特点是()。
.计算机之所以在金融、交通、通信等领域中能达到实时、快速的服务。
是因为其具有()特点。
.按年代来划分,第四代计算机应该是()。
.以微处理机为核心组成的微型计算机属于(第四代)计算机。
.依其处理数据的形态分类,计算机可分为模拟计算机、()、混合计算机三类。
.当前,计算机的发展趋势表现为()4种。
.计算机的圆周率目前已达到小数点后数百万位了,这主要是因为计算机具有(计算精度高)特点。
.计算机的五个基本部件是()。
.在ENIAC的研制过程中,()总结出计算机的基本结构,今天的计算机基本结构仍采用其提出的原理和思想。
.在计算机内部,程序和数据采用(二进制)代码表示。
.人类从记数、计数到计算,经历了漫长的历史阶段,即从手工阶段、机械阶段,一直发展到现今的___电子阶段_____..计算工具的发展动力,主要来自两个方面的需求:一是提高___计算能力_____,二是提高计算的方便性..计算机体系结构和___元器件____的进步决定着计算机向前发展的程度..1946年,在美国宾夕法尼亚大学,世界上第一台真正意义上的电子计算机____ENIAC____诞生。
《1.2.2 二进制与数制转换》作业设计方案

《二进制与数制转换》作业设计方案(第一课时)一、作业目标本作业旨在帮助学生掌握二进制数制的基本概念和转换方法,提高他们的计算思维和问题解决能力。
通过完成作业,学生将更好地理解二进制数制的特性,并能够进行有效的数制转换。
二、作业内容1. 基础概念:请学生阅读并理解二进制数的定义,了解二进制数的表示方法和特点。
2. 练习题:提供一些简单的二进制数转换题目,如十进制数转二进制数,二进制数转十进制数等。
3. 案例分析:给学生展示一些实际应用中的二进制数制转换案例,如计算机系统中的内存管理,网络协议中的数据编码等。
4. 小组讨论:组织学生进行小组讨论,分享他们对二进制数制的理解和应用看法,共同探讨二进制数制在实际问题中的价值。
三、作业要求1. 独立完成:学生需独立完成基础概念的阅读和理解,不依赖任何外部资源。
2. 认真解答:对于练习题和案例分析,学生需认真解答,确保答案的正确性。
3. 积极参与:小组讨论中,学生需积极参与,提出自己的观点和建议,共同推动小组讨论的进行。
4. 提交作业:学生需在规定时间内提交作业,可以通过网络平台或纸质文档的形式提交。
四、作业评价1. 答案正确性:根据学生提交的答案正确性给予相应的分数,对于基础概念的阅读和理解部分,答案正确即可获得满分;对于练习题和案例分析部分,教师将根据答案的准确性给予相应的分数。
2. 讨论积极性:根据学生在小组讨论中的表现,如是否积极参与讨论,是否提出有建设性的观点等,给予相应的加分,鼓励学生在讨论中发挥自己的思考能力。
3. 作业质量:根据学生提交的作业质量和完成情况,给予相应的综合评价分数。
4. 个性化反馈:对于每个学生,教师将给予个性化的反馈和建议,指出他们在作业中存在的问题和改进的方向。
五、作业反馈1. 学生提交的作业将通过网络平台或纸质文档进行收集和整理。
2. 教师将根据作业评价标准对学生的作业进行综合评价,并将评价结果反馈给学生。
3. 对于学生在作业中存在的问题和不足,教师将给予个性化的反馈和建议,帮助学生更好地改进和提高。
计算机基础---1、十进制0.1转二进制
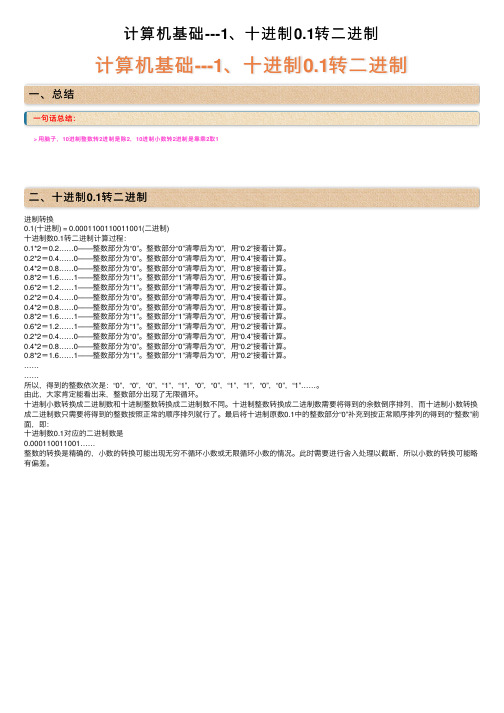
计算机基础---1、⼗进制0.1转⼆进制计算机基础---1、⼗进制0.1转⼆进制⼀、总结⼀句话总结:> ⽤脑⼦,10进制整数转2进制是除2,10进制⼩数转2进制是靠乘2取1⼆、⼗进制0.1转⼆进制进制转换0.1(⼗进制) = 0.0001100110011001(⼆进制)⼗进制数0.1转⼆进制计算过程:0.1*2=0.2……0——整数部分为“0”。
整数部分“0”清零后为“0”,⽤“0.2”接着计算。
0.2*2=0.4……0——整数部分为“0”。
整数部分“0”清零后为“0”,⽤“0.4”接着计算。
0.4*2=0.8……0——整数部分为“0”。
整数部分“0”清零后为“0”,⽤“0.8”接着计算。
0.8*2=1.6……1——整数部分为“1”。
整数部分“1”清零后为“0”,⽤“0.6”接着计算。
0.6*2=1.2……1——整数部分为“1”。
整数部分“1”清零后为“0”,⽤“0.2”接着计算。
0.2*2=0.4……0——整数部分为“0”。
整数部分“0”清零后为“0”,⽤“0.4”接着计算。
0.4*2=0.8……0——整数部分为“0”。
整数部分“0”清零后为“0”,⽤“0.8”接着计算。
0.8*2=1.6……1——整数部分为“1”。
整数部分“1”清零后为“0”,⽤“0.6”接着计算。
0.6*2=1.2……1——整数部分为“1”。
整数部分“1”清零后为“0”,⽤“0.2”接着计算。
0.2*2=0.4……0——整数部分为“0”。
整数部分“0”清零后为“0”,⽤“0.4”接着计算。
0.4*2=0.8……0——整数部分为“0”。
整数部分“0”清零后为“0”,⽤“0.2”接着计算。
0.8*2=1.6……1——整数部分为“1”。
整数部分“1”清零后为“0”,⽤“0.2”接着计算。
…………所以,得到的整数依次是:“0”,“0”,“0”,“1”,“1”,“0”,“0”,“1”,“1”,“0”,“0”,“1”……。
由此,⼤家肯定能看出来,整数部分出现了⽆限循环。
进制转换练习

进制转换练习简介进制转换是计算机科学中非常基础和重要的概念,它涉及将数字从一种进制表示转换为另一种进制表示。
常见的进制包括二进制、八进制、十进制和十六进制。
在本文档中,我们将介绍如何进行这些进制之间的转换,并提供一些练以巩固所学知识。
二进制转十进制二进制是计算机中最基础的进制,由0和1组成。
要将二进制数转换为十进制数,可以使用以下方法:1. 从二进制数的最右侧开始,将每个位上的数字乘以2的幂,并将它们相加。
2. 从右到左计算,第一个位乘以2的0次方,第二个位乘以2的1次方,第三个位乘以2的2次方,以此类推。
例如,将二进制数1101转换为十进制数:1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 13十进制转二进制十进制是我们最常使用的进制,由0到9的数字组成。
要将十进制数转换为二进制数,可以使用以下方法:1. 将十进制数除以2,记录余数。
2. 将得到的商再次除以2,继续记录余数。
3. 重复上述步骤,直到商为0为止。
4. 将记录的余数按照从下到上的顺序排列,得到二进制数。
例如,将十进制数23转换为二进制数:23 ÷ 2 = 11 余 111 ÷ 2 = 5 余 15 ÷ 2 = 2 余 12 ÷ 2 = 1 余 01 ÷2 = 0 余 1所以23的二进制表示为八进制和十六进制转换八进制和十六进制都是二进制的扩展表示形式,可以通过将二进制数分组来转换为这些进制。
每组长度为3的二进制数可以转换为一个八进制数,而每组长度为4的二进制数可以转换为一个十六进制数。
例如,将二进制数转换为八进制数和十六进制数:110 110 011 11 = 6 6 3 F所以的八进制表示为663,十六进制表示为6F练现在我们来做一些进制转换的练,以巩固所学知识:1. 将二进制数转换为十进制数。
2. 将十进制数58转换为二进制数。
3. 将十进制数123转换为八进制数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、十进制转换成其他进制
方法:(以转换成二进制数为例,转换成其它进制数同理)
十进制数的整数部分采用“除2取余法”,即十进制整数以及此期间产生的商逐次除以基数2,直到商为0,并按从后向前的次序,依次记下每一次相除所得的余数,即为转换后的二进制数。
十进制小数转换为二进制小数,采用“乘2取整法”。
即将十进制数的小数部分反复乘以2,直到没有小数或达到指定的精度为止。
再把各次乘2得到的整数(包含0)从前到后连接起来,就可得到相应的二进制整数。
1.将十进制数41转换成二进制数。
2.将十进制数153转换成八进制数。
3.将十进制数54转换成十六进制数。
4.将十进制数0.39转换成二进制数(舍入误差小于2-8)。
5.将十进制数0.513转换成八进制数(舍入误差小于8-6)。
二、其它进制转换成十进制
方法:将其它进制数的各位按位权展开相加。
1.将二进制数101001.1101转换成十进制数。
2.将十六进制数B67F转换成十进制数。
三、二进制、八进制和十六进制之间的转换
方法:
二进制与十六进制之间转换的方法:一位十六进制数可以转换为4位二进制数,反之亦然。
二进制与八进制之间转换的方法:一位八进制数可以转换为3位二进制数,反之亦然。
1.将二进制数10011101.01转换成八进制数。
2.将八进制数345.1转换成二进制数。
3.将二进制数111101000.011转换成十六进制数。
4.将十六进制数AF.26转换成二进制数。
