法拉第定律nzf
大学物理化学公式集

电解质溶液法拉第定律:Q =nzF m =M zFQ dE r U dl ++= dE r U dl--= t +=-+I I =-++r r r +=-+U U U ++=∞∞+Λm ,m λ=()FU U FU ∞∞+∞+-+r +为离子移动速率,U +( U -)为正(负)离子的电迁移率(亦称淌度)。
近似:+∞+≈,m ,m λλ +∞+≈,m ,m U U m m Λ≈Λ∞ (浓度不太大的强电解质溶液)离子迁移数:t B =I I B=Q Q B ∑B t =∑+t +∑-t =1 电导:G =1/R =I/U =kA/l电导率:k =1/ρ 单位:S ·m -1 莫尔电导率:Λm =kV m =k/c 单位S ·m 2·mol -1 cell lR K Aρρ== cell 1K R kR ρ==科尔劳乌施经验式:Λm =()c 1m β-∞Λ 离子独立移动定律:∞Λm =()m,m,+U U F λλ∞∞∞∞+--+=+ m U F λ∞∞+,+= 奥斯特瓦儿德稀释定律:Φc K =()mm m 2m c c ΛΛΛΛ∞∞Φ-平均质量摩尔浓度:±m =()v1v v m m --++平均活度系数:±γ=()1v v --+γγ+ 平均活度:±a =()v1v v a a --++=m mγ±±Φ 电解质B 的活度:a B =va ±=vm m ⎪⎭⎫ ⎝⎛Φ±±γ+v v v B +a a a a ±--== m +=v +m B m -=v -m B ()1v v vB m v vm +±+--=离子强度:I =∑i2i i z m 21德拜-休克尔公式:lg ±γ=-A|z +z --|I可逆电池的电动势及其应用(Δr G )T,p =-W f,max (Δr G m )T,p =zEFNernst Equation :若电池反应为 cC +dD =gG +hHE =E φ-dDc C hHg G a a a a ln zF RT 标准电动势E φ与平衡常数K φ的关系:E φ=φlnK zFRT还原电极电势的计算公式:ϕ=氧化态还原态-a a lnzF RT φϕ 计算电池反应的有关热力学函数变化值:m r S ∆=p T E zF ⎪⎭⎫⎝⎛∂∂m r H ∆=-zEF +p T E zFT ⎪⎭⎫ ⎝⎛∂∂ Q R =T m r S ∆=pT E zFT ⎪⎭⎫⎝⎛∂∂zF ⎪⎪⎭⎫ ⎝⎛∆⎪⎪⎭⎫ ⎝⎛21m r 1122T 1T 1H T E T E -=- zF ⎰⎪⎭⎫ ⎝⎛T2E2E 11T E d =dT T H 21T T 2mr ⎰∆ 电极书面表示所采用的规则:负极写在左方,进行氧化反应(是阳极),正极写在右方,进行还原反应(是阴极) 电动势测定的应用:(1) 求热力学函数变量Δr G m 、Δr G m Φ、m r H ∆、m r S ∆及电池的可逆热效应Q R 等。
法拉第电磁感应定律的原理及应用

法拉第电磁感应定律的原理及应用电磁现象一直是人们研究的热门话题,而法拉第电磁感应定律是电与磁的互相影响中最重要的定律之一。
本文将从定律的原理、实验方法以及在实际应用中的作用三个方面来探讨法拉第电磁感应定律的重要性。
一、定律的原理法拉第电磁感应定律是由英国物理学家迈克尔·法拉第于1831年发现的,主要表明磁场的变化会引起周围环状的导体中感应的电动势,而其大小与磁场变化速率成正比。
定律可以用公式来表示:在一定时间内,电动势的大小与导体中的通量变化率成正比,即E = -dΦ/dt ,其中E 是电动势的大小,dΦ/dt 是通量的变化率。
通量是一个物理量,指磁场对于体积内部每一个点的穿过面积的总和。
磁通量可以用一个称为韦伯 (Wb) 的单位来表示。
引入这个定律可以帮助我们更好地理解电与磁现象之间的关系。
同时,在应用方面,它也成为了许多电器和电子设备的基础。
二、实验方法想要验证法拉第电磁感应定律,可以进行以下一个简单的实验:1. 准备一个线圈:将一个导线弯成一个圆形。
线圈中的导线应该十分接近互相贴合,同时保证起点和终点不会接触。
2. 准备一个磁铁:一个永久磁铁或者一个电磁铁都可以。
3. 将磁铁附近的线圈中央:将线圈放置在磁铁附近中央,使其处于磁力线的作用范围里。
可以缓慢移动磁铁,看看线圈中是否能产生电流。
4. 记录电流变化:使用电表或记录装置,在线圈中记录磁力线穿过线圈的变化情况。
5. 改变磁力线:可以尝试使用磁铁移进或者移出线圈以观察电流变化的情况。
在实验过程中,可以通过这种方法来验证法拉第电磁感应定律的正确性。
实验也可以通过使用不同大小、不同形状的线圈以及外加电阻和电容器来探究这个定律的一些性质。
三、在实际应用中的作用法拉第电磁感应定律在现实生活中有广泛应用,这里介绍其中一些:1. 发电机:发电机的原理是利用磁场与线圈相互作用,产生感应电动势。
受到马克斯韦尔电磁理论的启发,发电机的设计师利用了法拉第电磁感应定律,使得发电机能够将机械能转化为电能,成为重要的能量来源之一。
物化公式
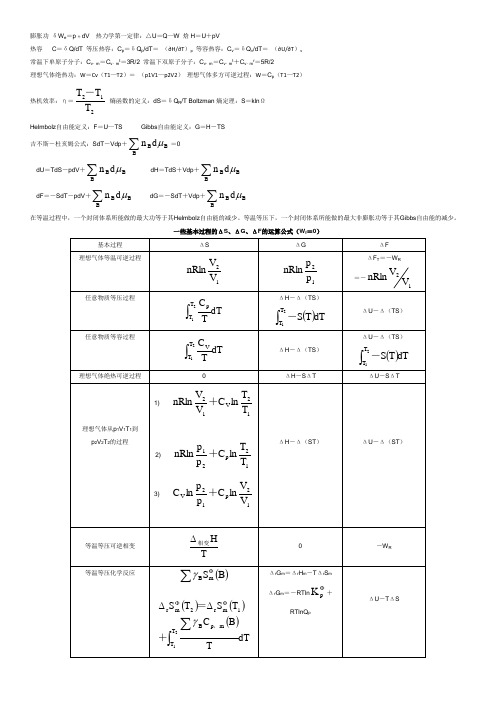
膨胀功 δW e =p 外dV 热力学第一定律:△U =Q —W 焓H =U +pV热容 C =δQ/dT 等压热容:C p =δQ p /dT = (∂H/∂T )p 等容热容:C v =δQ v /dT = (∂U/∂T )v 常温下单原子分子:C v ,m =C v ,m t =3R/2 常温下双原子分子:C v ,m =C v ,m t +C v ,m r =5R/2理想气体绝热功:W =Cv (T1—T2)= (p1V1—p2V2) 理想气体多方可逆过程:W =C p (T1—T2)热机效率:η=212T T T - 熵函数的定义:dS =δQ R /T Boltzman 熵定理:S =kln ΩHelmbolz 自由能定义:F =U —TS Gibbs 自由能定义:G =H -TS 吉不斯-杜亥姆公式:SdT -Vdp +∑BBBd nμ=0dU =TdS -pdV +∑B BBd nμ dH =TdS +Vdp +∑B BBd nμdF =-SdT -pdV +∑BBBd nμ dG =-SdT +Vdp +∑BBBd nμ在等温过程中,一个封闭体系所能做的最大功等于其Helmbolz 自由能的减少。
等温等压下,一个封闭体系所能做的最大非膨胀功等于其Gibbs 自由能的减少。
一些基本过程的ΔS 、ΔG 、ΔF 的运算公式(W f =0)基本过程ΔSΔGΔF 理想气体等温可逆过程12V V nRln12p p nRlnΔF T =-W R=-12V V nRln任意物质等压过程dTTC 21T T p ⎰ΔH -Δ(TS )()dTT S 21T T ⎰-ΔU -Δ(TS )任意物质等容过程dTTC 21T T V ⎰ΔH -Δ(TS )ΔU -Δ(TS )()dTT S 21T T ⎰-理想气体绝热可逆过程ΔH -S ΔT ΔU -S ΔT理想气体从p 1V 1T 1到p 2V 2T 2的过程1)12V 12T T lnC V V nRln+ 2)12p 21T T lnC p p nRln+3)12p 12V V V lnC p p ln C +ΔH -Δ(ST )ΔU -Δ(ST )等温等压可逆相变TH 相变∆-W R等温等压化学反应()B S m B∑Φγ()()()dTTB C T S T S 21T T m p B 1mr 2mr ⎰∑ΦΦ∆∆,+=γΔr G m =Δr H m -T Δr S m Δr G m =-RTln Φp K +RTlnQ pΔU -T ΔS溶液组成的表示法:(1)物质的量分数:B B n x n=(2)质量摩尔浓度:B B An m W =(3)物质的量浓度:B B n c V=(4)质量浓度B ω拉乌尔定律A A A p p x *= 亨利定律:x m B c Bp k x k m k c ===化学势的各种表示式和某些符号的物理意义: 气体:(1)纯理想气体的化学势()()T,p T RT ln ppμμΦΦ=+ 标准态:任意温度,p =p φ=101325Pa 。
大学化学公式

大学化学公式热力学第一定律功:δW =δW e +δW f(1) 膨胀功 δW e =p 外dV 膨胀功为正,压缩功为负。
(2) 非膨胀功δW f =xdy非膨胀功为广义力乘以广义位移。
如δW (机械功)=fdL ,δW (电功)=EdQ ,δW (表面功)=rdA 。
热 Q :体系吸热为正,放热为负。
热力学第一定律: △U =Q —W 焓 H =U +pV 理想气体的内能和焓只是温度的单值函数。
热容 C =δQ/dT(1)等压热容:C p =δQ p /dT = (∂H/∂T )p (2)等容热容:C v =δQ v /dT = (∂U/∂T )v 常温下单原子分子:C v ,m =C v ,m t =3R/2 常温下双原子分子:C v ,m =C v ,m t +C v ,m r =5R/2 等压热容与等容热容之差:(1)任意体系 C p —C v =[p +(∂U/∂V )T ](∂V/∂T )p (2)理想气体 C p —C v =nR 理想气体绝热可逆过程方程:pV γ=常数 TV γ-1=常数 p 1-γT γ=常数 γ=C p / C v 理想气体绝热功:W =C v (T 1—T 2)=11- (p 1V 1—p 2V 2)理想气体多方可逆过程:W =1nR-δ(T 1—T 2) 热机效率:η=212T T T - 冷冻系数:β=-Q 1/W 可逆制冷机冷冻系数:β=121T T T -焦汤系数: μJ -T =Hp T ⎪⎪⎭⎫⎝⎛∂∂=-()p T C p H ∂∂ 实际气体的ΔH 和ΔU :ΔU =dT T U V ⎪⎭⎫ ⎝⎛∂∂+dV V U T ⎪⎭⎫ ⎝⎛∂∂ ΔH =dT T H P ⎪⎭⎫⎝⎛∂∂+dp p H T ⎪⎪⎭⎫ ⎝⎛∂∂ 化学反应的等压热效应与等容热效应的关系:Q p =Q V +ΔnRT 当反应进度 ξ=1mol 时, Δr H m =Δr U m +∑BB γRT化学反应热效应与温度的关系:()()()dT B C T H T H 21T T m p B1m r 2m r ⎰∑∆∆,+=γ热力学第二定律Clausius 不等式:0TQS BA B A ≥∆∑→δ—熵函数的定义:dS =δQ R /T Boltzman 熵定理:S =kln Ω Helmbolz 自由能定义:F =U —TS Gibbs 自由能定义:G =H -TS 热力学基本公式:(1) 组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU =TdS -pdV dH =TdS +Vdp dF =-SdT -pdV dG =-SdT +Vdp (2) M axwell 关系:T V S ⎪⎭⎫⎝⎛∂∂=VT p ⎪⎭⎫ ⎝⎛∂∂ Tp S ⎪⎪⎭⎫ ⎝⎛∂∂=-p T V ⎪⎭⎫ ⎝⎛∂∂(3) 热容与T 、S 、p 、V 的关系:C V =T V T S ⎪⎭⎫ ⎝⎛∂∂ C p =T pT S ⎪⎭⎫⎝⎛∂∂Gibbs 自由能与温度的关系:Gibbs -Helmholtz 公式 ()pT /G ⎥⎦⎤⎢⎣⎡∂∆∂T =-2T H ∆ 单组分体系的两相平衡: (1)Clapeyron 方程式:dT dp=mX m X V T H ∆∆ 式中x 代表vap ,fus ,sub 。
《物理化学》公式集

热力学第一定律功:δW =δW e +δW f(1)膨胀功 δW e =p 外dV 膨胀功为正,压缩功为负。
(2)非膨胀功δW f =xdy非膨胀功为广义力乘以广义位移。
如δW (机械功)=fdL ,δW (电功)=EdQ ,δW (表面功)=rdA 。
热 Q :体系吸热为正,放热为负。
热力学第一定律: △U =Q —W 焓 H =U +pV 理想气体的内能和焓只是温度的单值函数。
热容 C =δQ/dT(1)等压热容:C p =δQ p /dT = (∂H/∂T )p (2)等容热容:C v =δQ v /dT = (∂U/∂T )v 常温下单原子分子:C v ,m =C v ,m t =3R/2常温下双原子分子:C v ,m =C v ,m t +C v ,m r =5R/2 等压热容与等容热容之差:(1)任意体系 C p —C v =[p +(∂U/∂V )T ](∂V/∂T )p (2)理想气体 C p —C v =nR 理想气体绝热可逆过程方程:pV γ=常数 TV γ-1=常数 p 1-γT γ=常数 γ=C p / C v 理想气体绝热功:W =C v (T 1—T 2)=11-γ(p 1V 1—p 2V 2) 理想气体多方可逆过程:W =1nR-δ(T 1—T 2) 热机效率:η=212T T T - 冷冻系数:β=-Q 1/W 可逆制冷机冷冻系数:β=121T T T -焦汤系数: μJ -T =H p T ⎪⎪⎭⎫⎝⎛∂∂=-()pT C p H ∂∂ 实际气体的ΔH 和ΔU :ΔU =dT T U V ⎪⎭⎫ ⎝⎛∂∂+dV V U T ⎪⎭⎫ ⎝⎛∂∂ ΔH =dT T H P ⎪⎭⎫ ⎝⎛∂∂+dp p H T⎪⎪⎭⎫ ⎝⎛∂∂ 化学反应的等压热效应与等容热效应的关系:Q p =Q V +ΔnRT 当反应进度 ξ=1mol 时, Δr H m =Δr U m +∑BB γRT化学反应热效应与温度的关系:()()()dT B C T H T H 21T T m p B1m r 2m r ⎰∑∆∆,+=γ热力学第二定律Clausius 不等式:0TQS BAB A ≥∆∑→δ—熵函数的定义:dS =δQ R /T Boltzman 熵定理:S =kln Ω Helmbolz 自由能定义:F =U —TS Gibbs 自由能定义:G =H -TS 热力学基本公式:(1)组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU =TdS -pdV dH =TdS +Vdp dF =-SdT -pdV dG =-SdT +Vdp (2)Maxwell 关系:T V S ⎪⎭⎫⎝⎛∂∂=V T p ⎪⎭⎫ ⎝⎛∂∂Tp S ⎪⎪⎭⎫ ⎝⎛∂∂=-p T V ⎪⎭⎫ ⎝⎛∂∂ (3)热容与T 、S 、p 、V 的关系:C V =T VT S ⎪⎭⎫⎝⎛∂∂ C p =T p T S ⎪⎭⎫ ⎝⎛∂∂Gibbs 自由能与温度的关系:Gibbs -Helmholtz 公式 ()pT /G ⎥⎦⎤⎢⎣⎡∂∆∂T =-2T H ∆ 单组分体系的两相平衡: (1)Clapeyron 方程式:dT dp=mX m X V T H ∆∆ 式中x 代表vap ,fus ,sub 。
法拉第定律

法拉第定律法拉第定律法拉第定律是描述电极上通过的电量与电极反应物重量之间的关系的,又称为电解定律。
法拉第定律又叫电解定律,是电镀过程遵循的基本定律。
法拉第(Michael Faraday l791-1867)是英国著名的自学成才的科学家,他发现的电解定律至今仍然指导着电沉积技术,是电化学中最基本的定律,从事电镀专业的工作者,都应该熟知这一著名的定律。
它又分为两个子定律,即法拉第第一定律和法拉第第二定律。
(1)法拉第第一定律法拉第的研究表明,在电解过程中,阴极上还原物质析出的量与所通过的电流强度和通电时间成正比。
当我们讨论的是金属的电沉积时,用公式可以表示为:M=KQ=KIt式中M一析出金属的质量;K—比例常数;Q—通过的电量;I—电流强度;t—通电时间。
法拉第第一定律描述的是电能转化为化学能的定性的关系,进一步的研究表明,这种转化有着严格的定量关系,这就是法拉第第二定律所要表述的内容。
(2)法拉第第二定律电解过程中,通过的电量相同,所析出或溶解出的不同物质的物质的量相同。
也可以表述为:电解1mol的物质,所需用的电量都是1个“法拉第”(F),等于96500 C或者26.8A?h。
1F=26.8A?h=96500C结合第一定律也可以说用相同的电量通过不同的电解质溶液时,在电极上析出(或溶解)的物质与它们的物质的量成正比。
由于现在标准用语中推荐使用摩尔数,也可以用摩尔数来描述这些定理。
所谓摩尔是表示物质的量的单位,每摩尔物质含有阿伏伽德罗常数个微粒。
摩尔简称摩,符号mol。
由于每mol的任何物质所含的原子的数量是一个常数,即6.023 × 10的23次方,这个数被叫作阿伏伽德罗常数。
阿伏伽德罗常数是很大的数值,但摩尔作为物质的量的单位应用极为方便。
因为1mol碳的质量是12g,即为6.023×10的23次方个碳原子的质量。
由此,我们可以推算1mol任何原子的质量。
一种元素的相对原子质量(原子量)是以l2C的质量的l/12作为标准。
155-174 第八章电解质溶液

=
a++
a − −
=+ +−
1
=
+ +
− −
1
1
m
=
m + +
m − −
=
+
+
−
−
mB
a
=
m m
aB
=
a + +
a − −
= a
离子强度: I
=1 2
B
mB zB2
德拜—休克尔极限公式
lg = − A z+ z− I 在 298K 时,使用简化公式时,A 值取
0.509(
mol kg
在。摩尔电导率随浓度的变化与电导率不同,浓度降低,粒子之间相互作用减弱,正、负讘
的运动速率因而增加,故摩尔电导率增加。
4.怎样分别求强电解质和弱电解质的无限稀释摩尔电导率?为什么要用不同的方法?
答:在低浓度下,强电解质溶液的摩尔电导率与 c 成线性关系。
( ) m = m 1− c
在一定温度下,一定电解质溶液来说, 是定值,通过作图,直线与纵坐标的交点即
B
= B
(T
)
+
RTInγm,B
mB mB
= B
(T ) + RTInam,B
电解质
B
=
B
(T ) + RTInaB
=
B
(T ) + RTIna+ν+
aν− −
活度因子表示式:非电解质
am,B
=
ν m,B
mB mB
电解质
aB
=
法拉第电磁感应定律

法拉第电磁感应定律法拉第电磁感应定律(Faraday's law of electromagnetic induction)是电磁学中的重要定律,描述了磁场的变化如何产生感应电流。
这个定律是由英国物理学家迈克尔·法拉第在1831年发现的,为电磁学的发展做出巨大贡献。
法拉第电磁感应定律可以用一个简洁的数学公式表达:感应电动势的大小等于导线中的磁通量的变化率。
即\epsilon = -\frac{d\Phi}{dt}其中,\epsilon 代表感应电动势,\Phi 代表磁通量,t代表时间。
负号表示感应电动势的方向和磁通量的变化方向相反。
这个定律的核心思想是,当一个导线被置于一个磁场中,并且磁场的强度发生变化时,导线中就会产生感应电流。
这个变化可以是磁场强度的增加或减少,也可以是磁场方向的改变。
这个定律对于理解电磁感应现象和发电原理非常重要,可以应用于实际生活和工程中。
为了更好地理解法拉第电磁感应定律,我们可以从几个方面来解释这个定律的原理和应用。
首先,我们来看一个简单的实验:在一个金属环上绕上一根导线,当将金属环放入强磁场中并旋转时,导线中就会有感应电流产生。
这是因为磁场随着金属环的旋转而发生变化,从而产生感应电动势和感应电流。
这个实验可以用法拉第电磁感应定律来解释:磁通量的变化引起了感应电动势的产生,进而产生了感应电流。
其次,法拉第电磁感应定律在发电中的应用非常重要。
根据这个定律,我们可以利用磁感线的变化来产生电流。
这就是电磁感应发电的原理。
当磁场通过一个线圈时,如果磁场的强度或方向发生变化,就会在线圈中产生感应电流。
这个原理广泛应用于发电机、变压器和电动机等设备中。
通过调节磁场的强度和方向,可以控制感应电动势和感应电流的大小和方向。
此外,法拉第电磁感应定律还与电磁波的产生和传播有关。
电磁波是由振动的电场和磁场所组成的一种波动现象。
根据法拉第电磁感应定律,磁场的变化可以引起电场的变化,进而产生电磁波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
法拉第定律nzf
法拉第定律,又称法拉第定律,是经典动力学理论的电磁学组成部分,于1820年由意大利物理学家米开朗基罗法拉第提出。
它提出了关于动作和反作用之间对称性的基本原理,改变了人们对物体运动和变形的看法,有力地支持了“质点观念”,使古希腊哲学家亚里士多德的“运动观念”成为古代物理学家们认可的论断。
法拉第定律认为,任何作用在物体上的力都必须有其相等的反作用,且反作用的矢量方向向反方向,作用的大小与反作用的大小相等。
例如,一个物体面对着另一个物体,把力施加在另一个物体上,那么另一个物体也必然施加同样大小的力反作用于前一个物体上,所施加的力的大小和方向都相等。
法拉第定律的认识,支持了“质点观念”,这个观念认为,物体在运动时,它们是在一个静止状态下。
静止状态意味着物体在动力学上处于不受外力影响的状态,而外力又是一种影响物体运动的力。
如果没有外力,物体就不会发生运动,也就不存在变形现象。
法拉第定律解释了物体在动力学上不受外力影响的原因。
法拉第定律的提出,不仅具有重要的科学含义,而且也改变了对物体的认识。
以往的认识中,人们认为物体运动和变形就是物体本身的一部分,由于某种原因,物体会发生变化。
然而,法拉第定律认为,物体是外力作用下发生变化的,而外力又有可能是压力、拉力、张力等形式,而这种变形又必然有与之相等的反作用。
也就是说,物体发生的运动和变形是物质的一种反作用,物体的变形就是外力的作用下
的物质反作用。
法拉第定律不仅改变了人们当时的观念,而且也为之后物理学家在研究动力学方面开辟了新的道路。
米开朗基罗法拉第的定律已被认为是经典动力学和电磁学的基础,激发了物理学家们研究并认识运动观念带来的新思路,为现代物理学研究打下了坚实的基础。
因此,法拉第定律可以被认为是将物理学从古希腊哲学家亚里士多德的“运动观念”推进到现代物理学的重要突破,它提出了物质运动和变形的基本原理,以及外力作用下的反作用现象,使现代物理学的研究有了一条新的发展路径。
法拉第定律开创了经典动力学的新篇章,以及电磁学的新世界,对于构建现代物理学的基础奠定了重要的作用,在物理学的研究中发挥了重要的作用。
