齿轮结构设计和校核
齿轮强度校核的新方法(图文)

齿轮强度校核的新方法(图文)论文导读:使用有限元分析软件ANSYS对齿轮进行强度分析,可对齿轮的强度设计提供可靠的根据,实现变速器齿轮的计算机辅助设计,能够加快设计进程、缩短研制周期、提高设计质量。
本文应用了APDL,即ANSYS参数化设计语言(ANSYSParametricDesignLanguage),设计直齿圆柱齿轮模块与应用ANSYS有限元软件进行有限元分析方面,做一些初步的探索。
关键词:ANSYS,直齿圆柱齿轮,接触应力,齿根弯曲应力0引言齿轮作为在机械结构中经常用到的重要的传动零件,其强度直接影响到整个机械结构的工作性能与寿命,然而在传统齿轮设计中,齿轮的强度校核过程与设计过程要紧是通过人工设计完成,计算繁琐,设计周期长且难以实现优化设计。
本文使用有限元分析法对渐开线标准圆柱直齿轮进行接触应力与齿根弯曲应力进行分析计算。
同时在有限元分析中,对AYSYS[1]软件进行二次开发,即应用了APDL[2]语言,自动实现了齿轮的参数精确建模,自习惯网格划分与有限元强度分析。
最后与传统经典方法进行了对比分析,证明了本方法的准确性。
具有实际操作性与推广价值。
论文发表。
1.齿轮强度分析的基本要求在机械专业中,减速机是要紧的重要的传动机构,而齿轮传动是其中最常见的实现方式。
论文发表。
因此齿轮零件的设计就显得尤为重要。
其中齿轮应力强度校核是齿轮结构设计的前提,只有相互啮合的齿轮通过了接触与弯曲强度校核计算,才能进行齿轮结构设计。
当然相互啮合的齿轮种类十分繁杂。
这里我们为方便起见,只考虑渐开线标准圆柱直齿轮的问题。
传统的应力强度校核计算十分烦琐,需要查阅机械设计手册中大量的数据(包含图形与图表)。
而传动机构中往往是多对齿轮啮合,其中有一对不符合要求,整个计算就得重来,耗费了设计者大量的精力。
因此借助计算机及相应软件完成对齿轮的优化设计十分必要。
使用有限元分析软件ANSYS对齿轮进行强度分析,可对齿轮的强度设计提供可靠的根据,实现变速器齿轮的计算机辅助设计,能够加快设计进程、缩短研制周期、提高设计质量。
齿轮的校核PPT课件

圆轴扭转时的许用切应力[ ]值是根据试验确定的,可查阅有关设计手册。
7.5 D22(1- 2)
所以,轴的刚度也满足要求。
=9550 x 100 = 716.3 (N.m) 5kW,n=100r/min,轴的许用切应力
=4பைடு நூலகம்M Pa,空心圆轴的内外径之比 = 0.
对于轴1: 要综合考虑扭矩和极惯性矩来确定最大单位长度扭角。
MAC
MCD
τ = 则: max MTmax / WP
= 902 x 10 3/ 0.2 x 50 3 = 14.4 Mpa < 38 MPa
所以,轴的强度足够。
例2:某拖拉机输出轴的直径d=50mm,其转速n=250r/min,
许用切应力[ ]=60MPa,试按强度条件计算该轴能传递 的最大功率。
PA=20kW,轴的转速n=180r/min,齿轮B、C、D的输出
功率分别为PB=3kW,Pc=10kW,PD=7kW,轴的许用切应
力[ ]=38M Pa,试校核该轴的强度。
解:求各轮的外力偶矩:
A
B
CD
MA = 9550 x 20/180
MB MC MD
A B
CD
用截面法可得:MAB
MA = 1061 N.m MB = 159 N.m MC = 531 N.m MD = 371 N.m
1000MT
Wp2
=
716300 0.2D2 3 (1- 4 )
= 40 ( M Pa)
D2 =
716300 0.2(1- 0.5 4) 40
= 46 mm
d 2 = 0.5D2=23 mm
A1 A2
d12 =D22(1-
2) =1.28
齿轮设计校核

齿轮设计校核齿轮作为机械传动的基础部件之一,在工业生产领域中应用广泛。
然而,由于工作条件的不同,齿轮的类型、尺寸及负载等参数不尽相同,因此在齿轮的设计时需要进行严格的校核才能确保其在实际使用中的安全可靠性。
一、齿轮参数设计1、齿轮类型根据使用的具体条件和要求,可以选择不同的齿轮类型,如圆柱齿轮、锥齿轮、螺旋齿轮、斜齿轮等。
不同类型的齿轮具有不同的传动效率、负载能力、精度要求等特点,应根据实际需要进行选择。
2、齿轮尺寸齿轮的尺寸包括齿数、模数、齿轮宽度等参数。
这些参数的选取应考虑到齿轮的负载、转速等因素,以便使齿轮的数据计算精确,并满足使用要求。
3、齿轮材料齿轮的材料需要具有良好的强度、硬度、韧性、耐磨性等特性,以满足工作条件下的负载和磨损要求。
通常选择的材料有合金钢、低碳钢、不锈钢、铜合金等。
模数是齿轮设计的关键参数之一,它与齿轮的齿数、圆径有关。
在设计时,需要根据负载情况、转速、尺寸等因素计算出具体的模数值。
齿数计算是齿轮设计中重要的部分,它直接影响到齿轮的传动比、噪声、载荷分布等性能。
在计算中,应考虑到齿轮传动的要求,并保证齿轮的强度和使用寿命。
3、齿轮载荷计算齿轮设计中的负载计算是根据齿轮所受的载荷和转矩计算得出的。
在设计中,应考虑到齿轮所受的载荷和转矩的不同作用方式,以及齿轮在使用过程中所承受到的动、静载荷等因素。
齿轮精度计算是指齿轮的基本圆直径、齿距误差等参数的计算。
在设计中,应考虑到齿轮传动的要求,以及齿轮间的配合情况,选取合适的精度要求。
齿轮设计校核是指针对齿轮设计过程中的各项计算进行检验和验证。
在校核中需要考虑到齿轮所承受的负载、强度、精度、磨损等因素,确保齿轮的设计参数满足使用要求。
1、强度校核强度校核是指对齿轮材料的强度、载荷、应力等因素进行检验和验证,以确保齿轮的强度能够满足工作要求和使用寿命。
精度校核是指对齿轮的齿距误差、跳动等参数进行检验和验证,以确保齿轮的精度符合设计要求,并满足传动的精度要求。
斜齿圆柱齿轮设计和校核计算

分度圆圆周力 材料接触应力 材料弯曲应力
承载能力计算
Ft σHlim σFE
93015.538 1300 18Cr2Ni4W 900
弧度
角度
传动比
t
1
端面模数 mt
6.0205
0.34906585
端面压力 角
αt
0.379139 21.72308008
0.41887902
βb 0.392184 22.47048266
161.50138 160.48751
136.762 135.749
分度圆直径 基圆直径 节圆直径 齿顶压力角 分度圆弧齿厚 重合度
滑动率
当量齿数 理论跨齿数 实际跨齿数 公法线长度
计算量棒直径 实际量棒直径
量棒中心所在圆上 的压力角
跨棒距
d=mt*cosβ db
ααt
ε=εα+εβ εα εβ η
630
计算中心距
244.493
分度圆直径
241.628 247.3578
计算法向模数
mn 5.93721
SIN() COS()
TAN()
ASIN ()
ACOS ()
ATAN() inv ()
0.3420201 0.9396926 0.36397023 0.35657 1.2142 0.3358 0.014904
0.4067366 0.9135455 0.44522869 0.43221 1.1386 0.3967 0.02635
0.370121 0.9289836 0.39841502 0.38887 1.1819 0.3624 0.019276
0.362053 0.9321575 0.38840325 0.37951 1.1913 0.3548 0.017934
齿轮校核

齿轮校核:软齿面齿轮按接触疲劳强度设计,按弯曲疲劳强度校核;硬齿面齿轮按弯曲疲劳强度设计,按接触疲劳强度校核。
齿轮:齿轮是指轮缘上有齿轮连续啮合传递运动和动力的机械元件。
齿轮在传动中的应用很早就出现了。
19世纪末,展成切齿法的原理及利用此原理切齿的专用机床与刀具的相继出现,随着生产的发展,齿轮运转的平稳性受到重视。
发展起源:历史在西方,公元前300年古希腊哲学家亚里士多德在《机械问题》中,就阐述了用青铜或铸铁齿轮传递旋转运动的问题。
希腊著名学者亚里士多德和阿基米德都研究过齿轮,希腊有名的发明家古蒂西比奥斯在圆板工作台边缘上均匀地插上销子,使它与销轮啮合,他把这种机构应用到刻漏上。
这约是公元前150年的事。
在公元前100年,亚历山人的发明家赫伦发明了里程计,在里程计中使用了齿轮。
公元1世纪时,罗马的建筑家毕多毕斯制作的水车式制粉机上也使用了齿轮传动装置。
到14世纪,开始在钟表上使用齿轮。
东汉初年(公元1世纪)已有人字齿轮。
三国时期出现的指南车和记里鼓车已采用齿轮传动系统。
晋代杜预发明的水转连磨就是通过齿轮将水轮的动力传递给石磨的。
史书中关于齿轮传动系统的最早记载,是对唐代一行、梁令瓒于725年制造的水运浑仪的描述。
北宋时制造的水运仪象台(见中国古代计时器)运用了复杂的齿轮系统。
明代茅元仪著《武备志》(成书于1621年)记载了一种齿轮齿条传动装置。
1956年发掘的河北安午汲古城遗址中,发现了铁制棘齿轮,轮直径约80毫米,虽已残缺,但铁质较好,经研究,确认为是战国末期(公元前3世纪)到西汉(公元前206~公元24年)期间的制品。
1954年在山西省永济县蘖家崖出土了青铜棘齿轮。
参考同坑出土器物,可断定为秦代(公元前221~前206)或西汉初年遗物,轮40齿,直径约25毫米。
关于棘齿轮的用途,迄今未发现文字记载,推测可能用于制动,以防止轮轴倒转。
1953年陕西省长安县红庆村出土了一对青铜人字齿轮。
根据墓结构和墓葬物品情况分析,可认定这对齿轮出于东汉初年。
2齿轮的设计及校核

2齿轮的设计及校核齿轮是一种常见的动力传递装置,广泛应用于机械传动中。
齿轮的设计和校核是确保齿轮传动系统正常工作的重要环节。
本文将从齿轮的设计和校核两个方面进行分析,详细介绍其原理和方法。
齿轮的设计是根据传动的要求和工作条件,确定齿轮的尺寸、型号、齿数等参数的过程。
首先需要确定传动的速比、转矩要求等。
然后根据这些参数,计算出齿轮的模数、齿轮的宽度、齿轮的材料等。
根据实际情况,可以选择使用标准齿轮或定制齿轮。
齿轮的校核是验证设计参数的合理性和齿轮传动系统的可靠性的过程。
主要包括以下几个方面:1.齿轮强度校核。
根据所选用的齿轮材料,计算其强度参数,并与设计需求进行比较。
常用的齿轮强度计算方法有弗赖德、路中曼等。
2.齿面接触强度校核。
通过计算齿轮齿面接触应力和接触应力分布,判断齿面接触是否能满足传动要求。
根据计算结果,可以调整齿轮的齿形和齿数等参数。
3.齿轮轴承能力校核。
根据齿轮传动的工作转矩,计算齿轮轴承的最大受力,并与轴承的额定负载进行比较。
如果超过了轴承的额定负载,需要重新选择适合的轴承。
4.齿轮的热强度校核。
计算齿轮的热强度参数,判断齿轮在长时间高速工作时的热强度能否满足要求。
如果不能满足,可能需要进行降速设计或采取散热措施。
5.齿轮的动态特性校核。
根据齿轮的质量、转动惯量等参数,计算齿轮系统的固有频率和谐振现象,并进行分析和校核。
如果存在谐振问题,需要采取减振措施。
在齿轮的设计和校核过程中,需要使用一些专业软件和标准规范进行计算和判断。
一般常用的计算软件有Ansys、AutoCAD等,相关的标准规范有GB/T 3456.2-2024等。
总之,齿轮的设计和校核是确保齿轮传动系统正常运行的关键步骤。
只有在设计和校核过程中充分考虑到齿轮的强度、接触、轴承、热强度和动态特性等方面的要求,才能保证齿轮传动系统的可靠性和稳定性。
齿轮强度校核的基本原则

齿轮强度校核的基本原则齿轮强度校核的基本原则主要包括以下几点:1.遵循国家标准和行业规范:在开展齿轮强度校核工作时,应严格遵循我国相关的国家标准和行业规范,确保校核结果的准确性和可靠性。
目前,我国有关齿轮设计及强度校核的主要标准有GB/T3478.1-1995《齿轮设计手册》和GB/T10095.1-2001《圆柱齿轮精度等级》等。
2.采用合理的计算方法:在进行齿轮强度校核时,应采用合理的计算方法,如有限元分析法、传统设计方法等。
其中,有限元分析法具有较高的计算精度,可有效模拟齿轮在工作过程中的受力情况,为强度校核提供可靠依据。
而传统设计方法则主要依据经验公式和图表进行计算,虽然过程较为简便,但精度相对较低。
3.考虑齿轮组合的强度平衡:在齿轮强度校核过程中,应充分考虑齿轮组合的强度平衡,确保各齿轮的强度足够且匹配合理。
此外,还需注意齿轮材料的选用,使其具有较高的强度和耐磨性。
4.遵循简化原则:为了便于计算和分析,可以在强度校核过程中对齿轮结构进行简化。
例如,将直齿锥齿轮传动中的齿数比、锥距等参数进行合理简化,以便于进行强度计算。
5.考虑齿轮传动的稳定性:在强度校核过程中,还需考虑齿轮传动的稳定性,避免因传动比过大或过小导致的齿轮失效。
此外,还需注意齿轮传动机构的润滑和防尘设计,以降低齿轮磨损和故障风险。
6.结合实际工况进行校核:齿轮强度校核应结合实际工况进行,充分考虑齿轮在工作过程中承受的载荷、转速、振动等因素。
此外,还需注意齿轮在安装和维护过程中的强度损失,确保校核结果的可靠性。
7.留有一定的安全系数:为了保证齿轮在使用过程中的安全性能,在校核强度时,应适当留有一定的安全系数。
安全系数的选取应根据实际工况和设计要求进行,一般取2~3较为合适。
综上所述,齿轮强度校核的基本原则包括遵循国家标准和行业规范、采用合理的计算方法、考虑齿轮组合的强度平衡、遵循简化原则、考虑齿轮传动的稳定性、结合实际工况进行校核以及留有一定的安全系数。
齿轮结构设计和校核
© R =1/3直齿锥齿轮传动是以大端参数为标准值的。
在强度计算时,则以齿宽中 点处的当量齿轮作为计算的依据。
对轴交角 刀=90。
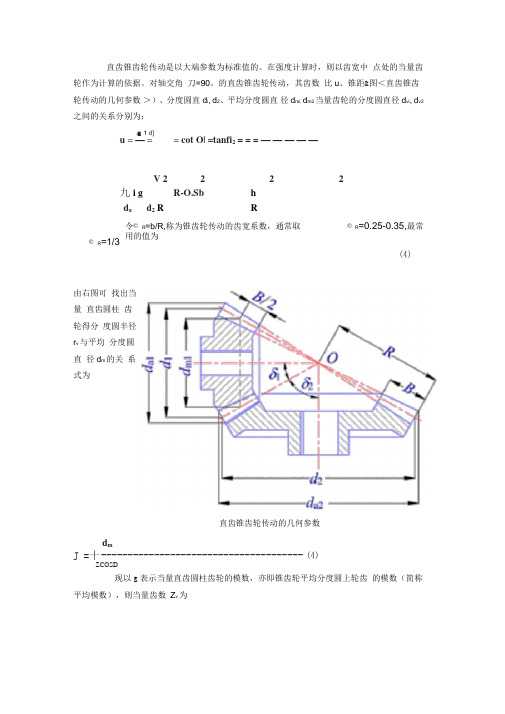
的直齿锥齿轮传动,其齿数 比u 、锥距&图<直齿锥齿轮传动的几何参数 >)、分度圆直d i , d 2、平均分度圆直 径d mi, d m2当量齿轮的分度圆直径d vi , d v2之间的关系分别为:連 1 d] u = — = = cot O| =tanfi 2 = = = — — — — —V 22 2 2九i gR-O.Sb h d x d 2 R R 令© R =b/R,称为锥齿轮传动的齿宽系数,通常取 © R =0.25-0.35,最常用的值为 ⑷由右图可 找出当量 直齿圆柱 齿轮得分 度圆半径r v 与平均 分度圆直 径d m 的关 系式为d mJ =十 -------------------------------------- ⑷ZCOSD现以g 表示当量直齿圆柱齿轮的模数,亦即锥齿轮平均分度圆上轮齿 的模数(简称平均模数),则当量齿数 Z v 为直齿锥齿轮传动的几何参数显然,为使锥齿轮不至发生根切,应使当量齿数不小于直齿圆柱齿轮的根切齿数。
另外,由式(d)极易得出平均模数mm和大端模数m的关系为111^=111(1-0.5^)--------------------------------------------------------- (h)、直齿圆锥齿轮的背锥及当量齿数为了便于设计和加工,需要用平面曲线来近似球面曲线,如下图OAB为分度圆锥,J和:为轮齿在球面上的齿顶高和齿根高,过点A作直线AO丄AQ与圆锥齿轮轴线交于点O,设想以OO为轴线, OA为母线作一圆锥QAB,称为直齿圆锥齿轮的背锥。
由图可见A B附近背锥面与球面非常接近。
因此,可以用背锥上的齿形近似地代替直齿圆锥齿轮大端球面上的齿形。
从而实现了平面近似球面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直齿锥齿轮传动是以大端参数为标准值的。
在强度计算时,则以齿宽中 点处的当量齿
轮作为计算的依据。
对轴交角 刀=90。
的直齿锥齿轮传动,其齿数 比u 、锥距R (图<直齿锥齿轮传动的几何参数 >)、分度圆直d i , d 2、平均分度圆直 径d m1 d m2当量齿轮的分度圆直径d v1, d v2之间的关系分别为:
—=cotO| =tan5j di
2 ' 2 】2
也亠= R-0.5b 亠05丄 _______________________________ 右 dj R
R
令© R =b/R,称为锥齿轮传动的齿宽系数,通常取
© R =0.25-0.35,最常用的值为
于是《^二即-0・5備 ------------------------------- (d )
由右图可 找出当量 直齿圆柱 齿轮得分 度圆半径 r v 与平均 分度圆直 径d m 的关 系式为
q= d 脏
V 2cos6
现以m m 表示当量直齿圆柱齿轮的模数,亦即锥齿轮平均分度圆上轮齿
的模数(简称平均模数),则当量齿数 Z v 为
(h)
R
=1/3 O
V)
R
2
巧
i
■ A
&
... =
直齿锥齿轮传动的几何参数
山 2片 Z
J =—=—=—--- m 肌 cos5
U =匹=乞.沁
V
c
Z 屮] Z] COSO 士
显然,为使锥齿轮不至发生根切,应使当量齿数不小于直齿圆柱齿轮
的根切齿数。
另外,由式(d )极易得出平均模数m 和大端模数m 的关系为
叫二呗―05 虬) -------------------------------------- (11)
、直齿圆锥齿轮的背锥及当量齿数
为了便于设计和加工,需要用平面曲线来近似球面曲线,如下图。
OAB 为分度圆锥,总』和用为轮齿在球面上的齿顶高和齿根高, 过点A 作直线AO
丄AO 与圆锥齿轮轴线交于点 O ,设想以OO 为轴线,OA 为母线作一圆锥OAB,称为直齿圆锥齿轮的背锥。
由图可见A B 附近背锥 面与球面非常接近。
因此,可以用背锥上的齿形近似地代替直齿圆锥齿轮大 端球面上的齿形。
从而实现了平面近似球面。
(g)
将背锥展成扇形齿轮,它的参数等于圆锥齿轮大端的参数,齿数就是圆锥齿轮的实际齿数2。
将扇形齿轮补足,则齿数增加为g。
这个补足后的直齿圆柱齿轮称为当量齿轮,齿数称为当量齿数。
其中
J = --- 7
当量齿数的用途:
1.仿形法加工直齿圆锥齿轮时,选择铣刀的号
码。
2.计算圆锥齿轮的齿根弯曲疲劳
强度时查取齿形系数。
标准直齿圆锥齿轮不发生根切的最少齿数Z血
与当量齿轮不发生根切的最少齿数兔皿的关系:
二、直齿圆锥齿轮的几何尺寸
标准直齿圆锥齿轮机构的几何尺寸计算公式
称名
号
代计算公式
小齿轮大齿轮
度圆锥角分
= arc cot
—
百2 = gtr P
顶高齿
札1 ■虬■札用
根高齿
=4 =(磴F)耕
度圆分
右■祕1-陀空
(
i
直径
顶圆直径齿
盅1 ■ & + 敢co;規£ =屈i + 2& 3S 6
根圆直径齿
dfi- d] - 2Af CE注Q
■如1 2人c<?s
爲
距锥
—檢/ M十兮细占2 I k
顶角齿
(收缩顶隙传动)
tan 為=tan % =沁 R
根角齿
tan 3门=tan^Q ~h^i R
度圆齿厚分
7^
E = --
2
隙
页
量齿数当
各广野hog细
锥页收缩顶隙传动
41弋弋1瓦1 ■爲十^*2
等顶隙传动
量
j_fc.
齿
轮
分
度
圆
半
径
量
齿
轮
齿
顶
圆
半
径
量
j_fc.
齿轮齿顶压力角
G泌-
arcc<?£
仏=arccos
如cos a
^T41
耳=7—0讥(tan务u - tan毋十玄歸0加込讹-tat 2冗
三、直齿圆锥齿轮传动的受力分析和强度计算
1、受力分析
在齿宽中点节线处的法向平面内,法向力可分解为三个分力: 力和轴向力。
(1)力的大小
F三竺L __________
"H血(1-0.阴)必
I
£1 = cos 靳=耳• cos 5]
I
巧1二El sin 151二耳]绘號血靳
⑵力的方向
圆周力:主动轮上的与转向相反,从动轮上的与转向相同;
径向力:分别指向各自轮心;
轴向力:分别由各轮的小端指向大端。
(3)力的对应关系
血=遇传】=你=%
2、计算载荷
式中:尤4按表查取;
扎“174 .©汀1“3•心.1。
三、齿面接触疲劳强度条件圆周力、径向因直齿圆锥
齿面接触疲劳强度按齿宽中点处的当量直齿圆柱齿轮进行计算。
齿轮一般制造精度较低,可忽略重合度的影响,并取有效齿宽,将当量齿轮的有 关参量代入直齿圆柱齿轮的强度计算公式,得
'
2
‘ 2曲\ 认温 代入上式,得到直齿锥齿轮的接触强
四、轮齿弯曲疲劳强度条件
与接触疲劳强度的计算相同,忽略重合度系数,按齿宽中点的当量直齿圆
柱 齿轮进行计算,将当量齿轮的参数代入,得:
(MPa)
加用等代入上式,得锥齿轮的齿根弯曲疲劳强度条件
校核式:
设计式:
in>3\-
- ---
\巴(1 - Q 如』'才%> J1 +/
m)
注意:
_ 2
1、『用、『31按当量齿数分别查图;
(MPa)
把 度计算的
校核式:
计算式: 4K7[ 咲S 可0,盹40环J 竝
(MPa)
式中:Z H 、Zp 、
V
I %丿
0朋与直齿圆柱齿轮相同。
(mm)
* _
4 皿&
蚣(1 一 0妙
-%
(MPa)
(m
%与直齿圆柱齿轮的相同;
2、
3、采用弯曲强度的设计式时,用大的口砌值代入;、按当量齿数分别查图;。
