Origin 常用小技巧1 分段线性拟合
origin拟合函数

origin拟合函数Origin是一款功能强大的数据分析软件,它提供了丰富的数据分析工具来处理实验数据,其中包括曲线拟合功能。
本文将着重介绍Origin中的曲线拟合功能,包括常见的拟合函数及其应用。
一、拟合函数在Origin中,可以通过选择不同的拟合函数来拟合所需的曲线。
常见的拟合函数有线性函数、二次函数、三次函数、指数函数、对数函数、幂函数、指数增长函数、正弦函数、余弦函数等。
下面将对这些函数进行详细介绍。
1. 线性函数一元线性函数的表达式为y=a+bx,其中a和b分别为截距和斜率,x为自变量,y为因变量。
线性函数是最简单的拟合函数之一,适用于线性关系较为明显的数据。
例如,当我们在光电效应实验中测量出光电子的动能和光子的频率时,它们之间就存在着线性关系,此时可以使用线性函数来拟合数据。
2. 二次函数三次函数的表达式为y=a+bx+cx^2+dx^3,其中a、b、c和d分别为常数,x为自变量,y为因变量。
三次函数通常用于描述抛物线,这种函数在物理和工程学中经常被应用。
例如,在材料科学中可以使用三次函数来描述一个材料的弹性行为。
4. 指数函数指数函数的表达式为y=ae^(bx),其中a和b为常数,x为自变量,y为因变量。
指数函数适用于描述随时间或位置而变化的某些现象。
例如,当我们观察放射性衰变时,衰变速率随时间的变化可以使用指数函数来拟合。
8. 正弦函数正弦函数的表达式为y=a sin(bx+c),其中a、b和c为常数,x为自变量,y为因变量。
正弦函数适用于描述像周期性的变化,例如,天文学中的多个现象,如日、月、星星的运动都是可以用正弦函数表示的。
二、常见应用在实际应用中,我们可以使用Origin中的曲线拟合功能来解决各种问题。
下面列举几种常见的应用。
1. 数据分析在实验数据分析中,使用拟合函数可以帮助我们理解和预测实验数据的变化趋势。
例如,在物理实验中,我们可以使用线性函数来分析位移和时间的关系,使用指数函数来分析辐射物质的衰变过程。
用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据

<
0.5,表明有95% 置信度认为可以拒绝零假
第6期
陈旭红:用 Origin 软件的线性拟合和非线性曲线拟合功能处理实验数据
89
设,也就是说可以接受拟合的参数的结果。 将相关的数据代入QV= Mm·C·ΔT,其中C为水当量,就可以求得QV:QV=- 5 541.8kJ·mol-1。 如果采用手工作图,不同的操作者处理同一组数据,得到的结果可能不同;即使由同一个操作者在不
摘 要:以物理化学实验中《 燃烧热的测定》实验为例,说明Origin软件在计算机上对实验数据进行作图、线性拟
合和非线性曲线拟合等处理而求得需要的实验参数,从而大大减少数据处理过程中产生的误差,而且方便快捷。
关键词:Origin软件;燃烧热;线性拟合;非线性曲线拟合
中图分类号:TP317
文献标识码:B
同时间处理同一组数据,其结果也不会完全一致。使用Origin软件可以克服上述问题,能够准确、快速、方 便地处理实验的数据。
参考文献:
[1] 郝红伟,施光凯. Origin6.0实例教程[M].北京:中国电力出版社,2000. [2] 夏春兰.Origin软件在物理化学实验数据处理中的应用[J].大学化学,2003,1(8 2):44- 46. [3] 复旦大学,武汉大学,中国科技大学.物理化学实验[M]. 3版.北京:高等教育出版社,2004.
0引言
提及Origin软件[1],许多人都知道它在实验数据作图上的应用。用Origin软件线性拟合和非线性曲线拟 合功能处理数据方面却很少有报道。实际上,Origin软件在线性拟合和非线性曲线拟合时,可屏蔽某些偏 差较大的数据点,以降低曲线的偏差[2],得到更为准确的结果,且方便快捷。
Origin软件有如下基本功能:①输入数据并作图。②将数据计算后作图。③数据排序。④选择需要的 数据范围作图。⑤数据点屏蔽。⑥Origin软件的线性拟合和非线性曲线拟合功能。
Origin 常用小技巧1 分段线性拟合
Origin 常用小技巧 1 分段线性拟合
By D. J. Liu
6 点上图中 From 和 To 后面的框中输入第二部确定的拟合范围,点击 OK,出现如下结果。
4
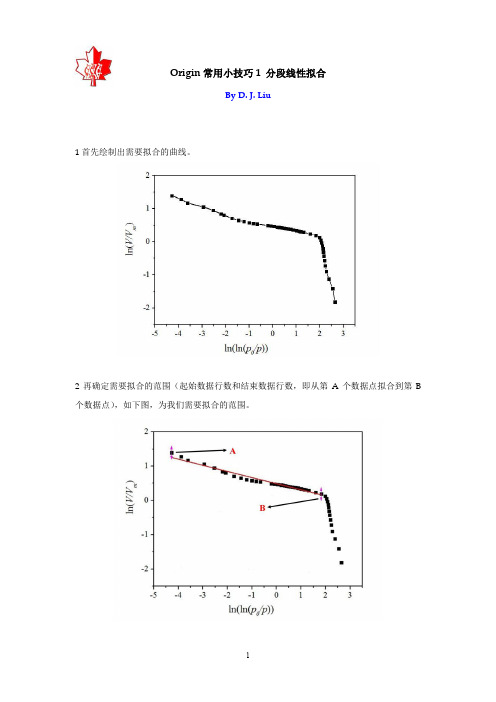
1 首先绘制出需要拟合的曲线。
2 再确定需要拟合的范围(起始数据行数和结束数据行数,即从第 A 个数据点拟合到第 B 个数据点) ,如下图,为我们需要拟合的范围。
1
3 Analysis → Fitting → Fitting Linear → Open Dialog
4 打开对话框后,如下图。
2
5 点击上图中红框的加号,展开对话框。
origin线性拟合的斜率和截距

origin线性拟合的斜率和截距
求origin线性拟合的斜率和截距,是求解一元线性回归问题的
基本步骤。
一元线性回归问题的模型可以表示为:y=ax+b,
其中a为斜率,b为截距。
要求求解origin线性拟合的斜率和截距,首先需要准备足够的
数据,即x和y的值,并将其分别放入x和y的数组中。
然后,根据x和y的值,计算出x的平均值和y的平均值,分别记为
x_mean和y_mean。
接下来,根据x和y的值,计算出x和y的方差,分别记为
x_var和y_var,以及x和y的协方差,分别记为x_cov和
y_cov。
最后,根据以上计算出的x_mean、y_mean、x_var、y_var、
x_cov和y_cov,可以计算出origin线性拟合的斜率a和截距b,其计算公式分别为:
a=x_cov/x_var
b=y_mean-a*x_mean
因此,求origin线性拟合的斜率和截距,需要准备足够的数据,并计算出x的平均值、y的平均值、x的方差、y的方差、x的
协方差和y的协方差,最后根据以上计算出的值,可以计算出origin线性拟合的斜率和截距。
origin 分段函数拟合

origin 分段函数拟合
分段函数拟合是一种常用的数学方法,用于逼近复杂函数。
它将整个定义域分成多个段落,每个段落内使用简单的函数进行拟合。
这样做的目的是用一组简单的函数来近似整个函数的行为,从而简化计算和分析过程。
在分段函数拟合中,我们首先确定分段点,即将整个定义域划分为不同的段落。
然后,针对每个段落,选择一种适当的函数类型进行拟合。
常用的函数类型包括线性函数、二次函数、指数函数和对数函数等等。
在每个段落内,我们通过调整函数的参数,使得拟合函数与实际函数的取值尽可能接近。
这可以通过最小二乘法等统计方法来实现。
通过不断优化参数,我们可以得到一个在整个定义域上都较好逼近原函数的分段函数。
分段函数拟合可以应用于多个领域,如物理学、经济学和工程学等。
它可以用于描述非线性关系、曲线拟合和数据分析等问题。
通过将问题分解为多个简单的段落,分段函数拟合可以简化复杂问题的处理,并提高计算效率。
总的来说,分段函数拟合是一种有效的数学方法,可以将复杂函数近似为一组简单的函数。
通过合理选择分段点和拟合函数,我们可以得到一个在整个定义域上都较好逼近原函数的分段函数,从而简化计算和分析过程。
origin分段函数拟合

origin分段函数拟合
拟合的函数形式为:
\[ f(x) =
\begin{cases}
a_1x + b_1 & \text{if } x < x_1 \\
a_2x + b_2 & \text{if } x_1 \leq x < x_2 \\
\vdots \\
a_{n-1}x + b_{n-1} & \text{if } x_{n-2} \leq x < x_{n-1} \\ a_nx + b_n & \text{if } x \geq x_{n-1} \\
\end{cases}
\]
其中,$a_i$和$b_i$为拟合参数,$x_i$为分段点。
拟合的过程可以分为以下几步:
1. 确定分段点$x_i$的个数和位置。
可以根据数据的分布情况和特点来选择合适的分段点。
2. 对每个区间$(x_{i-1}, x_i)$内的数据进行线性拟合,得到参数$a_i$和$b_i$。
3. 将每个区间的拟合结果拼接起来,得到最终的拟合函数。
具体的拟合算法可以使用最小二乘法来求解,最小化真实数据与拟合函数之间的误差。
可以使用数值优化算法,如梯度下降法或牛顿法来求解最优的参数值。
需要注意的是,拟合的结果可能会受到分段点的选择和初始参数值的影响,因此需要进行多次尝试和调整,以找到最优的拟合结果。
origin拟合曲线选取点

在Origin中拟合曲线时,选取合适的数据点非常重要。
以下是几个建议:
1. 代表性:选择具有代表性的数据点进行拟合。
这些点应该能够反映数据整体的变化规律。
2. 分布均匀:尽量选择分布均匀的数据点,避免在某些区域选择过多的点,而其他区域选择过少的点。
3. 考虑噪声和异常值:在选择数据点时,应考虑噪声和异常值的影响。
对于噪声,可以选择滤波或平滑处理来减少其影响。
对于异常值,可以将其去除或进行特殊处理。
4. 交互式拟合:可以在Origin中采用交互式拟合方式,即手动选择需要拟合的数据点,然后进行拟合。
这样可以更灵活地选择数据点,并获得更好的拟合效果。
5. 分段拟合:对于具有不同变化趋势的数据,可以考虑采用分段拟合方法。
这样可以更好地适应数据的局部变化规律,提高拟合精度。
6. 非线性拟合:如果数据呈现出非线性变化趋势,可以选择合适的非线性拟合函数进行拟合。
在Origin中,可以通过Analysis > Fitting > Nonlinear Curve Fit菜单进行非线性拟合。
7. 拟合曲线类型:根据数据的特征和变化规律,选择合适的拟合曲线类型。
例如,线性拟合、多项式拟合、指数拟合、对数拟合等。
总之,在Origin中拟合曲线时,需要仔细考虑数据点的选择,并根
据实际情况灵活调整拟合策略,以获得最佳的拟合效果。
origin数据拟合成曲线

origin数据拟合成曲线摘要:一、引言二、Origin数据拟合原理1.线性拟合2.非线性拟合三、拟合步骤1.数据准备2.添加拟合项3.设置拟合参数4.分析拟合结果四、优化拟合效果1.选择合适的拟合函数2.调整拟合参数3.增加或删除拟合项五、实例演示1.线性拟合实例2.非线性拟合实例六、总结与展望正文:一、引言作为一款强大的数据处理软件,Origin在科学计算、数据分析领域得到了广泛的应用。
其中,数据拟合功能可以帮助我们将实验或观测得到的数据转化为具有特定数学关系的曲线。
本文将详细介绍如何使用Origin进行数据拟合,以及如何优化拟合效果。
二、Origin数据拟合原理Origin数据拟合主要包括线性拟合和非线性拟合。
1.线性拟合:线性拟合是将数据点拟合成一条直线,其主要应用于数据呈线性关系的情况。
Origin软件会自动计算线性方程的斜率和截距,从而得到拟合方程。
2.非线性拟合:非线性拟合是将数据点拟合成一条非线性曲线,如二次曲线、指数曲线等。
Origin软件支持多种非线性拟合函数,用户可以根据实际情况选择合适的函数进行拟合。
三、拟合步骤1.数据准备:首先,在Origin软件中导入需要拟合的数据。
可以通过直接输入数据、导入文本文件或Excel文件等方式完成。
2.添加拟合项:在Origin中,选择需要拟合的数据集,右键点击,选择“拟合”菜单,添加拟合项。
用户可以根据需要选择线性拟合或非线性拟合。
3.设置拟合参数:在拟合项对话框中,可以设置拟合参数,如拟合函数、初始参数等。
根据实际需求,用户可以调整拟合参数以优化拟合效果。
4.分析拟合结果:完成拟合后,Origin软件会自动生成拟合报告,包括拟合方程、拟合参数、拟合精度等信息。
用户可以根据这些信息判断拟合效果是否满足要求。
四、优化拟合效果1.选择合适的拟合函数:根据数据特点,选择合适的拟合函数。
例如,当数据呈二次关系时,应选择二次拟合函数;当数据呈指数关系时,应选择指数拟合函数。
