数电答案第六章
数字电路答案第六章

第六章可编程逻辑器件PLD可编程逻辑器件PLD是由用户借助计算机和编程设备对集成电路进行编程,使之具有预定的逻辑功能,成为用户设计的ASIC芯片。
近年来,可编程逻辑器件从芯片密度上、速度上发展相当迅速,已成为集成电路的一个重要分支。
本章要求读者了解PLD器件的工作原理,掌握用可编程逻辑器件设计数字电路的方法。
为掌握使用电子设计自动化和可编程逻辑器件设计电路系统的后续课程打下良好的基础。
第一节基本知识、重点与难点一、基本知识(一)可编程逻辑器件PLD基本结构可编程逻辑器件PLD包括只读存储器ROM、可编程只读存储器PROM、可编程逻辑阵列PLA、可编程阵列逻辑PAL、通用阵列逻辑GAL和可擦写编程逻辑器件EPLD等。
它们的组成和工作原理基本相似,其基本结构由与阵列和或阵列构成。
与阵列用来产生有关与项,或阵列把所有与项构成“与或”形式的逻辑函数。
在数字电路中,任何组合逻辑函数均可表示为与或表达式,因而用“与门-或门”两级电路可实现任何组合电路,又因为任何时序电路是由组合电路加上存储元件(触发器)构成的,因而PLD的“与或”结构对实现数字电路具有普遍意义。
(二)可编程逻辑器件分类1.按编程部位分类PLD有着大致相同的基本结构,根据与阵列和或阵列是否可编程,分为三种基本类型:(1)与阵列固定,或阵列可编程;(2)与或阵列均可编程;(3)与阵列可编程,或阵列固定。
2.按编程方式分类(1)掩膜编程;(2)熔丝与反熔丝编程;(3)紫外线擦除、电可编程;(4)电擦除、电可编程;(5)在系统编程(Isp)。
(三)高密度可编程逻辑器件HDPLD单片高密度可编程逻辑器件HDPLD(High Density Programmable Logic Device)芯片内,可以集成成千上万个等效逻辑门,因此在单片高密度可编程逻辑器件内集成数字电路系统成为可能。
HDPLD器件在结构上仍延续GAL的结构原理,因而还是电擦写、电编程的EPLD 器件。
数电课后题答案(哈工大版)课后习题答案
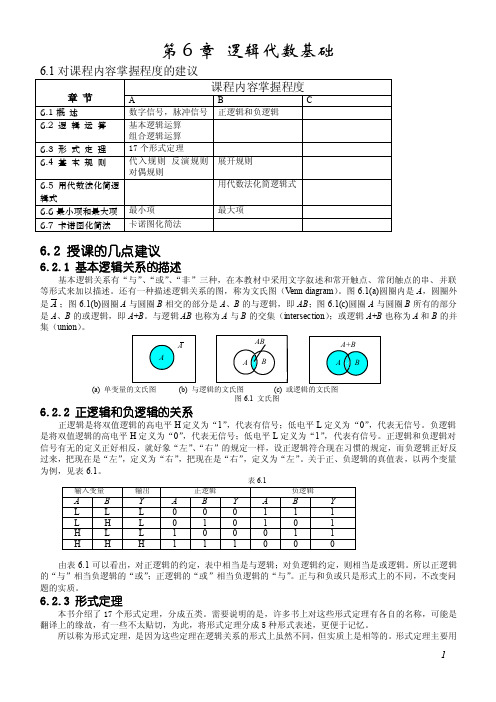
第6章 逻辑代数基础6.2 授课的几点建议6.2.1 基本逻辑关系的描述基本逻辑关系有“与”、“或”、“非”三种,在本教材中采用文字叙述和常开触点、常闭触点的串、并联等形式来加以描述。
还有一种描述逻辑关系的图,称为文氏图(V enn diagram )。
图6.1(a)圆圈内是A ,圆圈外是A ;图6.1(b)圆圈A 与圆圈B 相交的部分是A 、B 的与逻辑,即AB ;图6.1(c)圆圈A 与圆圈B 所有的部分是A 、B 的或逻辑,即A +B 。
与逻辑AB 也称为A 与B 的交集(intersection );或逻辑A +B 也称为A 和B 的并集(union )。
(a) 单变量的文氏图 (b) 与逻辑的文氏图 (c) 图6.1 文氏图6.2.2 正逻辑和负逻辑的关系正逻辑是将双值逻辑的高电平H 定义为“1”,代表有信号;低电平L 定义为“0”,代表无信号。
负逻辑是将双值逻辑的高电平H 定义为“0”,代表无信号;低电平L 定义为“1”,代表有信号。
正逻辑和负逻辑对信号有无的定义正好相反,就好象“左”、“右”的规定一样,设正逻辑符合现在习惯的规定,而负逻辑正好反过来,把现在是“左”,定义为“右”,把现在是“右”,定义为“左”。
关于正、负逻辑的真值表,以两个变量为例,见表6.1。
表6.1由表6.1可以看出,对正逻辑的约定,表中相当是与逻辑;对负逻辑约定,则相当是或逻辑。
所以正逻辑的“与”相当负逻辑的“或”;正逻辑的“或”相当负逻辑的“与”。
正与和负或只是形式上的不同,不改变问题的实质。
6.2.3 形式定理本书介绍了17个形式定理,分成五类。
需要说明的是,许多书上对这些形式定理有各自的名称,可能是翻译上的缘故,有一些不太贴切,为此,将形式定理分成5种形式表述,更便于记忆。
所以称为形式定理,是因为这些定理在逻辑关系的形式上虽然不同,但实质上是相等的。
形式定理主要用于逻辑式的化简,或者在形式上对逻辑式进行变换,它有以下五种类型:1.变量与常量之间的关系;2.变量自身之间的关系;3.与或型的逻辑关系;4.或与型的逻辑关系;5.求反的逻辑关系——摩根(Morgan )定理。
《数字电子技术基础》2版习题答案 6章习题解答
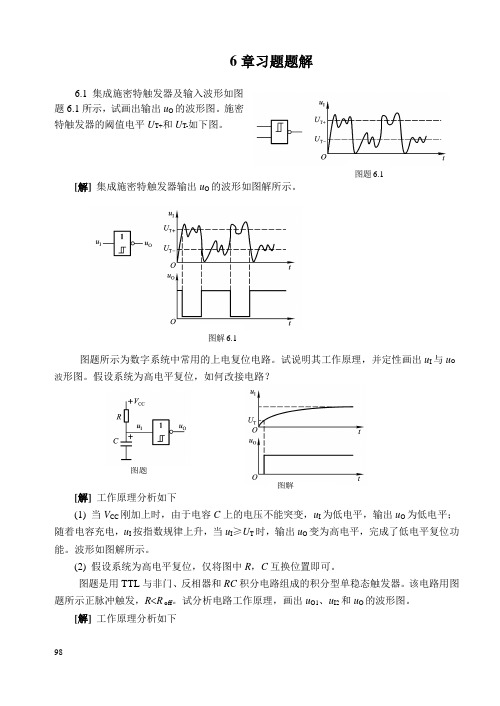
6章习题题解6.1 集成施密特触发器及输入波形如图题6.1所示,试画出输出u O的波形图。
施密特触发器的阈值电平U T+和U T-如下图。
图题6.1 [解]集成施密特触发器输出u O的波形如图解所示。
图解6.1图题所示为数字系统中常用的上电复位电路。
试说明其工作原理,并定性画出u I与u O 波形图。
假设系统为高电平复位,如何改接电路?图题图解[解] 工作原理分析如下(1) 当V CC刚加上时,由于电容C上的电压不能突变,u I为低电平,输出u O为低电平;随着电容充电,u I按指数规律上升,当u I≥U T时,输出u O变为高电平,完成了低电平复位功能。
波形如图解所示。
(2) 假设系统为高电平复位,仅将图中R,C互换位置即可。
图题是用TTL与非门、反相器和RC积分电路组成的积分型单稳态触发器。
该电路用图题所示正脉冲触发,R R off。
试分析电路工作原理,画出u O1、u I2和u O的波形图。
[解]工作原理分析如下9899触发信号未到来时,u I 为低电平,输出u O 为高电平;正触发脉冲到来时,u O1翻为低电平,此时由于u I2仍为高电平,输出u O 为高电平不变,电容通过R 放电,当u I2下降到U T 时〔u I 仍为高电平〕,输出u O 翻为高电平,暂稳态过程结束。
u O1、u I2和u O 的波形见图解。
6.4 集成单稳态触发器74121组成的延时电路如图题6.4所示,要求 (1)计算输出脉宽的调节范围; (2)电位器旁所串电阻有何作用?[解] (1) 输出脉宽:W ext ext W 0.70.7()t R C R R ==+,分别代入R W =0和22k Ω计算,可得t W的调节范围为:W 3.6mS 19mS t ≤≤。
(2) 电阻R 起保护作用。
假设无R ,当电位器调到零时,假设输出由低变高,那么电容C 瞬间相当于短路,V CC 将直接加于内部门电路输出而导致电路损坏。
6.5 集成单稳态触发器74121组成电路如图题6.5所示,要求(1)计算u O1、u O2的输出脉冲宽度;(2)假设u I 如图中所示,试画出输出u O1、u O2的波形图。
数字电路答案第六章

第六章可编程逻辑器件PLD可编程逻辑器件PLD是由用户借助计算机和编程设备对集成电路进行编程,使之具有预定的逻辑功能,成为用户设计的ASIC芯片。
近年来,可编程逻辑器件从芯片密度上、速度上发展相当迅速,已成为集成电路的一个重要分支。
本章要求读者了解PLD器件的工作原理,掌握用可编程逻辑器件设计数字电路的方法。
为掌握使用电子设计自动化和可编程逻辑器件设计电路系统的后续课程打下良好的基础。
第一节基本知识、重点与难点一、基本知识(一)可编程逻辑器件PLD基本结构可编程逻辑器件PLD包括只读存储器ROM、可编程只读存储器PROM、可编程逻辑阵列PLA、可编程阵列逻辑PAL、通用阵列逻辑GAL和可擦写编程逻辑器件EPLD等。
它们的组成和工作原理基本相似,其基本结构由与阵列和或阵列构成。
与阵列用来产生有关与项,或阵列把所有与项构成“与或”形式的逻辑函数。
在数字电路中,任何组合逻辑函数均可表示为与或表达式,因而用“与门-或门”两级电路可实现任何组合电路,又因为任何时序电路是由组合电路加上存储元件(触发器)构成的,因而PLD的“与或”结构对实现数字电路具有普遍意义。
(二)可编程逻辑器件分类1.按编程部位分类PLD有着大致相同的基本结构,根据与阵列和或阵列是否可编程,分为三种基本类型:(1)与阵列固定,或阵列可编程;(2)与或阵列均可编程;(3)与阵列可编程,或阵列固定。
2.按编程方式分类(1)掩膜编程;(2)熔丝与反熔丝编程;(3)紫外线擦除、电可编程;(4)电擦除、电可编程;(5)在系统编程(Isp)。
(三)高密度可编程逻辑器件HDPLD单片高密度可编程逻辑器件HDPLD(High Density Programmable Logic Device)芯片内,可以集成成千上万个等效逻辑门,因此在单片高密度可编程逻辑器件内集成数字电路系统成为可能。
HDPLD器件在结构上仍延续GAL的结构原理,因而还是电擦写、电编程的EPLD 器件。
数字电路答案第六章

A T V,、-、、/:第六章可编程逻辑器件PLD可编程逻辑器件PLD 是由用户借助计算机和编程设备对集成电路进行编程,使之具有预定的逻辑功能,成为用户设计的ASIC 芯片。
近年来,可编程逻辑器件从芯片密度上、速度上发展相当迅速,已成为集成电路的一个重要分支。
本章要求读者了解PLD 器件的工作原理,掌握用可编程逻辑器件设计数字电路的方法。
为掌握使用电子设计自动化和可编程逻辑器件设计电路系统的后续课程打下良好的基础。
第一节基本知识、重点与难点一、基本知识(一)可编程逻辑器件PLD 基本结构可编程逻辑器件PLD 包括只读存储器ROM 、可编程只读存储器PROM 、可编程逻辑阵列PLA、可编程阵列逻辑PAL、通用阵列逻辑GAL和可擦写编程逻辑器件EPLD等。
它们的组成和工作原理基本相似,其基本结构由与阵列和或阵列构成。
与阵列用来产生有关与项,或阵列把所有与项构成“与或”形式的逻辑函数。
在数字电路中,任何组合逻辑函数均可表示为与或表达式,因而用“与门-或门” 两级电路可实现任何组合电路,又因为任何时序电路是由组合电路加上存储元件(触发器)构成的,因而PLD 的“与或”结构对实现数字电路具有普遍意义。
(二)可编程逻辑器件分类1. 按编程部位分类PLD 有着大致相同的基本结构,根据与阵列和或阵列是否可编程,分为三种基本类型:(1)与阵列固定,或阵列可编程;(2)与或阵列均可编程;(3)与阵列可编程,或阵列固定。
2. 按编程方式分类(1)掩膜编程;(2)熔丝与反熔丝编程;(3)紫外线擦除、电可编程;(4)电擦除、电可编程;(5)在系统编程(Isp)。
(三)高密度可编程逻辑器件HDPLD单片高密度可编程逻辑器件HDPLD(High Density Programmable Logic Device )芯片内,可以集成成千上万个等效逻辑门,因此在单片高密度可编程逻辑器件内集成数字电路系统成为可能。
HDPLD 器件在结构上仍延续GAL 的结构原理,因而还是电擦写、电编程的EPLD 器件。
《数电》教材习题答案 第6章习题答案
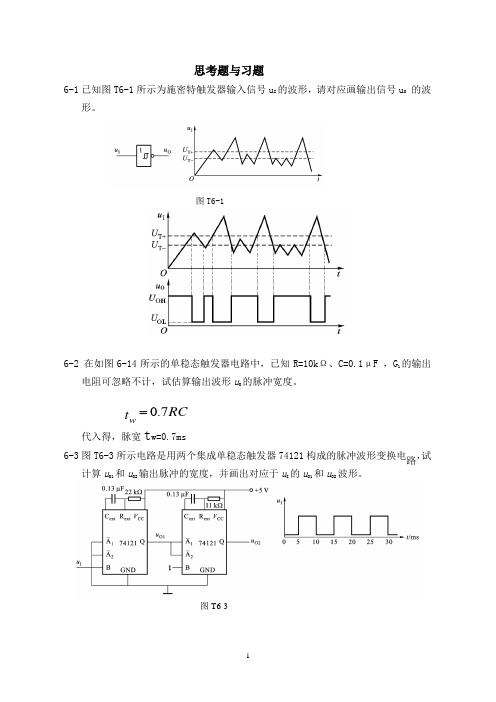
思考题与习题6-1已知图T6-1所示为施密特触发器输入信号u I 的波形,请对应画输出信号u O 的波形。
图T6-16-2 在如图6-14所示的单稳态触发器电路中,已知R=10k Ω、C=0.1μF ,G 1的输出 电阻可忽略不计,试估算输出波形u O 的脉冲宽度。
代入得,脉宽t w=0.7ms6-3图T6-3所示电路是用两个集成单稳态触发器74121构成的脉冲波形变换电路,试计算u O1和u O2输出脉冲的宽度,并画出对应于u I 的u O1和u O2波形。
图T6-3RCt w 7.06-4图T6-4所示电路为可控多谐振荡器,已知tW等于振荡器输出脉冲周期的5倍,请对应u k画u O1和u O2的波形。
图T6-46-5试构成一个如图6-23所示的RC环形振荡器电路,要求振荡器输出信号的频率为1kHZ ,请估算R和C的数值。
若要求振荡频率为1HZ,则R和C又该为多少?解:T≈2.2RC,f=1KHZ,则T=1ms,因此,当f=1KHZ时,RC=0.45ms;当f=1HZ 时,RC=0.45s。
6-6试用555定时器构成一个单稳态电路,要求输出脉冲幅度≥10V,输出脉冲宽度在1-10秒范围内连续可调。
解:根据题意,用555定时器设计得单稳态触发器取R1=22K,R2=18K,分压后输入端电压为6.75V(电源电压为15V),一般的,555定时器得输出高电平不低于其电源电压得90%,因此选15v.则UO输出脉宽t W=1.1RC设C=1000μF,则1≤1.1R×1000×10-6≤ 10 909≤R ≤9K6-7图T6-7是用两个555定时器接成的延迟报警器。
当开关S 断开后,经过一定的延 迟时间后扬声器开始发出声音。
如果在延迟时间内S 重新闭合,扬声器不会发出 声音。
在图中给定的参数下,试求延迟时间的具体数值和扬声器发出声音的频率。
图中的G 1是CMOS 反相器,电源电压为12V 。
数字电路第6章习题答案
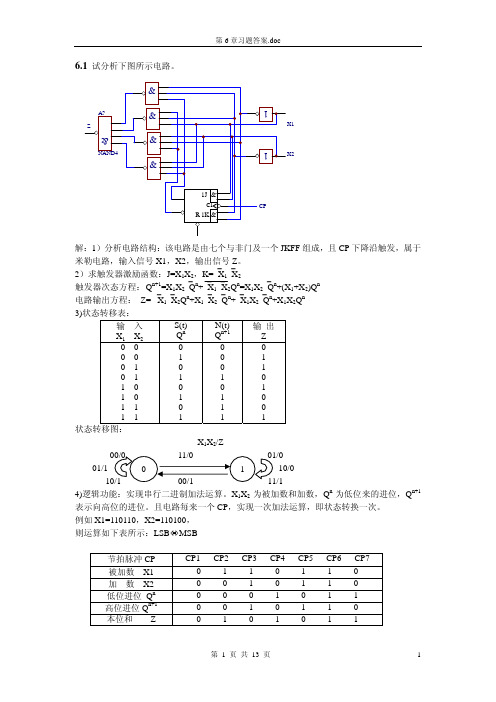
6.2 试作出101序列检测器得状态图,该同步电路由一根输入线X ,一根输出线Z ,对应与输入序列的101的最后一个“1”,输出Z=1。
其余情况下输出为“0”。
(1) 101序列可以重叠,例如:X :010101101 Z :000101001 (2) 101序列不可以重叠,如:X :010******* Z :0001000010 解:1)S 0:起始状态,或收到101序列后重新开始检测。
S 1:收到序列起始位“1”。
S 2:收到序列前2位“10”。
10101…X/Z0/01/0X/Z11…100…2)10101…X/Z0/0X/Z11…100…6.3对下列原始状态表进行化简:(a)解:1)列隐含表:A B CDC B ×A B CD C B ×AD BC ××(a)(b)2)进行关联比较 所有的等价类为:AD ,BC 。
最大等价类为:AD ,BC ,重新命名为a,b 。
3)列最小化状态表为:a/1b/0bb/0a/0aX=1X=0N(t)/Z(t)S(t)(b)N (t )/Z (t )S (t )X=0 X=1A B/0 H/0B E/0 C/1C D/0 F/0D G/0 A/1E A/0 H/0F E/1 B/1G C/0 F/0H G/1 D/1解:1)画隐含表:2)进行关联比较:AC,BD,EG ,HF,之间互为等价隐含条件,所以分别等价。
重新命名为: a, b, e, h 3)列最小化状态表:N (t )/Z (t ) S (t )X=0 X=1a b/0 h/0b e/0 a/1 e a/0 h/0 h e/1 b/1试分析题图6.6电路,画出状态转移图并说明有无自启动性。
解:激励方程:J1=K1=1;J2=Q1n⎯Q3n,K2=Q1nJ2=Q1n Q2n,K2=Q1n状态方程:Q1n+1=⎯Q1n·CP↓Q2n+1=[Q1n⎯Q3n⎯Q2n+⎯Q1n Q2n]·CP↓Q3n+1=[Q1n Q2n⎯Q3n+⎯Q1n Q3n]·CP↓状态转移表:序号Q3Q2Q10 1 2 3 4 5 000 001 010 011 100 101偏离状态110Æ111111Æ000状态转移图状态转移图:Q3Q2Q1偏离态能够进入有效循环,因此该电路具有自启动性。
数电第五版(阎石)第六章课后习题及答案
2 1 0 2 1 0 1 0 2 1 0 ' ' ' ' 2 1 0 1 0 1 0 1 0 ' ' ' ' ' 2 1 0 2 1 0 1 0 2 1 0
) Q (Q
) 0 (Q
电路图如下图所示:
【题6-34】设计一个控制步进电机三相六状态工作的逻辑电 路。如果用1表示电机绕组导通,0表示电机绕组截止,则三 个绕组ABC的状态转换图应如下图所示。M为输入的控制变 量,当M=1时 为正转,M为0时为反转。
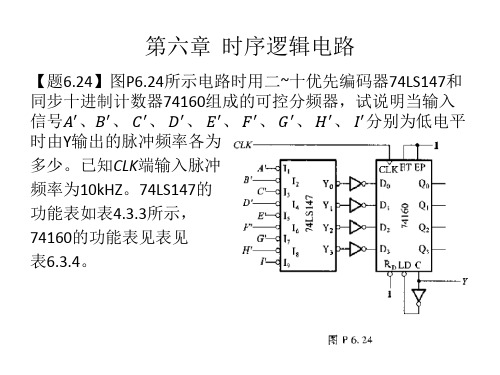
第六章 时序逻辑电路
解:74160的状态转换图如A6.24所示;当A=0时74LS147的输 ' ' ' ' 出为Y 3 Y 2 Y 1 Y 0 1110 ,74160的数据输入端 D 3 D 2 D 1 D 0 0001 则状态转换顺序将如图所示,即成为九进制计数器。输出的 脉冲Y的频率为CLK频率的1/9。以此类推可得:
低电平 输入端 1/9 1/8 1.11 1.25
1/7 1/6
1/5 1/4 1/3 1/2 0
1.43 1.67
2 2.5 3.33 5 0
【6.29】设计一个序列信号 发生器电路,使之在一系列 CLK信号作用下能周期性地 输出“0010110111”的序列 信号。 解:方案:十进制计数器 和8选1数据选择器 十进制计数器选用74160, 则计数器状态 Q 3 Q 2 Q 1 Q 0 与输出Z之间的关系真值 表如右图所示。
MQ MQ MQ
*
' 2 ' 3 ' 1
பைடு நூலகம்
M Q M Q M Q
' '
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
Q
j0
i 1
j
CLK
U
D
CLK
2
CLK
U
Q 1Q 0 CLK
D
Q 1Q 0
《数字电子技术基础》第五版
2. 同步十进制计数 器
①加法计数器 基本原理:在四位 二进制计数器基础 上修改,当计到 1001时,则下一个 CLK电路状态回到 0000。
T 3 Q 2 Q 1Q 0 Q 2 Q 1Q 0 Q 3 Q 0
0
1 0 0 3 2 1
2
1
0
1
0
1
2
3
T 3 Q 2 Q 1Q 0
《数字电子技术基础》第五版
能自启动
《数字电子技术基础》第五版
③十进制可逆计数器 基本原理一致,电路只用到0000~1001的十个状态 实例器件 单时钟:74190,168 双时钟:74192
《数字电子技术基础》第五版
二. 异步计数器
3 . 输出方程 Y Q 2Q 3
Q * J Q K Q ,得状态方程:
《数字电子技术基础》第五版 6.2.2 时序电路的状态转换表、状态转换图、状态 机流程图和时序图
一、状态转换表
Q3 Q2 Q1 Q3
*
Q2
*
Q1
*
Y
CLK
Q3
Q2
Q1
Y
0 0 0 0 0 1 0 0 1 0 1 1 1
《数字电子技术基础》第五版
1. 功能上:任一时刻的输出不仅取决于该时刻的输入,还 与电路原来的状态有关。 例:串行加法器,两个多位数从低位到高位逐位相加
2. 电路结构上 ①包含存储电路和组合电路
②存储器状态和输入变量共同决定输出
《数字电子技术基础》第五版
二、时序电路的一般结构形式与功能描述方法
《数字电子技术基础》第五版
( 3 ) 输出方程: Y [( A Q 1 Q 2 ) ( A Q 1Q 2 ) ] A Q 1 Q 2 A Q 1Q 2
《数字电子技术基础》第五版
(4)列状态转换表:
Q 2 * Q1 * Y
Q 2 Q1
A
00 01/0 11/1
01 10/0
10 11/0
③同步加减计数器
加/减 两种解决方案
加/减 计数器
计数结果
加/减 计数器
计数结果
《数字电子技术基础》第五版
a.单时钟方式 加/减脉冲用同一输入端, 由加/减控制线的高低电平决定加/减 器件实例:74LS191(用T触发器)
i 1 i 1 T i ( U ) Q j ( U ) Q j D D j0 j0 T0 1
状态方程 Q * H ( Z , Q )
《数字电子技术基础》第五版
三、时序电路的分类
1. 同步时序电路与异步时序电路 同步:存储电路中所有触发器的时钟使用统一的clk,状态变 化发生在同一时刻 异步:没有统一的clk,触发器状态的变化有先有后 2. Mealy型和Moore型 Mealy型: Y F ( X , Q ) Moore型:Y F ( Q )
可以用三个方程组来描述:
y1 f 1 ( x 1 , x 2 , , x i , q1 , q 2 , , q l ) y f ( x , x , , x , q , q , , q ) 1 1 2 i 1 2 l j 输出方程 Y F ( X , Q )
Q 1 * ( Q 2 Q 3 ) Q 1 Q 2 * Q 1 Q 2 Q 1Q 3 Q 2 Q * Q Q Q Q Q 1 2 3 2 3 3
Y Q 2Q 3
1
0 0 0 0
《数字电子技术基础》第五版
二、状态转换图
《数字电子技术基础》第五版
《数字电子技术基础》第五版
2、异步十进制加法计数器 原理: 在4位二进制异步加法计数器 上修改而成,
要跳过 1010 ~ 1111这六个状态
1 2 3 4 5 6 7 8 9 10
J=K=1 J=1 J=0
J=0
J=1
J=0
《数字电子技术基础》第五版
器件实例:二-五-十进制异步计数器74LS290
6.3.1 寄存器和移位寄存器 一、寄存器 ①用于寄存一组二值代码,N位寄存器由N个触发器组成, 可存放一组N位二值代码。 ②只要求其中每个触发器可置1,置0。 例1:
74 LS 75 clk 高电平期间 Q 随 D 改变
《数字电子技术基础》第五版
例:用维-阻触发器结构的74HC175
74 HC 175 CLK 时,将 D 0 ~ D 3 存入,与此前后的 有异步置 0 功能。 D 状态无关,
《数字电子技术基础》第五版
三、任意进制计数器的构成方法
用已有的N进制芯片,组成M进制计数器,是常用 的方法。
N进制
M进制
N M N M
《数字电子技术基础》第五版
1. N > M 原理:计数循环过程中设法跳过N-M个状态。 具体方法:置零法 置数法
异步置零法 同步置零法
异步预置数法 同步预置数法
CLK
I
S
LD
U D
工作状态 保持 预置数(异步) 加计数 减计数
X X
1 X 0 0
1 0 1 1
X X 0 1
b.双时钟方式 器件实例:74LS193(采用T’触发器,即T=1)
《数字电子技术基础》第五版
CLK
i
CLK CLK
0
U
Q
j0
i 1
j
CLK CLK
与 X 、 Q 有关 仅取决于电路状态
6.2 时序电路的分析方法
《数字电子技术基础》第五版
6.2.1 同步时序电路的分析方法 分析:找出给定时序电路的逻辑功能 即找出在输入和CLK作用下,电路的次态和输出。 一般步骤: ①从给定电路写出存储电路中每个触发器的驱动方程 (输入的逻辑式),得到整个电路的驱动方程。 ②将驱动方程代入触发器的特性方程,得到状态方程。 ③从给定电路写出输出方程。
②同步二进制减法计数器 原理:根据二进制减法运算 规则可知:在多位二进 制数末位减1,若第i位以 下皆为0时,则第i位应翻 转。 由此得出规律,若用T触发 器构成计数器,则第i位 触发器输入端Ti的逻辑 式应为:
T i Q i 1 Q i 2 ... Q 0 T0 1
《数字电子技术基础》第五版
T0 1
ቤተ መጻሕፍቲ ባይዱ
T1 Q 0 Q 0 Q 3
T 2 Q 1Q 2
《数字电子技术基础》第五版
能自启动
《数字电子技术基础》第五版
器件实例:74 160
CLK
R D
LD
EP
ET
工作状态 置 0(异步) 预置数(同步) 保持(包括C) 保持(C=0) 计数
X X X
0 1 1 1 1
X 0 1 1 1
《数字电子技术基础》第五版
一、同步计数器 1. 同步二进制计数器 ①同步二进制加法计数器 原理:根据二进制加法运算 规则可知:在多位二进 制数末位加1,若第i位以 下皆为1时,则第i位应翻 转。 由此得出规律,若用T触发 器构成计数器,则第i位 触发器输入端Ti的逻辑 式应为: i Q i 1 Q i 2 ... Q 0 T
R’D S1 S0 工作状态
0
1 1 1 1
X
0 0 1 1
X
0 1 0 1
置零
保持 右移 左移 并行输入
《数字电子技术基础》第五版
扩展应用(4位
8位)
《数字电子技术基础》第五版
6.3.2 计数器
• • 用于计数、分频、定时、产生节拍脉冲等 分类:按时钟分,同步、异步 按计数过程中数字增减分,加、减和可逆 按计数器中的数字编码分,二进制、二-十进制和 循环码… 按计数容量分,十进制,六十进制…
三、状态机流程图(State Machine Chart)
《数字电子技术基础》第五版
四、时序图
《数字电子技术基础》第五版
例:
D 1 Q 1 (1 ) 驱动方程: D 2 A Q1 Q 2
Q1 * D1 ( 2 ) 状态方程: Q 2 * A Q1 Q 2
z1 g 1 ( x 1 , x 2 , , x i , q1 , q 2 , , q l ) z g ( x , x , , x , q , q , , q ) 1 1 2 i 1 2 l k
驱动方程 Y F ( X , Q )
q 1 * h1 ( z 1 , z 2 , , z i , q 1 , q 2 , , q l ) q h ( z , z , , z , q , q , , q ) l 1 2 i 1 2 l l
11 00/1 10/0
0 1
00/0 01/0
(5)状态转换图
《数字电子技术基础》第五版
*6.2.3 异步时序逻辑电路的分析方法
各触发器的时钟不同时发生 例:
Q 2 * Q 2 clk 2
TTL电路
Q 1 * Q 3 Q 1 clk 1
《数字电子技术基础》第五版
6.3 若干常用的时序逻辑电路
《数字电子技术基础》第五版
例:
TTL电路
1 .写驱动方程: K1 1 J 1 ( Q 2 Q 3 ), K 2 ( Q 1Q 3 ) J 2 Q1 , J Q Q , K 3 Q2 1 2 3
2 . 代入 JK 触发器的特性方程( Q 1 * ( Q 2 Q 3 ) Q 1 Q 2 * Q 1Q 2 Q 1Q 3 Q 2 Q * Q Q Q Q Q 1 2 3 2 3 3
