高中数学 正弦函数的性质导学案(扫描版)北师大版必修4
高中数学第一章三角函数5.2正弦函数的性质学案北师大版必修4(2021年整理)

2018-2019学年高中数学第一章三角函数5.2 正弦函数的性质学案北师大版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年高中数学第一章三角函数5.2 正弦函数的性质学案北师大版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年高中数学第一章三角函数5.2 正弦函数的性质学案北师大版必修4的全部内容。
5.2 正弦函数的性质学习目标1。
理解、掌握正弦函数的性质。
2。
会求简单函数的定义域、值域.3.能利用单调性比较三角函数值的大小.知识点正弦函数的性质思考1 对于x∈R,sin(-x)=-sin x,这说明正弦函数具有怎样的性质?答案奇偶性。
思考2 正弦函数取得最大值、最小值时x的值是什么?答案对于正弦函数y=sin x,x∈R有:当且仅当x=π2+2kπ,k∈Z时,取得最大值1;当且仅当x=-π2+2kπ,k∈Z时,取得最小值-1.思考3 正弦函数的单调区间是什么?答案y=sin x的递增区间为错误!,k∈Z,递减区间为错误!,k∈Z.梳理函数正弦函数y=sin x,x∈R图像定义域R值域[-1,1]最值当x=错误!+2kπ(k∈Z)时,ymax=1;当x=-π2+2kπ(k∈Z)时,y min=-1周期性是周期函数,周期为2kπ(k∈Z,k≠0),2π是它的最小正周期奇偶性奇函数,图像关于原点对称单调性在区间错误!(k∈Z)上是增加的;在区间错误!(k∈Z)上是减少的对称轴x=错误!+kπ,k∈Z对称中心(kπ,0),k∈Z1.正弦函数在定义域上是单调函数.( ×)提示正弦函数不是定义域上的单调函数.2.已知y=k sin x+1,x∈R,则y的最大值为k+1。
【北师大版】2018-2019学年高中必修4数学:全一册学案第一章三角函数5.2正弦函数的性质

课堂达标 π x+ 6 的一个递减区间是( 1.函数 f(x)=sin π π - , 2 2 A. 2 2 - π, π 3 C. 3 解析 解得 答案 由 π π 3 ≤x+ ≤ π, 2 6 2 )
B.[-π,0] π 2 , π D. 2 3
π 4 ≤x≤ π.故选 D. 3 3 D ) B.y=sin(-|x|) D.y=xsin |x|
题型一 【例 1】
与正弦函数有关的值域问题 求下列函数的值域:
π π (1)y=sin(2x- ),x∈[0, ]; 3 2 (2)y=-2sin x+5sin x-2.
2
解
(1)∵0≤x≤
π π π 2π π π ,∴0≤2x≤π,- ≤2x- ≤ ,令 2x- =t,则原式转化为 y=sin t,t∈[- , 2 3 3 3 3 3
(1)f(x)=xsin x; (2)f(x)=|sin x|+1. 解 (1)∵x∈R,且关于原点对称,
又 f(-x)=-xsin(-x)=xsin x=f(x), ∴f(x)为偶函数. (2)∵x∈R,且关于原点对称,又 f(-x)=|sin(-x)|+1=f(x), ∴f(x)为偶函数.
方向 1
5.求函数 y=3-2sin 解 ∵-1≤sin
1 x≤1, 2
∴当 sin
1 1 π x=-1, x=2kπ- ,k∈Z, 2 2 2
即 x=4kπ-π,k∈Z,ymax=5, 此时自变量 x 的集合为{x|x=4kπ-π,k∈Z};
当 sin
1 1 π x=1, x=2kπ+ ,k∈Z, 2 2 2
所以 sin
54 56 2 - π - π+ π 7 7 7 (2)sin =sin 2 -8π+ π 2 7 =sin π, =sin 7 sin - 63 π π -8π+ π 8 8 =sin =sin , 8
正切函数的定义图像及性质(北师版必修4) 导学案
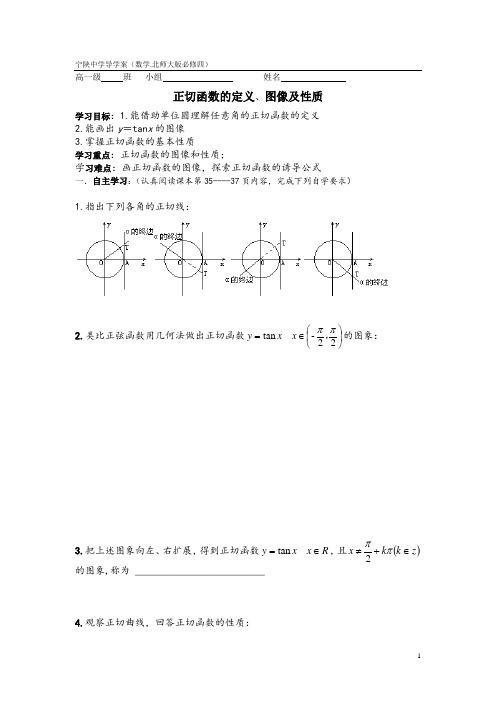
宁陕中学导学案(数学.北师大版必修四)高一级 班 小组 姓名正切函数的定义、图像及性质学习目标:1.能借助单位圆理解任意角的正切函数的定义2.能画出y =tan x 的图像3.掌握正切函数的基本性质学习重点:正切函数的图像和性质;学习难点:画正切函数的图像,探索正切函数的诱导公式一.自主学习:(认真阅读课本第35----37页内容,完成下列自学要求)1.指出下列各角的正切线:2.类比正弦函数用几何法做出正切函数⎪⎭⎫⎝⎛∈=22-tan ππ,x x y 的图象:3.把上述图象向左、右扩展,得到正切函数Rx x y ∈=tan ,且()z k k x ∈+≠ππ2的图象,称为 __________________________4.观察正切曲线,回答正切函数的性质:同学们,通过你的自主学习,你还有哪些疑惑,请把它填在下面的表格中:二.合作探究:例1.画出函数⎪⎭⎫⎝⎛+=4tan πx y 的图像并讨论其性质变式.求函数y =tan2x 的定义域、值域和周期.例2. 2tan ,3αα=若借助三角函数定义求角的正弦函数值和余弦函数值例3. tan 135tan 138︒︒比较与的大小三、反思总结:1、数学知识:2、数学思想方法:四.训练检测1. 1317tan()tan()45ππ--比较与的大小2. 函数)4tan(x y -=π的定义域为 ( )(A)},4|{R x x x ∈≠π(B)},4|{R x x x ∈-≠π(C) },,4|{Z k R x k x x ∈∈+≠ππ (D)},,43|{Z k R x k x x ∈∈+≠ππ3.下列函数中,同时满足(1)在(0, 2π)上递增, (2)以2π为周期, (3)是奇函数的是 ( )(A)x y tan = (B)x y cos = (C)xy 21tan = (D)x y tan -=4. 若tan 0x ≤,则( ).A .22,2k x k k Zπππ-<<∈ B .2(21),2k x k k Zπππ+≤<+∈C .,2k x k k Zπππ-<≤∈ D .,2k x k k Zπππ-≤≤∈5.tan 315tan 570tan(60)tan 675︒+︒-︒-︒求的值.(能力提升)6. 求出函数y =.7. 求函数y=lg(1-tanx)的定义域8.已知0cos 〉x ,且0tan 〈x ,求 (1)角x 的集合; (2)判断2x tan ,2cos x ,的符号.。
高中数学北师大版必修4第1章5《正弦函数的性质》word导学案

陕西省榆林育才中学高中数学第1章《三角函数》5正弦函数的性质导学案北师大版必修4【学习目标】1.会利用正弦函数的图像进一步研究和理解正弦函数的性质.2.能够灵活的应用正弦函数的性质解决相关问题.3.经历用正弦函数的图像研究正弦函数性质的过程,体会数形结合的思想.【重点难点】重点:正弦函数的性质及其应用.难点:应用正弦函数的性质解决相关问题.【使用说明】通过观察正弦函数的图像,总结正弦函数的性质,然后对照课本加以完善,最后通过小组讨论、合作探究进一步加深对正弦函数性质的理解.【自主学习】【合作探究】1. 利用五点法画出函数x y sin 1+=的简图,并根据图像讨论它的性质.2. 求下列函数的定义域:(1)1sin 1-=x y ; (2)1sin 2+=x y .3. 正弦函数的图像有对称轴吗?有对称中心吗?如果有,请写出对称轴方程 及对称中心的坐标;如果没有,请说明理由.【课堂检测】1. 函数x y sin 3=,当],[ππ-∈x 时,在区间_______________上是增加的,在区 间 ____________上是减少的;当=x ________时,y 取最大值______;当=x ______时,y 取最小值______.2. 与右图中曲线对应的函数是( )A. |sin |x y =B. ||sin x y =C. ||sin x y -=D. |sin |x y -=3. 求函数x y sin 21-=的单调增区间,并判断其奇偶性.【课堂小结】【课后训练】2. 函数x y sin 2-=的定义域为_______________.3. 讨论函数x y sin 211-=的性质.(定义域、值域、周期性、单调性和奇偶性)。
北师大版高中数学必修四教学案正弦函数图象与性质
年质1
授课时间
撰写人
时间
学习重点
“五点法”画y=sinx, x∈[0,2π]上的图象
学习难点
利用正弦线画出函数y=sinx, x∈[0,2π]的图像。
学习目标
①会用单位圆中的正弦线画出正弦函数图象;
②掌握正弦函数图象的“五点作图法”;
③掌握与正弦函数有关的简单图象平移变换和对称变换;
教学过程
一自主学习
1.什么叫正弦线?
2.画出函数y=sinx, x∈[0,2π]上的图象呢
3.五点作图法
二师生互动
例1用五点法画出下列函数在区间 上的简图。
(1)
(2)
三巩固练习
1用五点法画出下列函数在区间 上的简图:
⑴ ⑵ ⑶
四课后反思
五课后巩固练习
1.利用函数图像或单位圆求出满足条件 的集合
2.求函数 零点的个数
高中数学 第一章 三角函数 1.5 正弦函数的图像与性质学案 北师大版必修4(2021年整理)

高中数学第一章三角函数1.5 正弦函数的图像与性质学案北师大版必修4 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第一章三角函数1.5 正弦函数的图像与性质学案北师大版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第一章三角函数1.5 正弦函数的图像与性质学案北师大版必修4的全部内容。
1.5 正弦函数的图像与性质知识梳理1。
任意角的正弦函数(1)单位圆:圆心在原点O,半径等于1的圆称为单位圆.(2)定义如图1-4—1所示,单位圆与角α的终边交于P点.设P(a,b),则P点纵坐标b是角α的函数,称为正弦函数,记为b=sinα(α∈R)。
通常用x、y表示自变量和因变量,将正弦函数表示为y=sinx(x∈R).图1—4-1(3)正弦线如图1—4-1所示,过点P作x轴的垂线PM,垂足为M.单位圆中的有向线段MP叫做角α的正弦线。
当角α的终边在x轴上时,M与P重合,此时正弦线变成一个点.(4)正弦线所表示的正弦值可如下确定:正弦线的方向是表示正弦值的符号,同y轴一致,向上为正,向下为负;正弦线的长度是正弦值的绝对值.(5)正弦函数定义的推广如图1—4—2所示,设P(x,y)是α的终边上任意一点,图1-4—2P 到原点的距离|OP|=r ,有r=22y x ,则sinα=ry 。
对于每一个确定的角α,总有唯一确定的正弦值与之对应,所以这个对应法则是以角α为自变量的函数,叫做正弦函数。
正弦函数值与点P 在角α终边上的位置无关,只依赖于角α的大小。
2.周期函数一般地,对于函数y=f (x),如果存在一个不为零的常数T ,使得当x 取定义域内的每一个值时,f (x+T)=f(x)都成立,那么就把函数y=f(x)叫做周期函数,不为零的常数T 叫做这个函数的周期.对于周期函数来说,如果所有的周期中存在着一个最小的正数,就称它为最小正周期,今后提到的三角函数的周期,如没特别指明,一般都是指它的最小正周期.3.任意角的正弦值的符号(1)图形表示:各象限正弦函数符号,如图1—4—3所示.图1-4-3(2)表格表示.α的终边sinα x 非负半轴0 第一象限+y非负半轴+第二象限+x非正半轴0第三象限—y非正半轴-第四象限—4.正弦函数的图像和性质(1)图像:如图1-4-4所示.图1—4—4(2)性质.函数性质y=sinx 定义域R值域[-1,1]当x=2kπ+2π(k∈Z)时,y取最大值1;当x=2kπ-2π(k∈Z)时,y取最小值-1周期2π奇偶性奇函数单调性增区间[—2π+2kπ,2π+2kπ](k∈Z)减区间[—2π+2kπ,23π+2kπ](k∈Z)5。
高中数学 第一章 三角函数 1.5 正弦函数课堂导学案 北

1.5 正弦函数课堂导学三点剖析1.正弦函数的定义及诱导公式【例1】 sin (-2 010°)的值是( ) A.-21 B.23 C.21D.23-解析:∵-2 010°=-6×360°+150°,∴-2 010°的终边与150°角的终边相同.∴sin(-2 010°)=sin150°=sin(180°-30°) =sin30°=21. 答案:C 友情提示求解任意角的三角函数值时,应先将该任意角化负为正,化大为小(在0°—360°内),再利用诱导公式求值. 各个击破 类题演练 1求下列各式的符号:(1)sin(4π-);(2)sin 311π. 解:(1)∵4π-是第四象限角,∴sin(4π-)<0.(2)∵sin(311π)=sin(2π+35π),而35π是第四象限角,∴sin 311π<0变式提升 1已知x∈[0,6π],且sinx=2m+1,则m 的取值范围是_____________. 解析:由于0≤x≤6π,且y=sinx 在[0,6π]上为增函数,∴sin0≤sinx≤sin 6π,即0≤sinx≤21.∴0≤2m+1≤21,从而-21≤m≤-41.答案:[-21,-41]2.正弦函数性质的综合应用【例2】 判断函数f(x)=lg(sinx+x 2sin 1+)的奇偶性.思路分析:判断函数的奇偶性,主要依据定义,要注意一下两个要点:(1)定义域是否关于原点对称;(2)是否满足f(-x)=-f(x)或f(-x)=f(x).解:显然f(x)的定义域为R .f(-x)=lg [sin(-x)+)(sin 12x -+] =lg(-sinx+x 2sin 1+) =lg(xx 2sin 1sin 1++)=-lg(sinx+x 2sin 1+)=-f(x),∴f(x)为奇函数. 友情提示有些同学容易被函数解析式的复杂性所迷惑,当函数的式子较复杂时,我们可以用变形f(-x)+f(x)=0,则f(x)为奇函数;f(-x)-f(x)=0,则f(x)为偶函数. 类题演练 2求函数y=1sin 2+x 的定义域.解析:由题意知,需2sinx+1≥0,也即需sinx≥21-,① 在一周期[-2π,23π]上符合①的角为[67,6ππ-],由此可得函数定义域为 [2k π-6π,2k π+67π](k∈Z ). 变式提升 2(2005上海高考) 函数f(x)=sinx+2|sinx|,x∈[0,2π]的图象与直线y=k 有且仅有两个不同的交点,则k 的取值范围是_______.解析:f(x)=⎩⎨⎧∈-∈-]2,(,sin ],,0[,sin 3πππx x x x由图象知1<k <3.答案:1<k <3 3.正弦函数的图象【例3】 作出函数y=-sinx(0≤x≤2π)的图象.解析:利用“五点法”作图,关键是找出五个关键点,所以,最好利用列表整理数据,使问题既清晰又准确.(2)描点作图友情提示由于正弦曲线直观地表现了正弦函数的各种性态,因此要熟悉图象,理解几何法作图,掌握五点法作图.“五点”即y=sinx 的图象在一个最小正周期内的最高点、最低点和与x 轴的交点.一般地,观察y=sinx 的一个周期,常常是[0,2π]或[-2π,23π].类题演练 3用“五点法”画函数y=-1+sinx,x∈[0,2π]的简图.变式提升 3对于函数y=|sinx|,作出它的图象,写出它的定义域、值域、单调递增区间,并判断其奇偶性、周期性.解析:y=|sinx|的图象为: y=|sinx|的定义域是R ,值域为[0,1],单调递增区间:[k π,k π+2π],k∈Z ,它是偶函数,其周期为π.。
高中数学 第一章 三角函数 4.3 单位圆与正弦函数、余弦函数的基本性质学案 北师大版必修4

4.3 单位圆与正弦函数、余弦函数的基本性质学习目标 1.会利用单位圆研究正弦、余弦函数的基本性质.2.能利用正弦、余弦函数的基本性质解决相关的问题.知识点 正弦、余弦函数的性质思考1 正弦函数、余弦函数的最大值、最小值分别是多少?答案 设任意角x 的终边与单位圆交于点P (cos x ,sin x ),当自变量x 变化时,点P 的横坐标是cos x ,|cos x |≤1,纵坐标是sin x ,|sin x |≤1,所以正弦函数、余弦函数的最大值为1,最小值为-1.思考2 能否认为正弦函数在单位圆的右半圆是增加的?答案 不能,右半圆可以表示无数个区间,只能说正弦函数在每一个区间⎣⎢⎡⎦⎥⎤2k π-π2,2k π+π2(k ∈Z )上是增加的. 梳理 正弦、余弦函数的性质1.正弦函数在定义域上是单调函数.( × )提示 正弦函数不是定义域上的单调函数. 2.正弦函数在第一象限是增函数.( × )提示 正弦函数在第一象限不是增函数,因为在第一象限,如-5π3<π6,但sin ⎝ ⎛⎭⎪⎫-5π3=sin π3=32,sin π6=12,sin ⎝ ⎛⎭⎪⎫-5π3>sin π6.3.存在实数x ,使得cos x = 2.( × ) 提示 余弦函数最大值为1.4.余弦函数y =cos x 在区间[0,π]上是减函数.( √ ) 提示 由余弦函数的单调性可知正确.类型一 正弦、余弦函数的定义域 例1 求下列函数的定义域. (1)y =2sin x -3; (2)y =lg ⎝ ⎛⎭⎪⎫sin x -22+1-2cos x . 考点 正弦函数、余弦函数的定义域 题点 正弦函数、余弦函数的定义域 解 (1)自变量x 应满足2sin x -3≥0, 即sin x ≥32. 图中阴影部分就是满足条件的角x 的范围,即⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π+π3≤x ≤2k π+2π3,k ∈Z .(2)由题意知,自变量x 应满足不等式组⎩⎪⎨⎪⎧1-2cos x ≥0,sin x -22>0,即⎩⎪⎨⎪⎧cos x ≤12,sin x >22.则不等式组的解的集合如图(阴影部分)所示,∴⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π+π3≤x <2k π+3π4,k ∈Z. 反思与感悟 (1)求函数的定义域,就是求使解析式有意义的自变量的取值范围,一般通过解不等式或不等式组求得,对于三角函数的定义域问题,还要考虑三角函数自身定义域的限制. (2)要特别注意求一个固定集合与一个含有无限多段的集合的交集时,可以取特殊值把不固定的集合写成若干个固定集合再求交集.跟踪训练1 函数y =2sin x +1的定义域为 . 考点 正弦函数、余弦函数的定义域 题点 正弦函数、余弦函数的定义域 答案 ⎣⎢⎡⎦⎥⎤-π6+2k π,7π6+2k π,k ∈Z解析 要使2sin x +1有意义, 则必须满足2sin x +1≥0,即sin x ≥-12,结合单位圆,知x 的取值范围是⎣⎢⎡⎦⎥⎤-π6+2k π,7π6+2k π,k ∈Z . 类型二 正弦、余弦函数的值域与最值例2 (1)求函数y =cos x ⎝ ⎛⎭⎪⎫-π3≤x ≤5π6的值域.题点 正、余弦函数的值域解 ∵y =cos x 在区间⎣⎢⎡⎦⎥⎤-π3,0上是增加的, 在区间⎣⎢⎡⎦⎥⎤0,5π6上是减少的,∴当x =0时,y max =1,当x =5π6时,y min =cos 5π6=-32,∴y =cos x ⎝ ⎛⎭⎪⎫-π3≤x ≤5π6的值域是⎣⎢⎡⎦⎥⎤-32,1.(2)已知函数y =a sin x +1的最大值为3,求它的最小值. 考点 正、余弦函数的最值 题点 含参正、余弦函数的最值解 当a >0时,y max =a ×1+1=3,得a =2, ∴当sin x =-1时,y min =2×(-1)+1=-1; 当a <0时,y max =a ×(-1)+1=3,得a =-2, ∴当sin x =1时,y min =-2×1+1=-1. ∴它的最小值为-1.反思与感悟 (1)求正、余弦函数的值域或最值时应注意定义域,解题时可借助图像结合正、余弦函数的单调性进行分析.(2)对于含有参数的值域或最值,应注意对参数分类讨论.跟踪训练2 函数y =2+cos x ,x ∈⎝ ⎛⎦⎥⎤-π3,2π3的值域为 .考点 正、余弦函数的值域 题点 正、余弦函数的值域答案 ⎣⎢⎡⎦⎥⎤32,3解析 由单位圆,可知当x ∈⎝⎛⎦⎥⎤-π3,2π3时,cos x ∈⎣⎢⎡⎦⎥⎤-12,1,所以2+cos x ∈⎣⎢⎡⎦⎥⎤32,3,所以函数y =2+cos x ,x ∈⎝ ⎛⎦⎥⎤-π3,2π3的值域为⎣⎢⎡⎦⎥⎤32,3.类型三 正弦、余弦函数的单调性例3 函数y =cos x 的一个递增区间为( )A.⎝ ⎛⎭⎪⎫-π2,π2B.(0,π)C.⎝ ⎛⎭⎪⎫π2,3π2 D.(π,2π)题点 求正、余弦函数的单调区间 答案 D解析 ∵y =cos x 的递增区间为[2k π-π,2k π],k ∈Z ,令k =1得[π,2π],即为y =cos x 的一个递增区间,而(π,2π)⊆[π,2π],故选D. 反思与感悟 利用单位圆有助于理解记忆正弦、余弦函数的单调区间,特别注意不连贯的单调区间不能并.跟踪训练3 求下列函数的单调区间.(1)y =sin x ,x ∈[-π,π];(2)y =cos x ,x ∈[-π,π]. 考点 正、余弦函数的单调性 题点 求正、余弦函数的单调区间解 (1)y =sin x 在x ∈[-π,π]上的递增区间为⎣⎢⎡⎦⎥⎤-π2,π2,递减区间为⎣⎢⎡⎦⎥⎤-π,-π2,⎣⎢⎡⎦⎥⎤π2,π.(2)y =cos x 在x ∈[-π,π]上的递增区间为[-π,0],递减区间为[0,π].1.函数y =cos x -1的最小值是( ) A.0 B.1 C.-2 D.-1考点 正弦函数、余弦函数的最大值与最小值 题点 余弦函数的最大值与最小值 答案 C解析 cos x ∈[-1,1],所以y =cos x -1的最小值为-2.2.不等式2sin x -1≥0的解集为 . 考点 解三角不等式 题点 解三角不等式答案 ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪π4+2k π≤x ≤3π4+2k π,k ∈Z解析 由2sin x -1≥0得,sin x ≥22. 由单位圆可得π4+2k π≤x ≤3π4+2k π,k ∈Z .3.函数f (x )=-2sin x +1的最大值为 .答案 3解析 因为-1≤sin x ≤1,所以当sin x =-1时,f (x )取最大值2+1=3.4.求y =-2sin x ,x ∈⎣⎢⎡⎦⎥⎤-π6,π的值域. 考点 正、余弦函数的值域 题点 正、余弦函数的值域解 由x ∈⎣⎢⎡⎦⎥⎤-π6,π,得sin x ∈⎣⎢⎡⎦⎥⎤-12,1,∴y ∈[-2,1],∴y =-2sin x ,x ∈⎣⎢⎡⎦⎥⎤-π6,π的值域为[-2,1].利用单位圆来研究正弦、余弦函数的基本性质,能够加深对正弦、余弦函数性质的理解与认识,同时也有助于提升学生利用数形结合思想解决问题的意识.一、选择题1.函数y =sin x +-cos x 的定义域是( ) A.[k π,(k +1)π](k ∈Z ) B.⎣⎢⎡⎦⎥⎤2k π+π2,(2k +1)π(k ∈Z )C.⎣⎢⎡⎦⎥⎤k π+π2,(k +1)π(k ∈Z )D.[2k π,(2k +1)π](k ∈Z ) 考点 正弦函数、余弦函数的定义域 题点 正弦函数、余弦函数的定义域 答案 B解析 由已知,得⎩⎪⎨⎪⎧sin x ≥0,-cos x ≥0,∴⎩⎪⎨⎪⎧sin x ≥0,cos x ≤0,∴2k π+π2≤x ≤2k π+π(k ∈Z ).2.函数y =sin 2x 的递减区间是( ) A.⎣⎢⎡⎦⎥⎤π2+2k π,3π2+2k π(k ∈Z )B.⎣⎢⎡⎦⎥⎤k π+π4,k π+3π4(k ∈Z ) C.[π+2k π,3π+2k π](k ∈Z ) D.⎣⎢⎡⎦⎥⎤k π-π4,k π+π4(k ∈Z ) 考点 正弦函数、余弦函数的单调性 题点 正弦函数、余弦函数单调性的判断 答案 B解析 由2k π+π2≤2x ≤2k π+3π2,k ∈Z ,得k π+π4≤x ≤k π+3π4,k ∈Z ,∴y =sin 2x 的递减区间是⎣⎢⎡⎦⎥⎤k π+π4,k π+3π4(k ∈Z ).3.函数y =lg ⎝⎛⎭⎪⎫cos x -12的定义域为( )A.⎝ ⎛⎭⎪⎫-π3,π3B.⎝ ⎛⎭⎪⎫k π-π3,k π+π3,k ∈ZC.⎝⎛⎭⎪⎫2k π-π3,2k π+π3,k ∈Z D.R考点 正弦函数、余弦函数的定义域 题点 正弦函数、余弦函数的定义域 答案 C解析 ∵cos x -12>0,∴cos x >12,∴2k π-π3<x <2k π+π3,k ∈Z .∴函数y =lg ⎝ ⎛⎭⎪⎫cos x -12的定义域为⎝ ⎛⎭⎪⎫2k π-π3,2k π+π3,k ∈Z .4.函数y =4sin x +3在[-π,π]上的递增区间为( ) A.⎣⎢⎡⎦⎥⎤-π,-π2B.⎣⎢⎡⎦⎥⎤-π2,π2C.⎣⎢⎡⎦⎥⎤-π,π2 D.⎣⎢⎡⎦⎥⎤π2,π 考点 正、余弦函数的单调性 题点 求正、余弦函数的单调区间 答案 B解析 y =sin x 的递增区间就是y =4sin x +3的递增区间.5.y =3cos x ,x ∈⎝ ⎛⎦⎥⎤-π6,4π3的最大值与最小值分别为( )A.3,-3B.3,-332C.3,32D.3,-32考点 正、余弦函数的最值 题点 求正、余弦函数的最值 答案 A6.在[0,2π]内,使sin x ≥12成立的x 的取值范围是( )A.⎣⎢⎡⎦⎥⎤0,π6B.⎣⎢⎡⎦⎥⎤π6,56πC.⎣⎢⎡⎦⎥⎤π6,23πD.⎣⎢⎡⎦⎥⎤56π,π考点 解三角不等式 题点 解三角不等式 答案 B7.已知f (x )=cos ⎝⎛⎭⎪⎫πx +π3,x ∈Z ,则f (x )的值域为( )A.⎩⎨⎧⎭⎬⎫-12,12 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫-32,32 C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫-12,12,-32,32D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫12,32考点 余弦函数的值域 题点 余弦函数的值域 答案 A 二、填空题8.y =cos x ,x ∈⎣⎢⎡⎦⎥⎤-5π6,5π3的递增区间为 .考点 正、余弦函数的单调性 题点 求正、余弦函数的单调区间 答案 ⎣⎢⎡⎦⎥⎤-5π6,0,⎣⎢⎡⎦⎥⎤π,5π3 9.满足sin α-cos α>0的α的取值范围是 . 考点 解三角不等式 题点 解三角不等式答案 ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪π4+2k π<α<5π4+2k π,k ∈Z 解析 由图可解.10.y =3sin x ,x ∈⎣⎢⎡⎦⎥⎤-π3,4π3的值域为 .考点 正、余弦函数的值域 题点 正、余弦函数的值域答案 ⎣⎢⎡⎦⎥⎤-332,3解析 借助单位圆可知,函数f (x )=sin x ,x ∈⎣⎢⎡⎦⎥⎤-π3,4π3在x =π2处取最大值1,在x =-π3和x =4π3处同时取得最小值-32,即-32≤sin x ≤1,所以-332≤3sin x ≤3. 11.下列说法正确的是 .(只填序号) ①y =|sin x |的定义域为R ; ②y =3sin x +1的最小值为1; ③y =-sin x 为周期函数;④y =sin x -1的递增区间为⎣⎢⎡⎦⎥⎤2k π+π2,2k π+3π2(k ∈R ).考点 正、余弦函数的基本性质 题点 正、余弦函数的基本性质综合 答案 ①③解析 对于②,y =3sin x +1的最小值为-3+1=-2;对于④,y =sin x -1的递增区间为⎣⎢⎡⎦⎥⎤2k π-π2,2k π+π2,k ∈Z ,故②④错,填①③.三、解答题12.已知函数y =a cos x +b 的最大值是0,最小值是-4,求a ,b 的值. 考点 正、余弦函数的最值 题点 含参正、余弦函数的最值解 当a >0时,⎩⎪⎨⎪⎧a +b =0,-a +b =-4,解得⎩⎪⎨⎪⎧a =2,b =-2,当a <0时,⎩⎪⎨⎪⎧-a +b =0,a +b =-4,解得⎩⎪⎨⎪⎧a =-2,b =-2.∴a =2,b =-2或a =b =-2. 13.已知函数f (x )=12-sin x.(1)判定函数f (x )是否为周期函数; (2)求函数f (x )的递增区间;(3)当x ∈⎝ ⎛⎦⎥⎤-π6,5π6时,求f (x )的值域. 考点 正、余弦函数的基本性质 题点 正、余弦函数的基本性质综合 解 (1)函数f (x )的定义域是R .因为f (x +2π)=12-sin (2π+x )=12-sin x=f (x ),所以f (x )是周期函数.(2)由正弦函数的基本性质,可知在区间⎣⎢⎡⎦⎥⎤2k π-π2,2k π+π2(k ∈Z )上,函数y =sin x 是增加的,而此时函数h (x )=2-sin x 是减函数,从而可知此时函数f (x )是增函数, 故可知函数f (x )的递增区间为⎣⎢⎡⎦⎥⎤2k π-π2,2k π+π2(k ∈Z ).(3)设t =sin x ⎝ ⎛⎭⎪⎫x ∈⎝ ⎛⎦⎥⎤-π6,5π6,则t ∈⎝ ⎛⎦⎥⎤-12,1,所以1≤2-t <52,则25<12-t≤1.故f (x )的值域为⎝ ⎛⎦⎥⎤25,1. 四、探究与拓展14.函数y =-23cos x ,x ∈(0,2π),其单调性是( )A.在(0,π)上是增加的,在[π,2π)上是减少的B.在⎝ ⎛⎦⎥⎤0,π2,⎣⎢⎡⎭⎪⎫3π2,2π上是增加的,在⎝ ⎛⎦⎥⎤π2,3π2上是减少的C.在[π,2π)上是增加的,在(0,π)上是减少的D.在⎣⎢⎡⎦⎥⎤π2,3π2上是增加的,在⎝ ⎛⎭⎪⎫0,π2,⎝ ⎛⎭⎪⎫3π2,2π上是减少的考点 正、余弦函数的单调性题点 正、余弦函数的单调性答案 A15.已知f (x )=-sin x .(1)试写出f (x )的单调区间;(2)若f (x )在⎣⎢⎡⎦⎥⎤-π2,a 上是减少的,求实数a 的取值范围. 考点 正弦函数的单调性题点 正弦函数的单调性综合解 (1)∵f (x )=-sin x ,根据正弦函数y =sin x 的单调性可知,f (x )在⎣⎢⎡⎦⎥⎤2k π-π2,2k π+π2(k ∈Z )上是减少的, 在⎣⎢⎡⎦⎥⎤2k π+π2,2k π+3π2(k ∈Z )上是增加的. (2)∵f (x )在⎣⎢⎡⎦⎥⎤-π2,π2上是减少的, ∴⎣⎢⎡⎦⎥⎤-π2,a ⊆⎣⎢⎡⎦⎥⎤-π2,π2, 即-π2<a ≤π2. ∴a 的取值范围是⎝ ⎛⎦⎥⎤-π2,π2.。
