公务员考试1000道数字推理题详细讲解(精选)
国家公务员考试数字推理题附答案

国家公务员考试数字推理题附答案为了帮助参加国家公务员考试的考生复习数字推理题这一模块,接下来,本人为你分享国家公务员考试数字推理题附答案。
国家公务员考试数字推理题(一)1.17, 29, 43, 61, 87, ( )A.167B.115C.259D.1292.1, 11, 31, 512, 196, ( )A.9999B.999C.888D.88883.1/3,1,9,243,( )A.19683B.19785C.19827D.198694.2,1,6,14,40,108,( )A.288B.296C.304D.3125.3, 10,31,94,( ),850A.250B.270C.282D.283国家公务员考试数字推理题答案1.【解析】D.等差数列变式:2.【解析】D.数列各项的各位数字之和分别为1,2,4,8,16,(32),构成等比数列,只有D项各位数字之和为32,当选。
3.【解析】A.作商数列。
4.【解析】B.递推数列,递推规律为:后一项=前两项之和×2.因此,未知项为(40+108)×2=296.5.【解析】D.前一项×3+1=后一项,94×3+1=(283),(283)×3+1=850.国家公务员考试数字推理题(二)1. 4736,3728,3225,2722,2219,( )A.1514B.1532C.1915D.15622. 1.01,1.02,1.03,( ),1.08,1.13A.1.04B.1.05C.1.06D.1.073. 22,24,39,28,( ),16A.14B.11C.30D.154. 448,516,639,347,178,( )。
A.163B. 134C.785D. 8965. 23,57,1113,1317,( ),2331A.1921B.1715C.1723D.2129国家公务员考试数字推理题答案1.答案: A解析:将原数列机械划分47|36、37|28、32|25、27|22、22|19,每个数字的前半部分减后半部分构成一个公差为-2的等差数列,47-36=11,37-28=9,32-25=7,27-22=5,22-19=3,则未知项机械划分后前半部分减去后半部分应为1,只有选项A符合。
公务员考试数字推理基础知识各种特殊数字集(最全)
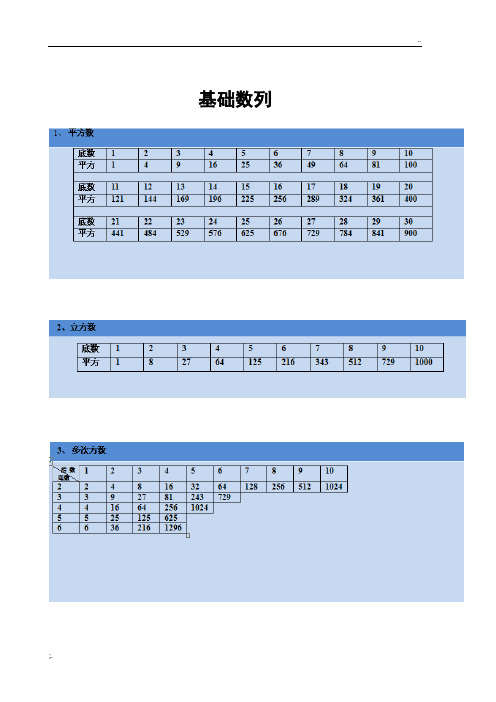
基础数列【例1】质数:2,3,5,7,1l,1 3,17,1 9,23.…【例2】合数:4,6,8,9,10,12,14,15,…【例】1,3,7,1,3,7,…1,7,1,7,l,7,…1,3,7,一1,一3,7,…【例】(1)6,12,19,27,35,( ),48答案:42,首尾相加为54。
(2)3,- l,5,5,11,( )答案:7,首尾相加为10。
等差数列及其变式一、基本等差数列【例】1,4,7,10,l 3,l 6,19,22,25,…【例1】(2007黑龙江,第8题)11,12,15,20,27,( ) A.32 B.34 C.36 D.38【答案】C【解题关键点】【例2】(2002国家,B类,第3题)32,27,23,20,18,( ) A.14 B.15 C.16 D.1 7【答案】D【解题关键点】【例3】(2002国家,B类,第5题)-2,1,7,16,( ),43 A.25 B.28 C.31 D.35【答案】B【解题关键点】【例】3,6,11,( ),27A.15 B.18 C.19 D.24【答案】B【解题关键点】二级等差数列。
(1)相邻两项之差是等比数列【例】0,3,9,21,( ),93A.40 B.45 C. 36 D.38【答案】B【解题关键点】二级等差数列变式(2)相邻两项之差是连续质数【例】11,13,16,21,28,( )A.37 B.39 C.41 D.47【答案】B【解题关键点】二级等差数列变式(3)相邻两项之差是平方数列、立方数列【例】1,2,6,15,()A.19B.24C.31D.27【答案】C【解题关键点】数列特征明显单调且倍数关系不明显,优先做差。
得到平方数列。
如图所示,因此,选C(4)相邻两项之差是和数列【例】2, 1, 5, 8, 15, 25, ( )A.41B.42C.43D.44【答案】B【解题关键点】相邻两项之差是和数列(5)相邻两项之差是循环数列【例】1,4,8,13,16,20,( )A. 20B. 25C. 27D. 28【答案】B【解题关键点】该数列相邻两数的差成3,4,5一组循环的规律,所以空缺项应为20+5=25,故选B。
公务员考试行测数字推理典型例题解析

(1)2、3、10、15、() 解析: 1的平⽅+1=2、2的平⽅-1=3、3的平⽅+1=10、4的平⽅-1=15、5的平⽅+1=(26) (2)10、9、17、50、() 解析: 10*1-1=9、9*2-1=17、17*3-1=50、50*4-1=(199) (3)2、8、24、64、() 解析: 2*2+4=8、8*2+8=24、24*2+16=64、64*2+32=(160) (4)0、4、18、48、100、() 解析: 这道题的关键是将每⼀项分解,0*1=0、2*2=4、6*3=18、12*4=48、20*5=100、30*6=(180) (5)4、5、11、14、22、() 解析: 前项与后项的和是到⾃然数平⽅数列。
4+5=9、5+11=16、11+14=25、14+22=36、22+(27)=49 (6)2、3、4、9、12、15、22、() 解析: 每三项相加,得到⾃然数平⽅数列。
2+3+4=9、3+4+9=16、4+9+12=25、9+12+15=36、12+15+22=49、15+22+(27)=64 (7) 1、2、3、7、46、() 解析: 后⼀项的平⽅减前⼀项得到第三项,2的平⽅-1=3、3的平⽅-2=7、7的平⽅-3=46、46的平⽅-7=(2109) (8)2、2、4、12、12、()、72 这是⼀个组合数列2*1=2、2*2=4、4*3=12、12*1=12、12*2=(24)、24*3=72 (9) 4、6、10、14、22、() 每项除以2得到质数列 2、3、5、7、11、(26)/2=13 (10)5、24、6、20、()、15、10、() 5*24=120、6*20=120、(8)*15=120、10*(12)=120 (11)763951、59367、7695、967、() 本题并未研究计算关系,⽽只是研究项与项之间的数字规律。
将第⼀项763951中的数字“1”去掉,并从后向前数得到下⼀项59367;将59367中的“3”去掉,并从后向前数得到7695;7695去掉“5”,从后向前数得到967;967去掉“7”,从后向前数得到(69)。
国家公务员考试数字推理习题附答案

国家公务员考试数字推理习题附答案国家公务员考试数字推理这一模块的复习,做习题是必不可少。
今天,本人为大家整理了国家公务员考试数字推理习题。
国家公务员考试数字推理习题(一)1. 10, 21, 44, 65, ( )A.122B.105C.102D.902. -1,2,1,8,19,( )A.62B.65C.73D.863. 4,5,15,6,7,35,8,9,( )A.27B.15C.72D.634. 2,4,12,60,420,( )A.4620B.840C.3780D.7205. 11,11,13,21,47,( )A.125B.126C.127D.128国家公务员考试数字推理习题答案1.答案: C解析: 因式分解数列。
列中的项一次拆分为2*5、3*7、4*11、5*13,我们发现2、3、4、5是等差数列,下一项为6;5、7、11、13为质数列,下一项为17,所以答案为6*17=102,即C选项。
2.答案: A解析:原数列为二级等比数列。
该数列两两相加可以得到1、3、9、27、(81),构成等比数列。
故未知项为81-19=62。
故正确答案为A。
3.答案: D解析:三三分组: [4,5,15] 、 [ 6,7,35] 、 [ 8,9,( )];组内关系:(4-1)×5=15, (6-1)×7=35, (8-1)×9=63;则未知项为63,故正确答案为D。
4.答案: A解析: 观察后发现数列单调递增,增速较快,且数字间有明显的倍数关系,考虑做商。
原数列:2,4,12,60,420;做一次商:2,3,5,7为质数数列,下一项应为11,故原数列下一项为420×11=4620。
因此,本题答案为A选项。
5.答案: C解析:原数列两次两两做差得0,2,8,26,(),再两两做差得:2,6,18,(54),为公比是3的等比数列,所以原数列=26+54+47=127。
因此,本题答案选择C选项。
行测:数字推理题100道(详解)

数字推理题500道详解【1】7,9,-1,5,( )A、4;B、2;C、-1;D、-3分析:选D,7+9=16;9+(-1)=8;(-1)+5=4;5+(-3)=2 , 16,8,4,2等比【2】3,2,5/3,3/2,( )A、1/4;B、7/5;C、3/4;D、2/5分析:选B,可化为3/1,4/2,5/3,6/4,7/5,分子3,4,5,6,7,分母1,2,3,4,5【3】1,2,5,29,()A、34;B、841;C、866;D、37分析:选C,5=12+22;29=52+22;( )=292+52=866【4】2,12,30,()A、50;B、65;C、75;D、56;分析:选D,1×2=2;3×4=12;5×6=30;7×8=()=56【5】2,1,2/3,1/2,()A、3/4;B、1/4;C、2/5;D、5/6;分析:选C,数列可化为4/2,4/4,4/6,4/8,分母都是4,分子2,4,6,8等差,所以后项为4/10=2/5,【6】4,2,2,3,6,()A、6;B、8;C、10;D、15;分析:选D,2/4=0.5;2/2=1;3/2=1.5;6/3=2;0.5,1,1.5, 2等比,所以后项为2.5×6=15【7】1,7,8,57,()A、123;B、122;C、121;D、120;分析:选C,12+7=8;72+8=57;82+57=121;【8】4,12,8,10,()A、6;B、8;C、9;D、24;分析:选C,(4+12)/2=8;(12+8)/2=10;(8+10)/2=9【9】1/2,1,1,(),9/11,11/13A、2;B、3;C、1;D、7/9;分析:选C,化成1/2,3/3,5/5 ( ),9/11,11/13这下就看出来了只能是(7/7)注意分母是质数列,分子是奇数列。
【10】95,88,71,61,50,()A、40;B、39;C、38;D、37;分析:选A,思路一:它们的十位是一个递减数字9、8、7、6、5 只是少开始的4 所以选择A。
公务员考试(图形数字推理)试题及答案详解

国家公务员考试行测冲刺备考举一反三灵活解答规律特征型图形推理题近年来国家公务员考试的难度在不断加大,反映在图形推理中就是规律越来越复杂隐蔽。
相比于数学运算、资料分析,图形推理似乎并无取巧之处。
这也造成了很多考生反映的图形推理完全没有思路,做了很多练习但临场就发懵的现状。
中公教育专家认为,突破图形推理,适度的练习是必要的,但关键在于通过这些练习学会举一反三。
图形问题在考察内容上主要分为:规律特征型推理思路、平面图形的空间还原与立体图形的平面展开、拼图及图形拆分与组合、意指型图形。
其中,以规律特征型推理思路考察得最为广泛和普遍,也是让考生最为头疼的题型。
在此,中公教育专家结合例题对这一类型的题目进行深入分析,正确引导考生的解题思路。
例题1:答案:B。
解题思路:定位此题,为组合图形的变化,故思维圈定于图形内部分割部分数;内部图形与外部图形的替代关系;图形求同。
图形内部分割部分数:第一组图的部分数分别为三部分、两部分、两部分,第二组图的部分数分别为九部分、三部分,不具有数字规律性,故此思维被否定。
内部图形与外部图形的替代关系:第一组图形中,图形一的外面正方形在图形二中移到内部,图形二中的六边形在图形三中并未发生替代关系,故此思维被否定。
图形求同:在第一组图中,均含有正方形,在第二组图中,均含有圆形,对照选项,只有B项含有圆形,可得题解。
例题2:答案:D。
解题思路:此题为细节变化问题,故思维圈定为前后图对比寻找细节差异。
第一图与第二图比较可发现,箭头方向发生变化、左边的小线段从最下面减少一条,对比第二图与第三图,箭头方向又发生变化、右边的小线段从最上面减少一条,即可推得可能性规律,以第三、四幅图进行验证,符合,对照选项,可得题解为D。
例题3:答案:C。
解题思路:定位此题为图形种类的变化,故思维圈定为某一或某几个图形的数量呈现规律性变化、每个图形总数量的恒定。
某一或某几个图形的数量呈现规律性变化:前五个图出现的六种图形的数量并未符合任何规律性分布,故此思维被否定。
国家公务员考试之数字推理习题精解(二).doc

国家公务员考试之数字推理习题精解(二)1. 20/9 ,4/3 ,7/9 ,4/9 ,1/4,()A.5/36B.1/6C.1/9D.1/144解析:这是一道分数难题,分母与分子均不同。
可将分母先通分,最小的分母是36,通分后分子分别是204=80,412=48,74=28,44=16,19=9,然后再从分子80、48、28、16、9 中找规律。
80=(48-28)4,48=(28-16)4,28=(16-9)4,可见这个规律是第一个分子等于第二个分子与第三个分子之差的4 倍,依此规律,()内分数应是16=(9-?)4,即(36-16)4=5。
故本题的正确答案为A。
2. 23 ,46 ,48 ,96 ,54 ,108 ,99 ,()A.200B.199C.198D.197解析:本题的每个双数项都是本组单数项的2 倍,依此规律,()内的数应为992=198。
本题不用考虑第2 与第3,第4 与第5,第6 与第7个数之间的关系。
故本题的正确答案为 C。
3. 1.1 ,2.2 ,4.3 ,7.4 ,11.5 ,()A.15.5B.15.6C.17.6D.16.6解析:此题初看较乱,又是整数又是小数。
遇到此类题时,可将小数与整数分开来看,先看小数部分,依次为0.1,0.2,0.3,0.4,0.5,那么,()内的小数应为0.6,这是个自然数列。
再看整数部分,即后一个整数是前一个数的小数与整数之和,2=1+1,4=2+2,7=4+3,11=7+4,那么,()内的整数应为11+5=16。
故本题的正确答案为D 。
4. 0.75 ,0.65 ,0.45 ,()A.0.78B.0.88C.0.55D.0.96解析:在这个小数数列中,前三个数皆能被0.05 除尽,依此规律,在四个选项中,只有C 能被0.05 除尽。
故本题的正确答案为C。
5. 1.16 ,8.25 ,27.36 ,64.49 ,()A.65.25B.125.64C.125.81D.125.01解析:此题先看小数部分,16、25、36、49 分别是4、5、6、7 自然数列的平方,所以()内的小数应为8.2=64,再看整数部分,1=13,8=23,27=33,64=43,依此规律,()内的整数就是5.3=125。
公务员考试数字推理题725道详解

公务员考试数字推理题725道详解【1】7,9,-1,5,( )A、4;B、2;C、-1;D、-3分析:选D,7+9=16;9+(-1)=8;(-1)+5=4;5+(-3)=2 , 16,8,4,2等比【2】3,2,5/3,3/2,( )A、1/4;B、7/5;C、3/4;D、2/5分析:选B,可化为3/1,4/2,5/3,6/4,7/5,分子3,4,5,6,7,分母1,2,3,4,5【3】1,2,5,29,()A、34;B、841;C、866;D、37分析:选C,5=12+22;29=52+22;( )=292+52=866【4】2,12,30,()A、50;B、65;C、75;D、56;分析:选D,1×2=2;3×4=12;5×6=30;7×8=()=56【5】2,1,2/3,1/2,()A、3/4;B、1/4;C、2/5;D、5/6;分析:选C,数列可化为4/2,4/4,4/6,4/8,分母都是4,分子2,4,6,8等差,所以后项为4/10=2/5,【6】4,2,2,3,6,()A、6;B、8;C、10;D、15;分析:选D,2/4=0.5;2/2=1;3/2=1.5;6/3=2;0.5,1,1.5, 2等比,所以后项为2.5×6=15【7】1,7,8,57,()A、123;B、122;C、121;D、120;分析:选C,12+7=8;72+8=57;82+57=121;【8】4,12,8,10,()A、6;B、8;C、9;D、24;分析:选C,(4+12)/2=8;(12+8)/2=10;(8+10)/2=9【9】1/2,1,1,(),9/11,11/13A、2;B、3;C、1;D、7/9;分析:选C,化成1/2,3/3,5/5 ( ),9/11,11/13这下就看出来了只能是(7/7)注意分母是质数列,分子是奇数列。
【10】95,88,71,61,50,()A、40;B、39;C、38;D、37;分析:选A,思路一:它们的十位是一个递减数字9、8、7、6、5 只是少开始的4 所以选择A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【1】7,9 ,-1 ,5,( )A、4;B、2;C、-1 ;D、-3分析:选D,7+9=16 ;9+ (-1 )=8 ;(-1 )+5=4 ;5+ (-3 )=2 , 16 ,8 ,4,2 等比【2】3,2,5/3 ,3/2 ,( )A、1/4 ;B、7/5 ;C、3/4 ;D、2/5分析:选B,可化为3/1 ,4/2 ,5/3 ,6/4 ,7/5, 分子3,4,5,6 ,7,分母1,2,3,4,5【3】1,2,5,29,()A、34;B、841 ;C、866 ;D、37分析:选C,5=1 2 +2 2;29=5 2+2 2 ;( )=29 2 +5 2=866【4】2,12,30,()A、50;B、65 ;C、75 ;D、56 ;分析:选D,1×2=2 ;3×4=12 ;5×6=30 ;7×8= ()=56【5】2,1,2/3 ,1/2 ,()A、3/4 ;B、1/4 ;C、2/5 ;D、5/6 ;分析:选C,数列可化为4/2 ,4/4 ,4/6 ,4/8 ,分母都是 4 ,分子2,4,6 ,8 等差,所以后项为4/10=2/5 ,【6】4,2,2,3,6,()A、6;B、8;C、10 ;D、15;分析:选D,2/4=0.5 ;2/2=1 ;3/2=1.5 ;6/3=2 ;0.5,1,1.5, 2 等比,所以后项为 2.5×6=15【7】1,7,8,57,()A、123 ;B、122 ;C、121 ;D、120 ;分析:选C,12 +7=8 ;72+8=57 ;82 +57=121 ;【8】4,12,8,10,()A、6;B、8;C、9;D、24 ;分析:选C,(4+12)/2=8 ;(12+8)/2=10 ;(8+10)/2=9【9】1/2 ,1,1,(),9/11,11/13A、2;B、3;C、1;D、7/9 ;分析:选C,化成1/2,3/3,5/5 ( ),9/11,11/13 这下就看出来了只能是(7/7) 注意分母是质数列,分子是奇数列。
【10】95,88 ,71,61 ,50 ,()A、40 ;B、39 ;C、38 ;D、37 ;分析:选A,思路一:它们的十位是一个递减数字9、8、7、6、5 只是少开始的 4 所以选择A。
思路二:95 - 9 - 5 = 81 ;88 - 8 - 8 = 72 ;71 - 7 - 1 = 63 ;61 - 6 - 1 = 54 ;50 - 5 - 0 = 45 ;40 - 4 - 0 = 36 ,构成等差数列。
【11】2,6,13,39,15,45,23,( )A. 46 ;B. 66 ;C. 68 ;D. 69 ;分析:选D,数字 2 个一组,后一个数是前一个数的 3 倍【12】1,3,3,5,7,9,13,15(),()A:19,21 ;B:19,23 ;C:21,23 ;D:27 ,30 ;分析:选C,1,3,3,5 ,7,9 ,13 ,15 (21 ),(30 )=> 奇偶项分两组1、3、7、13、21 和3、5 、9、15 、23 其中奇数项1、3、7、13 、21=> 作差2、4 、6、8 等差数列,偶数项3、5、9 、15 、23=> 作差2、4、6、8 等差数列【13】1,2,8,28,()A.72 ;B.100;C.64;D.56;分析:选B,1×2+2 ×3=8 ;2×2+8 ×3=28 ;8×2+28 ×3=100【14】0,4,18,(),100A.48 ;B.58 ;C.50 ;D.38 ;分析:A,思路一:0 、4、18 、48 、100=> 作差=>4 、14 、30 、52=> 作差=>10 、16 、22 等差数列;思路二:1 3-1 2=0 ;23-2 2 =4 ;33 -3 2=18 ;43 -4 2=48 ;53 -5 2=100 ;思路三:0 ×1=0 ;1×4=4 ;2×9=18 ;3×16=48 ;4×25=100 ;思路四:1 ×0=0 ;2×2=4 ;3×6=18 ;4×12=48 ;5×20=100 可以发现:0,2,6,(12),20 依次相差2,4,(6),8,思路五:0=1 2×0;4=2 2×1;18=3 2×2;( )=X 2 ×Y;100=5 2×4 所以()=4 2×3【15】23,89,43,2,()A.3;B.239 ;C.259 ;D.269 ;分析:选A,原题中各数本身是质数,并且各数的组成数字和2+3=5 、8+9=17 、4+3=7 、2 也是质数,所以待选数应同时具备这两点,选 A【16】1,1, 2, 2, 3, 4, 3, 5, ( )分析:思路一:1,(1,2),2,(3,4 ),3,(5,6)=> 分1、2、3 和(1,2),(3,4 ),(5,6 )两组。
思路二:第一项、第四项、第七项为一组;第二项、第五项、第八项为一组;第三项、第六项、第九项为一组=>1,2,3;1,3,5;2,4,6=> 三组都是等差【17】1,52, 313,174,( )A.5;B.515 ;C.525 ;D.545 ;分析:选B,52 中5 除以 2 余1(第一项);313 中31 除以 3 余1( 第一项);174 中17 除以 4 余1(第一项);515 中51 除以5 余1(第一项)【18】5, 15, 10, 215, ( )A、415 ;B、-115 ;C、445 ;D、-112 ;答:选B,前一项的平方减后一项等于第三项,5×5-15=10 ;15×15-10=215 ;10 ×10-215=-115【19】-7,0, 1, 2, 9, ( )A、12;B、18 ;C、24 ;D、28 ;答:选D,-7=(-2) 3+1 ;0=(-1) 3 +1 ;1=0 3 +1 ;2=1 3+1 ;9=2 3+1 ;28=3 3 +1【20】0,1,3,10,( )A、101 ;B、102 ;C、103 ;D、104 ;答:选B,思路一:0×0+1=1 ,1×1+2=3 ,3×3+1=10 ,10 ×10+2=102 ;思路二:0( 第一项)2+1=1( 第二项) 12 +2=3 32 +1=10 102 +2=102, 其中所加的数呈1,2,1,2 规律。
思路三:各项除以3,取余数=>0,1,0,1,0 ,奇数项都能被 3 整除,偶数项除 3 余1;【21】5,14,65/2,( ) ,217/2A.62 ;B.63 ;C. 64 ;D. 65 ;答:选B,5=10/2 ,14=28/2 , 65/2, ( 126/2), 217/2 ,分子=> 10=2 3+2 ;28=3 3+1 ;65=4 3+1 ;(126)=5 3+1 ;217=6 3 +1 ;其中2、1、1 、1、1 头尾相加=>1 、2、3 等差【22】124,3612,51020,()A、7084 ;B、71428 ;C、81632 ;D、91836 ;答:选B,思路一:124 是 1 、2、 4 ;3612 是 3 、6 、12 ;51020 是5、10 、20 ;71428 是7,14 28 ;每列都成等差。
思路二:124 ,3612 ,51020 ,(71428 )把每项拆成 3 个部分=>[1,2,4] 、[3,6,12] 、[5,10,20] 、[7,14,28]=> 每个[ ]中的新数列成等比。
思路三:首位数分别是1、3、5、(7 ),第二位数分别是:2 、6、10 、(14 );最后位数分别是:4、12 、20 、(28 ),故应该是71428 ,选B。
【23】1,1,2,6,24,( )A,25;B,27 ;C,120 ;D,125解答:选C。
思路一:(1+1 )×1=2 ,(1+2 )×2=6 ,(2+6 )×3=24 ,(6+24 )×4=120思路二:后项除以前项=>1 、2、3、4、5 等差【24】3,4,8,24,88,( )A,121 ;B,196 ;C,225 ;D,344解答:选D。
思路一:4=2 0 +3 ,8=2 2 +4 ,24=2 4 +8 ,88=2 6 +24 ,344=2 8 +88思路二:它们的差为以公比 2 的数列:4-3=2 0 ,8-4=2 2,24-8=2 4,88-24=2 6 ,?-88=2 8,?=344 。
【25】20,22,25,30,37,( )A,48;B,49 ;C,55 ;D,81解答:选A。
两项相减=>2 、3、5、7、11 质数列【26】1/9 ,2/27,1/27,( )A,4/27 ;B,7/9 ;C,5/18 ;D,4/243 ;答:选D,1/9,2/27,1/27,(4/243)=>1/9 ,2/27 ,3/81 ,4/243=> 分子,1、2、3 、4 等差;分母,9、27、81 、243 等比【27】√2,3,√28,√65,( )A,2 √14 ;B,√83 ;C,4√14 ;D,3√14 ;1 ;所以选√ 126 ,即D 3 √14【28】1,3,4,8,16,( )A、26;B、24 ;C、32 ;D、16 ;答:选C,每项都等于其前所有项的和1+3=4 ,1+3+4=8 ,1+3+4+8=16 ,1+3+4+8+16=32【29】2,1,2/3 ,1/2 ,( )A、3/4 ;B、1/4 ;C、2/5 ;D、5/6 ;答:选C ,2, 1 , 2/3 , 1/2 , (2/5 )=>2/1, 2/2, 2/3, 2/4 (2/5)=> 分子都为 2 ;分母,1、2 、3 、4 、5 等差【30】1,1,3,7 ,17 ,41 ,( )A.89;B.99 ;C.109 ;D.119 ;答:选B,从第三项开始,第一项都等于前一项的 2 倍加上前前一项。
2×1+1=3 ;2×3+1=7 ;2 ×7+3=17 ;;2 ×41+17=99【31】5/2 ,5 ,25/2 ,75/2 ,()答:后项比前项分别是2,2.5,3 成等差,所以后项为 3.5,()/(75/2 )=7/2 ,所以,()=525/4【32】6,15,35,77,( )A.106 ;B.117 ;C.136 ;D.163答:选D,15=6 ×2+3 ;35=15 ×2+5 ;77=35 ×2+7 ;163=77 ×2+9 其中3、5 、7、9 等差【33】1,3,3,6,7,12,15,( )A.17;B.27 ;C.30 ;D.24 ;答:选D,1,3,3,6,7,12 ,15 ,( 24 )=> 奇数项1、3、7、15=> 新的数列相邻两数的差为2、4、8 作差=> 等比,偶数项 3 、6 、12 、24 等比【34】2/3 ,1/2 ,3/7 ,7/18,()A、4/11 ;B、5/12 ;C、7/15 ;D、3/16分析:选A。
