人教版高一数学必修3第一章《算法初步》测试题及答案
最新人教版高中数学必修3第一章《四第1章 算法初步》本章测评

本章测评1.关于算法的描述正确的是()A.只有数学问题才会有算法B.算法过程要一步一步执行,每一步的操作都是明确的C.有的算法可能无结果D.一个算法执行了一年后才得出结果思路解析:算法具有确定性,有穷性,可行性,输入、输出的特性,它必须在有限的时间内完成,并输出结果.D 项没有实用价值,不具备可行性.答案:B2.下列符号框中表示处理框的是()A.菱形框B.平行四边形框C.矩形框D.圆角矩形框思路解析:菱形框是判断框,平行四边形框是输入、输出框,圆角矩形框是起止框.答案:C3.下列关于条件语句的叙述正确的是()A.条件语句中必须有ELSE和ENDIFB.条件语句中可以没有ENDIFC.条件语句中可以没有ELSE,但必须有ENDIFD.条件语句中可以没有ENDIF,也可以没有ELSE思路解析:条件语句又称为“块 IF语句”,之所以称为“块”,必须以IF开头,以ENDIF 结束,其中的ELSE可以 没有.答案:C4.下列语句不具备计算功能的是()A.输入语句B.输出语句C.赋值语句D.以上都对思路解析:输入语句 INPUT后跟变量,可给多个变量提供数据,运行时从键盘输入程序运行所需的数据,此时只能输入常量,不能是变量、函数或表达式,也就是说输入语句无计算功能.故选A.答案:A5.下面语句正确的是()A.b=2a+1 B.INPUT a;b;c C.PRINT 3*a+b D.INPUT a+b,c 思路解析:数学表达式中乘号不能省略,A不正确;输入语句后只能跟变量,不能是表达式,跟多个变量时要用逗号隔开,∴B、D不正确;输出语句后可跟表达式,故选C.答案:C6.用秦九韶算法求多项式f(x)=5x4-7x3+x+2当x=2的值时,需要次乘法运算,次加法运算. ()A.4 2 B.4 3 C.4 4 D.5 3思路解析:多项式可表示为f(x)=(((5x-7)x)x+1)x+2,需4次乘法,3次加法运算.答案:B7.用秦九韶算法求多项式f(x)=0.5x5+4x4-3x2+x-1当x=3的值时,先算的是() A.3×3=9 B.0.5×35 =121.5C.0.5×3+4=5.5 D.(0.5×3+4)×3=16.5思路解析:把多项式表示成如下形式:f(x)=((((0.5x+4)x)x-3)x+1)x-1,按递推方法,由里往外,先算0.5x+4的值.答案:C8.今天星期二,问再过42(7) 天是星期()A.二B.三C.四D.五思路解析:把42(7)转化为十进制数30,30/7=4(余2),余数为0时,还是星期二,所以余数为2时是星期四,故选C.答案:C9.运行以下程序时,循环体内语句执行的次数是()i=1WHILE i<10i=i+1i=i*iWENDPRINT iENDA.2 B.3 C.4 D.5思路解析:第一次执行循环体i=1→i=i+1→i=i*i,得到i=4,返回判断条件,满足条件i<10;第二次执行循环体i=4→i=i+1→i=i*i,得到i=25,不满足条件,退出循环体,共执行了2次.故选A.答案:A10.下列程序计算的数学式是()INPUT nT=1:s=0:i=1WHILE i<=nT=T*is=s+1/Ti=i+1WENDPRINT sENDA.1+2+3+…+n B.1!+2!+3!+…+n!C.1!+1/2!+1/3!+…+1/n! D.1+1/2+1/3+…+1/n思路解析:本题是一个递推累加问题,由T=T*i经过循环依次得到1!,2!,3!,…,n!,由s=s+1/T实现累加.故选C.答案:C11.用秦九韶算法求多项式f(x)=2+0.35x+1.8x2-3x3+6x4-5x5+x6在x=-1的值时,令v 0=a 6,v 1= v 0x+a 5,…,v 6=v 5x+a 0.则v 3的值是_______.思路解析:f(x)=(((((x-5)x+6)x-3)x+1.8)x+0.35)x+2,v 0=1,v 1=v 0x -5 =-6,v 2=v 1x+6=-6×(-1)+6=12,v 3=v 2x -3=-15.答案:-1512.分析下面的程序:INPUT xIF 9<x AND x<100 THENa=x/10b=x MOD 10x=10*b+aPRINT xELSEPRINT “输入有误!”END IFEND若输入38,运行上面的程序后,得到的结果是_______.思路解析:由条件可知输入的数应是两位,x=38,x/10取x 的十位是3,x MOD 10取x 的个位数是8,由x=10*b+a 得到83.答案:8313.把十进制数26记为32,这样的进制是________.思路解析:设该进制为k 进制,则3×k 1+2×k 0=26,∴k=8.答案:814.鸡兔同笼,已知鸡兔总头数h ,总脚数为f ,求鸡兔各有多少只?思路解析:设鸡x 只,兔y 只,则⎩⎨⎧=+=+,42,f y x h y x ∴ x=24f h -, y=22h f -. 解:程序框图如图 .程序:INPUT“输入鸡兔总头数:”;hINPUT“输入鸡兔总脚数:”;fX=(4*h-f)/2Y=(f-2*h)/2PRINT “鸡的只数为:”;xPRINT “兔的只数为:”;yEND15.将某科成绩分为3个等级:85~100为“A”;60~84为“B”;60以下为“C”.试用条件语句表示某个成绩等级的算法.思路解析:输入一个成绩,然后判断在哪个分数段内,从而输出相应的等级.解:程序框图如图:程序:INPUT “输入成绩:”;xIF x<60 THENPRINT “C”ELSEIF x<=84 THENPRINT “B”ELSEPRINT “A”ENDIFENDIFEND16.编程实现求310的值.思路解析:310是10个3相乘,可用循环来实现,循环10次.解:程序如下:S=1i=1WHILE i<=10S=3*Si=i+1WENDPRINT SEND程序框图:17.已知f(x)=⎪⎩⎪⎨⎧≥<<+≤1x 1,-x 1x 1,-1x --1x 1,-x -2,画出求 个n x f f f f )))(((n 个的程序框图. 思路解析:本题看似是一个简单的分段函数问题,用条件结构来实现,实际上所求的是一个n 重复合,所以还要引入循环结构,由里向外依次求解,注意在每次循环之前要用x=f(x)实现函数值到自变量的过渡转换.解:如图:18.2005年全国街舞电视大奖赛总决赛共有24个队参加,并请了12名评委,在计算每队选手的得分时,为了避免个别评委所给的极端分数的影响,按常规必须去掉一个最高分、一个最低分后再求平均分.如果采用百分制,试设计算法求某队的得分,画出程序框图,写出程序.思路解析:由于共有12位评委,所以每队会有12个分数,可以用循环来实现12个分数的输入,并实现累加、求和,按照题目要求,我们还要在这12个分数中找出最高分与最低分,即求12个数中的最大、最小值.用max表示最大值,min表示最小值,因为采用百分制,可设初值max=0,min=100(思考:为什么,反过来可以吗),在循环过程中,每输入一个分数x,就与max,min比较,如果x>max,则max=x,如果x<min,则min=x,如此循环下去,就能求出最大、最小值,最后从总和中减去这两个值,即为该队的最后得分.解:程序框图如图:程序:sum=0:i=1max=0:min=100 DOINPUT xsum=sum+xIF max<xTHENmax=xENDIFIF min>xTHENmin=xEND IFi=i+1LOOP UNTILi>12 s=sum-max-min a=s/10PRINTaEND。
人教A版高中数学必修三练习:第一章算法初步1.1算法与程序框图含答案

分层训练·进阶冲关A基(建用20分)1. 以下对于算法的法中正确的个数有( B )①求解某一的算法是独一的;②算法必在有限步操作以后停止;2③x-x>2 019 是一个算法 ;④算法行后必定生确立的果.A.1B.2C.3D.42.以下所中 , 不可以一个算法求解的是 ( D ) A. 用“二分法”求方程 x2-3=0 的近似解 ( 精准度 0.01)B.解方程C.求半径 2 的球的体D.求 S=1+2+3+⋯的3. 程序框符号“”可用于( B )A. 出 a=10B.a=10C.判断 a=10D.入 a=14.如所示的程序框 , 已知 a1=3, 出的果 7, a2的是( C )A.9B.10C.11D.125.以下图的流程图 , 当输入的值为 -5 时, 输出的结果是( D )A.-3B.-2C.-1D.26.依据以下图的程序框图 , 使适当作绩不低于 60 分时 , 输出“及格”, 当作绩低于 60 分时 , 输出“不及格” , 则 ( A )A. 框 1 中填“是” , 框 2 中填“否”B. 框 1 中填“否” , 框 2 中填“是”C.框 1 中填“是” , 框 2 中可填可不填D.框 2 中填“否” , 框 1 中可填可不填7.下边是某人出家门先打车去火车站 , 再坐火车去北京的一个算法 , 请增补完好 .第一步 , 出家门 .第二步 ,打车去火车站.第三步 , 坐火去北京 .8. 使用配方法解方程x2-4x+3=0 的算法的步是②①④③( 填序号).22①配方得 (x-2) =1; ②移得 x -4x=-3;9.行如所示的程序框 , 出的 S= 0.99 .10.行如所示的程序框 , 假如入的 x,t 均 2, 出的 S=7.11.求 1+3+5+7+⋯+31 的算法 , 并画出相的程序框 .【分析】第一步 :S=0;第二步 :i=1;第三步 :S=S+i;第四步 :i=i+2;第五步 :若 i 不大于 31, 返回履行第三步 ,不然履行第六步 ;第六步 :输出 S 值.程序框图如图 .12.设计一个算法求知足 10<x2<1 000 的全部正整数 , 并画出程序框图 . 【分析】算法步骤以下 :第一步 ,x=1.第二步 ,假如 x 2 >10, 那么履行第三步 ;不然履行第四步 .第三步 ,假如 x 2 <1 000, 那么输出 x; 不然结束程序 .第四步 ,x=x+1,转到第二步.程序框图如图 :B组提高练( 建议用时 20 分钟)13.履行以下图的程序框图 , 若输入 n=8, 则输出的 k= ( B )A.2B.3C.4D.514. 以下图的程序框图所表示的算法的功能是( C )A.算 1+ + +⋯+的B.算 1+ + +⋯+的C.算 1+ + +⋯+的D.算 1+ + +⋯+的15.行如所示的程序框 , 运转相的程序 , 最后出的果16.若框所示程序运转的出果 S=132,那么判断框中填入的对于 k 的判断条件是k≤10?或 k<11? .17. 已知直 l1:3x-y+12=0 和直 l 2:3x+2y-6=0, 一个算法 , 求 l 1和l2及 y 所成的三角形的面.【分析】算法以下 :第一步 ,解方程组得 l 1,l2的交点为 P(-2,6).第二步 ,在方程 3x-y+12=0中,令 x=0, 得 y=12, 进而获得 l1与 y 轴的交点为 A(0,12).第三步 ,在方程 3x+2y-6=0中,令 x=0, 得 y=3, 进而获得 l 2与 y 轴的交点为 B(0,3).第四步 ,求出△ABP 的边长 AB=12-3=9.第五步 ,求出△ABP 的边 AB 上的高 h=2.第六步 ,依据三角形的面积公式计算S=·AB·h=×9×2=9.第七步 ,输出 S.18.利用梯形的面积公式计算上底为 4, 下底为 6, 面积为 15 的梯形的高 . 请设计出该问题的算法及程序框图.【分析】依据梯形的面积公式S= (a+b)h,得h=,此中 a 是上底,b 是下底 ,h 是高 ,S 是面积 ,只需令 a=4,b=6,S=15,代入公式即可.算法以下 :第一步 ,输入梯形的两底a,b 与面积 S 的值 .第二步 ,计算 h=.第三步 ,输出 h.该算法的程序框图以下图:C组培优练 ( 建议用时 15 分钟 )19.履行以下图的程序框图所表达的算法 , 假如最后输出的 S值为, 那么判断框中实数 a 的取值范围是[2 015,2 016).20.运转以下图的程序框图 .(1) 若输入 x 的值为 2, 依据该程序的运转过程达成下边的表格, 并求输出的 i 与 x 的值 .第 i 次i=1i=2i=3i=4i=5ix=2×3(2)若输出 i 的值为 2, 求输入 x 的取值范围 .【分析】 (1)第 i 次i=1i=2i=3i=4i=5x=2 ×3 i61854162486由于 162<168,486>168,因此输出的 i 的值为 5,x 的值为 486.(2)由输出 i 的值为 2, 则程序履行了循环体 2 次,即解得<x ≤56.因此输入 x 的取值范围是.封闭 Word 文档返回原板块。
高中必修三数学第一章算法初步
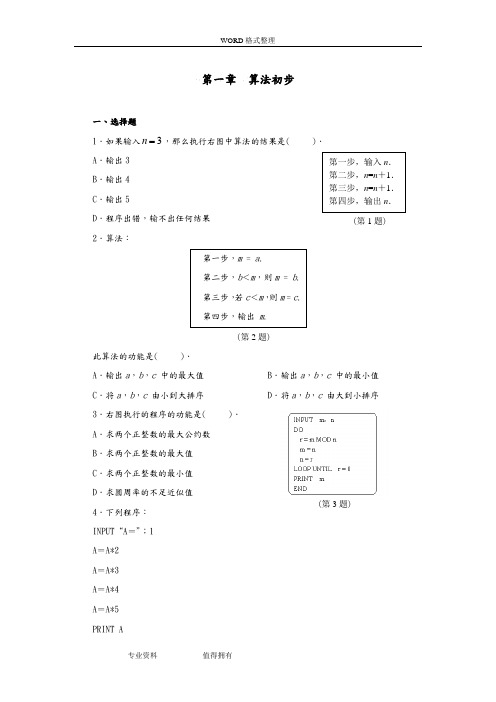
第一章 算法初步一、选择题1.如果输入3n ,那么执行右图中算法的结果是( ). A .输出3 B .输出4 C .输出5D .程序出错,输不出任何结果 2.算法:此算法的功能是( ). A .输出a ,b ,c 中的最大值 B .输出a ,b ,c 中的最小值 C .将a ,b ,c 由小到大排序D .将a ,b ,c 由大到小排序3.右图执行的程序的功能是( ). A .求两个正整数的最大公约数B .求两个正整数的最大值C .求两个正整数的最小值D .求圆周率的不足近似值 4.下列程序: INPUT “A =”;1 A =A *2 A =A *3 A =A *4 A =A *5 PRINT A(第1题)(第2题)(第3题)END输出的结果A 是( ). A .5B .6C .15D .1205.下面程序输出结果是( ).A .1,1B .2,1C .1,2D .2,26.把88化为五进制数是( ). A .324(5)B .323(5)C .233(5)D .332(5)7.已知某程序框图如图所示,则执行该程序后输出的结果是( ). A .1- B .1C .2D .12(第5题)(第7题)8.阅读下面的两个程序:甲 乙对甲乙两程序和输出结果判断正确的是( ).A .程序不同,结果不同B .程序不同,结果相同C .程序相同,结果不同D .程序相同,结果相同9.执行右图中的程序,如果输出的结果是4,那么输入的 只可能是( ).A .-4B .2C .2 或者-4D .2或者-410.按照程序框图(如右图)执行,第3个输出的数是( ). A .3 B .4 C .5 D .6二、填空题(第8题)(第9题)11.960与1 632的最大公约数为 .12.如图是某个函数求值的程序框图,则满足该程序的函数解析式为 _________.13.执行下图所示的程序,输出的结果为48,则判断框中应填入的条件为 .(第13题)14.下列所画流程图是已知直角三角形两条直角边a ,b 求斜边的算法,其中正确的是 .(写出正确的序号)(第12题)15.流程图中的判断框,有1个入口和 个出口. 16.给出以下问题:①求面积为1的正三角形的周长; ②求键盘所输入的三个数的算术平均数; ③求键盘所输入的两个数的最小数;④求函数⎩⎨⎧=22)(x x x f 当自变量取x 0时的函数值.其中不需要用条件语句来描述算法的问题有 . 三、解答题17.编写一个程序,计算函数f (x )=x 2-3x +5当x =1,2,3,…,20时的函数值.,x ≥3,x <318.编写程序,使得任意输入的3个整数按从大到小的顺序输出.19.编写一个程序,交换两个变量A和B的值,并输出交换前后的值.20.编写一个程序,计算两个非零实数的加、减、乘、除运算的结果(要求输入两个非零实数,输出运算结果).参考答案一、选择题1.C解析:本题通过写出一个算法执行后的结果这样的形式,来考查对算法的理解及对赋值语句的掌握.2.B解析:此算法为求出a,b,c中的最小值.3.A解析:本题通过理解程序语言的功能,考查求两个正整数最大公约数的算法.4.D解析:A=1×2×3×4×5=120.5.B解析:T=1,A=2,B=T=1.6.B解析:∵88=3×52+2×5+3,∴88为323(5).7.A解析:本题以框图为载体,对周期数列进行考查.数列以3项为周期,2 010除以3余数为0,所以它与序号3对应相同的数.8.B解析:结果均为 1+2+3+…+1 000,程序不同.9.B解析:如x≥0,则x2=4,得x=2;如x<0,则由y=x,不能输出正值,所以无解.10.C解析:第一个输出的数是1;第二个输出的数是3;第三个输出的数是5.二、填空题11.96.解析:(1 632,960)→(672,960)→(672,288)→(384,288)→(96,288)→(96,192)→(96,96).12.f (x )=⎩⎨⎧0 ,4- 50<,32x x x x -解析:根据程序框图可以知道这是一个分段函数. 13.答案:i ≥4?. 解析:根据程序框图分析:可知答案为i ≥4?. 14.①.解析:③、④选项中的有些框图形状选用不正确;②图中的输入变量的值应在公式给出之前完成.15.2.解析:判断框的两个出口分别对应“是”(Y)或“否”(N). 16.①②.解析:③④需用条件语句. 三、解答题 17.程序:(如图)18.第一步,输入3个整数a ,b ,c .第二步,将a 与b 比较,并把小者赋给b ,大者赋给a .第三步,将a 与c 比较.并把小者赋给c ,大者赋给a ,此时a 已是三者中最大的.≥ (第17题)第四步,将b 与c 比较,并把小者赋给c ,大者赋给b ,此时a ,b ,c 已按从大到小的顺序排列好.第五步,按顺序输出a ,b ,c . 程序:(如下图所示)19.程序:20.程序:。
高中数学人教A版必修三习题第一章-算法的概念含答案

答案:C
2.求过 P(a1,b1),Q(a ,b2)两点的直线斜率有如下的算法,请将算法补充完整: 2
S1 取 x1=a1,y1=b1,x2=a ,y2=b2. 2
S2 若 x1=x ,则输出斜率不存在;否则,________. 2
S 输出计算结果 k 或者无法求解信息.
3
解析:根据直线斜率公式可得此步骤.
第三步,依次从 2 到(n-1)检验能不能整除 n,若不能整除 n,则执行第四步;若能整
除 n,则执行第一步.
第四步,输出 n.
满足条件的 n 是( )
A.质数
B.奇数
C.偶数
D.约数
解析:此题首先要理解质数,只能被 1 和自身整除的大于 1 的整数叫质数.2是最小的
质数,这个算法通过对 2 到(n-1)一一验证,看是否有其他约数,来判断其是否为质数.
B 级 能力提升 1.结合下面的算法: 第一步,输入 x.
3
第二步,判断 x 是否小于 0,若是,则输出 x+2;否则,执行第三步.
第三步,输出 x-1.
当输入的 x 的值为-1,0,1 时,输出的结果分别为( )
A.-1,0,1
B.-1,1,0
C.1,-1,0
D.0,-1,1
解析:根据 x 值与 0 的关系选择执行不同的步骤.
第四步,得到方程组的解{x=10,)
y=20. 第五步,输出结果,鸡 10只,兔 20只.
4
答案:A
二、填空题
6.给出下列算法:
第一步,输入 x 的值.
第二步,当 x>4时,计算 y=x+2;否则执行下一步.
第三步,计算 y= 4-x.
第四步,输出 y.
当输入 x=0 时,输出 y=________.
高中数学 第一章 算法初步 1.3.1 辗转相除法与更相减损术练习(含解析)新人教A版必修3-新人教

第8课时辗转相除法与更相减损术知识点一辗转相除法1.有关辗转相除法,下列说法正确的是( )A.它和更相减损术一样是求多项式值的一种方法B.基本步骤是用较大的数m除以较小的数n得到除式m=nq+r,直至r<n为止C.基本步骤是用较大的数m除以较小的数n得到除式m=nq+r(0≤r<n),若r≠0,则将n的值赋给m,r的值赋给n,继续前面步骤,直至r=0为止D.以上说法皆错答案 C解析由辗转相除法的步骤易知C项正确.2.90与252的最大公约数是( )A.9 B.18 C.27 D.63答案 B解析利用辗转相除法求解.252=90×2+7290=72×1+1872=18×4+0,∴90与252的最大公约数为18.知识点二更相减损术3.更相减损术可解决下列问题中的( )A.求两个正整数的最大公约数B.求多项式的值C.进位制的转化计算D.排序问题答案 A解析更相减损术是解决求两个或两个以上的正整数的最大公约数的.4.如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )A.0 B.2C.4 D.14答案 B解析第一次执行,输入a=14,b=18,因为a<b,所以b=18-14=4;第二次执行,因为a=14,b=4,a>b,所以a=14-4=10;第三次执行,因为a=10,b=4,a>b,所以a =10-4=6;第四次执行,因为a=6,b=4,a>b,所以a=6-4=2;第五次执行,因为a =2,b=4,a<b,所以b=4-2=2,此时a=b=2.故选B.5.用更相减损术求319与261的最大公约数.解319-261=58,261-58=203,203-58=145,145-58=87,87-58=29,58-29=29,故319与261的最大公约数是29.易错点更相减损术求最大公约数时忽略乘约简数致误6.用更相减损术求612和468的最大公约数.易错分析当两个数均为偶数时,由于忽略用2约分,而导致错误.正解因为612和468都为偶数,所以两次用2约分化简,得153和117.用更相减损术求153和117的最大公约数,步骤如下:153-117=36,117-36=81,81-36=45,45-36=9,36-9=27,27-9=18,18-9=9,所以612和468的最大公约数为9×2×2=36.一、选择题1.用更相减损术求得81与135的最大公约数是( )A.54 B.27 C.9 D.81答案 B解析因为135-81=54,81-54=27,54-27=27,所以81与135的最大公约数是27.2.用“辗转相除法”求得459和357的最大公约数是( )A.3 B.9 C.17 D.51答案 D解析459=357×1+102,357=102×3+51,102=51×2,所以459和357的最大公约数为51.3.用辗转相除法计算60和48的最大公约数时,需要做的除法次数是( )A.1 B.2 C.3 D.4答案 B解析60=48×1+12,48=12×4+0,故只需要做两次除法运算.4.下列说法中正确的个数为( )①辗转相除法也叫欧几里得算法;②辗转相除法的基本步骤是用较大的数除以较小的数;③求最大公约数的方法,除辗转相除法之外,没有其他方法;④编写辗转相除法的程序时,要用到循环语句.A.1 B.2 C.3 D.4答案 C解析易知①②④正确;对于③,更相减损术也可求最大公约数,故③错误.5.运行下面的程序,当输入数据为78和36时,输出的值为( )INPUT “输入两个不同正整数m,n=”;m,nDOIF m>n THENm=m-nELSE n=n-mEND IFLOOP UNTIL m=nPRINT mENDA.24 B.18 C.12 D.6答案 D解析由程序语句知,此程序是用更相减损术求输入的两个数的最大公约数,因为78-36=42,42-36=6,36-6=30,30-6=24,24-6=18,18-6=12,12-6=6,所以选D.二、填空题6.用更相减损术求104与65的最大公约数是________.答案13解析由于65不是偶数,把104和65以大数减小数,并辗转相减,即104-65=39,65-39=26,39-26=13,26-13=13,所以104与65的最大公约数为13.7.三个数72,120,168的最大公约数是________.答案24解析120=72×1+48,72=48×1+24,48=24×2,168=24×7.8.阅读程序:INPUT “m,n=”;m,nIF n>m THENt=mm=nn=tEND IFDOr=m MOD nm=nn=rLOOP UNTIL r=0PRINT mEND若INPUT语句中输入m,n的值分别是161,368,则程序运行的结果为________.答案23解析该程序的功能是用辗转相除法求两个数的最大公约数.输入161,368,可求出它们的最大公约数为23.三、解答题9.用辗转相除法和更相减损术两种方法求80和36的最大公约数.解用辗转相除法:80=36×2+8,36=8×4+4,8=4×2+0.故80和36的最大公约数是4.用更相减损术:先用2约简得40和18,再用2约简得20和9,20-9=11,11-9=2,9-2=7,7-2=5,5-2=3,3-2=1,2-1=1,∴80和36的最大公约数是4.10.某化工厂有三种溶液,分别为4200毫升,3220毫升和2520毫升,现要将它们分别装入小瓶中,每个瓶子装入液体的体积相同,问:要使所有溶液都刚好装满小瓶且所用瓶子最少,则小瓶的容积应为多少毫升?解为了使所有溶液都装入瓶中,恰好都装满且所用瓶子最少,求所用瓶子的容积,也就是求这三种溶液的体积的最大公约数.先求4200和3220的最大公约数,4200=3220×1+980,3220=980×3+280,980=280×3+140,280=140×2,所以4200和3220的最大公约数是140.再求140和2520的最大公约数,2520=140×18,所以140和2520的最大公约数是140.综上,4200,3220和2520的最大公约数是140.所以小瓶的容积应为140毫升.。
中学人教版高中数学必修三同步练习:第一章算法初步单元测评(附答案)

单元测评(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷60分,第Ⅱ卷90分,共150分,考试时间120分钟.第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.算法有三种基本逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是()A.一个算法只能包含一种基本逻辑结构B.一个算法最多可以包含两种基本逻辑结构C.一个算法必须包含三种基本逻辑结构D.一个算法可能包含三种基本逻辑结构2.389化成的四进制数的末位是()A.1 B.2C.3 D.03.关于终端框的说法正确的是()A.表示一个算法的起始和结束,图形符号是B.表示一个算法输入和输出的信息,图形符号是C.表示一个算法的起始和结束,图形符号是D.表示一个算法输入和输出的信息,图形符号是4.执行图C11所示的程序框图,若输出的结果为11,则M处可填入的条件为()图C11A.k≥31 B.k≥15C.k>31 D.k>155.用秦九韶算法求多项式f(x)=12+35x+9x3+5x5+3x6当x=-1时的值,有如下说法:①要用到6次乘法;②要用到6次加法和15次乘法;③v0=12;④v3=11.其中说法正确的是()A.①③B.①④C.②④D.①③④6.执行图C12所示的程序框图,若输入x=-2,h=0.5,则输出的各个数的和等于()图C12A.3 B.3.5C.4 D.4.57.由辗转相除法得三个数720,120,168的最大公约数是()A.24 B.30 C.120 D.688.执行图C13所示的程序框图,若输出的S值为16,则输入的自然数n的最小值等于()图C13A.7 B.8 C.9 D.109.执行下面程序,若输出y的值为1,则输入x的值为()A.0 B.1 C.0或1 D.-1,0或110.如果下面程序执行后输出的结果是990,那么在程序中①处应为()A.i>10 B.i<8C.i<=9 D.i<911.某店一个月的收入或支出为a1,a2,…,a N,其中收入记为正数,支出记为负数.该店用如图C14所示的程序框图计算月总收入S和月净盈利V,那么在图中空白的判断框和处理框中应分别填入()图C14A.A>0,V=S-TB.A<0,V=S-TC.A>0,V=S+TD.A<0,V=S+T12.计算机中常用到的十六进制采用数字0~9和字母A~F共16个计数符号,各符号与十进制的对应关系如下表:例如用十六进制表示有D+E=1B,则A×B=()A.6E B.7C C.5F D.B0请将选择题答案填入下表:第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.若输入8,则执行下列程序后输出的结果是________.14.将二进制数101101(2)化为十进制数,结果为________;再将这个十进制数化为八进制数,结果为________.15.按如图C15所示的程序框图运算,若输入的x 的值为8,则输出的k 等于________.图C1516.阅读下面的程序,该算法的功能是______________________________________.三、解答题(本大题共6个小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)已知函数f (x )=⎩⎪⎨⎪⎧x 2-1(x ≥0),2x 2-5(x <0), 每输入一个x 值,都得到相应的函数值,画出程序框图并写出程序.18.(12分)图C16所示的程序框图表示了一个什么样的算法?试用当型循环写出它的算法并画出相应的程序框图.图C16 19.(12分)用秦九韶算法求多项式f(x)=x5+x3+x2+x+1当x=3时的值.20.(12分)(1)用更相减损术求184,253的最大公约数;(2)用辗转相除法求98,280的最大公约数.21.(12分)设计算法求11×2+ 12×3+ 13×4+…+ 199×100的值,要求画出程序框图,并用基本的算法语句编写程序.22.(12分)输入x ,求函数y =⎩⎪⎨⎪⎧3x -2,x ≥2,-2,x <2 的值的程序框图如图C17所示.(1)指出程序框图中的错误之处并写出正确的算法步骤. (2)重新绘制程序框图,并回答下面提出的问题. ①要使输出的值为7,则输入的x 的值应为多少? ②要使输出的值为正数,则输入的x 应满足什么条件?图C17单元测评(一)1.D2.A [解析] 将389化成四进制数是12011(4).3.C [解析] 终端框表示一个算法的起始和结束,图形符号是.4.B [解析] 依题意k =1,S =0,进入循环,循环过程依次为:S =0+1=1,k =2×1+1=3;S =1+3=4,k =2×3+1=7;S =4+7=11,k =2×7+1=15,终止循环,输出S =11.结合选项知,M 处可填k ≥15.5.B [解析] 因为x 的最高次数为6,所以①正确,②错误;v 0=3,故③错误;v 1=v 0x +5=2,v 2=v 1x +0=-2,v 3=v 2x +9=11,故④正确.6.B [解析] 按照程序框图依次执行为x =-2,h =0.5,输出y =0;x =-1.5,h =0.5,输出y =0;x =-1,h =0.5,输出y =0;x =-0.5,h =0.5,输出y =0;x =0,h =0.5,输出y =0;x =0.5,h =0.5,输出y =0.5;x =1,h =0.5,输出y =1;x =1.5,h =0.5,输出y =1;x =2,h =0.5,输出y =1,结束循环.故输出的各个数的和为3.5,选B.7.A [解析] 由辗转相除法得120和168的最大公约数是24,再由辗转相除法得24和720的最大公约数是24.故选A.8.C [解析] 根据程序框图可知i =2,k =1,S =1,进入循环后,循环次数与S ,i ,k 的值的变化如下表:第3次循环后,S =8,i =8,应满足条件“i <n ”,故自然数n ≥9;第4次循环后,S =16,i =10,应退出循环,不满足条件“i <n ”,故自然数n ≤10.所以9≤n ≤10,因此自然数n 的最小值等于9.9.C [解析] 由题意得⎩⎪⎨⎪⎧x ≥1,1=x 2 或⎩⎪⎨⎪⎧x <1,1=-x 2+1,解得x =1或x =0,故选C. 10.D [解析] 由程序易知①处为“i<9”.11.C [解析] 月总收入S 应当为本月的各项收入之和,故需满足A >0.月净盈利应当为月总收入减去本月各项支出的和,又T <0,所以V =S +T .因此,判断框内应填“A >0”,处理框内应填“V =S +T ”.12.A[解析] A×B对应的十进制数是110,所以用十六进制表示有A×B=6E.13.0.7[解析] 这是一个利用条件结构编写的程序,当输入t=8时,执行c=0.2+0.1×(t-3),得c=0.7.14.4555(8)[解析] 101101(2)=1×25+0×24+1×23+1×22+0×21+1×20=45,∴化为十进制数为45.又45=8×5+5,∴45=55(8).15.3[解析] 第一次循环x=88,k=1,通过判断得,需要继续循环;第二次循环x =888,k=2,通过判断得,需要继续循环;第三次循环x=8888,k=3,通过判断,结束循环,输出k=3.故最后输出的k值为3.16.求S=1+2+3+…+20和t=1×2×3×…×20的值17.解:程序框图和程序如下.18.解:这是一个计算10个数的平均数的算法.当型循环的算法如下:第一步,S=0.第二步,I=1.第三步,如果I小于等于10,执行第四步;否则,转第七步.第四步,输入G.第五步,S=S+G.第六步,I=I+1,返回第三步.第七步,A=S10. 第八步,输出A. 程序框图如图.19.解:f(x)=x5+x3+x2+x+1=((((x+0)x+1)x+1)x+1)x+1.当x=3时,v0=1,v1=1×3+0=3,v2=3×3+1=10,v3=10×3+1=31,v4=31×3+1=94,v5=94×3+1=283,∴f(3)=283.20.解:(1)用更相减损术,得253-184=69,184-69=115,115-69=46,69-46=23,46-23=23,∴184与253的最大公约数是23.(2)用辗转相除法,得280=98×2+84,98=84×1+14,84=14×6,∴98与280的最大公约数是14.21.解:程序框图和程序如下.22.解:(1)函数y =⎩⎪⎨⎪⎧3x -2,x ≥2,-2,x <2是分段函数,其程序框图中应该有判断框,应该有条件结构,不应该只用顺序结构.正确的算法步骤如下所示:第一步,输入x .第二步,判断x ≥2是否成立.若是,则y =3x -2;否则y =-2. 第三步,输出y .(2)根据(1)中的算法步骤,可以画出程序框图如图所示.①要使输出的值为7,则3x -2=7,故x =3,即输入的x 的值应为3.②要使输出的值为正数,则⎩⎪⎨⎪⎧x ≥2,3x -2>0,得x ≥2.故当x ≥2时,输出的值为正数.。
高中数学必修三第一章《算法初步》章节练习题(含答案)

《算法初步》章节练习题(30分钟50分)一、选择题(每小题3分,共18分)1.如图是某程序框图的一部分,其算法的逻辑结构为( )A.顺序结构B.判断结构C.条件结构D.循环结构2.下列各进位制数中,最大的数是( )A.11111(2)B.1221(3)C.312(4)D.56(8)3.如图所示,当输入x为2 006时,输出的y= ( )A.28B.10C.4D.2【补偿训练】执行如图所示的程序框图,若输出的结果是9,则判断框内m的取值范围是( )A.(42,56]B.(56,72]C.(72,90]D.(42,90]4.168,54,264的最大公约数是( )A.4B.6C.8D.95.下列程序的功能是( )S=1i=3WHILE S<=10000S=S ii=i+2WENDPRINT iENDA.求1×2×3×4×…×10 000的值B.求2×4×6×8×…×10 000的值C.求3×5×7×9×…×10 001的值D.求满足1×3×5×…×n>10 000的最小正整数n【补偿训练】如图程序框图中,语句“S=S×n”将被执行的次数是( )A.4B.5C.6D.76.执行如图所示程序框图,输出的k值为( )A.3B.4C.5D.6【补偿训练】如图是计算函数y=的值的程序框图,则在①、②和③处应分别填入的是( )A.y=-x,y=0,y=x2B.y=-x,y=x2,y=0C.y=0,y=x2,y=-xD.y=0,y=-x,y=x2二、填空题(每小题4分,共12分)7.执行如图所示的程序框图,若输入n的值为8,则输出s的值为.【补偿训练】某程序框图如图所示,若使输出的结果不大于37,则输入的整数i的最大值为.8.对任意非零实数a,b,若a⊗b的运算原理如图所示,则log8⊗= .29.阅读如图所示的程序框图,运行相应的程序,输出的结果s= .【补偿训练】阅读如图所示的程序框图,运行相应的程序,输出的S值等于.三、解答题(每小题10分,共20分)10.已知一个5次多项式为f(x)=5x5+2x4+3.5x3-2.6x2+1.7x-0.8,用秦九韶算法求这个多项式当x=5时的值.11.为了节约用水,学校改革澡堂收费制度,实行计时收费,洗澡时间在30分钟以内(含30分钟),每分钟收费0.1元,30分钟以上超出的部分每分钟0.2元,请设计程序,使用基本语句完成澡堂计费工作,要求输入时间,输出费用.【补偿训练】陈老师购买安居工程集资房62m2,单价为3 000元/m2.一次性国家财政补贴27 900元,学校补贴18 600元,余款由个人负担.房地产开发公司对教师实行分期付款(注①),每期为一年,等额付款.签订购房合同后一年付款一次,再经过一年又付款一次,共付10次,10年后付清.如果按年利率5.6%,每年按复利计算(注②),那么每年应付款多少元?画出程序框图,并写出计算所需的程序.注:①各期所付款的本息和的总和,应等于个人负担的购房余款的本息和.②每年按复利计算,即本年利息计入次年的本金中生息.《算法初步》章节练习题参考答案(30分钟50分)一、选择题(每小题3分,共18分)1.如图是某程序框图的一部分,其算法的逻辑结构为( )A.顺序结构B.判断结构C.条件结构D.循环结构【解析】选C.条件结构是处理逻辑判断并根据判断结果进行不同处理的结构,由算法流程图知,该算法的逻辑结构为条件结构.2.下列各进位制数中,最大的数是( )A.11111(2)B.1221(3)C.312(4)D.56(8)【解析】选C.11111(2)=1+1×2+1×22+1×23+1×24=1+2+4+8+16=31.1221(3)=1+2×3+2×32=1+6+18+27=52.312(4)=2+1×4+3×42=2+4+48=54.56(8)=6+5×8=6+40=46.3.(2015·陕西高考改编)如图所示,当输入x为2 006时,输出的y= ( )A.28B.10C.4D.2【解题指南】模拟执行程序框图,依次写出每次循环得到的x的值,当x=-2时不满足条件x ≥0,计算并输出y的值为10.【解析】选B.模拟执行程序框图,可得x=2 006,x=2 004满足条件x≥0,x=2 002满足条件x≥0,x=2 000…满足条件x≥0,x=0满足条件x≥0,x=-2不满足条件x≥0,y=10输出y的值为10.【补偿训练】执行如图所示的程序框图,若输出的结果是9,则判断框内m的取值范围是( )A.(42,56]B.(56,72]C.(72,90]D.(42,90]【解析】选B.第一次运行:S=2,k=2;第二次运行:S=6,k=3;…;第七次运行:S=56,k=8;第八次运行:S=2+4+6+…+16=72,k=9,输出结果.故判断框中m的取值范围是(56,72].4.(2015·襄阳高一检测)168,54,264的最大公约数是( )A.4B.6C.8D.9【解析】选B.168-54=114,114-54=60,60-54=6,54-6=48,48-6=42,42-6=36,36-6=30,30-6=24,24-6=18,18-6=12,12-6=6,故168和54的最大公约数为6.又因为264=44×6+0,所以6是264和6的最大公约数.所以这三个数的最大公约数为6.5.下列程序的功能是( )S=1i=3WHILE S<=10000S=S ii=i+2WENDPRINT iENDA.求1×2×3×4×…×10 000的值B.求2×4×6×8×…×10 000的值C.求3×5×7×9×…×10 001的值D.求满足1×3×5×…×n>10 000的最小正整数n【解析】选D.法一:S是累乘变量,i是计数变量,每循环一次,S乘以i一次且i增加2.当S>10 000时停止循环,输出的i值是使1×3×5×…×n>10 000成立的最小正整数n.法二:最后输出的是计数变量i,而不是累乘变量S.【补偿训练】如图程序框图中,语句“S=S×n”将被执行的次数是( )A.4B.5C.6D.7【解析】选B.由程序框图知:S=1×2×3×…×n.又1×2×3×4×5=120<200,1×2×3×4×5×6=720>200.故语句“S=S×n”被执行了5次,选B.6.(2015·北京高考改编)执行如图所示程序框图,输出的k值为( )A.3B.4C.5D.6【解题指南】按照程序框图顺序执行.【解析】选B.k=0,a=3,q=;a=,k=1;a=,k=2;a=,k=3;a=,k=4.【补偿训练】如图是计算函数y=的值的程序框图,则在①、②和③处应分别填入的是( )A.y=-x,y=0,y=x2B.y=-x,y=x2,y=0C.y=0,y=x2,y=-xD.y=0,y=-x,y=x2【解析】选B.当x> -1不成立时,y=-x,故①处应填“y=-x”;当x>-1成立时,若x>2,则y=x2,即②处应填“y=x2”,否则y=0,即③处应填“y=0”.二、填空题(每小题4分,共12分)7.(2015·苏州高一检测)执行如图所示的程序框图,若输入n的值为8,则输出s的值为.【解析】第一次循环,s=×(1×2)=2,i=4,k=2;第二次循环,s=×(2×4)=4,i=6,k=3;第三次循环,s=×(4×6)=8,i=8,k=4.此时退出循环,输出s的值为8.答案:8【补偿训练】某程序框图如图所示,若使输出的结果不大于37,则输入的整数i的最大值为.【解析】S=(20+1)+(21+1)+(22+1)+…+(2i-1+1).当i=1时,S=2;当i=2时,S=2+3=5;当i=3时,S=2+3+5=10;当i=4时,S=2+3+5+9=19;当i=5时,S=2+3+5+9+17=36;当i=6时,S=2+3+5+9+17+33>37.所以i的最大值为5.答案:58⊗= .8.对任意非零实数a,b,若a⊗b的运算原理如图所示,则log2【解析】log28<,则题意知,log28⊗=3⊗4==1.答案:19.(2015·大同高一检测)阅读如图所示的程序框图,运行相应的程序,输出的结果s= .【解析】程序在运行过程中各变量的值如下表示:第一次循环:当n=1时,得s=1,a=3.第二次循环:当n=2时,得s=4,a=5.第三次循环:当n=3时,得s=9,a=7,此时n=3,不再循环,所以输出s=9.答案:9【补偿训练】阅读如图所示的程序框图,运行相应的程序,输出的S值等于.【解析】第一次循环:S=1,k=1<4,S=2×1-1=1,k=1+1=2.第二次循环:k=2<4,S=2×1-2=0,k=2+1=3.第三次循环:k=3<4,S=2×0-3=-3,k=3+1=4,当k=4时,k<4不成立,循环结束,此时S=-3.答案:-3三、解答题(每小题10分,共20分)10.已知一个5次多项式为f(x)=5x5+2x4+3.5x3-2.6x2+1.7x-0.8,用秦九韶算法求这个多项式当x=5时的值.【解析】根据秦九韶算法,把多项式改写成如下形式:f(x)=((((5x+2)x+3.5)x-2.6)x+1.7)x-0.8,按照从内到外的顺序,依次计算一次多项式当x=5时的值;v0=5;v1=5×5+2=27;v2=27×5+3.5=138.5;v3=138.5×5-2.6=689.9;v4=689.9×5+1.7=3 451.2;v5=3 451.2×5-0.8=17 255.2;所以,当x=5时,多项式的值等于17 255.2.的值.”【延伸探究】若本题中已知条件不变,求“当x=2时v3【解析】v0=5;v1=5×2+2=12;v2=12×2+3.5=27.5;v3=27.5×2-2.6=52.4.故x=2时,v3=52.4.11.(2015·武汉高一检测)为了节约用水,学校改革澡堂收费制度,实行计时收费,洗澡时间在30分钟以内(含30分钟),每分钟收费0.1元,30分钟以上超出的部分每分钟0.2元,请设计程序,使用基本语句完成澡堂计费工作,要求输入时间,输出费用.【解题指南】题目为分段函数,用条件结构求解.【解析】设时间为t分钟,则费用y为y=程序框图如图所示.这里应用的是条件结构,应该用条件语句来表述,INPUT tIF t<=30 THENy=0.1tELSEy=3+(t-30)0.2END IFPRINT yEND【补偿训练】陈老师购买安居工程集资房62m2,单价为3 000元/m2.一次性国家财政补贴27 900元,学校补贴18 600元,余款由个人负担.房地产开发公司对教师实行分期付款(注①),每期为一年,等额付款.签订购房合同后一年付款一次,再经过一年又付款一次,共付10次,10年后付清.如果按年利率5.6%,每年按复利计算(注②),那么每年应付款多少元?画出程序框图,并写出计算所需的程序.注:①各期所付款的本息和的总和,应等于个人负担的购房余款的本息和.②每年按复利计算,即本年利息计入次年的本金中生息.【解析】设每年应付款x元,那么第一年付款的本息和为x×1.0569元,第二年付款的本息和为x×1.0568元,…第九年付款的本息和为x×1.056元,第十年付款为x元.所以各期所付款的本息和的总和为x(1+1.056+1.0562+…+1.0569).所购房余款的本息和为[3 000×62-(27 900+18 600)]×1.05610=139 500×1.05610,故有x(1+1.056+1.0562+…+1.0569)=139 500×1.05610,即x=.程序框图如下图所示:。
高中数学必修3(人教A版)第一章算法初步1.1知识点总结含同步练习及答案

描述:例题:高中数学必修3(人教A版)知识点总结含同步练习题及答案第一章 算法初步 1.1 算法与程序框图一、学习任务1. 了解算法的含义,了解算法的基本思想,能用自然语言描述解决具体问题的算法.2. 了解设计程序框图表达解决问题的过程,了解算法和程序语言的区别;了解程序框图的三种基本逻辑结构,会用程序框图表示简单的常见问题的算法.二、知识清单算法 程序框图三、知识讲解1.算法算法(algorithm)是指按照一定规则解决某一类问题的明确和有限的步骤 .可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤,或者看成按照要求设计好的有限的确切的计算序列,并且这样的步骤或序列能够解决一类问题.描述算法可以有不同的方式.例如,可以用自然语言和数学语言加以描述,也可以借助形式语言(算法语言)给出精确的说明,也可以用框图直观地显示算法的全貌.算法的要求:(1)写出的算法,必须能解决一类问题,并且能重复使用;(2)算法过程要能一步一步执行,每一步执行的操作必须确切,不能含混不清,而且经过有限步后能得到结果.下列对算法的理解不正确的是( )A.一个算法应包含有限的步骤,而不能是无限的B.算法中的每一个步骤都应当是确定的,而不应当是含糊的、模棱两可的C.算法中的每一个步骤都应当是有效地执行,并得到确定的结果D.一个问题只能设计出一种算法解:D算法的有限性是指包含的步骤是有限的,故 A 正确;算法的确定性是指每一步都是确定的,故 B正确;算法的每一步都是确定的,且每一步都应有确定的结果,故 C 正确;对于同一个问题可以有不同的算法,故 D 错误.下列叙述能称为算法的的个数为( )描述:2.程序框图程序框图简称框图,是一种用程序框、流程线及文字说明来表示算法的图形.其中,起、止框是任何流程不可少的,表明程序的开始和结束.输入和输出框可用在算法中任何需要输入、输出的位置.算法中间要处理数据或计算,可分别写在不同的处理框内.一个算法步骤到另一个算法步骤用流程线连接.如果一个框图需要分开来画,要在断开处画上连接点,并标出连接的号码.①植树需要运苗、挖坑、栽苗、浇水这些步骤;②依次进行下列运算:,,,,;③从枣庄乘火车到徐州,从徐州乘飞机到广州;④ ;⑤求所有能被 整除的正整数,即 .A. B. C. D.解:B①、②、③为算法.1+1=22+1=33+1=4⋯99+1=1003x >x +133,6,9,12,⋯2345写出解方程组的一个算法.解:方法一:代入消元法. 第一步,由 得 ;第二步,将 代入 ,得 ,解得 ;第三步,将 代入方程 ,得 ;第四步,得到方程组的解为 .方法二:加减消元法.第一步,方程 两边同乘以 ,得 ;第二步,将第一步所得的方程与方程 作差,消去 ,得 ,解得 ;第三步,将 代入方程 ,得 ,解得 ;第四步,得到方程组的解为 .{2x +y =74x +5y =112x +y =7y =7−2x y =7−2x 4x +5y =114x +5(7−2x )=11x =4x =4y =7−2x y =−1{x =4y =−12x +y =7510x +5y =354x +5y =11y 6x =24x =4x =42x +y =72×4+y =7y =−1{x =4y =−1例题:画程序框图的规则(1)使用标准的图形符号.(2)框图一般按从上到下、从左到右的方向画.(3)除判断框外,大多数流程图符号只有一个进入点和一个退出点.判断框是具有超过一个退出点的惟一符号.(4)判断框分两大类,一类判断框是“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果.(5)在图形符号内描述的语言要非常简练清楚.算法的三种基本逻辑结构顺序结构:语句与语句之间,框与框之间按从上到下的顺序进行.条件分支结构:在一个算法中,经常会遇到一些条件的判断,算法的流程条件是否成立有不同的流向,条件结构就是处理这种过程的结构.循环结构:在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是循环结构.下列程序框图分别是解决什么问题的算法.解:(1)已知圆的半径,求圆的面积的算法.(2)求两个实数加法的算法.执行如图的程序框图,输出的 ______ .解:T =30四、课后作业 (查看更多本章节同步练习题,请到快乐学)某程序框图如图所示,若输出的 ,则判断框内为( )A. B. C. D.解:AS =57k >4?k >5?k >6?k >7?已知函数 ,对每次输入的一个值,都得到相应的函数值,画出程序框图.解:f (x )={2x +3,3−x ,x 2x ⩾0x <0x答案:1. 关于算法的说法中,正确的是 A .算法就是某个问题的解题过程B .算法执行后可以产生不确定的结果C .解决某类问题的算法不是唯一的D .算法可以无限地操作下去不停止C()答案:解析:2. 下列运算不属于我们所讨论算法范畴的是 A .已知圆的半径求圆的面积B .随意抽 张扑克牌算到二十四点的可能性C .已知坐标平面内两点求直线方程D .加减乘除法运算法则B注意算法需按照一定的顺序进行.()4答案:解析:3. 执行如图所示的程序框图,如果输入的 ,则输出的 属于 .A .B .C .D .D取 ,得输出的 ,即可判断.t ∈[−2,2]S ()[−6,−2][−5,−1][−4,5][−3,6]t =−2S =64. 某批发商按客户订单数额的大小分别给予不同的优惠折扣.计算客户应付货款的算法步骤如下: :输入订单数额 (单位:件);输入单价 (单位:元);:若 ,则折扣率 ;若 ,则折扣率 ;若 ,则折扣率 ;若 ,则折扣率 ;:计算应付货款 (单位:元);:输出应付货款 .S 1x A S 2x <250d =0250⩽x <500d =0.05500⩽x <1000d =0.10x ⩾1000d =0.15S 3T =Ax (1−d )S 4T。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章《算法初步》测试题
一.选择题
1.下面的结论正确的是 ( )
A .一个程序的算法步骤是可逆的
B 、一个算法可以无止境地运算下去的
C 、完成一件事情的算法有且只有一种
D 、设计算法要本着简单方便的原则 2、早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个步骤、从下列选项中选最好的一种算法 ( )
A 、 S1 洗脸刷牙、S2刷水壶、S3 烧水、S4 泡面、S5 吃饭、S6 听广播
B 、 S1刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5 听广播
C 、 S1刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭 同时 听广播
D 、 S1吃饭 同时 听广播、S2泡面、S3烧水同时洗脸刷牙、S4刷水壶 3.算法 S1 m=a
S2 若b<m ,则m=b S3 若c<m ,则m=d S4 若d<m ,则 m=d
S5 输出m ,则输出m 表示 ( ) A .a ,b ,c ,d 中最大值
B .a ,b ,c ,d 中最小值
C .将a ,b ,c ,d 由小到大排序
D .将a ,b ,c ,d 由大到小排序 4.右图输出的是
A .2005
B .65
C .64
D .63 5、下列给出的赋值语句中正确的是( )
A. 5 = M
B. x =-x
C. B=A=3
D. x +y = 0
6、下列选项那个是正确的( ) (第4题) A 、INPUT A;B B. INPUT B=3 C. PRINT y=2*x+1 D. PRINT 4*x
7、以下给出的各数中不可能是八进制数的是( ) A.123 B.10 110 C.4724 D.7 857
8、如果右边程序执行后输出的结果是990,那么 在程序until 后面的“条件”应为( ) A.i > 10 B. i <8 C. i <=9 D.i<9 9.读程序 甲: i=1 乙: i=1000 S=0 S=0 WHILE i<=1000 DO S=S+i S=S+i i=i+l i=i 一1 WEND Loop UNTIL i<1 PRINT S PRINT S
END END
对甲乙两程序和输出结果判断正确的是
( )
A .程序不同结果不同
B .程序不同,结果相同
C .程序相同结果不同
D .程序相同,结果相同
10.在上题条件下,假定能将甲、乙两程序“定格”在i=500,即能输出i=500 时一个值,则输出结果 ( )
A .甲大乙小
B .甲乙相同
C .甲小乙大
D .不能判断 二.填空题.
11、有如下程序框图(如右图所示),则该程序框图表示的算法的功能是
( 第12题)
12、上面是求解一元二次方程)0(02≠=++a c bx ax 的流程图,根据题意填写:(1) (2) (3)
13.将二进制数1010 101(2) 化为十进制结果为 ;
再将该数化为八进制数,结果为 .
第一趟 第二趟 第三趟 第四趟
15.计算
11011(2)-101(2)= (用二进制表示) 三、解答题
16. 已知算法: ①将该算法用流程图描述之。
②写出该程序。
S1、 输入 X
S2 、 若X<1,执行 S3. 否则执行S6 S3 、 Y =X - 2 S4、输出 Y S5、 结束
S6、 若X=1 ,执行S7;否则执行S10;
(第11题) 第
S7 Y =0 S8 输出Y S9 结束 S10 Y= 2X+1 S11 输出Y S12 结束 17、设计算法求
50
491
431321211⨯+
⋅⋅⋅+⨯+⨯+⨯的值,写出用基本语句编写的程序. 18.用辗转相除法求210与162的最大公约数,并用更相减损术检验。
19、《中华人民共和国个人所得税法》规定,公民月工资,薪金所得不超过800元的部分不必纳税,超过800元的部分为全月应纳税 所得额,此项税款按下表分段累进计算:
20、给出30个数:1,2,4,7,……,其规律是:第1个数是1,第2个
数比第1个数大1, 第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),(I )请在图中判断框内(1)处和执行框中的(2)处填上合适的语句,使之能完成该题算法功能;(II )根据程序框图写出程序.
(第20题)
数学第一章测试题
姓名 座位号 班别
一、选择题
二、填空题
11..计算并输出使1×3×5×7…× >10 000成立的最小整数.
12.(1)
(2)x1= a
b 2∆
+- x2=a b 2∆-- (3) 输出x1,x2
13. 85 、 125(8)
14.用冒泡法对数3,6,9,5,1从小到大排序
第一趟 第二趟 第三趟 第四趟
15. 10110
三、解答题
16. 该算法是求函数
Y=⎪⎪⎪⎪
⎩
⎪⎪
⎪⎪
⎨⎧+==-=120
2X Y Y X Y )
1()
1()
1(>=<X X X
17、解 这是一个累加求和问题,共49项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.程序框图如下图所示
第17题 程序框图
18. 6 19.
y=
5800
2800%
15)2800(1502528001300%10)1300(251300800%5)800(8000
≤<⨯-++≤<⨯-+≤<⨯-≤x x x x x x x
20.解 (I )该算法使用了当型循环结构,因为是求30个数的和,故循环体应执行30次,其中i 是计数变量,因此判断框内的条件就是限制计数变量i 的,故应为30≤i .算法 中的变量p 实质是表示参与求和的各个数,由于它也是变化的,且满足第i 个数比其前一个数大1-i ,,第1+i 个数比其前一个数大i ,故应有i p p +=.故(1)处应填30≤i ;(2)处应填i p p +=。
