受控源电路的分析演示课件
合集下载
含受控源的电路分析

图3-18
解:以i1, i2和 i3为网孔电流,用观察法列出网孔 1和网孔2
的网孔方程分别为:
补充两个受控源控制变量 与网孔电流i1和i2关系的方程:
图3-18
代入 =1, =1和两个补充方程到网孔方程中,移项整 理后得到以下网孔方程:
解得网孔电流i1=4A, i2=1A和i3 =3A。
四、含受控源电路的结点方程
时间函数变化的电压和电流,从而在电路中产生电压和电
流。 受控源则描述电路中两条支路电压和电流间的一种约 束关系,它的存在可以改变电路中的电压和电流,使电路 特性发生变化。
图3-13
图(a)所示的晶体管在一定条件下可以用图(b)所示的
模型来表示。这个模型由一个受控源和一个电阻构成,这
个受控源受与电阻并联的开路电压控制,控制电压是ube,
图3-12
当受控源的控制系数r、g、和为常量时,它们是时 不变双口电阻元件。本书只研究线性时不变受控源,并采
用菱形符号来表示受控源 ( 不画出控制支路 ) ,以便与独立
电源相区别。 受控源与独立电源的特性完全不同,它们在电路中所 起的作用也完全不同。
独立电源是电路的输入或激励,它为电路提供按给定
由线性电阻和独立电源构成的单口网络,就端口特性
而言,可以等效为一个线性电阻和电压源的串联单口,或
等效为一个线性电阻和电流源的并联单口。 由线性受控源、线性电阻和独立电源构成的单口网络, 就端口特性而言,可以等效为一个线性电阻和电压源的串 联单口,或等效为一个线性电阻和电流源的并联单口。 同样,可用外加电源计算端口 VCR方程的方法,求得 含线性受控源电阻单口网络的等效电路。
将控制变量i3用网孔电流表示,即补充方程
图3-17
2.8 受控源和含受控源简单电路的分析

受控源与独立源的区别
1、两者都是电源; 2、独立源在电路中是能量转换装置; 3、受控源是描述电路器件中控制与被控制的关系; 4、含独立源的电路所有分析方法对含受控源的电路一样适用。
+
10V
-
+ 10I 1-
+
4Ω U
-
解:在应用叠加定理时,在各独立源单独作用
的电路中,受控源均要保留,控制量相应地变
4A 成各独立源单独作用时产生的电压或电流。 (1)10V电压源单独作用
I1′ 6Ω
+ 10I1′-
+
+
10V
4Ω U ′
-
-
I1
10 64
1A,
U I1 4 10I1 6V
2.8 受控源和含受控源简单电路的分析
一、受控源
电源分为独立电源和受控电源 (1)独立电源:能独立的对外电路提供能量的电源. (2)受控电源:
电压源的输出电压或电流源的输出电流受电路中其 它部分的电流或电压控制的电源,简称受控源。
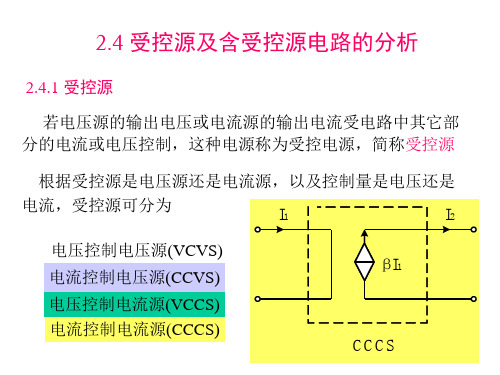
根据控制量是电压或电流,以及被控制量是电压源或电 流源,受控源可分为:
(2)4A电流源单独作用
I1′ ′6Ω
+ 10I1′′ -
+ 4A
4Ω U ′′
-
I1
4 64
(4)
1.6A
对大回路有:
6I
1
1 0I 1
U
0
U
1
6I
1
2 5.6V
(3)两个电源共同作用时
U U U
6 25.6 19.6V
注:含受控源电路的分析,受控源不能简单的看成独立电源。 要注意控制量与被控制量之间的关系,控制量存在,则被控制 量存在。
含受控源的电路分析

解:先将受控电压源和2电阻的串 联单口等效变换为受控电流源 0.5ri和2电阻的并联单口, 如图(b)所示。
图2-39
将2和3并联等效电阻1.2和受控电流源0.5ri并联, 等效变换为1.2电阻和受控电压源0.6ri的串联,如图(c)所 示。
由此求得
u (5 1.2 0.6r)i (8)i
单口等效电阻为
的网孔方程分别为:
(6)i1 (2)i2 (2)i3 16V (2)i1 (6)i2 (2)i3 u1
(6)i1 (2)i2 (2)i3 16V (2)i1 (6)i2 (2)i3 u1
补充两个受控源控制变量 与网孔电流i1和i2关系的方程:
u1 (2)i1 i3 i1 i2
G11v1 G12v2 ... G1(n1)vn1 iS11 G21v1 G22v2 ... G v 2(n1) n1 iS22
(2 30)
G( v n1)1 1 G(n1)2v2 G v (n1)(n1) n1 iS(n1((n1)
例2-29 列出图2-43电路的结点方程。
口等效电阻Ro=-R,这表明该电路可将正电阻变换为一个负 电阻。
例2-23 求图2-36(a)所示单口网络的等效电阻。
图2-36
解:设想在端口外加电压源u,写出端口电流i的表达式为
i
i1
i1
(
1)i1
1u
R
Gou
由此求得单口的等效电导为
Go
i u
(α
1)G
图2-36
由此求得单口的等效电导为
R11i1 R12i2 ... R1mim uS11
R21i1 R22i2 ... R2mim uS22 ........................
图2-39
将2和3并联等效电阻1.2和受控电流源0.5ri并联, 等效变换为1.2电阻和受控电压源0.6ri的串联,如图(c)所 示。
由此求得
u (5 1.2 0.6r)i (8)i
单口等效电阻为
的网孔方程分别为:
(6)i1 (2)i2 (2)i3 16V (2)i1 (6)i2 (2)i3 u1
(6)i1 (2)i2 (2)i3 16V (2)i1 (6)i2 (2)i3 u1
补充两个受控源控制变量 与网孔电流i1和i2关系的方程:
u1 (2)i1 i3 i1 i2
G11v1 G12v2 ... G1(n1)vn1 iS11 G21v1 G22v2 ... G v 2(n1) n1 iS22
(2 30)
G( v n1)1 1 G(n1)2v2 G v (n1)(n1) n1 iS(n1((n1)
例2-29 列出图2-43电路的结点方程。
口等效电阻Ro=-R,这表明该电路可将正电阻变换为一个负 电阻。
例2-23 求图2-36(a)所示单口网络的等效电阻。
图2-36
解:设想在端口外加电压源u,写出端口电流i的表达式为
i
i1
i1
(
1)i1
1u
R
Gou
由此求得单口的等效电导为
Go
i u
(α
1)G
图2-36
由此求得单口的等效电导为
R11i1 R12i2 ... R1mim uS11
R21i1 R22i2 ... R2mim uS22 ........................
第4章 受控源电路的

U + U1 I1 = Z1
i
U I2 = Z2
i
把它们代入[ 把它们代入[1]便得
1 1 U1 i = IS + U + Z1 Z1 Z 2
i i
[2]
含有解变量之外, 上式除 U含有解变量之外,还含有控制变量 U 故应再列出一个方程. 故应再列出一个方程.从图中看出
i 1
i
,
U = U 1 + U1
(a)
(b)
对结点1 以结点2为参考结点)可列出KCL式 对结点1(以结点2为参考结点)可列出KCL式 KCL i '1 iS + i ' 2 = 0 [l ] 由元件特性方程, 由元件特性方程,得
4.3受控源电路的简化分析 4.3受控源电路的简化分析
4.3.1叠加原理在分析受控流电路中的应 4.3.1叠加原理在分析受控流电路中的应 用 在使用叠加原理分析受控源电路时必须注 由于受控源受控制量的控制, 意:由于受控源受控制量的控制,不能独 立地作用于电路( 立地作用于电路(如果让受控源独立地作 用于电路, 用于电路,则该电路的所有支路电流均为 ).当某个独立源单独作用于电路时 当某个独立源单独作用于电路时, 零).当某个独立源单独作用于电路时, 受控源所在处既不能用断路代替, 受控源所在处既不能用断路代替,也不能 短路,只能保持原状不变. 短路,只能保持原状不变.
U m1 = jω M I 2
i i
(4-1-2a) 2a) (4-1-2b) 2b)
U m 2 = jω M I1
i
i
将其看作是特殊的电压源. 将其看作是特殊的电压源.
图4-1-2
虚线方框内的符号表示这 两个特殊的电压源. 两个特殊的电压源.它们 每一个都是有4 每一个都是有4个端钮的 元件, 元件,其中两个是输入端 ),另两个是输 (1和1 '),另两个是输 出端( 出端(2和2'). 输入端用导线连接, 输入端用导线连接,菱形 符号表示电压源, 符号表示电压源,其两端 电压受输入端电流的控制, 电压受输入端电流的控制, 它们之间的关系由式( 它们之间的关系由式(4 表示. -l-2)表示. 这个特殊电压源的输出电 压受输入电流的控制, 压受输入电流的控制,称 受控源. 为受控源.
i
U I2 = Z2
i
把它们代入[ 把它们代入[1]便得
1 1 U1 i = IS + U + Z1 Z1 Z 2
i i
[2]
含有解变量之外, 上式除 U含有解变量之外,还含有控制变量 U 故应再列出一个方程. 故应再列出一个方程.从图中看出
i 1
i
,
U = U 1 + U1
(a)
(b)
对结点1 以结点2为参考结点)可列出KCL式 对结点1(以结点2为参考结点)可列出KCL式 KCL i '1 iS + i ' 2 = 0 [l ] 由元件特性方程, 由元件特性方程,得
4.3受控源电路的简化分析 4.3受控源电路的简化分析
4.3.1叠加原理在分析受控流电路中的应 4.3.1叠加原理在分析受控流电路中的应 用 在使用叠加原理分析受控源电路时必须注 由于受控源受控制量的控制, 意:由于受控源受控制量的控制,不能独 立地作用于电路( 立地作用于电路(如果让受控源独立地作 用于电路, 用于电路,则该电路的所有支路电流均为 ).当某个独立源单独作用于电路时 当某个独立源单独作用于电路时, 零).当某个独立源单独作用于电路时, 受控源所在处既不能用断路代替, 受控源所在处既不能用断路代替,也不能 短路,只能保持原状不变. 短路,只能保持原状不变.
U m1 = jω M I 2
i i
(4-1-2a) 2a) (4-1-2b) 2b)
U m 2 = jω M I1
i
i
将其看作是特殊的电压源. 将其看作是特殊的电压源.
图4-1-2
虚线方框内的符号表示这 两个特殊的电压源. 两个特殊的电压源.它们 每一个都是有4 每一个都是有4个端钮的 元件, 元件,其中两个是输入端 ),另两个是输 (1和1 '),另两个是输 出端( 出端(2和2'). 输入端用导线连接, 输入端用导线连接,菱形 符号表示电压源, 符号表示电压源,其两端 电压受输入端电流的控制, 电压受输入端电流的控制, 它们之间的关系由式( 它们之间的关系由式(4 表示. -l-2)表示. 这个特殊电压源的输出电 压受输入电流的控制, 压受输入电流的控制,称 受控源. 为受控源.
最新电路(蔡小玲)精品课件02 受控源和基尔霍夫定律

.
.
_
1.5 电压源和电流源
电压源和电流源
实际电流源的产生:可由稳流电子设备产生。有些 电子器件输出具备电流源特性,如晶体管的集电极电 流与负载无关;光电池在一定光线照射下被激发产生 一定值的电流等
1.6 受控源
受控源
在电子电路中广泛使用各种晶体管、运算放大器等多端 器件。这些多端器件的某些端钮的电压或电流受到另一些端 钮电压或电流的控制。为了模拟多端器件各电压、电流间的
这种耦合关系,需要定义一些多端电路元件(模型)
本节介绍的受控源是一种非常有用的电路元件,常用来模
拟含晶体管、运算放大器等多端器件的电子电路。从事电子、
通信类专业的工作人员,应掌握含受控源的电路分析
1.6 受控源
若一个电源的输出电压(电流)受到电路中其 它支路的电压(电流)控制时,称为受控源 由两条支路构成(四端元件) 控制支路:开路或短路状态;
电压源
理想电压源 若一个二端元件输出电压恒定则称为理想电压源 电路符号
.
Us
.
.
u s ( t) _ +
.
1.5 电压源和电流源
理想电压源
基本性质: I + Us + _ 输出电压恒定,和外电路无关
其流过的电流由外电路决定
伏安特性曲线:
思考:什么情 况下U的曲线 会出现在第二 象限?
U
_
U
U U Us Us I R R
.
is Gs
isc
.+
u=0
u 0, isc is
(isc: 短路电流)
.
.
_
1.5 电压源和电流源
加载: i is Gsu
受控电源电路的分析-PPT

受控电源电路的分析
2.6 受控电源电路的分析 2.6.1受控电源 2.6.2受控电源电路的分析计算 2.6.3 输入电阻(输入阻抗) 2.6.4 输出电阻(输出阻抗)
2
§2.6 受控源电路的分析
2.6.1受控电源
电压源
电源
独立源
电流源
非独立源(受控源)
3
独立源和非独立源的异同
相同点:两者性质都属电源,均可向电路 提供电压或电流。
I1 (1 )I1 (1
27
R1R2
R1 (1 )R2
U i
) Ui R1
例5:R1=1k, R2=1k, R3=2k, U1=1V, U2=5V
求:电流I3
A
I1
R1
+
– U1
I2 I=40I1
R2
+
U2
–
I3 R3
B
用戴维南定理
(1)求开路电压 (2)求等效电阻(用开路电压
除短路电流法) (3)求I3
Us B
I2'
+
-
UD=0.4UAB
I1''
A
I2''
R1 R2 +
Is UD=0.4UAB
B
I1 I1' I1" 3.75 1.25 2.5A I2 I2' I2" 3.75 0.75 4.5A
14
受控源电路分析计算 - 要点(2)
可以用两种电源互换、等效电源定理等方法,简 化受控源电路。但简化时注意不能把控制量化简掉。 否则会留下一个没有控制量的受控源电路,使电路 无法求解。
6/7
UD' +
2.6 受控电源电路的分析 2.6.1受控电源 2.6.2受控电源电路的分析计算 2.6.3 输入电阻(输入阻抗) 2.6.4 输出电阻(输出阻抗)
2
§2.6 受控源电路的分析
2.6.1受控电源
电压源
电源
独立源
电流源
非独立源(受控源)
3
独立源和非独立源的异同
相同点:两者性质都属电源,均可向电路 提供电压或电流。
I1 (1 )I1 (1
27
R1R2
R1 (1 )R2
U i
) Ui R1
例5:R1=1k, R2=1k, R3=2k, U1=1V, U2=5V
求:电流I3
A
I1
R1
+
– U1
I2 I=40I1
R2
+
U2
–
I3 R3
B
用戴维南定理
(1)求开路电压 (2)求等效电阻(用开路电压
除短路电流法) (3)求I3
Us B
I2'
+
-
UD=0.4UAB
I1''
A
I2''
R1 R2 +
Is UD=0.4UAB
B
I1 I1' I1" 3.75 1.25 2.5A I2 I2' I2" 3.75 0.75 4.5A
14
受控源电路分析计算 - 要点(2)
可以用两种电源互换、等效电源定理等方法,简 化受控源电路。但简化时注意不能把控制量化简掉。 否则会留下一个没有控制量的受控源电路,使电路 无法求解。
6/7
UD' +
2.5受控源及含受控源电路的分析
本节小结 1、含受控源电路的分析与独立源电路基本相同,不同点是应用 叠加定理时受控源不能单独作用 2、含受控源和电阻的二端电路可等效为一个电阻 3、含独立源、受控源和电阻的二端电路,等效为一个电压源 和一个电阻的串联 4、含受控源电路的等效电阻需采用外加电源法或短路电流法 求解
课堂练习: 1、求下图所示电路的戴维宁等效电路
U T R 1 (1 )R 2 I T
RO UT R 1 (1 )R 2 IT
I I T
原电路的戴维宁等效电路
RO
+ U OC I
R3
U OC I S (R 1 R 2 ) U S I R O R 3 R 1 R 3 (1 )R 2
对三极管的输入回路,有
+ U -
I
Ib rbe
β Ib
RC RE Ie
RB
E
( I I b ) RB I b rbe (1 ) I b RE U
RB Ib I R B rbe (1 )R E
二端电路的输入电阻
RB rbe (1 ) RE U rbe (1 ) RE I b I RB rbe (1 ) RE
I1 + U1 -
+ μU 1 -
+ U2 -
+ γ I1 -
+ U2 -
(a) V C V S
I2 + U1 I1
(b) C C V S
I2
gU 1
β I1
(c) V C C S
受控源的四种类型
Hale Waihona Puke (d) C C C SR2 a
R3
1-6受控源100914
电路原理
例题分析
例4:求图示电路a、b端口的等效电阻Rab。 在端口施加一激励源(可加电压 解:
3u 1Ω
源,也可加电流源)
a
2Ω R + ab u 2Ω
b
1 2 u 2( 3u 1) 1 1 2 8 1A u V 15 u 8 Rab 1 15
电路原理
由此看出含受控源的网络其等效电阻可以为负值。
-
i2 电路原理
§16 受 控 源 · 分类
控制支路(输入端口) 控制量
电压控受控源
受控支路(输出端口)
u1 (i1=0)
VCVS
受控量
u2 受控电压源
CCVS
VCCS
电流控受控源
i1 (u1=0)
CCCS
i2
受控电流源
①电压控电压源(VCVS:Voltage Controlled Voltage Source) ②电压控电流源(VCCS:Voltage Controlled Current Source) ③电流控电流源(CCCS:Current Controlled Current Source) ④电流控电压源(CCVS:Current Controlled Voltage Source) 电路原理
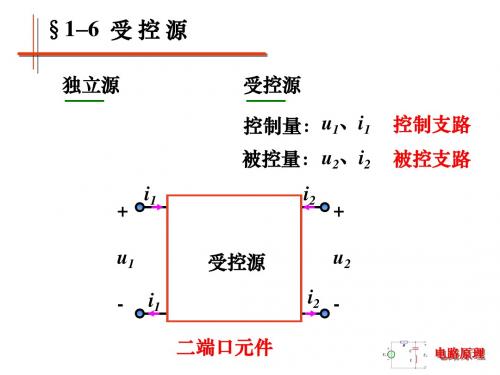
§16 受 控 源
独立源 受控源 控制量: u1、i1
被控量: u2、i2 + u1 i1 控制 被控 受控源 支路 支路 i1 二端口元件 i2 + u2 控制支路 被控支路
-
i2 电路原理
§16 受 控 源 · 定义
电路中有一条支路的电压(或电流)受另一 条支路的电压或电流控制,这两条支路就构 成一个受控源。这两条支路分别称为受控支 路和控制支路。 i1 i2 + + u1 控制 被控 受控源 支路 支路 i1 二端口元件 u2
例题分析
例4:求图示电路a、b端口的等效电阻Rab。 在端口施加一激励源(可加电压 解:
3u 1Ω
源,也可加电流源)
a
2Ω R + ab u 2Ω
b
1 2 u 2( 3u 1) 1 1 2 8 1A u V 15 u 8 Rab 1 15
电路原理
由此看出含受控源的网络其等效电阻可以为负值。
-
i2 电路原理
§16 受 控 源 · 分类
控制支路(输入端口) 控制量
电压控受控源
受控支路(输出端口)
u1 (i1=0)
VCVS
受控量
u2 受控电压源
CCVS
VCCS
电流控受控源
i1 (u1=0)
CCCS
i2
受控电流源
①电压控电压源(VCVS:Voltage Controlled Voltage Source) ②电压控电流源(VCCS:Voltage Controlled Current Source) ③电流控电流源(CCCS:Current Controlled Current Source) ④电流控电压源(CCVS:Current Controlled Voltage Source) 电路原理
§16 受 控 源
独立源 受控源 控制量: u1、i1
被控量: u2、i2 + u1 i1 控制 被控 受控源 支路 支路 i1 二端口元件 i2 + u2 控制支路 被控支路
-
i2 电路原理
§16 受 控 源 · 定义
电路中有一条支路的电压(或电流)受另一 条支路的电压或电流控制,这两条支路就构 成一个受控源。这两条支路分别称为受控支 路和控制支路。 i1 i2 + + u1 控制 被控 受控源 支路 支路 i1 二端口元件 u2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例6 用电源等效变换法求U.
3
+
I1
2I1
-4V 4 3A
+ U
-
+ 6I1 - 3
+ 4V I1
+ U
-
4
-
解: 据KVL
6I1-3×3+U-4I1=0
I1=
4 4
A
=1A
U=7V
例7 化简
解
I+
6Ω 3Ω
+
+
U
6V _
_0.3U
-
1A
U=(I+1+0.1U) ×2 0.8U=2I+2
U10 24V
U20 8V
U20 U
I U10 U20 16A 2
受控源电路分析计算 - 要点(2)
可以用两种电源互换、等效电源定理等方法,简化受控源 电路。但简化时注意不能把控制量化简掉。(应保留控制量所 在支路)否则会留下一个没有控制量的受控源电路,使电路无 法求解。
解法2:用叠加原理
电压源作用:
电流源作用:
I1' 2
1
I1" 2
1
+ –10V
+ _ 2I1'
+ 3A _ 2I1"
2I1'+ I1' +2I1' =
对大回路:
10
2I1" +(3+ I1")1+2I1"= 0
I1 I=1'I1=' 2+AI1"= 2 – 0.6=1. I41A"= – 0.6A
20 15
I1
2
2.5A
I 2 I1 I S 2.5 2 4.5A
例3 I1 2 A 2 I2
Es +
R1 R3
20V -
R2
1
+
_ ED
2A Is
ED = 0.4UAB B 求I1,I2 .
根据迭加定理
I1 I1' I1" I2 I2' I2"
I
Bs
I2''
+
-
ED=0.4U”AB
I1 I1' I1" 2.5A I2 I2' I2" 4.5A
例4 求I
3U
1
① I 2 ② +
2A
4
O
1
U -
解:
以O为参考节点, 列节点电压方程.
11
1
( 2
4 )U10
2 U20
2 3U
1
1
2 U10 (1 2)U20 3U
(2)在用迭加原理求解受控源电路时,只应分别考虑独立 源的作用;而受控源仅作一般电路参数处理。
例1 试求电流 I1 。 解法1:用支路电流法
I1 2 a 1 I2
对结点 a:I1+I2= –
+ –10V
Hale Waihona Puke 3A+ _
2I1
对3 大回路: 2I1 – I2 +2I1 解得:I1 = 1. 4 A
=
1
应用:用于晶体管电路的分析。
受控源举例
ic
ib
C
B E
ib
ic= ib
rbe
四种理想受控电源的模型
电 I1=0
压
控+
制 电 压
U1 -
I2
+
+
_ U1
U2 -
源
(a)VCVS
电 压
I1=0
控+
制 电
U1
流-
源
I2
+ gU1 U2
-
(c) VCCS
电 I1
流
控+
制 电
U1=0 -
压
I2
+
+
_
U2
6 I1
R1
E+
R2
_ 9V
1
6 ID’
I D'
ED 6
I1 6
A
SUCCESS
THANK YOU
2019/6/26
I1 6
E
+
R1
6 7
9V _
R1
6
6/7
E
+
I1
+
-
ID'
9V
ED'
_
I D'
I1 6
A
ED'
I1 7
V
6 7
6
I1
I1 7
9
I1 1.3 A
例5 I1 6
R1 E+ 9V _ R2
R3 4 1
R5
ID 2
已知:
ID 0.5I1
求: I1
例5 两种电源互换
6
I1
+ E R1
4
R5
_
R2 1
2
9V
ID
I D 0.5I1
I1 6
E
+
R1
6 7
9V _
ID'
I1
6
4
R1
E+ _
9V
R2 1
2 + _
ED
ED 2ID I1 V
U=2.5I+2.5
1A I+
2.5
+
U
_ 2.5V -
0.1U 6Ω
I+
3Ω U -
I+
0.1U
U
2Ω -
受控源电路分析计算 - 要点(3)
应用戴维南定理求解受控源电路时:
(1)如果二端网络内除了受控源外没有其他独立源, 则此二端网络的开端电压必为0。因为,只有在独立源 作用后产生控制作用,受控源才表现出电源性质。 (2)求等效电阻时,网络中的独立源去除,受控源应 保留。 (3)可以用“加压求流法”或“开路、短路法”求等 效电阻。
例2 电路参数如图所示
ED= 0.4 UAB
求:I1、 I2
解: 根据节点电压法
设 VB = 0
则:
U AB
ES R1
1
ED R2
IS
1
R1 R2
ED 0.4U AB
I1 2 A 2
Es + 20V -
R1 R3
2A
R2 1
Is
B
解得: U AB 15 V
I2
+ _ ED
代入数据得:
解得
Es -
ED=0.4U’AB
U AB' 20 2I1' 0.6U AB' 2I2'
B
I1' I2'
(2) Is 单独作用 节点电压法:
UAB' 12.5V I1' I2' 3.75 A
I '' 1
A R1
Is
I '' 2
R2 +
U AB"
-
ED=0.4U’AB
2.8 受控源电路的分析
独立源 电源
电压源 电流源
非独立源(受控源)
独立电源:指电压源的电压或电流源的电流不受
外电路的控制而独立存在的电源。 受控电源:指电压源的电压或电流源的电流受电路中
其它部分的电流或电压控制的电源。 受控源的特点:当控制电压或电流消失或等于零时,
受控源的电压或电流也将为零。
对含有受控源的线性电路,可用前几节所讲的电路分析方 法进行分析和计算 ,但要考虑受控的特性。
(1) Es 单独作用
I1'
A
I2'
+ R1 Es -
R2 +
-
ED= 0.4U’AB
B
(2) Is 单独作用
I1''
A
I2''
R1 R2 +
Is
-
ED= 0.4U”AB
B
(1) Es 单独作用
I1'
A
I2'
+ R1 R2 +
U AB' ES R1I1' U AB' 0.4U AB' R2I2'
I1 -
源
(b)CCVS
电 I1
流
控+
制 电 流
U1=0
-
I2
+
I1 U2
-
源
(d) CCCS
受控源电路的分析计算
一般原则:
电路的基本定理和各种分析计算方法仍可使用,只是 在列方程时必须增加一个受控源关系式。
受控源电路分析计算- 要点(1)
(1) 在节点电压法中,先视受控源为独立源,再列受控量 与节点电压变量的关系作为辅助方程。
ED R2
IS
11 R1 R2
0.4 U AB" 2 2
11 22
B U AB" 2.5 V
I1"
2.5 2
1.25A
I 2"
0.4 2.5 2.5 2
