数值分析(计算方法)
数值分析-计算方法-插值a
500 5
18
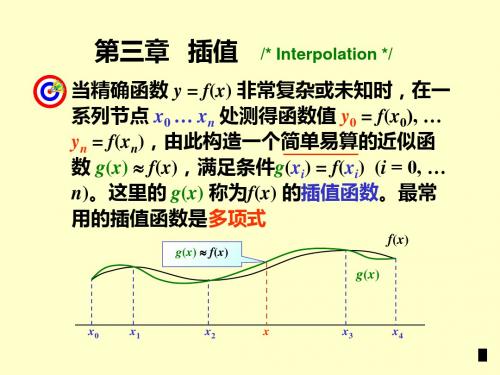
解: n = 1 分别利用x0, x1 以及 x1, x2 计算
x0
x1
x2
利用
x0 6 , x1 4
L 1 (x ) x /6 /4 /4 1 2 x /4 /6 /6 1 2
sin
而
50 0
Lf1内要( (5端1x 8插计)点 ) 通算s,0 常的i.x 7插n 7 优x6值12 2 所于4效,在外果R 1 的推(x 较) 区。f 好(f x 间选)2 ( 。 ! 的择x s )(x ix ,n 6 f)x (( x 4 )) 4 s 2 |( ix x n , 6 )x x ( ( 4 6 )|, 4)
Ln ( xi ) yi , i 0, ... , n
条件:无重合节点,即 i j xi xj
n=1
线性插值
已称知为x拉0 氏, x基1 ;函y0数, y1/*,La求graL n1 g(exB)asa is0 */,a1x 使得
L满1( 足x0 )条 件y0 l,i(Lx1j)(=x1 )ij/*yK1 ronecker Delta */
f(x)L (x) n
f ( ) (n1)
ni
i
项式是唯一存在的。
证明: 由插值条件可知,插值多项式Ln(x)的系数ai满足线性
方程组
1
x 0
xn 0
a0
y 0
1
x 1
xn 1
a1
y 1
1
x n
数值分析1-误差及有效数字

(避免绝对值很大的数为乘数)
x1 1 x1 e e x ex 2 (避免 x2 为很小的数为除数) 1 2 x x x2 2 2
er x1 x2 x1 x2 er x1 er x 2 x1 x2 x1 x2
er x1 x2
这里,主要介绍计算机中浮点数的表示形式及 表示范围(4个参数):
x s p
其中, s =±0.a1a2a3………at 称为尾数∈[-1,1],
s 中的正负号用一位数字区分;
β为基数,如取2、10、8、16; p为阶数,有上限U和下限L, 由计算机存储字节长度决定。
1.4 误差危害的防止 (1)使用数值稳定的计算公式
数值稳定是指计算过程中舍入误差对计算影响不大的算法, 若第n+1步的误差en+1 与第n步的误差en满足
en 1 1 en
,则称该计算公式是绝对稳定的
例:建立积分In=
1
0
xn dx x5
(n=0,1.........,20)
递推关系式,并分析误差传播影响。
解: I +5I
n
n-1=
x 5x 0 x 5 dx
1 n n -1
1
0
x n-1dx
x n
n
1
0
1 n
I 0=
1 0 x 5dx
1
ln x 5
1 0
=ln6-ln5
1 In -5In -1 n ∴递推式: I 0 ln6 - ln5
2
x1 x 2
2
e x1 e x 2
数值分析计算方法实验报告

end;
end;
X=x;
disp('迭代结果:');
X
format short;
输出结果:
因为不收敛,故出现上述情况。
4.超松弛迭代法:
%SOR法求解实验1
%w=1.45
%方程组系数矩阵
clc;
A=[2,10,0,-3;-3,-4,-12,13;1,2,3,-4;4,14,9,-13]
b=[10,5,-2,7]'
b=[10,5,-2,7]'
[m,n]=size(A);
if m~=n
error('矩阵A的行数和列数必须相同');
return;
end
if m~=size(b)
error('b的大小必须和A的行数或A的列数相同');
return;
end
if rank(A)~=rank([A,b])
error('A矩阵的秩和增广矩阵的秩不相同,方程不存在唯一解');
3.实验环境及实验文件存档名
写出实验环境及实验文件存档名
4.实验结果及分析
输出计算结果,结果分析和小结等。
解:1.高斯列主元消去法:
%用高斯列主元消去法解实验1
%高斯列主元消元法求解线性方程组Ax=b
%A为输入矩阵系数,b为方程组右端系数
%方程组的解保存在x变量中
format long;
A=[2,10,0,-3;-3,-4,-12,13;1,2,3,-4;4,14,9,-13]
return;
end
c=n+1;
A(:,c)=b;
for k=1:n-1
数值分析-计算方法-方程求根a-文档资料

6.3 Fixed-Point Iteration
例 用收敛定理考察例题6.1两种解法的收敛性。 解 考察等价方程:
3 x g ( x ) x 1 1
当x∈[1.4, 1.6]时g1(x)∈[1.4, 1.6], 并且有 1 g ( x ) 1 1 2 33 (x 1 ) 所以迭代方程 xk+1= g1(xk) 收敛。 考察等价方程:
k k 1 0
( k = 1, 2, … )
且存在极限
1 L x * x k 1 x lim g * k x * x k
6.3 Fixed-Point Iteration
证明:① g(x) 在[a, b]上存在不动点?
令 f a g ( x ) b ( x ) g ( x ) x
( b ) g ( b ) b 0 f ( a ) g ( a ) a 0 ,f
f (x) 有根
② 不动点唯一?
~ ~ g ( x ) 反证:若不然,设还有 x ,则 ~ ~ ~ ~ 在 x* 和x 之间。 g ( x *) g ( x ) g ( ξ ) ( x * x ), x* x
对于给定的精度 ,可估计二分法所需的步数 k :
b a b a k k |x x*| k k 2 2
b a ln b a ln ε ε k k 2 ln 2
①简单; ② 对f (x) 要求不高(只要连续即可) . ①无法求复根及偶重根 ② 收敛慢 请同学们自行设计计算程序。
xk
k xk
1
6 1.32470
1.25992
7 1.32471
数值分析与数值计算方法

数值分析与数值计算方法数值分析与数值计算方法是现代科学与工程领域中的重要学科,它涉及到利用计算机和数值方法解决数学问题的理论和技术。
本文将从数值分析的基本概念、应用领域以及常见的数值计算方法等方面进行探讨。
一、数值分析的基本概念数值分析是一门研究数学算法与计算机实现相结合的学科,旨在通过数学模型的建立和数值计算方法的选择,对实际问题进行定量分析和计算。
它不仅包括了数值计算方法的研究,还包括了误差分析、计算复杂性和算法设计等内容。
数值分析的核心任务是将问题转化为数学模型和计算机可处理的形式,通过数值计算方法求解模型得到近似解。
数值分析的基本思想是通过将连续问题离散化,将其转化为离散的代数问题,然后利用数值计算方法进行求解。
二、数值分析的应用领域数值分析广泛应用于科学和工程领域,例如物理学、化学、生物学、经济学、计算机科学等。
在实际的科学研究和工程应用中,常常需要对现象进行数值建模和计算求解,以获得更加准确的结果。
在物理学中,数值分析用于求解微分方程、积分方程等物理模型,并模拟和预测天体运动、流体流动等自然现象。
在化学和生物学中,数值分析被用于计算分子结构、化学反应动力学等问题。
在经济学中,数值分析可以用于建立经济模型、进行风险评估和决策分析。
三、常见的数值计算方法1. 插值和拟合方法:插值和拟合方法用于根据已知数据点的函数值,构造出一个逼近原函数的函数。
常见的插值方法有拉格朗日插值和牛顿插值;拟合方法包括最小二乘拟合、多项式拟合等。
2. 数值积分方法:数值积分方法用于计算函数在一定区间上的定积分。
常见的数值积分方法有梯形规则、辛普森规则等。
3. 数值微分方法:数值微分方法用于在离散数据点上估计函数的导数。
常见的数值微分方法有中心差分法和向前差分法等。
4. 常微分方程数值解法:常微分方程数值解法用于求解常微分方程的数值解。
常见的数值解法有欧拉法、龙格-库塔法等。
5. 线性方程组的数值解法:线性方程组的数值解法用于求解线性代数方程组的数值解。
数值分析计算方法试题集及答案

数值分析复习试题第一章 绪论 一. 填空题 1.*x为精确值x 的近似值;()**x f y =为一元函数()x f y =1的近似值;()**,*y x f y =为二元函数()y x f y ,2=的近似值,请写出下面的公式:**e x x =-:***r x xe x -=()()()*'1**y f x x εε≈⋅ ()()()()'***1**r r x f x y x f x εε≈⋅()()()()()**,**,*2**f x y f x y y x y x yεεε∂∂≈⋅+⋅∂∂()()()()()****,***,**222r f x y e x f x y e y y x y y y ε∂∂≈⋅+⋅∂∂ 2、 计算方法实际计算时,对数据只能取有限位表示,这时所产生的误差叫 舍入误差 。
3、 分别用2.718281,2.718282作数e 的近似值,则其有效数字分别有6 位和7 位;又取 1.73≈-211.73 10 2≤⨯。
4、 设121.216, 3.654x x ==均具有3位有效数字,则12x x 的相对误差限为0.0055 。
5、 设121.216, 3.654x x ==均具有3位有效数字,则12x x +的误差限为0.01 。
6、 已知近似值 2.4560A x =是由真值T x 经四舍五入得到,则相对误差限为0.0000204 .7、递推公式,⎧⎪⎨⎪⎩0n n-1y =y =10y -1,n =1,2,如果取0 1.41y ≈作计算,则计算到10y 时,误差为8110 2⨯;这个计算公式数值稳定不稳定 不稳定 . 8、精确值 14159265.3*=π,则近似值141.3*1=π和1415.3*2=π分别有 3位和 4 位有效数字。
9、若*2.71828x e x =≈=,则x 有 6 位有效数字,其绝对误差限为1/2*10-5。
10、 设x*的相对误差为2%,求(x*)n的相对误差0.02n11、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字;12、计算方法主要研究( 截断 )误差和( 舍入 )误差; 13、为了使计算 ()()2334610111y x x x =++---- 的乘除法次数尽量地少,应将该表达式改写为11,))64(3(10-=-++=x t t t t y ,为了减少舍入误差,应将表达式19992001-改写为199920012+。
数值分析与计算方法 第一章 插值法

同 理 : (t) 至 少 有n 个 互 异 零 点;
(t) 至 少 有n 1 个 零 点 ;
(n1) (t ) 至 少 有 一 个 零 点 ; 即 (a ,b),
(n1) (
)
R(n1) n
(
)
K ( x)n1(n1) (
)
R(n1) n
(
)
K ( x) (n
1)!
f (n1) ( ) K ( x) (n 1)! 0
x x0 x1 x2 xn , y f ( x)? y y0 y1 y2 yn
(1)有的函数没有表达式,只是一种表格函数,而我们需要的 函数值可能不在该表格中。
(2)如果函数表达式本身比较复杂,计算量会很大;
对于这两种情况,我们都需要寻找一个计算方便且表达简单
的函数 P x来近似代替 f ( x),求 P x 的方法称为插值法。
Ln1( x)
为此我们考虑对Lagrange插值多项式进行改写; ——由唯一性,仅是形式上的变化
期望:Ln ( x) 的计算只需要对Ln1( x)作一个简单的修正.
考虑 h( x) Ln ( x) Ln1( x) h( x) 是次数 n 的多项式,且有
h( x j ) Ln ( x j ) Ln1( x j ) 0 ,j 0 ,1,2 ,L ,n 1 ;
)
3
)
1 2
(x
(
4
6
6
)( x
)(
4
3
)
3
)
1
(
x
6
)(
x
4
)
2
(
3
6
)(
3
4
)
3 2
数值分析计算方法复习(典型例题)解析

6
626
复化 Simpson 公式
h
ba 2n
,
xj
a
jh
( j 0,1,,2n)
x2 j2
x2 j1
x2 j
I( f )
n j 1
h 3
[
f
(
x2
j2
)
4
f
(
x2
) j 1
f (x2 j )]
Sn( f )
n j 1
h 3
[
f
(
x2
j
2
)
4
f
(
x2
j 1
)
f ( x2 j )]
b a
则迭代格式为
xk 1
2
x3 k
1
取初值 x0 0
x1
2
x3 0
1
1
x2
2
x3 1
1
3
x3
2
x3 2
1
55
由此可见,这种迭代格式是发散的
(2) 如果将原方程化为等价方程 x 3 x 1 2
仍取初值
x0 0 x1 3
x0 1 3 2
1 0.7937 2
x2 3
x1 1 3 1.7937 0.9644
h(1 f (xn1, y(xn1)) f (xn , y(xn )) 1 f (xn1, y(xn1)))
y(xn1) ( y(xn ) y(xn1))
h(1 y(xn1) y(xn ) 1 y(xn1))
y(xn ) hy(xn )
h2 2
y(xn )
h3 6
y(xn )
计算方法复习
Final Exam Review
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017/2/21
J. G. Liu
数值计算方法既有数学类课程中理论上的抽象性和严谨 性,又有实用性和实验性等技术特征,它是一门理论性 和实践性都很强的课程。在20世纪70年代,大多数学校 仅在数学系的计算数学专业和计算机系开设计算方法这 门课程。随着计算机技术的迅速发展和普及,现在计算 方法课程几乎已成为所有理工科大学生的一门必修课程。
则有方程 设人龟起初相距 S ,两者的速度分别为 V 和 v ,
Vt vt S
易得人追上龟所花的时间是
(1)
S t* V v
School of Math. & Phys.
16
North China Elec. P.U.
Numerical Analysis
2017/2/21
J. G. Liu
v0 a0
vk x vk 1 ak
(k 1,2,)
——考虑问题1
算 法 流 程 图
School of Math. & Phys.
15
North China Elec. P.U.
Numerical Analysis
2017/2/21
J. G. Liu
2 迭代法的校正技术
有些问题的“大事化小”过程似乎无法了结。Zeno悖论 强调人“永远”赶不上龟正是为了突出这层含义。这是 一类无限逼近的过程,适于用所谓预报校正技术来处理。
10
North China Elec. P.U.
Numerical Analysis
2017/2/21
J. G. Liu
tk-1
tk
V
v
Sk-1
V Sk
v
图示: 人龟追赶过程
耐人寻味的是,尽管Zeno悖论的论断极其荒谬,但从算法设计思 想的角度来看它却是极为精辟的。Zeno悖论将人龟追赶问题表达 为一连串追赶步的逐步逼近过程。设人与龟的速度分别为与,记 表示逼近过程的第步人与龟的间距,另以表示相应的时间,相邻 两步的时间差。Zeno悖论将人龟追赶问题分解为一追一赶两个过 程:
若用bk表示前k项的部分和,则有
(1)
b0 a0 bk bk 1 ak , k 1,2,, n
则计算结果即为所求的和值:
(2 )
S bn
School of Math. & Phys. 13
(3)
North China Elec. P.U.
Numerical Analysis
School of Math. & Phys.
14
North China Elec. P.U.
Numerical Analysis
2017/2/21
J. G. Liu
考虑
P( x) a0 x a1x
n
n 1
an1x an
ak x
k 0
n
nk
利用缩减技术可得如下算法:
4
North China Elec. P.U.
Numerical Analysis
2017/2/21
J. G. Liu
数值计算方法,是一种研究如何求解数学问题数值近
似解的方法,是在计算机上使用的解数学问题的方法, 简称计算方法。包括直接方法和迭代方法!
数值计算方法的计算对象是线性代数,微积分,常微
S vtk tk 1 , k 0,1,2, V
(2)
Zeno悖论所描述的逼近过程正是这种迭代过程,当 k→∞时,tk →t* ( ——考虑问题2 )。大家知道, 任何形式的重复都可看成是“时间”的量度。Zeno在 刻画人龟追赶问题中设置了两个“时钟”:一个是日 常的钟,另外Zeno又将迭代次数视为另一种时钟,不 妨称之为Zeno钟。Zeno公式(2)表明,当Zeno钟趋于 ∞时人才能追上龟,Zeno正是据此断言人永远追不上 龟。
分方程中的数学问题。内容包括: 求解线性方程组的数值方法; 计算矩阵特征值和特征向量的数值方法; 非线性方程和非线性方程组的迭代解法; 插值与拟合; 数值微积分; 常微分方程数值解等问题。
School of Math. & Phys.
5
North China Elec. P.U.
追的过程:先令龟不动,计算人追上龟所费的时间
tk
Sk 1
赶的过程:再令人不动,计算龟在这段时间内爬行的路程
School of Math. & Phys. 11
Sk vtk
V
North China Elec. P.U.
Numerical Analysis
2017/2/21
J. G. Liu
Numerical Analysis
2017/2/21
J. G. Liu
数
值
分
析
——插值、拟合与数值微积分
主讲:
刘敬刚
School of Math. & Phys.
1
North China Elec. P.U.
Numerical Analysis
2017/2/21
J. G. Liu
一、引例 考虑如下线性方程组 a11 x1 a1n xn b1 a x a x b nn n n n1 1 或者: Ax b
9
North China Elec. P.U.
Numerical Analysis
2017/2/21
J. G. Liu
引例
§ 1.1 算法设计技术
古希腊哲学家 Zeno( 芝诺 ) 在两千多年前提出过一个骇人 听闻的命题:一个人不管跑得多快,也追不上爬在他前 面的一只乌龟。这就是著名的Zeno悖论。
School of Math. & Phys. 2 North China Elec. P.U.
Numerical Analysis
2017/2/21
J. G. Liu
首先看一个简单的例子:
x1 x2 1 2 x1 x2 0
x1 1 x2 2
(若是更高阶的
School of Math. & Phys. 3 North China Elec. P.U.
Numerical Analysis
2017/2/21
J. G. Liu
二、研究对象和主要内容
实际问题 数学模型 算法设计
应用数学
程序设计
计 算 数 学
上机求解
School of Math. & Phys.
方程组呢?)
若行列式用按行(列)展开的方法计算 , 用克莱姆法则求解(1)需做乘除法的次数: (n 1)(n 1)n ! 当方程组阶数较高时,计算量很大,因此克莱姆法则通常仅有 理论上的价值,计算线性方程组的解还要考虑:
数值解法 = 算法 + 计算机。
人类的计算能力是计算工具和计算方法效率的乘积,提高计算方 法的效率与提高计算机硬件的效率同样重要。科学计算已用到科 学技术和社会生活的各个领域中,成为继实验和理论研究之后的 第三种研究方法。
School of Math. & Phys.
8
North China Elec. P.U.
Numerical Analysis
2017/2/21
J. G. Liu
数值分析的基本概念
内容:
1、算法设计技术 2、误差 3、数值计算中需要注意的一些问题 4、算法的稳定性 5、病态问题
School of Math. & Phys.
Zeno在论证这个命题时采取了如下形式的逻辑推理:设 人与龟同时同向起跑,如果龟不动,那么人经过某段时 间便能追上它;但实际上在这段时间内龟又爬了一段路 程,从而人又得重新追赶,如下图所示,这样每追赶一 次所归结的是同样类型的追赶问题,因而这种追赶过程 “永远”不会终结。
School of Math. & Phys.
School of Math. & Phys. 12 North China Elec. P.U.
S0 S , Sk Sk 1 v
V
k 1, 2,
Numerical Analysis
2017/2/21
J. G. Liu
1 直接法的缩减技术 数列求和问题:
S a0 a1 an
若以人和龟之间的距离 Sk 定义问题的规模大小,则 上述过程将问题规模压缩了 v V 倍:
V v 由于龟的速度远远小于人的速度,故 V 很小,因此
S k S k 1 v
按上述步骤很快问题的规模 Sk 就可以忽略不计,从而 得到人追上龟所花时间 t k ,Zeno的解释可用如下过程 表示:
——Zeno算法 可见,Zeno算法的设计思想是,将人龟追赶计算化归为简单的行 程计算的重复,它的设计方法是逐步压缩计算模型的规模,这种 “化大为小”的设计策略称为规模缩减技术,简称缩减技术。 算法的设计精髓:“简单”的重复生成复杂!
2017/2/21
J. G. Liu
参考书目:
1 钟尔杰.数值分析.高等教育出版社,2004. 2 颜庆津.数值分析.修订版.北京航空航天大学出版社,2000. 3 李庆扬. 数值分析.清华大学出版社,2001. 4 白峰杉.数值计算引论.高等教育出版社,2004.
5 王能超.计算方法.北京: 高等教育出版社, 2005.
学习过程中应该注意以下几个方面: 认清算法的计算对象; 掌握基本的计算方法及其原理; 用C++语言编制程序,在计算机上对算法进行验
证; 对于算法要勤思考多比较!
School of Math. & Phys.
