信号分析与处理模拟试卷(答案)
信号分析与处理答案第二版完整版

信号分析与处理答案第二版HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第二章习题参考解答求下列系统的阶跃响应和冲激响应。
(1)解当激励为时,响应为,即:由于方程简单,可利用迭代法求解:,,…,由此可归纳出的表达式:利用阶跃响应和冲激响应的关系,可以求得阶跃响应:(2)解 (a)求冲激响应,当时,。
特征方程,解得特征根为。
所以:…(2.1.2.1)通过原方程迭代知,,,代入式(2.1.2.1)中得:解得,代入式(2.1.2.1):…(2.1.2.2)可验证满足式(2.1.2.2),所以:(b)求阶跃响应通解为特解形式为,,代入原方程有,即完全解为通过原方程迭代之,,由此可得解得,。
所以阶跃响应为:(3)解(4)解当t>0时,原方程变为:。
…(2.1.3.1)…(2.1.3.2)将(2.1.3.1)、式代入原方程,比较两边的系数得:阶跃响应:求下列离散序列的卷积和。
(1)解用表格法求解(2)解用表格法求解(3)和如题图2.2.3所示解用表格法求解(4)解(5)解(6)解参见右图。
当时:当时:当时:当时:当时:(7) ,解参见右图:当时:当时:当时:当时:当时:(8) ,解参见右图当时:当时:当时:当时:(9) ,解(10),解或写作:求下列连续信号的卷积。
(1) ,解参见右图:当时:当时:当时:当时:当时:当时:(2) 和如图2.3.2所示解当时:当时:当时:当时:当时:(3) ,解(4) ,解(5) ,解参见右图。
当时:当时:当时:当时:(6) ,解(7) ,解(8) ,解(9) ,解试求题图示系统的总冲激响应表达式。
解已知系统的微分方程及初始状态如下,试求系统的零输入响应。
(1) ;解,,(2) ;,解,,,,可定出(3) ;,解,,,可定出某一阶电路如题图所示,电路达到稳定状态后,开关S 于时闭合,试求输出响应。
解由于电容器二端的电压在t=0时不会发生突变,所以。
信号分析与处理14~15上期末试卷A答案

浙江大学宁波理工学院2014–2015学年第一学期《信号分析与处理》课程期末考试试卷A 答案一、选择题(共10分,每空2分)1、一信号⎩⎨⎧><=2/1||02/1||1)(t t t x ,,,则其傅立叶变换为 C 。
A.ωsin B.ω2sin C.)2/sin(ω D.πωsin 23A –4A.5 A.1、(2、(78/π=Ω 3分742=Ωπ为有理数,分母为其基波周期,即N=7 4分 3、(10分)求出下列信号的拉氏反变换。
236512-<<-+++}Re{s s s s (反变换) 解:21326512+-+=+++=s s s s s S X )( 5分根据收敛域的双边情况,可求出反变换为双边信号如下:[])()()()(t u e t u e S X L t x t t -+==---2312 5分4、(15分)已知2112523)(---+--=zz z z X ,试问,)(n x 在以下三种收敛域下,哪一种是左边序列?哪一种是右边序列?哪一种是双边序列?并求出各对应的)(n x 。
(1)2||>z ; (2)5.0||<z ; (3)2||5.0<<zX ( ((2(35、(15分)已知)(t5(tx-的波形,要求画出分阶段变换的步骤x的波形如下,试画出)2下面画出6、(10分)求周期矩形脉冲信号的傅立叶级数(指数形式),并大概画出其频谱图。
解:指数级傅里叶展开如下 8分k c 的谱线图如下,只要绘制出趋势图即可2分四.论述题(25分)1、(10分)阐述拉普拉斯变换和傅立叶变换的关系,并用适当的公式加以说明。
答:1)傅立叶变换到拉氏变换:信号的傅立叶变换需满足狄立赫利收敛条件,不满足该条件的信号不存在傅立叶变换,对于部分不满足收敛条件的信号)(t x ,乘以衰减因子t e δ-后只要δ满足一定范围,t e t x δ-)(的傅立叶变换是存在的。
信号分析与处理_绝密模拟试卷1_(2)

以下面题目来复习,考个好成绩很容易一、选择题(10分,每题2分)1. 若f (t) 是已录制在磁带的声音信号,则下列表述错误的是 Ba) f (−t) 表示将磁带倒转播放产生的信号b) f (2t) 表示将磁带以二倍速度播放的信号c)f (2t) 表示将磁带速度降低一半播放的信号d) 2 f (t) 表示将磁带音量放大一倍播放的信号2.一个理想低通滤波器由h(t) = sin c( Bt) 冲激响应描述。
由于这个h(t) 在t<0时不为零,且s in c 函数不是绝对可积的,故 Ca) 该滤波器物理上不可实现,但它是稳的。
b) 该滤波器物理上可实现,但它不稳定。
c) 该滤波器物理上可实现,也是稳定的。
d) 该滤波器物理上不可实现,也不稳定。
3. z 变换的收敛域决定了序列x(n) 的性质。
在下列关于序列x(n) 的性质的表述中,错误的是a) 有限长序列x(n) 的z 变换X( z) 的收敛域是整个z 平面,有时要除去z= 0 或z为无穷。
b) 右边序列x(n) 的z变换X( z) 的收敛域位于以最大极点的模为半径的圆外部分c) 左边序列x(n) 的z变换X( z) 的收敛域位于以最大极点的模为半径的圆内部分d) 双边序列x(n) 的z变换X( z) 的收敛域是以最大和最小极点半径为界的环形4.周期性非正弦连续时间信号的频谱,其特点为( A) 。
(a) 频谱是连续的,收敛的(b) 频谱是离散的,谐波的,周期的(c) 频谱是离散的,谐波的,收敛的(d) 频谱是连续的,周期的5. 如某一因果线性时不变系统的系统函数H(S) 的所有极点的实部都小于零,则( C) 。
(a) 系统为非稳定系统(b)|h(t)|< ∞(c) 系统为稳定系统(d) |h(t)| =03)IIR数字滤波的基本网络结构有直接型、级联型、并联型FIR数字滤波的基本网络结构有直接型、级联型、线性型。
4)计算积分的结果为 8 。
信号分析与处理模拟试卷(答案)

信号分析与处理模拟试卷答案一. 填充题(每小题2分,共20分)1. 指信号能量有限,平均功率为零的信号。
2. ()()nn X z x n z∞-=-∞=∑3. 0()F ωω-4. 极点5. )(s F s n6. 响应信号与激励信号相比,只是响应大小和出现的时间不同,而无波形上的变化。
7. z z a z a-8. 没有外加激励信号的作用,只由起始状态所产生的响应。
9. 冲激响应,()h t 。
10.系统参数不随时间变化的系统。
二. 利用函数或变换性质求函数值(每小题4分,共12分)1. )()(ωωF j dt t df ↔ (1分))()(2)(2)()12()()())(()(ωω-ω'ω-ω-↔-∴ω'ω-ω-=ωωω↔F j F F dtt df t F F F j d dj dt t df t(1分)(2分)2. ()119dF s ds s s =-+ (1分) 91()()()t f t u t e u t -=- (2分)919()()()()1()(1)()t t tf t f t u t e u t f t e u t t---==-=- (1分)3。
求函数1()2nu n 的Z 变换。
解:()1zu n z ↔- 1z > (1分)21()(1)z d z z nu n z dz z ⎛⎫ ⎪-⎝⎭↔-=- (2分) 21()22(1)znu n z ↔- 1z > (1分) 三、)(t f 的波形如图所示,请给出变换)22(t f -的步骤,试画出其波形。
(6分) 解:)]1(2[]2[)()(--→-→-→t f t f t f t f (3分)(3分)四.求像函数2()4(1)se F s s s -=+的拉氏反变换。
(12分)解: 1221()()4(1)4(1)s s se F s e F s e s s s s ---===++ 112121()4(1)A B B F s s s s s i s i==++++- (2分) 11211()04(1)4A sF s s s ====+ (2分) 1111()()4()8B s i F s s i s s i =+==-=-- (2分)2111()()4()8B s i F s s i s s i =-===-+ (2分)121111884()4(1)F s s s s s i s i==--++- 111()()cos ()44f t u t tu t =- (2分)11()(1)(1)s e F s f t u t -↔--1()[1cos (1)](1)4f t t t u t =--- (2分)五。
信号分析与处理习题答案(P155)

信号分析与处理习题答案(P155)3、绘图程序:%sinusoidal sequence n=0:29;x=sin(16*pi/5*n+pi/4); stem(n,x);xlabel('n');ylabel('x(n)');title('Sinusoidal sequence'); grid;55825162=∴===N N m序列为周期序列为有理数πππω4、绘图程序:%delta sequencen=[-5 -4 -3 -2 -1 0 1 2 3 4 5]; x=[0 5 0 0 2 0 -4 0 3 0 0]; stem(n,x);xlabel('n');ylabel('x(n)');title('delta sequence'); grid;8、根据DTFT 性质, (1)时域尺度变换特性:连续时间傅里叶变换的尺度变换表示为:⎪⎭⎫ ⎝⎛↔a X a at x ω1)( 然而,在离散时间的情况下,若a 不是整数,x[an]就不是一个序列。
另一方面,如果a 是一个整数,例如a=2,那么x[2n]仅包含x[n]的偶数样点。
因此,离散时间中的时域尺度变换与上式有些不同。
令m 为一正整数,则序列的傅里叶变换为⎩⎨⎧≠===km n kmn k x m n x n x m 0][]/[][)(()a b{})(][][][][)()()()(Ω====∑∑∑∞-∞=Ω-∞-∞=Ω-∞-∞=Ω-m X ek x ekm xen xn x F n km j n kmj m n nj m m所以)(0]/[][)(Ω↔⎩⎨⎧≠==m X km n km n m n x n x m⎪⎭⎫⎝⎛Ω↔a X an x )( (3)时域位移:)(][00Ω↔-Ω-X en n x n j)()1()()()2()(22Ω-=Ω-Ω↔--Ω-Ω-X e X eX n x n x j j10.(2)根据P109式3-26)())(()(1)()()(00101000Ω=Ω+=ΩΩ=∑∑-=Ω--=Ωk X qN k X en x Nk X e k X n x N k njk N k njk根据题意,序列x(n)的基本周期为N=8,Ω0=2π/N=π/4 根据欧拉公式,nj nj njnjee een 002121214cos 44Ω-Ω-+=⎪⎪⎭⎫ ⎝⎛+=πππ则x(n)的傅里叶系数为X(1)=1/2,X(-1)= X(-1+8)= X(7)=1/2,其他系数等于0。
信号分析与处理 模拟试卷2

信号分析与处理 模拟试卷2一、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(10分,每小题2分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )二.填空题(15分,每空1分)1)数字信号处理的步骤:预滤波、模数转换器、数字信号处理、数模转换器、平缓滤波2)计算积分dt t t t )3(')142(23-++⎰+∞∞-δ的结果为 -78 。
3)系统阶跃响应的上升时间和系统的 截止频率 成反比。
4)若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8Hz 。
5)白噪声是指 功率谱密度在整个频率范围内均匀分布的噪声 。
6))()(5241n R x n R x ==,只有当循环卷积长度L =8 时,二者的循环卷积等于线性卷计。
7)数字角频率ω与模拟角频率Ω的关系式T *Ω=ω 。
8)当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
9)激励为单位脉冲信号)(t δ作用下所产生的 零状态响应 ,简称冲激响应。
10)从采样信号(s f )中无失真的恢复原连续信号(c f ),采样频率与原连续信号的应满足c s f f 2≥ 。
三.简答题(30分,每小题6分)1..请简述傅里叶变换的意义,并写出非周期连续信号的傅里叶变换和逆变换表达式; 答:傅里叶变换将时域问题转化到频域中解答,从而简化了问题的处理。
(回答这些就给满分,多答更好)傅里叶变换:dtet f w F jwt⎰+∞∞--=)()(傅里叶逆变换:dwew F t f jwt⎰∞+∞-=)(21)(π2.若要让抽样后的信号不产生频谱混叠,在抽样过程中应该满足什么条件答:抽样频率满足奈奎斯特采样定理,信号频谱的最高频率小于折叠频率。
信号分析与处理答案(苪坤生 潘孟贤 丁志中 第二版)习题答案

第二章习题参考解答2.1 求下列系统的阶跃响应和冲激响应。
(1) )()1(31)(n x n y n y =--解 当激励为)(n δ时,响应为)(n h ,即:)()1(31)(n n h n h δ+-=由于方程简单,可利用迭代法求解:1)0()1(31)0(=+-=δh h ,31)0(31)1()0(31)1(==+=h h h δ,231)1(31)2()1(31)2(⎪⎭⎫ ⎝⎛==+=h h h δ…,由此可归纳出)(n h 的表达式:)()31()(n n h n ε=利用阶跃响应和冲激响应的关系,可以求得阶跃响应:)(])31(2123[311)31(1)31()()(10n k h n s n n k nk nk ε-=--===+=-∞=∑∑(2) )()2(41)(n x n y n y =--解 (a)求冲激响应)()2(41)(n n h n h δ=--,当0>n 时,0)2(41)(=--n h n h 。
特征方程0412=-λ,解得特征根为21,2121-==λλ。
所以: n n C C n h )21()21()(21-+= …(2.1.2.1)通过原方程迭代知,1)0()2(41)0(=+-=δh h ,0)1()1(41)1(=+-=δh h ,代入式(2.1.2.1)中得:121=+C C0212121=-C C 解得2121==C C , 代入式(2.1.2.1):0,)21(21)21(21)(>-+=n n h n n …(2.1.2.2)可验证)0(h 满足式(2.1.2.2),所以:)(])21()21[(21)(n n h n n ε-+=(b)求阶跃响应通解为 n n c C C n s )21()21()(21-+=特解形式为 K n s p =)(,K n s p =-)2(,代入原方程有 141=-K K , 即34=K完全解为34)21()21()()()(21+-+=+=n n p c C C n s n s n s通过原方程迭代之1)0(=s ,1)1(=s ,由此可得13421=++C C134212121=+-C C 解得211-=C ,612=C 。
信号处理分析试卷及解答
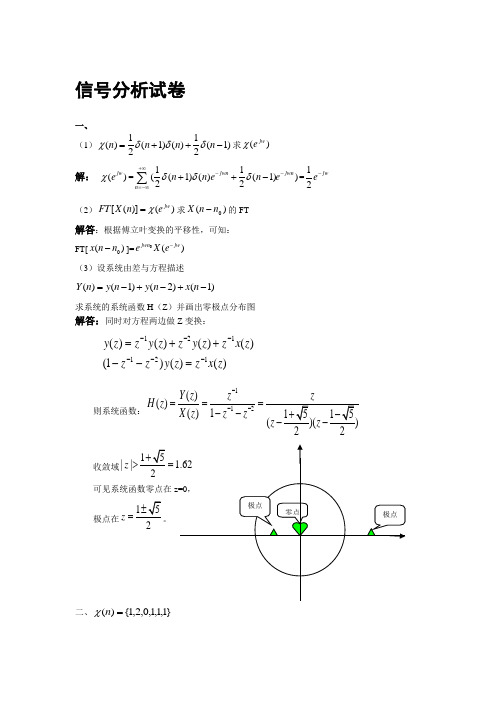
信号分析试卷一、 (1))1(21)()1(21)(-++=n n n n δδδχ求)(jw e χ 解: ()jwe χ=11((1)()(1))22jwn jwnn n n e n e δδδ+∞--=-∞++-∑=12jw e - (2))()]([jw e n X FT χ=求)(0n n X -的FT解答:根据傅立叶变换的平移性,可知:FT[0()x n n -]=0()jwn jw eX e -(3)设系统由差与方程描述)1()2()1()(-+-+-=n x n y n y n Y求系统的系统函数H (Z )并画出零极点分布图解答:同时对方程两边做Z 变换:)()()1()()()()(121121z x z z y z z z x z z y z z y z z y ------=--++=则系统函数:112()()()122Y z z H z X z z z---===--收敛域1||2z >=可见系统函数零点在极点在12z =二、}1,1,1,0,2,1{)(=n χ(1)求X (Z ) (2)求X (K )解答:(1)X (Z )=()nn n zχ+∞-=-∞∑=1*0z -+2* 1z -+0+1* 3z -+1*4z -+1*5z -根据公式:X(K)=∑-=-10/2)(N n Nkn j en x π,可得:X(0)=1*1+2*1+0*1+1*1+1*1+1*1=6; X(1)=1+2**2*/6j eπ-+*2**3/6*2**4/6*2**5/60j j j ee e πππ---+++=1+2*/3j eπ-⨯**2*/3**5/3j j j e e e πππ---+++);X (2)=1+2/328/310/320j j j j ee e e ππππ-⨯-⨯⨯-⨯⨯-⨯⨯⨯++++X (3)=1+*2j e π-⨯32450j j j j e e e e ππππ-⨯⨯-⨯⨯-⨯-⨯⨯+++++;X (4)=1+24/3j e π-⨯⨯⨯416/320/30j j j e e e πππ-⨯⨯-⨯⨯-⨯⨯++++;X(5)=1+5/32j eπ-⨯⨯⨯520/325/30j j j e e e πππ-⨯⨯-⨯⨯-⨯⨯++++三 、对某实信号进行谱分析,要求频率分辩F=2HZ ,信号的上限频率fm=1KHZ (1)确定采样频率s f ,采样间隔s T (2)采样长度p T 和点数N解答:(1)s f ≥2fm=2 KHZs T ≤1sf =0.5310-⨯s (2)N=sf F =1000 p T =1F=0.5s四、某系统由方程描述)1(21)()1(21)(-++-=n x n x n y n y 设系统是因果的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号分析与处理模拟试卷(答案)
信号分析与处理模拟试卷答案
一.
填充题(每小题2分,共20分)
1. 指信号能量有限,平均功率为零的信号。
2. ()()n
n X z x n z
∞
-=-∞
=
∑
3. 0()F ωω-
4. 极点
5. )(s F s n
6. 响应信号与激励信号相比,只是响应大小和出现的时间不同,而无波形上的变化。
7.
z z a z a
-
8. 没有外加激励信号的作用,只由起始状态所产生的响应。
9. 冲激响应,()h t 。
10.
系统参数不随时间变化的系统。
二.
利用函数或变换性质求函数值(每小题4分,共12分)
1.
)()
(ωωF j dt
t df ↔ (1分) )
()(2)(2)
()12()()())(()(ωω-ω'ω-ω-↔-∴ω'ω-ω-=ωωω
↔F j F F dt
t df t F F F j d d
j dt t df t
(1分)
(2分) 2.
()11
9
dF s ds s s =-+ (1分) 91()()()t f t u t e u t -=- (2分)
919()()()()
1
()(1)()
t t tf t f t u t e u t f t e u t t
---==-=- (1分)
3.求函数1()2
nu n 的Z 变换。
解:()1
z
u n z ↔
- 1z > (1分) 2
1()(1)
z d z z nu n z dz z ⎛⎫ ⎪-⎝⎭↔-=- (2分) 21()22(1)
z
nu n z ↔- 1z > (1分) 三、)(t f 的波形如图所示,请给出变换)22(t f -的步骤,试画出其波形。
(6分) 解:
)]1(2[]2[)()(--→-→-→t f t f t f t f (3分)
(3分)
四.求像函数2()4(1)
s
e F s s s -=+的拉氏反变换。
(12分)
解: 1
221()()4(1)4(1)
s s s
e F s e F s e s s s s ---===++ 112121
()4(1)A B B F s s s s s i s i
=
=++++- (2分)
11211
()04(1)
4
A sF s s s ====
+ (2分)
1111
()()4()8
B s i F s s i s s i =+==-=-- (2
分)
2111
()()4()8
B s i F s s i s s i =-===-+ (2
分)
12111
1884()4(1)F s s s s s i s i
==--++- 111
()()cos ()44
f t u t tu t =- (2分)
11()(1)(1)s e F s f t u t -↔--
1
()[1cos (1)](1)4f t t t u t =--- (2分)
五.已知)(2)(1t u t
t f e -=,2()()(1)f t u t u t =--,求)()()(
21t f t f t g *= (10分)
解:
121222
2
1
2
2
22(1)()()()()()(2)()[()(1)(2)()()()(1)(2)()(1)
(2)11(1)()(1)(1)(2)
22
t
t t t g t f t f t f f t d u u t u t d u u t d u u t d d u t d u t u t u t e e e e e e e τ
ττ
ττ
τττττττ
ττττττ
ττ∞-∞
∞
--∞∞
∞
---∞-∞
------=*=-=----=----=--=----⎰
⎰
⎰⎰⎰⎰分分分分分
六.已知像函数231
)(2+++=z z z z X ,2>z ,求))(n χ (10分)
解:
12()1
(2)2
A A X z z z z z z ==+++ (2分) 0,2z z ==- 为单根 (2分)
1022()1
[]2
()1
[(2)]2z z X z A z
z X z A z z ==-===+=-
(2分)
1()22(2)
z X z z =
-+ (2分) 11()()(2)()22
n n n u n χδ=-- (2分)
七.已知激励信号为)()(t u t
t e e
-=
,求系统的冲激响应
2
3)(-=
s s
s H ,求系统的零状态响应。
(10分) 解: 1
1
)(+=
s s E (2分) 123()()()(1)(2)
12
zs s
R s E s H s s s A A s s ==
+-=+
+- (2分)
1,2s s =-=为单根 (2分)
1122[(1
)()]1[(2)()]2zs s zs s A s R s A s R s =-==+==-= (2分)
12()12
zs R s s s =++-
2()(
2)()t
t
zs r t u t e
e -=+ (2分)
八.
电路如图所示,已知激励信号为)(t e ,电容-=0t 时电感
初始电流为A i l 2)0(=,电容初始电压为(0)1c u V =。
试求回路中的零输入电流响应)(t i 。
(14分)
解: (0)12()(0)s s
c l u s
E s Li -=
-=
(2分) 等效电路图如右图 (4分)
2
21
21212()1(1)[](1)(1)
s s
I s s s sL R sc k k s s --=
=+++=+
++ (2分)
1s =-为双重极点,221[(1)()]3s k s I s =-=+= (2分)
211
[(1)()]2s k s I s =-'
=+=- (2
分)
2
32
()(1)1
I s s s -=
+++ ()(32)()t t zi i t te e u t --∴=- (2分)
九.已知系统的微分方程为2
()()2()3()2
d y t dy t y t t dt
dt χ++=,试画出系统线
性模拟框图。
(6分)
解:2()()2()3()2d y t dy t y t t dt dt
χ=--+(2分)
(4分)。
