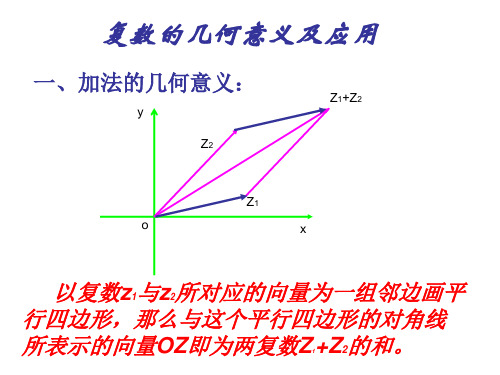
复数加法的几何意义
复数的基本运算与几何意义解释

复数的基本运算与几何意义解释复数是由实部和虚部构成的数,其表示形式为a + bi,其中a和b 分别为实部和虚部的实数部分,i为虚数单位,满足i^2 = -1。
复数的运算包括加法、减法、乘法和除法,下面将基本运算进行详细解释,并探讨其在几何中的意义。
一、加法运算对于两个复数z1 = a1 + b1i和z2 = a2 + b2i而言,它们的和z = z1 + z2的实部等于两个复数实部的和,虚部等于两个复数虚部的和,即:z = z1 + z2 = (a1 + a2) + (b1 + b2)i几何意义:将复数z1和z2表示在复平面上,实部表示在实轴上,虚部表示在虚轴上。
加法运算就是将两个复数的向量相加,得到新的向量的终点,即通过终点相加的法则得到。
二、减法运算对于两个复数z1 = a1 + b1i和z2 = a2 + b2i而言,它们的差z = z1 - z2的实部等于两个复数实部的差,虚部等于两个复数虚部的差,即:z = z1 - z2 = (a1 - a2) + (b1 - b2)i几何意义:将复数z1和z2表示在复平面上,减法运算就是将z2的向量从z1的向量终点出发得到新的向量的终点,即通过终点减去起点的法则得到。
三、乘法运算对于两个复数z1 = a1 + b1i和z2 = a2 + b2i而言,它们的乘积z = z1 * z2的实部等于两个复数实部的乘积减去虚部的乘积,虚部等于两个复数实部的乘积加上虚部的乘积,即:z = z1 * z2 = (a1a2 - b1b2) + (a1b2 + b1a2)i几何意义:将复数z1和z2表示在复平面上,乘法运算就是将z1的向量的长度与z2的向量的长度相乘(模的乘积),同时将z1的向量的方向与z2的向量的方向相加(幅角的叠加),得到新的向量,即将两个向量的长度相乘,诱导出新的长度,将两个向量的角度相加,诱导出新的角度。
四、除法运算对于两个复数z1 = a1 + b1i和z2 = a2 + b2i而言,它们的商z = z1 / z2为复数,可以通过以下步骤求解:1. 乘以共轭复数:将除数z2的虚部取相反数,即z2* = a2 - b2i;2. 乘以共轭复数得到分子:z1 * z2* = (a1 + b1i)(a2 - b2i);3. 化简分子:z1 * z2* = (a1a2 + b1b2) + (a1b2 - b1a2)i;4. 除以分母的模的平方:z = (a1a2 + b1b2)/(a2^2 + b2^2) + (a1b2 -b1a2)/(a2^2 + b2^2)i。
复数加法的几何意义.

我们设z1=a+bi z2=c+di 则z1+z2=(a+c)+(b+d)I
如何作出与z1+z2对应的向量? Y
先作出(a+c)+bi 再作出(a+c)+(b+d)I
Z Z2
Z1
X
O
证明的关键:
如何证明OZ2与Z1Z平行? 法一:用平面几何的知识 延长ZZ1 法二:用解析几何的斜率
复数加法的几何意义
问题提出:
在物理学中,我们知道两个 力的合成--两个向量的和满 足平行四边形法则。既然复数 可以表示平面上的向量,那么 复数的加法与向量的加法是否 具有一致性?
问题剖析:
如图, 复数z1+ z2与向量OZ是 否对应? Y
Z
Z2
Z1
X
O
思路分析:
思路一:考察OZ是否对应z1+z2? 思路二:考察z1+z2是否对应OZ ?
意义 上述结论的意义:
一、我们可以用复数的加法 来解决向量的加法
二、可以用向量的加法来表 示复数的加法
三、虚数越来越实在了。
作业:
P1பைடு நூலகம்9.2
复数代数形式的加减运算及其几何意义

在信号处理中的应用
信号合成与分解
复数代数形式的加减运算可以用于信 号的合成与分解,例如在频谱分析和 滤波器设计中。通过加减运算,可以 将信号分解为不同的频率分量,便于 分析和处理。
调制与解调
在通信系统中,复数代数形式的加减 运算用于信号的调制和解调过程。通 过加减运算,可以实现信号的相位和 幅度调整,从而实现信号的传输和接 收。
复数减法的几何意义
复数减法可以理解为在复平面上的向量减法。给定两个复数 $z_1 = a + bi$ 和 $z_2 = c + di$,它们的差 $z_1 - z_2 = (a-c) + (b-d)i$ 可以看作是两个向量在复平面上的差分。
向量差分:在复平面上,将 $z_1$ 的向量起点固定,然后 平移至 $z_2$ 的起点,得到向量差。这个过程对应于复数 减法运算。
部对应横轴,虚部对应纵轴。
03
复数代数形式的几何意义
复数加法的几何意义
复数加法可以理解为在复平面上的向量加法。给定两个复数 $z_1 = a + bi$ 和 $z_2 = c + di$,它们的和 $z_1 + z_2 = (a+c) + (b+d)i$ 可以看作是两个向量在复平面上的合成。
向量合成:在复平面上,将 $z_2$ 的向量起点固定,然后平 移至 $z_1$ 的起点,得到向量和。这个过程对应于复数加法 运算。
复数代数形式的加减运算 及其几何意义
• 引言 • 复数代数形式的加减运算 • 复数代数形式的几何意义 • 复数代数形式的加减运算的应用 • 结论
Hale Waihona Puke 1引言复数的基本概念
01
复数是由实部和虚部构成的数,一 般形式为$z=a+bi$,其中$a$和 $b$是实数,$i$是虚数单位,满足 $i^2=-1$。
复数的加减法几何意义2
C
z2 z2-z1
z1 A
z1+z2
B
4、 |z1|= |z2|,| z1+ z2|= | z1- z2| 则平行四边形OABC是正方形
三、复数乘法的几何意义:
两个复数Z1与Z2相乘时,可以先画出分别与之相对应的 向量OP1、OP2,然后把向量OP1按逆时针方向旋转一个角, 再把它的模变为原来的r2倍,所得的向量就表示积。
Z1
x
O
1、 两个复数的差z2-z1与连结两个向量终点并指向被减数的向量对应。 2、复平面上两点间的距离|Z1Z2|=|z2-z1|
1、2(|z1|2+|z2|2)=| z1+ z2|2+ | z1- z2|2
2、|z1|= |z2| 则平行四边形OABC是菱形
o 3、 | z1+ z2|= | z1- z2|
4、(1)若arg(-2-i)=α,arg(-3-i)=β,求α +β
(2)若z1=-2,z2=1+
√3 i,z3=1-i,求arg[(z1z2)/z3]
5、若|z1|=3,|z2|=5,|z1-z2|=7,求z1/z2
6.已知ABC的三个顶点A, B,C对应的复数分别为
z1,
z2 ,
z3 , 若
z2 z3
4
(C) 11
4
(D) 5
4
2、在复平面内,直角三角形ABC的直角顶点C对应的
复数为-2,30度的顶点A对应的复为 则点B所对应的复数为
5 3i
3.复平面内点A对应的复数为1,点B对应的复数 为3 i, 将向量AB绕A按顺时针方向旋转900并 将模扩大到原来的2倍得向量A C, 则点C对应 的复数为
复数加法的几何意义

复数加法的几何意义1. 复数加法的几何意义啊,就像是给你一个神奇的工具,能把两个图形巧妙地组合在一起呢!比如说,一个复数代表一个向量,那两个复数相加不就是这两个向量的合成嘛!就像你走路,先向东走一段,再向北走一段,那你最终的位置不就是这两段的组合嘛,是不是很有意思?2. 嘿,你知道复数加法的几何意义吗?它简直就是数学世界里的魔法呀!好比你有两个图形,通过复数加法,就能看到它们融合后的奇妙样子。
就像拼积木一样,把不同的部分拼在一起,形成新的形状,太神奇啦!3. 哇塞,复数加法的几何意义可太重要啦!这就好像是在构建一个独特的世界呀。
比如在地图上,一个复数是一个地点到另一个地点的路线,那两个复数相加不就是把这两条路线合起来嘛,这多让人惊叹啊!4. 复数加法的几何意义,你可别小瞧它呀!它就像是一个超级导演,能指挥着各种图形的变换呢。
比如说在一个游戏里,两个复数分别代表不同的动作,那它们相加就是新的组合动作,这多有趣啊,你能明白吗?5. 哎呀呀,复数加法的几何意义真的很奇妙呢!就好像是在搭积木,每个复数都是一块积木,加在一起就搭出了不同的造型。
比如一个复数是向左平移,另一个是向上平移,那它们相加不就是斜着平移啦,是不是很神奇呀?6. 复数加法的几何意义,真的就像一把神奇的钥匙呀!能打开好多未知的大门呢。
想想看,两个复数就像两条不同的路,它们相加就是找到一条新的路,这是多么令人兴奋的发现啊!7. 哇哦,复数加法的几何意义,那可是超级厉害的呢!就好比是把不同的故事片段连接起来。
例如一个复数是一个冒险的开始,另一个是遇到的挑战,那它们相加就是整个精彩的冒险过程呀,是不是特别吸引人?8. 嘿呀,复数加法的几何意义可真是不简单呐!它就像在拼图,把不同的部分拼在一起,呈现出完整的画面。
就像一个复数是一片云朵,另一个是一阵风,它们相加就是云朵被风吹动的样子,多有意思呀!9. 复数加法的几何意义,真的如同一个神秘的宝藏呀!能挖掘出好多惊喜呢。
复数加减法的几何意义 PPT

1.
有序实数对(a,b)
一一对应
复数z=a+bi
直角坐标系中的点Z(a,b)
(数)
(形)
一一对应 向量 OZ
一一对应
2.复数与其相对应的向量的模相等,即: 对应平面向量OZ 的模|OZ |,即复数 z=a+bi在复
平面上对应的点Z(a,b)到原点的距离。
(5). z 1
点( x, y)到点(0,1)的距离
练习:
1.若复数z满足z 1 z 1 ,求z 1的最小值。
z 1 min 1
2.若z1 1, z2 2,求z1 z2 的最值。
z1 z2 max 3, z1 z2 min 1
y
(x, y)
B
y
2
1
A
(1,0) o (1,0) x
1.复数加、减法的运算法则:
(1)运算法则:设复数z1=a+bi,z2=c+di,
那么:z1+z2=(a+c)+(b+d)i; z1-z2=(a-c)+(b-d)i.
即:两个复数相加(减)就是实部与 实部,虚部与虚部分别相加(减).
(2)复数的加法满足交换律、结合律,
即对任何z1,z2,z3∈C,有
所以
| z | = a2 b2
问题: 复数的模为一实数。则复数的模可以
进行加、减、乘、除四则运算。 那么,复数本身是否也可以进行加、
减、乘、除四则运算呢?
1.复数代数形式的加、减法运算法则,即:
z1+z2=?
z1-z2=?
2.复数代数形式的加、减运算的几何意义;
3.特别的:z1 z2 的几何意义。
复数的加减法及其几何意义

复数的加减法及其几何意义一、复数的加减法1. 复数的定义- 设z = a+bi,其中a,b∈ R,a称为复数z的实部,记作Re(z)=a;b称为复数z的虚部,记作Im(z) = b。
- 例如,z = 3 + 2i,实部a = 3,虚部b=2。
2. 复数的加法法则- 设z_{1}=a_{1}+b_{1}i,z_{2}=a_{2}+b_{2}i,则z_{1}+z_{2}=(a_{1}+a_{2})+(b_{1}+b_{2})i。
- 例如,若z_{1}=2 + 3i,z_{2}=1 - 2i,则z_{1}+z_{2}=(2 + 1)+(3-2)i=3 + i。
3. 复数的减法法则- 设z_{1}=a_{1}+b_{1}i,z_{2}=a_{2}+b_{2}i,则z_{1}-z_{2}=(a_{1}-a_{2})+(b_{1}-b_{2})i。
- 例如,若z_{1}=4+5i,z_{2}=2 + 3i,则z_{1}-z_{2}=(4 - 2)+(5 -3)i=2+2i。
二、复数加减法的几何意义1. 复数的几何表示- 在复平面内,复数z = a+bi可以用点Z(a,b)来表示,也可以用向量→OZ来表示,其中O为坐标原点。
- 例如,复数z = 3+2i对应的点为(3,2),对应的向量→OZ,起点为O(0,0),终点为Z(3,2)。
2. 复数加法的几何意义- 设z_{1}=a_{1}+b_{1}i,z_{2}=a_{2}+b_{2}i,它们对应的向量分别为→OZ_{1}和→OZ_{2}。
- 那么z_{1}+z_{2}对应的向量为→OZ_{1}+→OZ_{2},即平行四边形法则:以→OZ_{1}和→OZ_{2}为邻边作平行四边形,则对角线→OZ对应的复数就是z_{1}+z_{2}。
- 例如,z_{1}=2 + i,z_{2}=1+2i,→OZ_{1}=(2,1),→OZ_{2}=(1,2),以→OZ_{1}和→OZ_{2}为邻边的平行四边形的对角线向量→OZ=→OZ_{1}+→OZ_{2}=(3,3),对应的复数z_{1}+z_{2}=3 + 3i。
高二数学复数的加减运算

二.复数的加减法及几何意义
3、共轭复数:
实部相等而虚部互为相反数的两个复数,叫做 互为共轭复数,也称这两个复数互相共轭。
Z的共轭复数用Z来表示即Z a bi时, Z a bi
复数的加减运算 及其几何意义
一.回顾复数的几何意义
一一对应
复数z=a+bi
直角坐标系中的点Z(a,b)
(数)
(ห้องสมุดไป่ตู้)
一一对应 平面向量 OZ
|z|=|a+bi|
点Z(a,b)到原点的距离
(数)
(形)
一一对应 平面向量 OZ 的模|OZ |.
| z z0 | 复平面上点Z(a,b)到Z0 (a’,b’)的距离
例2:证明:1 | Z || Z |
Z Z
2 Z1 Z2 Z1 Z2
Z1 Z2 Z1 Z2
例3.(1)若Z1 3 i, Z2 4i 1, Z1 Z Z2, 求Z
(2)设f (Z ) Z , Z1 3 4i, Z2 i 2,则求f (Z1 Z2 ).
(3)已知Z C,且2Z 3Z 1 3i,求复数Z.
;宁波象山出海捕鱼 宁波象山出海捕鱼 ;
不影响其存在和意义。 地址是死的,地点是活的。地址仅仅被用以指示与寻找,地点则用来生活和体验。 安东尼·奥罗姆是美国社会学家,他有个重大发现:现代城市太偏爱“空间”却漠视“地点”。在他看来,地点是个正在消失的概念,但它担负着“定义我们生存状态”的使命。 “地点是人类活动最重
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上述结论的意义:
意义
一、我们可以用复量的加法来表示复数的加法
三、虚数越来越实在了。
作业:
P189.2
复数加法的几何意义
问题提出:
在物理学中,我们知道两个力的合成--两个向量的和满足平行 四边形法则。既然复数可以表示平面上的向量,那么复数的加法与 向量的加法是否具有一致性?
问题剖析:
如图, 复数z1+ z2与向量OZ是否对应? Y
Z Z2
X Z1 O
思路分析:
思路一:考察OZ是否对应z1+z2? 思路二:考察z1+z2是否对应OZ ?
教科书采用的是思路一,我们这里采用思路二.
我们设z1=a+bi z2=c+di 则z1+z2=(a+c)+(b+d)I
如何作出与z1+z2对应的向量? Y
先作出(a+c)+bi 再作出(a+c)+(b+d)I
Z Z2
Z1 X
O
证明的关键:
如何证明OZ2与Z1Z平行? 法一:用平面几何的知识延长ZZ1
