t检验和x2检验doc
一文搞懂Z检验,T检验,x2检验

一文搞懂Z检验,T检验,x2检验作者:Bob大叔,香港精益六西格玛黑带
三种检验方法的介绍
Z检验举例:
某产品,其装量服从N(2.1,0.012),即均值2.1,标准差0.01。
抽取15个样品,其测量值如下:
2.08 2.10 2.10
2.09 2.10 2.10
2.09 2.09 2.11
2.09 2.12 2.10
2.10 2.10 2.10
建立假设H0:μ=2.1,H1 μ≠2.1,由于σ已知,故选择Z检验
操作如下:
P=0.36>0.05,无法拒绝原假设H0, 所以认为取样的平均装量没有变化。
t检验举例:
某设备的OEE目标为70%,连续15天的OEE如下,请判断OEE是否已达到70%目标?
由于σ(标准差)未知,且为小样本,故而选择,t检验
建立假设:HO: μ=70%, H1>70%,
操作如下:
P=0.252>0.05,无法拒绝原假设,说明0EE并未大于70%。
X2检验举例:
已知某产品装量,符合N(μ,σ2)分布,μ未知,但是要求标准差不能超过0.01,随机抽取30个样品,请问标准差是否有变化?
由于μ未知,故而选择X2检验,
建立假设:H0:σ=0.01, H1:σ≠0.01
操作如下:
(weixin gongzhonghao: HK_BobUncle)
P=0.303>0.05, 无法拒绝原假设,说明标准差无变化。
第二单元 T检验与x2检验

---------------------------------------------------------------最新资料推荐------------------------------------------------------1 / 5第二单元 T 检验与x2检验422 通过本课的学习, 熟练掌握单正态总体方差未知时均值的检验方法( T 检验法) , 掌握单正态总体方差的检验方法检验法) . (T 检验法) 我们数理统计面对的是随机现象, 面对的研究对象总体并不完全了解, 如期望未知, 解决的方法有三个: 点估计:用样本的均值作为总体的均值的估计值, 从另一个角度提出解决未知参数的问题; 区间估计: 未知参数落在区间内的概率是, 另一种问题就是要回答数学期望是不是等于的问题, 这就是假设检验的问题问题: 已知总体其中未知, 现要通过抽样检测判断假设, 选取样本统计量,在假设成立的条件下,)根据显著性水平确定接受域[-),其中满足关系查t 分布表,由自由度和查出, 满足 〕 =1-即:-此时接受, 否则拒绝假设. 问题: 已知总体其中未知, 现要通过抽样检测判断假设, 2. 选取样本的统计量因为在假设时,根据显著性水平确定拒绝域,和拒绝域(0,和,+其中,分别满足下列条件2)) ,具体由和查分布表而得到. 4.计算样本值,视其属于什么区域而判断接受假设,还是拒绝假设. 问题思考:检验的接受域是[-,吗?答案:不是,应为,对一批新的存贮缸进行耐裂试验, 抽测五个, 得爆破压力为(单位:克/米2) :545, 545, 530, 550, 545。
爆压是服从正态分布的, 过去这种缸的平均爆压为 549,问这批新缸的平均爆压有否显著差别? 解: 假设=549,因未知故采用统计量由=0. 05, 和自由度n-1==0. 025,查 t 分布表得=2. 7764 由样本计算得:x=543,2s==-1. 77[-2. 7764, 2. 7764] 故接受假设=549,即新缸平均爆压和旧缸无显著差别. 已知总体从中抽取一组样本测得数据 5. 0, 4. 8, 5. 1,5. 2, 5. 0。
T检验法Microsoft Office Word 文档
T检验法
T检验法常用于检验多组测定值的平均值的一致性,也可以用它来检验同组测定值中个测定之的一致性。
一同一组测定值中数据一致性的检验为例,来介绍他的检验步骤。
(1)将各数据按从大到小的顺序排列:x1
、x2、x3、……x n。
求出算术平均值x和标准偏差。
将最大值记为x max,最小值记为x min,这两个值是否可疑,则需计算T值。
(2)计算公式可以使用下式
T=x−x min
s 或T=x min−x
s
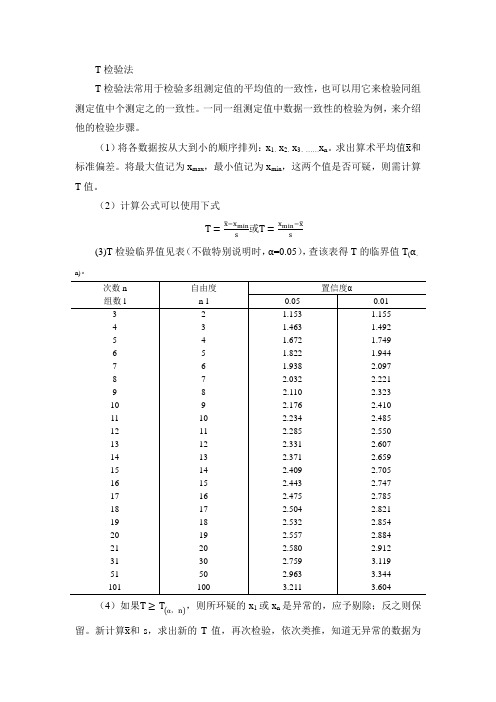
(3)T检验临界值见表(不做特别说明时,α=0.05),查该表得T的临界值T(α,n)。
(4)如果T≥T
α,n
,则所环疑的x1或x n是异常的,应予剔除;反之则保留。
新计算x和s,求出新的T值,再次检验,依次类推,知道无异常的数据为
止。
(5)在第1个异常数据剔除舍弃后,如果仍有可疑数据需要判别时,则应重对多组测定值的检验,只要把平均值作为1个数据用以上步骤进行计算与检验。
u检验、t检验、F检验、X2检验

u检验、t检验、F检验、X2检验常用显著性检验1.t检验适用于计量资料、正态分布、方差具有齐性的两组间小样本比较。
包括配对资料间、样本与均数间、两样本均数间比较三种,三者的计算公式不能混淆。
2.t'检验应用条件与t检验大致相同,但t′检验用于两组间方差不齐时,t′检验的计算公式实际上是方差不齐时t检验的校正公式。
3.U检验应用条件与t检验基本一致,只是当大样本时用U检验,而小样本时则用t检验,t检验可以代替U检验。
4.方差分析用于正态分布、方差齐性的多组间计量比较。
常见的有单因素分组的多样本均数比较及双因素分组的多个样本均数的比较,方差分析首先是比较各组间总的差异,如总差异有显著性,再进行组间的两两比较,组间比较用q检验或LST检验等。
5.X2检验是计数资料主要的显著性检验方法。
用于两个或多个百分比(率)的比较。
常见以下几种情况:四格表资料、配对资料、多于2行*2列资料及组内分组X2检验。
6.零反应检验用于计数资料。
是当实验组或对照组中出现概率为0或100%时,X2检验的一种特殊形式。
属于直接概率计算法。
7.符号检验、秩和检验和Ridit检验三者均属非参数统计方法,共同特点是简便、快捷、实用。
可用于各种非正态分布的资料、未知分布资料及半定量资料的分析。
其主要缺点是容易丢失数据中包含的信息。
所以凡是正态分布或可通过数据转换成正态分布者尽量不用这些方法。
8.Hotelling检验用于计量资料、正态分布、两组间多项指标的综合差异显著性检验。
计量经济学检验方法讨论计量经济学中的检验方法多种多样,而且在不同的假设前提之下,使用的检验统计量不同,在这里我论述几种比较常见的方法。
在讨论不同的检验之前,我们必须知道为什么要检验,到底检验什么?如果这个问题都不知道,那么我觉得我们很荒谬或者说是很模式化。
检验的含义是要确实因果关系,计量经济学的核心是要说因果关系是怎么样的。
那么如果两个东西之间没有什么因果联系,那么我们寻找的原因就不对。
SPSS简明教程X2检验和T检验

SPSS最适用的统计学方法(X2检验和T检验)1.SPSS的启动(1)在windows[开始]→[程序]→[spss20],进入SPSS for Windows对话框,2.创建一个数据文件三个步骤:(1)选择菜单【文件】→【新建】→【数据】新建一个数据文件。
(2)单击左下角【变量视窗】标签进入变量视图界面,定义每个变量类型。
(3)单击【数据视窗】标签进入数据视窗界面,录入数据库单元格内。
3.读取外部数据当前版本的SPSS可以很容易地读取Excel数据,步骤如下:(1)按【文件】→【打开】→【数据】的顺序使用菜单命令调出打开数据对话框,在文件类型下拉列表中选择数据文件,如图2.2所示。
图2.2 Open File对话框(2)选择要打开的Excel文件,单击“打开”按钮,调出打开Excel数据源对话框,如图2.3所示。
对话框中各选项的意义如下:工作表下拉列表:选择被读取数据所在的Excel工作表。
范围输入框:用于限制被读取数据在Excel工作表中的位置。
图2.3 Open Excel Data Source对话框4.数据编辑在SPSS中,对数据进行基本编辑操作的功能集中在Edit和Data菜单中。
5.SPSS数据的保存SPSS数据录入并编辑整理完成以后应及时保存,以防数据丢失。
保存数据文件可以通过【文件】→【保存】或者【文件】→【另存为】菜单方式来执行。
在数据保存对话框(如图2.5所示)中根据不同要求进行SPSS数据保存。
图2.5 SPSS数据的保存5. 数据分析在SPSS中,数据整理的功能主要集中在【数据】和【分析】两个主菜单下6.语言切换:编辑(E)—选项(N)--用户界面-语言--简体中文第六章:描述性统计分析(X2检验)完成计数资料和等级资料的统计描述和一般的统计检验,我们常用的X2检验也在其中完成。
6.1.1界面说明界面如下所示:分析—描述统计—频率用于定义需要计算的其他描述统计量。
现将各部分解释如下:Percentile Values复选框组定义需要输出的百分位数,可计算1.四分位数(Quartiles)、2.每隔指定百分位输出当前百分位数(Cut points for equal groups)3.直接指定某个百分位数(Percentiles),如直接P2.5和P97.5o Central tendency复选框组用于定义描述集中趋势的一组指标:均数(Mean)、中位数(Median)、众数(Mode)、总和(Sum)。
两样本t检验计算公式

两样本t检验计算公式我们来看一下两样本t检验的计算公式。
两样本t检验的计算公式如下:t = (x1 - x2) / sqrt(s1^2/n1 + s2^2/n2)其中,t为检验统计量,x1和x2分别为两个样本的均值,s1和s2为两个样本的标准差,n1和n2分别为两个样本的样本容量。
在进行两样本t检验时,我们需要先计算出两个样本的均值和标准差,然后代入上述公式进行计算。
计算得到的t值可以与t分布的临界值进行比较,从而判断两个样本的均值是否存在显著差异。
接下来,我们将通过一个实例来说明如何使用两样本t检验进行分析。
假设我们想要比较两个不同班级的学生在数学考试中的平均成绩是否有显著差异。
我们随机抽取了班级A和班级B各30名学生的成绩数据,现在我们想要利用两样本t检验来进行分析。
我们计算出班级A和班级B的平均成绩和标准差。
假设班级A的平均成绩为80,标准差为10,班级B的平均成绩为85,标准差为12。
样本容量分别为30。
将这些数据代入两样本t检验的计算公式中,我们可以得到:t = (80 - 85) / sqrt(10^2/30 + 12^2/30)计算得到的t值为-2.73。
接下来,我们需要查找t分布表,找到相应自由度下的临界值。
如果t值小于临界值,则可以认为班级A和班级B的平均成绩存在显著差异。
通过查表,我们发现当自由度为58时,t分布的临界值为-2.00。
由于计算得到的t值(-2.73)小于临界值(-2.00),因此我们可以得出结论:班级A和班级B的数学成绩存在显著差异,班级B的平均成绩高于班级A。
两样本t检验是一种常用的统计方法,可用于比较两个独立样本均值是否存在显著差异。
通过计算得到的t值与t分布的临界值进行比较,我们可以判断两个样本的均值是否存在显著差异。
在实际研究中,我们可以利用两样本t检验来进行数据分析,从而得到有关样本之间差异的结论。
需要注意的是,两样本t检验的计算公式只适用于满足一定假设条件的情况下。
t检验总结
t检验总结t检验是统计学中常用的一种假设检验方法,用于判断两组数据之间是否存在显著差异。
在实际应用中,t检验在医学、生物学、社会科学等领域被广泛使用。
本文将对t检验的原理、应用以及注意事项进行总结,旨在使读者对t检验有一个全面的了解。
一、t检验的原理及公式t检验是基于样本均值之间的差异来判断总体均值是否有显著区别的一种假设检验方法。
主要应用于两组样本的均值比较。
不同于z 检验,t检验适用于小样本(样本量较小)的情况。
t检验的基本原理是,计算两组样本的均值差异,然后根据样本的方差和样本量来估计总体均值之间的差异是否显著。
计算t值的公式如下:t = (x1 - x2) / (s√(1/n1 + 1/n2))其中,x1和x2分别为两组样本的均值,s为样本的标准差,n1和n2为两组样本的样本量。
通过计算t值,可以与t分布表中的临界值进行比较,从而判断两组样本均值之间的差异是否显著。
二、t检验的应用场景t检验在实际应用中具有广泛的应用场景。
以下是一些典型的应用场景:1. 医学研究:在药物的临床试验中,常用t检验来比较接受不同治疗方法的患者之间的效果差异。
2. 社会科学:在调查研究中,t检验可以用来比较不同群体之间的某种特征的差异,如男性与女性在某项指标上的差异。
3. 生物学:在实验室研究中,t检验可用来比较不同处理组的实验结果是否存在显著差异。
4. 工程领域:在质量控制方面,可以使用t检验来判断两种质量控制方法的差异是否显著。
以上仅是一些常见的应用场景,实际上t检验在各个领域都有广泛的应用。
三、t检验的注意事项在进行t检验时,需要注意以下几点:1. 样本的随机性:确保样本是随机抽取的,以减少抽样偏差对结果的影响。
2. 样本的独立性:确保样本之间是相互独立的,即一个样本的观测值不受另一个样本的影响。
3. 正态分布假设:在t检验中,通常假设两个总体是正态分布。
如果数据的正态性不满足,可以使用非参数检验方法。
4. 方差齐性假设:t检验中还需要满足方差齐性假设,即两组样本的方差相等。
两样本t检验计算公式
两样本t检验计算公式1.对于两个独立样本的t检验:t=(x1-x2)/√(s1^2/n1+s2^2/n2)其中t表示t值;x1和x2分别表示两个样本的均值;s1和s2分别表示两个样本的标准差;n1和n2分别表示两个样本的样本容量。
2.对于两个相关样本的t检验:t = (x1 - x2) / (sdiff / √n)其中t表示t值;x1和x2分别表示两个样本的均值差;sdiff表示两个样本的均值差的标准差;n表示样本容量。
接下来,我们将具体介绍两个不同情况下的两样本t检验计算过程。
一、独立样本t检验计算过程:1.收集两个样本的数据并计算样本均值和样本标准差;2.计算两个样本的样本容量;3.计算两个样本的方差;4.根据计算得到的数据,带入公式计算t值;5.查表或使用统计软件计算得到的t值对应的P值;6.对比P值与设定的显著性水平(通常为0.05),如果P值小于显著性水平,则可以拒绝原假设,即认为样本均值存在显著差异;反之,接受原假设,即认为样本均值不存在显著差异。
二、相关样本t检验计算过程:1.收集两个样本的相关数据并计算样本均值差;2.计算样本均值差的标准差;3.计算样本容量;4.根据计算得到的数据,带入公式计算t值;5.查表或使用统计软件计算得到的t值对应的P值;6.对比P值与设定的显著性水平(通常为0.05),如果P值小于显著性水平,则可以拒绝原假设,即认为样本均值存在显著差异;反之,接受原假设,即认为样本均值不存在显著差异。
需要注意的是,在进行两样本t检验前,需要满足以下前提条件:1.数据来自正态分布的总体;2.数据具有相同的方差;3.对于独立样本t检验,两个样本之间应相互独立;4.对于相关样本t检验,两个样本之间应具有相关性。
总结起来,两样本t检验是一种比较两个样本均值是否有显著差异的统计方法,通过计算t值和P值来进行假设检验。
根据计算得到的P值是否小于设定的显著性水平,判断两个样本的均值是否存在显著差异。
第二讲X2检验、第三讲t检验
例:某奶牛场有奶牛500头,每年 每年产奶油20,000斤左右, 每年
现随意抽取10头奶牛为样本,测得产奶油为每头平均45斤, 标准差为13.2斤,问样本平均数(45)与总体平均数(40) 之间的差异是否显著?
生物统计学
黄冈师范学院 解:A、假设波动是抽样误差,样本平均数与总体平均
数之间没有显著差异。 B、依据已知数据求出标准误
样本是总体的一部分,统计值与参数之间只能逼近不可能完全符合, 就有误差存在,称为抽样误差。在不同总体中抽样,样本间也存在误差, 称为本质的差别。显著性测验的作用主要是检验两种假设,即两个 检验两种假设,
总体是否相等,两个样本是否来自同一总体 总体是否相等,两个样本是否来自同一总体。 二、t分布及其测验步骤 分布及其测验步骤
生物统计学
黄冈师范学院 例:检查F2代400株中红花281株、白花119株、理论为300株、100株。
∑=(300-281)+(100-119)=0 无意义。 = 无意义。 = b、改进 K ∑(0-T)² 若结果=0,说明观察值与理论值完全吻合; ( ) 若结果= ,说明观察值与理论值完全吻合; i=1 ∑(0-T)²的数值越小,说明实际次数与理论次数越接近, 但不能说明实际次数和理论次数之间的差异程度 差异程度。 差异程度
一)、t分布的意义 1、t分布 、 分布 分布(t·Distribution)。从总体中抽取很多样本,样本平均数与 从总体中抽取很多样本, 从总体中抽取很多样本 总体平均数之差,除以该样本的标准误差, 总体平均数之差,除以该样本的标准误差,称为 x −µ t= 差值是标准误的多少倍。 差值是标准误的多少倍 sx 这样,一个样本有一个t值,抽多少个样本就有多少个t值,集合很多 值的概率分布 t值,就形成t值的概率分布。
第8章t检验
第八章 t 检验t 检验(t test)亦称Student’s t 检验,是以t 分布为基础定量资料分析中常用的假设检验方法,用于两均数间的比较。
t 检验的应用条件为:①在单样本t 检验中,总体标准差σ未知且样本含量较小,要求样本来自正态分布总体;②配对t 检验是单样本t 检验的特殊情况,配对设计是指同质受试对象配成对子分别接受两种不同处理或同一受试对象分别接受两种不同处理;③两小样本均数比较时,要求两样本均来自正态分布总体,且两样本总体方差相等;若两样本总体方差不相等,则用t '检验;④对两大样本(12n n 、均大于50)的均数比较,可用Z 检验。
但在实际应用时,与上述条件略有偏差,只要其分布为单峰且近似对称分布即可。
第一节 样本均数与总体均数的比较样本与总体均数比较的检验亦称为单样本t 检验(one sample t test),用于样本均数代表的未知总体均数μ与已知总体均数0μ(一般为理论值或标准值)的比较。
在00:H μμ=成立的条件下,检验统计量的计算公式如下01X X X t v n S μ-===- (8.1) 式中,X 为样本均数,S 为样本标准差,v 为自由度。
例8.1 已知某地新生儿出生体重均数为3.36 kg 。
从该地农村随机抽取40名新生儿,测得其平均体重为3.27 kg ,标准差为0.44 kg ,问该地农村新生儿出生体重是否与该地新生儿平均出生体重不同?1.建立检验假设,确定检验水准0: 3.36H μ=,该地农村新生儿体重与该地新生儿平均出生体重相同 1: 3.36H μ≠,该地农村新生儿体重与该地新生儿平均出生体重不同0.05α=2.计算检验统计量 由式(8.1),得1.294140139X X X t S v n μ-====-=-=-= 3.确定P 值,作出统计推断根据39v =和 1.294t =-的绝对值查t 界值表(附表3),得0.20.4P <<,则按0.05α=的检验水准,不拒绝0H ,差异无统计学意义,尚不能认为该地农村新生儿体重与该地新生儿平均出生体重不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
---------------------------------------------------------------最新资料推荐------------------------------------------------------
t检验和x2检验doc
实验一 t-检验实验目的及要求掌握利用Excel 数据分析中提供t-检验工具进行假设检验的方法,并能够解释实验结果。
实验内容及步骤例1-7:
双样本等均值检验是在一定置信水平之下, 在两个总体方差相等的假设之下,检验两个总体均值的差值等于指定平均差的假设是否成立的检验。
假设某工厂为了比较两种装配方法的效率,分别组织了两组员工,每组9 人,一组采用新的装配方法,另外一组采用旧的装配方法。
18个员工的设备装配时间图1-18 中表格所示。
根据以下数据,是否有理由认为新的装配方法更节约时间?图1-18 操作步骤:
STEP1:
选择工具菜单的数据分析子菜单,双击t-检验: 双样本等方差假设选项,则弹出图1-19 所示对话框。
(注: 如果没有数据分析,则请加载分析工具库加载宏。
操作方法:
在工具菜单上,单击加载宏。
在可用加载宏列表中,选中分析工具库框,再单击确定。
如果必要,请按安装程序中的指示进行操作。
1 / 5
) 2)在数据分析对话框中,单击t-检验,再单击确定。
3)在出现的对话框中,设置所需的参数。
图1-19 STEP2:
分别填写变量1 的区域:
$B$1: $B$10,变量2 的区域:
$D$1: $D$10,由于我们进行的是等均值的检验,填写假设平均差为0,由于数据的首行包括标志项选择标志选项,所以选择标志选项,再填写显著水平为0. 05, 然后点击确定按扭。
则可以得到图1-20所示的结果。
图1-20 结果分析:
如图1-20中所示,表中分别给出了两组装配时间的平均值、方差和样本个数。
其中,合并方差是样本方差加权之后的平均值, Df 是假设检验的自由度它等于样本总个数减2, t 统计量是两个样本差值减去假设平均差之后再除于标准误差的结果, P(T=t) 单尾是单尾检验的显著水平, t 单尾临界是单尾检验t 的临界值, P(T=t) 双尾是双尾检验的显著水平, t 双尾临界是双尾检验t 的临界值。
由下表的结果可以看出t 统计量均小于两个临界值,所以,在5%显著水平下,不能拒绝两个总体均值相等的假设,即两种装配方法所耗时间没有显著的不同。
Excel 中还提供了以下类似的假设检验的数据分析工具,它们的名称和作用如下:
---------------------------------------------------------------最新资料推荐------------------------------------------------------ t-检验:
双样本异方差假设 t-检验:
成对双样本均值分析 z-检验:
双样本均值分析实验二 x实验目的及要求 x关关系。
该实验要求学生掌握利用Excel实现x2检验 2检验经常用来判断同一个调查的对象的两个特性之间是否存在明显相2检验的方法步骤,并能够解释实验结果。
实验内容及步骤例1-9:
如图1-27所示,表中是某装修公司的调查报告,试用x2检验方法分析在顾客的所在地区和所选房子的地板类型之间是否存在明显的相关关系。
图1-27 操作步骤:
STEP1:
建立期望频数表。
如图1-28所示,先建立期望频数表的框架,然后在B10 单元格输入公式=B$7*$F4/$F$7 ,再利用填充柄将公式复制到表格的其它单元格,最后利用Excel 的求和函数sum 计算行和与列和。
图1-28 2 概率值。
在A15 单元格输入标志项卡方概率值,先点击B15单元格,从插入菜单中函数子菜单,选择统计函数中的CHITEST 函数,单击确定按扭,然后在弹出的对话框中分别添入实际频数范围B4: E6
3 / 5
和预期频数范围B10: E12 。
最后单击确定按扭即可得到计算结果1. 3E-07, 如图1-29 所示。
STEP2:
计算X 图1-29 STEP3:
建立X2 统计表。
如图1-30 所示,先建立表格的框架,然后在B20单元格输入公式=(B4-B10) /B10 ,再利用填充柄将公式复制到表格的其它单元格。
最后计算X入标志项与计算公式。
2 卡方统计量,分别在A24 与B24 单元输图1-30 STEP4:
进行假设检验。
如图1-31所示,分别输入置信水平、临界值和假设检验的结果其中CHIINV 函数的自由度=(第一类属性的分类数-1) *( 第二类属性的分类数-1) =(3-1) *(4-1) =6。
图1-31 结果分析:
以上的操作步骤完成整个列联表的分析。
其中, B15单元格的卡方概率值与B24 单元格的卡方统计量是表格的两个重要计算结果。
其中卡方概率值等于1. 3E-07 表明:
如果总体的两类属性,即所在地区和所选地板类型,是不相关的,那么得到以上观察的样本的概率是0. 00000013。
---------------------------------------------------------------最新资料推荐------------------------------------------------------ 这个概率几乎接近于0,所以可以认为总体的这两个属性是显著相关的。
5 / 5。
