4节点、8节点
3-8四节点矩形单元讲解

(3-48)
其中 (xi , yi)是节点i的整体坐标,i =1,2,3,4。
返回
在局部坐标系中,节点i的坐标是(i , i ),其值分别 为±1。取位移模式
u 1 2 3 4 v 5 6 7 8
(a)
该函数称为双线性函数。将节点的局部坐标值代入上 式,可列出四个节点处的位移分量,即两组四元联立方程 ,由此可求得位移模式中的8个未知参数1,2,…,8,
x x0 a
y y0 b
式中
x0 ( x1 x2 ) / 2 ( x3 x4 ) / 2 y0 ( y2 y3 ) / 2 ( y1 y4 ) / 2 a ( x2 x1 ) / 2 ( x3 x4 ) / 2 b ( y3 y2 ) / 2 ( y4 y1 ) / 2
返回
求出α1, α2, α3, α4;α 5, α 6 , α7 , α8
u1 u2 u3 u4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 2 1 3 4 1 1 1 1 4
(3-51)
(i=1,2,3,4)
(3-49)
由虎克定律我们可以得出用节点位移表示的单元应力,即
D S1
S2
S3
S4
e
(3-50)
返回
式中
Si D Bi
E
(i=1,2,3,4)
(h)
对于平面应力问题
Si
4ab 1 2
a i 1 0 b i 1 0 b 1 a i 1 0 i 0 1 1 a i 1 0 b i 1 0 2 2
07-Tekla常用节点编号
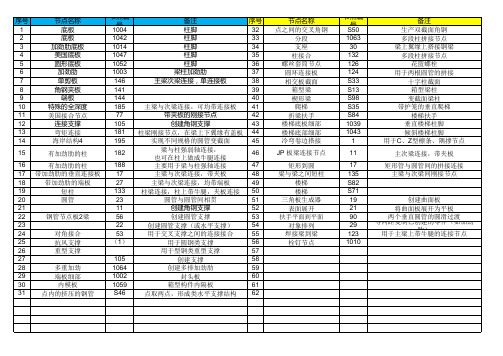
节点名称 底板 底板
加劲肋底板 美国底板 圆形底板 加劲肋 单剪板 角钢夹板 端板
特殊的全深度 美国接合节点
连接支撑 弯矩连接 海岸结构4
15
有加劲肋的柱
16
有加劲肋的柱
17 带加劲肋的垂直连接板
18
带加劲肋的端板
19
短柱
20
圆管
主次梁连接,带夹板
矩形管与圆管间的拼接连接 主梁与次梁间刚接节点
创建曲面板 将曲面板展开为平板 等间两距个复垂制直已圆创管建的的圆零滑件过(渡如加劲 用于主梁上带肋牛)腿的连接节点
46
47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62
节点名称 点之间的交叉角钢
分段 支座 柱接合 螺丝套筒节点 圆环连接板 相交板截面 箱型梁 楔形梁 爬梯 折梁扶手 楼梯底板细部 楼梯底部细部 冷弯卷边搭接
JP 板梁连接节点
矩形到圆 粱与梁之间短柱
楼梯 楼梯 三角板生成器 表面展开 扶手平面到平面 对象排列 焊接梁到梁 栓钉节点
柱梁连接,柱上带牛腿,夹板连接 圆管与圆管间相贯 创建角钢支撑 创建圆管支撑
创建圆管支撑(或水平支撑) 用于交叉支撑之间的连接接合
用于圆钢类支撑 用于型钢类重型支撑
创建支撑 创建多排加劲肋
封头板 箱型构件内隔板 点取两点,形成类水平支撑结构
序号 32 33 34 35 36 37 38 39 40 41 42 43 44 45
105 1064 1002 1059 S46
备注 柱脚 柱脚 柱脚 柱脚 柱脚 梁柱加劲肋 主梁次梁连接,单连接板
2015广联达钢筋软件算量常见问题百问百答

29 节点设置
柱/墙柱
是否可以设置桩上柱插筋弯折 桩上柱插筋弯折长度,软件能否设
长度?
置?一般软件默认的是多少?
可以设置,在工程设置——节点设置——桩上柱插 筋节点,直接修改即可,软件默认的弯折长度是 10d
4
序 一级分类 二级分类
号
问题
问题描述
解决方案
30 节点设置 31 节点设置 32 节点设置 33 节点设置 34 节点设置
柱/墙柱 柱/墙柱
修改计算设置中柱基础插筋弯 折长度为特定数值后节点设置 中不关联?
如何设置伸入基础锚固区长度 不一样的框架柱角筋和边筋?
修改计算设置中柱基础插筋弯折长度 为特定数值后,节点设置中的插筋节 点还是默认为 a,没有变化?
原因分析:节点设置中基础插筋节点构造中默认弯 折数值为 a.是从计算设置中设定的进行取值,修改 计算设置为具体数值,a 的显示不会变化。解决方 案:节点显示的 a 不会变化,计算时会按照计算设 置中设定的数值计算。
钢筋弯折是多少?
弯折是多少?
15d,软件将多种节点构造内置,自动处理。
为什么女儿墙里面计算了插 筋?
为什么女儿墙里面计算了插筋?
软件里面选中剪力墙——右键——其他属性——节 点设置——剪力墙——梁/板上墙节点,所以软件会 计算插筋.
21 节点设置 22 节点设置 23 节点设置
框架梁/非框 框架梁端部支座是柱,需要采用 框架梁端部支座是柱时,需要采用机 计算设置--节点设置--框架梁/非框架梁--楼层框
桩承台遇集水坑图纸要求桩承台钢筋锚入集水坑一个固定长度如何实1146版本之前桩承台上是无法绘制集水坑用筏板代替桩承台调整筏板遇集水坑节点lae为具体数值便可实现1146版本之后软件新增桩承台上可以绘制集水坑修改桩承台遇集水坑节点lae一级分类二级分类问题问题描述解决方案24节点设置基础什么不按承台底筋锚入防水底板构造锚固的节点计算
ls-dyna壳单元类型 -回复

ls-dyna壳单元类型-回复LSDYNA壳单元类型(Shell Element Types in LSDYNA)引言:有限元模拟是当今工程界广泛使用的一种重要工具,用于研究和预测结构、材料和系统的行为。
在这种模拟中,壳单元是最常用的元素类型之一。
壳单元能够模拟各种结构,如板、薄膜和薄壁结构。
LSDYNA是一种流行的有限元分析软件,广泛用于汽车、航空航天和其他工程领域。
本文将介绍LSDYNA中的壳单元类型,以及它们的特性、应用和限制。
第一部分:LSDYNA壳单元类型概述LSDYNA提供了多种不同的壳单元类型,以适应各种模拟需求。
以下是其中一些常见的类型:1. 8节点壳单元(SHELL8):这是LSDYNA中最常用的壳单元类型之一。
它具有8个节点和6个自由度(3个位移和3个转动),可以模拟目标结构的复杂几何形状和变形。
8节点壳单元适用于复杂的结构,如汽车车身和飞机机翼。
2. 4节点壳单元(SHELL4):与8节点壳单元相比,4节点壳单元具有更简单的几何形状和变形模型。
它只有4个节点和3个自由度(2个位移和1个转动),适用于相对简单的结构,如平板和薄膜。
3. 9节点壳单元(SHELL9):这种类型的壳单元具有9个节点和6个自由度。
它在模拟中提供了更高的精度和准确性,特别是对于具有弯曲性质的结构。
这种壳单元类型常用于分析曲面结构,如汽车车身表面。
4. DKT(Dissipative Kirchhoff Theory)壳单元:DKT壳单元基于基尔霍夫理论,用于模拟薄板和薄壁结构的弯曲行为。
这种壳单元类型适用于在弯曲过程中发生大变形和应变的结构,比如复合材料。
第二部分:LSDYNA壳单元特性和应用LSDYNA的壳单元具有多种特性和功能,使其适用于不同的工程模拟需求。
1. 优势功能:- 非线性材料特性:LSDYNA的壳单元支持非线性材料特性,如大变形、弹塑性和断裂。
这使得可以模拟更复杂的结构和材料行为。
- 大变形和刚体运动耦合:壳单元能够同时模拟大变形和刚体运动,适用于需要考虑结构挤压和扭转等情况的模拟。
MARC培训手册

FEM\MARC培训手册.docMARC培训手册目录1. MARC程序介绍1.1 MARC程序结构特点1.2 MARC安装后的有关目录1.3 MARC程序手册的组成1.4 MARC的文件系统1.5 MARC软件运行1.6 运行MARC所需的Job文件的数据构成2.弹塑性分析2.1理论概要2.2选项的使用方法2.3应力分析的控制2.3.1 增量步迭代算法2.3.2 迭代求解控制(CONTROL选项)3.热传导分析3.1理论概要3.2自动步长控制3.3选项的使用方法4.热应力分析4.1理论概要4.2自动步长控制4.3选项的使用方法5.实例分析5.1弹塑性分析5.2热传导分析热传导分析的输入数据与结果5.3热应力分析热应力分析的输入数据与结果附录Ⅰ有限单元法的基本步骤Ⅱ单元的使用方法及数值积分Ⅲ求解器Ⅳ内存分配和空间需求Ⅴ重起动与后处理Ⅵ用TYING实现节点自由度间的线性约束ⅦSingularity Ratio(奇异比)1.MARC程序介绍MARC Analysis Research Corporation(简称MARC)始创于1967年,总部设在美国加州的Palo Alto,是全球第一家非线性有限元软件公司。
创始人是美国著名布朗大学应用力学系教授,有限元分析的先驱Pedro Marcel。
MARC 公司在创立之初便独具慧眼,瞄准非线性分析这一未来分析发展的必然,致力于非线性有限元技术的研究、非线性有限元软件的开发、销售和售后服务。
对于学术研究机构,MARC公司的一贯宗旨是提供高水准的CAE 分析软件及其超强灵活的二次开发环境,支持大学和研究机构完成前沿课题研究。
对于广阔的工业领域,MARC软件提供先进的虚拟产品加工过程和运行过程的仿真功能,帮助市场决策者和工程设计人员进行产品优化和设计,解决从简单到复杂的工程应用问题。
经过三十余年的不懈努力,MARC 软件得到学术界和工业界的大力推崇和广泛应用,建立了它在全球非线性有限元软件行业的领导者地位。
9-有限元四面体及六面体单元
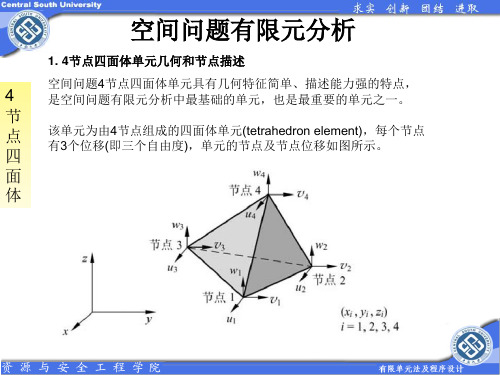
4 节 点 四 面 体
基本概念 空间问题有限元分析
7.单元刚度矩阵
4 节 点 四 面 体
基本概念 空间问题有限元分析
8. 4节点四面体单元的常系数应变和应力
4 节 点 四 பைடு நூலகம் 体
基本概念 空间问题有限元分析
1. 单元的几何和节点描述
8 节 点 正 六 面 体
该单元为由8节点组成的正六面体单元(hexahedron element),每个节点有3 个位移(即3个自由度),单元的节点及节点位移如图所示
(4-115)
(4-116)
基本概念 空间问题有限元分析
2.单元位移场的表达
8 节 点 正 六 面 体
该单元有8个节点,因此每个方向的位移场可以设定8个待定系数, 根据确定位移模式的基本原则(从低阶到高阶、唯一确定性),选 取该单元的位移模式为
(4-117)
(4-118)
基本概念 空间问题有限元分析
基本概念 空间问题有限元分析
1. 4节点四面体单元几何和节点描述
4 节 点 四 面 体
(4-102) (4-103)
基本概念 空间问题有限元分析
2.单元位移场的表达
4 节 点 四 面 体
该单元有4个节点,单元的节点位移有12个自由度(DOF)。因此每个方向的 位移场可以设定4个待定系数,根据节点个数以及确定位移模式的基本原则 (从低阶到高阶的完备性、唯一确定性),选取该单元的位移模式为
2.空间8节点六面体单元分析的算例
空 间 问 题 分 析 的 算 例
基本概念 空间问题有限元分析
2.空间8节点六面体单元分析的算例 (1)结构的离散化与编号
空 间 问 题 分 析 的 算 例
dyna实体单元类型

dyna实体单元类型在有限元分析(Finite Element Analysis,FEA)中,"Dyna" 通常是指LS-DYNA,这是一种广泛用于模拟动态加载和非线性材料行为的有限元软件。
在LS-DYNA 中,实体单元(Element)是构成有限元模型的基本组成单元之一。
LS-DYNA 支持多种实体单元类型,以适应不同类型的模拟问题。
以下是LS-DYNA 中的一些常见实体单元类型:1. Solid Element(实体单元):•Type 1: 8 节点固体元素(Solid Element)•Type 2: 20 节点固体元素(Solid Element)•Type 3: 15 节点固体元素(Solid Element)2. Shell Element(壳单元):•Type 4: 4 节点壳单元(Shell Element)•Type 5: 8 节点壳单元(Shell Element)•Type 6: 3 节点三角形壳单元(Shell Element)3. Beam Element(梁单元):•Type 7: 2 节点梁单元(Beam Element)•Type 8: 3 节点梁单元(Beam Element)4. Rigid Body Element(刚体单元):•Type 9: 刚体单元1/ 2以上只是LS-DYNA 支持的一些基本实体单元类型,实际上还有更多的单元类型和变种可供选择,以适应不同的仿真场景。
选择合适的实体单元类型取决于模型的几何形状、材料特性、加载条件等因素。
在LS-DYNA 的用户手册和文档中,可以找到详细的关于每个单元类型的信息,包括其数学表达式、适用范围以及用法示例。
2/ 2。
第五讲 等参单元

•
关于高斯积分有如下结论: 采用N个积分点的高斯积分,如果被积函数是2N-1阶及以
下的多项式,则高斯求积公式给出准确结果。
•
对于二、三维高斯积分,有:
I
I
1
1
1 1
1
1
f ( , )dd f (i , j ) wi w j
i 1 j 1
1
L
M
1 1 1
平面内的任意四边形单元称为实际单元或子单元。显然, 母单元的节点对应于不同的x,y坐标就得到不同的任意 四边形单元。
•变实例
• 建立了局部坐标系或映射后,我们可以在ξ -η 平面上 的母单元中描述实际单元的位移模式和力学特性。 • 任意四边形单元在母单元中的位移模式插值公式(或者
称为ξ -η 坐标系下的位移模式)可以参考矩形单元的 位移模式写为:
1)形函数导数的坐标变换 • 等参单元中形函数是局部坐标ξ ,η 的显函数,而计算 应变时需要形函数对x,y坐标的导数。根据等参变换式, ξ ,η 和 x,y之间有一定函数关系,由复合函数求导规 则有:
N i x N x i y N i N i x x N J N y i i y y
k B DBhd
e T
e
由于[B]矩阵已是ξ,η的函数,上式积分应该在自然坐标系下 进行,或者说进行积分变量替换。
在整体坐标系中,面积微元为x 方向和y 方向微矢量的叉乘 的模量,
• 由二维重积分变量替换公式得到:
k 1 1 B DBh J dd
任意直边四边形
任意六面体
