计量经济学(单选)第二三章习题说课讲解
第二、三章习题

一、单选题:1.最小二乘准则是指使()达到最小值的原则确定样本回归方程。
A.()∑=-n t t t Y Y 1ˆ B.∑=-n t t t Y Y 1ˆ C.tt Y Y ˆmax - D.()21ˆ∑=-nt tt Y Y2.下图中“{”所指的距离是()i YA. 随机误差项B. 残差C. i Y 的离差D.i Y ˆ的离差3.参数估计量βˆ是i Y 的线性函数称为参数估计量具有( )的性质。
A.线性B.无偏性C.有效性D.一致性4.参数β的估计量βˆ具备有效性是指()A.0)ˆ(=βVarB.)ˆ(βVar 为最小C.0ˆ=-ββD.)ˆ(ββ-为最小5.回归模型i i i X Y μββ++=10,i = 1,…,25中,总体方差未知,检验010=β:H 时,所用的检验统计量1ˆ11ˆβββS -服从()。
A.)(22-n χB.)(1-n tC.)(12-n χ D.)(2-n t 6.对回归模型应用普通最小二乘法,会得到一组正规方程组,下列方程中不是正规方程组的是()A.0)(10=--∑i i X Y ββB. 0)(10=--∑i i i X X Y ββC.0)ˆ(2=-∑i i Y YD.0=∑i i X e7.样本可决系数2R 的取值范围是()A.12≤RB. 12≥RC. 102≤≤RD. 112≤≤-R 8.一元线性回归模型i i i X Y μββ++=10的最小二乘结果显示,残差平方和RSS=92,样本容量n=25,则回归模型的标准差σ为()A.1.270B.2.324C.2.000D.1.7539.总体平方和TSS 、残差平方和RSS 与回归平方和ESS 三者的关系是()。
A.RSS=TSS+ESSB.TSS=RSS+ESSC.ESS=RSS-TSSD.ESS=TSS+RSS10.设k 为回归模型中的参数个数(包括截距项),n 为样本容量,ESS 为残差平方和,RSS 为回归平方和。
《计量经济学》第三版课后题问题详解李子奈

第一章绪论参考重点:计量经济学的一般建模过程第一章课后题(1.4.5)1.什么是计量经济学?计量经济学方法与一般经济数学方法有什么区别?答:计量经济学是经济学的一个分支学科,是以揭示经济活动中客观存在的数量关系为容的分支学科,是由经济学、统计学和数学三者结合而成的交叉学科。
计量经济学方法揭示经济活动中各个因素之间的定量关系,用随机性的数学方程加以描述;一般经济数学方法揭示经济活动中各个因素之间的理论关系,用确定性的数学方程加以描述。
4.建立与应用计量经济学模型的主要步骤有哪些?答:建立与应用计量经济学模型的主要步骤如下:(1)设定理论模型,包括选择模型所包含的变量,确定变量之间的数学关系和拟定模型中待估参数的数值围;(2)收集样本数据,要考虑样本数据的完整性、准确性、可比性和—致性;(3)估计模型参数;(4)检验模型,包括经济意义检验、统计检验、计量经济学检验和模型预测检验。
5.模型的检验包括几个方面?其具体含义是什么?答:模型的检验主要包括:经济意义检验、统计检验、计量经济学检验、模型的预测检验。
在经济意义检验中,需要检验模型是否符合经济意义,检验求得的参数估计值的符号与大小是否与根据人们的经验和经济理论所拟订的期望值相符合;在统计检验中,需要检验模型参数估计值的可靠性,即检验模型的统计学性质;在计量经济学检验中,需要检验模型的计量经济学性质,包括随机扰动项的序列相关检验、异方差性检验、解释变量的多重共线性检验等;模型的预测检验主要检验模型参数估计量的稳定性以及对样本容量变化时的灵敏度,以确定所建立的模型是否可以用于样本观测值以外的围。
第二章经典单方程计量经济学模型:一元线性回归模型参考重点:1.相关分析与回归分析的概念、联系以及区别?2.总体随机项与样本随机项的区别与联系?3.为什么需要进行拟合优度检验?4.如何缩小置信区间?(P46)由上式可以看出(1).增大样本容量。
样本容量变大,可使样本参数估计量的标准差减小;同时,在同样置信水平下,n 越大,t 分布表中的临界值越小。
计量经济学习题(第一、二章)

第一章绪论一单项选择题1、计量经济学是一门()学科A、测量B、经济C、统计D、数学2、同一统计指标按时间顺序记录的数据列称为()A、横截面数据B、时间序列数据C、虚变量数据D、面板数据3、样本数据的质量问题,可以概括为完整性、准确性、可比性和()A、时效性B、一致性C、广泛性D、系统性4、描述微观主体经济活动中的变量关系的计量经济模型是()A微观计量经济模型 B 宏观计量经济模型C 理论计量经济模型D 应用计量经济模型5、下面属于横截面数据的是()A 1991-2003年各年某地区20个乡镇企业的平均工业产值B 1991-2003年各年某地区20个乡镇企业各镇的工业产值C 某年某地区20个乡镇工业产值的合计数D 某年某地区20个乡镇各镇的工业产值6、下列属于时间序列数据的是()A某月全厂各班组的出勤率B 某日30个大中城市的最高气温C 某上市公司股票每天的收盘价D 全国第二次工业普查按行业划分的工业总产值7、经济计量分析工作的基本步骤是()A建立模型、收集样本数据、估计参数、检验模型、应用模型B 设定模型、估计参数、检验模型、应用模型、模型评价C 个体设计、总体设计、估计模型、应用模型、检验模型D 确定模型导向、确定变量及方程式、估计模型、检验模型、应用模型8、计量经济分析工作的研究对象是()A.经济理论B.经济数学方法C.经济数学模型D.社会经济系统9、有人采用全国大中型煤炭企业的截面数据,估计生产函数模型,然后用该模型预测未来煤炭行业的产出量,这是违反了数据的()原则。
A.一致性B.准确性C.可比性D.完整性10、对模型参数估计值的符号和大小合理性进行的检验,属于( )A 、经济意义检验B 、计量经济学检验C 、统计检验D 、预测检验 11、对下列模型进行经济意义检验,哪一个模型通常被认为没有实际价值的( ) A. (i C i 消费)=500+0.8I (收入)B. di i i Q (商品需求)=10+0.8I(收入)+0.9P(价格)C. si i Q (商品供给)=20+0.75P(价格)D. 0.60.4()()i i L i Y(产出量)=0.65K 资本劳动12、流动性偏好函数为:μβββ+++=r Y M 210,设M 为货币需求量,Y 为收入水平,r 为利率,论,有()的估计值,根据经济理和分别为和21^2^1ββββ A 、应为负值应为正值,^2^1ββ B 、应为正值应为正值,^2^1ββ C 、应为负值应为负值,^2^1ββ D 、应为正值应为负值,^2^1ββ二 多项选择题1、计量经济学是以下哪些学科相结合的综合性学科( ) A 统计学 B 数理经济学 C 经济统计学 D 数学 E 经济学2、计量经济模型的应用在于( )A 结构分析B 经济预测C 政策评价D 检验和发展经济理论E 设定和检验模型 3、一个模型用于预测前必须经过的检验有( )A 、经济检验B 、统计检验C 、计量经济学检验D 、模型预测检验E 、实践检验4、样本数据的质量问题可以概括为( )A 、完整性B 、准确性C 、可比性D 、一致性E 、同质性5、下面属于截面数据的是()A、1980—2005年各年全国31省市自治区的服务业产值B、1980—2005年各年某地区的财政收入C、2004年全国31个省市自治区的工业产值D、2004年30个重点调查的工业产值E、2004年全国国内生产总值的季度数据6、在模型的经济意义检验中,包括检验下面的哪几项()A、参数估计量的符号B、参数估计量的大小C、参数估计量的相互关系D、参数估计量的显著性E、随机干扰项检验三简答题1、为什么说计量经济学是一门经济学科?2、计量经济模型有哪些应用?3、计量经济学的研究对象是什么?如何运用计量经济学研究经济问题?第二章 一元线性回归模型一 单项选择题1.变量之间的关系可以分为两大类( )。
计量经济学讲义_2.doc

第二章经典单方程计量经济学模型:一元线性回归模型§2.1 回归分析概述一回归分析的概念无论自然现象之间还是社会经济现象之间,大都存在着不同程度的联系,计量经济学的主要任务之一就是寻找各种经济变量之间的相互联系程度、联系方式以及经济变量之间的运动规律。
一般来说,变量之间的关系可以分为两类:一类是确定性的函数关系。
例如,表示。
圆的半径与圆面积之间的关系,可以用函数关系S=2r另一类是非确定性的统计相关关系。
例如,商品房的价格Y与房屋面积X 的关系,随着X的增加,Y也增加。
但是,在给定X时,Y并不能确定。
原因在于,商品房的价格Y不仅与房屋面积X有关,而且还与所在的区域、楼层和小区的人文环境等等因素有关。
这样,虽然人们无法得到商品房的价格Y与房屋面积X之间的函数关系,但是,人们可以将商品房的价格Y作为随机变量,通过统计计量的方法研究它们之间的统计相关关系。
研究随机变量间统计相关关系的方法主要有两种,一种是相关分析法,另一种是回归分析法。
1 相关分析相关分析主要研究随机变量间的相关形式和相关程度。
(1)相关的定义与分类定义:相关(correlation)指两个或两个以上随机变量间相互关系的程度或强度。
分类:①按强度分完全相关:变量间存在函数关系。
例,圆的周长,L = 2πr高度相关(强相关):变量间近似存在函数关系。
例,我国家庭收入与支出的关系。
弱相关:变量间有关系但不明显。
例,近年来我国耕种面积与产量。
零相关:变量间不存在任何关系。
例,某班学生的学习成绩与年龄。
2004006008001020304050YX121020304050YX0.51.01.52.02.53.02.02.53.03.54.04.5YX完全相关 高度相关、线性相关、正相关 弱相关②按变量个数分按形式分:线性相关, 非线性相关 简单相关:指两个变量间相关按符号分:正相关, 负相关, 零相关 复相关(多重相关):指一个变量与两个或两个以上变量间的相关。
伍德里奇《计量经济学导论》(第4版)笔记和课后习题详解(2-8章)

GPA GPA Ai
ˆ 5.8125 / 56.875 0.1022 。 根据公式 2.19 可得: 1
ˆ 3.2125 0.1022 25.875 0.5681 。 根据公式 2.17 可知: 0
????2222211112222221111varvarvar?nnnniiiiiiiiiinnniiiiiixxuxxuxxx??????????????????????????????????????????????????????????????????根据公式257????2211?varniixx????????????对任何数据样本??2211nniiiixxx??????除非0x?
7.利用 Kiel and McClain(1995)有关 1988 年马萨诸塞州安德沃市的房屋出售数据,如下方程给出了房屋 价格( price )和距离一个新修垃圾焚化炉的距离( dist )之间的关系:
log price 9.40 0.312log dist n 135 , R 2 0.162
因此 GPA 0.5681 0.1022 ACT 。 此处截距没有一个很好的解释, 因为对样本而言,ACT 并不接近 0。 如果 ACT 分数提高 5 分,预期 GPA 会提高 0.1022× 5=0.511。 (Ⅱ)每次观测的拟合值和残差表如表 2-3 所示: 表 2-3
i
GPA
GPA
^
^
ˆ u
1 2 3 4 5 6 7 8
^
2.8 3.4 3.0 3.5 3.6 3.0 2.7 3.7
2.7143 3.0209 3.2253 3.3275 3.5319 3.1231 3.1231 3.6341
庞皓计量经济学第三版课后习题及答案 顶配
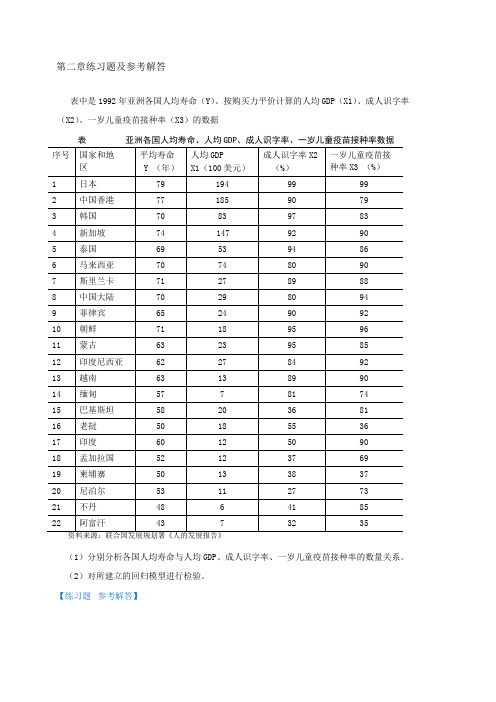
第二章练习题及参考解答表中是1992年亚洲各国人均寿命(Y)、按购买力平价计算的人均GDP(X1)、成人识字率(X2)、一岁儿童疫苗接种率(X3)的数据表亚洲各国人均寿命、人均GDP、成人识字率、一岁儿童疫苗接种率数据(1)分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。
(2)对所建立的回归模型进行检验。
【练习题参考解答】(1)分别设定简单线性回归模型,分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系(2)对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显着影响.(3)分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为人均寿命与成人识字率回归的可决系数为人均寿命与一岁儿童疫苗接种率的可决系数为相对说来,人均寿命由成人识字率作出解释的比重更大一些为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:表浙江省财政预算收入与全省生产总值数据的显着性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年,全省生产总值为32000 亿元,比上年增长%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学生独立完成由12对观测值估计得消费函数为:(1)消费支出C的点预测值;(2)在95%的置信概率下消费支出C平均值的预测区间。
第四讲(计量经济学第二章)PPT课件

12
六、参数估计量的概率分布及随机扰 动项方差的估计
13
经典假设下,普通最小二乘估计的分布
^
0 0 wii
ˆ1 1 ki i
^
0~N(0,2
w2) i
^
1~N(1,2
k2) i
14
古典假设下,随机扰动项方差的估计
^
2
1
n2
ei2
^2
(n2)2 ~2(n2) (证明略)
6
2、一元线性回归模型普通最小二乘估 计量的性质
高斯—马尔可夫定理(Gauss-Markov theorem)
在古典回归模型的基本假定下,最小 二乘估计量是具有最小方差的线性 无偏估计量,具有一致性。
7
无偏性:即
^
^
E00,E11
证: ˆ1 1 ki i
E ( ˆ 1 ) E ( 1 k ii ) 1 k i E ( i ) 1
1
x12i x22i(x1ix2i)2
[( x2 2i)x1iyi][( x1ix2i)x2iyi]
[ ]y x1 2i x2 2i(x1ix2i)2
( x2 2i)x1i( x1ix2i)x2i x12i x2 2i(x1ix2i)2 i
^
( x22i)x1i( x1ix2i)x2i
参数β0的区间估计所需要的统计量:
~t(n2) ^
T 00
0
S^
0
设置信水平 1
p{T|0|t}1
2
^
^
得置信区间: ( 0t2S^0, 0t2S^0)
17
二元线性回归模型
二元线性回归模型 Y i01 X 1 i2 X 2 i u i
《计量经济学(第二版)》习题解答(第1-3章)

《计量经济学(第二版)》习题解答第一章1.1 计量经济学的研究任务是什么?计量经济模型研究的经济关系有哪两个基本特征? 答:(1)利用计量经济模型定量分析经济变量之间的随机因果关系。
(2)随机关系、因果关系。
1.2 试述计量经济学与经济学和统计学的关系。
答:(1)计量经济学与经济学:经济学为计量经济研究提供理论依据,计量经济学是对经济理论的具体应用,同时可以实证和发展经济理论。
(2)统计数据是建立和评价计量经济模型的事实依据,计量经济研究是对统计数据资源的深层开发和利用。
1.3 试分别举出三个时间序列数据和横截面数据。
1.4 试解释单方程模型和联立方程模型的概念,并举例说明两者之间的联系与区别。
1.5 试结合一个具体经济问题说明计量经济研究的步骤。
1.6 计量经济模型主要有哪些用途?试举例说明。
1.7 下列设定的计量经济模型是否合理,为什么?(1)ε++=∑=31i iiGDP b a GDPε++=3bGDP a GDP其中,GDP i (i =1,2,3)是第i 产业的国内生产总值。
答:第1个方程是一个统计定义方程,不是随机方程;第2个方程是一个相关关系,而不是因果关系,因为不能用分量来解释总量的变化。
(2)ε++=21bS a S其中,S 1、S 2分别为农村居民和城镇居民年末储蓄存款余额。
答:是一个相关关系,而不是因果关系。
(3)ε+++=t t t L b I b a Y 21其中,Y 、I 、L 分别是建筑业产值、建筑业固定资产投资和职工人数。
答:解释变量I 不合理,根据生产函数要求,资本变量应该是总资本,而固定资产投资只能反映当年的新增资本。
(4)ε++=t t bP a Y其中,Y 、P 分别是居民耐用消费品支出和耐用消费品物价指数。
答:模型设定中缺失了对居民耐用消费品支出有重要影响的其他解释变量。
按照所设定的模型,实际上假定这些其他变量的影响是一个常量,居民耐用消费品支出主要取决于耐用消费品价格的变化;所以,模型的经济意义不合理,估计参数时可能会夸大价格因素的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、单选题:
1.回归分析中定义的()
A.解释变量和被解释变量都是随机变量
B.解释变量为非随机变量,被解释变量为随机变量
C.解释变量和被解释变量都为非随机变量
D.解释变量为随机变量,被解释变量为非随机变量
2.最小二乘准则是指使()达到最小值的原则确定样本回归方程。
A.()∑=-n
t t t Y Y 1ˆ B.∑=-n t t t Y Y 1
ˆ C.t t Y Y ˆmax - D.()2
1ˆ∑=-n
t t t Y Y 3.下图中“{”所指的距离是()
A.
残差 C. i Y 的离差 D. i Y ˆ的离差
4.最大似然准则是从模型总体抽取该n 组样本观测值的()最大的准则
确定样本回归方程。
A.离差平方和
B.均值
C.概率
D.方差
5.参数估计量βˆ是i Y 的线性函数称为参数估计量具有( )的性质。
A.线性
B.无偏性
C.有效性
D.一致性
X 10ˆˆβ+
6.参数β的估计量βˆ具备有效性是指()
A.0)ˆ(=βVar
B.)ˆ(βVar 为最小
C.0ˆ=-ββ
D.)ˆ(ββ-为最小
7.要使模型能够得出参数估计量,所要求的最小样本容量为()
A.n ≥k+1
B.n ≤k+1
C.n ≥30
D.n ≥3(k+1)
8.已知含有截距项的三元线性回归模型估计的残差平方和为8002=∑
t e ,估计用样本容量为24=n ,则随机误差项t u 的方差估计量为( )。
A.33.33
B.40
C.38.09
D.36.36
9.最常用的统计检验准则包括拟合优度检验、变量的显著性检验和()。
A.方程的显著性检验
B.多重共线性检验
C.异方差性检验
D.预测检验
10.反映由模型中解释变量所解释的那部分离差大小的是( )。
A.总体平方和
B.回归平方和
C.残差平方和
11.总体平方和TSS 、残差平方和RSS 与回归平方和ESS 三者的关系是()。
A.RSS=TSS+ESS
B.TSS=RSS+ESS
C.ESS=RSS-TSS
D.ESS=TSS+RSS
12.下面哪一个必定是错误的()。
A. i i X Y 2.030ˆ+= 8.0=XY r
B. i i X Y 5.175ˆ+-= 91.0=XY r
C. i i
X Y 1.25ˆ-= 78.0=XY r D. i i
X Y 5.312ˆ--= 96.0-=XY r 13.产量(X ,台)与单位产品成本(Y ,元/台)之间的回归方程为X Y 5.1356ˆ-=,这说明()。
A.产量每增加一台,单位产品成本增加356元
B.产量每增加一台,单位产品成本减少1.5元
C.产量每增加一台,单位产品成本平均增加356元
D.产量每增加一台,单位产品成本平均减少1.5元
14.回归模型i i i X Y μββ++=10,i = 1,…,25中,总体方差未知,
检验010=β:H 时,所用的检验统计量1
ˆ11ˆβββS -服从()。
A.)(22-n χ B.)(1-n t
C.)(12-n χ
D.)(2-n t
15.设k 为回归模型中的参数个数(包括截距项),n 为样本容量,ESS 为
残差平方和,RSS 为回归平方和。
则对总体回归模型进行显著性检验 时构造的F 统计量为()。
A. /(1)/()ESS k F RSS n k -=- B.)/()1/(1k n ESS k RSS F ---= C.ESS RSS F = D.RSS ESS F =
16.根据可决系数R 2与F 统计量的关系可知,当R 2=1时有()。
A.F=1
B.F=-1
C.F →+∞
D.F=0
17.线性回归模型的参数估计量βˆ是随机变量i Y 的函数,即
()Y X X X '1
'ˆ-=β。
所以βˆ是()。
A.随机变量 B.非随机变量
C.确定性变量
D.常量
18.由 βˆˆ00X Y =可以得到被解释变量的估计值,由于模型中参数估计量的
不确定性及随机误差项的影响,可知0ˆ
Y 是()。
A.确定性变量
B.非随机变量
C.随机变量
D.常量
19.下面哪一表述是正确的()。
A.线性回归模型i i i X Y μββ++=10的零均值假设是指011=∑=n i i n μ
B.对模型i i i i X X Y μβββ+++=22110进行方程显著性检验(即F
检验),检验的零假设是
02100===βββ:H C.相关系数较大并不意味着两个变量存在较强的因果关系
D.当随机误差项的方差估计量等于零时,说明被解释变量与解释变量
之间为函数关系
20.在双对数线性模型μββ++=X Y ln ln 10中,参数1β的含义是()。
A.Y 关于X 的增长量
B.Y 关于X 的发展速度
C.Y 关于X 的边际倾向
D.Y 关于X 的弹性
21.根据样本资料已估计得出人均消费支出Y 对人均收入X 的回归方程为 X Y ln 75.000.2ln +=),这表明人均收入每增加1%,人均消费支出将增加()。
A.2%
B.0.2%
C.0.75%
D.7.5%
22.半对数模型μββ++=X Y ln 10中,参数1β的含义是()。
A .X 的绝对量变化,引起Y 的绝对量变化
B .Y 关于X 的边际变化
C .X 的相对变化,引起Y 的期望值绝对量变化
D .Y 关于X 的弹性
23.半对数模型μββ++=X Y 10ln 中,参数1β的含义是()。
A.X 的绝对量发生一定变动时,引起因变量Y 的相对变化率
B.Y 关于X 的弹性
C.X 的相对变化,引起Y 的期望值绝对量变化
D.Y 关于X 的边际变化
24.双对数模型
μ
β
β+
+
=X
Y ln
ln
1
0中,参数1
β的含义是()。
A.X的相对变化,引起Y的期望值绝对量变化
B.Y关于X的边际变化
C.X的绝对量发生一定变动时,引起因变量Y的相对变化率
D.Y关于X的弹性
简答题:
1.随机误差项包含哪些因素影响。
2.最小二乘法的基本原理。
3.为什么要计算调整后的可决系数?
一、单选题:
1-5. B D B C A 6-10 B A B A B
11-15 B C D D A 16-20 C A C C D 21-24 C C A D
1. 答:
随机误差项主要包括下列因素的影响:
(1)解释变量中被忽略的因素的影响;
(2)变量观测值的观测误差的影响;
(3)模型关系的设定误差的影响;
(4)其它随机因素的影响。
2、答
最小二乘法的基本原理是当从模型总体随机抽取n组样本观测值后,最合理的参数估计量应该使得模型能最好地拟合样本数据。
3、答:
剔除样本容量和解释变量个数的影响。
