应用统计 大工 期末复习综合1
应用统计分析复习要点和答案
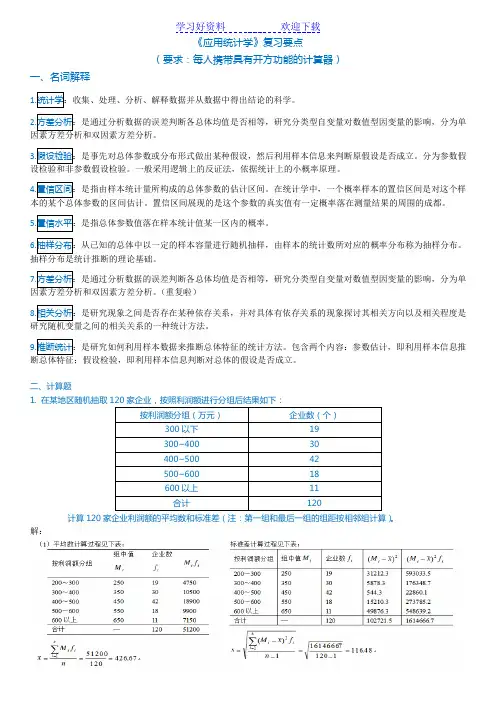
《应用统计学》复习要点（要求：每人携带具有开方功能的计算器）一、名词解释（重复啦）二、计算题1. 在某地区随机抽取计算120。
解：2.某银行为缩短顾客到银行办理业务等待的时间，准备了两种排队方式进行试验。
为比较哪种排队方式使顾客等待的时间更短，两种排队方式各随机抽取9名顾客，得到第一种排队方式的平均等待时间为7.2分钟，标准差为1.97分钟，第二(1)(2)比较两种排队方式等待时间的离散程度。
(3)如果让你选择一种排队方式，你会选择哪一种？试说明理由。
解：3. 某大学为了解学生每天上网的时间，在全校学生中随机抽取36人，调查他们每天上网的时间（单位：小时），得到的数据如下：z(0.01)统计量值分别为1.65、1.96和2.58）解：4. 利用下面的信息，构建总体均值μ的置信区间。
(1)总体服从正态分布，且已知σ=500，n=15，=8900，置信水平为95%。
（注：z统计量值为1.96）(2)总体不服从正态分布，且已知σ=500，n=35，=8900，置信水平为95%。
（注：z统计量值为1.96）(3)总体不服从正态分布，σ未知，n=35，=8900，s=500，置信水平为90%。
（注：z统计量值为1.65）(4)总体不服从正态分布，σ未知，n=35，=8900，s=500，置信水平为99%。
（注：z统计量值为2.58）解：5.对消费者的一项调查表明，17%的人早餐饮料是牛奶。
某城市的牛奶生产商认为，该城市的人早餐饮用牛奶的比例更高。
为验证这一说法，生产商随机抽取550人的一个随机样本，其中115人早餐饮用牛奶。
在α=0.05的显著性水平下，检验该生产商的说法是否属实？（注：z统计量值为1.96）解：6.一项包括了200个家庭的调查显示，每个家庭每天看电视的平均时间为7.25小时，标准差为2.5小时。
据报道，10年前每天每个家庭看电视的平均时间是6.7小时。
取显著性水平α=0.01，这个调查能否证明“如今每个家庭每天收看电视的平均时间增加了”？（注：z统计量值为1.96）解：7.下面是7个地区2000年的人均国内生产总值GDP（Y）和人均消费水平（X）的统计数据（注：此题对应的t统计量值为2.57（1（2）人均GDP作自变量，人均消费水平作因变量，利用最小二乘法求出估计的回归方程，并解释回归系数的实际意义。
大连理工大学22春“工商管理”《应用统计》期末考试高频考点版(带答案)试卷号：4
大连理工大学22春“工商管理”《应用统计》期末考试高频考点版（带答案）一.综合考核(共50题)1.随机变量X~N(0，1)，Y~N(0，1)，且相互独立，则2X-Y服从N(0，3)。
()A.正确B.错误参考答案：B2.对任意两事件A与B，等式()成立。
A.P(AB)=P(A)P(B)B.P(A∪B) =P(A)+P(B)C.P(A|B)=P(A)(P(B)≠0)D.P(AB)=P(A)P(B|A)(P(A)≠0)参考答案：D3.自总体X抽得一个容量为5的样本8，2，5，3，7，则样本均值是()A.8B.2C.5D.3参考答案：C4.有两箱同种类的元件，第一箱装50只，其中10只为一等品; 第二箱装30只，其中18只为一等品。
今从两箱中选出一箱，然后从该箱中作不放回抽取，每次一只，则第一次取出的元件是一等品的概率是()。
A.0.5B.0.2C.0.4D.0.35.对于常数a，b，随机变量X，Y，有E(aX+bY)=aE(X)+bE(Y)。
()A.错误B.正确参考答案：B6.如果随机变量X的分布函数F(X)可以表示成一个非负可积函数f(x)的积分，则称X为连续型随机变量。
()A.错误B.正确参考答案：B7.将3只不同的球投到4个不同的杯子中去，则每个杯中球的个数最多为1个的概率是3/8。
()A.正确B.错误参考答案：A8.如果X与Y独立，D(X)=2，D(Y)=1，则D(X-2Y+3)=6。
()A.正确B.错误参考答案：A9.对于常数C，有E(C)=0。
()A.正确B.错误10.设样本x1，x2，...，xn取自正态总体(σ>0)，则=()。
A.N(0，1)B.C.N(u，1)D.参考答案：A11.每张奖券中尾奖的概率为1/10，某人购买了20张奖券，则中尾奖的张数X服从什么分布?()A.二项B.泊松C.指数D.正态参考答案：A12.设随机事件A与B互不相容，P(A)=0.2，P(A∪B)=0.5，则P(B)=0.3。
应用统计分析总复习
《应用统计分析》复习由于老师要求试卷个性化，我们尽量调整语句顺序或用近义词替换，变成自己白话的语气，特别是要求结合本单位情况的，可以提前思考一下如何把别人的答案套用到自己单位（特别是论述题）。
一、名词解释1.总体：调查研究的事物或现象的全体称为总体。
2.个体：组成总体的每个元素（成员）称为个体。
3.指标：是指用来刻画于描述总体基本状况和各个变量分布特征的综合数量。
4.随机变量：表示随机试验各种结果的实值单值函数，例如电话交换台在一定时间内收到的呼叫次数等等。
5.样本平均值：是指在一组样本中所有数据之和再除以样本的个数。
6.样本方差：其中 E(x)为样本均值。
7.系统抽样：一般指等距抽样，它是首先将总体中各单位按一定顺序排列，根据样本容量要求确定抽选间隔，然后随机确定起点，每隔一定的间隔抽取一个单位的一种抽样方式。
8.随机抽样：按照随机的原则，即保证总体中每一个对象都有已知的、非零的概率被选入作为研究的对象，保证样本的代表性。
9.无偏性：一个总体参数的无偏性是，其期望值等于参数真值的统计量，这意味着无论你取无数个样本，计算每个样本的估计值，估计量的平均值将会等于参数估计值，也就是说样本统计量平均来说等于参数。
估计量是随机变量，对于不同的样本值会得到不同的估计值，我们希望在未知参数真值附近摆动，而它的期望值等于未知参数的真值。
这就导致无偏性这个标准。
10.一致性:一致性也称为相合性，是样本容量非常大时估计量的性质，即渐进性质或大样本性质,如果随着样本容量的增大，估计量和参数的差变小，那么我们说这个无偏估计量具有一致性,用方差来测度二者相似的程度。
二、简答题1.为什么实际工作中经常使用平均值（如人均工资）？平均值也称均值,它是一组数据相加后除以数据的个数得到的结果，采用平均值这种描述数据水平的方式时，数据采集以及统计计算都相对简单和方便，可以很容易得出数据水平的统计量，很容易被多数人理解和接受，因此在实际工作中经常使用。
应用统计学复习题精编版
应用统计学复习题精编版MQS system office room 【MQS16H-TTMS2A-MQSS8Q8-MQSH16898】应用统计学复习题简答题1.简述普查和抽样调查的特点。
答：普查是指为某一特定目的而专门组织的全面调查，它具有以下几个特点：（1）普查通常具有周期性。
（2）普查一般需要规定统一的标准调查时间，以避免调查数据的重复或遗漏，保证普查结果的准确性。
（3）普查的数据一般比较准确，规划程度也较高。
（4）普查的使用范围比较窄。
抽样调查指从调查对象的总体中随机抽取一部分单位作为样本进行调查，并根据样本调查结果来推断总体数量特征的一种数据收集方法。
它具有以下几个特点：（1）经济性。
这是抽样调查最显着的一个特点。
（2）时效性强。
抽样调查可以迅速、及时地获得所需要的信息。
（3）适应面广。
它适用于对各个领域、各种问题的调查。
（4）准确性高。
2.为什么要计算离散系数？答：离散系数是指一组数据的标准差与其相应得均值之比，也称为变异系数。
对于平均水平不同或计量单位不同的不同组别的变量值，是不能用方差和标准差比较离散程度的。
为消除变量值水平高低和计量单位不同对离散程度测度值的影响，需要计算离散系数。
离散系数的作用主要是用于比较不同总体或样本数据的离散程度。
离散系数大的说明数据的离散程度也就大，离散系数小的说明数据的离散程度也就小。
3、加权算术平均数受哪几个因素的影响？若报告期与基期相比各组平均数没变，则总平均数的变动情况可能会怎样？请说明原因。
答：加权算术平均数受各组平均数喝次数结构（权数）两因素的影响。
若报告期与基期相比各组平均数没变，则总平均数的变动受次数结构（权数）变动的影响，可能不变、上升、下降。
如果各组次数结构不变，则总平均数；如果组平均数高的组次数比例上升，组平均数低的组次数比例下降，则总平均数上升；如果组平均数低的组次数比例上升，组平均数高的组次数比例下降，则总平均数下降。
4.解释相关关系的含义，说明相关关系的特点。
大工13秋应用统计辅导资料一
目录主题：准备知识 .................................................................................................... 错误!未定义书签。
主题：准备知识 .................................................................................................... 错误!未定义书签。
主题：第一章随机事件及其概率1—3节........................................................ 错误!未定义书签。
主题：第一章随机事件及其概率4—6节........................................................ 错误!未定义书签。
主题：第二章随机变量及其分布1—3节...................................................... 错误!未定义书签。
主题：第二章随机变量及其分布4—5节...................................................... 错误!未定义书签。
主题：第二章随机变量及其分布6-7节 ........................................................ 错误!未定义书签。
主题：第二章随机变量及其分布8-9节 ........................................................ 错误!未定义书签。
主题：第三章随机变量的数字特征1—2节.................................................. 错误!未定义书签。
大工15春《应用统计》开卷考试期末复习题
大工15春《应用统计》开卷考试期末复习题一、单项选择题（本大题共60小题，每小题2分，共120分）1、从一幅52张的扑克牌（去掉大小王）中，任意取5张，其中没有K 字牌的概率为552548C C 2、事件A 与B 互不相容，,3.0)(0.4,)(==B P A P 则=)(B A P 0.33、设B A 、为两个随机事件，则B A -不等于B A 4、设B A 、为两个随机事件，则B A AB ⋃等于A5、已知事件A 与事件B 互不相容，则下列结论中正确的是)()()(B P A P B A P +=+6、已知事件A 与B 相互独立，则下列等式中不正确的是P(A)=1-P(B)7、设电灯泡使用寿命在2000小时以上的概率为0.15，欲求12个灯泡在使用2000小时以后只有一个不坏的概率，则只需用什么公式即可算出贝努利概型计算公式8、随意地投掷一均匀骰子两次，则两次出现的点数之和为8的概率为3659、盒中有10个木质球，6个玻璃球，玻璃球中有2个红色4个蓝色，木质球中有3个红色7个蓝色，现从盒中任取一球，用A 表示“取到蓝色球”，用B 表示“取到玻璃球”，则P(B|A)=11410、6本中文书和4本外文书，任意在书架上摆放，则4本外文书放在一起的概率是)!7!4(11、设随机变量X 的分布列为X 0123P0.10.30.40.2)(x F 为其分布函数，则=)2(F 0.812、在相同条件下，相互独立地进行5次射击，每次射中的概率为0.6，则击中目标的次数X 的概率分布为二项分布B(5,0.6)13、)(),(),,(y F x F y x F Y X 分别是二维连续型随机变量),(Y X 的分布函数和边缘分布函数，),,(y x f ),(x f X )(y f Y 分别是),(Y X 的联合密度和边缘密度，则一定有X 与Y 独立时，)()(),(y F x F y x F Y X =14、设随机变量X 对任意参数满足2)]([)(X E X D =，则X 服从指数分布15、X 服从参数为1的泊松分布，则有()C、)0(11}|1{|2>-≥<-εεεX P 16、设二维随机变量),(Y X 的分布列为则==}0{XY P 317、若)(),(,)(),(21X E X E Y E X E 都存在，则下面命题中错误的是),()-,(Y X Cov Y X Cov =18、若D(X),D(Y)都存在，则下面命题中不一定成立的是X 与Y 独立时，D(XY)=D(X)D(Y)19、设)()(x X P x F ≤=是连续型随机变量X 的分布函数，则下列结论中不正确的是F(x)是不增函数20、每张奖券中尾奖的概率为101，某人购买了20张奖券，则中尾奖的张数X 服从什么分布二项21、设θˆ是未知参数θ的一个估计量，若θθ≠)ˆ(E ，则θˆ是θ的有偏估计22、设总体22),,(~σσu N X 未知，通过样本n x x x ,,,21 检验00:u u H =时，需要用统计量ns u x t /-0=23、设4321,,,x x x x 是来自总体),(2σu N 的样本，其中u 已知，2σ未知，则下面的随机变量中，不是统计量的是)(14212x x x ++σ24、设总体X 服从参数为λ的指数分布，其中0>λ为未知参数，n x x x ,,,21 为其样本，∑==ni i x n x 11，下面说法中正确的是x 是)(x E 的无偏估计25、作假设检验时，在哪种情况下，采用t 检验法对单个正态总体，未知总体方差，检验假设00u u H =：26、设随机变量 ,,,,21n X X X 相互独立，且),,,2,1( n i X i =都服从参数为1的泊松分布，则当n充分大时，随机变量∑==n i i X n X 11的概率分布近似于正态分布1,1(n N 27、设n x x x ,,,21 是来自总体X 的样本，)1,0(~N X ，则∑=ni ix12服从)(2n χ28、设总体X 服从),(2σu N ，n x x x ,,,21 为其样本，x 为其样本均值，则212)-(1x x ni i∑=σ服从)1-(2n χ29、设总体X 服从),(2σu N ，n x x x ,,,21 为其样本，212-(1-1x x n s n i i ∑==，则22)1-(σs n 服从)1-(2n χ30、10021,,,x x x 是来自总体）（22,1~N X 的样本，若)1,0(~,10011001N b x a y x x i i +==∑=，则有5-,5==b a 31、对任意事件A,B，下面结论正确的是)()()(AB P A P B A P -=32、已知事件A 与B 相互独立，6.0)(,5.0)(==B P A P ，则)(B A P ⋃等于0.733、盒中有8个木质球，6个玻璃球，玻璃球中有2个红色4个蓝色，木质球中有4个红色4个蓝色，现从盒中任取一球，用A 表示“取到蓝色球”，用B 表示“取到玻璃球”，则=)|(A B P 3134、设321,,A A A 为任意的三事件，以下结论中正确的是若321,,A A A 相互独立，则321,,A A A 两两独立35、若)](1)][(1[)(B P A P B A P --=⋃，则A 与B 应满足的条件是A 与B 相互独立36、设B A ,为随机事件，且B A ⊂，则AB 等于A37、设C B A ,,为随机事件，则事件“C B A ,,都不发生”可表示为CB A 38、甲、乙、丙三人独立地破译一密码，他们每人译出的概率都是1/4，则密码被译出的概率为643739、掷一颗骰子，观察出现的点数，则“出现偶数”的事件是随机事件40、若A,B 之积为不可能事件，则称A 与B 互不相容41、下列函数中可以作为某个二维随机变量的分布函数的是⎩⎨⎧>>--=--其他,00,0),1)(1(),(4y x e e y x F y x 42、设(X,Y)的联合分布列为则下面错误的是()C、51,151==q p 43、下列函数中，可以作为某个二维连续型随机变量的密度函数的是⎩⎨⎧>>=+-其他,00,0,),()(2y x e y x f y x44、设(X,Y)的联合分布列为则关于X 的边缘分布列为45、若随机变量X 服从[0,2]上的均匀分布，则=2)]([)(X E X D 3146、某人打靶的命中率为0.8，现独立地射击5次，那么5次中有2次命中的概率为3225)2.0()8.0(C 47、设c b a ,,为常数，b X E a X E ==)(,)(2，则=)(cX D )(22a b c -48、设),(~2σu N X i 且i X 相互独立，n i ,,2,1 =，对任意∑==>ni i X n X 11,0ε所满足的切比雪夫不等式为221}|{|εσεn u X P -≥<-49、若随机变量X 的方差存在，由切比雪夫不等式可得≤≥-}1|)({|X E X P )(X D 50、若随机变量X 服从二项分布B(n,p)，且E(X)=6，D(X)=3.6,则有p=0.4，n=1551、设总体X 服从泊松分布， 2,1,0,}{===-k e k X P k λλ，其中0>λ为未知参数，n x x x ,,,21 为X的一个样本，∑==n i i x n x 11，下面说法中错误的是x 是2λ的无偏估计52、总体X 服从正态分布)1,(u N ，其中u 为未知参数，321,,x x x 为样本，下面四个关于u 的无偏估计中，有效性最好的是321313131x x x ++53、样本n x x x ,,,21 取自总体X，且2)(,)(σ==X D u X E ，则总体方差2σ的无偏估计是21)(11x x n ni i --∑=54、对总体),(~2σu N X 的均值u 作区间估计，得到置信度为0.95的置信区间，意义是指这个区间有95%X 01P0.50.5的机会含u 的值55、设3621,,,x x x 为来自总体X 的一个样本，)36,(~u N X ，则u 的置信度为0.9的置信区间长度为3.2956、设总体22),,(~σσu N X 未知，通过样本n x x x ,,,21 检验00:u u H =时，需要用统计量ns u x t /0-=57、对假设检验问题0100:,:u u H u u H ≠=，若给定显著水平0.10，则该检验犯第一类错误的概率为0.1058、从一批零件中随机抽出100个测量其直径，测得的平均直径为5.2cm，标准方差为1.6cm，若想知这批零件的直径是否符合标准直径5cm，因此采用了t 检验法，那么，在显著性水平α下，接受域为)99(||αt t ≤59、总体服从正态分布),(2σu ，其中2σ已知，随机抽取20个样本得到的样本方差为100，若要对其均值u 进行检验，则用u 检验法60、下列说法中正确的是如果原假设是正确的，但作出接受备择假设结论，则犯了拒真错误二、判断题（本大题共60小题，每小题2分，共120分）1、若事件B A 、互不相容，则A B A P =⋃)(。
应用统计期末复习题及参考答案
一简答题 (共10题，总分值100分 )1. 联系实际论述统计的基本职能。
（10 分）2. 下面是20个职工的一次业务考核成绩，请以5分为组距对它们进行分组整理，编制出次数分布表。
96 84 76 85 95 84 86 78 79 7580 82 83 82 87 92 90 92 96 83 （10 分）3. 联系实际论述变异指标的作用和类型（10 分）4. 联系实际阐述统计调查方案的内容（10 分）5. 下面是20个职工的年龄，请以5岁为组距对它们进行分组整理，编制出次数分布表。
51 28 37 46 35 43 37 39 40 2642 43 42 33 29 30 45 37 46 46 （10 分）6. 联系实际论述统计工作的过程（10 分）7. 某企业2015、2016、2017年的产量分别为：410万件、480万件、510万件，请计算该企业2016年和2017年产量的：⑴逐期增长量；⑵累积增长量；⑶环比增长速度；⑷定基增长速度（10 分）8. 结合实例阐述相关关系的种类（10 分）9. 联系实际论述典型调查的意义和作用（10 分）10. 某公司2014、2015、2016年的利润分别为：400万元、800万元、900万元，请计算该公司2015和2016年利润的：⑴逐期增长量；⑵累积增长量；⑶环比增长速度；⑷定基增长速度（10 分）一简答题 (共10题，总分值100分 )1. 答案：统计的基本职能包括：信息职能、咨询职能、监督职能。
信息职能表现在根据科学的统计指标和统计调查方法，全面、系统地搜集、处理和提供大量的以数据描述为基本特征的社会经济信息。
统计工作者通过对统计资料经过反复筛选，提炼出有价值的、接受者尚未掌握的数字情报资料等信息，向这些信息使用人提供服务。
咨询职能指利用已经掌握的丰富的统计信息资源，运用科学的分析方法和先进的技术手段，深入开展综合分析和专题研究，为科学决策和现代管理提供各种可供选择的咨询建议和对策方案。
应用统计学期末复习试卷8套含答案大学期末复习资料
2009
2010
五.综合分析题(20%，20分)
4、引入价格同度量因素，使价格固定在基期
销售量总指数
(万元)
引入销售量同度量因素，使销售量固定在报告期
价格总指数
(万元)
总销售额指数
(万元)
分析报告：由于销售量增加使总销售额增长了19%，使总销售额增加的绝对额为32100万元；由于销售价格上涨使总销售额增长了13%，使总销售额增加的绝对额为26100万元。以上两个因素共同作用的结果使总成本增加了34%，增加的绝对额是12万元。
E．平均增长速度
7．某企业产品总成本报告期为183150元，比基期增长10%，单位成本综合指数为104%，则（ABC）。
A．总成本指数为110%
B．产量增长了%
C．基期总成本为166 500元
D．单位成本上升使总成本增加了7 044元
E．产量增产使总成本增加了9 606元
8．简单随机抽取调查单位时其方法有（ABE）。
BDE
BCD
AB
ABCDE
AD
ABC
ABE
ABCDE
BCE
三.判断题(10%,每题1分)
1
2
3
4
5
6
7
8
9
10
√
×
×
×
√
√
×
×
√
√
四.计算题(20%,每题10分)
1、该厂工人的平均月工资 （元）
2、
年份
产值
（万元）
与上年比较
增长量（万元）
发展速度（%）
增长速度（%）
增长1%的绝对值（万元）
2006
2007
应用统计学期末复习题
A人口按年龄分组 B家庭按收入分组 C 企业按职工人数分组 D 产品按等级分组 17企业按资产总额分组（ B ）。 A只能用单项式分组 B 只能 使用组距式分组 C 可以用单项式分组，也可以用组距式分 组 D 无法分组 18统计分组的关键问题在于（ C ）。 A确定分组的组数 B确定分组的组距 C确定分组的标志 D 计算各组的组中值 19.在进行组距式分组时，凡遇到某单位的标志值刚好等于相邻两组上 下限时，一般的做法是( B ) A将此值归入上限所在组 B将此值归入下 限所在组 C将此值归入上限所在组或下限所在组均可 D另行分组 20 某连续变量数列分为五组：50以下，50－60，60－70，70－80，80 以上，则下面说法正确的是（C ） A 50在第一组，70在第四组 B 60在第二组，80在第五组 C 70在第四组，80在第五组 D 50在第二组，80在第四组 21某连续变量数列，其末组为500以上，其邻近组的组中值为480，则末 组的组中值为（ A ）。 A 520 B 510 C 500 D 490 22.某商场销售电视机，2008年共销售6000台，年末库存100台。这两个 指标是( C ) A时期指标 B时点指标 C前者是时期指标，后者是时点指标 D前 者是时点指标，后者是时期指标 23 下列指标中的强度相对指标是（ A ）。 A 1998年我国人均国内生产总值为6392元 B 1998年我国国内生 产总值比上年增长7.8% C 1998年我国每个职工平均工资为7497元 D 1997年我国钢产量 为美国的 115% 24下列哪个指标属于比较相对指标( B ) A男性人口数与女性人口数比例 B中国人口数与印度人口 数比例 C.合格品数与不合格品数的比例 D.GDP与人口数的比例 25 .某企业职工工资总额计划比去年提高12%，实际提高14%，则其计划 完成程度为（ A ） A.101.79% B.102% C.112% D.114.25% 26．下列属于位置平均数的是( C ) A算术平均数 B调和平均数 C众 数 D几何平均数 27定基增长速度等于（ D ）。 A环比增长速度之和 B环比增长速度之积 C环比发展速度的总和-1 D环比发展速度的连乘积-1 28. 以1980年为基期，2004年为报告期，计算某现象的平均发展速度应 开( B ) A.23次方 B.24次方 C.25次方 D.26次方 29.某地区的生产总值2012年比2007年增长了60%，则该时期该地区生产 总值的年平均增长速度为（C ） A. B. C. D. 30用按季平均法测定季节比率时，各季的季节比率之和应等于（ C ） A100％ B120％ C400％ D1200％
应用统计学复习试题
Z722e；对于有限总体, Z2/2 N------------------- 时磊忖呎….... . ... ... ....应用统计学复习题一简述1统计调查的方法有那几种？答：三种主要调查方式：普查，抽样调查，统计报表。
实际中有时也用到重点调查和典型调查。
2•表示数据分散程度的特征数有那几种？答：全距（又称极差），方差和标准差，交替标志的平均数和标准差，变异系数，标准分数3为什么对总体均值进行估计时，样本容量越大，估计越精确？答：因为总体是所要认识的研究对象的全体，它是具有某种共同性质或特征的许多单位的集合体•总体的单位数通常用N来表示，N总是很大的数. 样本是总体的一部分，它是从总体中随机抽取出来、代表总体的那部分单位的集合体. 样本的单位数称为样本容量，通常用n表示。
样本容量n越大，就越接近总体单位数N，样本均值就越接近总体均值，对总体均值进行估计时，估计越精确。
4•区间估计与点估计的结果有何不同？答：点估计是使用估计量的单一值作为总体参数的估计值；区间估计是指定估计量的一个取值范围都为总体参数的估计。
5•在统计假设检验中，如果轻易拒绝了原假设会造成严重后果时，应取显著性水平较大还是较小，为什么？答：取显著性水平较小，因为如果轻易拒绝了原假设会造成严重后果，那就说明在统计假设检验中，拒绝原假设的概率要小，而假设检验中拒绝原假设的概率正是事先选定的显著性水平a 6•简述算术平均数、几何平均数、调和平均数的适用范围。
答：几何平均数主要适用于比率的平均。
一般地说，如果待平均的变量x与另外两个变量f和m有fx=m的关系时，若取f为权数，应当采用算术平均方法；若取m为权数，应当采用调和平均方法。
7•对总体均值的假设检验中，如何通过确定样本容量大小以控制两类错误？答：要控制两类错误就要减小误差，也就是提高精确性，决定样本大小的影响因素主要有：（1 ）总体方差o2的大小•总体方差大，抽样误差大，则应多抽一些样本容量•问题是实际工作中我们往往不知道总体方差，因而必须作试验性调查，或以过去的历史资料作参考.（2）可靠性程度的高低•要求可靠性越高，所必需的样本容量就越大. （3）允许误差的范围•这主要由研究目的而定. 若要求推断比较精确，允许误差范围应该小一些，随之抽取的样本单位数就要多一些.可用最大允许抽样误差e来表示区间估计的准确程度，其中对于无限总体,------------------- 时磊5说----- - ---- -------8•假设检验的基本思想是什么？答：假设检验的基本思想是：根据所获得的样本，运用统计分析方法对总体的某种假设作出拒绝或接受的判断。
大学应用统计学期末复习
D.2倍
8、某企业总成本报告期比基期增长30%，产量增长
20%，则单位成本增长（
A.10% B.8.33%
）。
C.50% D.80%
某企业劳动生产率资料如下表，计算该企业下半 年平均月劳动生产率。
6月 总产值（万元） 87 月末职工人数（人） 460 劳动生产率（元/人） 1948 7月 91 470 1957 8月 94 480 1979 9月 96 480 2000 10月 102 490 2103 11月 98 480 2021 12月 91 450 1957
复习：第二章-统计调查
• 调查对象（总体）、调查单位（个体）、报告单位（提交 资料单位） • 调查时间（如果调查的是时点现象，调查时间就是规定的 统一标准时间；如果调查的是时期现象，调查时间就是资 料所反映的起止日期） • 调查时限（调查期限）（指进行调查工作的期限） • 统计调查分类：
– （1）统计报表和专门调查 – （2）全面调查和非全面调查
– 按作用与计算方法不同：总量指标、相对指标和平均 指标 – 按反映总体特征不同：数量指标和质量指标 – 按反映时间、地点不同：时点指标和时期指标 – 按计量单位不同：实物指标和价值指标
例题
• 1、在人口总体中，个体是“ ”，“文化程度”是 标志。 • 2、要了解一个企业的产品质量情况，总体是 、个体 是 。 • 3、性别是 标志，标志表现则具体为 或 两种结果。 • “统计”一词从不同的角度去理解，可以有三种含义，即 、统 计资料和统计学。 • 4、几位学生的某门课成绩分别是67分、78分、88分、89分、96分， 则“成绩”是（ ）。 • A、品质标志 B、数量标志 C、标志值 D、数量指标 • 5、对某地区工业企业职工收入情况进行研究，统计总体是（ ）。 • A、每个工业企业 B、该地区全部工业企业 • C、每个工业企业的全部职工 D、该地区全部工业企业的全部 职工 • 6、要了解100名学生的学习情况，则个体是（ ）。 • A、100名学生 B、每一名学生 • C、100名学生的学习成绩 D、每一名学生的学习成绩
《应用统计学》复习题库
第一章思考题及练习题（一）填空题1．统计工作与统计资料的关系是和的关系。
2．统计工作与统计学的关系是和的关系。
3．统计活动具有...和的职能。
4．统计指标反映的是的数量特征，数量标志反映的是的数量特征。
5．在人口总体中，个体是“”，“文化程度”是标志。
6．统计研究过程的各个阶段，运用着各种专门的方法，如大量观察法..综合指标法.和统计推断法等。
7．统计标志是总体中各个体所共同具有的属性或特征的名称。
它分为和两种。
8．要了解一个企业的产品质量情况，总体是.个体是。
9．性别是标志，标志表现则具体为或两种结果。
10．一件商品的价格在标志分类上属于。
11．一项完整的统计指标应该由....和等构成。
12．统计指标按所反映的数量特点不同，可以分为和。
13．反映社会经济现象相对水平或工作质量的指标称为指标。
14.统计活动过程通常被划分为.和三个阶段。
15．经过余年的发展，形成了今天的统计学。
16．古典统计学时期有两大学派，它们分别是和。
17．《关于死之表的自然和政治观察》一书的作者是，他第一次编制了“生命表”。
18.提出了著名的误差理论和“平均人”思想。
19.统计研究的数量性是指通过数来反映事物的量的.量的.量的和量的。
20.统计学包括和两部分内容。
21.总体中所包含的个体数量的多少称为；样本中所包含的个体数量的多少称为。
22.总体中的一个组或类，可被称为一个研究域或。
23.从总体中随机抽取的一部分个体所组成的集合称为。
24.统计理论与方法，事实上就是关于的理论和方法。
25.总体的三大特征是.和。
26.总体的差异性要求体现在至少具有一个用以说明个体特征的。
27.企业性质标志适用的测定尺度是，产品质量等级标志适用的测定尺度是，企业利润标志适用的测定尺度是，企业产量标志适用的测定尺度是。
28.可变的数量标志的抽象化称为。
它按其所受影响因素不同，可分为和两种，按其数值的变化是否连续出现，可分为和两种。
29.个体是的承担者。
应用统计大工期末复习综合1
应用统计大工期末复习综合1本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March2、典型例题解析题型：基本概念、公式与简单运算例1、计算题：写出下列随机试验的样本空间及下列事件所包含的样本点：掷一颗骰子，出现奇数点。
解：掷一颗骰子，其结果有6种可能：出现1点，2点，3点，……，6点，可以记样本空间Ω={1，2，3，4，5，6}，那么“出现奇数点”的事件为{1，3，5}。
例2、计算题：口袋里装有若干个黑球与若干个白球，每次任取一个球，共抽取两次，设事件A 表示第一次取到黑球，事件B 表示第二次取到黑球，用A,B 的运算表示下列事件：（1）第一次取到白球且第二次取到黑球 （2）两次都取到白球（3）两次取到球的颜色不一致 （4）两次取到球的颜色一致解：（1）第一次取到白球且第二次取到黑球，意味着第一次不取到黑球且第二次取到黑球，即事件A 不发生且事件B 发生，可用积事件B A _表示（2）两次都取到白球，意味着第一次取到白球且第二次也取到白球，即事件A 与 B 同时不发生，可用积事件__B A 表示（3）两次取到球的颜色不一致，意味着第一次取到黑球且第二次取到白球，或者第一次取到白球且第二次取到黑球，即积事件B A _发生或积事件_B A 发生，可用和事件B A _+_B A 表示（4）两次取到球的颜色一致，意味着两次都取到黑球，或者两次都取到白球，即积事件AB 发生或积事件__B A 发生，可用和事件AB +__B A 表示例3、填空题：设.60)(.30)(=⋃=B A P A P ，。
（1）若A 和B 互不相容，则P(B)=（2）若B A ⊂，则P(B)= （3）若P(AB)=，则P(B)=解题思路：根据概率的性质P(A+B)=P(A)+P(B)-P(AB)=， （1）若A 和B 互不相容，则AB=Φ，P(AB)=0， 因此P(B)=P(A+B)-P(A)=。
应用统计学复习一
复习思考题一一、单选（每小题2分，共20分）1、统计认识过程是（）。
A、从质到量B、从量到质C、从质到量，再到质和量的结合D、从总体到个体2、调查某市职工家庭的生活状况时，统计总体是（）。
A、该市全部职工家庭B、该市每个职工家庭C、该市全部职工D、该市职工家庭户数3、通过调查大庆、胜利等几大主要油田来了解我国石油生产的基本情况，这种调查方式属于（）。
A、普查B、典型调查C、重点调查D、抽样调查4、了解某企业的期末在制品数量，由调查人员亲自到现场观察计数，这种收集资料的方式属于（）。
A、采访法B、直接观察法C、大量观察法D、报告法5、统计分组的关键在于（）。
A、正确选择分组标志B、正确划分各组界限C、正确确定组数和组限D、正确选择分布数列种类6、在出生婴儿中，男性占53%，女性占47%，这是（）。
A、比例相对指标B、强度相对指标C、比较相对指标D、结构相对指标7、序时平均数又称作（）。
A、平均发展速度B、平均发展水平C、平均增长速度D、静态平均数8、相关关系是（）。
A、现象间客观存在的依存关系B、现象间的一种非确定性的数量关系C、现象间的一种确定性的数量关系D、现象间存在的函数关系9、抽样调查的主要目的是（）。
A、了解现象发展的具体过程和变化趋势B、对调查单位作深入具体的研究C、用样本指标对总体综合数量特征作出具有一定可靠程度的推断估计D、为计划和决策提供详细生动的资料10、从总体中选取样本时必须遵循的基本原则是（）。
A、可靠性B、随机性C、代表性D、准确性和及时性二、多选（每小题2分，共10分）1、全国人口普查中（）。
A、全国人口数是统计总体B、总体单位是每一个人C、全部男性人口数是统计指标D、男女性别比是总体的品质标志2、专门调查包括（）。
A、普查B、抽样调查C、定期报表D、全面报表3、下列指标中属于时期指标的有（）。
A、全年出生人数B、国民生产总值C、粮食总产量D、商品销售额4、下列指标中属于时点指标的有（）。
《应用统计学》期末总复习
三、统计表与统计图
1、统计表的一般结构 2、从内容上看，统计表的构成 3、统计表的设计原则 4、 常用的统计图有哪些？
第３章
统计数据的特征描述
一、平均数（不包括几何平均数） 二、众数（未分组） 三、中位数（未分组） 四、分位数（未分组） 五、极差和四分位差（未分组） 六、方差和标准差（未分组） 七、变异系数和异众比率（未分组） 要求：知道哪些是集中趋势测度值，哪些是 离散程度测度值，会计算并进行评价。
第５章
统计假设检验
一、两类判断错误的定义和关系 二、Ｐ值和显著性水平α的含义 三、根据实际建立假设（单边、双边） 五、如何用P值进行决策 六、均值的t检验（包括单样本、独立样本、 配对样本）、方差的检验的条件和步骤， （重点会用SPSS软件处理并熟悉输出结果 解读）
上机实验：熟悉以下功能选项
一、SPSS的中文全称 二、SPSS数据编辑窗口左下角两个视区 三、定义变量包括哪些 四、分类整理（功能选项及输出表解读） 五、数据排序 六、频数分析（功能选项及输出表解读） 七、计算基本描述统计量（功能选项及输出表解读） 八、假设检验（三种，功能选项及输出表解读）
《统计学》期末总复习
2011.12.14
考试要求
考试时间：90分钟 题型： 一、单选题（10分） 二、多选题（10分）（多、少、错选都无分） 三、填空题（20分） 四、计算题（20分） 五、实验简答题(30分） 六．论述题（10分）
考Leabharlann 大纲考试大纲第１章
统计学与统计数据
一、统计与统计学（统计学的定义和分类） 二、总体与样本（理解二者定义和之间的关 系） 三、参数与统计量（定义及最常用的统计量 和参数） 四、标志与指标（定义和分类） 五、统计数据的类型（从不同角度说明） 要求：结合实际背景理解基本概念
应用统计学期末复习参考
应用统计学期末复习参考一、简答题（30分）1、统计学研究的对象是什么？答：统计学的研究对象是客观对象的数量方面，具体说，是研究总体现象的数量特征与规律性，以帮人们科学地认识客观事物。
2、在应用统计学研究实际问题时，需要兼备哪两方面的知识？答：一方面要掌握统计学的基本理论与方法，另一方面要具有实际问题的知识背景。
这样才能把定量分析与定性分析结合起来，在应用统计方法进行定量分析的基础上，再应用各学科的专业知识对统计分析的结果做出合理的解释。
3、统计学中总体、个体和样本的定义？答：总体就是某一特定研究中所有单元的集合。
通常由具有相同性质的许多单元构成，而构成总体的每个单元被称为个体。
个体是我们借以收集数据的对象，可以由人、单位或物充当。
样本是指从总体中抽取的部分个体构成的集合4、统计研究中抽样的必要性？答：统计研究的目的是认识总体的数量特征，但有时构成总体的个体数量很大，实际工作中不可能或不必要对每个个体的数量特征逐一调查，通常是以某种方式从总体中抽取一部分个体代表总体进行研究。
样本是总体的代表，从统计中抽取样本的目的就是通过对样本特征的分析去推断总体的特征。
5、品质型变量和数值型变量的定义？答：品质型变量又称定性变量，是指反映事物品质特征的变量，其表现为类别，通常是用文字来表示的；数值型变量又称定量变量，是指反映事物特征的变量，通常使用自然或度量衡单位进行计量，其结果表现为具体的数值。
数值型变量根据其取值是否连续，又可以分为离散变量和连续变量两种形式。
6、参数与统计量的定义以及它们在统计研究中的关系？答：参数是用来描述总体特征的概括性值，通常用大写字母表示，如总体均值，标准差，总体比例等；统计量是用来描述样本特征的概括性值，通常用小写字母表示，如样本均值，样本标准差，样本比例等。
在进行统计推断时，总体数据通常是不完全的，所以参数是一个未知的常数，但样本是经过抽样所确定下来的，所以统计量总是可以计算出来的，通过样本统计量来对总体参数进行推断与检验。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、典型例题解析
题型：基本概念、公式与简单运算
例1、计算题：写出下列随机试验的样本空间及下列事件所包含的样本点：掷一颗骰子，出现奇数点。
解：掷一颗骰子，其结果有6种可能：出现1点，2点，3点，……，6点，可以记样本空间Ω={1，2，3，4，5，6}，那么“出现奇数点”的事件为{1，3，5}。
例2、计算题：口袋里装有若干个黑球与若干个白球，每次任取一个球，共抽取两
次，设事件A 表示第一次取到黑球，事件B 表示第二次取到黑球，用A,B 的运算表示下列事件：
（1）第一次取到白球且第二次取到黑球
（2）两次都取到白球
（3）两次取到球的颜色不一致
（4）两次取到球的颜色一致
解：（1）第一次取到白球且第二次取到黑球，意味着第一次不取到黑球且第二次取到黑球，即事件A 不发生且事件B 发生，可用积事件B A _
表示
（2）两次都取到白球，意味着第一次取到白球且第二次也取到白球，即事件A 与 B 同时不发生，可用积事件__B A 表示
（3）两次取到球的颜色不一致，意味着第一次取到黑球且第二次取到白球，或者第一次取到白球且第二次取到黑球，即积事件B A _发生或积事件_B A 发生，可用和事件B A _+_
B A 表示
（4）两次取到球的颜色一致，意味着两次都取到黑球，或者两次都取到白球，即积事件AB 发生或积事件__B A 发生，可用和事件AB +__B A 表示
例3、填空题：设.60)(.30)(=⋃=B A P A P ，。
（1）若A 和B 互不相容，则P(B)=
（2）若B A ⊂，则P(B)=
（3）若P(AB)=0.2，则P(B)=
解题思路：根据概率的性质P(A+B)=P(A)+P(B)-P(AB)=0.6，
（1）若A 和B 互不相容，则AB=Φ，P(AB)=0，
因此P(B)=P(A+B)-P(A)=0.6-0.3=0.3。
（2）若B A ⊂，则P(AB)=P(A)，
因此P(B)=P(A+B)-P(A)+P(A)=0.6。
（3）若P(AB)=0.2，则P(B)=P(A+B)-P(A)+P(AB)=0.6-0.3+0.2=0.5。
答案：（1）0.3；（2）0.6；（3）0.5。
附：知识拓展—概率的历史
第一个系统地推算概率的人是16世纪的卡尔达诺。
记载在他的著作《<iber de Ludo Aleae 》中。
卡尔达诺的数学著作中有很多给赌徒的建议。
这些建议都写成短文。
例如：《谁，在什么时候，应该赌博？》、《为什么亚里斯多德谴责赌博？》、《那些教别人赌博的人是否也擅长赌博呢？》等。
然而，首次提出系统研究概率的是在帕斯卡和费马来往的一系列信件中,他们用不
同的组合方法给出了这类问题的正确答案。
1655年，荷兰数学家惠更斯访问巴黎时了解到帕斯卡与费马的通信研究,对这类问题产生兴趣并著《论赌博中的计算》,探讨概率问题的原理。
讨论的情况与结果被惠更斯总结成《关于赌博中的推断》（1657年）一书，这是公认的有关或然数学的奠基之作。
本空间Ω={1，2，3，4，5，6}，那么“出现奇数点”的事件为{1，3，5}。
例2、口袋里装有若干个黑球与若干个白球，每次任取一个球，共抽取两次，设事件A 表示第一次取到黑球，事件B 表示第二次取到黑球，用A,B 的运算表示下列事件：（题型1）
（1）第一次取到白球且第二次取到黑球
（2）两次都取到白球
（3）两次取到球的颜色不一致
（4）两次取到球的颜色一致
解：（1）第一次取到白球且第二次取到黑球，意味着第一次不取到黑球且第二次取到黑球，即事件A 不发生且事件B 发生，可用积事件B A _表示
（2）两次都取到白球，意味着第一次取到白球且第二次也取到白球，即事件A 与B 同时不发生，可用积事件_
_B A 表示
（3）两次取到球的颜色不一致，意味着第一次取到黑球且第二次取到白球，或者第一次取到白球且第二次取到黑球，即积事件B A _发生或积事件_B A 发生，可用和事件B A _+_B A 表示
（4）两次取到球的颜色一致，意味着两次都取到黑球，或者两次都取到白球，即积事件AB 发生或积事件__B A 发生，可用和事件AB +__B A 表示
例3、罐中有12粒围棋子，其中8粒白子，4粒黑子，从中任取3粒，求(题型2)
（1）取到的都是白子的概率
（2）取到两粒白子，一粒黑子的概率
（3）至少取到一粒黑子的概率
（4）取到的3粒棋子颜色相同的概率
解：设A 表示“取到的都是白子”，B 表示“取到两粒白子，一粒黑子”，C 表示“至少取到一粒黑子”，D 表示“取到的3粒棋子颜色相同”。
基本事件总数n=C 312
(1)因为3粒棋子都从8粒白棋中取得，A 包含的基本事件数为C 38，则
P(A)=C C
31238
=
55
14
(2)B 包含的基本事件数为C 28C 14，则P(B)=C C C 3121
428=55
28 (3)因为3粒棋子中至少有一粒黑子，那么这三粒棋子的颜色有三种可能：一种是一粒黑子，两粒白子；一种是两粒黑子，一粒白子；一种是三粒都是黑子，故C 包含的
基本事件数为C 14C 28+C 24C 18+C 34，则P(C)=C
C C C C C 312
3418242814 ++=5541 或者由于各事件的关系可看出，C=_A ,所以P(C)=P(_A )=1-P(A)=1-5514=55
41 (4)取到的3粒棋子颜色相同，要么全是白的，要么全是黑的，共有C 38+C 34种取
法，故P(D)=C C C 312
3438
+=5515=113 例4、甲、乙二人独立地各向同一目标射击一次，其命中率分别为0.6和0.7（题型3）
（1）求目标被命中的概率
（2）若已知目标被命中，求它是甲射中的概率
解：设1A 表示“甲命中目标”，2A 表示“乙命中目标”，B 表示“目标被命中”，所求概率为P(B)和P(1A |B)
已知P(1A )=0.6，P(2A )=0.7，因1A 与2A 相互独立，利用事件之间的运算，B=1A +2A （或写成B=1A ⋃2A ）表示事件1A 与2A 至少有一个发生。
又利用加法公式，P(B)=P(1A )+(2A )-P(1A 2A )，则
（1）P(B)=P(1A )+(2A )-P(1A 2A )=P(1A )+(2A )-P(1A )P(2A )
=0.6+0.7-0.6⨯0.7=0.88
又因B 1⊂A ，则
（2）P(B |1A )=)
()P(1B P B A =)()P(1B P A =88.06.0=2215 例5、设工厂A 和工厂B 的产品的次品率分别是1%和2%，现在从由A 和B 的产品分别是60%和40%的产品中随机抽取一件，发现是次品，则该次品属于A 生产的概率是多少？（题型4）
解：该次品可能是A 生产的也可能是B 生产的，工厂A 和工厂B 的产品的次品率都
已知。
产品可能是A 生产的也可能是B 生产的，构成样本空间的一个划分。
随机抽取一件，发现是次品，求该次品属A 生产的概率实际是由结果来求原因发生的概率，用贝叶斯公式。
设事件C 为“产品是次品”，事件A 为“产品属A 生产”，事件B 为“产品属B 生产”，因为,.60)(=A P ,4.0)(=B P ,1.00)|(=A C P 02.0)|(=B C P
由全概率公式，有014.0)|()()|()()(=⨯+⨯=B C P B P A C P A P C P 又由贝叶斯公式，有)
()|()()|(C P A C P A P C A P ⨯= 说明：由结果来求原因发生的概率，用贝叶斯公式解决此类问题。
此题的计算结果表明：工厂A 和工厂B 的产品的次品率分别是1%和2%，但从由A 和B 的产品分别占60%
和40%的产品中随机抽取一件，发现是次品，该次品属A 生产的概率变为7
3，该次品属B 生产的概率变为7
4。
P(C|A)的意思是在属A 生产的产品中发现次品的概率，正好是A 产品的次品率，所以不能混淆P(A|C)和P(C|A)，否则只会得出错误的结果。