【免费下载】第9章光学作业参考答案
大物 上海交大课后答案 第九章

习题99-1.杨氏双缝的间距为m m 2.0,距离屏幕为m 1,求:(1)若第一级明纹距离为2.5mm ,求入射光波长。
(2)若入射光的波长为6000A,求相邻两明纹的间距。
解:(1)由Lx k dλ=,有:xd k L λ=,将0.2mm d =,1m L =,1 2.5mm x =,1k =代入,有:3372.5100.210 5.0101m λ---⨯⨯⨯==⨯;即波长为:500nm λ=; (2)若入射光的波长为 A 6000,相邻两明纹的间距:73161030.210D x mm d λ--⨯⨯∆===⨯。
9-2.图示为用双缝干涉来测定空气折射率n 的装置。
实验前,在长度为l 的两个相同密封玻璃管内都充以一大气压的空气。
现将上管中的空气逐渐抽去,(1)则光屏上的干涉条纹将向什么方向移动;(2)当上管中空气完全抽到真空,发现屏上波长为λ的干涉条纹移过N 条。
计算空气的折射率。
解:(1)当上面的空气被抽去,它的光程减小,所以它将 通过增加路程来弥补,条纹向下移动。
(2)当上管中空气完全抽到真空,发现屏上波长为λ的干涉条纹移过N 条,可列出:λN n l =-)(1 得:1+=lN n λ。
9-3.在玻璃板(折射率为50.1)上有一层油膜(折射率为30.1)。
已知对于波长为nm 500和nm 700的垂直入射光都发生反射相消,而这两波长之间没有别的波长光反射相消,求此油膜的厚度。
解:因为油膜( 1.3n =油)在玻璃( 1.5n =玻)上,所以不考虑半波损失,由反射相消条件有:2(21)122n e k k λ=-= 油,,, 当12500700nm nmλλ==⎧⎪⎨⎪⎩时,11222(21)22(21)2n e k n e k λλ=⎧-=-⎪⎪⎨⎪⎪⎩油油⇒2121217215k k λλ-==-, 因为12λλ<,所以12k k >,又因为1λ与2λ之间不存在'λ以满足'2(21)2n e k λ=-油式,即不存在21'k k k <<的情形,所以1k 、2k 应为连续整数,可得:14k =,23k =; 油膜的厚度为:17121 6.73104k e m n λ--==⨯油。
工程光学郁道银第二版第九章 课后答案

工程光学郁道银第二版第九章课后答案9.1 背景知识在工程光学的第九章中,我们将讨论光学系统中的配焦、色差、球差等问题,并提供相应的课后答案。
这一章的内容将帮助我们更好地理解和掌握光学系统的设计和优化。
9.2 配焦与球差问题 1在一折射球面透镜中,根据配焦公式可以得到:$$ \\frac{n_1}{u} + \\frac{n_2}{v} = \\frac{n_2 - n_1}{R} $$其中,$ n_1 $ 和 $ n_2 $ 分别为入射介质和透镜介质的折射率,$ R $ 为球面的曲率半径,$ u $ 和 $ v $ 分别为物距和像距。
请根据上述配焦公式回答以下问题:a.如果 $ u = \infty $,透镜为凹球面,试推导出透镜的焦距公式。
b.推导出透镜的主焦距公式。
c.如果透镜为凸球面,$ v \gt 0 $,根据配焦公式,物距 $ u $ 的取值范围会有什么限制?答案a.当 $ u = \infty $ 时,代入配焦公式得到:$$ 0 + \\frac{n_2}{v} = \\frac{n_2 - n_1}{R} $$整理得到:$$ v = \\frac{R}{n_2 - n_1}$$b.主焦距定义为当物体距离无限远时透镜成像于焦点上的距离。
当 $ u = \infty $ 时,根据配焦公式得到:$$ \\frac{n_2}{v} = \\frac{n_2 - n_1}{R} $$整理得到:$$ v = \\frac{R}{n_2 - n_1} $$由于 $ v $ 表示物距,代入光学系统中物像关系公式$ \frac{1}{f} = \frac{1}{u} + \frac{1}{v} $,得到主焦距公式:$$ \\frac{1}{f} = \\frac{1}{\\infty} + \\frac{1}{v} =\\frac{1}{v} $$所以主焦距 $ f = \frac{R}{n_2 - n_1} $。
《光学》答案(吴强版)

f nAD f n(r cos f )
r
f (1 n) 1 n cos
1-4 解:参看课本 P 16 图 1-13 考 虑 三 角 形 PSC , 有 PS ( x1 R) R 2( x1 R) R cos
l1
l
1 const 2n sin
所以,
1
l2
2
2
1
l1
l2
带相关参数得未知波长为
6429
2n 2.73 107 m
2-14 设相邻两条纹对应的高度差为 h , h
h 则 sin l
D L tan L sin
(1)由于
d 0.5mm
所以,
d dc 0 . 4 3 6 8 mm
故屏上看不到干涉条纹。
(2) 由 得
l
பைடு நூலகம்db
, 代
d 0.5*103 m, b 0.25*103 m
l 22.849cm
所以,
l l R 2.89cm
2-13 解:
l
2n sin
从而得出:
cos 0 0, 或 sin 0 0
所以,
3 0, , ,
2 2
满足以上条件的角度为实际光线。 1-3 解: 由题意知,经过镜具 的出射光为平行光, 又由折射定律得,
M r S
N
MN // AC
则有
f
A D
C
r cos f AD A D rc o s f
2
喀蔚波09章习题解答

3第九章几何光学习题解答9-1 一只坛子装了 100.0cm 深的甘油,观察者观察坛底好像提高了 32.5cm , 求甘油的折射率.解:由题意知n 2=1, u=100cm , v=-67.5cm , r = x,代入单球面成像公式得n ! 1 1 - m100 -67.5 一 ::n i =1.489-2如图9-2所示,光导纤维是由圆柱形的玻璃芯和玻璃包层组成,其折射率分别为m 和n 2 ((n 1>口).设在垂直端面外介质的折射率为 n 。
.证明光线能在 纤维内芯和包层间发生全反射的入射光线最大孔径角 二m 满足:n ° sin 如=• n ; _ n ;证明如下:n 0 sinv m 十 sin :(1) n 〔 cos 二 n 2(2)将(1)和(2)平方后相加的9-3 折射率为1.5的月牙形透镜,凸面的曲率半径为15cm,凹面的曲率半径 为30cm,如果用平行光束沿光轴对着凹面入射(1)求空气中的折射光线的相交 点;(2)如果将此透镜放在水中,问折射的交点又在何处?解:(1)因为n=1.5, n 0=1, r 1=-30cm , r 2=-15cm 代入薄透镜焦距公式得(2) n=1.5, n °= 4/3, r 1= -30cm, r 2= -15cm 代入薄透镜焦距公式得- 1—%=60cm=240cm2 . 2 - 2 2 n ° sin 為二 n 1 「门2 2-n 29-4 眼睛的光学结构可简化为一折射单球面 ,共轴球面的曲率半径为5.55mm,内部平均折射率为4/3,计算两个焦距•若月球在眼睛节点所张的角度为 1° ,问视网膜上月球的像有多大?眼节点到视网膜的距离取 15mm.解:根据题意n 1=1,n 2=4/3,r=5.55mm 代入单球面焦距公式得1f 1 5.55 =16.65 mm 4 -1 3 视网膜上月球的像的大小为 15ta n1° =0.26mm9-5将折射率为1.50,直径为10cm 的玻璃棒的两端磨成凸的半球面,左端 的半径为5cm 而右端的半径为10cm.两顶点间的棒长为60cm,在左端顶点左方 20cm 处有一物(在光轴上).(1)作为右端面的物是什么? ( 2)右端面的物距为 多少? ( 3)此物是实的还是虚的?( 4)最后所成的像在何处?解:(1)根据题意可知左端面的像作为右端面的物(2) 已知n 1=1, n 2=1.5, u=20cm, n=5cm, d=60cm 代入单球面成像公式得1 1.5 1.5-1 --- + ------ = --------- 20 v 5v = 30cm所以右端面的物距为60cm-30cm=30cm(3) 此物是实物(4) 将u=30cm , n 1=1.5, n 2=1, r= -10cm 代入单球面成像公式得1.5 1 1-1.5---- 十—= ------------30 v -10v =::9-6将折射率为1.5,直径为8.0cm,端面为凸半球形的玻璃棒,置于液体中, 在棒5.55 =22.2mm3 3轴上离端面60cm处有一物体,成像在棒内l.0m处,求液体的折射率.解:已知u=60cm,n2=1.5,r= 4cm,v=100cm代入单球面成像公式得n i 1.5 1.5 - n i60 而一4~m =1.359-7直径为8cm的玻璃球,中心处镶有一小红物,求观察者看到小红物的位解:已知u=4cm,n i=1.5,n2=1,r=-4cm,代入单球面成像公式得1.5 1 1-1.5+ =4 v -4v - -4cm所以观察者看到小红物位于球心处9-8 一极地探险者在用完了火柴后,用冰做了个透镜聚焦阳光来点火,若他做的是曲率半径为25cm的平凸透镜,此透镜应离火绒多远?(设冰的折射率为1.31)解:已知n =1.31, n°=1, r1=25cm, r2=x代入薄透镜焦距公式得- 1 1「f 二(”1)伝-二)=81cm9-9 一透镜将一物成像在离透镜12cm的屏幕上,当把此透镜背离物体移远2cm时,屏幕必须向物移近2cm,以便重新对它聚焦,此透镜的焦距是多少?解:设物与透镜的距离为x,透镜的焦距f,则根据题意可知1 1 1(1)——I ----- = -------x 12 f解得f=4cm9-10 一弯月形薄透镜两表面的曲率半径分别为5cm和10cm,其折射率为1.5,若将透镜的凹面朝上且盛满水,求水与透镜组合后的等效焦距.解:组合薄透镜可看成是由水组成的薄透镜和弯月形薄透镜密切接触组合而成.假定光从水一侧射入,设由水组成的薄透镜的焦距为f1,弯月形薄透镜的焦距为f2,根据题意可列出下列方程1-4 1 i irf^ ( 1)( ) =30cm1[3 ::-10仇= |(1.5-1)( 1- J =20cm-10 - 51 1 1 1 1 1f =71 12=30 20=12f =12cm9-11有焦距为10cm的凸透镜焦矩为40cm的凹透镜放在同一光轴上,两者相距10cm,在凸透镜前20cm处放一物体(在光轴上),求最后像的位置,并作图.解:对于凸透镜U1=20cm, f1=10cm, d=10cm代入薄透镜成像公式得1 .丄_丄20 V1 一10v1= 20cm对于凹透镜U2=10cm-20cm=-10cm,f2=-40cm,代入薄透镜成像公式得1 1 1-------------------- T -------------------- = ---------------------------------10 v 2 - 40V2 - 13.3cm9-12把一物放在会聚透镜前方适当距离处时,像落在离透镜20cm处的屏幕上.现将一发散透镜放在会聚透镜与屏幕中间,我们发现,为了得到清晰的像必须把屏幕向离开透镜的方向移远20cm.这发散透镜的焦距是多少?解:一物经会聚透镜所成的像作为发散透镜的物,此物距U2= -10cm,V2=30cm代入薄透镜成像公式得1 1 1-10 30 一ff = -15cm9-13眼睛不调节时能看清的物点到眼睛之间的距离称为远点.视力正常者的远点在无穷远处,即平行光进入眼睛后刚好会聚于视网膜上.眼睛最大调节时能看清的物点到眼睛之间的距离称为近点,视力正常者的近点约为10~12cm.与正常眼相比较,近视眼的近点近,远视眼的近点远,这就是近视眼和远视眼名称的来历.某人眼睛的远点为2m,他应配戴怎样的眼镜?解:配戴的眼镜必须使无穷远的物体在眼前2m处成一虚像,即u=x, v = -2 m 代入薄透镜成像公式得1 1 1—+ ——=—-2 f0.5D = -50,度f9-14 一远视眼的近点为1.0m,要看清眼前25cm处的物体,问需要配戴怎样的眼镜?解:所配戴的眼镜应使眼前25cm处的物体在眼前1m处成一虚像,即u=25cm, v = -1m代入薄透镜成像公式得1 1 1----- r -------- =——---- +----- =0.25 -1f13D f= 300度9-15 一显微镜物镜焦距为10.0mm,目镜焦距为25.0mm,两镜间距为180mm.若物体最后成一虚像于明视距离处,求物距及显微镜的放大率.解:已知f1=1cm,f2=2.5cm, d=18cm, V2=-25cm代入薄透镜成像公式得物镜成像1 1 1----- r -------- = ---------u1v1f1(1)目镜成像1 1 .1(2)d -v1v2f2代入数据得1 1 1=U1 v1 1(3)1 11(4)+18 7 -25 2.5解得V1=15.7cm U1=1.07cmV1 2515.725M-------- X147U1 f2 1.07 2.5。
全部光学作业解答Word版
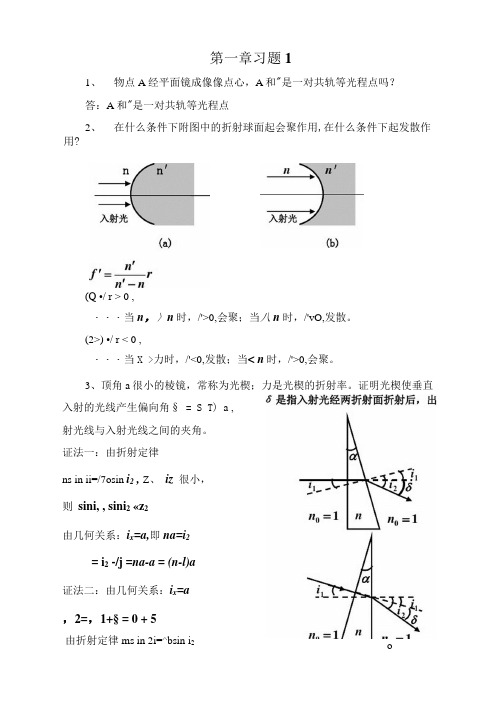
第一章习题11、物点A经平面镜成像像点心,A和"是一对共轨等光程点吗?答:A和"是一对共轨等光程点2、在什么条件下附图中的折射球面起会聚作用,在什么条件下起发散作用?(Q •/ r > 0 ,・・・当n,〉n时,/'>0,会聚;当八n时,/'vO,发散。
(2>) •/ r < 0 ,・・・当X >力时,/'<0,发散;当< n时,/'>0,会聚。
3、顶角a很小的棱镜,常称为光楔;力是光楔的折射率。
证明光楔使垂直入射的光线产生偏向角§ = S T) a ,射光线与入射光线之间的夹角。
证法一:由折射定律ns in ii=/7osin i2 , Z、iz很小,则sini, , sini2 «z2由几何关系:i x=a,即na=i2= i2 -/j =na-a = (n-l)a证法二:由几何关系:i x=a,2=,1+§ = 0 + 5由折射定律ms in 2i=^bsin i2o _V N 很小,sinq =a, sin/2 »i2, 且n0 «1则有na-a + 5, /• 8 = na-a = (n- l)a4>若空气中一均匀球形透明体能将平行光束会聚于其背面顶点上.此透明体的折射率应等于多少?解:设球形透明体的半径为r,其折射率为川已知H =1,p = -g, p' = 2r根据单球面折射成像公式= 得:工=上1 :. n f = 2p p r 2r r5、试证明:一束平行光相继经过几个平行分界面的多层介质折射时,出射光线的方向只与入射光的方向及入射空间和出射空间介质的折射率有关,与中间各层介质无关。
证明:V 坷sinh = //o sin/on2 sini2 = n l smi xn3 sin匚=n2 sin/2ii■g】sinL ijsini—n k sini* sini AU:.n k sini k =n o sin«o即sin/x = (/i0 sini0)/«A,命题成立。
第9章习题及参考答案
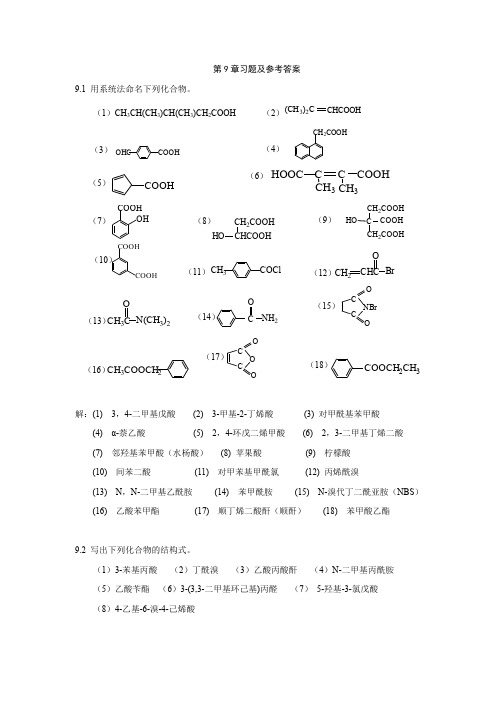
第9章习题及参考答案9.1 用系统法命名下列化合物。
(1)CH 3CH(CH 3)CH(CH 3)CH 2COOH (2)CHCOOH (CH 3)2COHCCOOHCH 2COOHCOOHHOOCC CH 3CH 3C COOHCOOHOH CHCOOH CH 2COOHHOCH 2COOHCCOOHHOCH 2COOHCOOHCOOHCH 3COClCH 2OBr CHCCH 3C ON(CH 3)2C O NH 2CC O O NBrCH 3COOCH 2CC O OOCOOCH 2CH 3解:(1) 3,4-二甲基戊酸 (2) 3-甲基-2-丁烯酸 (3) 对甲酰基苯甲酸 (4) α-萘乙酸 (5) 2,4-环戊二烯甲酸 (6) 2,3-二甲基丁烯二酸 (7) 邻羟基苯甲酸(水杨酸) (8) 苹果酸 (9) 柠檬酸 (10) 间苯二酸 (11) 对甲苯基甲酰氯 (12) 丙烯酰溴(13) N ,N-二甲基乙酰胺 (14) 苯甲酰胺 (15) N-溴代丁二酰亚胺(NBS ) (16) 乙酸苯甲酯 (17) 顺丁烯二酸酐(顺酐) (18) 苯甲酸乙酯9.2 写出下列化合物的结构式。
(1)3-苯基丙酸 (2)丁酰溴 (3)乙酸丙酸酐 (4)N-二甲基丙酰胺 (5)乙酸苄酯 (6)3-(3,3-二甲基环己基)丙醛 (7) 5-羟基-3-氯戊酸 (8)4-乙基-6-溴-4-己烯酸(3) (4)(5)(6) (7)(10)(13) (16) (8)(11) (14) (17)(9) (12) (15)(18)解:CH 2CH 2COOH BrOOOO (1)3-苯基丙酸(2)丁酰溴(3)乙酸丙酸酐NHCH 3O (4)N -二甲基丙酰胺OPhO (5)乙酸苄酯CHOHOCOOHClCOOHBr(6)3-(3,3-二甲基环己基)丙醛(7)5-羟基-3-氯戊酸(8)4-乙基-6-溴-4-己烯酸9.3 将下列各组化合物的酸性由强到弱排列成序。
光学教程参考答案

光学教程参考答案光学教程参考答案光学是一门研究光的传播、反射、折射、干涉、衍射等现象的学科,它在我们的日常生活中扮演着重要的角色。
从眼镜到激光,从相机到光纤通信,光学技术的应用无处不在。
然而,光学作为一门科学,其原理和理论并不容易理解。
为了帮助大家更好地掌握光学知识,本文将提供一些光学教程的参考答案,希望能对读者有所帮助。
1. 光的传播光的传播是光学研究的基础。
光的传播遵循直线传播的原则,即光在均匀介质中传播时呈直线传播。
当光传播到介质边界时,会发生反射和折射。
反射是指光从介质表面反射回去,而折射是指光从一种介质传播到另一种介质时改变传播方向的现象。
2. 反射定律反射定律是描述光在界面上的反射规律的定律。
根据反射定律,入射光线、反射光线和法线三者在同一平面上,并且入射角等于反射角。
这个定律对于理解镜面反射现象非常重要,也是光学中的基础概念之一。
3. 折射定律折射定律是描述光在界面上的折射规律的定律。
根据折射定律,入射光线、折射光线和法线三者在同一平面上,并且入射角、折射角和两种介质的折射率之间满足一个简单的关系式:入射角的正弦值与折射角的正弦值成正比,比例常数为两种介质的折射率之比。
4. 光的干涉光的干涉是指两束或多束光波相互叠加产生的干涉现象。
干涉现象可以分为两种类型:构造干涉和破坏干涉。
构造干涉是指两束或多束光波相互叠加形成明暗条纹的现象,如杨氏双缝干涉实验。
破坏干涉是指两束或多束光波相互叠加形成干涉消除的现象,如牛顿环实验。
5. 光的衍射光的衍射是指光通过一个或多个孔径或障碍物时发生的波的传播现象。
衍射现象是光的波动性质的直接证据,也是光学中的重要现象之一。
衍射可以通过菲涅尔衍射和菲涅耳-柯西衍射公式进行定量描述。
6. 光的色散光的色散是指光在不同介质中传播时由于折射率的不同而产生的颜色分散现象。
光的色散是由于不同波长的光在介质中的折射率不同而引起的,这是光学中的一个重要现象。
著名的色散现象包括光的折射色散和光的衍射色散。
工程光学第三版下篇物理光学第九章光的电磁理论基础课后习题答案

第九章光的电磁实际根底zc141.一个立体电磁波能够表现为E0,E2cos[2 10( t)],E0,求(1)该 z2x y电磁波的频率、波长、振幅跟原点的初相位?〔2〕拨的传达偏向跟电矢量的振动偏向? 〔3〕响应的磁场B的表白式? z 解:〔1〕立体电磁波EAcos[2(t) , ] c146310m 。
对应有A2,10Hz,2〔2〕波传达偏向沿z 轴,电矢量振动偏向为 y 轴。
B 与E 垂直,传达偏向一样,∴ByBz0〔3〕 8EyCEy610[21014(zcBxt) ] 2z E y 0,E0,E10cos1015( 2t),2.在玻璃中传达的一个线偏振光能够表现z x0.65c试求〔1〕光的频率跟波长;〔2〕玻璃的折射率。
z z 2 15解:〔1〕EAcos[2(t) ]10cos[10( t)]c 0.65c1514∴210v510Hz72/k2/0.65c3.910mncv31081.54c〔2〕n3.910751014n3.在与一平行光束垂直的偏向上拔出一片通明薄片, 薄片的厚度h0.01mm ,折射率n=1.5,假定光波的波长为500nm ,试盘算通明薄片拔出前后所惹起的光程跟相位的变更。
解:光程变更为(n1)h0.005mm0.0051062 500相位变更为2 20(rad)4.地球外表每平方米接纳到来自太阳光的功率为 1.33kw,试盘算投射到地球外表的太阳光的电场强度的巨细。
假定太阳光收回波长为 600nm 的单色光。
1 21 2 IA 2cA 2 0解:∵1 22I 3∴A()10v/mc 085.写出立体波E100exp{i[(2x3y4z)1610t]}的传达偏向上的单元矢量 k。
解:∵EAexp[i(kr t)]krkxkykz xyzk x 2,k y 3,k4zkkxkykz2x3y4z 0 x 0 y 0 z 0 0 02 3 4 k 0x 0y 0z 02929296.一束线偏振光以45度角从氛围入射到玻璃的界面, 线偏振光的电矢量垂直于入射面,试求反射系数跟透射系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9章 光学习题解9.1在双缝干涉实验中,波长nm 的单色光入射在缝间距500=λm 的双缝上,屏到双缝的距离为2m ,求(1)每条明纹的宽度;(2)中央
4102-⨯=a 明纹两侧的两条第10级明纹中心的间距;(3)若用一厚度为m 的云6106.6-⨯=e 母片覆盖其中一缝后,零级明纹移到原来的第七级明纹处;则云母片的折射率为多少?
解:(1)m 10510
2105002349---⨯=⨯⨯⨯==∆d D x λ(2)两条10级明纹间距为
20=0.1m x ∆(3)由于,所以有()λ71=-n e 53.171=+=e n λ9.2 某单色光照射在缝间距为d =m 的杨氏双缝上,屏到双缝的
4102.2-⨯距离为D =m ,测出屏上20条明纹之间的距离为m ,则该单色光的81⋅210849-⨯⋅波长是多少?
解: m 1084.9202-⨯=∆==∆x x d D x λnm 3.6018.1201084.9102.22
4=⨯⨯⨯⨯=∴--λ9.3白光垂直照射到空气中一厚度m 的肥皂膜(n = 1.33)上,在
μ380=e 可见光的范围内(),哪些波长的光在反射中增强?nm 760nm 400--解:由于光垂直入射,光程上有半波损失,即时,干涉加强。
λλ
k ne =+22
所以
10101220216124-⨯-=-=
k k ne λ在可见光范围内 nm 9.6732= 时,λ=k nm 3.4043= 时,λ=k 9.4如题图9.4所示,在双缝实验中入射光的波长为550nm ,用一厚度为的透明薄片盖住S 1缝,发现中央明纹移动3个条纹,向上移至cm 1085.24-⨯=e 。
求透明薄片的折射率。
‘O 题图9.4 解:当用透明薄片盖住S 1缝,以单色光照射时,经S 1缝的光程,在相同的
几何路程下增加了,于是原光程差为零的中央明纹位置从O 点向上移动,其他条纹随之平动,但条纹宽度不变。
依题意,图中为中央明条纹的位置,加透'O 明薄片后,①光路的光程为,②光路的光程为r 2。
因为e n r ne e r )1(11-+=+-点是中央明条纹的位置,其光程差为零,所以有,即'O 0])1([12=-+-=e n r r δ (1)e n r r )1(12-=-在不加透明薄片时,出现中央明条纹的条件为 (2)λk r r =-12由式(1)和式(2)可得 ,λk e n =-)1(
所以介质的折射率为 1+=
e k n λ依题意k = 3,代入已知条件和e 的数值得λ 此介质薄片是云母片。
58.111085.210550369=+⨯⨯⨯=--n 9.9 在一块玻璃基片上交替镀上不同材料的多层介质膜,组成一个反射式
滤波片,使它能对波长为632.8nm 的红光的反射率达99%以上,已知高折射率介
质为ZnS ,折射率为=2.35,低折射率介质为MgF 2,折射率为=1.38。
求每1n 2n 层膜的最小厚度(设光线垂直照射)如题9.9图所示。
题图9.9
解:反射式滤色片是让反射光在膜的上表面干涉加强。
第一层为ZnS 膜,厚度为e 1,第二层为MgF 2膜,厚度为e 2,第三层为ZnS 膜,厚度为e 1,第四层
为MgF 2膜,厚度为e 2,膜的层数愈多,总反射率愈高,但由于光的吸收,实际上层数不能过多,一般最佳值为15层或17层。
入射光在第一层膜上下表面反射形成的两束相干光,考虑到存在半波损失和垂直入射的条件,所以光程差为 2211λδ+=e n 根据干涉加强条件 λλ
k e n =+2211依题意,要求镀的膜厚度最小,即k =1故有 λλ=+2211e n
所以 nm 3.6735.248.632411=⨯==n e λ同理,入射光在第二层膜上下表面反射形成的两束相干光,其光程差为 λλδ=+=2222e n 所以 nm 6.11438.148.632422=⨯==n e λ依此类推,各层膜的厚度,即为上面所求之值。
9.14 用波长为0.63m 的激光束垂直照射到单缝上,若测得两个第五级μ暗纹之间的距离为6.3 cm ,屏与缝间距离为5 m ,求单缝缝宽。
解:由单缝衍射公式 λθ5sin =a 而 52103.6tan sin 2⨯⨯=≈-θθ所以 m 1054-⨯=a 9.16在夫琅禾费单缝衍射实验中,用单色光垂直照射缝面,已知入射光波长为500 nm ,第一级暗纹的衍射角为300,求(1)缝宽是多少;(2)缝面所能分成的半波带数。
解:(1)由单缝衍射暗纹公式λθk a ±=sin 则1=k λθ=sin a θ
λsin =a 代入数据,得m 1030sin nm 5006-== a (2)根据题意,此时的为半个波长的2倍,所以缝面分成的半波带θsin a 数为2个。
9.20 用一个每毫米500条缝的衍射光栅观察钠光谱线,波长为589.0nm 。
求(1)当光线垂直入射到光栅上时,能看到的光谱线的最高级次;(2)当光
线以300角斜入射时,能看到的光谱线的最高级次是多少。
解:(1)依题意,光栅常数为 ()m 10250010163--⨯=⨯=+b a 入射光垂直入射时,设能看到的最高级次为K m 。
根据光栅公式,有
()λθm k b a =+sin 因为 , 即 1sin ≤θλ
b a k m +=
代入数据,得 39.3=m k 因为应取整数,所以=3m k m k (2)入射光斜入射时,设能看到的最高级次为。
m k '根据光栅公式,有()()λθm k b a 'sin 30sin =++ 因为 ,即 1sin ≤θ()()λ130sin '++= b a k m 代入数据,得 =5.09m k '因为应取整数,m k '所以 =5m k '9.28 两偏振片的偏振化方向成夹角时,透射光强为I 1 , 若入射光不变,而
030两偏振片的偏振化方向夹角变为,则透射光强如何变化?045解:由马吕斯定律可知02O 130cos 2I I =0
2O 245cos 2I I =
两式相比可得1232I I = 9.29 使自然光通过两偏振化方向成夹角的偏振片,透射光强为I ,在0601这两个偏振片之间再插入另一偏振片,它的方向与前两个偏振片均成角,则030透射光强为多少?分析
设入射自然光强为,偏振片Ⅰ对入射的自然光起起偏作用,透射
0I 的偏振光光强恒为,而偏振片Ⅱ对入射的偏振光起检偏作用,此时透射与入20I 射的偏振光强满足马吕斯定律。
若偏振片插入两块偏振片之间,则偏振片Ⅱ、Ⅲ均起检偏作用,故透射光强必须两次应用马吕斯定律才能求出。
解:根据以上分析,入射光通过偏振片Ⅰ和Ⅱ后,透射光强为02O 160cos 2I =I 插入偏振片Ⅲ后,其透射光强为
0202O 230cos )30cos 2I (
=I 两式相比可得1
225.2I I =9.30 分别求出光在空气与玻璃(n =1.50)和空气与水(n =1.33)的界面上反射时的起偏振角。
解:由布儒斯特角满足的关系式1tan 1120==n n n i 且 可知,光在空气——玻璃界面上反射时的起偏角
013.5650.1arctan ==i 光在空气——水界面上反射时的起偏角0
021.5333.1arctan ==i。
