河南省三门峡市灵宝市2019—2020年学年上期期末考试试题(1—8单元)【试题+答案】
2019-2020学年河南省三门峡市高三(上)期末数学试卷(理科)
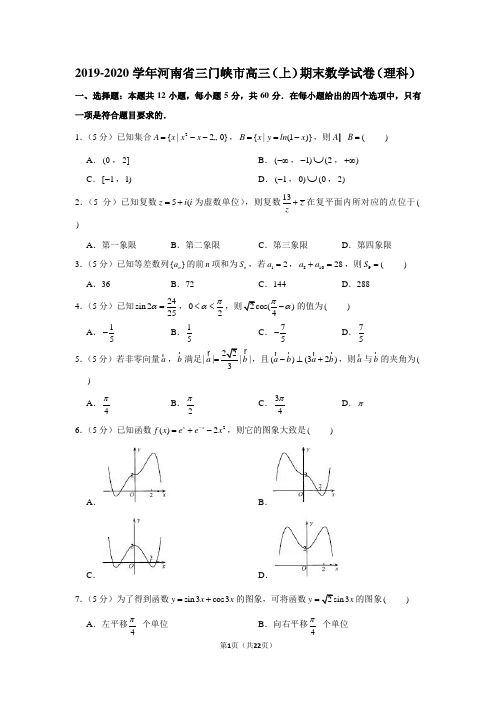
2019-2020学年河南省三门峡市高三(上)期末数学试卷(理科)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合2{|20}A x x x =--…,{|(1)}B x y ln x ==-,则(A B =I ) A .(0,2] B .(-∞,1)(2-⋃,)+∞C .[1-,1)D .(1-,0)(0⋃,2)2.(5分)已知复数5(z i i =+为虚数单位),则复数13z z+在复平面内所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3.(5分)已知等差数列{}n a 的前n 项和为n S ,若12a =,81028a a +=,则9(S = ) A .36B .72C .144D .2884.(5分)已知24sin 225α=,02πα<<,则2cos()4πα-的值为( )A .15-B .15C .75-D .755.(5分)若非零向量a r ,b r 满足22||||a b =r r ,且()(32)a b a b -⊥+r r r r ,则a r与b r 的夹角为( ) A .4π B .2π C .34π D .π6.(5分)已知函数2()2x x f x e e x -=+-,则它的图象大致是( )A .B .C .D .7.(5分)为了得到函数sin3cos3y x x =+的图象,可将函数23y x =的图象( ) A .左平移4π个单位 B .向右平移4π个单位C .向右平移12π个单位 D .向左平移12π个单位8.(5分)如图所示,在一个边长为1的正方形AOBC 内,曲线3(0)y x x =>和曲线y x =围成一个叶形图(阴影部分),向正方形AOBC 内随机投一点(该点落在正方形AOBC 内任何一点是等可能的),则所投的点落在叶形图内部的概率是( )A .512B .16C .14 D .139.(5分)运行下列程序框图,若输出的结果是2222222511234795⨯⨯⨯⨯⨯,则判断框内的条件是( )A .91i „?B .100i „?C .191i „?D .200i „?10.(5分)某三棱锥的三视图如图所示,则该三棱锥的体积为( )A .60B .30C .20D .1011.(5分)已知1F ,2F 为双曲线22221(0,0)x y a b a b-=>>的左、右焦点,以12F F 为直径的圆与双曲线右支的一个交点为P ,1PF 与双曲线相交于点Q ,且1||2||PQ QF =,则该双曲线的离心率为( ) A 5B .2C 3D 512.(5分)若关于x 的不等式21202xlnx x x kx k +---<的解集为(,)a b ,且(,)a b 内只有一个整数,则实数k 的取值范围是( ) A .342[,]43ln --B .324(,]43ln -C .324[,]43ln -D .342(,]43ln --二、填空题:本题共4小题,每小题5分,共20分.13.(5分)定义在R 上的偶函数()f x 满足,当0x <时,()1xf x x =-,则曲线()y f x =在点(2,f (2))处的切线的斜率为 .14.(5分)设n S 为等比数列{}n a 的前n 项和,若11a =,且13S ,22S ,3S 成等差数列,则n a = .15.(5分)市扶贫工作组从4男3女共7名成员中选出队长1人,副队长1人,普通队员2人组成4人工作小组下乡,要求工作组中至少有1名女同志,且队长和副队长不能都是女同志,共有 种安排方法.16.(5分)已知函数22()()()x a f x x a e e =+++,若存在0x ,使得024()1f x e +…,则实数a 的值为 .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题都必须作答,第22、23题为选考题,考生根据要求作答.一、必做题:共60分.17.(12分)在ABC ∆中,角A ,B ,C 对应的边分别是a ,b ,c ,已知cos23cos()1A B C -+=. (Ⅰ)求角A 的大小;(Ⅱ)若ABC ∆的面积53S =,5b =,求sin sin B C 的值.18.(12分)如图,已知ABCD ∆中,90BCD ∠=︒,AB ⊥平面BCD ,2BC =,3CD =,3AB =,E 是AC 的中点.(Ⅰ)若F 是AD 的中点,求证:平面BEF ⊥平面ABC ;(Ⅱ)若2AF FD =,求平面BEF 与平面BCD 所成的锐二面角的大小.19.(12分)我市为改善空气环境质量,控制大气污染,政府相应出台了多项改善环境的措施,其中一项是为了减少燃油汽车对大气环境污染,从2018年起大力推广使用新能源汽车,鼓励市民如果需要购车,可优先考虑选用新能源汽车,政府对购买使用新能源汽车进行购物补贴,同时为了地方经济发展,对购买本市企业生产的新能源汽车比购买外地企业生产的新能源汽车补贴高,所以市民对购买使用本市企业生产的新能源汽车的满意度也相应有所提高,有关部门随机抽取本市本年度内购买新能源汽车的100户,其中由70户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行,满分100分,将分数按照[0,20),[20,40),[40,60),[60,80),[80,100]分成5组,得如下频率分布直方图.(Ⅰ)若本次随机抽取的样本数据中购买使用本市企业生产的新能源汽车的用户中有52户满意度得分不少于60分,得分不少于60分为满意,根据提供的条件数据,完成下面的列联表,并判断是否有90%的把握认为购买使用新能源汽车的满意度与产地有关?满意 不满意 总计 购本市企业生产的新能源汽车户数 购外地企业生产的新能源汽车户数总计(Ⅱ)以频率作为概率,政府对购买使用新能源汽车的补贴标准是:购买本市企业生产的每台补贴2(1)a a >万元,购买外地企业生产的每台补贴a 万元,但本市本年度所有购买新能源汽车的补贴每台的期望值不超过3.4万元,则购买外地产的新能源汽车每台最多补贴多少万元?附:22()()()()()n ad bc k a b c d a c b d -=++++,其中n a b c d =+++.20()P k k …0.100 0.050 0.025 0.010 0.001 0k2.7063.8415.0246.63510.82820.(12分)实轴长为43的椭圆的中心在原点,其焦点1F ,2F 在x 轴上.抛物线的顶点在原点O ,对称轴为y 轴,两曲线在第一象限内相交于点A ,且12AF AF ⊥,△12AF F 的面积为3.(Ⅰ)求椭圆和抛物线的标准方程;(Ⅱ)过点A 作直线l 分别与抛物线和椭圆交于B ,C ,若2AC AB =u u u r u u u r,求直线l 的斜率k .21.(12分)已知函数21()2f x ax alnx x =-+.(1)讨论函数()f x 的单调性;(2)若0a <,设()()g x f x x =-,()22h x xlnx x =-+,若对任意1x ,2[1x ∈,12)()x x +∞≠,2121|()()||()()|g x g x h x h x --…恒成立,求实数a 的取值范围.二、选做题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系xOy 中,曲线1C 的参数方程为3cos (sin x y θθθ=⎧⎨=⎩为参数,[0θ∈,2))π,曲线2C 的参数方程为3(12x a t y t ⎧=⎪⎪⎨⎪=⎪⎩为参数). (Ⅰ)求曲线1C ,2C 的普通方程;(Ⅱ)若曲线1C 上一点P 到曲线2C 的距离的最大值为23a . [选修4-5:不等式选讲]23.已知函数2()4f x x ax =++,()|2||2|g x x x =++-. (Ⅰ)当4a =-时,求不等式()()f x g x …的解集;(Ⅱ)若不等式()()f x g x „的解集包含[2,4],求a 的取值范围.2019-2020学年河南省三门峡市高三(上)期末数学试卷(理科)参考答案与试题解析一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合2{|20}A x x x =--„,{|(1)}B x y ln x ==-,则(A B =I ) A .(0,2] B .(-∞,1)(2-⋃,)+∞C .[1-,1)D .(1-,0)(0⋃,2)【解答】解:解220x x --„可得12x -剟,∴集合2{|20}[1A x x x =--=-„,2]若使函数(1)y ln x =-的解析式有意义 则10x ->,即1x <故{|(1)}(B x y ln x ==-=-∞,1) [1A B ∴=-I ,1),故选:C .2.(5分)已知复数5(z i i =+为虚数单位),则复数13z z+在复平面内所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【解答】解:5z i =+Q ,∴131313(5)153555(5)(5)22i z i i i z i i i -+=+-=+-=-++-. ∴复数在复平面内对应的点的坐标为153(,)22-,位于第四象限. 故选:D .3.(5分)已知等差数列{}n a 的前n 项和为n S ,若12a =,81028a a +=,则9(S = ) A .36B .72C .144D .288【解答】解:等差数列的首项为12a =,设公差为d , 由817a a d =+,101193()a a d a d =+=+, 81028a a +=Q即41628d +=得32d =, 那么9983297222S ⨯=⨯+⨯=. 故选:B .4.(5分)已知24sin 225α=,02πα<<cos()4πα-的值为( )A .15-B .15C .75-D .75【解答】解:Q 24sin 225α=,02πα<<,12sin cos 25αα∴=, 22sin cos 1αα+=Q249(sin cos )12sin cos 25αααα∴+=+=,7cos())cos sin 45πααααα-==+=.故选:D .5.(5分)若非零向量a r ,b r满足||||a b =r r ,且()(32)a b a b -⊥+r r r r ,则a r与b r 的夹角为()A .4π B .2π C .34π D .π【解答】解:()(32)a b a b -⊥+r r r rQ ,()(32)0a b a b ∴-+=r r r rg , 即22320a b a b --=r rr r g , 即2222323a b a b b =-=r r r r r g ,cos a ∴<r,22||||b a b b a b >===r r r r g r r , 即a <r,4b π>=r ,故选:A .6.(5分)已知函数2()2x x f x e e x -=+-,则它的图象大致是( )A .B .C .D .【解答】解:函数2()2()x x f x e e x f x --=+-=,函数是偶函数,排除A ,B 选项; 当2x =时,f (2)222222280.50e e e e --=+-⨯=+-≈-<. 可知D 不正确, 故选:C .7.(5分)为了得到函数sin3cos3y x x =+的图象,可将函数2sin 3y x =的图象( )A .左平移4π个单位 B .向右平移4π个单位 C .向右平移12π个单位D .向左平移12π个单位【解答】解:函数sin3cos32sin(3)2sin3()412y x x x x ππ=+=+=+,应将函数2sin 3y x =的图象向左平移12π个单位即可.故选:D .8.(5分)如图所示,在一个边长为1的正方形AOBC 内,曲线3(0)y x x =>和曲线y x =围成一个叶形图(阴影部分),向正方形AOBC 内随机投一点(该点落在正方形AOBC 内任何一点是等可能的),则所投的点落在叶形图内部的概率是( )A .512B .16C .14 D .13【解答】解:可知此题求解的概率类型为关于面积的几何概型,由图可知基本事件空间所对应的几何度量()1S Ω=, 满足所投的点落在叶形图内部所对应的几何度量: S (A )31341200215()()|3412x x dx x x =-=-=⎰. 所以P (A )512=.故选:A .9.(5分)运行下列程序框图,若输出的结果是2222222511234795⨯⨯⨯⨯⨯,则判断框内的条件是( )A .91i „?B .100i „?C .191i „?D .200i „?【解答】解:第一次2i =满足条件,22122S =⨯=,5i =, 第二次5i =满足条件,2225S =⨯,11i =, 第三次11i =满足条件,2222511S =⨯⨯,23i =, 第四次23i =满足条件,2222251123S =⨯⨯⨯,47i =, 第五次47i =满足条件,2222225112347S =⨯⨯⨯⨯,95i =, 第六次95i =满足条件,2222222511234795S =⨯⨯⨯⨯⨯,190i =, 此时190i =不满足条件. 故条件为100i „? 故选:B .10.(5分)某三棱锥的三视图如图所示,则该三棱锥的体积为( )A .60B .30C .20D .10【解答】解:由三视图可知:该几何体为三棱锥, 该三棱锥的体积115341032=⨯⨯⨯⨯=.故选:D .11.(5分)已知1F ,2F 为双曲线22221(0,0)x y a b a b-=>>的左、右焦点,以12F F 为直径的圆与双曲线右支的一个交点为P ,1PF 与双曲线相交于点Q ,且1||2||PQ QF =,则该双曲线的离心率为( ) A 5B .2C 3D 5【解答】解:Q 点P 是以12F F 为直径的圆与C 右支的一个交点,∴即12F PF ∠为直角,∴则设1||QF m =,||2PQ m =,则12||2F F c =,则222||49PF c m =-,222||45QF c m =- 则2212||||3492PF PF m c m a -=-=,①21||||2QF QF m a -==,②,则32m m a ==,即4m 平方整理得224516m c =,则221645m c =,代回②2a =,即c =即离心率ce a= 故选:A .12.(5分)若关于x 的不等式21202xlnx x x kx k +---<的解集为(,)a b ,且(,)a b 内只有一个整数,则实数k 的取值范围是( ) A .342[,]43ln --B .324(,]43ln -C .324[,]43ln -D .342(,]43ln --【解答】解:根据题意,不等式21202xlnx x x kx k +---<即212(1)2xlnx x x k x +-<+,设21()22f x xlnx x x =+-,()(1)g x k x =+,若不等式21202xlnx x x kx k +---<的解集为(,)a b ,则在区间(,)a b 上,()f x 的图象在()g x 的下方;()g x 为过点(1,0)-的直线,k 为直线(1)y k x =+的斜率,设(1,0)M -; 对于21()22f x xlnx x x =+-,其导数()1f x lnx x '=+-,有f '(1)0=,在区间(0,1)上,()0f x '<,()f x 为减函数, 在区间(1,)+∞上,()0f x '>,()f x 为增函数; 据此可得()f x 的大致图象如图:设3(1,)2A -,(2,42)B ln -为函数()f x 上两点,则有30321(1)4MAk --==---,420422(1)3MB ln ln k ---==--,若(,)a b 内只有一个整数,则有34243ln k --<…,即k 的取值范围为3(4-,42]3ln -;故选:D .二、填空题:本题共4小题,每小题5分,共20分.13.(5分)定义在R 上的偶函数()f x 满足,当0x <时,()1xf x x =-,则曲线()y f x =在点(2,f (2))处的切线的斜率为 19. 【解答】解:设0x >,则()()11x xf x f x x x -=-==--+, 0x ∴>,21()(1)f x x '=+,f ∴'(2)19=, 故答案为19.14.(5分)设n S 为等比数列{}n a 的前n 项和,若11a =,且13S ,22S ,3S 成等差数列,则n a = 13n - .【解答】解:设等比数列的公比为q ,n S 为等比数列{}n a 的前n 项和,若11a =,且13S ,22S ,3S 成等差数列,可得23143S S S =+,11a =, 即24(1)13q q q +=+++,3q =.13n n a -∴=.故答案为:13n -.15.(5分)市扶贫工作组从4男3女共7名成员中选出队长1人,副队长1人,普通队员2人组成4人工作小组下乡,要求工作组中至少有1名女同志,且队长和副队长不能都是女同志,共有 348 种安排方法.【解答】解:根据题意,分2种情况讨论: ①,正副队长都是男同志,需要先在4名男成员中任选2人,分别担任队长和副队长,有2412A =种情况, 再在剩下的5人中选出2人,担任普通队员,要求至少有1名女同志,有2519C -=种情况, 此时有129108⨯=种安排方法; ②,正副队长一男一女,需要先在男女同志中各选一人,分别担任队长和副队长,有11243224C C A =种情况, 再在剩下的5人中选出2人,担任普通队员,有2510C =种情况, 此时有2410240⨯=种安排方法; 则一共有108240348+=种安排方法; 故答案为:348.16.(5分)已知函数22()()()x a f x x a e e =+++,若存在0x ,使得024()1f x e +„,则实数a 的值为 2211e e -+ .【解答】解:函数22()()()x af x x a e e=+++,函数()f x 可以看作是动点(,)x M x e 与动点(,)aN a e --之间距离的平方,动点M 在函数x y e =的图象上,N 在直线1y x e=的图象上,问题转化为求直线上的动点到曲线的最小距离,由x y e =得,1x y e e'==,解得1x =-, 所以曲线上点1(1,)Me -到直线1y x e =的距离最小,最小距离d =,则24()1f x e +…,根据题意,要使024()1f x e +„,则024()1f x e =+,此时N恰好为垂足,由11MNae ek ea--==--+,解得2211eae-=+.故答案为:2211ee-+.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题都必须作答,第22、23题为选考题,考生根据要求作答.一、必做题:共60分.17.(12分)在ABC∆中,角A,B,C对应的边分别是a,b,c,已知cos23cos()1A B C-+=.(Ⅰ)求角A的大小;(Ⅱ)若ABC∆的面积53S=,5b=,求sin sinB C的值.【解答】解:(Ⅰ)由cos23cos()1A B C-+=,得22cos3cos20A A+-=,即(2cos1)(cos2)0A A-+=,解得122cosA cosA==-或(舍去).因为0Aπ<<,所以3Aπ=.(Ⅱ)由13sin532S bc A bc===,得到20bc=.又5b=,解得4c=.由余弦定理得2222cos25162021a b c bc A=+-=+-=,故21a=.又由正弦定理得222035sin sin sin sin sin2147b c bcB C A A Aa a a===⨯=g.18.(12分)如图,已知ABCD∆中,90BCD∠=︒,AB⊥平面BCD,2BC=,3CD=,3AB=,E是AC的中点.(Ⅰ)若F是AD的中点,求证:平面BEF⊥平面ABC;(Ⅱ)若2AF FD=,求平面BEF与平面BCD所成的锐二面角的大小.【解答】(Ⅰ)证明:AB⊥Q平面BCD,AB CD∴⊥.又CD BC⊥Q,CD∴⊥平面ABC.E Q 、F 分别为AC 、AD 的中点,//EF CD ∴.EF ∴⊥平面ABC , EF ⊂Q 平面BEF ,∴平面BEF ⊥平面ABC .(Ⅱ)解:如图建立空间直角坐标系C xyz -,则 (2B ,0,0),(0D ,3,0),(2A ,0,3) Q 1AEEC=,(1E ∴,0,3)Q2AFFD=,223(,3,)33F ∴ ∴(1BE =-u u u r ,0,3),423(,3,)33BF =-u u u r , 设(n x =r ,y ,)z ,则n ⊥r 平面BEF ,∴304233033x z x y z ⎧-+=⎪⎪⎨⎪-++=⎪⎩,取31(,,1)2n =rQ 平面BCD 的法向量是(0m =r,0,1),2cos ,||||n m n m n m ∴<>==r rg r r r r∴平面BEF 与平面BCD 所成的锐二面角为45︒.19.(12分)我市为改善空气环境质量,控制大气污染,政府相应出台了多项改善环境的措施,其中一项是为了减少燃油汽车对大气环境污染,从2018年起大力推广使用新能源汽车,鼓励市民如果需要购车,可优先考虑选用新能源汽车,政府对购买使用新能源汽车进行购物补贴,同时为了地方经济发展,对购买本市企业生产的新能源汽车比购买外地企业生产的新能源汽车补贴高,所以市民对购买使用本市企业生产的新能源汽车的满意度也相应有所提高,有关部门随机抽取本市本年度内购买新能源汽车的100户,其中由70户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行,满分100分,将分数按照[0,20),[20,40),[40,60),[60,80),[80,100]分成5组,得如下频率分布直方图.(Ⅰ)若本次随机抽取的样本数据中购买使用本市企业生产的新能源汽车的用户中有52户满意度得分不少于60分,得分不少于60分为满意,根据提供的条件数据,完成下面的列联表,并判断是否有90%的把握认为购买使用新能源汽车的满意度与产地有关?满意不满意总计购本市企业生产的新能源汽车户数购外地企业生产的新能源汽车户数总计(Ⅱ)以频率作为概率,政府对购买使用新能源汽车的补贴标准是:购买本市企业生产的每台补贴2(1)a a>万元,购买外地企业生产的每台补贴a万元,但本市本年度所有购买新能源汽车的补贴每台的期望值不超过3.4万元,则购买外地产的新能源汽车每台最多补贴多少万元?附:22()n ad bck-=,其中n a b c d=+++.2()P k k…0.1000.0500.0250.0100.001k 2.706 3.841 5.024 6.63510.828【解答】解:()I.根据样本频率分布直方图可知:满意度得分不少于6的用户数:(200.0200200.0150)10070⨯+⨯⨯=,又因为本市企业生产用户有52户满意,所以外地企业生产的用户有18户满意,得如下列联表:则2100(52121818) 2.041 2.70670307030k ⨯⨯-⨯=≈<⨯⨯⨯,故没有90%的把握认为购买使用新能源汽车的满意度与产地有关.()II .设政府对购买新能源汽车的补贴每台为x 万元,则2x a =或x a =,270()0.7100P x a ===,30()0.3100P x a ===, 随机变量x 的分布列为:则2()0.70.3E x a a =+,由() 3.4E x „,即20.70.3 3.4a a +„,即273340a a +-„,解得1727a -剟, 又因为1a >,故12a <„,所以,购买外地产的新能源汽车每台最多补贴2万元.20.(12分)实轴长为的椭圆的中心在原点,其焦点1F ,2F 在x 轴上.抛物线的顶点在原点O ,对称轴为y 轴,两曲线在第一象限内相交于点A ,且12AF AF ⊥,△12AF F 的面积为3.(Ⅰ)求椭圆和抛物线的标准方程;(Ⅱ)过点A 作直线l 分别与抛物线和椭圆交于B ,C ,若2AC AB =u u u r u u u r,求直线l 的斜率k .【解答】解:(Ⅰ)设椭圆方程为22221(0)x y a b a b+=>>,1AF m =,2AF n =由题意知2224436m n c m n mn ⎧+=⎪⎪+=⋯⎨⎪=⎪⎩(2分)解得29c =,21293b ∴=-=.∴椭圆的方程为221123x y +=⋯(4分)3A y c ⨯=Q ,1A y ∴=,代入椭圆的方程得22A x =将点A 坐标代入得抛物线方程为28x y =. ⋯(6分) (Ⅱ)设直线l 的方程为1(2)y k x -=-,1(B x ,1)y ,2(C x ,2)y 由2AC AB =u u u r u u u r得21222(2)x x -=-,化简得12222x x -=(8分)联立直线与抛物线的方程21(22)8y k x x y ⎧-=-⎪⎨=⎪⎩,得28280x kx k -+-=∴128x k +=①⋯(10分)联立直线与椭圆的方程221(22)412y k x x y ⎧-=-⎪⎨+=⎪⎩ 得2222(14)(8162)32280k x k k x k k ++-+--=∴2x +=⋯(12分)∴1222(8x x k -=-=整理得:(160k -=∴k ,所以直线l. ⋯(14分)21.(12分)已知函数21()2f x ax alnx x =-+.(1)讨论函数()f x 的单调性;(2)若0a <,设()()g x f x x =-,()22h x xlnx x =-+,若对任意1x ,2[1x ∈,12)()x x +∞≠,2121|()()||()()|g x g x h x h x --…恒成立,求实数a 的取值范围.【解答】解:(1)2()1a ax x af x ax x x+-'=-+=,令2()t x ax x a =+-,①当0a =时,()0()0t x x f x '=>⇒>,所以()f x 在(0,)+∞上单调递增;②当0a <时,令1()00t x x =⇒<,20x =>,所以()f x 在上单调递增,在)+∞上单调递减;③当0a >时,令1()00t x x =⇒>,20x =<,所以()f x 在上单调递减,在)+∞上单调递增. (2)2(1)()a a x g x ax x x-'=-=,因为0a <,当1x …时,()0g x '„,()g x 在[1,)+∞单调减; ()2h x lnx '=-,当1x …时,()0h x '„,()h x 在[1,)+∞单调减. 因为对任意1x ,2[1x ∈,)+∞,2121|()()||()()|g x g x h x h x --…, 不防设12x x <,则由两函数的单调性可得: 1212()()()()g x g x h x h x --…,所以:1122()()()()g x h x g x h x --…对任意12[1x x <∈,)+∞恒成立; 令21()()()222F x g x h x ax alnx xlnx x =-=-+-,则12()()F x F x …对任意12[1x x <∈,)+∞恒成立;即:()y F x =在[1x ∈,)+∞上单调减, 即:()20a F x ax lnx x'=-+„在[1x ∈,)+∞上恒成立, 令()2a G x ax lnx x=-+,222()ax x a G x x ++'=, 当1a -„时,220ax x a ++„在[1x ∈,)+∞恒成立,所以()0G x '„,()G x 在[1,)+∞单调减,所以()G x G „(1)0=,满足题意,当10a -<<时,()G x 有两个极值点1x ,2x且11x =>,21x =<, 所以在1(1,)x 上,()G x 单调增,即:()G x G >(1)0=对任意1(1,)x x ∈上恒成立,不满足题意,舍!综上,当1a -„时,不等式2121|()()||()()|g x g x h x h x --…在1x ,2[1x ∈,)+∞恒成立.二、选做题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系xOy 中,曲线1C 的参数方程为3cos (sin x y θθθ=⎧⎨=⎩为参数,[0θ∈,2))π,曲线2C的参数方程为(12x a t y t ⎧=⎪⎪⎨⎪=⎪⎩为参数). (Ⅰ)求曲线1C ,2C 的普通方程;(Ⅱ)若曲线1C 上一点P 到曲线2C的距离的最大值为a .【解答】解:(Ⅰ)曲线1C 的参数方程为3cos (sin x y θθθ=⎧⎨=⎩为参数,[0θ∈,2))π,利用平方关系可得:22:19x C y +=. 由曲线2C的参数方程为(12x a t y t ⎧=+⎪⎪⎨⎪=⎪⎩为参数),消去参数可得::0C x a --=. (Ⅱ)设点(3cos ,sin )P θθ,点P 到2C的距离|)|32a d πθ---==,当0a …时,有sin()13πθ-=时,max d =,∴a = 当0a <时,有sin()13πθ-=-时,max d =,∴a =-;综上,a =a =-.[选修4-5:不等式选讲] 23.已知函数2()4f x x ax =++,()|2||2|g x x x =++-.(Ⅰ)当4a =-时,求不等式()()f x g x …的解集;(Ⅱ)若不等式()()f x g x „的解集包含[2,4],求a 的取值范围.【解答】解:(Ⅰ)当4a =-时,2()44f x x x =-+.又2,2()|2||2|4,222,2x x g x x x x x x --⎧⎪=++-=-<<⎨⎪⎩„…,∴当2x -„时,2442x x x -+-…,解得2x -„;当22x -<<时,2444x x -+…,解得20x -<„;当2x …时,2442x x x -+…,解得3x ….综上,不等式的解集为{|03x x x 或剠.(Ⅱ)()()f x g x „的解集包含[2,4]等价于24|2||2|x ax x x ++++-„在[2,4]上恒成立, 即2(2)40x a x +-+„对于[2x ∈,4]上恒成立,令2()(2)4h x x a x =+-+,要使()0h x „在[2,4]恒成立,只需(2)0(4)0h h ⎧⎨⎩„„, 即82(2)0204(2)0a a +-⎧⎨+-⎩„„,3a ∴-„, a ∴的取值范围为(-∞,3]-.。
2019-2020学年河南省三门峡市高一上学期期末数学试题及答案解析版

2019-2020学年河南省三门峡市高一上学期期末数学试题及答案解析版一、单选题1.设集合{|24}A x x =≤<,{|3782}B x x x =-≥-,则A B 等于( )A .{|34}x x ≤<B .{|3}x x ≥C .{|2}x x >D .{|2}x x ≥【答案】D【解析】先求得集合B,根据并集运算即可求解. 【详解】因为{|3782}B x x x =-≥-,即{|3}B x x =≥ 集合{|24}A x x =≤<由并集运算可得{|24}{|3}{|2}A B x x x x x x ⋃=≤<⋃≥=≤ 故选:D 【点睛】本题考查了集合并集的简单运算,属于基础题.2.已知直线l 过点()1,1且平行于直线4x y 80+-=,则直线l 的方程是( )A .x 4y 30-+=B .x 4y 50--=C .4x y 50++=D .4x y 50+-=【答案】D【解析】根据直线平行设出平行直线方程为4x +y +c =0,代入点的坐标求出c 即可.【详解】解:设与直线4x +y ﹣8=0平行的直线方程为4x +y +c =0, ∵直线4x +y +c =0过(1,1), ∴4+1+c =0, 即c =﹣5,则直线方程为4x +y ﹣5=0, 故选D . 【点睛】本题主要考查直线平行的求解,利用平行直线系是解决本题的关键. 3.函数()ln(32)f x x =+-的定义域为( )A .3[1,)2B .3(1,)2C .3[1,]2D .3(,)2+∞【答案】B 【解析】要使函数()()ln 32f x x =+-有意义,则10320x x ->⎧⎨->⎩,解得312x <<. 故选B.4.麻团又叫煎堆,呈球形,华北地区称麻团,是一种古老的中华传统特色油炸面食,寓意团圆.制作时以糯米粉团炸起,加上芝麻而制成有些包麻茸、豆沙等馅料,有些没有.一个长方体形状的纸盒中恰好放入4个球形的麻团,它们彼此相切,同时与长方体纸盒上下底和侧面均相切,其俯视图如图所示,若长方体纸盒的表面积为2576cm ,则一个麻团的体积为( )A .336cm πB .348cm πC .324cm πD .372cm π【答案】A【解析】设麻团的半径为r ,根据题意,得到长宽高,从而求得r 及麻团体积. 【详解】设麻团的半径为r ,因为麻团与长方体纸盒上下底和侧面均相切, 故长方体的长4a r =,宽4b r =,高2h r =, 又长方体表面积为576,故:223232576r r +=, 解得3r =,故麻团的体积为:334363V r cm ππ==. 故选:A. 【点睛】本题考查球体与长方体相切问题,涉及球体的体积计算与长方体表面积计算.5.三个数0.377,0.3,ln 0.3a b c ===大小的顺序是( ) A .a c b >> B .a b c >> C .b a c >> D .c a b >>【答案】B【解析】试题分析:根据指数函数和对数函数的单调性知:0.30771a =>=,即1a >;7000.30.31b <=<=,即01b <<;ln0.3ln10c =<=,即0c <;所以a b c >>,故正确答案为选项B .【考点】指数函数和对数函数的单调性;间接比较法. 6.已知函数1()()x x f x e e =-( 2.71828e ≈),则()f x ( ) A .是偶函数,且在R 上是增函数 B .是奇函数,且在R 上是增函数C .是偶函数,且在R 上是减函数D .是奇函数,且在R 上是减函数 【答案】B 【解析】函数()1xx f x e e ⎛⎫=- ⎪⎝⎭满足()()11 0xxx x f x f x e e e e ⎛⎫⎛⎫+-=-+-= ⎪ ⎪⎝⎭⎝⎭,即()() f x f x =--. 所以()f x 是奇函数,又因为y x e =和1y xe ⎛⎫=- ⎪⎝⎭均为增函数,所以()1xx f x e e ⎛⎫=- ⎪⎝⎭也为增函数, 故选B.7.如图,在直角梯形ABCD 中,0190,//,12A AD BC AD AB BC ∠====,将ABD ∆沿BD 折起,使得平面ABD ⊥平面BCD .在四面体A BCD -中,下列说法正确的是( )A .平面ABD ⊥平面ABCB .平面ACD ⊥平面ABC C .平面ABC ⊥平面BCD D .平面ACD ⊥平面BCD【答案】B【解析】由平面ABD ⊥平面BCD 的性质定理得CD ⊥AB ,又由AD ⊥AB ,从而得到AB ⊥平面ADC ,又AB ⊂平面ABC ,可得平面ABC ⊥平面ADC . 【详解】∵在直角梯形ABCD 中,AD ∥BC ,AD=AB=12BC=1,∠A =90°,在BCD ∆中,,BC=2,45DBC ∠= ,由余弦定理得90BDC ∠= ,∴BD ⊥CD ,又平面ABD ⊥平面BCD ,且平面ABD∩平面BCD =BD ,故CD ⊥平面ABD ,则CD ⊥AB ,又由AD ⊥AB ,CDAD D =∴AB ⊥平面ADC ,又AB ⊂平面ABC ,∴平面ABC ⊥平面ADC . 故选B . 【点睛】本题考查平面与平面垂直的性质和判定定理,考查逻辑思维能力,属于中档题. 8.已知函数7(13)10,(7)(),(7)x a x a x f x a x --+≤⎧=⎨>⎩是定义域R 上的减函数,则实数a 的取值范围是( )A .11(,)32B .16(,]311C .12[,)23D .16(,]211【答案】B【解析】根据分段函数单调性的性质建立不等式关系进行求解.【详解】若f (x )是定义域(-∞,+∞)上的减函数, 则满足()7701130713101a a a a a -⎧⎪-⎨⎪-+≥⎩<<<= 即0113611a a a ⎧⎪⎪⎪⎨⎪⎪≤⎪⎩<<> ,整理得16311a <≤.故选:B 【点睛】本题考查了分段函数单调性的应用,根据分段函数的性质建立不等式是解决本题的关键.9.某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )A .快、新、乐B .乐、新、快C .新、乐、快D .乐、快、新【答案】A【解析】根据四棱锥图形,正好看到“新年快乐”的字样,可知顺序为②年①③,即可得出结论. 【详解】根据四棱锥图形,正好看到“新年快乐”的字样,可知顺序为②年①③, 故选A . 【点睛】本题考查四棱锥的结构特征,考查学生对图形的认识,属于基础题.10.中国古代数学名著《九章算术》中,将顶部为一线段,下底为一矩形的拟柱体称之为刍甍(méng),如图几何体为刍甍,已知面ABCD 是边长为3的正方形,//EF AB ,2,EF EF =与面ABCD 的距离为2,则该多面体的体积为( )A .6B .152 C .8 D .9【答案】C【解析】根据题意,把该几何体分成一个四棱锥和一个三棱锥,各自求出它的体积再求和即可. 【详解】不妨设EF ⊥面BCF ,如图所示,,连接BE ,CE ,则多面体ABCDEF 的体积为:V =V 四棱锥E﹣ABCD+V 三棱锥E ﹣BCF=13×32×2+13×12×3×2×2=6+2=8. 故选C. 【点睛】本题考查了空间几何体体积的计算问题,把几何体分成一个四棱锥和一个三棱锥是解题的关键,属于基础题. 11.已知函数()f x 的定义域为R .当0x <时,3()1f x x =-;当11x -≤≤时,()()f x f x -=-;当12x >时,11()()22f x f x +=-.则(6)f =( ) A .2- B .1- C .0 D .2【答案】D【解析】试题分析:当时,11()()22f x f x +=-,所以当时,函数是周期为的周期函数,所以,又函数是奇函数,所以,故选D .【考点】函数的周期性和奇偶性.12.已知点(,)P x y 是直线240x y -+=上一动点,直线,PA PB 是圆22:20C x y y ++=的两条切线,,A B 为切点,则直线AB 必过的定点是( )A .42,55⎛⎫-⎪⎝⎭B .42,55⎛⎫--⎪⎝⎭C .24,55⎛⎫-⎪⎝⎭D .24,55⎛⎫--⎪⎝⎭【答案】D【解析】设点()00,P x y ,写出直线AB 的方程,利用相交直线系来求解直线恒过的定点. 【详解】设点()00,P x y ,因为点P 在直线240x y -+=上, 故:00240x y -+=,解得:0024y x =+;① 又过点P ,作圆()2211x y ++=的两条切线,切点为A 、B ,故:直线AB 的方程为:()()00111x x y y +++=;② 将①代入②可得:()022540x x y y ++++=故直线AB 恒过定点为直线220x y ++=与540y +=的交点,即:220540x y y ++=⎧⎨+=⎩,解得2545x y ⎧=-⎪⎪⎨⎪=-⎪⎩故选:D. 【点睛】本题综合考查直线与圆,涉及切线问题,直线恒过定点问题,属中档题.二、填空题13.已知直线21y kx k =++,则直线恒经过的定点______. 【答案】()2,1-【解析】试题分析:将直线21y kx k =++化简为点斜式,可得12y k x -=+(),∴直线经过定点21-(,),且斜率为k .即直线21y kx k =++恒过定点()2,1-.故答案为()2,1-. 【考点】恒过定点的直线.【方法点晴】本题给出含有参数k的直线方程,求直线经过的定点坐标.着重考查了直线的基本量与基本形式等知识,属于基础题;如果一条直线经过某一定点,那么这条直线就是过该定点的直线.这里面可以看出,过一个定点的直线是不唯一的,事实上是由无数条直线组成,将直线化简成点斜式的形式得:12(),可得直线的斜率为ky k x-=+且经过定点()-,从而得到答案.2,114.给出下列命题:①任意三点确定一个平面;②三条平行直线最多可以确定三个个平面;③不同的两条直线均垂直于同一个平面,则这两条直线平行;④一个平面中的两条直线与另一个平面都平行,则这两个平面平行;其中说法正确的有_____(填序号).【答案】②③【解析】对四个选项进行逐一分析即可.【详解】对①:根据公理可知,只有不在同一条直线上的三点才能确定一个平面,故错误;对②:三条平行线,可以确定平面的个数为1个或者3个,故正确;对③:垂直于同一个平面的两条直线平行,故正确;对④:一个平面中,只有相交的两条直线平行于另一个平面,两平面才平行,故错误. 综上所述,正确的有②③. 故答案为:②③. 【点睛】本题考查立体几何中的公理、线面平行的判定,属综合基础题.15.已知点(3,0)A -,(1,2)B ,若圆222:(3)(4)(0)C x y r r -+-=>与以线段AB 为直径的圆相外切,则实数r 的值是__________. 【答案】5【解析】()3,0A -,()1,2B ,则AB ==AB 中点为:()1,1-.以线段AB 为直径的圆圆心为()1,1-圆C 与以线段AB 为直径的圆相外切,所以圆心距5r ==+所以5r =故答案为5点睛:这个题目考查的是两圆的位置关系;两圆的位置关系有相交,外切,内切,内含,外离这几种情况.判断两圆的位置关系时的常用方法是找两圆心距和两半径之和或差的关系.常考的题型是已知位置关系求参或者找公切线的条数.16.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设x ∈R ,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,例如: []2.13-=-,[]3.13=,已知函数()121123x xf x +=-+,则函数[()]y f x =的值域是__________. 【答案】{}1,0,1- 【解析】()()1221221152123123312xx x x xf x ++-=-=-=-+++.()()()225215121,,0,2,2,0,,121231223x x x x⎛⎫+∈+∞∈-∈--∈- ⎪+++⎝⎭. []x 表示不超过x 的最大整数,所以{}521,0,1312x ⎡⎤-∈-⎢⎥+⎣⎦. 故答案为{}1,0,1-.三、解答题 17.已知函数21()f x x =.(1)判断函数()f x 的奇偶性,并说明理由;(2)用函数单调性的定义证明函数()f x 在(0,)+∞上是减函数.【答案】(1)见解析;(2)见解析【解析】(1)先判断函数定义域关于原点对称,然后利用奇偶性定义即可判断;(2)任取()12,0,x x ∈+∞,且12x x <,利用函数单调性的定义作差分析即可得到证明. 【详解】(1)函数()f x 的定义域为()(),00,-∞⋃+∞.对于定义域内的每一个x ,都有()()2211f x x x -==-,()()f x f x ∴-=.∴函数()f x 为偶函数(2)设任意()12,0,x x ∈+∞,且12x x <,则()()12221211f x f x x x -=- 22212212x x x x -== ()()21212212x x x x x x +-. 由120x x <<,得120x x +>,210x x ->,22120x x > 于是()()120f x f x ->,即()()12f x f x >.∴函数()f x 在()0,+∞上是减函数.【点睛】本题考查函数奇偶性和函数单调性定义的应用,属于基础题. 18.分别求出适合下列条件的直线方程: (1)经过点且在轴上的截距等于在轴上截距的2倍; (2)经过直线与的交点,且和,等距离. 【答案】(1)或;(2)或【解析】试题分析:(1)分两种情况讨论:当直线不过原点时,设出直线的截距式方程,代点求解即可;当直线过原点时,先利用两点求出斜率,利用点斜式方程进行求解;(2)先联立两直线方程求出两条直线的交点,再分直线是否存在斜率设出直线方程,利用点到直线的距离公式进行求解.试题解析:(1)当直线不过原点时,设所求直线方程为,将代入所设方程,解得,此时,直线方程为;当直线过原点时,斜率,直线方程为,即.综上可知,所求直线方程为或.(2)由解得交点坐标为,当直线的斜率存在时,设的方程是,即,由、两点到直线的距离相等得,解得,方程为;当斜率不存在时,即直线平行于轴,方程为时也满足条件.综上可知,所求直线方程为或.点睛:在设直线方程时,要注意其限制条件,如直线的点斜式和斜截式适用于存在斜率的情况,直线的截距式适用于与坐标轴不平行且不过原点的直线;且处理平面解析几何时,要注意利用初中的平面几何知识,如第(2)问中,由平面几何知识可判定所求直线与直线平行或过线段的中点,可减小计算量.19.已知()=是定义域为R的奇函数,当[)y f xx∈+∞时,0,()22=-.f x x x(1)写出函数()y f x =的解析式;(2)若方程()f x a =恰3有个不同的解,求a 的取值范围. 【答案】(1)()222,02,0x x x f x x x x ⎧-≥=⎨--<⎩(2) ()1,1-【解析】(1)由奇函数的定义求解析式,即设0x <,则有x ->0,利用()f x -可求得()f x ,然后写出完整的函数式;(2)作出函数()f x 的图象,确定()f x 的极值和单调性,由图象与直线y a =有三个交点可得a 的范围. 【详解】解:(1)当(),0x ∈-∞时,()0,x -∈+∞,()f x 是奇函数,()()f x f x ∴=--=-()()2222x x x x ⎡⎤---=--⎣⎦()222,02,0x x x f x x x x ⎧-≥∴=⎨--<⎩. (2)当[)0,x ∈+∞时,()()22211f x x x =-=--,最小值为1-;当(),0x ∈-∞,()()22211f x x x x =--=-+,最大值为1. 据此可作出函数的图象,如图所示,根据图象得,若方程()f x a =恰有3个不同的解, 则a 的取值范围是()1,1-. 【点睛】本题考查函数奇偶性,考查函数零点与方程根的关系.在求函数零点个数(或方程解的个数)时,可把问题转化为一个的函数图象和一条直线的交点个数问题,这里函数通常是确定的函数,直线是动直线,由动直线的运动可得参数取值范围.20.如图,在四棱锥P ABCD -中,四边形ABCD 为平行四边形,090BAP CDP ∠=∠=,E 为PC 中点,(1)求证://AP 平面EBD ;(2)若PAD ∆是正三角形,且PA AB =.(Ⅰ)当点M 在线段PA 上什么位置时,有DM ⊥平面PAB ? (Ⅱ)在(Ⅰ)的条件下,点N 在线段PB 上什么位置时,有平面DMN ⊥平面PBC ?【答案】(1)详见解析;(2)(Ⅰ) 点M 在线段PA 中点时;(Ⅱ)当14PN PB =时. 【解析】(1)连接AC ,BD ,AC BD=O ,连接OE ,由O 为AC 中点,E 为PC 中点,得OE //PA ,推出AP //平面EBD ;(2)(Ⅰ) 当点M 在线段PA 中点时,由线面垂直的判定定理得DM ⊥平面PAB ;(Ⅱ)当1PN PB 4=时由(Ⅰ)得PB ⊥平面DMN ,推出平面DMN ⊥平面PBC . 【详解】(1)证明:连接AC ,BD ,AC BD ⋂=O ,因为ABCD 是平行四边形,则O 为AC 中点,连接OE ,又E 为PC 中点,OE //PA,OE ∴⊂面EBD ,PA ⊄面EBD ∴ AP //平面EBD .(2)解(Ⅰ)当点M 在线段PA 中点时,有DM ⊥平面PAB 取PA 中点M ,连接DMCD PD ⊥,又AB//CDAB PD ∴⊥,又AB PA ⊥,PA PD P ⋂=,AB ∴⊥平面PAD AB DM ∴⊥,又ΔPAD 是正三角形, DM PA,PA AB A,∴⊥⋂=∴ DM ⊥平面PAB(Ⅱ)当1PN PB 4=时,有平面DMN ⊥平面PBC过M 作MN PB ⊥于N ,由(Ⅰ)知DM PB,MN DM M ⊥⋂=,PB ∴⊥平面DMN ,所以平面DMN ⊥平面PBC易得1PN PB 4= 【点睛】本题考查了线面平行和线面垂直,面面垂直的判定定理,数量掌握判定定理的内容是关键,属于中档题.21.已知点P 是圆22:(3)4C x y -+=上的动点,点(3,0)A - ,M 是线段AP 的中点(1)求点M 的轨迹方程;(2)若点M 的轨迹与直线:20l x y n -+=交于,E F 两点,且OE OF ⊥,求n 的值.【答案】(1)221x y +=;(2)n =±.【解析】(1)设()M x,y 为所求轨迹上任意的一点,其对应的P 点为()11x ,y .M 因为是线段AP 的中点,由相关点法化简即可;(2)联立方程22x y 120x y n ⎧+=⎨-+=⎩设()()1122E x ,y ,F x ,y 由OE OF ⊥得1212x x y y 0+=化简即可.【详解】解:(1)设()M x,y 为所求轨迹上任意的一点,其对应的P 点为()11x ,y ,则()2211x 3y 4-+=①又M 是AP 的中点,11x 32y 2x y -⎧=⎪⎪∴⎨⎪=⎪⎩,则11x 23y 2x y =+⎧⎨=⎩,代入①式得 22x y 1+=(或用定义法亦可)(2)联立方程22x y 120x y n ⎧+=⎨-+=⎩消去y 得225x 4nx n 10++-=由Δ0>得n <<又设()()1122E x ,y ,F x ,y ,则122124n x x 5n 1x x 5⎧+=-⎪⎪⎨-⎪=⎪⎩③ 由OE OF ⊥可得1212x x y y 0+=,而y 2x n =+()()1212x x 2x n 2x n 0∴+++=,展开得()212125x x 2n x x n 0+++=由③式可得22n 14n 52n n 055-⎛⎫⨯+⨯-+= ⎪⎝⎭,化简得25n 2=④ 根据②④得n 2=±.【点睛】本题考查了由相关点代入法求轨迹方程,也考查了直线与圆的位置关系等知识,属于中档题.22.设函数()f x 定义域为I ,对于区间D I ⊆,如果存在12,x x D ∈,12x x ≠,使得122f x f x ,则称区间D 为函数()f x 的λ区间.(1)判断(,)-∞+∞是否是函数31x y =+的λ区间;(2)若1,22⎡⎤⎢⎥⎣⎦是函数log a y x =(其中0a >,1a ≠)的λ区间,求a 的取值范围.【答案】(1)不是;(2)()1 ,11,22⎛⎫⋃⎪⎝⎭. 【解析】(1)由对数型函数的值域可以进行判断; (2)根据()()122f x f x +=,得对数方程,求解即可得范围. 【详解】(1)因为30x >,则311x y =+>,故任取12,x x ,则122y y +>,根据题意,区间(),-∞+∞不是函数31x y =+的λ区间. (2)根据题意,若1,22⎡⎤⎢⎥⎣⎦是函数log ?a y x =的λ区间,则: 存在12,x x ,使得:12log log 2a a x x +=,整理得:212x x a =;因为1,22x ⎡⎤∈⎢⎥⎣⎦,故121,44x x ⎛⎫∈ ⎪⎝⎭,即21,44a ⎛⎫∈ ⎪⎝⎭, 解得:()1,11,22a ⎛⎫∈⋃⎪⎝⎭. 【点睛】本题属于函数与新定义问题的综合,考查了指数型函数的值域,与对数方程的求解,属综合基础题.。
2019-2020学年河南省三门峡市七年级(上)期末数学试卷-带答案

2019-2020学年河南省三门峡市七年级(上)期末数学试卷一、选择题(本大题共10小题,共30.0分)1.若是一元一次方程,则m等于.A. 1B. 2C. 1或2D. 任何数2.关于x的方程与的解相同,则A. B. C. 2 D.3.解方程时,去分母正确的是A. B.C. D.4.已知,则等于A. B. C. D.5.在有理数范围内定义运算“”,其规则为,则方程的解为A. B. C. D. 556.方程中被阴影盖住的是一个常数,此方程的解是这个常数应是A. 1B. 2C. 3D. 47.x是一个两位数,y是一个三位数,把x放在y的左边构成一个五位数,则这个五位数的表达式是A. xyB.C.D.8.某试卷由26道题组成,答对一题得8分,答错一题倒扣5分.今有一考生虽然做了全部的26道题,但所得总分为零,他做对的题有A. 10道B. 15道C. 20道D. 8道9.设,,且,则y的值是A. B. C. D.10.某个体商贩在一次买卖中,同时卖出两件上衣,售价都是135元,若按成本计,其中一件盈利,另一件亏本,在这次买卖中他A. 不赚不赔B. 赚9元C. 赔18元D. 赚18元二、填空题(本大题共5小题,共15.0分)11.在方程,,,,,中,是一元一次方程的有______ .12.当______时,式子与的值互为相反数.13.若是关于x的一元一次方程,则______,方程的解是______.14.若a,b互为相反数,c,d互为倒数,p的绝对值等于2,则关于x的方程的解为______.15.某商店将彩电按成本价提高,然后在广告上写“大酬宾,八折优惠”,结果每台彩电仍获利270元,那么每台彩电成本价是______.三、计算题(本大题共3小题,共18.0分)16.x等于什么数时,代数式的值比的值的2倍小1?17.已知关于x的方程:与有相同的解,求以y为未知数的方程的解.18.在“节能减排,做环保小卫士”活动中,小明对两种照明灯的使用情况进行了调查,得出如表所示的数据:已知这两种灯的照明效果一样,小明家所在地的电价是每度元.注:用电度数功率千瓦时间小时,费用灯的售价电费请你解决以下问题:如果选用一盏普通白炽灯照明1000小时,那么它的费用是多少?在白炽灯的使用寿命内,设照明时间为x小时,请用含x 的式子分别表示用一盏白炽灯的费用和一盏节能灯的费用;照明多少小时时,使用这两种灯的费用相等?如果计划照明4000小时,购买哪一种灯更省钱?请你通过计算说明理由.四、解答题(本大题共5小题,共40.0分)19.解下列方程.;;20.方程的根,比关于x的方程的根的2倍还多,求关于x的方程的解.21.某车间有62个工人,生产甲、乙两种零件,每人每天平均能生产甲种零件12个或乙种零件23个,已知每3个甲种零件和2个乙种零件配成一套,问应分配多少人生产甲种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好配套?22.甲、乙两工程队开挖一条水渠各需10天、15天,两队合作2天后,甲有其他任务,剩下的工作由乙队单独做,还需多少天能完成任务?23.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米小时,水速为2千米时,则A港和B 港相距多少千米.答案和解析1.【答案】A【解析】【分析】解题的关键是根据一元一次方程的未知数x的次数是1这个条件,此类题目应严格按照定义解答.若一个整式方程经过化简变形后,只含有一个未知数,并且未知数的次数都是1,系数不为0,则这个方程是一元一次方程.据此列出关于m的等式,继而求出m的值.【解答】解:根据一元一次方程的特点可得,解得.故选A.2.【答案】C【解析】解:解第一个方程得:,解第二个方程得:解得:故选:C.可以分别解出两方程的解,两解相等,就得到关于k的方程,从而可以求出k的值.本题考查解的定义,关键在于根据同解的关系建立关于k的方程.3.【答案】C【解析】解:方程两边同时乘以6得:,去括号得:.故选C.去分母的方法是方程两边同时乘以各分母的最小公倍数6,在去分母的过程中注意分数线起到括号的作用,以及去分母时不能漏乘没有分母的项.在去分母的过程中注意分数线起到括号的作用,并注意不能漏乘没有分母的项.4.【答案】D【解析】解:方法1:方法2:故选D.先去括号,分别把等式两边展开并且合并同类项得,然后利用等式的性质对式子进行变形,即可得到的值.本题主要考查等式的性质,利用等式性质对等式进行变形即可得到结果.5.【答案】D【解析】【分析】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键原式利用题中的新定义计算即可求出值.【解答】解:根据题中的新定义得:,整理得:,解得:.故选D.6.【答案】C【解析】解:设阴影部分表示的数为a,将代入,得:,解得:,故选:C.设这个常数为a,将y的值代入方程计算即可求出a的值.此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.7.【答案】C【解析】解:根据题意得,这个五位数的表达式是,故选C.此题考查了数字的表示方法,每位上的数字乘以位数再相加即为此数,比如:个位上数字为a,十位上数字为b,则此两位数为此题中还要注意整体思想的应用,x是一个两位数,y是一个三位数,把x放在y的左边构成一个五位数,可以看做x位于千位上,y位于个位上,所以这个五位数的表达式是.此题要把握好数字的表示方法,还要特别注意整体思想的应用,此题中数学思想的学习是关键.8.【答案】A【解析】解:设他作对了x道题,则:,解得:.故选A.本题的等量关系为:得分扣分;根据题意设出作对了x道题,可得关于x的方程式,求解可得答案.本题的关键点和难点在等量关系上:对题得分错题扣分实际得分.9.【答案】B【解析】【分析】本题考查了解一元一次方程和等式的性质,主要考查学生运用等式的性质解方程的能力,题目比较好,难度不大.把P和Q的值代入,得出关于y的方程,求出方程的解即可.【解答】解:,,,代入得:,,,.故选B.10.【答案】C【解析】解:设在这次买卖中原价都是x元,则可列方程:解得:比较可知,第一件赚了27元第二件可列方程:解得:,比较可知亏了45元,两件相比则一共亏了18元.故选:C.要知道赔赚,就要先算出两件衣服的原价,要算出原价就要先设出未知数,然后根据题中的等量关系列方程求解.此题的关键是先算出两件衣服的原价,才能知道赔赚.不可凭想象答题.11.【答案】【解析】解:是分式方程;符合一元一次方程的形式;是一元二次方程;符合一元一次方程的形式;是二元一次方程;符合一元一次方程的形式;故是一元一次方程.只含有一个未知数元,并且未知数的指数是次的方程叫做一元一次方程,它的一般形式是b是常数且.本题主要考查了一元一次方程的一般形式,只含有一个未知数,未知数的指数是1,一次项系数不是0,这是这类题目考查的重点.12.【答案】【解析】解:根据题意得:,去分母得:,去括号得:,移项、合并同类项得:,系数化1得:.即当时式子与的值互为相反数.式子与的值互为相反数就是已知这两个式子的和是0,就可以得到一个关于x的方程,解方程就可以求出x的值.本题主要考查相反数的概念,已知相反数就是已知一个相等关系,可以利用方程解决.13.【答案】【解析】解:是关于x的一元一次方程,,且,解得:,方程为,解得:,故答案为:;.利用一元一次方程的定义判断求出a的值,即可确定出方程的解.此题考查了一元一次方程的定义,熟练掌握一元一次方程的定义是解本题的关键.14.【答案】【解析】解:,b互为相反数,c,d互为倒数,p的绝对值等于2,,,,将其代入关于x的方程中,可得:,解得:.由相反数得出,由倒数得出,由绝对值得出,然后将其代入关于x的方程中,从而得出x的值.主要考查了相反数,倒数,绝对值的概念及其意义,并利用这些概念得到的数量关系代入含有字母系数的方程中,利用一元一次方程求出未知数的值.15.【答案】1350元【解析】解:设每台彩电成本价是x元,依题意得:,解得:.故答案是:1350元.根据利润售价成本价,设每台彩电成本价是x元,列方程求解即可.本题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.16.【答案】解:根据题意得:,去分母得:,移项合并得:,解得:.【解析】根据题意列出方程,求出方程的解即可得到x的值.此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.17.【答案】解:解方程得:将代入得:解得:将,代入得:,解得:.【解析】根据方程1可直接求出x的值,代入方程2可求出m,把所求m和x代入方程3,可得到关于y的一元一次方程,解答即可.本题解决的关键是能够求解关于x的方程,根据同解的定义建立方程.18.【答案】解:根据题意得:元,则一盏普通白炽灯照明1000小时,费用为53元;用一盏白炽灯的费用为元;一盏节能灯的费用为元;根据题意得:,解得:,则照明800小时时,使用这两种灯的费用相等;用节能灯省钱,理由为:当时,用白炽灯的费用为元;用节能灯的费用为元,则用节能灯省钱.【解析】根据表格列出算式,计算即可得到结果;根据表格中的数据列出代数式即可;令两代数式相等列出方程,求出方程的解即可得到结果;根据照明4000小时,求出各自的费用,比较即可得到结果.此题考查了一元一次方程的应用,列代数式,以及代数式求值,弄清题意是解本题的关键.19.【答案】解:去括号得:,移项合并得:,解得:;去分母得:,移项合并得:,解得:;去分母得:,移项合并得:,解得:;方程整理得:,即,移项合并得:,解得:.【解析】方程去括号,移项合并,把x系数化为1,即可求出解;方程去分母,去括号,移项合并,把x系数化为1,即可求出解;方程去分母,去括号,移项合并,把x系数化为1,即可求出解;方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解.此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.20.【答案】解:,解得,方程的根,比关于x的方程的根的2倍还多,得的根是.把代入方程,得.解得.把代入,得.解得.【解析】根据解方程,可得第一个方程的解,根据两个方程的解的关系,可得第二个方程的解,根据把方程的解代入方程,可得关于a的方程,根据解方程,可得a的值,根据巴a的值代入方程,可得关于x的一元一次方程,根据解方程,可得答案.本题考查了一元一次方程的解,利用把方程的解代入方程得出关于x的方程是解题关键.21.【答案】解:设应分配x人生产甲种零件,则由题意得,解得,人.故应分配46人生产甲种零件,16人生产乙种零件才能使每天生产的甲种零件和乙种零件刚好配套.【解析】设应分配x人生产甲种零件,人生产乙种零件才能使每天生产的甲种零件和乙种零件刚好配套,根据每人每天平均能生产甲种零件12个或乙种零件23个,可列方程求解.本题考查了一元一次方程的应用.关键是设出生产甲种零件和乙种零件的人数,以配套的比例列方程求解.22.【答案】解:设还需x天能完成任务,根据题意可得方程:.解得.答:还需10天能完成任务.【解析】此题属于工程问题,基本公式是:工作量工作时间工作效率,由此公式可得甲、乙的工作效率分别为、;甲的工作时间是2天,乙的工作时间是天,相等关系为:甲、乙两天的工作量乙x天的工作量总工作量1.此题考查一元一次方程的应用,关键是找出题目中的相等关系,工程问题的基本公式是:工作量工作时间工作效率.23.【答案】解:设A港和B港相距x千米,根据题意得:,解得:.故A港和B港相距504千米.【解析】此题考查顺流与逆流的关系,顺水速度水流速度静水速度,逆水速度静水速度水流速度.根据时间关系列方程求解.此题考查了学生对顺水速度,逆水速度的理解,这与顺风逆风类似.。
2019-2020学年河南省灵宝市第一高级中学高三语文上学期期末考试试题及答案解析

2019-2020学年河南省灵宝市第一高级中学高三语文上学期期末考试试题及答案解析一、现代文阅读(36分)(一)现代文阅读I(9分)阅读下面的文字,完成下列小题。
对城市而言,文明弹性是一个城市体在生存、创新、适应、应变等方面的综合状态、综合能力,是公共性与私人性之间、多样性与共同性之间、稳定性与变迁性之间、柔性与刚性之间的动态和谐,过于绵柔、松散,或者过于刚硬、密集,都是弹性不足或丧失的表现,是城市体出现危机的表征。
当代城市社会,尤其需要关注以下文明弹性问题。
其一,空间弹性。
城市具有良好空间弹性的一个重要表现,是空间的私人性与公共性关系能够得到较为合理的处理。
任何城市空间都是私人性与公共性的统一,空间弹性的核心问题,就是如何实现空间的公共性与私人性的有机统一、具体转换。
片面地强调空间的公共性或片面地强调空间的私人性,都会使城市发展失去基础,目前,人们更多地要求空间的私人性,注重把空间固化为永恒的私人所有物、占有物。
这种以私人化为核心的空间固化倾向,造成城市空间弹性不足,正在成为制约城市发展的一个重要原因。
其二,制度弹性,一种较为理想的、有弹性的城市制度,是能够在秩序与活力、生存与发展间取得相对平衡的制度。
城市有其发展周期、发展阶段,对一个正在兴起的城市而言,其主要任务是聚集更多的发展资源、激活发展活力,而对一个已经发展起来的城市而言,人们会更为注重城市制度的稳定功能。
但问题在于,即使是正在崛起的城市,也需要面对秩序与稳定的问题;即使是一个已经发展起来的城市,也需要面对新活力的激活问题。
过于注重某种形式的城市制度,过于注重城市制度的某种目标,都是城市制度弹性不足,走向僵化的表现,都会妨害城市发展。
其三,意义弹性。
所谓城市的意义弹性,是指城市能够同时满足多样人群的不同层面的意义需要,并能够使不同的意义与价值在总体上达到平衡与和谐,不断形成具体的意义共同性。
当一个城市体只允许一种、一个层面的意义存在时,这个城市体可能繁荣一时,但必然会走向衰落。
河南省三门峡市2019-2020学年高一上学期期末数学试卷 (有解析)

河南省三门峡市2019-2020学年高一上学期期末数学试卷一、选择题(本大题共12小题,共60.0分)1. 设集合A ={x|−1≤x ≤2},B ={x|0≤x ≤4},则A ∪B =( )A. {x|0≤x ≤2}B. {x|1≤x ≤2}C. {x|0≤x ≤4}D. {x|−1≤x ≤4}2. 过L 1:3x −5y −10=0和L 2:x +y +1=0的交点,且平行于L 3:x +2y −5=0的直线方程为 ( )A. 8x −16y +21=0B. 8x +16y −21=0C. 8x +16y +21=0D. 8x −16y −21=03. 函数y =lg(1−x)+√−x 2+x +2的定义域是( )A. [2,1]B. (1,2]C. [−1,2]D. [−1,1)4. 如图,在长方体ABCD −A 1B 1C 1D 1中,AB =AD =6,AA 1=4,则三棱锥D 1−AB 1D 的体积为( )A. 8B. 12C. 24D. 725. 三个数a =0.52,b =log 20.5,c =20.5的大小关系是( )A. a <c <bB. b <c <aC. a <b <cD. b <a <c6. 若f(x)=e x −ae −x 为奇函数,则满足f(x −1)>1e 2−e 2的x 的取值范围是( )A. (−2,+∞)B. (−1,+∞)C. (2,+∞)D. (3,+∞)7. 已知PA ⊥矩形ABCD 所在的平面,则侧面和底面所在平面中互相垂直的平面有( )A. 1对B. 2对C. 3对D. 5对8. 若函数f(x)={a(x −1)+1,x <−1a −x,x ≥−1(a >0,且a ≠1)是R 上的单调函数,则实数a 的取值范围是( )A. (0,13)B. (13,1)C. (0,13]D. [13,1)9. 如图所示,已知四棱锥P −ABCD 的高为3,底面ABCD 为正方形,PA =PB =PC =PD 且AB =√6,则四棱锥P −ABCD 外接球的半径为( )A. 32B. 2C. √3D. 310. 如图,在多面体ABCDEF 中,已知面ABCD 是边长为3的正方形,EF//AB ,EF =32,EF 与面ABCD 的距离为2,则该多面体的体积为 ( )A. 92B. 5C. 6D. 15211. 已知函数f (x )对于任意实数x 满足条件f(x +2)=−1f(x),若f(0)=12,则f(2018)=( )A. −12B. 12C. −2D. 212. 已知圆M :x 2+(y −2)2=1,Q 是x 轴上的动点,QA ,QB 分别切圆M 于A ,B 两点,则直线AB 恒过定点( )A. (0,32)B. (0,1)C. (2,0)D. (0,2)二、填空题(本大题共4小题,共20.0分)13. 直线l:(2m +1)x +(m +1)y −3m −1=0(m ∈R )经过的定点为________________. 14. 判断下列命题是否正确.(正确的打“√”,错误的打“×”)(1)空间不同三点确定一个平面( )(2)空间两两相交的三条直线确定一个平面( )(3)和同一直线都相交的三条平行线在同一平面内()15.圆x2+y2=r2(r>0)与圆(x−3)2+(y−4)2=1相外切,则半径r的值为______.(x≥2)的值域为______ .16.函数y=3x+2x+1三、解答题(本大题共6小题,共70.0分).且f(1)=5.17.已知函数f(x)=x+ax(1)求a的值;(2)判断函数f(x)的奇偶性;(3)判断函数f(x)在(2,+∞)上的单调性并用定义证明你的结论.18.在平面直角坐标系中,已知直线m:ax−3y+2=0.(1)若直线m在x轴上的截距为−2,求实数a的值,并写出直线m的截距式方程;(2)若过点M(3,1)且平行于直线m的直线n的方程为:4x−6y+b=0,求实数a,b的值,并求出两条平行直线m,n之间的距离.19.设函数f(x)=3x,且f(a+2)=18,函数g(x)=3ax−4x(x∈R).(1)求g(x)的解析式.(2)若方程g(x)−b=0在x∈[−2,2]上有两个不同的解,求实数b的取值范围.20.如图,在四棱锥P−ABCD中,AB//CD,CD=2AB,E为PC的中点,且∠PAB=∠PDC=90°.(Ⅰ)证明:BE//平面PAD;(Ⅱ)证明:平面PAB⊥平面PAD.21.已知A为圆T:(x−4)2+y2=16上的动点,B的坐标为(−4,0),P在线段AB的中点.(Ⅰ)求P的轨迹C的方程.(Ⅱ)过点(−1,3)的直线l与C交于M,N两点,且,求直线l的方程.22.已知函数f(x)=log a(2+x),g(x)=log a(2−x),a>0且a≠1,设函数ℎ(x)=f(x)+g(x).(1)当a=2时,求ℎ(x)的定义域和值域;(2)当f(x)>g(x)时,求x的取值范围.-------- 答案与解析 --------1.答案:D解析:本题主要考查集合的基本运算,属于基础题. 根据并集定义进行求解即可.解:∵A ={x|−1≤x ≤2},B ={x|0≤x ≤4}, ∴A ∪B ={x|−1≤x ≤4}, 故选:D .2.答案:C解析:本题考查了直线方程的应用问题,是基础题.求出两直线L 1、L 2的交点坐标,再设与x +2y −5=0平行的直线方程为x +2y +m =0,代入交点坐标求出m 的值,即可写出方程.解:两直线L 1:3x −5y −10=0,L 2:x +y +1=0的交点为{3x −5y −10=0x +y +1=0, 解得{x =58y =−138,即(58,−138); 设与x +2y −5=0平行的直线方程为x +2y +m =0, 则58+(−138)×2+m =0, 解得m =218,所求的直线方程为8x +16y +21=0. 故选C .3.答案:D解析:本题考查函数定义域的概念及求法,对数函数的定义域,一元二次不等式的解法. 要使得原函数有意义,则需满足{ 1−x >0 −x 2+x +2≥0,解出x 的范围即可.解:要使原函数有意义,则:{ 1−x >0 −x 2+x +2≥0;解得−1≤x <1,∴原函数的定义域是:[−1,1). 故选D .4.答案:C解析:【分析】本题考查三棱锥的体积,属于基础题.利用等体积转换得V D 1−AB 1D =V B 1−AD 1D =13S △AD 1D ⋅A 1B 1可得解.【解答】解:由题意,得V D 1−AB 1D =V B 1−AD 1D =13S △AD 1D ⋅A 1B 1=13×12×6×4×6=24. 故选C .5.答案:D解析:本题考查对数值大小的比较,掌握对数函数与指数函数的性质是关键,利用对数函数与指数函数的性质,将a ,b ,c 与0和1比较即可. 解:∵0<a =0.52<1, b =log 20.5<log 21=0, c =20.5>20=1,∴b <a <c故选D .6.答案:B解析:解:根据题意,若f(x)=e x −ae −x 为奇函数,f (0)=0得a =1, 则f(x)=e x −e −x ,又由f′(x)=e x +e −x ,则函数f(x)为R 上为增函数, 则f(x −1)>1e −e 2⇒f(x −1)>f(−2)⇒x −1>−2,解可得x>−1,即x的取值范围为(−1,+∞);故选:B.根据题意,由奇函数的性质可得f(0)=0,计算可得a=1,即可得函数的解析式,求出函数的导数,−e2⇒f(x−1)>f(−2)⇒x−1>−2,分析可得函数f(x)为R上为增函数,进而可得f(x−1)>1e2解可得x的值,即可得答案.本题考查函数的奇偶性与单调性的综合应用,关键是求出a的值,确定函数的解析式.7.答案:D解析:【分析】本题考查线面垂直的判定,面面垂直的性质,属于基础题.由线面垂直的判定定理及面面垂直的性质,可得在侧面与底面所在平面中互相垂直的平面共有5对.【解答】解:由题意,因为PA⊥平面ABCD,且PA⊂平面PAB,PA⊂平面PAD,所以平面PAB⊥平面ABCD,平面PAD⊥平面ABCD.因为底面ABCD为矩形,所以AB⊥AD,又PA⊥AB,PA∩AD=A,所以AB⊥平面PAD,所以平面PAD⊥平面PAB.因为底面ABCD为矩形,所以AB⊥BC,又PA⊥BC,PA∩AB=A,所以BC⊥平面PAB,所以平面PAB⊥平面PBC.同理,平面PAD⊥平面PCD.所以在侧面与底面所在平面中互相垂直的平面共有5对,故选D.8.答案:D解析:解:∵a>0,∴当x<−1时,函数f(x)为增函数,∵函数在R上的单调函数,∴函数为单调递增函数,则当x≥−1时,f(x)=(1a)x,为增函数,则1a>1,即0<a<1,同时a≥−2a+1,即3a≥1,即a≥13,综上13≤a<1,故选:D.根据分段函数单调性的关系进行求解即可.本题主要考查函数单调性的应用,根据分段函数单调性的性质是解决本题的关键.9.答案:B解析:本题考查正四棱锥、考查球的半径,比较基础.四棱锥为正四棱锥,根据该四棱锥的高为3 ,底面是边长为√6的正方形,即可求得球的半径.解:由题意,四棱锥为正四棱锥高为3 ,底面是边长为√6的正方形,设球的半径为R,则有R2=(√22×√6)2+(3−R)2,解得R=2,故选B.10.答案:D解析:解:法一:如下图所示,连接BE、CE则四棱锥E−ABCD的体积V E−ABCD=13×3×3×2=6,又∵整个几何体大于四棱锥E−ABCD的体积,∴所求几何体的体积V求>V E−ABCD,故选D.法二:分别取AB、CD的中点G、H连EG,GH,EH,把该多面体分割成一个四棱锥与一个三棱柱,可求得四棱锥的体积为3,三棱柱的体积92,整个多面体的体积为152. 故选D .由已知中多面体ABCDEF 中,已知面ABCD 是边长为3的正方形,EF 与面AC 的距离为2,我们易求出四棱锥E −ABCD 的体积,然后根据整个几何体大于部分几何体的体积,分析已知中的四个答案,利用排除法,得到答案.本题考查的知识点是棱柱、棱锥、棱台的体积,其中根据根据整个几何体大于部分几何体的体积,求出四棱锥E −ABCD 的体积,并与已知中的四个答案进行比较,利用排除法是解答此类问题的捷径.11.答案:C解析:本题考查的知识点是函数的周期性,函数的值.根据已知中函数f(x)对于任意实数x 满足条件f(x +2)=−1f(x),判断出函数f(x)是以4为周期的周期函数,是解答本题的关键.解:f(x +2)=−1f(x),f (x +4)=f (x +2+2)=−1f x+2=f (x )即函数的周期是4, 所以f(2018)=f (504×4+2)=f (2) 又因为f(0)=12, 所以f (2)=−1f (0)=−2, 故选C .12.答案:A解析:解:设点Q(t,0),由几何性质可以知道,A ,B 在以QM 为直径的圆上, 又M(0,2),∴QM 的中点为(t2,1),而|QM|=√t 2+4, ∴此圆的方程为x 2+y 2−tx −2y =0,AB 为两圆的公共弦,两圆方程相减得tx −2y +3=0, ∴直线AB :y =t2x +32恒过定点(0,32). 故选:A .设点Q(t,0),求出以QM 为直径的圆的方程,与圆M 的方程联立求得AB 所在直线方程,则答案可求.本题考查直线与圆的位置关系,考查圆系方程的应用,是基础题.13.答案:(2,−1)解析:本题主要考查直线经过定点问题,属于基础题.先分离参数m ,再令m 的系数等于零,求得x 、y 当的值,可得定点的坐标.解:直线l :(2m +1)x +(m +1)y −3m −1=0(m ∈R),即直线l :m(2x +y −3)+(x +y −1)=0,令2x +y −3=0,得x +y −1=0,由{2x +y −3=0x +y −1=0,解得x =2,且y =−1, 可得直线l 经过定点(2,−1),故答案为(2,−1).14.答案:(1)×(2)×(3)√解析:(1)本题考查的是公理3,是容易题.解:由公理3得过不共线的三点有且只有一个平面,故本题的说法是错误的.故答案为×.(2)本题考查的是公理3及其推论,是基础题.解:比如墙角处的三条交线,就不能确定一个平面,只有空间两两相交且不共点的三条直线确定一个平面,故本题的说法是错误的.故答案为×.(3)本题考查的是公理3及其推论,是基础题.解:设直线l 和三条平行线a ,b ,c ,由公理3的推论3得,a ,b 确定平面α,b ,c 确定平面β,再由公理1得直线l 均在α,β内,即过b ,l 的两条相交直线有两个平面,这与公理3的推论2矛盾,故α,β重合,即本题的说法是正确的.故答案为√.15.答案:4解析:本题考查圆与圆的位置关系,两圆外切,两圆圆心距等于两圆半径之和是解题的关键,本题属于基础题.用两圆外切,两圆圆心距等于两圆半径之和来求出r 的值.解:圆x 2+y 2=r 2(r >0)的圆心坐标(0,0),半径为r ;圆(x −3)2+(y −4)2=1的圆心坐标(3,4),半径为1,∵两圆外切,∴两圆圆心距等于两圆半径之和,∴√32+42=5=1+r ,∴r =4,故答案为:4.16.答案:[83,3)解析:分离常数得到y =3−1x+1,根据x 的范围可以求出1x+1的范围,从而得出y 的范围,即得出该函数的值域.考查值域的概念,分离常数法的运用,根据不等式的性质求函数值域的方法.解:y =3(x+1)−1x+1=3−1x+1; x ≥2;∴0<1x+1≤13;∴83≤y <3;∴该函数的值域为[83,3).故答案为:[83,3). 17.答案:解:(1)由f(1)=5,得:5=1+a ,∴a=4;(2)f(x)=x+4x,∵x∈(−∞,0)∪(0,+∞)且f(−x)=−(x+4x)=−f(x),∴f(x)为奇函数;(3)任取:2<x1<x2,∵f(x1)−f(x2)=x1+4x1−x2−4x2=(x1−x2)+4(x2−x1)x1x2=(x1−x2)(1−4x1x2),∵2<x1<x2,∴x1−x2<0,x1x2>4,4x1x2<1∴f(x1)−f(x2)<0,∴f(x)在(2,+∞)上为增函数.解析:本题主要考查函数奇偶性和单调性的判断和应用,结合函数奇偶性和单调性的定义是解决本题的关键.(1)根据条件解方程即可.(2)根据函数奇偶性的定义进行判断即可.(3)根据函数单调性的定义进行证明即可.18.答案:解:(1)因为直线m在x轴上的截距为−2,所以直线经过点(−2,0),代入直线方程得−2a+ 2=0,所以a=1.所以直线m的方程为x−3y+2=0,当x=0时,y=23,所以直线m的截距式方程为:x−2+y23=1(负号写在前面或是3变为分子y的系数都不给分)(2)把点M(3,1)代入直线n的方程为:4x−6y+b=0,求得b=−6,由两直线平行得:a4=−3−6≠2−6,所以a=2,因为两条平行直线m,n之间的距离就是点M(3,1)到直线m的距离,所以d=√22+(−3)2=5√1313.解析:本题考查了直线关于点对称的直线方程的求法,考查了斜率公式的运用,是基础题.(1)因为直线m在x轴上的截距为−2,所以直线经过点(−2,0),代入直线方程得−2a+2=0,解得a.可得直线m的方程,化为直线m的截距式方程.(2)把点M(3,1)代入直线n的方程为:4x−6y+b=0,求得b.根据两直线平行得:a4=−3−6≠2−6,解得a.利用两条平行直线m ,n 之间的距离就是点M(3,1)到直线m 的距离即可得出.19.答案:解:(1)∵f (x )=3x ,且f (a +2)=18,∴3a+2=18⇒3a =2.∵g (x )=3ax −4x ,∴g (x )=2x −4x .(2)方法一 方程为2x −4x −b =0,令t =2x ,x ∈[−2,2], 则14≤t ≤4,且方程t −t 2−b =0在[14,4]上有两个不同的解.设y =t −t 2=−(t −12)2+14,y =b , 则两函数图象在[14,4]内有两个交点.画出y =t −t 2,t ∈[14,4]的大致图象,如图所示.由图知b ∈[316,14)时,方程有两个不同的解.方法二 方程为2x −4x −b =0,令t =2x ,x ∈[−2,2],则14≤t ≤4,∴方程t −t 2−b =0在[14,4]上有两个不同的解.设f (t )=−t 2+t −b,t ∈[14,4],∴{Δ=1−4b>0⇒b<14, f(14)≤0⇒b≥316,f(4)≤0⇒b≥−12,解得b∈[316,14).解析:本题考查函数的解析式的求法,函数的零点的求法,考查数形结合,考查计算能力.(1)利用已知条件求出3a=2,代入g(x)=3ax−4x即可求解函数的解析式.(2)方法一:化简方程,构造函数,利用数形结合求解实数b的取值范围;方法二:方程为2x−4x−b=0,令t=2x,x∈[−2,2],则14≤t≤4,设f(t)=−t2+t−b,t∈[14,4],结合题意,根据二次函数的性质列不等式即可求解.20.答案:证明:(Ⅰ)取PD的中点F,连接EF,AF,因为E为PC的中点,所以EF=12CD,EF//CD,因为AB//CD,AB=12CD,所以AB//EF,AB=EF,所以四边形ABEF为平行四边形,所以BE//AF,因为BE⊄平面PAD,AF⊂平面PAD,所以BE//平面PAD;(Ⅱ)由已知∠PAB=∠PDC=90°,得AB⊥AP,CD⊥PD,由于AB//CD,故AB⊥PD,又因为AP ⊂平面PAD,PD ⊂平面PAD,AP ∩PD =P从而AB ⊥平面PAD ,又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .解析:本题考查了线面平行的判定,面面垂直的判定,属于中档题.(Ⅰ)先取PD 的中点F ,连接EF ,AF ,可证四边形ABEF 为平行四边形,得到BE//AF ,即可证明BE//平面PAD ;(Ⅱ)先由已知∠PAB =∠PDC =90°,得AB ⊥AP ,CD ⊥PD ,再由AB//CD ,得到AB ⊥PD ,可证AB ⊥平面PAD ,即可证明平面PAB ⊥平面PAD .21.答案:解:(Ⅰ)设点P 的坐标为(x,y),点A 的坐标为(x 0,y 0),依题意得x =x 0−42,y =y 02,解得x 0=2x +4,y 0=2y ,又(x 0−4)2+y 02=16,所以4x 2+4y 2=16,即x 2+y 2=4,所以点P 的轨迹C 的方程为x 2+y 2=4;(Ⅱ)因为直线l 与曲线C 交于M ,N 两点,且|MN|=2√3,所以原点O 到直线l 的距离d =√4−3=1.若l 斜率不存在,直线l 的方程为x =−1,此时符合题意;若l 斜率存在,设直线l 的方程为y −3=k(x +1),即kx −y +k +3=0,则原点O 到直线l 的距离d =√1+k 2=1,解得k =−43, 此时直线l 的方程为4x +3y −5=0,所以直线l 的方程为4x +3y −5=0或x =−1.解析:本题考查了点的轨迹方程以及直线和圆的位置关系,属于中档题.(Ⅰ)设点P 的坐标为(x,y),点A 的坐标为(x 0,y 0),根据中点坐标公式即可求出;(Ⅱ)若l 斜率不存在,直线l 的方程为x =−1,此时符合题意;若l 斜率存在,设直线l 的方程为y −3=k(x +1),即,根据点到直线的距离公式即可求出.22.答案:解:(1)由{2+x >02−x >0,得:−2<x <2, ∴ℎ(x)的定义域为{x|−2<x <2},∴ℎ(x)=log 2(4−x 2),令u =4−x 2,则0<u ≤4,∴log 2u ≤2,即log 2(4−x 2)≤2,∴ℎ(x)的值域为(−∞,2].(2)∵f(x)>g(x),∴log a (2+x)>log a (2−x),当a >1时,{2+x >2−x 2−x >0∴0<x <2; 当0<a <1时,{2+x <2−x 2+x >0∴−2<x <0, 综上所述,当a >1时,x 的取值范围为{x|0<x <2};当0<a <1时,x 的取值范围为{x|−2<x <0}.解析:本题考查了对数函数的性质,考查求函数的定义域、值域问题,考查分类讨论思想,是一道中档题.(1)根据对数函数的性质求出ℎ(x)的定义域,通过换元,求出函数的值域即可;(2)问题转化为log a (2+x)>log a (2−x),通过讨论a 的范围,得到关于x 的不等式组,解出即可.。
【解析版】三门峡市2019-2020学年度八年级上期末数学试卷

【解析版】三门峡市2019-2020学年度八年级上期末数学试卷~学年度八年级上学期期末数学试卷一、填空题(每小题2分,共20分)1.已知空气的单位体积质量为0.00124g/cm3,将它用科学记数表示为g/cm3.2.计算:(﹣)×[()1007]2=.3.分解因式:﹣x2+4xy﹣4y2=.4.若等腰三角形两边长分别为8,10,则这个三角形的周长为.5.三角形三内角的度数之比为1:2:3,最大边的长是8cm,则最小边的长是cm.6.一个多边形内角和是一个四边形内角和的4倍,则这个多边形的边数是.7.如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线MN交AC于D,CD=1cm,连接BD,则AC的长为cm.8.若a+b=7,ab=12,则a2+b2的值为.9.如图,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,那么∠C=度.10.已知:a+=5,则=.二、选择题:(每小题2分,共20分)11.下列计算正确的是()A. x2+x3=x5 B. x2•x3=x6 C.(x2)3=x5 D. x5÷x3=x212.下面有4个汽车标志图案,其中是轴对称图形的是()A.②③④ B.①③④ C.①②④ D.①②③13.已知点P(1,a)与Q(b,2)关于x轴成轴对称,则a﹣b的值为()A.﹣1 B. 1 C.﹣3 D. 314.如图,△ABC≌△A DE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为()A. 40° B. 35° C. 30° D. 25°15.下列各式变形中,是因式分解的是()A. a2﹣2ab+b2﹣1=(a﹣b)2﹣1 B. 2x2+2x=2x2(1+)C.(x+2)(x﹣2)=x2﹣4 D. x4﹣1=(x2+1)(x+1)(x﹣1)16.若分式的值为零,则x等于()A.﹣1 B. 1 C.﹣1或1 D. 1或217.等腰三角形的一个角是48°,它的一个底角的度数是()A. 48° B. 48°或42° C. 42°或66° D. 48°或66°18.下列命题中,正确的是()A.三角形的一个外角大于任何一个内角B.三角形的一条中线将三角形分成两个面积相等的三角形C.两边和其中一边的对角分别相等的两个三角形全等D.三角形的三条高都在三角形内部19.不能用尺规作出唯一三角形的是()A.已知两角和夹边 B.已知两边和夹角C.已知两角和其中一角的对边 D.已知两边和其中一边的对角20.如图,△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=5cm,BC=3cm,则△PBC的周长等于()A. 4cm B. 6cm C. 8cm D. 10cm三.解答题(本题7小题,共60分)21.计算:(1)(﹣2xy2)2÷(xy)+b﹣4a2b÷b.22.因式分解:(1)2﹣(x+2y)2(a﹣b)2+4ab.23.先化简代数式,再从﹣2,2,0三个数中选一个恰当的数作为a的值代入求值.24.解方程:25.如图,在平面直角坐标系XOY中,A(﹣1,5),B(﹣1,0),C(﹣4,3).(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);直接写出A′,B′,C′三点的坐标:A′(),B′(),C′()(3)计算△ABC的面积.26.如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CD于点E,交CB于点F(1)求证:CE=CF.将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图所示.试猜想:BE′与CF有怎样的数量关系?请证明你的结论.27.某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的倍,购进数量比第一次少了30支.(1)求第一次每支铅笔的进价是多少元?若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?~学年度八年级上学期期末数学试卷参考答案与试题解析一、填空题(每小题2分,共20分)1.已知空气的单位体积质量为0.00124g/cm3,将它用科学记数表示为 1.24×10﹣3g/cm3.考点:科学记数法—表示较小的数.分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.解答:解:0.00124=1.24×10﹣3.故答案为:1.24×10﹣3.点评:本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.2.计算:(﹣)×[()1007]2=﹣.考点:幂的乘方与积的乘方.分析:先根据幂的乘方进行计算,再根据积的乘方进行计算,最后求出即可.解答:解:(﹣)×[()1007]2=(﹣)×()=[(﹣)×]×(﹣)=1×(﹣)=﹣,故答案为:﹣.点评:本题考查了幂的乘方和积的乘方的应用,能灵活运用运算法则进行计算是解此题的关键,注意:a m•b m=(ab)m.3.分解因式:﹣x2+4xy﹣4y2=﹣(x﹣2y)2.考点:提公因式法与公式法的综合运用.分析:先提取公因式﹣1,再根据完全平方公式进行二次分解.完全平方公式:a2﹣2ab+b2=(a﹣b)2.解答:解:﹣x2+4xy﹣4y2,=﹣(x2﹣4xy+4y2),=﹣(x﹣2y)2.故答案为:﹣(x﹣2y)2.点评:本题考查了提公因式法,公式法分解因式,提取公因式后利用完全平方公式进行二次分解,注意分解要彻底.4.若等腰三角形两边长分别为8,10,则这个三角形的周长为26或28.考点:等腰三角形的性质;三角形三边关系.分析:分腰长为8和10两种情况,可求得三角形的三边,再利用三角形的三边关系进行验证,可求得其周长.解答:解:当腰长为8时,则三角形的三边长分别为8、8、10,满足三角形的三边关系,此时周长为26;当腰长为10时,则三角形的三边长分别为10、10、8,满足三角形的三边关系,此时周长为28;综上可知三角形的周长为26或28,故答案为:26或28.点评:本题主要考查等腰三角形的性质,掌握等腰三角形的两腰相等是解题的关键,注意利用三角形的三边关系进行验证.5.三角形三内角的度数之比为1:2:3,最大边的长是8cm,则最小边的长是4cm.考点:含30度角的直角三角形.分析:先求出三角,再解直角三角形求边.解答:解:三角形三内角的度数之比为1:2:3,则最小的角是30度,最大角是直角,因而最小边是30°的锐角所对的边,等于斜线的一半是4cm.故填4cm.点评:本题主要考查了直角三角形中.30度的锐角所对的直角边等于斜边的一半.6.一个多边形内角和是一个四边形内角和的4倍,则这个多边形的边数是10.考点:多边形内角与外角.分析:多边形的外角和是360度,多边形的外角和是内角和的4倍,则多边形的内角和是360×4=1440度,再由多边形的内角和列方程解答即可.解答:解:设这个多边形的边数是n,由题意得,(n﹣2)×180°=360°×4解得n=10.故答案为:10.点评:本题主要考查了多边形的内角和定理与外角和定理,熟练掌握定理是解题的关键.7.如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线MN交AC于D,CD=1cm,连接BD,则AC的长为3cm.考点:线段垂直平分线的性质.分析:根据线段垂直平分线的性质可得AD=BD,可得到∠CBD=30°,在Rt△CBD中可求得BD=2CD,可求得AD,可得到AC.解答:解:∵MN是AB的垂直平分线,∴AD=BD,∴∠DBA=∠A=30°,∴∠CDB=60°,又∠C=90°,∴∠CBD=30°,∴AD=BD=2CD=2cm,∴AC=AD+CD=2cm+1c m=3cm,故答案为:3.点评:本题主要考查线段垂直平分线的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.8.若a+b=7,ab=12,则a2+b2的值为25.考点:完全平方公式.分析:根据完全平方公式得出a2+b2=(a+b)2﹣2ab,代入求出即可.解答:解:∵a+b=7,ab=12,∴a2+b2=(a+b)2﹣2ab=72﹣2×12=25.故答案为:25.点评:本题考查了对完全平方公式的应用,注意:完全平方公式有:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2.9.如图,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,那么∠C=20度.考点:等腰三角形的性质.专题:计算题.分析:由AB+BD=DC,易想到可作辅助线DE=D B,然后连接AE,从而可出现两个等腰三角形,一个是△ABE,一个是△ACE,利用三角形外角的性质,易求∠B=2∠C,再利用三角形内角和定理可求∠C.解答:解:在DC上截取DE=DB,连接AE,设∠C=x,∵AB+BD=DC,DE=DB,∴CE=AB,又∵AD⊥BC,DB=DE,∴直线AD是BE的垂直平分线,∴AB=AE,∴CE=AE,∴∠B=∠AEB,∠C=∠CAE,又∵∠AEB=∠C+∠CAE,∴∠AEB=2x,∴∠B+∠C=3x=180°﹣120°=60°,∴∠C=20°.故答案是:20°.点评:本题考查了线段垂直平分线的判定和性质、等腰三角形的性质、三角形内角和定理、三角形外角性质.10.已知:a+=5,则=24.考点:分式的乘除法.专题:计算题.分析:本题可以从题设入手,然后将化简成含有a+的分式,再代入计算即可.解答:解:=;∵a+=5,∴==52﹣1=24.故答案为24.点评:本题化简过程比较灵活,运用了提取公因式、配方法.二、选择题:(每小题2分,共20分)11.下列计算正确的是()A. x2+x3=x5 B. x2•x3=x6 C.(x2)3=x5 D. x5÷x3=x2考点:同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.分析:根据合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变;同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加;幂的乘方法则:底数不变,指数相乘;同底数幂的除法法则:底数不变,指数相减,分别进行计算,即可选出答案.解答:解:A、x2与x3不是同类项,不能合并,故此选项错误;B、x2•x3=x2+3=x5,故此选项错误;C、(x2)3=x6,故此选项错误;D、x5÷x3=x2,故此选项正确;故选:D.点评:此题主要考查了同底数幂的除法,合并同类项,同底数幂的乘法,幂的乘方,很容易混淆,一定要记准法则才能做题.12.下面有4个汽车标志图案,其中是轴对称图形的是()A.②③④ B.①③④ C.①②④ D.①②③考点:轴对称图形.分析:利用轴对称图形性质,关于某条直线对称的图形叫轴对称图形得出即可.解答:解:只有第4个不是轴对称图形,其它3个都是轴对称图形.故选:D.点评:此题主要考查了轴对称图形的性质,轴对称的关键是寻找对称轴,两边图象折叠后可重合.13.已知点P(1,a)与Q(b,2)关于x轴成轴对称,则a﹣b的值为()A.﹣1 B. 1 C.﹣3 D. 3考点:关于x轴、y轴对称的点的坐标.分析:关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得a、b的值.解答:解:∵点P(1,a)与Q(b,2)关于x轴成轴对称,∴b=1,a=﹣2,∴a﹣b=﹣3,故选:C.点评:此题主要考查了关于x轴对称点的坐标,关键是掌握点的坐标的变化规律.14.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为()A. 40° B. 35° C. 30° D. 25°考点:全等三角形的性质.分析:根据三角形的内角和定理列式求出∠BAC,再根据全等三角形对应角相等可得∠DAE=∠BAC,然后根据∠EAC=∠DAE﹣∠DAC代入数据进行计算即可得解.解答:解:∵∠B=80°,∠C=30°,∴∠BAC=180°﹣80°﹣30°=70°,∵△ABC≌△ADE,∴∠DAE=∠BAC=70°,∴∠EAC=∠DAE﹣∠DAC,=70°﹣35°,=35°.故选B.点评:本题考查了全等三角形对应角相等的性质,熟记性质并准确识图是解题的关键.15.下列各式变形中,是因式分解的是()A. a2﹣2ab+b2﹣1=(a﹣b)2﹣1 B. 2x2+2x=2x2(1+)C.(x+2)(x﹣2)=x2﹣4 D. x4﹣1=(x2+1)(x+1)(x﹣1)考点:因式分解的意义.分析:根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.解答:解:A a2﹣2ab+b2﹣1=(a﹣b)2﹣1中不是把多项式转化成几个整式积的形式,故A错误;B 2x2+2x=2x2(1+)中不是整式,故B错误;C (x+2)(x﹣2)=x2﹣4是整式乘法,故C错误;D x4﹣1=(x2+1)(x2﹣1)=(x2+1)(x+1)(x﹣1),故D正确.故选:D.点评:本题考查了因式分解的意义,因式分解是把一个多项式转化成几个整式积的形式,注意B不是整式的积,A、C不是积的形式.16.若分式的值为零,则x等于()A.﹣1 B. 1 C.﹣1或1 D. 1或2考点:分式的值为零的条件.专题:计算题.分析:分式的值为0的条件是:(1)分子=0;分母≠0.两个条件需同时具备,缺一不可.据此可以解答本题.解答:解:依题意得|x|﹣1=0,且x2﹣3x+2≠0,解得x=1或﹣1,x≠1和2,∴x=﹣1.故选A.点评:此题考查的是对分式的值为0的条件的理解和因式分解的方法的运用,该类型的题易忽略分母不为0这个条件.17.等腰三角形的一个角是48°,它的一个底角的度数是()A. 48° B. 48°或42° C. 42°或66° D. 48°或66°考点:等腰三角形的性质.专题:分类讨论.分析:分底角为48°和顶角48°,根据等腰三角形的性质和三角形内角和定理求解即可.解答:解:当底角为48°时,则底角为48°;当顶角为48°时,则底角==66°;综上可知三角形的一个底角为48°或66°,故选D.点评:本题主要考查等腰三角形的性质,掌握等腰三角形的两底角相等是解题的关键.18.下列命题中,正确的是()A.三角形的一个外角大于任何一个内角B.三角形的一条中线将三角形分成两个面积相等的三角形C.两边和其中一边的对角分别相等的两个三角形全等D.三角形的三条高都在三角形内部考点:命题与定理.分析:根据三角形外角性质对A进行判断;根据三角形中线性质和三角形面积公式对B进行判断;根据三角形全等的判定对C进行判断;根据三角形高线定义对D进行判断.解答:解:A、三角形的一个外角大于任何一个不相邻的一个内角,所以A选项错误;B、三角形的一条中线将三角形分成两个面积相等的三角形,所以B选项正确;C、两边和它们的夹角分别对应相等的两个三角形全等,所以C选项错误;D、钝角三角形的高有两条在三角形外部,所以D选项错误.故选B.点评:本题考查了命题:判断事物的语句叫命题;正确的命题称为真命题;错误的命题称为假命题.19.不能用尺规作出唯一三角形的是()A.已知两角和夹边 B.已知两边和夹角C.已知两角和其中一角的对边 D.已知两边和其中一边的对角考点:全等三角形的判定.分析:把尺规作图的唯一性转化成全等三角形的判定,根据全等三角形的判定方法逐项判定即可.解答:解:A、已知两角和夹边,满足ASA,可知该三角形是唯一的;B、已知两边和夹角,满足SAS,可知该三角形是唯一的;C、已知两角和其中一角的对边,满足AAS,可知该三角形是唯一的;D、已知两边和其中一边的对角,满足SSA,不能确定三角形是唯一的.故选D.点评:本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL,注意AAA和SSA不能证明三角形全等.20.如图,△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=5cm,BC=3cm,则△PBC的周长等于()A. 4cm B. 6cm C. 8cm D. 10cm考点:线段垂直平分线的性质;等腰三角形的性质.分析:先根据等腰三角形的性质得出AC=AB=5cm,再根据线段垂直平分线的性质得出AP=BP,故AP+PC=AC,由此即可得出结论.解答:解:∵△ABC中,AB=AC,AB=5cm,∴AC=5cm,∵AB的垂直平分线交AC于P点,∴BP+PC=AC,∴△PBC的周长=(BP+PC)+BC=AC+BC=5+3=8cm.故选C.点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.三.解答题(本题7小题,共60分)21.计算:(1)(﹣2xy2)2÷(xy)+b﹣4a2b÷b.考点:整式的混合运算.分析:(1)先算乘方,再算除法;先利用平方差公式和整式的乘除计算,再进一步合并同类项即可.解答:解:(1)原式=(4x2y4)÷(xy)=12xy3;原式=4a2﹣b2+2ab+b2﹣4a2=2ab.点评:此题考查整式的混合运算,掌握计算公式和计算方法是解决问题的关键.22.因式分解:(1)2﹣(x+2y)2(a﹣b)2+4ab.考点:因式分解-运用公式法.分析:(1)用平方差公式进行因式分解即可;先利用完全平方公式展开(a﹣b)2+4ab,再利用完全平方公式因式分解即可.解答:解:(1)2﹣(x+2y)2=[+(x+2y)][﹣(x+2y)]=(3x+3y)(x﹣y)=3(x+y)(x﹣y);(a﹣b)2+4ab=a2﹣2ab+b2+4ab=a2+2ab+b2=(a+b)2.点评:本题考查了因式分解,公式法分解因式,熟练掌握完全平方公式和平方差公式的结构特点是解题的关键.23.先化简代数式,再从﹣2,2,0三个数中选一个恰当的数作为a的值代入求值.考点:分式的化简求值.专题:计算题.分析:原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分得到最简结果,将a=0代入计算即可求出值.解答:解:原式=÷=•=,当a=0时,原式==2.点评:此题考查了分式的化简求值,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式.24.解方程:考点:解分式方程.专题:计算题.分析:观察可得方程最简公分母为(x﹣2)(x+1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.解答:解:去分母,得:(x+1)2+x﹣2=(x﹣2)(x+1)整理得:4x=﹣1,x=﹣.经检验x=﹣是原方程的解.所以原方程的解为x=﹣.点评:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.25.如图,在平面直角坐标系XOY中,A(﹣1,5),B(﹣1,0),C(﹣4,3).(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);直接写出A′,B′,C′三点的坐标:A′(),B′(),C′()(3)计算△ABC的面积.考点:作图-轴对称变换.分析:(1)分别找到y轴右侧与y轴左侧的点在同一水平线上,且到y轴的距离相等的点,顺次连接即可;根据点所在的象限及距离y轴,x轴的距离分别写出各点坐标即可;(3)易得此三角形的底边为5,高为3,利用三角形的面积公式计算即可.解答:解:(1);A′(1,5),B′(1,0),C′(4,3);(3)∵A(﹣1,5),B(﹣1,0),C(﹣4,3),∴AB=5,AB边上的高为3,∴S△ABC=.点评:用到的知识点为:两点关于某条直线对称,那么这两点的连线被对称轴垂直平分;三角形的面积等于底×高÷2.26.如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CD于点E,交CB于点F(1)求证:CE=CF.将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图所示.试猜想:BE′与CF有怎样的数量关系?请证明你的结论.考点:全等三角形的判定与性质;等腰三角形的判定与性质;平移的性质.专题:几何综合题;压轴题.分析:(1)根据平分线的定义可知∠CAF=∠EAD,再根据已知条件以及等量代换即可证明CE=CF,根据题意作辅助线过点E作EG⊥AC于G,根据平移的性质得出D′E′=DE,再根据已知条件判断出△CEG≌△BE′D′,可知CE=BE′,再根据等量代换可知BE′=CF.解答:(1)证明:∵AF平分∠CAB,∴∠CAF=∠EAD,∵∠ACB=90°,∴∠CAF+∠CFA=90°,∵CD⊥AB于D,∴∠EAD+∠AED=90°,∴∠CFA=∠AED,又∠AED=∠CEF,∴∠CFA=∠CEF,∴CE=CF;猜想:BE′=CF.证明:如图,过点E作EG⊥AC于G,连接EE′,又∵AF平分∠CAB,ED⊥AB,EG⊥AC,∴ED=EG,由平移的性质可知:D′E′=DE,∴D′E′=GE,∵∠ACB=90°,∴∠ACD+∠DCB=90°∵CD⊥AB于D,∴∠B+∠DCB=90°,∴∠ACD=∠B,在△CEG与△BE′D′中,,∴△CEG≌△BE′D′(AAS),∴CE=BE′,由(1)可知CE=CF,∴BE′=CF.点评:本题主要考查了平分线的定义,平移的性质以及全等三角形的判定与性质,难度适中.27.某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的倍,购进数量比第一次少了30支.(1)求第一次每支铅笔的进价是多少元?若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?考点:分式方程的应用;一元一次不等式组的应用.专题:计算题.分析:(1)设第一次每支铅笔进价为x元,则第二次每支铅笔进价为x元,根据题意可列出分式方程解答;设售价为y元,求出利润表达式,然后列不等式解答.解答:解:(1)设第一次每支铅笔进价为x元,根据题意列方程得,﹣=30,解得x=4,经检验:x=4是原分式方程的解.答:第一次每支铅笔的进价为4元.设售价为y元,第一次每支铅笔的进价为4元,则第二次每支铅笔的进价为4×=5元根据题意列不等式为:×(y﹣4)+×(y﹣5)≥420,解得y≥6.答:每支售价至少是6元.点评:本题考查了分式方程的应用和一元一次不等式的应用,弄清题意并找出题中的数量关系并列出方程是解题的关键.最后不要忘记检验.。
2019-2020学年河南省三门峡市高三(上)期末数学试卷(文科)

第1页(共20页)2019-2020学年河南省三门峡帀咼三(上)期末数学试卷(文科)一、选择题:本题共 12小题,每小题 5分,共60分•在每小题给出的四个选项中,只有一 项是符合题目要求的•1 . (5 分)若集合 A {0 , 1, 2} , B {x|x2 3x, 0},则 A | B 为()A . {1 , 2}B . {0 , 1 , 2}C . {0 , 1, 2, 3}D . {x|0剟x 3}132. (5分)已知复数z 5 i (i 为虚数单位),则复数一z 在复平面内所对应的点位于(z )A .第一象限B .第二象限C .第三象限D .第四象限3. ( 5分)已知函数 f(x) 2 2,x, 1 Iog 2(x 1),x ,且f 1(a ) 3,则 f (6 a)( )7531A .B .CD .-444 44. ( 5 分)若 sin (― 1 )-小 2 ,则 cos()的值为 ()6 3 37.(5 分)已知函数 f(x) sin( x )(5. 7 - 9(5分)正项等比数列 {%}中,现 2玄3玄716,且a 5与a ?的等差中项为4,则{ a n }2的公比是()C . 3_40J |2),其图象相邻两条对称轴之间距离为将函数y f (x )的向右平移一个单位长度后,得到关于y 轴对称,则( )6A.f (x )的关于点(一,0)对称6B . f (x )的图象关于点(一,0)对称 6C . f (x )在(一,一)单调递增6. ( 5分)若非零向量a , b 满足| a | J 22 2ibi ,且(a b) (3aC . D. ■■ 22b ),则a 与b 的夹角为(2D • f(x)在(—,)单调递增3 6& (5分)底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内 有一内接正四棱锥 S ABCD ,该四棱锥的体积为 4-2,现在半球内任取一点,39.( 5分)在 ABC 中,内角A , B ,C 所对应的边分别为 a ,b ,c,若bsi nA 3acosB 0 , 且b 2 ac ,则亍的值为()A .二210. ( 5分)某三棱锥的三视图如图所示,则该三棱锥的体积为俯视團则该点在正C 」 C . 2侧〔左) 视图2与双曲线右支的一个交点为 P , PR 与双曲线相交于点 Q ,A . 6030C . 20102 x11. (5分)已知F , F 2为双曲线一2a2b 1(a0,b 0)的左、 右焦点,以 F 1F 2为直径的圆且|PQ| 2|QR|,则该双曲线的离心率为( A . 5)B.2C. ,3D V212. ( 5分)已知函数f(x)al nx 2x,若不等式f(x 1)ax 2e x在x(0,)上恒成立,则实数a的取值范围是()A. a, 2B.a…2C. a, 0D. 0剟a 2二、填空题:本题共4小题,每小题5分,共20分.13. (5分)已知f(x)为偶函数,当x0 时,f (x) ln( x)3x ,则曲线y f(x)在点(1,处的切线方程是x 2y 5, 014. (5分)设变量x , y满足约束条件x y 2, 0,则目标函数z 2x 3y 1的最大值为___ .15. ________________________________________________________________ ( 5分)等比数列{a.}前n项的和为2n1,则数列{a:}前n项的和为________________________ .2 2 216. (5分)斜率为1的直线I过抛物线y 2px(p 0)的焦点F ,若I与圆(x 5) y 8相切,则p等于_____ .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤•第17〜21题为必考题,每个试题都必须作答,第22、23题为选考题,考生根据要求作答•17. (12分)设等差数列{a n}的前n项和为S n , n N*,公差d 0 , S3 15,已知印,, a13成等比数列.(I)求数列{a n}的通项公式;(H)设b n a2n,求数列{b n}的前n项和T n .18. (12分)如图,已知四棱锥P ABCD的底面ABCD是菱形,BAD 60 , PA PD ,O为AD边的中点,点M在线段PC 上.(I)证明:平面POB 平面PAD ;(2)若AB 2 3 , PA .7 , PB J3 , PA//平面MOB,求四棱锥M BODC 的体积.第6页(共20页)19. ( 12分)某省在2017年启动了 “ 3 3 ”高考模式.所谓“ 3 3 ”高考模式,就是语文、 数学、外语(简称语、数、外)为高考必考科目,从物理、化学、生物、政治、历史、地理(简称理、化、生、政、史、地)六门学科中任选三门作为选考科目.该省某中学 高一新生共有990人,学籍号的末四位数从 0001到0990 .专业受陨百分比(I )现从高一学生中抽样调查 110名学生的选考情况, 问:采用什么样的抽样方法较为恰 当?(只写出结论,不需要说明理由)(H )据某教育机构统计,学生所选三]学科在将来报考专业时受限制的百分比是不同的.该机构统计了受限百分比较小的十二种选择的百分比值 x (i 1, 2,, 12),制作出如条形图.设以上条形图中受限百分比的均值为x ,标准差为s •如果一个学生所选三门学科专业受限百分比在区间(X s , x s )内,我们称该选择为“恰当选择”.该校李明同学选择了化学, 然后从余下五门选考科目中任选两门•间李明的选择为“恰当选择“的概率是多少?(均值X ,标准差s 均精确到0.1)1 n 1 n 12 (参考公式和数据:一 (x x )2 一 X 2 X 2 , X 2 2644.83)2017 级 30 2S 201510 5 Q化史政生史政理化生理生地化地政理优地理生史理化史理史政理地政理主政理化政23n i 1 n i 1 i 120. (12分)已知点M (- - , 3)在椭圆C:% 芯 1(a b 0)上,且点M到C的左、3 3 a b右焦点的距离之和为22(1 )求C的方程umr ujur (2)设0为坐标原点,若C的弦AB的中点在线段0M (不含端点0 , M)上,求OA?OB的取值范围1 221. (12 分)已知函数f(x) —x2 (a 1)x alnx . 2(1 )当a 1时,讨论函数f(x)的单调性;2x 1(2)若不等式f(x) (a 1)x… x a1 e对于任意x [e , e]成立,求正实数a的取值范围.(二)选做题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分•[选修4-4 :坐标系与参数方程](本小题满分10分)x 3cos22. ( 10分)在直角坐标系xOy中,曲线G的参数方程为(为参数,y sin■ t2 (t为参数). 1t2(i)求曲线G , C2的普通方程;(H)若曲线G上一点P到曲线C2的距离的最大值为2 3,求a .[选修4-5:不等式选讲](本小题满分0分)223. 已知函数f(x) x ax 4 , g(x) | x 21 | x 21.(i)当a 4时,求不等式f(x)…g(x)的解集;(H)若不等式f(x), g(x)的解集包含[2 , 4],求a的取值范围.[0,2 )),曲线C2的参数方程为第8页(共20页)2019-2020学年河南省三门峡市高三(上)期末数学试卷(文科)参考答案与试题解析12小题,每小题 5分,共60分•在每小题给出的四个选项中,只有项是符合题目要求的【解答】解:B {x|0剟収3};A |B {0 , 1, 2}. 故选:B .【解答】解:Qz 5 i ,a 1 时,log 2 (a 1) 3,7, 1 17 f(6 a) f( 1) 2 1 12 4故选:A . 1 2) ,则cos( 2 )的值为(33C .、选择题:本题共 1. ( 5分)若集合A {0,1, 2} , B{x|x 23x, 0},则 A | B 为(A . {1 , 2}B . {0 , 1 , 2}C . {0 , 1, 2, 3}D . {x|0剟X 3}2. ( 5分)已知复数 z 5 i (i 为虚数单位)13,则复数一 zZ 在复平面内所对应的点位于A •第一象限B. 第二象限C. 第三象限D. 第四象限13 _13z z 5 i13(5 i) (5 i)(5 i)15 3i .2 2 复数在复平面内对应的点的坐标为15 3(仝,-),位于第四象限. 2 2故选:D .x 12 2,x, 1 Iog 2(x 1),x 3,则 f (6 a)(A . 1 B. § 4 4 C .3 【解答】解:由题意,a, 1时,2 12 3,无解; 4.( 5分)若叫3. ( 5分)已知函数f (x ) 1,且 f ( a )【解答】解:Q sin( )1, 631cos 冷)35. (5分)正项等比数列{&}中,a i a 5 2a 3a y 8589 的公比是()运LA . 1B . 2C .D . . 22【解答】解:正项等比数列{a n }中, a 〔a 5 2a 3a 7 a 5 a 9 16 , 可得 a 3 2a 3a 7 a 7 (a 3 a 7) 16 ,即 a 3 a 74,a 5与a 9的等差中项为4,即a 5 a 9 8 , 设公比为q ,则q 2 (a 3 a 7) 4q 2 8, 则q 2 (负的舍去), 故选:D .r r r 2\f3 r r r r r r r6. ( 5分)若非零向量a , b 满足|a| —2|b|,且(a b) (3a 2b),则a 与b 的夹角为(3)cos(-3 2)COS2(3)2cos 216,且a 5与a 9的等差中项为4,则{ a n }第10页(共20页)故选:A .ra3一42 r IP rG g 65 ra1 1orer a2ra2r b2 - 3rar b rar br a3-2-2ra ra -lbg H ra7. (5分)已知函数f(x) sin( x )(0,| |),其图象相邻两条对称轴之间距离为—,22将函数y f(x)的向右平移—个单位长度后,得到关于 y 轴对称,则()6A . f (x)的关于点(_,0)对称6 B . f (x)的图象关于点(—,0)对称6C . f (x)在(孑3)单调递增2D . f (x)在(一,-)单调递增3 62 , f (x) sin(2 x ).将函数y f (x)的向右平移一个单位长度后,可得y sin(2x —63根据得到的图象关于 y 轴对称,可得— k - , k Z ,- , f(x) sin(2x -). 3 2661当x —时,f(x)-,故f (x)的图象不关于点(一,0)对称,故A 错误;6 2 6—时,f (x)1,故f (x)的图象关于直线 x —对称,不不关于点(―,0)对称,6 6 6故B 错误;故选:C .& (5分)底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内 有一内接正四棱锥 S ABCD ,该四棱锥的体积为 口,现在半球内任取一点, 则该点在正3【解答】解:Q 函数f (x) sin( x )(0,| | -),其图象相邻两条对称轴之间距离为)的图象,在(-^)上,2xf (x)单调递增,故C 正确; [3T ,-],f (x)单调递减,故 D 错误,四棱锥内的概率为(32 ,B .厘【解答】解:连结AC , BD 交点为0,设球的半径为由题意可知SO AO OC OD OB r .则 AB 2r , 四棱锥的体积为 1( 2r )24.2 3解得r 2 ,四棱锥的外接球的体积现在半球内任取一点,则该点在正四棱锥内的概率为:4.2 T ;<24- 2 3a,b ,c ,若 bsi nA 3acosB 0,且b 2ac ,A .丄2C . 2【解答】解: ABC 中,由 bsin A ;/3agcosB 0,利用正弦定理得sin BsinA .3sin AcosB tan B 3,故 B由余弦定理得b 22acccos B2 2c ac ,即 b (ac)2 3ac ,又b 2ac ,所以 24b(a 2a cc ),求得盲故选:C .32 ,10. ( 5分)某三棱锥的三视图如图所示,则该三棱锥的体积为【解答】 解:由三视图可知:该几何体为三棱锥,该三棱锥的体积1丄5 3 4 10 . 3 22■y^ 1(a 0,b 0)的左、右焦点,以bP ,Ph 与双曲线相交于点 Q ,且| PQ | 2 | QR |,则该双曲线的离心率为( )A . 5B . 2C . 3【解答】解:Q 点P 是以FE 为直径的圆与C 右支的一个交点,即 FPF 2为直角,则设 IQF 1 | m ,|PQ | 2m , 则|旺| 2c ,则 |PF 2 | 4c 2 9m 2,| QF 2 | 4c 2 5m 2, 则 |PF | |PF 2 | 3m4c 2 9m 2 2a ,①正〔主)视图 侧〔左)视團A . 60B . 30C . 20D . 10FF 2为直径的圆与双曲线右支的一个交点为22 5m2m 2a , ②,IQF21IQF1 |、.4c则3m4c29m4c25m m2a,4c25m2,即4m4c29m2平方整理得45m216c2,则m2性,代回②得.4c2 5 16C竺c 2a,45 \ 4515即c 5a即离心率e - 5 ,a故选:A.12. (5分)已知函数f(x) alnx 2x,若不等式f(x 1) ax 2e x在x (0,)上恒成立,则实数a的取值范围是()A . a, 2B . a--2 C. a, 0 D. 0剟a 2 【解答】解:f(e x) ax 2e x,所以f(x 1) ax 2^在(0,)上恒成立,等价于f(x 1) f (e x)在(0,)上恒成立,因为x (0,)时,1 x 1 e x,所以只需f (x)在(1,)上递减,即x 1 , f (x), 0恒成立,即x 1时,-,2恒成立,a, 2x,x所以a, 2,故选:A.二、填空题:本题共4小题,每小题5分,共20分.13. (5分)已知f(x)为偶函数,当x 0时,f(x) ln( x) 3x ,贝U曲线y f(x)在点(1, 3)处的切线方程是—2x y 1 0_ .【解答】解:f (x)为偶函数,可得f( x) f (x),3第17页(共20页)当x 0 时,f (x) ln( x) 3x,即有31 x 0 时,f(x) Inx 3x , f (x) 3 , x 可得 f (1) In1 33, f (1)1 32,则曲线y f (x)在点(1, 3)处的切线方程为y ( 3) 2(x 1),即为2x y 10 .故答案为:2x y 1 0 .x 2y 5, 014. (5分)设变量x , y 满足约束条件x y 2, 0,则目标函数z 2x 3y 1的最大值为 10 .【解答】 解:不等式表示的平面区域如图所示:2 1 目标函数z 2x 3y 1,即y x _(z 1),3 3则直线过点C 时,纵截距最大, 丄 x 2y 50 口由,可得x 3, y 1 ; x y 2目标函数z 2x 3y 1的最大值为2 3 3 1 1 10 , 目标函数z 2x 3y 1的最大值为:10,1,则数列{a :}前n 项的和为【解答】解:Q 等比数列{a n }前n 项的和为2n 1 , at & 2 1 1 ,第12页(共20页)15. (5分)等比数列{a n }前n 项的和为2n第19页(共20页)a 2 4n 1 316. (5分)斜率为1的直线l 过抛物线y 2 2px(p 0)的焦点F ,若I 与圆2 2(X 5) y 8 相切,贝U p 等于 2或18【解答】解:斜率为1的直线I 过抛物线2y 2px(p 0)的焦点F (扌,0),设直线I 的方程为y若I 与圆(x 5)2 y 2 8相切,可得解得p 2或1& 故答案为:2或18 •三、解答题:共 70分.解答应写出文字说明、证明过程或演算步骤 第17〜21题为必考题,每个试题都必须作答,第 22、23题为选考题,考生根据要求作答17. (12分)设等差数列{a n }的前n 项和为S , n N ,公差d 0 , S 315 ,已知 a 1 , a 4,a 13成等比数列.(I)求数列{a n }的通项公式;(H)设b n a 2n,求数列{b n }的前n 项和「.【解答】 解:(1)依题意,a , a 4, a 3成等比数列.即有a 2 a 1 ai 3 ,则3a(a 1 3 2d 15 2 ,23d)a 1(a 1 12d).2.因此 a n a 1 (n 1)d 3 2(n 1) 2n 1 ,即 a n 2n 1 .(H)依题意,解得a 13a2s, s (4 1)1 2,故公比为qai1 (1 4n)故数列a n2的首项为1,公比等于4,数列a n2前n项的和为32 3 n 1T n b l b2 b n (2 1) (2 1) (2 1),2 3 n 1 4(1 2n) n 222 3242n 1n n 2 n 4 •1 218. (12分)如图,已知四棱锥P ABCD的底面ABCD是菱形,BAD 60 , PA PD ,O为AD边的中点,点M在线段PC 上.所以ABD是正三角形,(1分)因为O为AD边的中点, PA PD ,所以AD PO,AD BO , PO|BO O ,所以AD平面POB,(3 分)因为AD平面PAD,所以平面POB 平面PAD •(5分)(2)连接AC,交OB于点N,连接MN ,因为PA/ /平面MOB,所以PA//MN,(6分)易知点N为ABD的重心,所以AN 1 AC,31故PM -PC,3(7 分)因为AB 2 3 , PA PD.7,所以OB 3 , OP 2,因为PB13 ,所以POB 90,即OP OB,且AD PO , 所以OP 平面BODC , (8分)2 2由PM -PC知CM -CP,4 3BODC的体积. BAD60 ,(1)证明:平面POB 平面PAD ;求四棱锥M 【解答】(1)证明:连BD,因为底面ABCD是菱形,19.( 12分)某省在2017年启动了 “ 3 3 ”高考模式.所谓“ 3 3 ”高考模式,就是语文、 数学、外语(简称语、数、外)为高考必考科目,从物理、化学、生物、政治、历史、地理(简称理、化、生、政、史、地)六门学科中任选三门作为选考科目.该省某中学 高一新生共有990人,学籍号的末四位数从 0001到0990 .专业受限百分比(I )现从高一学生中抽样调查 110名学生的选考情况,问:采用什么样的抽样方法较为恰当?(只写出结论,不需要说明理由)(H )据某教育机构统计,学生所选三]学科在将来报考专业时受限制的百分比是不同的.该机构统计了受限百分比较小的十二种选择的百分比值 x (i 1 , 2,, 12),制作出如条形图.设以上条形图中受限百分比的均值为 x ,标准差为s •如果一个学生所选三门学科专业受限 百分比在区间(X s , x s )内,我们称该选择为“恰当选择”.该校李明同学选择了化学,故点M 到平面BODC 的距离为2 P0 4 ,(9分)3 3因为S BODC 所以四棱锥?S ABCD 3 2 1 (2 3)2 sin60 空,4 4 2 2M BODC 的体积为1 口3 2(10 分)(12分)2017 级化史政生史政理化生理生地化地政理优地理生史理化史理史政理地政理生政理优政“的概率是多少?(均值然后从余下五门选考科目中任选两门•间李明的选择为“恰当选择第23页(共20页)2x ,标准差s 均精确到0.1)(参考公式和数据:n n 12| 21 2 2 2(X i X)2X i 2 X 2 , X i 2 2644.83)【解答】解:(I )根据题意,用系统抽样方法比较合适;右焦点的距离之和为 22(1 )求C 的方程的取值范围y 2).直线OM 的方程为:y代入椭圆方程可得: 3X 2 4mx 2 m 2 2 0 .【解答】解:(1)由题意可得:厶丄1 , 2a3a 2 3b 22 2,解得aX 2椭圆的标准方程为:丄弦AB 的中点在线段OM (不含端点O , M )上,X 1 X 2化为:X 1 X 2 2( y y 2). 2 y 1 Q X 1 X 2 2X 22X 12 y 2 相减可得: (X 1 X 2)(X 1 X 2)(y 1 y 2)(wy ?) 0.(y 1y 1 y 2y 2)1 20 .X 1 X 2y 1y 2k AB .iX12(3.33.6 9 10.5 12 12^14 14忆7但919・513.4.S 21 1212 2X i丄 2644.83 13.42220.4025 179.56 40.8412所以S 6.4,所以(X s, X s) (7.0,19.8). 从化学学科以外五门任选两门,共有10种基本情况, 分别为化理生、化理政、化理史、化理地、化生政、化生史、化生地、化政史、化政地、化史地, 而满足在(X4种情况.所以,李明的选择成为“恰当选择”的概率4 P0.4 .10X 2C : 2 a2b 21(a b 0)上,且点M到C 的左、(2)设O 为坐标原点,若C 的弦AB 的中点在线段OM (不含端点O , M )上,求umr ujur OA?OB设直线AB 的方程为:y 20. (12分)已知点M ,乜)在椭圆3x22o24( m 1)8(3 m )0 .解得 m 3.口 x 1 x 2 2m 又(0, —) ,0 m .3.由根与系数的关系可得:x 1 x 2, *x 23uuu uuu 2 40A?0B m -3(1 )当a 1时,讨论函数f (x)的单调性;x 2(2)若不等式f (x) (a 1)x … x a 1 e 对于任意x [e 1 , e ]成立,求正实数范围.【解答】 解:(1)函数 f (x)的定义域为(0,),f (x)x (a 1) a(x a)(x 1)x x若0 a 1,当0 x a 或x 1时, f (x)0 , f (x)单调递增;当a x 1 时,f (x) 0 , f (x)单调递减,若a,,当0 x 1 时,f (x) 0 , f (x)单调递减; 当x1 时,f (x)f (x)单调递增.综上所述,当a, 0时,函数f(x)在(1,)上单调递增,在(0,1)上单调递减; 当0 a 1时,函数f(x)在(a,1)上单调递减,在(0,a)和(1,)上单调递增.(2)原题等价于对任意x [丄,e ],有alnx x a , e 1成立,ealnx x a , a 0,所以 g(x)max , e 1 ,uun uun 0A?0B xx 2%y 2 x<,x 2 ( xm)( X 2 m) 2%X 2m(% X 2)2 222m 2 4m m 2 -3321. (12分)已知函数f(x) -x 22(a 1)x alnx .g(x)a(x a 1)A2△ 16m 2m 2 2 34 - 3,3)a 的取值设 g(x)令g (x) 0 ,得 0 x 1 ;令g (x) 0 ,得x 1 ,1所以函数g(x)在[1, 1]上单调递减,在(1 , e]上单调递增,eg(x)max max(g(!) a e a, g (e) a e a),e、 1设h (a) g (e) g(一)e a e a 2a(a 0),e则h (a) e a e a 2 2 e a ge a 2 0,所以h (a)在(0,)上单调递增,故h ( a) h(0) 0 ,所以g (e) g($ ,e从而g(x)max g (e) a e a,所以 a e a, e 1,即e a a e 1 0,设(a) e a a e 1(a 0),贝U (a) e a 1 0,所以(a)在(0,)上单调递增,又(1) 0 ,所以e a a e 1, 0的解为a, 1 ,因为a 0 ,所以正实数a的取值范围为(0 , 1].(二)选做题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第」题计分•[选修4-4 :坐标系与参数方程](本小题满分10分)x 3cos22.(10分)在直角坐标系xOy中,曲线G的参数方程为(为参数,y sin[0,2 )),曲线C2的参数方程为t2 (t为参数). 1t2(I)求曲线G , C2的普通方程;(n)若曲线C1上一点P到曲线C2的距离的最大值为2 3,求a .x 3cos【解答】解:(I)曲线G的参数方程为(为参数,y sin2系可得:C:— y2 1 .9 [0 , 2 )),利用平方关第27页(共20页)(H)设点 P(3cos ,sin ),|3cos/3sin a |I ^^sin(-)a l点P 到C 2的距离d l 3cos 空——-1322当 a-0 时,有 sin( ) 1 时,d max 匸3 - 2 3 , a 2 3 ;3 2 当 a 0 时,有 sin( )1 时,d max 乙3 -2 3, a 23 ;32综上,a 2 3或a 2 3 .[选修4-5:不等式选讲](本小题满分0分)223.已知函数 f(x) x ax 4 , g(x) | x 21 | x 21.(I)当a4时,求不等式 f(x)…g(x)的解集;(H)若不等式f(x), g(x)的解集包含[2 , 4],求a 的取值范围.【解答】解:(I)当 i a4 时,f (x) 2 x 4x 42x, x, 2又 g(x) |x 2||x 2|4, 2 x 2 ,2x,x-2当x 2时, 2x4x 4…2x ,解得 x, 2 ;当2 x2时,2x4x4…4,解得 2人 0 ;当 x---2 时,x 24x 4…2x ,解得x ・・3 5.综上,不等式的解集为 x | x^^0或x 35 .(n) f (x), g(x)的解集包含[2 , 4]等价于 x 2 ax 4, |x 2 | |x 2 | 在[2 ,即x 2 (a 2)x 4, 0对于x [2 , 4]上恒成立,令 h(x) x 2 (a 2)x4 ,由曲线C 2的参数方程为t 2(t 为参数)1-t 2,消去参数可得: a 0 .要使h(x), 0在[2 , 4]恒成立,只需h(2), 0 h(4), 04]上恒成立,a, 3 ,8 2(a 2),0即20 4(a 2), 0a 的取值范围为(,3] .(2)设A(X , yj , B(X2 ,第28页(共20页)。
2019-2020学年河南省三门峡市高三(上)期末数学试卷(文科)

2019-2020学年河南省三门峡市高三(上)期末数学试卷(文科)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若集合{0A =,1,2},2{|30}B x x x =-„,则A B I 为( ) A .{1,2}B .{0,1,2}C .{0,1,2,3}D .{|03}x x 剟2.(5分)已知复数5(z i i =+为虚数单位),则复数13z z+在复平面内所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3.(5分)已知函数1222,1()(1),1x x f x log x x -⎧-⎪=⎨-+>⎪⎩„,且f (a )3=-,则(6)(f a -= )A .74-B .54-C .34-D .14-4.(5分)若1sin()63πα-=,则2cos(2)3πα+的值为( )A .13-B .79-C .13D .795.(5分)正项等比数列{}n a 中,153759216a a a a a a ++=,且5a 与9a 的等差中项为4,则{}n a 的公比是( )A .1B .2 CD6.(5分)若非零向量a r ,b r满足||||3a b =r r ,且()(32)a b a b -⊥+r r r r ,则a r与b r 的夹角为() A .4π B .2π C .34π D .π7.(5分)已知函数()sin()(0,||)2f x x πωϕωϕ=+><,其图象相邻两条对称轴之间距离为2π,将函数()y f x =的向右平移6π个单位长度后,得到关于y 轴对称,则( ) A .()f x 的关于点(,0)6π对称B .()f x 的图象关于点(,0)6π-对称C .()f x 在(,)63ππ-单调递增D .()f x 在2(,)36ππ--单调递增 8.(5分)底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S ABCD -,该四棱锥的体积为423,现在半球内任取一点,则该点在正四棱锥内的概率为( )A .1πB .2C .3D .2π9.(5分)在ABC ∆中,内角A ,B ,C 所对应的边分别为a ,b ,c ,若sin 3cos 0b A a B -=,且2b ac =,则a cb+的值为( ) A .22B .2C .2D .410.(5分)某三棱锥的三视图如图所示,则该三棱锥的体积为( )A .60B .30C .20D .1011.(5分)已知1F ,2F 为双曲线22221(0,0)x y a b a b-=>>的左、右焦点,以12F F 为直径的圆与双曲线右支的一个交点为P ,1PF 与双曲线相交于点Q ,且1||2||PQ QF =,则该双曲线的离心率为( ) AB .2CD12.(5分)已知函数()2f x alnx x =-,若不等式(1)2x f x ax e +>-在(0,)x ∈+∞上恒成立,则实数a 的取值范围是( ) A .2a „B .2a …C .0a „D .02a 剟二、填空题:本题共4小题,每小题5分,共20分.13.(5分)已知()f x 为偶函数,当0x <时,()()3f x ln x x =-+,则曲线()y f x =在点(1,3)-处的切线方程是 .14.(5分)设变量x ,y 满足约束条件250200x y x y x +-⎧⎪--⎨⎪⎩„„…,则目标函数231z x y =++的最大值为 .15.(5分)等比数列{}n a 前n 项的和为21n -,则数列2{}na 前n 项的和为 . 16.(5分)斜率为1的直线l 过抛物线22(0)y px p =>的焦点F ,若l 与圆22(5)8x y -+=相切,则p 等于 .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题都必须作答,第22、23题为选考题,考生根据要求作答.17.(12分)设等差数列{}n a 的前n 项和为n S ,*n N ∈,公差0d ≠,315S =,已知1a ,4a ,13a 成等比数列.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设2n n b a =,求数列{}n b 的前n 项和n T .18.(12分)如图,已知四棱锥P ABCD -的底面ABCD 是菱形,60BAD ∠=︒,PA PD =,O 为AD 边的中点,点M 在线段PC 上.(1)证明:平面POB ⊥平面PAD ;(2)若AB =PAPB =//PA 平面MOB ,求四棱锥M BODC -的体积.19.(12分)某省在2017年启动了“33+”高考模式.所谓“33+”高考模式,就是语文、数学、外语(简称语、数、外)为高考必考科目,从物理、化学、生物、政治、历史、地理(简称理、化、生、政、史、地)六门学科中任选三门作为选考科目.该省某中学2017级高一新生共有990人,学籍号的末四位数从0001到0990.(Ⅰ)现从高一学生中抽样调查110名学生的选考情况,问:采用什么样的抽样方法较为恰当?(只写出结论,不需要说明理由)(Ⅱ)据某教育机构统计,学生所选三]学科在将来报考专业时受限制的百分比是不同的.该机构统计了受限百分比较小的十二种选择的百分比值(1i x i =,2,⋯,12),制作出如条形图.设以上条形图中受限百分比的均值为x ,标准差为s .如果一个学生所选三门学科专业受限百分比在区间(x s -,)x s +内,我们称该选择为“恰当选择”.该校李明同学选择了化学,然后从余下五门选考科目中任选两门.间李明的选择为“恰当选择“的概率是多少?(均值x ,标准差s 均精确到0.1)(参考公式和数据:2221111()n n i i i i x x x x n n ==-=-∑∑,12212644.83)i i x ==∑20.(12分)已知点23(M 3)在椭圆2222:1(0)x y C a b a b+=>>上,且点M 到C 的左、右焦点的距离之和为(1)求C 的方程(2)设O 为坐标原点,若C 的弦AB 的中点在线段OM (不含端点O ,)M 上,求?OA OBu u u r u u u r的取值范围21.(12分)已知函数21()(1)2f x x a x alnx =-++. (1)当1a <时,讨论函数()f x 的单调性;(2)若不等式2()(1)12a x f x a x x e ++++-…对于任意1[x e -∈,]e 成立,求正实数a 的取值范围.(二)选做题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](本小题满分10分)22.(10分)在直角坐标系xOy 中,曲线1C 的参数方程为3cos (sin x y θθθ=⎧⎨=⎩为参数,[0θ∈,2))π,曲线2C的参数方程为(12x a t y t ⎧=⎪⎪⎨⎪=⎪⎩为参数). (Ⅰ)求曲线1C ,2C 的普通方程;(Ⅱ)若曲线1C 上一点P 到曲线2C的距离的最大值为a . [选修4-5:不等式选讲](本小题满分0分)23.已知函数2()4f x x ax =++,()|2||2|g x x x =++-. (Ⅰ)当4a =-时,求不等式()()f x g x …的解集;(Ⅱ)若不等式()()f x g x „的解集包含[2,4],求a 的取值范围.2019-2020学年河南省三门峡市高三(上)期末数学试卷(文科)参考答案与试题解析一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若集合{0A =,1,2},2{|30}B x x x =-„,则A B I 为( ) A .{1,2}B .{0,1,2}C .{0,1,2,3}D .{|03}x x 剟【解答】解:{|03}B x x =剟; {0A B ∴=I ,1,2}.故选:B .2.(5分)已知复数5(z i i =+为虚数单位),则复数13z z+在复平面内所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【解答】解:5z i =+Q ,∴131313(5)153555(5)(5)22i z i i i z i i i -+=+-=+-=-++-. ∴复数在复平面内对应的点的坐标为153(,)22-,位于第四象限. 故选:D .3.(5分)已知函数1222,1()(1),1x x f x log x x -⎧-⎪=⎨-+>⎪⎩„,且f (a )3=-,则(6)(f a -= )A .74-B .54-C .34-D .14-【解答】解:由题意,1a „时,1223α--=-,无解; 1a >时,2log (1)3a -+=-,7α∴=,117(6)(1)224f a f --∴-=-=-=-.故选:A .4.(5分)若1sin()63πα-=,则2cos(2)3πα+的值为( )A .13-B .79-C .13D .79【解答】解:Q 1sin()63πα-=,1cos()33πα∴+=,∴2217cos(2)cos2()2()12133399cos πππααα+=+=+-=⨯-=-. 故选:B .5.(5分)正项等比数列{}n a 中,153759216a a a a a a ++=,且5a 与9a 的等差中项为4,则{}n a 的公比是( ) A .1B .2CD【解答】解:正项等比数列{}n a 中,153759216a a a a a a ++=,可得2223377372()16a a a a a a ++=+=, 即374a a +=,5a 与9a 的等差中项为4,即598a a +=,设公比为q ,则2237()48q a a q +==,则q , 故选:D .6.(5分)若非零向量a r ,b r满足||||a b =r r ,且()(32)a b a b -⊥+r r r r ,则a r与b r 的夹角为()A .4π B .2π C .34π D .π【解答】解:()(32)a b a b -⊥+r r r rQ ,()(32)0a b a b ∴-+=r r r rg , 即22320a b a b --=r r r r g , 即2222323a b a b b =-=r r r r r g ,cos a ∴<r,22||||b a b b a b >===r r r r g r r , 即a <r,4b π>=r ,故选:A .7.(5分)已知函数()sin()(0,||)2f x x πωϕωϕ=+><,其图象相邻两条对称轴之间距离为2π,将函数()y f x =的向右平移6π个单位长度后,得到关于y 轴对称,则( ) A .()f x 的关于点(,0)6π对称B .()f x 的图象关于点(,0)6π-对称C .()f x 在(,)63ππ-单调递增D .()f x 在2(,)36ππ--单调递增 【解答】解:Q 函数()sin()(0,||)2f x x πωϕωϕ=+><,其图象相邻两条对称轴之间距离为1222ππω=g ,2ω∴=,()sin(2)f x x ϕ=+. 将函数()y f x =的向右平移6π个单位长度后,可得sin(2)3y x πϕ=-+ 的图象, 根据得到的图象关于y 轴对称,可得32k ππϕπ-+=+,k Z ∈,6πϕ∴=-,()sin(2)6f x x π=-.当6x π=时,1()2f x =,故()f x 的图象不关于点(,0)6π对称,故A 错误;当6x π=-时,()1f x =-,故()f x 的图象关于直线6x π=-对称,不不关于点(,0)6π对称,故B 错误;在(,)63ππ-上,2[62x ππ-∈-,]2π,()f x 单调递增,故C 正确;在2(,)36ππ--上,32[62x ππ-∈-,]2π-,()f x 单调递减,故D 错误, 故选:C .8.(5分)底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S ABCD -,该四棱锥的体积为423,现在半球内任取一点,则该点在正四棱锥内的概率为( )A .1πB .2C .3D .2π【解答】解:连结AC ,BD 交点为0,设球的半径为r , 由题意可知SO AO OC OD OB r =====. 则2AB r =,四棱锥的体积为2142(2)3V r r =⨯⨯=,解得2r =,四棱锥的外接球的体积为:3141824223233V r πππ=⨯=⨯=;∴现在半球内任取一点,则该点在正四棱锥内的概率为:421342ππ=,故选:A .9.(5分)在ABC ∆中,内角A ,B ,C 所对应的边分别为a ,b ,c ,若sin 3cos 0b A a B =,且2b ac =,则a cb+的值为( ) A 2B 2C .2D .4【解答】解:ABC ∆中,由sin 3cos 0b A a B =g ,利用正弦定理得sin sin 3sin cos 0B A A B =, tan 3B ∴3B π=.由余弦定理得222222cos b a c ac B a c ac =+-=+-g ,即22()3b a c ac =+-, 又2b ac =,所以224()b a c =+,求得2a cb+=, 故选:C .10.(5分)某三棱锥的三视图如图所示,则该三棱锥的体积为( )A .60B .30C .20D .10【解答】解:由三视图可知:该几何体为三棱锥, 该三棱锥的体积115341032=⨯⨯⨯⨯=.故选:D .11.(5分)已知1F ,2F 为双曲线22221(0,0)x y a b a b-=>>的左、右焦点,以12F F 为直径的圆与双曲线右支的一个交点为P ,1PF 与双曲线相交于点Q ,且1||2||PQ QF =,则该双曲线的离心率为( ) A 5B .2C 3D 5【解答】解:Q 点P 是以12F F 为直径的圆与C 右支的一个交点,∴即12F PF ∠为直角,∴则设1||QF m =,||2PQ m =,则12||2F F c =,则222||49PF c m =-,222||45QF c m =- 则2212||||3492PF PF m c m a -=-=,①21||||2QF QF m a -==,②,则32m m a ==,即4m 平方整理得224516m c =,则221645m c =,代回②2a =,即c =即离心率ce a= 故选:A .12.(5分)已知函数()2f x alnx x =-,若不等式(1)2x f x ax e +>-在(0,)x ∈+∞上恒成立,则实数a 的取值范围是( ) A .2a „B .2a …C .0a „D .02a 剟【解答】解:()2x x f e ax e =-,所以(1)2x f x ax e +>-在(0,)+∞上恒成立, 等价于(1)()x f x f e +>在(0,)+∞上恒成立, 因为(0,)x ∈+∞时,11x x e <+<, 所以只需()f x 在(1,)+∞上递减, 即1x >,()0f x '„恒成立, 即1x >时,2ax„恒成立,2a x „,所以2a „, 故选:A .二、填空题:本题共4小题,每小题5分,共20分.13.(5分)已知()f x 为偶函数,当0x <时,()()3f x ln x x =-+,则曲线()y f x =在点(1,3)-处的切线方程是 210x y ++= .【解答】解:()f x 为偶函数,可得()()f x f x -=, 当0x <时,()()3f x ln x x =-+,即有0x >时,()3f x lnx x =-,1()3f x x'=-, 可得f (1)133ln =-=-,f '(1)132=-=-,则曲线()y f x =在点(1,3)-处的切线方程为(3)2(1)y x --=--, 即为210x y ++=. 故答案为:210x y ++=.14.(5分)设变量x ,y 满足约束条件250200x y x y x +-⎧⎪--⎨⎪⎩„„…,则目标函数231z x y =++的最大值为 10 .【解答】解:不等式表示的平面区域如图所示: 目标函数231z x y =++,即21(1)33y x z =-+-,则直线过点C 时,纵截距最大, 由25020x y x y +-=⎧⎨--=⎩,可得3x =,1y =;∴目标函数231z x y =++的最大值为2331110⨯+⨯+=,目标函数231z x y =++的最大值为:10, 故答案为:10.15.(5分)等比数列{}n a 前n 项的和为21n-,则数列2{}na 前n 项的和为 413n - .【解答】解:Q 等比数列{}n a 前n 项的和为21n -,11211a s ∴==-=,221(41)12a s s =-=--=,故公比为212a q a ==. 故数列{}2n a 的首项为1,公比等于4,数列{}2na 前n 项的和为1(14)41143n n ⨯--=-, 故答案为413n -.16.(5分)斜率为1的直线l 过抛物线22(0)y px p =>的焦点F ,若l 与圆22(5)8x y -+=相切,则p 等于 2或18 .【解答】解:斜率为1的直线l 过抛物线22(0)y px p =>的焦点(2pF ,0), 设直线l 的方程为2py x =-, 若l 与圆22(5)8x y -+=|5|p -=, 解得2p =或18. 故答案为:2或18.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题都必须作答,第22、23题为选考题,考生根据要求作答.17.(12分)设等差数列{}n a 的前n 项和为n S ,*n N ∈,公差0d ≠,315S =,已知1a ,4a ,13a 成等比数列.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设2n n b a =,求数列{}n b 的前n 项和n T . 【解答】解:()I 依题意,1a ,4a ,13a 成等比数列.即有24113a a a =, 则12111323152(3)(12).a d a d a a d ⨯⎧+=⎪⎨⎪+=+⎩, 解得132.a d =⎧⎨=⎩,因此1(1)32(1)21n a a n d n n =+-=+-=+, 即21n a n =+.(Ⅱ)依题意,1222121n n n n b a +==⨯+=+.23112(21)(21)(21)n n n T b b b +=++⋯+=++++⋯++,23124(12)2222412n n n n n n ++-=++⋯++=+=+--.18.(12分)如图,已知四棱锥P ABCD -的底面ABCD 是菱形,60BAD ∠=︒,PA PD =,O 为AD 边的中点,点M 在线段PC 上.(1)证明:平面POB ⊥平面PAD ;(2)若23AB =,7PA =,13PB =,//PA 平面MOB ,求四棱锥M BODC -的体积.【解答】(1)证明:连接BD ,因为底面ABCD 是菱形,60BAD ∠=︒, 所以ABD ∆是正三角形,⋯(1分) 因为O 为AD 边的中点,PA PD =, 所以AD PO ⊥,AD BO ⊥,PO BO O =I , 所以AD ⊥平面POB ,⋯(3分) 因为AD ⊂平面PAD ,所以平面POB ⊥平面PAD . ⋯(5分) (2)连接AC ,交OB 于点N ,连接MN , 因为//PA 平面MOB ,所以//PA MN ,⋯(6分) 易知点N 为ABD 的重心,所以13AN AC =,故13PM PC =,⋯(7分)因为23AB =7PA PD ==,所以3OB =,2OP =,因为13PB = 所以90POB ∠=︒,即OP OB ⊥,且AD PO ⊥, 所以OP ⊥平面BODC ,⋯(8分) 由13PM PC =知23CM CP =,故点M 到平面BODC 的距离为2433PO =,⋯(9分)因为2331932(23)sin 60442BODC ABCD S S ==⨯⨯⨯⨯︒=,⋯(10分)所以四棱锥M BODC -的体积为19342333⨯⨯=. ⋯(12分)19.(12分)某省在2017年启动了“33+”高考模式.所谓“33+”高考模式,就是语文、数学、外语(简称语、数、外)为高考必考科目,从物理、化学、生物、政治、历史、地理(简称理、化、生、政、史、地)六门学科中任选三门作为选考科目.该省某中学2017级高一新生共有990人,学籍号的末四位数从0001到0990.(Ⅰ)现从高一学生中抽样调查110名学生的选考情况,问:采用什么样的抽样方法较为恰当?(只写出结论,不需要说明理由)(Ⅱ)据某教育机构统计,学生所选三]学科在将来报考专业时受限制的百分比是不同的.该机构统计了受限百分比较小的十二种选择的百分比值(1i x i =,2,⋯,12),制作出如条形图.设以上条形图中受限百分比的均值为x ,标准差为s .如果一个学生所选三门学科专业受限百分比在区间(x s -,)x s +内,我们称该选择为“恰当选择”.该校李明同学选择了化学,然后从余下五门选考科目中任选两门.间李明的选择为“恰当选择“的概率是多少?(均值x ,标准差s 均精确到0.1)(参考公式和数据:2221111()n n i i i i x x x x n n ==-=-∑∑,12212644.83)i i x ==∑【解答】解:(Ⅰ)根据题意,用系统抽样方法比较合适; (Ⅱ)根据题意,1222221111(3.3 3.6910.51212.3141417.718.919.526.3)13.4.2644.8313.4220.4025179.5640.84121212i i x s x x -=+++++++++++≈=-≈⨯-=-≈∑.所以 6.4s ≈,所以(,)(7.0,19.8)x s x s -+=.从化学学科以外五门任选两门,共有10种基本情况,分别为化理生、化理政、化理史、化理地、化生政、化生史、化生地、化政史、化政地、化史地,而满足在(,)x s x s -+内的有理化史、理化地、化地政、理化生,共4种情况. 所以,李明的选择成为“恰当选择”的概率40.410P ==. 20.(12分)已知点M在椭圆2222:1(0)x y C a b a b+=>>上,且点M 到C 的左、右焦点的距离之和为(1)求C 的方程(2)设O 为坐标原点,若C 的弦AB 的中点在线段OM (不含端点O ,)M 上,求?OA OBu u u r u u u r的取值范围【解答】解:(1)由题意可得:2241133a b+=,2a =a =1b =. ∴椭圆的标准方程为:2212x y +=.(2)设1(A x ,1)y ,2(B x ,2)y .直线OM 的方程为:12y x =.弦AB 的中点在线段OM (不含端点O ,)M 上,∴12121222y y x x ++=⨯,化为:12122()x x y y +=+.由221112x y +=,222212x y +=,相减可得:12121212()()()()02x x x x y y y y +-++-=. 120x x -≠Q ,∴12121212()02x x y y y y x x +-++=-. ∴12121AB y y k x x -=-=-. 设直线AB 的方程为:y x m =-+,代入椭圆方程可得:2234220x mx m -+-=.△2221624(1)8(3)0m m m =--=->.解得23m <.又12223x x m +=∈,∴0m <<. 由根与系数的关系可得:1243m x x +=,212223m x x -=.∴222221212121212122244?()()2()2333m m OA OB x x y y x x x m x m x x m x x m m m -=+=+-+-+=--++=⨯-+=-u u u r u u u r .而0m <<.∴2445?(,)333OA OB m =-∈-u u u r u u u r.21.(12分)已知函数21()(1)2f x x a x alnx =-++. (1)当1a <时,讨论函数()f x 的单调性;(2)若不等式2()(1)12a x f x a x x e ++++-…对于任意1[x e -∈,]e 成立,求正实数a 的取值范围.【解答】解:(1)函数()f x 的定义域为(0,)+∞, ()(1)()(1)a x a x f x x a x x--'=-++=, 若01a <<,当0x a <<或1x >时,()0f x '>,()f x 单调递增; 当1a x <<时,()0f x '<,()f x 单调递减, 若0a „,当01x <<时,()0f x '<,()f x 单调递减; 当1x >时,()0f x '>,()f x 单调递增.综上所述,当0a „时,函数()f x 在(1,)+∞上单调递增,在(0,1)上单调递减; 当01a <<时,函数()f x 在(,1)a 上单调递减,在(0,)a 和(1,)+∞上单调递增. (2)原题等价于对任意1[x e∈,]e ,有1a alnx x e -+-„成立,设()a g x alnx x =-+,0a >,所以()1max g x e -„,(1)()a a x g x x-'=,令()0g x '<,得01x <<;令()0g x '>,得1x >,所以函数()g x 在1[e ,1]上单调递减,在(1,]e 上单调递增,1()(()a g x max max g a e e -==+,g (e ))aa e =-+,设h (a )g =(e )1()2(0)a a g e e a a e--=-->,则h '(a)220a a e e -=+->=, 所以h (a )在(0,)+∞上单调递增, 故h (a )(0)0h >=, 所以g (e )1()g e>,从而()max g x g =(e )a a e =-+, 所以1a a e e -+-„,即10a e a e --+„,设ϕ(a )1(0)a e a e a =--+>,则ϕ'(a )10a e =->, 所以ϕ(a )在(0,)+∞上单调递增,又ϕ(1)0=,所以10a e a e --+„的解为1a „, 因为0a >,所以正实数a 的取值范围为(0,1].(二)选做题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](本小题满分10分)22.(10分)在直角坐标系xOy 中,曲线1C 的参数方程为3cos (sin x y θθθ=⎧⎨=⎩为参数,[0θ∈,2))π,曲线2C的参数方程为(12x a t y t ⎧=⎪⎪⎨⎪=⎪⎩为参数). (Ⅰ)求曲线1C ,2C 的普通方程;(Ⅱ)若曲线1C 上一点P 到曲线2C的距离的最大值为a .【解答】解:(Ⅰ)曲线1C 的参数方程为3cos (sin x y θθθ=⎧⎨=⎩为参数,[0θ∈,2))π,利用平方关系可得:22:19x C y +=.由曲线2C的参数方程为(12x a t y t ⎧=+⎪⎪⎨⎪=⎪⎩为参数),消去参数可得::0C x a --=. (Ⅱ)设点(3cos ,sin )P θθ,点P 到2C的距离|)|32a d πθ---==,当0a …时,有sin()13πθ-=时,max d =,∴a =当0a <时,有sin()13πθ-=-时,max d =,∴a =-;综上,a =a =-.[选修4-5:不等式选讲](本小题满分0分)23.已知函数2()4f x x ax =++,()|2||2|g x x x =++-. (Ⅰ)当4a =-时,求不等式()()f x g x …的解集;(Ⅱ)若不等式()()f x g x „的解集包含[2,4],求a 的取值范围. 【解答】解:(Ⅰ)当4a =-时,2()44f x x x =-+. 又2,2()|2||2|4,222,2x x g x x x x x x --⎧⎪=++-=-<<⎨⎪⎩„…,∴当2x -„时,2442x x x -+-…,解得2x -„;当22x -<<时,2444x x -+…,解得20x -<„;当2x …时,2442x x x -+…,解得3x ….综上,不等式的解集为{|03x x x 或剠.(Ⅱ)()()f x g x „的解集包含[2,4]等价于24|2||2|x ax x x ++++-„在[2,4]上恒成立, 即2(2)40x a x +-+„对于[2x ∈,4]上恒成立, 令2()(2)4h x x a x =+-+,要使()0h x „在[2,4]恒成立,只需(2)0(4)0h h ⎧⎨⎩„„,即82(2)0204(2)0aa+-⎧⎨+-⎩„„,3a∴-„,a∴的取值范围为(-∞,3]-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灵宝市2019-2020学年度上期期末考试九年级化学试卷注意事项:1.本试卷共6页,四个大题,满分50分,考试时间60分钟。
请用黑色墨水的钢笔或签字笔直接答在答题卡上。
2.闭卷考试。
3.答题前请将密封线内的项目填写清楚。
相对原子质量:H:1 O:16 C:12 Ca:40 Al:27 C:12 S:32 N:14 F:19一、选择题(本题包括14个小题,每题只有一个选项符合题意,每小题1分,共14分)1.现代的生产和生活要消耗大量能量。
下列活动中,通过化学反应提供能量的是A.发射航天飞机B.水车汲水灌溉C. 太阳能供热D. 风力发电2.加油站、面粉加工厂、煤矿井内、纺织厂必贴的图标是AB C D3.下列选项正确的是A.检验甲烷燃烧有CO2生成B.读取液体体积C.带有残液的滴管倒持D.吹灭酒精灯4.从化学角度看,下列叙述中不正确的是A.开发清洁新能源可以有效减少和防止酸雨的形成B.扑灭图书档案火灾最适宜用液态二氧化碳灭火器甲烷内壁涂有澄清石灰水C.CO 2、O 3、CH 4、氟氯代烷都能产生温室效应D.常用钢丝球擦洗铝壶可以使其光亮洁净和更耐用 5. 中学生应有一定的安全常识。
下列做法不合理的是A. 在山林中遇火灾时,向顺风方向奔跑,逃离火灾区B. 被围困在火灾区时,应用湿毛巾捂住口鼻并尽量贴近地面逃离C. 室内起火,不要急于打开所有门窗D. 夜间发现燃气泄漏应关闭阀门并开窗通风,不能立即开灯 6.下列有关验证二氧化碳性质的实验中,不能证明二氧化碳化学性质的是A B C D 7.我国科学家用滤纸和二氧化钛(TiO 2)薄膜制出一种新型“纳米纸”,又在纳米纸上“铺”一层“萘胺” (C 10H 9N)染料,制成一种试纸,用于检测食品中亚硝酸盐浓度的高低。
下列说法正确的是A .二氧化钛中Ti 的化合价为+2价B .萘胺中氮元素的质量分数约为11.9%C .这种试纸是一种新型化合物D .萘胺中碳、氢、氮三种元素的质量比为120∶9∶148.某同学在研究物质燃烧的条件时,做了下图所示的实验:把一条粗金属丝绕成线圈,罩在一支蜡烛的火焰上,火焰很快就熄灭了。
对这一实验的说法不正确的是 A.金属丝有良好的导热性B.金属线圈内的气体温度升高了C.可燃物的温度降到了着火点以下D.若预先将金属丝加热,蜡烛就不会很快熄灭 9.以科学原理和事实为依据进行推理是学习化学的一种重要方法,下列推理合理的是A .物质世界是由一百多种元素组成的,因此可以利用周期表中的元素任意组合新物质B .化合物是由不同元素组成的纯净物,所以只含一种元素的物质一定不是化合物C .原子和分子都是构成物质的微粒,因此物质不是由分子构成,就一定是由原子构成D .CO 和CO 2的元素组成相同,所以它们的性质也完全相同 10. 下列除去杂质的方法错误的是 选项 物质 杂质 除杂方法A 硝酸铜溶液 硝酸银溶液 加过量铜粉,充分反应后过滤B 氮气 氧气 将气体缓缓通过灼热的铜网C 二氧化碳 一氧化碳 将混合气体通过灼热的氧化铜D铜碳在空气中灼烧稀盐酸 石灰石矿泉水 塑料瓶 清石灰CO 2紫色石蕊试液 CO 2CO 2氢气质量11.为比较4种金属X 、Y 、Z 、W 的活动性,小刚进行了一系列实验,结果如下表所示。
其则它们的金属活动性顺序为A .Y >W >X >ZB .Y >W >Z >X C.Y >X >W >Z D .X >Y >W >Z 12.等质量的M 、N 两种金属,分别与相同质量分数的足量稀盐酸反应(已知M 、N 在生成物中均为+2价),生成氢气质量和反应时间的关系如右图所示,下列叙述正确的是 A.M 、N 两种金属中较活泼的是N B.生成H 2的质量M <N C.相对原子质量较大的是N D.产生H 2的速率N >M 13.“愚人金”实为铜锌合金,外观和黄金极为相似,常被不法商贩冒充黄金牟取暴利,下列关于鉴别“愚人金”与黄金的实验方案,合理的是 ①“愚人金”比较硬度,硬度小的是“愚人金” ②灼烧表面变色的是“愚人节”③浸没在稀硫酸中表面有气泡产生的是“愚人金”④浸没在硫酸锌溶液中表面附着银白色物质的是“愚人金” A. ①③ B. ②④C. ①④D. ②③14.下列图象不能正确反映对应变化关系的是 A B C D A .电解水一段时间B .加热一定量高锰酸钾固体C .加热氯酸钾制氧气D .实验室利用双氧水制取氧气二、填空题(本题包括6个小题,每空1分,共16分)15.(3分)现有乙醇、水银、铝、一氧化碳、二氧化硫四种物质,其中(用化学式填写):①常温下为液体的金属是 ;②属于可再生能源的是 ; ③造成酸雨的主要气体是 。
16.(2分)右下图是某反应的微观示意图,反应前后化合价没有发生变化的元素为_______;气体体积时间s 固中元的量剩固的量氧的量参加反应的甲物质和生成的丙物质分子数目比为________。
17.(4分)A 、B 、C 、D 、E 是初中化学中常见的不同物质,其中A 为黑色固体,C 为难溶于水的固体。
其转化关系如右图所示:(1)A 的化学式为________,E 的化学式为________。
(2)写出由B →E 、E →C 的化学方程式_________________、______________________。
18.(4分)钢铁在生产、生活中有广泛的用途。
(1)钢铁属于__________(填“纯净物”或“混合物”);(2)炼铁厂常以焦炭、赤铁矿(主要成分是氧化铁Fe 2O 3)、空气等为主要原料炼铁,请写出一氧化碳与氧化铁在高温下反应的化学方程式_____________________。
(3)市场上有一种含铁粉的麦片,食用后在胃酸(主要成分为盐酸)作用下将铁粉转化为人体可吸收的铁元素,反应的化学方程式为______________________。
这种麦片必须真空保存,原因是__________________________________________________________。
19.(1分)对比实验是实验探究的重要方法,下列对比实验设计不能实现相应实验目的的是________。
A B C D A. 烧杯中的蜡烛逐渐熄灭,说明燃烧的条件之一是可燃物要与氧气接触 B. 探究温度对分子运动快慢的影响C. 若将图中的小石头换成小煤块能得到与图设计相同的结论D. 热水的作用之一是隔绝氧气20.(2分)某化合物完全燃烧,需要氧气4.8g ,同时生成4.4g 二氧化碳和2.7g 水,则化合物中含有_________元素(写出元素符号),各元素的原子个数比是________(和上空中的元素相对应)。
三、简答题(本题包括4个小题,共10分)21.(2 分)根据要求写出下列反应的化学方程式. (1)铝是活泼金属,为什么通常铝锅却很耐腐蚀?氢原子 氧原子 氮原子甲 乙 各加一滴红墨水50mL 冷水 50mL 热水小石头 小木块 白磷红磷80℃白磷 热水(4)硅是信息技术的关键材料。
高温下氢气与四氯化硅(SiCl 4)反应可制得高纯度的硅,同时生成氯化氢。
22.(2分)在使用体温计测量体温时,若不慎将体温计打破,散落出来的汞和汞蒸气会对人体产生危害。
此时撒一些硫粉在上面,使硫与汞发生化学反应生成固体硫化汞(HgS )。
(1)写出硫与汞反应的化学方程式。
(2)用分子、原子的观点解释体温计测量体温时汞柱上升的现象。
23. (3分)如图是初中化学中的三个小实验,请回答:(1) 图甲中水的作用是什么?(2) 图乙实验在操作无误的情况下可得出的结论是_______________________。
(3) 图丙实验可得出CO 2具有什么的化学性质?24.(3分)下图为某同学探究铁、铜、银三种金属活动性顺序的一组实验。
(1)上述实验中,有气泡产生的是_______________。
(2)通过上述实验,还不能证明铁、铜、银三种金属的金属活动性顺序,请你在此基础上补充一个实验帮助这位同学达到实验目的(写出实验步骤、现象及结论)_______________________________________________________________________________。
(3)某同学将一小包铜粉和锌粉的混合物放入一定量的硝酸银溶液中,使其充分反应后过滤,得到固体和蓝色滤液,并对滤液的组成进行探究。
同学们对滤液中所含的溶质做出多种猜想,其中有两种猜想可能成立,这两种猜想是:【以下填写滤液中物质的化学式(水除外)】图甲图乙图丙氧气铁丝 水 电热棒足量红磷空气水CO 2干燥紫色石蕊布条湿润紫色石蕊布条铁稀硫酸铜 稀硫酸铁铁硫酸铜溶液硝酸银溶液① ② 。
四、综合应用题(共10分)25.某兴趣小组根据下列装置进行实验,请你参与并回答:A B C D (1)②仪器的名称是________。
(2)若用A 装置制取氧气,则①中可观察到的现象是_________________________________ (任答一点);写出该反应的化学方程式______________________________。
(3) B 和C 装置均可制取CO 2,与B 相比较,C 的主要优点_______________________。
(4)常用金属锌和稀硫酸反应制取。
若实验室要制取少量氢气最好选择发生装置________(填字母);若用试管排空气法收集氢气,请在D 处方框中画出装置图(只画试管和导气管)。
(5) 某研究性学习小组为了测定某矿山石灰石中碳酸钙的质量分数,取来了一些矿石样品,并取稀盐酸200g,平均分成4份,进行实验,结果如下:(杂质不与稀盐酸反应)①表格中m 的数值是________。
②求石灰石中碳酸钙的质量分数。
实 验 1 2 3 4 加入样品的质量/g 5 10 15 20 生成CO 2的质量/g 1.76 3.52 4.4 m棉花有空塑料板 ①②灵宝市2019-2020学年度上期期末考试化学试题参考答案一、选择题(本题包括14个小题,每小题1分,共14分)题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 答案AAADADDBBDACDC15. ① Hg ②C 2H 5OH ③ SO 2 16. 氢 2:1 17. (1)C CO 2 (2)2CO+O 2高温 2CO 2 CO 2+Ca(OH)2==CaCO 3↓+H 2O18.(1) 混合物 (2) 3CO+Fe 2O 3高温2Fe+3CO 2(3) Fe+2HCl=FeCl 2+H 2↑ 防止铁与氧气、水蒸气等反应而变质 19. C 20. C H O 2:6:1 三、简答题(本题包括4个小题,共10分) 21.(2分)(1)2A1+O 2==A12O 3 (2)2H 2+SiCl 4高温Si +4HCl22.(2分)(1)Hg+S==HgS (2)受热后,汞原子的间隔变大,汞柱上升 23.(3分)(1) 防止高温生成物溅落炸裂瓶底 (2) 氧气约占空气体积的1/5(2)二氧化碳能与水反应生成碳酸24. (3分)(1)A (1分)(2)将铜丝或铜片放入到AgNO 3溶液中,若铜表面有银白色固体析出,说明铜比银活泼(1分) (3)①Zn(NO 3)2和Cu(NO 3)2 ②Zn(NO 3)2、Cu(NO 3)2和AgNO 3 (1分) 四、综合应用题【(1)—(3)每空1分共6分,(4)4分,共计10分】 25.(6分)(1)长颈漏斗(2) 固体颜色由暗紫色变为黑色;2KMnO 4 △K 2MnO 4+MnO 2+O 2↑(3) 能随时控制反应的发生和停止 (4) C (5) ①4.4②解:设5g 石灰石中碳酸钙的质量为x CaCO 3+2HCl====CaCl 2+H 2O+CO 2↑ 10044 x1.76 g100/44=x/1.76g x=4g石灰石中碳酸钙的质量分数4g/5g ×100%=80% 答:石灰石中碳酸钙的质量分数为80%。
