第六章自由空间中的平面电磁波
第六章 平面电磁波

一维电磁波,设电场仅为z的函数:
∂2Ex ∂z 2
−1 υ2
∂2Ex ∂t 2
=0
此方程的通解为
Ex ( z, t)
=
f
(t
−
z υ
)
+
f
(t
+
z υ
)
f ( t- z / v ) f ( t- z / v )
图 7-1 向+z方向传播的波
1
无界媒质中,一般没有反射波存在,只有单一行进方向的波。 假设平面波沿+z方向传播,只有Ex(z, t)分量,方程式的解
旋圆极化波 其它情况是椭圆极化波。
例1:试求下列均匀平面波的极化方式和传播方向。
(1) E = ex Em sin (ωt − kz ) + ey Em cos (ωt − kz )
(2) E = ex E0e− jkz − ey jE0e− jkz
(3)
E
=
ex
Em
sin
⎛⎜⎝ ωt
−
kz
+
π 4
入射波和反射波的形式
Ex
=
E e j(ωt−kz) 0
+
E e' j(ωt+kz) 0
自由空间:
∂Ex = ∂z
Ex
=
E e j(ωt−kz) 0
− jkE0e j(ωt−kz) = −μ
∂H ∂t
y
= − jωμH y
Hy =
E0
e = E e j(ωt−kz)
0 j(ωt−kz)
μ /ε
η
η具有阻抗的量纲,单位为欧姆(Ω),与媒质参数有关,称为媒
自由空间中的电磁波

电磁场量与介质特性量的关系
2020/5/23
6
自由空间中的电磁波— 电磁波的基本特征 为了学习更加复杂形式的电磁波,首先对均匀平面波进行了解和学习。
均匀平面波的解(公式推导)
均匀平面波的传输特性
电磁波谱特性
2020/5/23
7
自由空间中的电磁波— 电磁波的基本特征
2020/5/23
紫外线应用方面如下: 化学:涂料固化,颜料固化,光刻 生物学:紫外线灭菌法,促进植物生长,诱杀蚊虫 仪器分析:矿石,药物,食品分析 应用:人体保健照射,诱杀害虫,油烟氧化,光触酶(二氧化钛)
2020/5/23
13
自由空间中的电磁波— 电磁波的基本特征
6)X 射线
波长为 0.1 ~ 10 nm,在大气中全部被吸收,不能用于遥感 。
干涉的数学模型分析?(公式推导)
干涉产生需要满足的条件
电场强度和磁场强度都必须分别具备相同的振 动方向
频率必须相同 路程差不能太大 振幅不能悬殊太大
干涉结果公式表示
干涉现象
2020/5/23
干涉示意图
20
自由空间中的电磁波— 电磁波的衍射
在物理学中,衍射是指波遇到障碍物或小孔后通过散射继续传播的 现象,孔隙越小,波长越大,现象越显著
2020/5/23
16
自由空间中的电磁波— 电磁波的极化特征 极化的形式数学模型分析(线极化、圆极化和椭圆极化)?(公式推导)
2020/5/23
不同形式极化17 示意图
自由空间中的电磁波— 电磁波的极化特征
极化波的描述
极化方向的定义 ➢ 在一定的坐标系中定义 ➢ 坐标系的选择是任意的 ➢ 极化平面是垂直于传播方向的平面
第6章 自由空间的电磁波

教案课程: 电磁场与电磁波内容: 第6章自由空间的电磁波课时:4学时教师:刘岚。
)线、γ射线等也都是电磁波,科学研究证明电磁波是一个大家族。
所有这些电磁波仅在波长λ(或频率f )上有所差别,而在本质上完全相同,且波长不同的电磁波在真空中的传播速度都是8001/310c εμ=≈⨯(m/s )。
因为波的频率和波长满足关系式f c λ⋅=,所以频率不同的电磁波在真空中具有不同的波长。
电磁波的频率愈高,相应的波长就越短。
无线电波的波长最长(频率最低),而γ射线的波长最短(频率最高)。
目前人类通过各种方式已产生或观测到的电磁波的最低频率为2210f Hz -=⨯,其波长为地球半径的3510⨯倍,而电磁波的最高频率为2510f Hz =,它来自于宇宙的γ射线。
为了对各种电磁波有个全面的了解,人们按照波长或频率的顺序把这些电磁波排列起来,这就是电磁波谱。
多媒体课件展示:电磁波谱图电磁波谱无线电波微波红外线可见光紫外线X 射线伽马射线可见光: 红 | 橙 | 黄 | 绿 | 蓝 | 靛 | 紫由于辐射强度随频率的减小而急剧下降,因此波长为几百千米(105米)的低频电磁波强度很弱,通常不为人们注意。
实际使用的无线电波是从波长约几千米(频率为几百千赫)开始:波长3000米~50米(频率100千赫~6兆赫)的属于中波段;波长50米~10米(频率6兆赫~30兆赫)的为短波;波长10米~1厘米(频率30兆赫~3万兆赫)甚至达到1毫米(频率为3×105兆赫)以下的为超短波(或微波)。
有时按照波长的数量级大小也常出现米波,分米波,厘米波,毫米波等名称。
中波和短波用于无线电广播和通信,微波用于电视和无线电定位技术(雷达)。
可见光的波长范围很窄,大约在7600~4000(在光谱学中常采用埃()作长度单位来表示波长,1=10~8厘米)、从可见光向两边扩展,波长比它长的称为红外线,波长大约从7600直到十分之几毫米。
红外线的热效应特别显著;波长比可见光短的称为紫外线,它的波长为50~4000,它有显著的化学效应和荧光效应。
第六章自由空间传播的电磁波

第 6 章自由空间中的电磁波◇波动无界空间中方程解之一——均匀平面波。
◇该电磁波在无界空间理想介质中的传播特点和各项参数的物理意义。
◇电磁波极化的概念。
实际空间充满了各种不同电磁特性的介质。
电磁波在不同介质中传播表现出不同的特性。
人们正是通过这些不同的特性获取介质或目标性质性的理论依据。
因此电波传播是无线通信、遥感、目标定位和环境监测的基础。
1. 散度的概念2. 旋度的概念 3. 梯度的概念1. 麦克斯韦方程及内涵2. 坡印廷矢量及内涵3. 时谐场的概念主要内容回顾自由空间是一个没有电荷因而也就不存在电流的空间。
这并不是说在整个空间中没有源存在而只是指在我们所感兴趣的区域不存在源这个区域应有0和0。
J 0D/EBt0B/HDt 自由空间中存在着电波波和磁波波BE表明 变化的电场产生变化的磁场 变化的磁场产生变化的电场 二者相互依存。
λ波长观看波形图两边取旋度 6.1 波动方程考虑均匀无耗媒质的无源区域000J00ttEHHEBDtEH2tEEH得2220tEE电场E的波动方程2220tHH磁场H的波动方程得2EEE将矢量恒等式式中2为拉普拉斯算符 在直角坐标系中2222222xyz而波动方程在直角坐标系中可分解为三个标量方程222222220xxxxEEEExyzt222222220yyyyEEEExyzt222222220zzzzEEEExyzt?? 波动方程的解是空间一个沿特定方向传播的电磁波。
?? 电磁波的传播问题归结为在给定边界条件和初始条件下求解波动方程。
复数形式的波动方程——亥姆霍兹方程设为时谐场22222ReRejtjtmmeettEEE得220kEE220kHH亥姆霍兹方程式中22k·用复数形式研究时谐场称为频域问题。
6.2 理想介质中的均匀平面波·平面波——等相位面为平面·均匀平面波——平面等相位面上 场强大小、方向、相位处处相等的平面波。
·均匀平面波是一种理想情况。
平面波电磁场
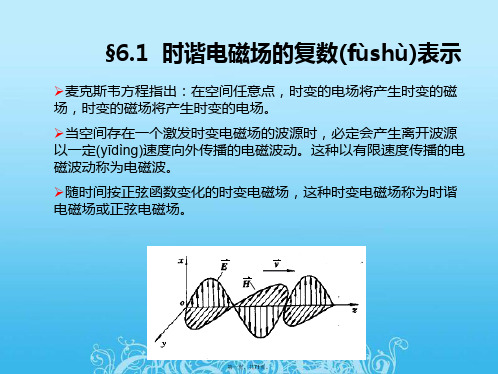
无功功率
Pi 1 2UsIin u(i)Im 1 2U I*
第十八页,共71页。
二、复坡印廷定理(dìnglǐ)
S
Re12EH*ds V
1EJ*dv
2
V
1E2dv
2
S
Im12EH*ds2V
1H21E2dv
4
4
说明:
(1)式表示有功功率平衡(pínghéng),即输入封闭面的 有功功率等于体积中热损耗功率的平均值。
➢波长(bōcλháng):
空 间 相 位 (xiàngwèi)kz 变 化 2π 所 经 过 的 距 离 称 为 波 长 或 相 位
(➢xi波àn数gw: èi)波k 长2
由kλ=2π
➢频率: ➢相速:
f 1 一秒内相位变化2π的次数称为频率
T 2
等相面传播的速度
vp
dz
dt k
1
公式推导: cos(ωt-kz)=const.
一、 复数(fùshù)形式麦克斯韦方程组
t
Ex(t)Ret
(E xejt)Rej[E xejt]
2 t2
2 Ex(t)Ret2
(E xejt)Re[2E xejt]
t
Ex(t)
jEx
E
B
t
RE ej t[ ] Rje B e [j t]
E jB 结论(jiélùn):复数形式麦
ab | a | | b | e j(a ) a | a | e j(a ) b |b|
第三页,共71页。
aa*
aa*
a'
, a"
2
2j
二、复矢量(shǐliàng)
角频率
电磁场计算题

重要习题例题归纳第二章 静电场和恒定电场一、例题:1、例2.2.4(38P )半径为0r 的无限长导体柱面,单位长度上均匀分布的电荷密度为l ρ。
试计算空间中各点的电场强度。
解:作一与导体柱面同轴、半径为r 、长为l 的闭合面S ,应用高斯定律计算电场强度的通量。
当0r r <时,由于导体内无电荷,因此有0=⋅⎰→→SS d E ,故有0=→E ,导体内无电场。
当0r r>时,由于电场只在r 方向有分量,电场在两个底面无通量,因此2ερπl rl E dS E dS a a E S d E l r Sr r Sr r r r S=⋅=⋅=⋅=⋅⎰⎰⎰→→→→则有:r E l r 02περ=2、例2.2.6(39P )圆柱坐标系中,在m r2=与m r 4=之间的体积内均匀分布有电荷,其电荷密度为3/-⋅m C ρ。
利用高斯定律求各区域的电场强度。
解:由于电荷分布具有轴对称性,因此电场分布也关于z 轴对称,即电场强度在半径为r 的同轴圆柱面上,其值相等,方向在r 方向上。
现作一半径为r ,长度为L 的同轴圆柱面。
当m r20≤≤时,有02=⋅=⋅⎰→→rL E S d E r Sπ,即0=r E ;当m rm 42≤≤时,有)4(1220-=⋅=⋅⎰→→r L rL E S d E r Sπρεπ,因此,)4(220-=r rE r ερ;当m r 4≥时,有L rL E S d E r Sπρεπ0122=⋅=⋅⎰→→,即r E r 06ερ=。
3、例2.3.1(41P )真空中,电荷按体密度)1(220ar -=ρρ分布在半径为a 的球形区域内,其中0ρ为常数。
试计算球内、外的电场强度和电位函数。
解:(1)求场强:当a r >时,由高斯定律得2224επQ E r S d E S==⋅⎰→→而Q 为球面S 包围的总电荷,即球形区域内的总电荷。
300242002158)(44)(a dr a r r dr r r Q aaπρπρπρ=-==⎰⎰因此20302152r a a E rερ→→=当a r <时)53(44)(1425300020121a r r dr r r E r S d E rS -===⋅⎰⎰→→επρπρεπ因此)33(23001a r r a E r-=→→ερ (2)球电位;当a r >时,取无穷远的电位为零,得球外的电位分布为ra r d E r r03022152)(ερ=⋅=Φ⎰∞→→当a r =时,即球面上的电位为20152ερa S =Φ 当a r <时)1032(2)(24220011a r r a r d E r a rS +-=⋅+Φ=Φ⎰→→ερ4、例2.4.1(48P )圆心在原点,半径为R 的介质球,其极化强度)0(≥=→→m r a P m r 。
谢处方《电磁场与电磁波》(第4版)章节习题-第6章 均匀平面波的反射与透射【圣才出品】

第6章 均匀平面波的反射与透射一、判断题电磁波垂直入射至两种媒质分界面时,反射系数与透射系数之间的关系为ρτ1+=。
( )ρτ【答案】√二、填空题电磁波从理想介质1垂直向理想介质2入射,介质1和2的本征阻抗分别为30Ω和70Ω,则分界面处的反射系数Γ和透射系数τ分别是_______,_______。
【答案】0.4;1.4三、简答题1.简述平面电磁波在媒质分界面处的反射现象和折射现象满足的斯耐尔(Snell )定律;并具体说明什么条件下发生全反射现象,什么是临界角,给出临界角的计算公式。
答:(1)斯耐尔(Snell )定律:①反射线和折射线都在入射面内;②反射角等于入射角,即;r i θθ=③折射角的正弦值与入射角的正弦值之比等于入射波所在的媒质的折射率与折射波所在媒质的折射率之比,即,式中sin sin ii n n ττθθ=n =(2)全反射现象:①理想导体全反射。
在电磁波入射到理想导体表面时,由理想导体表面切向电场为零的条件,反射系数为±1,称为理想导体全反射现象;②理想介质全反射。
当电磁波由光密介质入射到光疏介质时,由于,根据斯耐12n n >尔定律有。
当入射角增加到某一个角度时,折射角就可能等于。
因此,i τθθ>i θπ2c θ<τθπ2在时,就没有向介质2内传播的电磁波存在,即发生全反射现象。
c θθ>能使的入射角称为临界角,有:π2τθ=c θ21sin c n n θ==2.什么是电磁波在媒质分界面的全反射现象和全折射现象?什么是临界角和布儒斯特角?一个任意极化波由空气斜入射到一介质界面,以什么角度入射才能使反射波为线极化波?说明原因。
答:(1)当电磁波由光密介质入射到光疏介质时,由于,根据斯耐尔定律有12n n >。
当入射角增加到某一个角度时,折射角就可能等于。
因此,在i τθθ>i θπ2C θ<τθπ2时,就没有向介质2内传播的电磁波存在,即发生全反射现象。
第6章习题解答

根据题意,可知:平面波的角频率ω = 18π ×106 rad s ;波数 k = 1π rad m 3
由此得出
频率: f = ω = 9×106 Hz ; 2π
相速: vp = f λ = 54 ×106 m s
波长: λ = 2π = 6m k
能流密度矢量为
S
=
E
×
H
=
ex
1 η
sin2 (18π
e
z
A/m
(3)当t = 10−8 s 时,为使电场强度为最大正值,应有
PDF 文件使用 "pdfFactory Pro" 试用版本创建
2π ×108 t − 4π x + π = 2π ×108×10−8 − 4π x + π = ±2nπ
36
36
解之得的电场强度最大正值的位置在
(V/m)
f = c = 3×108 = 45 ×108 = 1.43×109 (Hz) λ π /15 π
于是可知
H = −e y 3π cos(9 ×109 t + 30z) (A/m)
E = e x 360π 2 cos(9 ×109 t + 30z) (V/m)
6-4 在自由空间中,某电磁波的波长为 0.2m。当该波进入到理想电介质后,波长变为 0.09m。
x = 13 m 3 n = 13 m nλ 82 8
(n = 0,1,2L)
6-9 某电台发射 600KHz 的电磁波,在离电台足够远处可以认为是平面波。设在某一点 a, 某瞬间的电场强度为10−4 V/m,求该点瞬间的磁场强度。若沿电磁波的传播方向前行 100 m,到达另一点 b,问该点要迟多少时间,才具有10−4 V/m 电场。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面直角坐标系
矢量: A ex Ax ey Ay ez Az
Ax Ay Az 散度: A x y z ex 旋度: A x Ax ey y Ay ez z Az
柱坐标系
矢量: A er Ar e A ez Az
波动过程中,等相面和传播方向是垂直的。
平面波
定义 平面波,是三维波中最简单的一种。这个波在空 间传播过程中,对应于任意时刻t,在其传播空间 具有相同相位的点所构成的等相位面(也称为波 阵面)为平面,于是就称其为平面波。
理解
均匀平面波是研究起来最简单同时也是最容易理 解的。 均匀(Uniform):在任意时刻,在所在的平面中 场的大小和方向都是不变的。
J
作为一个矢量方程,上式包含了三个常微分方程,每 一个分别对应着一个分矢量 ,其方程 ex , e y , e z 形式为:
d2 f 2 2 f 2 dz c
根据高等数学知识,由于f仅为z的函数,f对z二次微分后与本身仅差一个 常数,所以,方程的解必为z的指数函数,设为:
f C exp( z )
J
因此 ES exC1 exp(i z / c) eyC2 exp(i z / c) ezC3 exp(i z / c) 或
ES E0 exp(i z / c)
其中 E0 表示一个任意的常矢量
平面波可表示为
E(r, t ) Es ( z) exp(i zt ) E0 exp(i z / c) exp(i zt )
式中C和β都是常数,从β所具有的性质看,我们称其为相位常数,通过代 入方程解得: 2
2
C2
或
i
C
f a exp(i z / C ) b exp(i z / C )
f C exp(i z / C )
物理意义:+z方向传播的 波与-z方向传播的波叠加 其中的±符号表示C是两个 可能的任意常数
1 rAr 1 A Az 散度: A r r r z er r 旋度: A r Ar e rA ez r z Az
球坐标系
矢量: A eR AR e A e A 散度:
1 R AR 1 1 A A 2 sin A R r R sin R sin
其中
(i / c)E0 z exp[(i / c)( z ct )] 0
已知 E0 是一个常量,要使上式对任意 z 与t均成立,则只有 z 由麦克斯韦第一方程可知,平面电波没有沿z轴的分量, 即在波的传播方向上不存在电场分量,换句话说,平面电波是横波。
E0 z=0
相伴而生的B波
如果存在一个随时间变化的电场,那么同时必将会出现一个磁场, 在自由空间中,这两种场的关系为
结论
在自由空间中的电波和磁波,均以光 速传播,彼此互为因果,相伴产生。其波 动方程均满足Helmholtz方程,不发生衰减。
2 1 E 0 2 2 c t B
2
单频电磁波
随时间正弦变化(单频)的波在空间传 播过程中,按波前等相位面(或波振面)的 形状,可分为平面波、柱面波和球面。若等 相位面上各点波的振幅也相同就,则称为均 匀波。否则,称为非均匀波。
自由空间中的平面电磁波
目 的
研究平面单色(单波长)波(plane monochromatic wave), 探索E波和B波在自由空间的传播过程中是如何相互关联的。
随时间变化的波
E(r, t ) ES ( z)exp(it )
该式表示一种随时间变化的波,即角频率为ω的正弦波,它只在Z方向上传播, 由于其频率一定,我们称这种波为平面“单色”波。
由此可以看出±号的意义:表示了波沿着Z轴正方向 传播和沿着Z轴负方向传播。
结论:
E (r , t ) EA f ( z ct ) EB g ( z ct )
1. 方程解中常数C所包含的±号分别表示了波沿 着Z轴正方向传播和沿着Z轴负方向传播。 2. 一旦确定了任意常矢量,电场波传播的方向也 就随之而定。即电波将会随着时间的变化而沿 着确定的传播方向以正弦波的形式向前传播。
2
eR 1 旋度: A 2 R sin R AR
Re RA
R sin e R sin A
Maxwell方程组预言电磁波的存在
B E t D H t D B BE H
*
赫 兹 实 验
赫兹实验在人类历史上首次发射和接收了电磁波,且通
一维波动方程
( z, t ) 1 ( z, t ) 2 0 2 2 z v t
2 2
解为行波
f ( z vt ) g ( z vt )
一维波的数学形式 自变量为(z-vt)的函数f(z-vt)表示以速度 v 沿着 Z 方向传播的行波(Traveling wave)
2 2 1 1 2 拉普拉斯算子: 2 r 2 2 r r r r z
球坐标系
1 1 哈密顿算子: eR e e R r r sin 拉普拉斯算子:
2 1 1 1 2 2 2 R 2 sin 2 2 R R R R sin R sin 2
微分形式:
积分形式:
D B E t B 0 D H J t
D dS Q
S
B l E dl S t B dS 0
S
D l H dl I S t
或 E(r, t ) EA exp(i z / c)exp(it ) EB exp(i z / c)exp(it ) 即 E(r, t ) EA exp[(i z / c)( z ct )] EB exp[(i z / c)( z ct )]
EA f ( z ct ) EB g ( z ct )
过多次实验证明了电磁波与光波一样能够发生反射、折射、 干涉、衍射和偏振,验证了麦克斯韦预言,揭示了光的电磁 本质,从而将光学与电磁学统一起来。
变化的磁场产生电场
B E t
自由空间中电场的波动方程
B E E B t t 2 E ( E ) E E 并且有: B , E 0 t 2 E 2 E 2 0 t
三、平面电磁波的特性
平面电波必定是横波
因为 所以
E 0
其中 E ex Ex ey E y ez Ez
Ex E y Ez 0 x y z
而平面电波 E 的分量都与x ,y无关
E E0 exp(i / c)( z ct )
Ez 0 z
E0 ex E0 x ey E0 y ez E0 z
自由空间中电磁场的波动方程—Helmholtz方程
2 2 E 0 2 t B
一维行波波动图
电磁波的波速
三维波动方程一般形式
2 1 ( x, y, z, t ) 2 ( x, y, z, t ) 2 0 2 v t
自由空间中的电磁波
第六章
时变电流或 加速运动的 电荷向空间 辐射电磁波
能量存在的一种形式 作为探求未知物质世界 的手段应用于雷达、导 航、遥测、遥感和遥控 作为信息的载体应用于 通信、广播、电视 电磁波辐射问题
研究设计产 生能满足各 种应用要求 的电磁波
电 磁 波
电磁波的产生与传播
由麦克斯韦的电磁场理论,变化的电场产生变化的磁场, 而变化的磁场又产生变化的电场,这样,变化电场和变化磁场 之间相互依赖,相互激发,交替产生。在迅变情况下,电磁场 以波动形式存在。变化着的电场和磁场互相激发,形成在空间 中传播的电磁波。由于在广播通讯、光学和其他科学技术中的 广泛应用,电磁波的传播、辐射和激发问题已发展为独立的学 科,具有十分丰富的内容。
变化的电场产生磁场
D B E H t t E B t
自由空间中磁场的波动方程
E B B E t t 2 B ( B) B B 并且有: E , B 0 t 2 B 2 B 2 0 t
2 2
解为行波
X ( x vt ) Y ( y vt ) Z ( z vt )
平面直角坐标系
哈密顿算子: ex ey ez x y z 拉普拉斯算子: 2 2 2 x y z
2 2 2 2
柱坐标系
1 哈密顿算子: er e ez r r z
将该平面“单色”波的函数代入一般的三维电波方程得
2 1 E 2 E 2 2 c t
1 exp(it ) Es 2 Es ( 2 ) exp(it ) c
2
2 2 2 2 d Es 2 Es ( 2 2 2 ) Es x y z dz 2
d 2 Es 2 2 Es 2 dz c
微分形式:
积分形式:
D 0 B E t B 0 D H t
D dS 0
S
B l E dl S t SB dS 0 D l H dl S t
E B / t
c B E / t
2
E(r, t ) E0 exp(i / c)( z ct )
平面电波不存 在着Z分量
E (r , t ) {ex E0 x eY E0 y eZ 0}exp(i / c)( z ct )
