【最新试题库含答案】巴蜀中学数学试题
重庆巴蜀中学2024年高一下学期7月期末考试数学试题+答案

高2026届高一 (下) 期末考试数学试卷注意事项:1.答题前,考生务必将自己的姓名、准考证号、班级、学校在答题卡上填写清楚。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试卷上作答无效。
3.考试结束后,请将答题卡交回,试卷自行保存。
满分150分,考试用时120分钟。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设△ABC的内角A,B,C所对的边分别为aa,bb,cc, 若aa=√3,bb=1,AA=ππ3,则B= ( )A. ππ3 B、ππ2 C. ππ6 D. ππ42. 某校高一年级有四个班共有学生200人, 其中1班60人, 2班50人, 3班50人, 4班40人.该校要了解高一学生对食堂菜品的看法,准备从高一年级学生中随机抽取40人进行访谈,若采取按比例分配的分层抽样,且按班级来分层,则高一2班应抽取的人数是( )A. 12B. 10C. 8D. 203.已知平面四边形OABC用斜二测画法画出的直观图是边长为1的正方形OO′AA′BB′CC′,则原图形OABC中的AB= ( )A. √2BB.2√2C. 3D. 24.已知m,n,β是两个不重合的平面,则下列结论正确的是( )A. 若α∥β, m∥β, 则m∥αB. 若m⊥α, n⊥α, 则m∥nC. 若m∥α, m∥β, 则α∥βD. 若m⊥n, m⊂α, 则n⊥α5.甲、乙、丙3人独立参加一项挑战,已知甲、乙、丙能完成挑战的概率分别为13、13、14,则甲、乙、丙中有人完成挑战的概率为 ( )A. 15B. 13 c. 25 D. 236.平行六面体. AABBCCAA−AA₁BB₁CC₁AA₁中, 底面ABCD 为正方形, ∠AA1AAAA=∠AA1AABB=ππ3, AAAA₁=AABB=1,E为C₁D₁的中点,则异面直线BE和DC所成角的余弦值为 ( )A. 0 BB.√32C. 12AA.√347.甲在A处收到乙在航行中发出的求救信号后,立即测出乙在方位角(是从某点的正北方向线起,依顺时针方向到目标方向线之间的水平夹角) 为45°、距离A处为10n mile的 C处,并测得乙正沿方位角为105°的方向, 以6n mile/h的速度航行, 甲立即以14n mile/h的速度前去营救,甲最少需要 ( )小时才能靠近乙.A. 1B. 2C. 1.5D. 1.28.已知向量OOAA满足|OOAA在OOAA方向上的投影向量为OOAA12,则CCAA�����⃗⋅CCBB�����⃗的最小值为( )AA.−12BB.4−2√63CC.1−√72AA.5−2√74二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 设复数z的共轭复数为zz̅,ii为虚数单位, 若(zz+2)ii=1+ii, 则( )A. 复数z的虚部为-1B. |z|=2C. zz̅在复平面内对应的点在第一象限AA.zz⁸=1610.一个袋子中有大小相同,标号分别为1,2,3,4的4个小球.采用不放回方式从中任意摸球两次,一次摸一个小球.设事件A=“第一次摸出球的标号小于3”,事件B=“第二次摸出球的标号小于3”,事件C=“两次摸出球的标号都是偶数”,则 ( )A. P(A)=P(B) BB.PP(AABB)=16CC.PP(AA∪BB)=23AA.PP(AACC)=11211. 如图, 在棱长为2的正方体ABCD-A₁B₁C₁D₁(中,点M 分别为CC₁上的动点,O为正方体内一点,则以下命题正确的是 ( )A. B₁M+DM 取得最小值2 √5B.当M为中点时,平面BMD₁截正方体所得的截面为平行四边形C. 四面体ABMD的外接球的表面积为5π时, CM=1D. 若AO=CO, A₁O=2, 则点O的轨迹长为. √2ππ三、填空题:本题共3小题,每小题5分,共15分.12. 已知向量aa⃗=(1,1),bb�⃗=(mm,−)若aa⃗//�aa⃗+bb�⃗�,则m= .13.若圆锥的轴截面是边长为2的等边三角形,则圆锥的侧面积为 .14. 记△ABC的内角A, B, C所对的边分别为a, b, c, 已知aaaaii aa AA+ccaaii aa CC=aaccaaaaCC+ccccaaaaAA,若△ABC的面积, SS=ttbb²(tt>0),则tt的最大值为 .四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.15.(本小题满分13分)为调查外地游客对洪崖洞景区的满意程度,某调查部门随机抽取了100位游客,现统计参与调查的游客年龄层次,将这100人按年龄(岁)(年龄最大不超过65岁,最小不低于15岁的整数) 分为5组, 依次为[15,25),[25,35),[35,45),[45,55),[55,65], 并得到频率分布直方图如下:(1)求实数aa的值;(2)估计这 100人年龄的样本平均数(同一组数据用该区间的中点值作代表);(3)估计这 100人年龄的第80百分位数.(结果保留一位有效数字,四舍五入)16.(本小题满分15分)如图,在直四棱柱. AABBCCAA−AA₁BB₁CC₁AA₁中, 四边形ABCD是一个菱形, ∠DAB=60°, ∠AAAABB=60°,点P为BC₁上的动点.(1) 证明: DP//平面AB₁D₁;(2)试确定点P的位置,使得. BBCC⊥AAPP.17.(本小题满分15分)在. △AABBCC中,角A,B,C所对的边分别为aa,bb,cc, aa=2,√3�cosAA sinAA+cosBB sinBB�=2cc bb.(1) 求A的大小;�����⃗=AABB�����⃗3+2AAAA�����⃗3,若A 为钝角,求△AABBAA面积的取值范围.(2) 已知AAAA18.(本小题满分17分)已知三棱台−AA₁BB₁CC₁中, △ABC为正三角形, AA1BB1=AAAA1=BBBB1=12AABB=1,点E为线段AB 的中点.(1) 证明: A₁E∥平面B₁BCC₁;(2) 延长AA₁, BB₁, CC₁交于点 P, 求三棱锥P-ABC的体积最大值;(3)若二面角AA−CCCC₁−BB的余弦值为13,求直线BB₁与平面. AACCCC₁AA₁所成线面角的余弦值.19.(本小题满分17分)球面三角学是研究球面三角形的边、角关系的一门学科.如图,球O 的半径为R.A、B、C为球面上三点,劣弧BC的弧长记为aa,设O。
重庆市渝中区巴蜀中学校2023-2024学年八年级上学期期末数学试题(含答案)

数学一、选择题(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑.1.在下列几种汽车标识图中,不是轴对称图形的是( )A .B .C .D .2.若分式有意义,则的取值范围是( ).A . B . C . D .且3.下列运算正确的是()A . B . C . D .4.下列多项式中,在实数范围内不能进行因式分解的是( )A .B .C .D .5.如图,圆柱体的底面周长为是底面圆的直径,在圆柱表面的高上有一点,,一只蚂蚁从点出发,沿圆柱的表面爬行到点的最短路程是( )A .B .C .D .21a a -a 0a ≠12a≠12a ≥12a ≥-0a ≠632x x x ÷=325a a a ⋅=33(2)6x x =32254a a a-=22x y -244b b -+-322a a a ++222m mn n--6cm,AB BC D 2,6cm BD CD BC ==A D 5cm6的运算结果应在( )A.4与5之间 B .5与6之间 C .6与7之间 D .7与8之间7.下列四个命题中,是假命题的是( )A .对角线互相平分的四边形是平行四边形B .对角线相等的四边形是矩形C.对角线互相垂直且平分的四边形是菱形D .对角线互相垂直的矩形是正方形8.如图,在中,的角平分线交于边上一点,且,线段的长为()A .B .C .D .39.如图,在菱形中,对角线与相交于点是上任一点,于于,若,则的值为( )A .B .C .D .10.如图,在矩形中,对角线相交于点平分交于,以为边向矩形内作等边三角形,连接的度数为( )A .B .C .D .+ABCD ABC BCD ∠∠、ABE BE AB ==CEABCD AC BD ,O P AC PE AB ⊥,E PF BC ⊥F 8,6AC BD ==PE PF +65125245485ABCD AC BD 、,,O AB BO AE =BAD ∠BC E EC ECF .DF BDF ∠10︒12︒15︒17︒11.若关于的不等式组有且只有两个偶数解,且关于的分式方程有解,则所有满足条件的整数的和是()A .5B .7C .10D .1512.如图,为正方形内一点,过作直线交于点,过作直线交、于,且.若.以下结论:①为等边三角形;②③.其中正确的有()A .1个 B .2个 C.3个 D .4个二、填空题(本大题8个小题,每小题4分,共32分)请将每小逶的答案直接填写在答题卡中对应的横线上.13.用科学计数法表示的数,用小数表示为______.14是同类二次根式,那么的值为______.15.在中,若,则的度数为______度.16.若,则______.17.如图,四边形是菱形,交于点交手点,连接,若,则______.x 2112123x a x x -≤-⎧⎪⎨+-<⎪⎩y 46222ay y y y ++=---a P ABCD P PD BC E P GH AB DC G H 、GH DE =,15APD DEC EDC ∠=∠∠=︒ABP △PG =234PBE S PD =△PE PG =+35.1210-⨯x ABCD 50A B ∠=∠+︒B ∠57x x y =+y x=ABCD AC BD 、,E DF AB ⊥AB F EF 16,6AC EF ==DF =18.如图,在平行四边形中,分别为边的中点,连接,当平分时,的长为______.19.如图,矩形中,为边上一点,为边上一点,连接,将四边形沿翻折,点恰好落在边上处,点的对应点为,则的长为______.20.一个四位数,且满足各数位上的数字互不相同,且都不为零.若将的个位数字与千位数字交换,百位数字与十位数字交换,得到新的一个数,记,若为整数,我们称为“善雅数”.例如:,为“善雅数”.求______;若是“善雅数”,当最大时,______.三、解答题:(本大题共8个小题,21-25题每小题8分,26-28题每小题10分共70分)解答时每小题都必须写出必要的演算过程或推理步聙,请将解答过程书写在答题卡中对应的位置上.21.计算:(1(2)22.已知:如图,在矩形中,是边上的点,连接.(1)尺规作图,以为边,为顶点作交线段于点.(要求:基本作图,保留作图痕迹,不写作法,不下结论).(2)求证:四边形为平行四边形(请完善下面的证明过程).ABCD AD E F =、BC CD 、EF AE BD 、、AE BEF ∠BD ABCD E AB ,BE BC F =CD EF BEFC EF B AD G C .39H AB AG ==EF n abcd =n n m ()27n m F n -=()F n n ()341221433412,4727n F n -=== n ∴()6472F =n ()F n m =)2+2224124421x x x x x x x ⎫⎫⎛⎛---⋅⎪⎪ -+-+⎝⎝⎭⎭ABCD E CD AE BC C ,BCF DAE CF ∠=∠AB F AFCE证明:四边形为矩形在和中②______③______即四边形为平行四边形(④______)(填写推理依据).23.先化简再求值:,其中24.如图,在直角中,是边上一点,连接为的中点,过作交延长线于,且平分,连接.(1)求证:四边形是菱形.(2)连接交于,求的度数.25.会一门艺术、优雅生活!巴蜀中学一年一度的艺术节于12月26日开幕,同学们编排节目、设计活动、制作海报,热情高涨.如图是初二某班同学设计制作的艺术节海报展示支架,其中支架底坐长长为支撑杆,支撑点可以沿着上下自由滑动,从而实现倾斜程度的改变.(1)当支撑点在中点时,连接,测得,求支撑杆的长度.(2)当支撑点在处时,连接比长,求此时到的距离.ABCD ,,,90AB CD AD BC AB CD B D ∴==∠=∠=︒∥ADE △CBF △D B AD BC∠=∠⎧⎪=⎨⎪⎩①______()ASA ADE CBF ∴△≌△DE ∴=CD DE AB ∴-=-CE AF=∴AECF 22691232183x x x x x x ++⎫⎛÷-+ ⎪--⎝⎭3x =-AEC △90,E B ∠=︒AE ,BC O AC C CD AB ∥BO D AC BCD ∠AD ABCD OE BC ,27F ACD ∠=︒CFO ∠OA 1.5m,OK 1.8m,AM M OK OK OK AK AK AO =AM M ',,AK AM AK AK ⊥''''OM '0.6m A OK '26.“元旦节”假期最后一天,李老师驾车从老家沿高速路回主城,途中依次经过四地,其中和路程均为为高速出口,且在出口旁有加油站,的路程为.李老师用2小时通过路段,其中通过路段的平均速度是通讨路段的1.2倍.(1)求李老师通过路段的平均速度.(2)李老师所驾驶汽车的“最佳油耗时速”为(以此速度行驶时油耗最低),以“最佳油耗时速”行驶,每100公里耗油为,速度每增加,每100公里耗油增加.当他经过地时的时间为上午9:30,发现此时油箱里还剩余燃油.若李老师要在中午12:00前通过地,同时通讨地时燃油未耗尽,求他在路段的平均时速的取值范围.27.在平面直角坐标系中,直线与轴交于点,与轴交于点,且,.(1)如图1,点为线段上一点,若,求点的坐标;(2)如图2,点在线段上,是直线上的两个动点且是轴上任意一点,连接,求的最小值;(3)在(2)的条件下,当取最小值时,为直线上一动点,是平面内任意一点,当四点构成的四边形是以为边的菱形时,请直接写出点的坐标.28.如图,中,点分别在边上,连接.(1)如图1,连接,若的长.(2)如图2,平分交于,连接为延长线上一点,连接.求证:.(3)如图3,在(2)的条件下,为平面内一点,,当最大时,直接写出的面积.A B C D 、、、AB BC 90km,D CD 240km AC BC AB AB 80km /h 5L 2km /h 0.1L C 14.4L D D CD AB x A yB 30OAB ∠=︒9OA =CAB AOC S =△C D OA 2,OD DA E F =、AB EF =G x DE GF 、DE EF FG ++DE EF FG ++M FG N A B M N 、、、AB N ABC △D E 、BC AC 、,AD AD AB =DE ,60,2DC AE AD BAD AB ==∠=︒=+DE AF DAC ∠DC ,30F AFB ∠=︒,.FE FEC ABC G ∠=∠AD ,60GE GB EGB ∠=︒、BG EG +=2AC AB P ==AP =2PC PB -APC △参考答案一、选择题:(每题4分,共48分)1-5:ABBDA 6-10:CBDCC 11-12:AC二、填空题:(每题4分,共32分)13.0.00512 14.6 15.65 16. 17.9.6 18. 1920.138,1289三、解答题:21.(1)解:原式(2)解:原式22.(1)(2)①②③④一组对边平行且相等的四边形是平行四边形23.解:原式2522=--+0=()()()22221(2)21x x x x x x x ⎡+-⎤-=-⋅⎢⎥--+⎣⎦()()22212121x x x x x x x x x --+=⋅-⋅-+-+()211x x x x x +=-++21x x x +=+x=DAE BCF∠=∠BFBF()()22(3)(3)122333x x x x x x ⎡⎤+-+=÷⎢⎥+--⎣⎦()2369233x x x x x +++=÷--将代入原式24.解:(1)为中点在和中又四边形是平行四边形又平分又,又是平行四边形四边形是菱形(2)为中点,又又为中点,()23323(3)x x x x +-=⨯-+()123x =+3x =-==CD AB∥BAO DCO∴∠=∠O BD BO DO∴=AOB △COD △BAO DCO AOB CODBO DO ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS AOB COD ∴△≌△AB CD ∴=AB CD∥∴ABCD AC BCD∠BCO DCO ∴∠=∠DCO BAO∠=∠BCO BAO∴∠=∠AB BC ∴=ABCD ∴ABCD ,CD CB O = BD 27BCO DCO ∴∠=∠=︒CD AB∥27BAO DCO ∴∠=∠=︒O AC AE EC⊥54EOC ∴∠=︒25.解:(1)为中点答:支撑杆长(2)设,则在中由勾股定理过作于则答:到的距离为.26.解:(1)设李老师通过路段的平均速度为,则通过路段的平均速度为解得:经检验:是原方程的解且符合题意(不检验扣1分)答:李老师通过路段的平均速度为.(2)设李老师在路段的平均速度比增加了个由题意得:99CFO ∴∠=︒,AK AO M = OK ,0.9AM OK OM ∴⊥= 1.2mAM ∴==1.2mOM x '=0.6AK x =+'1.8OA ∴= 1.8M K x∴='-'RT AM K ''△2221.2(0.6)(1.8)x x ++=-0.3x ∴=0.9, 1.5AK M K ='='∴'A AH OK ⊥'HM K AH AK AM ⋅='⋅'''1.50.9 1.2AH =⨯18m 25AH ∴=A OK '18m 25AB km /h x BC 1.2km /hx 909021.2x x+=82.5x =82.5x =AB 82.5km /h CD 80km /h a 2km /h()()2.580224024050.114.4100a a ⎧⨯+>⎪⎨+⨯<⎪⎩解得:.答:李老师通过路段的速度应大于小于27.解:(1)由过作,得在中,(2)将延方向平移则刚好落在轴上作关于直线的对称点可得810a <<16220a∴<<96802100a ∴<+<CD 96km /h 100km /h9AOC S OA ==△C CH OA⊥1S 2AOC OA CH =⨯⨯△CH =t R AHC =△30OAC ∠=︒6,3AH OH ∴==(C ∴2OD DA= 6OD ∴=DE EF D 'y D 'EF D ''OD D B D B ''''===ID OI =''=(3)28.解:(1)过作交于为等边三角形,设,则,即(2)法一:过作交于,延长到使,连接32D ⎛∴ ⎝''11315,22M N ⎛⎛-+ ⎝⎝22315,,,22M N ⎛⎛-+ ⎝⎝33321,22M N ⎛⎛+ ⎝⎝44321,,,22M N ⎛⎛+ ⎝⎝E EH CD ⊥CD H,60ADAB BAD =∠=︒ABD ∴△60,120ADB ADC ∠=︒∠=︒,30AD DC DAE DCE =∴∠=∠=︒AD AE= 75,45ADE EDC ∴∠=︒∠=︒EH x =,DH x CH ==2x ∴+=+2x ∴=2EH =DE ∴=A AM BC ⊥BC M GB N BN EG =AN ,AB AD EFC ABC=∠=∠在和中在和中法二:延长到使,连接证得由得ADB CEF∴∠=∠ADF AEF∴∠=∠ADF △AEF △ADF AEF DAF EAFAF AF ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS ADF AEF ∴△≌△AD AE AB∴==30AFB ∠=︒60MAF ∴∠=︒,BAM DAM DAF EAF∠=∠∠=∠ 120BAC ∴∠=︒60120180BAC EGB ∠+∠=︒+︒=︒180ABG AEG ∴∠+∠=︒ABN AEG∴∠=∠ABN △AEG △AB AE ABN AEGNB EG =⎧⎪∠=∠⎨⎪=⎩()SAS ABN AEG ∴△≌△,AN AG NAB GAE∴=∠=∠120BAD GAE BAD NAB NAG ∴∠+∠=∠+∠=∠=︒BG BN ∴+=BG EG ∴+=GE Q EQ BG =AQ ADF AEF △≌△AB AE=GEC ABG ∠=∠60,120BAE BGE BAE ∠+∠=︒∠=︒证(3)ABG AEQ△≌△6。
重庆市巴蜀中学校2024-2025学年八年级上学期第一次月考数学试卷(含答案)

数学一、选择题(本大题10个小题,每小题4分,共40分)1.的相反数是()A.B.C.3D.2.地铁是城市轨道交通的一种,截止2024年年初,重庆已运营12条轨道交通线路,建成全国规模最大的山地城市交通运营网络,进入世界级轨道交通城市行列.下列分别是我国深圳、石家庄、重庆、北京的地铁图标,其中是轴对称图形的是()A.B.C.D.3.下列式子中,运算正确的是()A.B.C.D.4.如图,在中,,在的延长线上取点D,过点D作.若,则的度数为()A.38°B.42°C.52°D.62°5.设n为正整数,且,则n的值为()A.3B.4C.5D.66.为了促进A,B两小区居民的阅读交流,区政府准备在街道上设立一个读书亭C,使其分别到A,B两小区的距离之和最小,则下列作法正确的是()A.B.C.D.7.《九章算术》中有这样一道题:“今有善行者一百步,不善行者六十步.今不善行者先行一百步,善行者追之,问几何步及之?”意思是:走路快的人走100步时,走路慢的人只走60步,走路慢的人先走100步,走路快的人要走多少步才能追上?设走路快的人走m步才能追上走路慢的人,此时走路慢的人走了n 步,则可列方程组为()3-13-3-13224a a a+=358a a a⋅=632a a a÷=()32626a a=Rt ABC△90A∠=︒AB DE BC∥38C∠=︒D∠1n n<<+A .B .C .D .8.下列说法正确的是( )A .等腰三角形是一个轴对称图形,它的对称轴是底边的高线B .三角形三边垂直平分线的交点到三角形三个顶点的距离相等C .有两个角相等的等腰三角形是等边三角形D .全等的两个图形一定关于某条直线成轴对称9.如图,在长方形中,点E 是边上一点,连接、,将沿着翻折,点C 恰好落在边上的点F 处.若,,则面积是( )A .9B .12C .15D .1810.已知单项式串:,,,,…,,其中n ,为非负整数,,,,…,均为正整数.规定:,,,…,,整式的所有系数的和记作.如:因为,所以;因为,所以;因为,所以.以下说法:①若,,,,则;②若,则所有满足条件的整式的和为;③若,则所有满足条件的整式有9个.其中正确的个数是( )A .0B .1C .2D .3二、填空题(本大题8个小题,每小题4分,共32分)11.计算:______.12.已知一个多边形的内角和是外角和的3倍,则这个多边形的边数为______.13.如图,在中,,的垂直平分线交于点E ,交于点D ,连接.若10010060m n m n =+⎧⎪⎨=⎪⎩10060100m n m n =+⎧⎪⎨=⎪⎩10010060m n m n =-⎧⎪⎨=⎪⎩10060100m n m n =-⎧⎪⎨=⎪⎩ABCD BC AE DE CDE △DE AE 75DEC ∠=︒3CD =ADE △0a 1a x 22a x 33a x n n a x 0a 1a 2a 3a na 00M a =11M a x =2222020M a x M a x a =+=+()22n n n n M a x M n -=+≥n M ()n F M 00M a =()00F M a =11M a x =()11F M a =2220M a x a =+()220F M a a =+01a =12a =23a =34a =()36F M =()34F M =3M 3610x x +()6n n F M +=n M ()201π32⎛⎫--= ⎪⎝⎭ABC △6cm AC =AC BC AC AE的周长为,则的周长为______cm .14.若,则______.15,则以a 、b 为边的等腰三角形的底边长为______.16.若关于x 的不等式组的解集为,且点关于y 轴对称的点在第二象限,则所有满足条件的整数m 的值之和为______.17.如图,在中,,点D 为外一点,连接、、,使得,,,则的度数是______.18.如果一个四位自然数的各数位上的数字互不相等且均不为0,满足千位数字与十位数字之和等于百位数字与个位数字之和,且都为8,则称这个四位数为“拜拜数”.例如:对于7216,因为,所以7216为“拜拜数”.请写出符合条件的最小“拜拜数”是______.已知一个“拜拜数”M 的千位数字是,百位数字是b ,十位数字是(其中,,,且a ,b ,c ,d 均为整数),记M 的千位数字与个位数字的乘积为,百位数字与十位数字的乘积为.若是一个自然数的平方,则满足此条件的最大“拜拜数”是______.三、解答题(本大题8个小题,共78分)19.(1);(2);(3);(4).20.(6分)化简求值:,其中,.21.(8分)在学习了全等三角形的知识后,一位同学进行了如下的探究,他发现:在一组对边平行且相等ABE △14cm ABC △2340x y +-=927x y⋅=30b +-=12333x m x x -⎧≥-⎪⎨⎪-<+⎩3x >-()27,4m +ABC △AB AC =ABC △AD BD CD 60ABD ∠=︒79ADB ∠=︒22BDC ∠=︒CBD ∠71268+=+=2a 2c d +14a ≤≤17b ≤≤127c d ≤+≤()F M ()K M ()()442F M K M a c d --++242x y xy ⋅()()23x x y ⋅-()1323a b a b ⎛⎫-⋅+ ⎪⎝⎭()()()23a b b a a a b +⋅-+-()()11222x x y x y x y ⎛⎫+-+- ⎪⎝⎭2x =1y =-的四边形中,它的一组对角顶点到另一组对角顶点所连线段的距离存在着一定的数量关系.这位同学利用三角形全等证明了他的猜想,请根据他的想法与思路,完成以下作图与填空.(1)如图,在四边形中,,,连接,于点F .利用尺规作图,过点B 作的垂线,垂足为点E (不写作法,保留作图痕迹)·(2)在(1)问所作的图形中,求证:.证明:∵,∴___①___,∵,,∴在和中,∴.∴___③___.于是这位同学得到的结论是:在一组对边平行且相等的四边形中,___④___.22.(8分)为了解某校八年级学生的体育测试情况,随机抽取了该校若干名八年级学生的体育测试成绩进行了统计分析,并根据抽取的成绩绘制了如下的频数分布表和频数分布直方图:成绩x /分频数频率40a b0.4550c 200.1请根据所给信息,解答下列问题:(1)上述图表中______,______,______,(2)请补全频数分布直方图;(3)若该校八年级共有2200名学生参加此次体育测试,估计该年级体育成绩不低于36分的学生人数是多ABCD AB CD =AB CD ∥AC DF AC ⊥AC BE DF =AB CD ∥BE AC ⊥DF AC ⊥90AEB CFD ∠=∠=︒ABE △CDF △______BAE DCF AB CD ∠=∠⎧⎪⎨⎪=⎩②()AAS ABE CDF ≌△△4350x ≤≤3643x ≤<2936x ≤<2229x ≤<a =b =c =少?23.(10分)如图,在和中,点C 在线段上,与交于点F .若,,.(1)求证:;(2)若,,求的度数.24.(10分)“金秋墨彩庆华诞,笔落惊云书国魂.”为庆祝建国75周年,年级决定举行书法比赛,为奖励在比赛中表现优秀的同学,年级提前购买了甲、乙两种奖品。
2024年重庆市巴蜀中学(巴本)小升初数学真题试卷附详细答案

2024年重庆市巴蜀中学(巴本)小升初数学真题试卷2024.01.041、甲、乙、丙出去探险,他们三个人路上觉得无聊,开始玩游戏。
第一轮,乙、丙获胜,他们的卡牌分别翻了一倍;第二轮甲、乙获胜,他们的卡牌翻了一倍;第三轮甲、丙获胜。
他们的卡牌翻了一倍,最后他们三人的卡牌相等。
细心的甲数了一下,他的卡牌比原来的卡牌少了100张。
那么请问他们原来各有多少张卡牌?2、简算292728×1415。
3、一个两位数为N ,在前面任意添加任何数,数字和为N ,这种数不被N 整除,被称为“开心数”,问最小的“开心数”是________。
4、已知正方形的边长为10cm ,求阴影部分面积(π=3.14)。
5、S △AED 是20cm 2,S △BEF 是12cm 2,求S △FDC 面积。
6、如图,已知正六边形ABCDEF 的面积是314平方厘米,那么阴影部分面积总和是多少?ED CFBA ABE C DF7、王老师在黑板上写了这样的乘法算式:12345679×___=□□□□□□□□□,然后说道:“只要同学们告诉我你喜欢1、2、3、4、5、6、7、8、9中的哪个数,我在横线上填上适当的乘数,右边的积一定全由你喜欢的数字组成。
”小明抢着说:“我喜欢3”,王老师填上乘数“27”,结果积就出现九个3:12345679×27=333333333。
小字说:“我喜欢7”。
只见王老师填上乘数“63”,积就出现九个7:12345679×63=777777777。
小丽说:“我喜欢8。
”那么算式中应填上的乘数是________。
8、学校修建一个圆形喷水池,周长是12.56米,在水池周围要修一条1米宽的环线小路,这条小路的面积是________。
9、设l 1,l2,...,l n是有序的数,已知l 1=1.l n={1+l n2(n为偶数)1l n−1(n为奇数),若l m=37,求m的值。
10、童童和乐乐是医院疫情期间新引进的两款智能机器人,每天早上童童和乐乐“唱着歌”穿梭在104米长的病区走廊上,童童负责配送药物,只要护士下单,它就能准确的送达。
2024-2025学年重庆市江北区巴蜀中学九年级数学第一学期开学教学质量检测试题【含答案】

2024-2025学年重庆市江北区巴蜀中学九年级数学第一学期开学教学质量检测试题题号一二三四五总分得分A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)甲、乙、丙、丁四位选手各射击10次,每人的平均成绩都是9.3环,方差如表:选手甲乙丙丁方差(环2)0.0350.0160.0220.025则这四个人种成绩发挥最稳定的是()A .甲B .乙C .丙D .丁2、(4分)甲、乙、丙三个旅游团的游客人数都相等,且每个团游客的平均年龄都是35岁,这三个团游客年龄的方差分别是2 1.44S =甲,218.8S =乙,225S =丙,导游小方最喜欢带游客年龄相近的团队,若在这三个团中选择一个,则他应选()A .甲队B .乙队C .丙队D .哪一个都可以3、(4分)如图,将△ABC 绕点B 逆时针旋转α,得到△EBD ,若点A 恰好在ED 的延长线上,则∠CAD 的度数为()A .90°﹣αB .αC .180°﹣αD .2α4、(4分)若式子2-2x -有意义,则x 的取值范围为().A .x≥2B .x≠2C .x≤2D .x <25、(4分)下列四组线段中,可以组成直角三角形的是()A .4,5,6B .3,4,5C .5,6,7D .1,36、(4分)下列性质中,平行四边形不一定具备的是()A .邻角互补B .对角互补C .对边相等D .对角线互相平分7、(4分)下列图案,既是轴对称图形又是中心对称图形的个数是().A .1B .2C .3D .48、(4分)矩形ABCD 中,AB =3,BC =4,点E 是BC 边上一点,连接AE ,把∠B 沿AE 折叠,使点B 落在点B′处,当△CEB′为直角三角形时,BE 的长为()A .3B .32C .2或3D .3或32二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)如图,直线2y x =-+与x 轴、y 轴分别交于A B 、两点,过B 点作BC y ⊥轴与双曲线(0)k y k x =<交于C 点,过C 作CD x ⊥轴于D .若梯形ABCD 的面积为4,则k 的值为_____.A BC D O xy10、(4分)计算:=_________.11、(4分)若最简二次根式能合并成一项,则a =_____.12、(4分)平行四边形ABCD 中,若240A C ∠+∠=︒,A ∠=_____.13、(4分)已知菱形有一个锐角为60°,一条对角线长为4cm ,则其面积为_______cm 1.三、解答题(本大题共5个小题,共48分)14、(12分)如图,在平面直角坐标系xOy 中,一次函数6y x =-+的图象与正比例函数y kx =的图象交于点A (2,m ),一次函数6y x =-+的图象分别与x 轴、y 轴交于B 、C 两点.(1)求m 、k 的值;(2)求∠ACO 的度数和线段AB 的长.15、(8分)如图,∠AOB =30°,OP =6,OD =,PC =PD ,求OC 的长.16、(8分)某花卉基地出售文竹和发财树两种盆栽,其单价为:文竹盆栽12元/盆,发财树盆栽15元/盆。
重庆市巴蜀中学2023-2024学年九年级上学期期末数学试题(含答案)
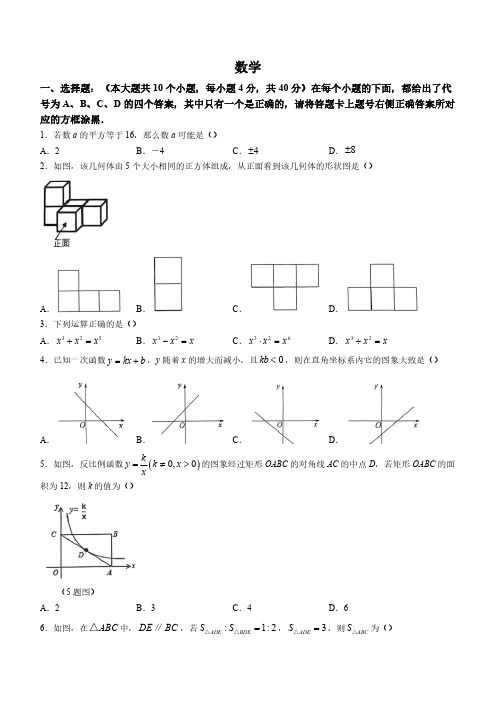
数学一、选择题:(本大题共10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑.1.若数a 的平方等于16,那么数a 可能是()A .2B .-4C .D .2.如图,该几何体由5个大小相同的正方体组成,从正面看到该几何体的形状图是()A .B .C .D .3.下列运算正确的是()A .B .C .D .4.已知一次函数,y 随着x 的增大而减小,且,则在直角坐标系内它的图象大致是()A .B .C .D .5.如图,反比例函数的图象经过矩形OABC 的对角线AC 的中点D ,若矩形OABC 的面积为12,则k 的值为()(5题图)A .2B .3C .4D .66.如图,在中,,若,,则为()4±8±325x x x +=32x x x-=326x x x ⋅=32x x x÷=y kx b =+0kb <()0,0ky k x x=≠>ABC △DE BC ∥:1:2ADE BDE S S =△△3ADE S =△ABC S △(6题图)A .9B .12C .24D .277.平面直角坐标系中,A 、B 、C 三点坐标分别为,,,以这三点为平行四边形的三个顶点,则第四个顶点不可能在()A .第一象限B .第二象限C .第三象限D .第四象限8.如图,过上一点P 的切线与直径AB 的延长线交于点C ,点D 是圆上一点,且,则的度数为()(8题图)A .32°B .33°C .34°D .35°9.菱形ABCD ,,E ,F 分别是CB ,CD 上两点,连接AE ,AF ,EF ,且,如果,则下列说法错误的是()(9题图)A .B .C .D .10.对于以下式子:,,,,下列说法正确的有()(1)如果,则无论y 取何常数,A ,B ,C ,D 调整顺序后可组成一列数,这列数后项减去前项的差均相等;(2)代数式一定是非负数;(3)如果A 为第1项,B 为第2项,C 为第3项,第1项与第2项的和减去第3项的结果为第4项,第2项()0,0()0,4-()3,3-O e 29BDP ∠=︒C∠60B ∠=︒60EAF ∠=︒BAE α∠=CEF α∠=60FAD α∠=︒-60EFC α∠=︒-90AFD α∠=︒-A x y =+B x y =-2C x y =-D xy =0x =222A B C D ⋅--与第3项的和减去第4项的结果为第5项,……,依此类推,则第2024项为.A .0个B .1个C .2个D .3个二、填空题(本大题共8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卡中对应的横线上.11______.12.一个正多边形的内角和是1080°,则这个正多边形有______条边.13.已知当时,整式的值等于10,则当时,则的值为______.14.某次车展活动设计了一种有奖竞猜游戏,游戏规则如下:在5个相同商标牌中,有3个商标牌的背面贴有一个笑脸,其余2张商标牌的背面贴一张哭脸,每个人每次翻两张牌,只有两张都是笑脸才得奖,则观众每次获奖的概率是______.15.如图,已知,,,B 、D 、E 在同一直线上,则的度数为______.(15题图)16.如图,扇形AOB ,点O 为圆心,半径OB 长为2,,再以点B 为圆心,OB 为半径作弧,交弧AB 于点C ,则阴影部分的面积是______.(16题图)17.若整数a 使关于x 的不等式组无解,且使关于y 的分式方程有非负整数解,则满足条件的a 的值之和为______.18.一个四位正整数M ,如果千位数字与十位数字之和的两倍等于百位数字与个位数字之和,则称M 为“共进退数”,并规定等于M 的前两位数所组成的数字与后两位数所组成的数字之和,等于M 的前两位数所组成的数字与后两位数所组成的数字之差,如果,那么M 各数位上的数字之和为3032x y +0122⎛⎫--= ⎪⎝⎭2x =35bx cx +-2x =-37bx cx ++AB AC =AD AE =52BAC DAE ∠=∠=︒BEC ∠90AOB ∠=︒232x a x a ->⎧⎨-<-⎩5355ay y y -=---()F M ()G M ()60F M =______;有一个四位正整数(,,,且为整数)是一个“共进退数”,且是一个平方数,是一个整数,则满足条件的数N 是______.三.解答题(本大题共8个小题,第19题8分,其余每题各10分,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.19.(本小题满分8分)计算:(1)(2)20.(本小题满分10分)如图:正方形ABCD 中,直线经过点D ,与AB 交于点E ,(1)用直尺和圆规作图:过点C 作DE 的垂线,垂足为G ,交AD 于点F ,(请保留作图痕迹,不要求写作图过程)(2)同学们作图完成后,通过测量发现,并且推理论证了该结论,请你根据他们的推理论证过程完成以下证明:如图:已知正方形ABCD 中,DE 、CF 分别是直线,直线被一组对边截得的线段,当时,求证:.证明:∵正方形ABCD ,∴,∴,∴,∵,∴,∴ ② ,∴,在和中,1101100010N x y z =+++08x ≤≤09y ≤≤08z ≤≤()F N ()7G N ()()()212141a a a a -+--211121xx x x ⎛⎫-÷ ⎪+++⎝⎭1l 2l DE CF =1l 2l DE CF ⊥DE CF =AD DC =90EAD CDF ∠=∠=︒90+∠=︒AED ①DE CF ⊥90FGD ∠=︒AED DFG ∠=∠DAE △CDF △,∴,∴.同学们进一步研究发现,一条直线被正方形的一组对边所截得的线段与另一条直线被正方形的另一组对边所截得的线段垂直时均具备此特征,请你依据题目中的相关描述,完成下列命题:两条直线分别被正方形的一组对边所截,若所截得的线段④.21.(本小题满分10分)为了激发同学们对古诗词学习的兴趣,2023年9月我市某中学开展了“课外古诗词赏析比赛”.为了解学生课外古诗词的学习情况,现从该校七、八年级中各随机抽取10名学生的比赛成绩(成绩为百分制,学生得分均为整数且用x 表示,)进行整理、描述和分析,并将其共分成四组:A :,B :,C :,D :)下面给出了部分信息:七年级10名学生的比赛成绩是:84,85,86,88,89,95,96,99,99,99.八年级10名学生的比赛成绩在C 组中的数据是:90,94,94.七、八年级抽取的学生比赛成绩统计表年级七年级八年级平均数9292中位数92b 众数c100根据以上信息,解答下列问题:(1)______,______,______;(2)根据以上数据,你认为该校七、八年级中哪个年级学生古诗词掌握得较好?请说明理由(一条理由即可);(3)该校七年级有1420名学生、八年级有1300名学生参加了此次“课外古诗词赏析比赛”,请估计参加此次比赛成绩不低于90分的学生人数是多少?22.列方程解应用题(本小题满分10分)中国最重要的传统节日之一春节,除了有热烈的庆祝活动和丰盛的美食外,长辈发压岁钱给晚辈表达美好的祝福也是春节习俗的重要组成部分.为迎接2024年龙年春节的到来,某工厂计划安排甲车间生产16000个龙年布艺红包袋.根据现有设备和工艺,甲车间每天可生产360个布艺红包袋,甲车间单独先工作4天后,工厂安排乙车间加入一起赶工,且乙车间每天可生产680个布艺红包袋,EAD CDF AED DFG⎧∠=∠⎪⎨⎪∠=∠⎩③DAE CDF △≌△DE CF =85x <8590x ≤<9095x ≤<95100x ≤≤a =b =c =(1)从开始加工到完成这批布艺红包袋一共需要多少天?(2)由于市场需求增大,甲车间按原生产效率单独生产4天后,工厂改进了两个车间的生产工艺,并将剩下的生产任务平均分给了甲、乙两车间.改进后甲、乙两车间每天生产的布艺红包袋数量之比为,且改进工艺后两个车间完成剩下生产任务的天数之和为10天,问改进工艺后甲车间每天生产多少个布艺红包袋?23.(本小题满分10分)如图,平行四边形ABCD 中,,,连接AC ,,动点P 以每秒1个单位的速度从点C 出发沿折线运动,设点P 运动时间为x 秒,的面积为,(1)请直接写出关于x 的函数表达式,并注明自变量x 的取值范围;(2)在给定的平面直角坐标系中画出这个函数图象,并写出该函数的一条性质;(3)的函数图象如图所示,当时请直接写出x 的取值范围.(结果保留一位小数,误差小于0.2)24.(本小题满分10分)今年10月“愉悦创造营”的同学们积极参加劳动实践,在校园“耕读园”里播种了近百粒萝卜种子.某周日下午返校时涵涵和静静约好一起去“耕读园”看看萝卜的生长情况.如图,已知“耕读园”在点A 处,涵涵家位于点A 正南方一条东西走向的街道BD 上,且在耕读园西南方向800米的C 处;静静家位于点D 正北方米且位于“耕读园”南偏西60°方向上的点E 处,图中点A 、B 、C 、D 、E 在同一平面内,(1)求静静家离耕读园的距离是多少?(结果保留根号)7:133AB =5BC =90BAC ∠=︒C A D →→ABP △1y 1y 24y x=12y y ≥(2)涵涵周日下午5:40出门,先以80米/分钟的速度从C 出发,往正西方向走到点D 处后再向正北方向到静静家楼下两人碰面,然后两人以此速度一起前往“耕读园”,请问她们能在5:55前到达耕读园吗?(参考数据:,结果精确到十分位)25.(本小题满分10分)如图1:平面直角坐标系中,抛物线与x 轴交于点和点B ,与y轴交于点C ,点是抛物线上一点,图1图2 图3(1)求抛物线表达式;(2)如图2:点是y 轴上一点,连接AD ,点P 是直线AD 上方抛物线上一个动点,过点P 作轴交直线AD 于点E ,在射线ED 上取一点F ,使得,求周长的最大值及此时点P 的坐标.(3)如图3:将原抛物线沿射线AD 方向平移4个单位长度,平移后抛物线的对称轴与x 轴交于点N ,射线AD 上有一点G ,连接GN ,过点G 作GN 的垂线与抛物线交于点M ,连接MN ,若,请直接写出点M 的坐标.26.(本小题10分)已知,中,,,交BC 于点D ,.图1 图2 图3(1)如图1,将BD 绕点B 逆时针旋转得线段BE ,且点E 在DA 的延长线上,求BE 的长.(2)如图2,在(1)的条件下,连接CE ,F 为AB 上一点,且满足:,作于点G ,求证:.(3)如图3,在(1)的条件下,P 、Q 分别为线段BA 、EB 上的两个动点,且满足,当1.414≈ 2.449≈292y ax bx =++()A -()()0,3D PE y ∥PE PF =PEF △292y ax bx =++1y 1y 30GMN ∠=︒ABC △AB AC =120BAC ∠=︒AD AB ⊥6AD =BEF AFG ∠=∠FG CE ⊥CG =BP EQ =PD QD+最小时,M 为平面内一动点,将沿EM 翻折得,请直接写出的最大值.BEM △B EM '△PB '参考答案一、选择题(每题4分,共48分)1-5:CADAB6-10:DAADB二、填空题(每题4分,共32分)19.计算:(1)解:原式.(2)解:原式.20.①②③④互相垂直,那么这两条线段相等21.(1)40,94,99;(2)解:八年级学生的古诗词掌握得较好.从平均数看,七年级平均分92分=八年级平均分92分,从中位数看,七年级92分<八年级中位数94分,所以八年级学生的古诗词掌握得较好.(3)(人)答:估计参加本次比赛成绩不低于90分的学生约为1620人.22.解:(1)设从开始加工到完成这批布艺红包袋一共需要x 天.答:从开始加工到完成这批布艺红包袋.一共需要18天.()()()212141a a a a -+--224141a a a a =--+=-211121xx x x ⎛⎫-÷ ⎪+++⎝⎭2(1)11x x x x x+=⨯=++ADE ∠90ADE DFG ∠+∠=︒AD CD =571420130016201010⨯+⨯=()()3603603204160003604x ++-=-⨯⎡⎤⎣⎦18x =(2)设甲车间每天生产7m 个,乙车间每天生产13m 个布艺红包袋.(个)经检验:是原分式方程的解,且符合题意.∴改进后甲每天产量:(个).答:改进工艺后,甲车间每天生产1120个布艺红包袋.23.(1)(2)当时,随x 增大而减小,当时,随x 增大而增大.(3)或(结果保留一位小数,误差不超过0.2).24.解:(1)过E 作于H ,,,∵中,,,∴,∴,∴,∴∵,EDBH 为矩形.∴,,∵,,,∴(米),答:静静家离耕读园距离为米.(2)∵,,∴∵矩形EDBH ,,∴,16000360472802-⨯=7280728010713m m+=160m =160m =16071120⨯=()()360426244955x x y x x ⎧-+≤<⎪⎪=⎨⎪-<≤⎪⎩04x <<1y 49x <<1y 0.8 3.2x ≤≤ 4.79.0x ≤≤EH AB ⊥90EHA BHE ∠==︒800AC =ABC △90B ∠=︒45BAC ∠=︒9045ACB BAC BAC ∠=︒-∠=︒=∠BA BC =222AC AB BC =+AB BC ==90D B BHE ∠=∠=∠=︒ED =HE BD =ED HB ==90AHE ∠=︒60EAH ∠=︒AH =cos AH AE EAH ===∠90AHE ∠=︒60EAH ∠=︒AE =sin EH AE EAH =⋅∠==BD EH ==CD BD BC =-=-∴总用时:(分),∵5:50-5:40=15(分),∴,∴她们能在5:55前到达耕读园.25.解:(1),代入,,∴.(2)过P 作于点H ,则,设,,,∴,,∴,∴,∴PE最大时,最大,直线AD :,,,,开口向下,对称轴直线,,∴时,,.14.4814.580CD DE EA ++=≈≈14.515<()A -()927029362a a ⎧-+=⎪⎪⎨⎪-+=⎪⎩12a b ⎧=-⎪⎨⎪=⎩21922y x =-+PH EF ⊥90PHE ∠=︒219,22P p p ⎛⎫-+ ⎪⎝⎭∠=∠PHE DOA EPH DAO ∠=∠EPH DAO △∽△PH AO PE AD ==PH PE =()(22PEF C PE PH PE =+=+△PEF C △3y x =+3E p p ⎛⎫+ ⎪ ⎪⎝⎭212526PE p ⎛=-++ ⎝102-<x =0p -<<x =PEF C △356P ⎛⎫ ⎪ ⎪⎝⎭(3),,.26.解:(1).(2)延长EF 至M ,使得,连接BM 、CM 、CF ,,∴,∴,,∴,,,∴,,∴,,,∴,∴,∴,∴,,∴(3)1223M ⎫⎪⎪⎭)2M ()316M --12BE =EM CM =BEF AFG ∠=∠AFE EBF BEF EFG AFG ∠=∠+∠=∠+∠30EBF EFG ∠=∠=︒FG CE ⊥60FEG ∠=︒EM CM BEM DEC EB EC =⎧⎪∠=∠⎨⎪=⎩()SAS BEM DEC △≌△BM CD =120EAM EDC ∠=∠=︒180EBM AEB ∠+∠=︒BM AE ∥CD AD AE ==BM AE =()ASA AEF BMF △≌△FE FM =CF EM ⊥30FCG ∠=︒CG =()max 12PB '=+-。
重庆市巴蜀中学教育集团2024-2025学年高二上学期10月月考数学试题及答案

重庆市巴蜀中学教育集团高2026届高二(上)月考数学试题注意事项:1.答题前,考生务必将自己的姓名、准考证号、班级、学校在答题卡上填写清楚。
2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试卷上作答无效。
3.考试结束后,请将答题卡交回,试卷自行保存。
满分150分,考试用时120分钟。
一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、直线30x y --=的倾斜角为()A .π3B .π6C .π4D .2π32、平面内,动点P 的坐标(),x y ,则动点P 的轨迹方程为()A .2212421x y +=B .22163x y +=C .22169x y +=D .22196x y +=3、以点()1,5C --为圆心,且过原点的圆的方程是()A .()()221525x y -+-=B .()()22151x y +++=C .()()22159x y -+-=D .()()221526x y +++=4、已知圆1C :224x y +=,圆2C :224440x y x y +--+=,则两圆的公共弦方程为()A .20x y ++=B .20x y +-=C .40x y ++=D .40x y +-=5、直线l 过点()1,2,且与圆C :()()222410x y -+-=相交所形成的长度为)A .3B .2C .1D .06、若点()2,1A 关于直线l :y kx b =+(k ,b ∈R )的对称点为()4,3A '-,则b =()A .3-B .1-C .3D .57、已知椭圆E :221106x y +=的左,右焦点分别为1F ,2F ,过2F 且斜率为3直线交E 于P ,Q 两点,则1PQF △的内切圆半径为()A .8B .4C .4D .88、点M 是椭圆()222210x y a b a b+=>>上的点,以M 为圆心的圆与x 轴相切于椭圆的焦点F ,与y 轴相交于P ,Q 两点,若PQM △是直角三角形,则该椭圆的离心率为()A .2B .12-C .2-D .2二、选择题:本题共3小题,每小题6分,共18分。
2025届重庆市渝中学区巴蜀中学九年级数学第一学期开学考试试题【含答案】

2025届重庆市渝中学区巴蜀中学九年级数学第一学期开学考试试题题号一二三四五总分得分A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)下列几组数中,不能作为直角三角形三边长度的是()A .3,4,5B .5,7,8C .8,15,17D .12、(4分)已知四边形ABCD 是平行四边形,下列结果正确的是()A .当AB =BC 时,它是矩形B .AC BD ⊥时,它是菱形C .当∠ABC =90°时,它是菱形D .当AC =BD 时,它是正方形3、(4分)某种药品原价为36元/盒,经过连续两次降价后售价为25元/盒。
设平均每次降价的百分率为x ,根据题意所列方程正确的是()A .236(1)3625x -=-B .236(12)25x -=C .236(1)25x -=D .225(1)36x -=4、(4分)下列计算正确的是()。
A -=B 3=-C =D .=5、(4分)如图,在△ABC 中,点D 、E 、F 分别是边AB 、AC 、BC 的中点,要判定四边形DBFE 是菱形,下列所添加条件不正确的是()A .AB=ACB .AB=BC C .BE 平分∠ABCD .EF=CF6、(4分)不等式2x-1≤3的解集是()A .x≤1B .x≤2C .x≥1D .x≤-27、(4分)已知249x mx ++是完全平方式,则m 的值为()A .6B .6±C .12D .12±8、(4分)下列关于x 的方程中,有实数解的为()A 0=B 0=C .()30x -=D 3x =-二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)已知等腰三角形两条边的长为4和9,则它的周长=______.10、(4分)如图,在△MBN 中,已知:BM =6,BN =7,MN =10,点A C ,D 分别是MB ,NB ,MN 的中点,则四边形ABCD 的周长是_____.11、(4分)已知:等腰三角形ABC 的面积为302m ,AB=AC=10m ,则底边BC 的长度为_________m.12、(4分)若分式方程122x m x x -=--无解,则m 等于___________13、(4分)某公司招聘英语翻译,听、说、写成绩按3∶3∶2计入总成绩.某应聘者的听、说、写成绩分别为80分,90分,95分(单项成绩和总成绩满分均为百分制),则他的总成绩为____________分.三、解答题(本大题共5个小题,共48分)14、(12分)如图,在矩形ABCD 中,AB =1,对角线AC 、BD 相交于点O ,过点O 作EF ⊥AC 分别交射线AD 与射线CB 于点E 和点F ,联结CE 、AF .(1)求证:四边形AFCE 是菱形;(2)当点E 、F 分别在边AD 和BC 上时,如果设AD =x ,菱形AFCE 的面积是y ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)如果△ODE 是等腰三角形,求AD 的长度.15、(8分)五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.(1)求甲、乙两种商品每件的进价分别是多少元?(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.16、(8分)计算:+(π-2)0-|-5|+23⎛⎫ ⎪⎝⎭-2;14⎛⎫ ⎪⎝⎭-1--1).17、(10分)某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:候选人面试笔试形体口才专业水平创新能力甲86909692乙92889593若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照4:6:5:5的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?18、(10分)某网络约车公司近期推出了“520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(千米),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图.组别单次营运里程“x”(千米)频数第一组0<x≤572第二组5<x≤10a第三组10<x≤1526第四组15<x≤2024第五组20<x≤2530根据以上信息,解答下列问题:(1)表中a=,样本中“单次营运里程”不超过15千米的频率为;(2)请把频数分布直方图补充完整;(3)估计该公司5000个“单次营运里程”超过20千米的次数.(写出解答过程)B卷(50分)一、填空题(本大题共5个小题,每小题4分,共20分)19、(4分)如图,∠XOY=45°,一把直角三角尺△ABC的两个顶点A、B分别在OX,OY上移动,其中AB=10,那么点O到顶点A的距离的最大值为_____.20、(4分)一组数据为5,7,3,x,6,4.若这组数据的众数是5,则该组数据的平均数是______.21、(4分)如图, ABCD 的对角线AC ,BD 交于点O ,M 是CD 的中点,连接OM ,若OM=2,则BC 的长是______________.22、(4分)计算:_______________.23、(4分)在函数y=中,自变量x 的取值范围是_______.二、解答题(本大题共3个小题,共30分)24、(8分)已知关于x 的一元二次方程x 2﹣2(k ﹣1)x+k(k+2)=0有两个不相等的实数根.(1)求k 的取值范围;(2)写出一个满足条件的k 的值,并求此时方程的根.25、(10分)八年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名八年级学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图均不完整),请根据图中所给信息解答下列问题:(1)在这次评价中,一共抽查了多少名学生?(2)求扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数;(3)请将条形统计图补充完整.26、(12分)如图,在△ABC 中,AC ⊥BC ,AC=BC ,延长BC 至E 使BE=BA ,过点B 作BD ⊥AE 于点D ,BD 与AC 交于点F ,连接EF .(1)求证:△ACE ≌△BCF.(2)求证:BF=2AD ,(3)若CE=,求AC 的长.参考答案与详细解析一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、B【解析】根据勾股定理的逆定理依次判断各项后即可解答.【详解】选项A,32+42=52,符合勾股定理的逆定理,能作为直角三角形三边长度;选项B,52+72≠82,不符合勾股定理的逆定理,不能作为直角三角形三边长度;选项C,82+152=172,符合勾股定理的逆定理,能作为直角三角形三边长度;选项D,12+)22,符合勾股定理的逆定理,能作为直角三角形三边长度.故选B.本题考查了勾股定理的逆定理,熟练运用勾股定理的逆定理判定三角形是否为直角三角形是解决问题的关键.2、B【解析】根据矩形、菱形、正方形的的判定方法判断即可.【详解】解:A、当AB=BC时,平行四边形ABCD为菱形,所以A选项的结论错误;B、当AC⊥BD时,平行四边形ABCD为菱形,所以B选项的结论正确;C、当∠ABC=90°时,平行四边形ABCD为矩形,所以C选项的结论错误;D、当AC=BD时,平行四边形ABCD为矩形,所以D选项的结论不正确.故选:B.本题考查了正方形的判定,也考查了菱形、矩形的判定方法.正方形的判定方法:先判定四边形是矩形,再判定这个矩形有一组邻边相等;先判定四边形是菱形,再判定这个菱形有一个角为直角.3、C【解析】试题解析:第一次降价后的价格为36×(1-x),两次连续降价后售价在第一次降价后的价格的基础上降低x ,为36×(1-x )×(1-x ),则列出的方程是36×(1-x )2=1.故选C .4、C 【解析】根据二次根式的运算法则即可求出答案.【详解】解:(A )原式A 错误;(B )原式=3,故B 错误;(C )原式,故C 正确;(D )原式,故D 错误;故选:C 本题考查二次根式,解题的关键是熟练运用二次根式的运算法则,本题属于基础题型.5、A 【解析】当AB=BC 时,四边形DBFE 是菱形.根据三角形中位线定理证明即可;当BE 平分∠ABC 时,可证BD=DE ,可得四边形DBFE 是菱形,当EF=FC ,可证EF=BF ,可得四边形DBFE 是菱形,由此即可判断;【详解】解:当AB=BC 时,四边形DBFE 是菱形;理由:∵点D 、E 、F 分别是边AB 、AC 、BC 的中点,∴DE ∥BC ,EF ∥AB ,∴四边形DBFE 是平行四边形,∵DE=12BC ,EF=12AB ,∴DE=EF ,∴四边形DBFE 是菱形.故B 正确,不符合题意,当BE 平分∠ABC 时,∴∠ABE=∠EBC∴∠CBE=∠DEB∴∠ABE=∠DEB∴BD=DE∴四边形DBFE是菱形,故C正确,不符合题意,当EF=FC,∵BF=FC∴EF=BF,∴四边形DBFE是菱形,故D正确,不符合题意,故选A.本题考查三角形的中位线定理,平行四边形的判定和性质,菱形的判定等知识,解题的关键是熟练掌握三角形中位线定理,属于中考常考题型.6、B【解析】首先移项,把-1移到不等式的右边,注意要变号,然后合并同类项,再把x的系数化为1,即可求出不等式的解集.【详解】解:2x-1≤3,移项得:2x≤3+1,合并同类项得:2x≤4,把x的系数化为1得:x≤2,故选:B.此题主要考查了一元一次不等式的解法,解不等式时要注意:①移项时要注意符号的改变;②把未知数的系数化为1时,两边同时除以或乘以同一个负数时要改变不等号的方向.7、D【解析】根据完全平方式的结构特征,即可求出m的值.【详解】解:∵249x mx ++是完全平方式,∴22312m =±⨯⨯=±;故选择:D.此题主要考查了完全平方公式的应用,要熟练掌握,解答此题的关键是要明确:(a±b )1=a 1±1ab+b 1.8、C 【解析】根据二次根式必须有意义,可以得到选项中的无理方程是否有解,从而可以解答本题.【详解】0=Q ,2030x x ∴->->且 ,即23x x <>且 故无解.A 错误;0=Q ,又0≤Q 00==,即=32x x =且 故无解,B 错误;()30x -=Q ,3002x x ∴-==-或 ,即32x x ==或 有解,C 正确;3x =-Q ,02,2x x ∴≤-≤,2,30x x ≤-<Q 又,故无解.故选C.此题考查无理方程,解题关键在于使得二次根式必须有意义.二、填空题(本大题共5个小题,每小题4分,共20分)9、1【解析】分9是腰长与底边长两种情况讨论求解即可.【详解】①当9是腰长时,三边分别为9、9、4时,能组成三角形,周长=9+9+4=1,②当9是底边时,三边分别为9、4、4,∵4+4<9,∴不能组成三角形,综上所述,等腰三角形的周长为1.故答案为:1.本题考查了等腰三角形的两腰相等的性质,难点在于要分情况讨论求解.10、13【解析】根据中位线性质可以推出CD∥AB,AD∥BC,可得四边形ABCD为平行四边形,由中点可得四边形ABCD的周长【详解】∵点A,C,D分别是MB,NB,MN的中点,∴CD∥AB,AD∥BC,∴四边形ABCD为平行四边形,∴AB=CD,AD=BC.∵BM=6,BN=7,点A,C分别是MB,NB的中点,∴AB=3,BC=3.5,∴四边形ABCD的周长=(AB+BC)×2=(3+3.5)×2=13.故答案为13本题考查了中位线的性质,以及平行四边形的判定及性质,掌握中位线的性质及平行四边形的性质是解题的关键.11、或【解析】作CD ⊥AB 于D ,则∠ADC=∠BDC=90°,由三角形的面积求出CD ,由勾股定理求出AD ;分两种情况:①等腰△ABC 为锐角三角形时,求出BD ,由勾股定理求出BC 即可;②等腰△ABC 为钝角三角形时,求出BD ,由勾股定理求出BC 即可.【详解】作CD ⊥AB 于D ,则∠ADC=∠BDC=90°,△ABC 的面积=12AB ⋅CD=12×10×CD=30,解得:CD=6,∴AD==8m ;分两种情况:①等腰△ABC 为锐角三角形时,如图1所示:BD=AB−AD=2m,∴;②等腰△ABC 为钝角三角形时,如图2所示:BD=AB+AD=18m ,∴综上所述:BC 的长为或故答案为:或本题考查等腰三角形的性质,解题的关键是掌握等腰三角形的性质,分情况讨论等腰三角形.12、1【解析】先去分母,把分式方程的增根代入去分母后的整式方程即可得到答案.【详解】解:122x m x x -=--,去分母得:1x m -=,所以:1m x =-,因为:方程的增根是2x =,所以:此时1m =,故答案为:1.本题考查分式方程无解时字母系数的取值,掌握把增根代入去分母后的整式方程是解题关键.13、87.1【解析】分析:运用加权平均数的公式直接计算.用80分,90分,91分,分别乘以3,3,2,再用它们的和除以8即可.详解:由题意知,总成绩=(80×3+90×3+91×2)÷(3+3+2)=87.1(分).故答案为:87.1.点睛:本题考查的是加权平均数的求法.本题易出现的错误是直接求出80,90,91的平均数.三、解答题(本大题共5个小题,共48分)14、(1)见解析;(2)21(1)2x y x x +=≥;(3)AD 或3.【解析】(1)由△DOE ≌△BOF ,推出EO=OF ,∵OB=OD ,推出四边形EBFD 是平行四边形,再证明EB=ED 即可.(2)由cos ∠DAC=AD OAAC AE =,求出AE 即可解决问题;(3)分两种情形分别讨论求解即可.【详解】(1)①证明:如图1中,∵四边形ABCD 是矩形,∴AD ∥BC ,OB =OD ,∴∠EDO =∠FBO ,在△DOE和△BOF 中,EDO FBO OD OB EOD BOF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△DOE ≌△BOF ,∴EO =OF ,∵OB =OD ,∴四边形EBFD 是平行四边形,∵EF ⊥BD ,OB =OD ,∴EB =ED ,∴四边形EBFD 是菱形.(2)由题意可知:AC =,1OA OC 2==,∵AD OA cos DAC AC AE ∠==,∴21x AE 2x +=,∴21x y AE CD 2x +=⋅=,∵AE≤AD ,∴212x x x + ,∴x 2≥1,∵x >0,∴x≥1.即21x y 2x +=(x≥1).(3)①如图2中,当点E 在线段AD 上时,ED =EO ,则Rt △CED ≌Rt △CEO ,∴CD =CO =AO =1,在Rt △ADC 中,AD ===如图3中,当的E 在线段AD 的延长线上时,DE =DO ,∵DE =DO =OC ,EC =CE ,∴Rt △ECD ≌Rt △CEO ,∴CD =EO ,∵∠DAC =∠EAO ,∠ADC =∠AOE =90°,∴△ADC ≌△AOE ,∴AE =AC ,∵EO 垂直平分线段AC ,∴EA =EC ,∴EA =EC =AC ,∴△ACE 是等边三角形,∴AD =CD•tan30°=3,综上所述,满足条件的AD 或3.本题考查四边形综合题、矩形的性质,等边三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会转化的思想思考问题.15、(1)甲商品每件进价30元,乙商品每件进价70元;(2)甲商品进80件,乙商品进20件,最大利润是1200元.【解析】(1)根据购进甲商品1件和乙商品3件共需240元,甲商品2件和乙商品1件共需130元可以列出相应的方程组,从而可以求得甲、乙两种商品每件的进价分别是多少元;(2)根据题意可以得到利润与购买甲种商品的函数关系式,从而可以解答本题.【详解】(1)设商品每件进价x 元,乙商品每件进价y 元,得32402130x y x y +=⎧⎨+=⎩解得:3070x y =⎧⎨=⎩,答:甲商品每件进价30元,乙商品每件进价70元;(2)设甲商品进a 件,乙商品(100﹣a )件,由题意得,a ≥4(100﹣a ),a ≥80,设利润为y 元,则,y =10a +20(100﹣a )=﹣10a +2000,∵y 随a 的增大而减小,∴要使利润最大,则a 取最小值,∴a =80,∴y =2000﹣10×80=1200,答:甲商品进80件,乙商品进20件,最大利润是1200元.本题考查一次函数的应用、二元一次方程组的应用、一元一次不等式的应用,解答本题的关键是明确题意,利用一次函数的性质和不等式的性质解答.16、(1)14【解析】(1)根据二次根式的性质、零指数幂的性质、绝对值的性质及负整数指数幂的性质依次计算后合并即可求解;(2)根据二次根式的性质、负整数指数幂的性质及平方差公式依次计算后合并即可求解.【详解】(1)原式=2+1-5+94=14;(2)原式=(5-1)=+4-4=.本题考查了二次根式的混合运算,熟练运用二次根式的性质、零指数幂的性质、绝对值的性质、负整数指数幂的性质、平方差公式及二次根式的混合运算顺序是解决问题的关键.17、选择乙.【解析】由形体、口才、专业水平、创新能力按照4:6:5:5的比确定,根据加权平均数的计算方法分别计算不同权的平均数,比较即可,【详解】形体、口才、专业水平、创新能力按照4:6:5:5的比确定,则甲的平均成绩为8649069659254655⨯+⨯+⨯+⨯+++=91.2.乙的平均成绩为9248869559354655⨯+⨯+⨯+⨯+++4+6+5+5=91.8.乙的成绩比甲的高,所以应该录取乙.本题考查加权平均数,熟练掌握计算方法是解题的关键.18、(1)48,0.1;(2)见解析;(3)750次.【解析】(1)①由各组频数之和等于数据总数200可得出a 的值;用第一、二、三组的频数和除以200可得;(2)根据频数分布表中的数据可把频数分布直方图补充完整;(3)用5000乘以样本中“单次营运里程”超过20公里的次数所占比例即可得.【详解】(1)a=200-(72+26+24+30)=48;样本中“单次营运里程”不超过15公里的频率为724826200++=0.1.故答案为48,0.1;(2)补全图形如下:(3)5000×30200=750(次).答:该公司这5000个“单次营运里程”超过20公里的次数约为750次.本题考查读频数分布直方图的能力和利用统计表获取信息的能力;利用统计表获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.也考查了利用样本估计总体.一、填空题(本大题共5个小题,每小题4分,共20分)19、【解析】当∠ABO=90°时,点O 到顶点A 的距离的最大,则△ABC 是等腰直角三角形,据此即可求解.【详解】解:∵sin 45sin AB AOABO=∠∴当∠ABO=90°时,点O 到顶点A 的距离最大.则OA=.故答案是:.本题主要考查了等腰直角三角形的性质,正确确定点O 到顶点A 的距离的最大的条件是解题关键.20、5【解析】首先根据众数的定义:是一组数据中出现次数最多的数值,即可得出5x =,进而可求得该组数据的平均数.【详解】解:根据题意,可得5x =则该组数据的平均数为57356456+++++=故答案为5.此题主要考查众数的理解和平均数的求解,熟练掌握,即可解题.21、1【解析】证明OM 是DBC ∆的中位线即可求解.【详解】解:四边形ABCD 是平行四边形,OD OB ∴=,M 是CD 中点,DM MC ∴=,∴OM 是DBC ∆的中位线,24BC OM ∴==,故答案为:1.本题考查平行四边形的性质、三角形中位线定理等知识,解题的关键是根据平行四边形性质判断出OM 是DBC ∆的中位线.22、123、x≥﹣2且x≠0【解析】根据题意得x+2≥0且x≠0,即x≥-2且x≠0.二、解答题(本大题共3个小题,共30分)24、方程的根120=2x x =-或【解析】(1)根据方程的系数结合根的判别式,即可得出关于k 的一元一次不等式,解之即可得出k 的取值范围;(1)取k=0,再利用分解因式法解一元二次方程,即可求出方程的根.【详解】(1)∵关于x 的一元二次方程x 1﹣1(k ﹣a )x+k (k+1)=0有两个不相等的实数根,∴△=[﹣1(k ﹣1)]1﹣4k (k ﹣1)=﹣16k+4>0,解得:k <14.(1)当k=0时,原方程为x 1+1x=x (x+1)=0,解得:x 1=0,x 1=﹣1.∴当k=0时,方程的根为0和﹣1.本题考查了根的判别式以及因式分解法解一元二次方程,解题的关键是:(1)牢记“当△>0时,方程有两个不相等的实数根”;(1)取k=0,再利用分解因式法解方程.25、(1)560人;(2)54°;(3)补图见解析.【解析】分析:(1)由“专注听讲”的学生人数除以占的百分比求出调查学生总数即可;(2)由“主动质疑”占的百分比乘以360°即可得到结果;(3)求出“讲解题目”的学生数,补全统计图即可;详解:(1)根据题意得:224÷40%=560(名),则在这次评价中,一个调查了560名学生;故答案为:560;(2)根据题意得:84560×360°=54°,则在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为54度;故答案为:54;(3)“讲解题目”的人数为560-(84+168+224)=84,补全统计图如下:点睛:此题考查了频率(数)分布直方图,扇形统计图,以及用样本估计总体,弄清题中的数据是解本题的关键.26、(1)证明见解析;(2)证明见解析;(3)2+.【解析】(1)由△ABC 是等腰直角三角形,得到AC=BC ,∠FCB=∠ECA=90°,由于AC ⊥BE ,BD ⊥AE ,根据垂直的定义得到∠CBF+∠CFB=90°,∠DAF+∠AFD=90°,由于∠CFB=∠AFD ,于是得到∠CBF=∠CAE ,证得△BCF ≌△ACE ;(2)由(1)得出AE=BF ,由于BE=BA ,BD ⊥AE ,于是得到AD=ED ,即AE=2AD ,即可得到结论;(3)由(1)知△BCF ≌△ACE ,推出CF=CE=,在Rt △CEF 中,EF==2,由于BD ⊥AE ,AD=ED ,求得AF=FE=2,于是结论即可.【详解】(1)∵AC ⊥BC ,BD ⊥AE∴∠FCB=∠BDA=90°∠CBF+∠CFB=90°,∠DAF+∠AFD=90°∵∠CFB=∠AFD∴∠CBF=∠CAE∵AC=BC∴△ACE ≌△BCF (2)由(1)知△ACE ≌△BCF 得AE=BF ∵BE=BA ,BD ⊥AE ∴AD=ED ,即AE=2AD ∴BF=2AD (3)由(1)知△ACE ≌△BCF ∴CF=CE=∴在Rt △CEF 中,EF==2,∵BD ⊥AE ,AD=ED ,∴AF=FE=2,∴AC=AF+CF=2+.本题考查了全等三角形的判定和性质,等腰直角三角形的性质,勾股定理,熟练掌握全等三角形的判定和性质定理是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巴蜀中学数学试题
:
篇一:重庆巴蜀中学高2017级高一(上)期末数学试卷及其答案
重庆巴蜀中学高2017级高一(上)期末考试
数学试题
第Ⅰ卷(选择题共50分)
一、选择题(本大题共10小题,每小题5分,共计50分。
在每小题给出的四个选项中,只有一项是符合题目要求的)
1、已知集合A??0,1?,B???1,0,a?3?,且A?B,则a=() A.1 B.0 C.?2 D.?3
2、不等式
x?2
?0的解集是() x?1
A.??1,2? B.???,?1????1,2? C.???,?1???2,??? D.??1,2? 3、已知点P(tan?,cos?)在第三象限,则角?的终边在() A.第一象限 B.第二象限 C.第三象限
?1?x2,x≤11
)的值为() 4、函数f(x)??,则f(f(3)?2x?3,x?17
A.?
3
D.第四象限
B.3 C.
158 D.
169
1
6、已知函数f(x)?x?lnx,则f(x)满足()
3
?1??1?
A.在区间?,1?,?1,e?内均有零点 B.在区间?,1?,?1,e?内均无零点
?e??e??1??1?
C.在区间?,1?内有零点,?1,e?内无零点D.在区间?,1?内无零点,?1,e?内有零点
?e??e??????
7、已知a?1,b?6,a?(b?a)?2则向量和向量的夹角是()π
A.6
πππ
B.4C.3 D.2
8、已知函数f(x)?
2x?a?11
在??1,???上是减函数,则函数y?loga的图像大致为()
x?1x
得f?f?y0???y0,则a的取值范围是() A.???,4?ln2?
B.?3,4? C.?3,4?ln2? D.?2?ln2,4?
第Ⅱ卷(非选择题共100分)
二、填空题:本大题共5小题,每小题5分,共25分.把答案填写在答题卡相应位置上。
11. sin1920?=___________
?1?
12. 若幂函数y?f(x)的图像经过点?3,?,则f(5)=___________
?9?
2???)=_____________ 13. 设tan?,tan?是方程x?3x?2?0的两个根,。
