(新)混沌通信中QCSK调制matlab代码
通信原理的MATLAB实验 QPSK的调制解调报告
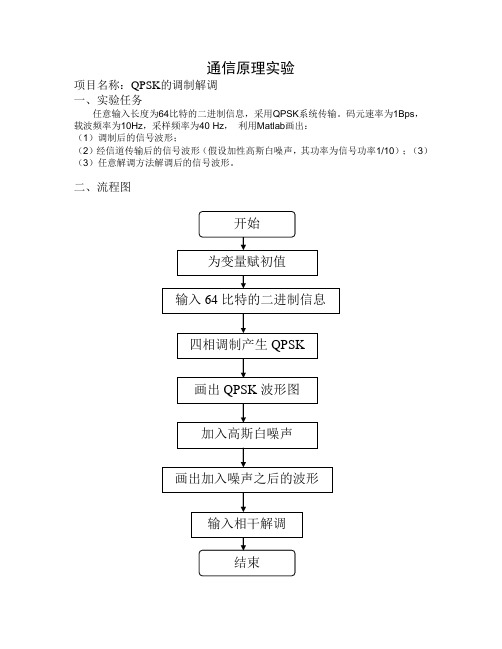
通信原理实验项目名称:QPSK的调制解调一、实验任务任意输入长度为64比特的二进制信息,采用QPSK系统传输。
码元速率为1Bps,载波频率为10Hz,采样频率为40 Hz,利用Matlab画出:(1)调制后的信号波形;(2)经信道传输后的信号波形(假设加性高斯白噪声,其功率为信号功率1/10);(3)(3)任意解调方法解调后的信号波形。
二、流程图三、完整程序Fd=1; %码元速率Fc=10; %载波频率Fs=40; %采样频率N=Fs/Fd;df=10;x=[ 1 1 0 1 1 0];%任意输入64比特的二进制信息M=2; %进制数SNRpBit=10;%加性高斯白噪声,其功率为信号功率的1/10,即信噪比为10 SNR=SNRpBit/log2(M); %转换为码元速率seed=[12345 54321];numPlot=length(x);figure(1)%画出输入二进制序列subplot(211);stem([0:numPlot-1],x(1:numPlot),'bx');title('输入波形’)%调制y=dmod(x,Fc,Fd,Fs,'fsk',M,df);numModPlot=numPlot*Fs;t=[0:numModPlot-1]./Fs;subplot(212);%画出调制后的信号plot(t,y(1:length(t)),'b-');axis([min(t) max(t) -1.5 1.5]);title('调制后的信号')%在已调信号中加入高斯白噪声randn('state',seed(2));y=awgn(y,SNR-10*log10(0.5)-10*log10(N),'measured',[],'dB');%相干解调figure(2)subplot(211);plot(t,y(1:length(t)),'b-');%画出经过信道的实际信号axis([min(t) max(t) -1.5 1.5]);title('加入高斯白噪声后的已调信号')%带输出波形的相干M元频移键控解调subplot(212);stem([0:numPlot-1],x(1:numPlot),'bx');hold on;stem([0:numPlot-1],z1(1:numPlot),'ro');hold off;axis([0 numPlot -0.5 1.5]);title('相干解调后的信号')四、波形。
qpsk调制 matlab代码

QPSK(Quadrature Phase Shift Keying)调制是一种常用的数字调制方式,它使用4个相互正交的相位来表示数字信号,从而实现信号的传输和识别。
在无线通信、数字通信和数字电视等领域都有着广泛的应用。
在本文中,我们将使用Matlab编写QPSK调制的代码,以帮助读者更好地理解QPSK调制的原理和实现。
1. QPSK调制简介QPSK调制是一种常用的相位调制方式,它将两路独立的数据流分别调制到正交的载波上,实现了频谱的高效利用和传输速率的提高。
QPSK调制共有4种状态,分别是0°、90°、180°、270°,对应的二进制数据为00、01、10、11。
通过改变相位来表示不同的数字信号,QPSK调制在噪声干扰下具有一定的抗干扰能力,因此在实际应用中得到了广泛的应用。
2. Matlab实现QPSK调制在Matlab中,我们可以利用其强大的信号处理工具箱实现QPSK调制的模拟,并通过仿真结果来验证QPSK调制的正确性。
以下是实现QPSK调制的Matlab代码:```matlab设置参数fc = 1000; 载波频率fs = 0; 采样频率T = 1; 信号持续时间t = 0:1/fs:T-1/fs; 时间序列data = randi([0 1],1,100); 随机生成100个二进制数据数据映射为QPSK调制信号data_I = 2*data(1:2:end)-1; I路数据data_Q = 2*data(2:2:end)-1; Q路数据s = (data_I + 1i*data_Q).*exp(1i*2*pi*fc*t); QPSK调制信号显示QPSK调制信号subplot(211)plot(t,real(s))title('QPSK调制信号-I路')xlabel('时间')ylabel('幅度')subplot(212)plot(t,imag(s))title('QPSK调制信号-Q路')xlabel('时间')ylabel('幅度')```在上述代码中,我们首先设置了载波频率fc、采样频率fs、信号持续时间T和时间序列t,然后随机生成了100个二进制数据,并分别将其映射到I路和Q路数据中。
qpsk调制 matlab代码

qpsk调制 matlab代码我们需要了解QPSK调制的基本原理。
QPSK调制是一种相位调制技术,它将数字信号分为两个部分,分别表示为I路和Q路。
I路和Q 路分别是正交的,即它们的相位差为90度。
通过调整I路和Q路信号的幅度和相位,可以实现不同的调制方式。
QPSK调制使用两个比特来表示一个符号,因此可以表示四个不同的相位状态。
这四个相位状态分别为0度、90度、180度和270度。
我们可以将这四个相位状态分别表示为00、01、10和11。
在QPSK 调制中,将这四个相位状态映射到一个星座图上,星座图的每个点表示一个相位状态。
接下来,我们使用Matlab来实现QPSK调制。
首先,我们需要生成一组二进制数据,这些数据将被映射到星座图上。
我们可以使用randi函数生成一组随机的二进制数据。
然后,我们将这组二进制数据分为两个部分,分别表示为I路和Q路。
```matlabdata = randi([0, 1], 1, N); % 生成随机二进制数据data_I = data(1:2:end); % 提取I路数据data_Q = data(2:2:end); % 提取Q路数据```接下来,我们需要将I路和Q路数据映射到星座图上。
我们可以使用qammod函数来实现这个过程。
qammod函数将I路和Q路数据作为输入,输出对应的星座图点的复数值。
```matlabM = 4; % 星座图中的点的数量symbols = qammod(data_I * 2 + data_Q, M); % 将I路和Q路数据映射到星座图上```然后,我们可以通过添加高斯白噪声来模拟无线信道的影响。
我们可以使用awgn函数来实现这个过程。
awgn函数将星座图点的复数值作为输入,输出经过信道影响后的复数值。
```matlabSNR = 10; % 信噪比symbols_noisy = awgn(symbols, SNR); % 添加高斯白噪声```我们可以使用qamdemod函数将经过信道影响后的复数值解调为二进制数据。
matlab qpsk调制 差分编码

MATLAB中的QPSK调制和差分编码一、QPSK调制概述QPSK是一种数字调制技术,它是Quadrature Phase Shift Keying 的缩写,顾名思义,QPSK调制就是基于正交相位的移相键控技术。
在QPSK调制中,将输入的数字比特流分为两个独立的序列,分别对应正弦信号和余弦信号,然后分别将这两个序列经过平移操作,最终将它们相加得到调制后的信号。
二、QPSK调制的原理和公式1. QPSK调制的过程可以用以下数学公式表示:\[ s(t) = \sqrt{\frac{2}{T}} \cdot (I(t) \cdot \cos(2\pi f_c t) - Q(t) \cdot \sin(2\pi f_c t))\]其中,s(t)表示QPSK调制的信号,I(t)和Q(t)分别为输入的两个正交序列,T为每个符号的持续时间,fc为信号的载频。
2. 在Matlab中利用QPSK调制函数进行调制的示例代码如下:```matlabM = 4; 4种相位k = log2(M); 每个符号的位数numBits = xxx; 待调制的比特数dataIn = randi([0 1],numBits,1); 随机产生待调制的比特数据dataInMatrix = reshape(dataIn,length(dataIn)/k,k); 重新排列比特数据dataSymbolsIn = bi2de(dataInMatrix); 将比特数据转换为十进制数据modObj =modem.pskmod('M',M,'PhaseOffset',0,'SymbolOrder','Gray','Inp utType','Bit');dataMod = modulate(modObj,dataSymbolsIn); 进行QPSK调制```三、差分编码的概念差分编码是一种用于增强数字通信系统性能的编码技术,它的基本思想是根据相邻符号之间的变化来产生调制信号。
qpsk 信号 matlab仿真代码

1. 介绍QPSK信号QPSK (Quadrature Phase Shift Keying) 是一种数字调制技术,常用于无线通信和数字通信系统中。
它是通过改变相位来传输数字信息的一种调制方式,相较于单相位调制方式,QPSK可以提高信号传输效率和频谱利用率。
2. QPSK信号的生成原理QPSK信号的产生可以通过正交调制的方式完成,即将数据流分为两个独立的流并分别与正弦和余弦信号相乘,经过合并后即可生成QPSK信号。
具体过程如下:(1) 将二进制数据流分为实部和虚部,分别代表I信号和Q信号;(2) 分别对I信号和Q信号进行调制,得到两路调制信号;(3) 将两路调制信号通过信号合并器得到QPSK信号。
3. QPSK信号的Matlab仿真代码在Matlab中,可以通过编程实现QPSK信号的生成和仿真。
以下是一个简单的QPSK信号Matlab仿真代码示例:```Matlab设置QPSK调制参数M = 4; 调制阶数msg = randi([0 M-1],10000,1); 随机生成10000个0到M-1的整数,模拟二进制信息流txSig = qammod(msg,M); QAM调制绘制星座图scatterplot(txSig) 绘制QPSK星座图添加高斯噪声rxSig = awgn(txSig, 10); 添加信道噪声,信噪比为10dB解调rxMsg = qamdemod(rxSig,M); QPSK解调[numErrors,ber] = biterr(msg,rxMsg); 计算比特错误率disp(['比特错误率为:',num2str(ber)])```4. QPSK信号仿真结果分析通过上述Matlab代码,我们可以得到QPSK信号的仿真结果。
通过绘制星座图可以直观地观察到QPSK信号在复平面上的分布情况。
随后,我们可以添加高斯噪声,模拟信道中的干扰,然后进行解调并计算比特错误率。
5. 结论通过以上QPSK信号的Matlab仿真代码,我们可以成功生成和仿真QPSK信号,并得到比特错误率等性能指标。
matlab qpsk调制函数

matlab qpsk调制函数QPSK调制函数是一种常用的数字调制方法,广泛应用于无线通信系统中。
在Matlab中,我们可以使用qpskmod函数来实现QPSK调制。
本文将介绍QPSK调制的原理、实现方法以及在通信系统中的应用。
我们来了解一下QPSK调制的原理。
QPSK调制是一种基于正交载波的调制方式,它将每个符号映射为一个复数,复数的实部和虚部分别表示正交载波的两个相位。
QPSK调制共有4个不同的符号,每个符号代表两个比特,因此它可以传输更多的信息量。
具体来说,QPSK调制将两个比特映射为一个复数,共有4种可能的映射方式,分别是00、01、10和11。
这四种映射方式对应的复数分别为1+j、-1+j、-1-j和1-j。
在Matlab中,我们可以使用qpskmod函数来实现QPSK调制。
该函数的基本语法为:y = qpskmod(x,M),其中x是输入的比特序列,M 是调制的方式,对于QPSK调制来说,M的取值为4。
函数的输出y 是调制后的复数序列。
QPSK调制函数的实现非常简单,我们只需要将输入的比特序列按照两个比特一组进行分组,然后根据映射关系进行映射即可。
下面是一个简单的示例代码:```matlab% 生成随机比特序列bits = randi([0 1], 1, 1000);% QPSK调制qpsk = qpskmod(bits, 4);```上述代码首先生成了一个随机的比特序列,长度为1000。
然后使用qpskmod函数对比特序列进行QPSK调制,调制后的结果存储在变量qpsk中。
QPSK调制在无线通信系统中有着广泛的应用。
由于QPSK调制可以传输更多的信息量,因此在有限的带宽资源下能够达到更高的数据传输率。
此外,QPSK调制还具有抗噪声性能较好的特点,可以在较差的信道条件下实现可靠的通信。
在实际的通信系统中,QPSK调制往往与其他技术结合使用,以提高系统的性能。
例如,在OFDM系统中,QPSK调制常用于每个子载波上,以实现高速数据传输。
matlabask调制解调

MATLAB中实现ASK(振幅键控)调制解调的步骤如下:
生成随机比特流:使用MATLAB的随机数生成函数生成二进制比特流。
映射比特流到振幅:将二进制比特流映射到相应的振幅值,通常使用高电平和低电平表示二进制比特流的1和0。
调制信号:使用生成的振幅信号调制高频载波信号。
通常可以使用MATLAB的信号处理函数进行调制,如modulate函数。
传输信号:将调制后的信号通过信道传输。
解调信号:在接收端,使用适当的解调方法将调制信号解调为原始比特流。
常用的解调方法包括相干解调和非相干解调。
在MATLAB中,可以使用相关函数进行相干解调,如demodulate函数。
比特流同步:在解调过程中,需要确保解调器与发送端保持同步,以便正确解调出原始比特流。
可以使用适当的同步算法实现比特流的同步。
误码率分析:最后,可以使用MATLAB的误码率分析工具计算解调后的比特流的误码率,以评估调制解调性能。
以上是MATLAB实现ASK调制解调的大致步骤。
QPSK调制与解调在MATLAB平台上的实现(word文档良心出品)
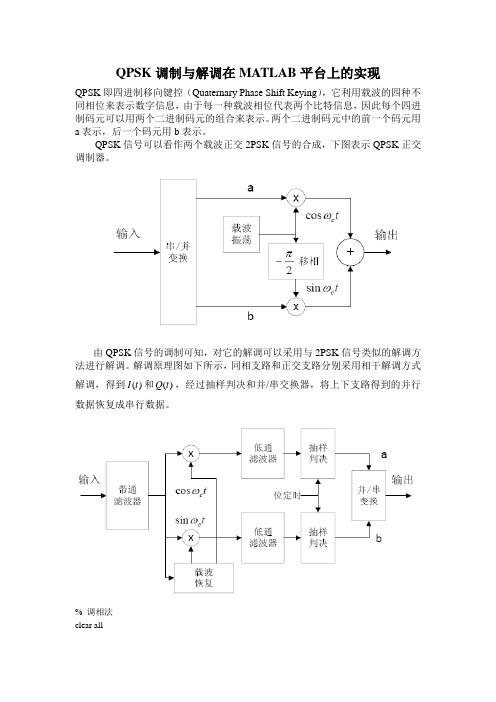
QPSK调制与解调在MATLAB平台上的实现QPSK即四进制移向键控(Quaternary Phase Shift Keying),它利用载波的四种不同相位来表示数字信息,由于每一种载波相位代表两个比特信息,因此每个四进制码元可以用两个二进制码元的组合来表示。
两个二进制码元中的前一个码元用a表示,后一个码元用b表示。
QPSK信号可以看作两个载波正交2PSK信号的合成,下图表示QPSK正交调制器。
由QPSK信号的调制可知,对它的解调可以采用与2PSK信号类似的解调方法进行解调。
解调原理图如下所示,同相支路和正交支路分别采用相干解调方式解调,得到()Q t,经过抽样判决和并/串交换器,将上下支路得到的并行I t和()数据恢复成串行数据。
% 调相法clear allclose allt=[-1:0.01:7-0.01];tt=length(t);x1=ones(1,800);for i=1:ttif (t(i)>=-1 & t(i)<=1) | (t(i)>=5& t(i)<=7);x1(i)=1;else x1(i)=-1;endendt1=[0:0.01:8-0.01];t2=0:0.01:7-0.01;t3=-1:0.01:7.1-0.01;t4=0:0.01:8.1-0.01;tt1=length(t1);x2=ones(1,800);for i=1:tt1if (t1(i)>=0 & t1(i)<=2) | (t1(i)>=4& t1(i)<=8);x2(i)=1;else x2(i)=-1;endendf=0:0.1:1;xrc=0.5+0.5*cos(pi*f);y1=conv(x1,xrc)/5.5;y2=conv(x2,xrc)/5.5;n0=randn(size(t2));f1=1;i=x1.*cos(2*pi*f1*t);q=x2.*sin(2*pi*f1*t1);I=i(101:800);Q=q(1:700);QPSK=sqrt(1/2).*I+sqrt(1/2).*Q;QPSK_n=(sqrt(1/2).*I+sqrt(1/2).*Q)+n0;n1=randn(size(t2));i_rc=y1.*cos(2*pi*f1*t3);q_rc=y2.*sin(2*pi*f1*t4);I_rc=i_rc(101:800);Q_rc=q_rc(1:700);QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);QPSK_rc_n1=QPSK_rc+n1;figure(1)subplot(4,1,1);plot(t3,i_rc);axis([-1 8 -1 1]);ylabel('a序列');subplot(4,1,2);plot(t4,q_rc);axis([-1 8 -1 1]);ylabel('b序列');subplot(4,1,3);plot(t2,QPSK_rc);axis([-1 8 -1 1]);ylabel('合成序列'); subplot(4,1,4);plot(t2,QPSK_rc_n1);axis([-1 8 -1 1]);ylabel('加入噪声');效果图:% 设定T=1,加入高斯噪声clear allclose all% 调制bit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3);bit_Q = bit_in(2:2:1e3);data_I = -2*bit_I+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);end;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=conv(data_I2,xrc)/5.5;data_Q2_rc=conv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;n0=rand(size(t1));I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*sin(2*pi*f1*t1); QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc); QPSK_rc_n0=QPSK_rc+n0;% 解调I_demo=QPSK_rc_n0.*cos(2*pi*f1*t1);Q_demo=QPSK_rc_n0.*sin(2*pi*f1*t1);% 低通滤波I_recover=conv(I_demo,xrc);Q_recover=conv(Q_demo,xrc);I=I_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;% 抽样判决data_recover=[];for i=1:20:10000data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)];end;bit_recover=[];for i=1:20:20000if sum(data_recover(i:i+19))>0data_recover_a(i:i+19)=1;bit_recover=[bit_recover 1];elsedata_recover_a(i:i+19)=-1;bit_recover=[bit_recover -1];endenderror=0;dd = -2*bit_in+1;ddd=[dd'];ddd1=repmat(ddd,20,1);for i=1:2e4ddd2(i)=ddd1(i);endfor i=1:1e3if bit_recover(i)~=ddd(i)error=error+1;endendp=error/1000;figure(1)subplot(2,1,1);plot(t2,ddd2);axis([0 100 -2 2]);title('原序列');subplot(2,1,2);plot(t2,data_recover_a);axis([0 100 -2 2]);title('解调后序列'); 效果图:% 设定T=1, 不加噪声clear allclose all% 调制bit_in = randint(1e3, 1, [0 1]);bit_I = bit_in(1:2:1e3);bit_Q = bit_in(2:2:1e3);data_I = -2*bit_I+1;data_Q = -2*bit_Q+1;data_I1=repmat(data_I',20,1);data_Q1=repmat(data_Q',20,1);for i=1:1e4data_I2(i)=data_I1(i);data_Q2(i)=data_Q1(i);end;t=0:0.1:1e3-0.1;f=0:0.1:1;xrc=0.5+0.5*cos(pi*f);data_I2_rc=conv(data_I2,xrc)/5.5;data_Q2_rc=conv(data_Q2,xrc)/5.5;f1=1;t1=0:0.1:1e3+0.9;I_rc=data_I2_rc.*cos(2*pi*f1*t1);Q_rc=data_Q2_rc.*sin(2*pi*f1*t1); QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);% 解调I_demo=QPSK_rc.*cos(2*pi*f1*t1);Q_demo=QPSK_rc.*sin(2*pi*f1*t1);I_recover=conv(I_demo,xrc);Q_recover=conv(Q_demo,xrc);I=I_recover(11:10010);Q=Q_recover(11:10010);t2=0:0.05:1e3-0.05;t3=0:0.1:1e3-0.1;data_recover=[];for i=1:20:10000data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)]; end;ddd = -2*bit_in+1;ddd1=repmat(ddd',10,1);for i=1:1e4ddd2(i)=ddd1(i);endfigure(1)subplot(4,1,1);plot(t3,I);axis([0 20 -6 6]);subplot(4,1,2);plot(t3,Q);axis([0 20 -6 6]);subplot(4,1,3);plot(t2,data_recover);axis([0 20 -6 6]); subplot(4,1,4);plot(t,ddd2);axis([0 20 -6 6]);效果图:% QPSK误码率分析SNRindB1=0:2:10;SNRindB2=0:0.1:10;for i=1:length(SNRindB1)[pb,ps]=cm_sm32(SNRindB1(i));smld_bit_err_prb(i)=pb;smld_symbol_err_prb(i)=ps;end;for i=1:length(SNRindB2)SNR=exp(SNRindB2(i)*log(10)/10);theo_err_prb(i)=Qfunct(sqrt(2*SNR)); end;title('QPSK误码率分析');semilogy(SNRindB1,smld_bit_err_prb,'*');axis([0 10 10e-8 1]);hold on;% semilogy(SNRindB1,smld_symbol_err_prb,'o'); semilogy(SNRindB2,theo_err_prb);legend('仿真比特误码率','理论比特误码率'); hold off;function[y]=Qfunct(x)y=(1/2)*erfc(x/sqrt(2));function[pb,ps]=cm_sm32(SNRindB)N=10000;E=1;SNR=10^(SNRindB/10);sgma=sqrt(E/SNR)/2;s00=[1 0];s01=[0 1];s11=[-1 0];s10=[0 -1];for i=1:Ntemp=rand;if (temp<0.25)dsource1(i)=0;dsource2(i)=0;elseif (temp<0.5)dsource1(i)=0;dsource2(i)=1;elseif (temp<0.75)dsource1(i)=1;dsource2(i)=0;elsedsource1(i)=1;dsource2(i)=1;end;end;numofsymbolerror=0;numofbiterror=0;for i=1:Nn=sgma*randn(size(s00));if((dsource1(i)==0)&(dsource2(i)==0))r=s00+n;elseif((dsource1(i)==0)&(dsource2(i)==1)) r=s01+n;elseif((dsource1(i)==1)&(dsource2(i)==0)) r=s10+n;elser=s11+n;end;c00=dot(r,s00);c01=dot(r,s01);c10=dot(r,s10);c11=dot(r,s11);c_max=max([c00 c01 c10 c11]);if (c00==c_max)decis1=0;decis2=0;elseif(c01==c_max)decis1=0;decis2=1;elseif(c10==c_max)decis1=1;decis2=0;elsedecis1=1;decis2=1;end;symbolerror=0;if(decis1~=dsource1(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(decis2~=dsource2(i))numofbiterror=numofbiterror+1;symbolerror=1;end;if(symbolerror==1)numofsymbolerror=numofsymbolerror+1;end;end;ps=numofsymbolerror/N;pb=numofbiterror/(2*N);效果图:11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
clear all;
x=randsrc(20,1,[0:1]); %产生二进制随机码stairs(x);
axis([0,20,-0.1,1.1]);
title('二进制随机序列');
clc
clear
close all
% q=99;
%k=[1:99];
%x(k)=sin(k*pi/q);
x(1)=0.212345;
for k = 1:99;
x(k+1) =4 * x(k) * (1 - x(k));
end
plot(x);
legend('混沌信号x');
grid on;%加网格
clc
clear
close all
% q=99;
%k=[1:99];
%x(k)=sin(k*pi/q);
x(1)=0.212345;
for k=1:99;
x(k+1)=4*x(k)*(1-x(k)); end
y=hilbert(x);
figure(1)
plot(imag(y));
legend('希尔伯特变换y'); grid on
clc
clear
close all
% q=99;
%k=[1:99];
%x(k)=sin(k*pi/q);
x(1)=0.212345;%x的初植
for k=1:99;
x(k+1)=4*x(k)*(1-x(k)); end
y=hilbert(x);%x的希尔伯特变换figure(1)
plot(imag(y));
grid on
legend('加密后的信号ms');
clc
clear
close all
% q=99;
%k=[1:99];
%x(k)=sin(k*pi/q);
x(1)=0.212345;
for k=1:99;
x(k+1)=4*x(k)*(1-x(k));
end
y=hilbert(x);%希尔伯特变换
figure(1)
plot(imag(y));
grid on
legend('加密后的信号ms');
y2=AWGN(imag(y),0.8,1);%imag(y)为已调信号,0.8为信噪比,1为信号功率figure(2)
plot(y2);
grid on
legend('加噪声后的调制信号y2');
bs=1;
Eb=1;
Zb=bs.*Eb;%解调出的信号stem(Zb,'r');
title('解调出的信号Zb')
clc;
x=0:18;%信噪比的取植范围
xSNR=10.^(x/20);%化成dB形式
for i=1:length(x);
k=2;
y1(i)=1/2*erfc(1/(sqrt(4*1/xSNR(i)+k*((1/xSNR(i))^2))));%求k=2的系统理论的误码率end
semilogy(x,y1);%绘出x和y1的图
for i=1:length(x)
hold on;
plot(x(i),y1(i),'g*')
end
gtext('QCSK,K=2');%在光标的位置放置给定的文字
for i=1:length(x);
k=16;
y2(i)=1/2*erfc(1/(sqrt(4*1/xSNR(i)+k*((1/xSNR(i))^2))));%求k=16的系统理论的误码率end
semilogy(x,y2);%绘出x和y2的图
for i=1:length(x)
hold on;
plot(x(i),y2(i),'r.')
end
gtext('QCSK,K=16');
for i=1:length(x);
k=64;
y3(i)=1/2*erfc(1/(sqrt(4*1/xSNR(i)+k*((1/xSNR(i))^2))));%求k=64的系统理论的误码率end
semilogy(x,y3);%绘出x和y3的图
for i=1:length(x)
hold on;
plot(x(i),y3(i),'b+')
end
gtext('QCSK,K=64');
grid on
xlabel('Eb/No[dB]');
ylabel('BER');
title('QCSK的系统误码率');
clc;
x=0:18;%信噪比的取植范围
xSNR=10.^(x/20);%化成dB形式
for i=1:length(x);
k=2;
y1(i)=1/2*erfc(1/(sqrt(4*1/xSNR(i)+k*((1/xSNR(i))^2))));%求QCSK,k=2的系统理论的误码率
end
semilogy(x,y1);
for i=1:length(x)
plot(x(i),y1(i),'g*')
end
for i=1:length(x);
k=2;
y2(i)=1/2*erfc(1/(sqrt(4*1/xSNR(i)+2*k*((1/xSNR(i))^2))));%求DCSK,k=2的系统理论的误码率
end
semilogy(x,y2);
for i=1:length(x)
hold on;
plot(x(i),y2(i),'r.')
end
gtext('绿色的*表示QCSK K=2;红色的.表示DCSK K=2');
grid on
xlabel('Eb/No[dB]');
ylabel('BER');
title('K=2的系统误码率');
clc;
x=0:18;%信噪比的取植范围
xSNR=10.^(x/20);%化成dB形式
for i=1:length(x);
y1(i)=1/2*erfc(1/(sqrt(4*1/xSNR(i)+k*((1/xSNR(i))^2))));%求QCSK,k=16的系统理论的误码率
end
semilogy(x,y1);
for i=1:length(x)
hold on;
plot(x(i),y1(i),'g*')
end
gtext('QCSK,K=16');
for i=1:length(x);
k=16;
y2(i)=1/2*erfc(1/(sqrt(4*1/xSNR(i)+2*k*((1/xSNR(i))^2))));%求DCSK,k=16的系统理论的误码率
end
semilogy(x,y2);
for i=1:length(x)
hold on;
plot(x(i),y2(i),'r.')
end
gtext('DCSK,K=16');
grid on
xlabel('Eb/No[dB]');
ylabel('BER');
title('K=16时的系统误码率');
clc;
x=0:18;%信噪比的取植范围
xSNR=10.^(x/20);%化成dB形式
for i=1:length(x);
k=64;
y1(i)=1/2*erfc(1/(sqrt(4*1/xSNR(i)+k*((1/xSNR(i))^2))));%求QCSK,k=64的系统理论的误码率
end
semilogy(x,y1);
for i=1:length(x)
hold on;
plot(x(i),y1(i),'g*')
end
gtext('QCSK K=64');
for i=1:length(x);
k=64;
y2(i)=1/2*erfc(1/(sqrt(4*1/xSNR(i)+2*k*((1/xSNR(i))^2))));%求DCSK,k=64的系统理论的误码率
end
semilogy(x,y2);
for i=1:length(x)
所谓的光辉岁月,并不是以后,闪耀的日子,而是无人问津时,你对梦想的偏执。
hold on;
plot(x(i),y2(i),'r.')
end
gtext('DCSK K=64');
grid on
xlabel('Eb/No[dB]');
ylabel('BER');
title('K=64的系统误码率');
同是寒窗苦读,怎愿甘拜下风!11。
