高三文科数学三角函数知识点归纳
高考三角函数知识点总结

高考三角函数知识点总结一、基本概念和性质1.弧度制:单位圆上的弧所对应的圆心角的大小定义为该弧的弧度。
1弧度等于圆周的1/2π。
2. 三角函数:正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)、余切函数cot(x)、正割函数sec(x)和余割函数csc(x)。
3.三角恒等式:包括同角三角恒等式、余角三角恒等式、反三角函数同角恒等式等。
4.周期性:正弦函数、余弦函数、正割函数和余割函数的周期都是2π;正切函数和余切函数的周期是π。
二、基本关系式1.正弦函数:在直角三角形中,正弦函数是指对于一个锐角三角形,三角形的对边和斜边的比值。
- sin(x) = a / c,其中a是对边,c是斜边。
- sin(x) = y / r,其中y是斜边在y轴上的投影,r是半径。
2.余弦函数:在直角三角形中,余弦函数是指对于一个锐角三角形,三角形的邻边和斜边的比值。
- cos(x) = b / c,其中b是邻边,c是斜边。
- cos(x) = x / r,其中x是斜边在x轴上的投影,r是半径。
3.正切函数:在直角三角形中,正切函数是指对于一个锐角三角形,三角形的对边和邻边的比值。
- tan(x) = a / b,其中a是对边,b是邻边。
- tan(x) = y / x,其中y是斜边在y轴上的投影,x是斜边在x轴上的投影。
4.余切函数:余切函数是正切函数的倒数。
- cot(x) = 1 / tan(x)。
5.正割函数:在直角三角形中,正割函数是指对于一个锐角三角形,三角形的斜边和邻边的比值的倒数。
- sec(x) = 1 / cos(x)。
6.余割函数:在直角三角形中,余割函数是指对于一个锐角三角形,三角形的斜边和对边的比值的倒数。
- csc(x) = 1 / sin(x)。
三、平面内角与弧度制之间的关系1.弧度制与度数之间的转换:-弧度=度数×π/180-度数=弧度×180/π2.弧度制下的角的性质:-一个圆上的圆心角的弧度数等于该弧所对应的弧的弧度数。
高中三角函数知识点归纳总结(通用10篇)

高中三角函数知识点归纳总结(通用10篇)高中数学三角函数知识点总结:三倍角公式篇一sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)高中数学三角函数知识点总结:三倍角公式推导篇二sin3a=sin(2a+a)=sin2acosa+cos2asina高中数学三角函数知识点总结:半角公式篇三tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)高中数学三角函数知识点总结:辅助角公式篇四Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))高中数学三角函数知识点总结:和差化积篇五sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)高中三角函数知识点归纳篇六1.做高中数学题的时候千万不能怕难题!有很多人数学分数提不动,很大一部分原因是他们的畏惧心理。
高考数学之三角函数知识点总结

高考数学之三角函数知识点总结高考数学中,三角函数是一个重要的知识点。
它在解三角形、解三角方程和求极限等方面都有广泛应用。
下面是对高考数学中三角函数的知识点进行总结:一、基本概念和性质:1.三角函数的定义:正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数的定义。
2.三角函数的周期性:正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数的周期性。
3.三角函数的奇偶性:正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数的奇偶性。
4.三角函数的范围:正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数的范围。
二、基本公式和恒等变换:1.三角函数的和差化积公式。
2.三角函数的倍角公式。
3.三角函数的半角公式。
4.三角函数的和差化积公式的逆运算。
三、极坐标与三角函数:1.极坐标下的坐标转换。
2.极坐标下的两点间距离公式。
四、三角函数的解析式:1.任意角的解析式。
2.一些特殊角的解析式。
五、三角函数的图像与性质:1.正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数的图像和性质。
2.三角函数图像的平移、伸缩和翻转。
3.三角函数的性态。
六、三角函数的应用:1.三角函数在测量中的应用:测量高度、测量角度、计算地理位置等。
2.三角函数在力学中的应用:力的合成、平衡条件等。
3.三角函数在电路中的应用:交流电的正弦表达式等。
4.三角函数在几何中的应用:解三角形、求面积等。
5.三角函数在物理中的应用:波动现象、振动现象等。
以上是高考数学中三角函数的主要知识点总结。
掌握这些知识点,对于解答相关题目、理解相关概念都有很大帮助。
在备考高考数学时,应不断强化基础知识,多进行题目练习和真题训练,同时注重理解和巩固基本概念和性质,提高解题的能力和技巧。
高中数学三角函数知识点总结精品版资料

高中数学三角函数知识点总结精品版资料高中数学中,三角函数是一个重要的章节,它是数学的基础,在其他学科中也有广泛的应用。
以下是关于高中数学三角函数的知识点总结。
一、三角函数的定义1. 正弦函数 sin(x):在直角三角形中,对于角度x对应的角的正弦值定义为:正弦值 = 对边/斜边。
2. 余弦函数 cos(x):在直角三角形中,对于角度x对应的角的余弦值定义为:余弦值 = 邻边/斜边。
3. 正切函数 tan(x):在直角三角形中,对于角度x对应的角的正切值定义为:正切值 = 对边/邻边。
二、三角函数的基本关系1. 正弦函数、余弦函数、正切函数的基本关系:sin(x)² + cos(x)² = 12. 正切函数与正弦函数、余弦函数的关系:tan(x) =sin(x)/cos(x)。
三、三角函数的性质1. 周期性:sin(x + 2π) = sin(x),cos(x + 2π) = cos(x),tan(x + π) = tan(x)。
2. 奇偶性:sin(-x) = -sin(x),cos(-x) = cos(x),tan(-x) = -tan(x)。
3. 正负性:sin(x)在0 < x < π范围内为正,余弦函数cos(x)在0 < x < π范围内为负,正切函数tan(x)在0 < x < π范围内为正。
4. 三角函数的特殊值:sin(0) = 0,cos(0) = 1,tan(0) = 0。
四、三角函数的图像1. 正弦函数的图像:y = sin(x)的图像在[0, 2π]区间内的图像是一条连续的波浪曲线,振幅为1,周期为2π。
2. 余弦函数的图像:y = cos(x)的图像在[0, 2π]区间内的图像是一条连续的波浪曲线,振幅为1,周期为2π。
3. 正切函数的图像:y = tan(x)的图像在(-π/2, π/2)区间内是一条连续的曲线,具有无穷多个渐近线。
高考文科数学三角函数知识点
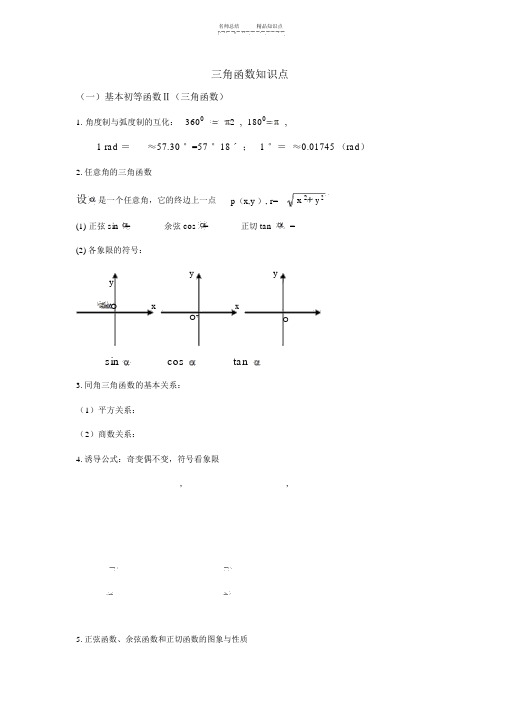
名师总结精品知识点三角函数知识点(一)基本初等函数Ⅱ(三角函数)1. 角度制与弧度制的互化:3600 2 , 1800,1 rad =≈57.30 °=57 °18ˊ; 1 °=≈0.01745 (rad)2.任意角的三角函数设是一个任意角,它的终边上一点p(x,y ), r=x 2y 2(1) 正弦 sin =余弦 cos =正切 tan=(2)各象限的符号:y yycossin O x x2O+Osin cos tan3.同角三角函数的基本关系:(1)平方关系:(2)商数关系:4.诱导公式:奇变偶不变,符号看象限,,5.正弦函数、余弦函数和正切函数的图象与性质函y sin xy cosxy tan x性 质数图象定义域RRx x k, k2值域1,11,1R当 x2kk当 x2k k时,2时, y max 1 ;ymax1;最值既无最大值也无最小值当 x2kk当 x 2kk时,2ymin1 .时, y min1.周期性 22奇偶性奇函数偶函数 奇函数在 2k, 2k 22在 2k,2 k k 上k上是增函数;是增函数;在 k2, k 单调性2在 2k, 2k 3在 2k,2 kkk上是增函数.22上是减函数.k 上是减函数.对称中心对称中心对称中心k,0 kk 对称性k,0 k2,0 k对称轴2对称轴 x k k无对称轴x kk26.三角函数的伸缩变化,先平移后伸缩y s ix 的n图象向左 (>0) 或向右 ( 0)平移个单位长度得的图象得的图象横坐标伸长(0< <1) 或缩短 (>1)1到原来的( 纵坐标不变)纵坐标伸长 ( A 1) 或缩短 (0<A<1)为原来的 A倍( 横坐标不变 )得的图象得的图象。
先伸缩后平移向上 ( k 0) 或向下 (k 0)平移 k 个单位长度y sin x 的图象纵坐标伸长 ( A 1)或缩短 (0 A 1)为原来的 A倍( 横坐标不变 )横坐标伸长 (01) 或缩短 ( 1)得的图象得的图象到原来的1(纵坐标不变 )向左 ( 0)或向右 ( 0)平移个单位向上 (k 0) 或向下 ( k0)得的图象平移 k 个单位长度得的图象。
高三文科数学三角函数概念、同角关系、诱导公式

义的应用原点)的角为,OB为终边的角为,那么 sin(+ )等于多少?
(第103页例1)
二、三角函数定义的应用
例2 直线y=2x+m和圆x2+y2=1交于 以x轴正方向为始边,OA为终边(
典例分析
原点)的角为,OB为终边的角为 sin(+ )等于
典例分析
二、三角函数定义的应用
例3 如图,已知点A(3,4),C(2,0),
点B在第二象限,且OB=3,O为坐标原点,
记AOC= . (1)求sin2的值;
y
A
(2)若AB=7, 求 BOC的面积.
B
O
C
x
典例分析
三、
-7 例4
已知-
2
x
0, sin
x
cos
x
1 5
,
5 求sin x cos x 的值.
sin x cos x与方程思想
典例分析
sin x cos x与方程思想
复习回顾
二、三角函数 定义的应用
1.齐次式的问题
一、同角关系的应用
2.已知一个角的三角函数值,求其它的 三角函数值
典例分析
若角的终边落在射线y=二-、x三(角函x数定义0的)应上用 ,
in
1 cos2 的值为 (第104页第6题)2 直线y=2x+m和圆x2+y2=1交于点A,B, 以x轴正方向为始边,OA为终边(O是坐标
例5
已知 (0,),sin2
-24 , 25
-7
求 cos sin 的值.
5
三、
三角函数的概念 同角 三角函数的关系 诱导
公式
单击此处添加副标题
高三数学三角函数知识点

高三数学三角函数知识点一、概述数学中的三角函数是一个重要的概念,主要包括正弦函数、余弦函数、正切函数等。
在高三数学学习中,掌握三角函数的相关知识点可以帮助我们解决各种复杂的几何问题,同时也是高考数学必考的内容。
二、正弦函数与余弦函数1.定义正弦函数(sin):在直角三角形中,对于一个锐角A,正弦函数的值等于对边与斜边的比值,即sinA=对边/斜边。
余弦函数(cos):在直角三角形中,对于一个锐角A,余弦函数的值等于邻边与斜边的比值,即cosA=邻边/斜边。
2.性质- 正弦函数的定义域为实数集,值域为[-1,1]。
- 余弦函数的定义域为实数集,值域为[-1,1]。
- 正弦函数与余弦函数的图像均为周期函数,周期为2π或360°。
三、正切函数与余切函数1.定义正切函数(tan):在直角三角形中,对于一个锐角A,正切函数的值等于对边与邻边的比值,即tanA=对边/邻边。
余切函数(cot):在直角三角形中,对于一个锐角A,余切函数的值等于邻边与对边的比值,即cotA=邻边/对边。
2.性质- 正切函数的定义域为实数集,值域为全体实数。
- 余切函数的定义域为实数集,值域为全体实数。
- 正切函数与余切函数的图像均为周期函数,周期为π或180°。
四、三角函数的基本关系1.正弦函数与余弦函数的关系- sin(π/2 - A) = cosA- cos(π/2 - A) = sinA2.正切函数与余切函数的关系- tanA = 1 / cotA- cotA = 1 / tanA3.正弦函数与余切函数的关系- sinA / cotA = cosA- cotA / sinA = cosA五、三角函数的图像与性质1.正弦函数与余弦函数的图像- 正弦函数为奇函数,图像关于原点对称。
- 余弦函数为偶函数,图像关于y轴对称。
2.正切函数与余切函数的图像- 正切函数为奇函数,图像关于原点对称。
- 余切函数为奇函数,图像关于原点对称。
(完整版)高中三角函数知识点总结

(完整版)高中三角函数知识点总结高中三角函数知识点总结1. 基本三角函数概念- 三角函数是以单位圆为基础的函数,包括正弦函数、余弦函数和正切函数。
- 正弦函数(sin):在直角三角形中,对于一个锐角,其对边与斜边的比值称为正弦值。
即:sinA = 对边/斜边。
- 余弦函数(cos):在直角三角形中,对于一个锐角,其邻边与斜边的比值称为余弦值。
即:cosA = 邻边/斜边。
- 正切函数(tan):在直角三角形中,对于一个锐角,其对边与邻边的比值称为正切值。
即:tanA = 对边/邻边。
2. 基本三角函数性质和公式- 三角函数的周期性:正弦函数和余弦函数的周期都是2π;正切函数的周期是π.- 三角函数的奇偶性:正弦函数是奇函数,余弦函数是偶函数,正切函数是奇函数。
- 三角函数的同角关系:sinA/cosA = tanA。
- 三角函数的和差化积公式和积化和差公式:具体公式可根据需要进行查阅。
3. 三角函数图像和性质- 正弦函数图像:在0到2π的区间内,正弦函数的图像为一条周期性的波浪线,最高点为1,最低点为-1,对应于最大值和最小值,0点对应于零值。
- 余弦函数图像:在0到2π的区间内,余弦函数的图像为一条周期性的波浪线,最高点为1,最低点为-1,对应于最大值和最小值,0点对应于最大值。
- 正切函数图像:在0到π的区间内,正切函数的图像无法在x=π/2和3π/2时定义,其他点对应的图像为一条连续的射线。
4. 三角函数的应用- 三角函数广泛应用于科学和工程领域中的周期性现象的描述和计算,例如电流的正弦波,声波的波动等。
- 在几何学中,三角函数也应用于测量角度和距离等问题的解决。
以上为高中三角函数的基本知识点总结,更详细的内容和公式可以参考相关教材或资料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三文科数学三角函数知识点归纳
角的概念的推广.弧度制.
任意角的三角函数.单位圆中的三角函线.同角三角函数的基本关系式.正弦、余弦的
诱导公式.
两角和与差的正弦、余弦、正切.二倍角的正弦、余弦、正切.
正弦函数、余弦函数的图像和性质.周期函数.函数y=Asinωx+φ的图像.正切函数的图像和性质.已知三角函数值求角。
1理解任意角的概念、弧度的意义能正确地进行弧度与角度的换算.
2掌握任意角的正弦、余弦、正切的定义;了解余切、正割、余割的定义;掌握同角三角函数的基本关系式;掌握正弦、余弦的诱导公式;了解周期函数与最小正周期的意义.
3掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式.
4能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明.
5理解正弦函数、余弦函数、正切函数的图像和性质,会用“五点法”画正弦函数、余弦函数和函数y=Asinωx+φ的简图,理解A.ω、φ的物理意义.
6会由已知三角函数值求角,并会用符号arcsinx\arc-cosx\arctanx表示.
7掌握正弦定理、余弦定理,并能初步运用它们解斜三角形.
8“同角三角函数基本关系式:sin2α+cos2α=1,
sinα/cosα=tanα,tanα•cotα=1”。
感谢您的阅读,祝您生活愉快。
