【重点推荐】新高中数学 课时分层作业10 双曲线的简单几何性质 新人教A版选修1-1练习试卷
数学人教A版选择性必修第一册3.2.2双曲线的简单几何性质

3 2
x y
横坐标 xM 以及它到直线 0 的距离 d .沿曲线向
3 2
右上方拖动点 M ,视察 xM 与 d 的大小关系,你发现
了什么?
4.渐近线
经过1 , 2 作轴的平行线 = ± ,经过1 , 2 作 轴的平
3.2.2 双曲线的简单几何性质
双曲线定义
图
平面内与两个定点F1,F2的距离的差的绝对值
等于非零常数(小于|F1F2|)的点的轨迹.
形
焦点坐标
标准方程
a、b、c 的关系
F1 c ,0,F2 c ,0.F1 0 ,
c ,F2 0 ,c .
x2
y2
2 1
2
a
b
y2
例4 双曲线冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲
面,它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m,试
建立适当的坐标系,求出此双曲线的方程(精确到1m).
解:根据双曲线的对称性,在冷却塔的轴截面所在平面建立如图所示的
平面直角坐标系Oxy,使小圆的直径AA’在x轴上,圆心与原点重合.
x2
2 1
2
a
b
c2=a2+b2
思考:类比对椭圆几何性质的研究,你认为应该研究双曲线
的哪些几何性质?如何研究这些性质?
范围、对称性、顶点、离心率…
利用双曲线的标准方程研究双曲线的几何性质
2
2
x
y
以 2 2 1 (a>0,b>0)为例
a
b
1.范围
2
由双曲线的标准方程可知, 2
2019-2020学年高中数学课时作业双曲线的简单几何性质新人教A版选修

2.已知双曲线的实轴和虚轴等长.且过点(5,3).则双曲线方程为( )
A. - =1 B. - =1
C. - =1 D. - =1
解析:由题意知.所求双曲线是等轴双曲线.设其方程为x2-y2=λ(λ≠0).将点(5,3)代入方程.可得λ=52-32=16.所以双曲线方程为x2-y2=16.即 - =1.
A. - =1 B. - =1
C. - =1 D. - =1
解析:设双曲线的标准方程为 - =1(a>0.b>0).由题意知c=3.a2+b2=9.设A(x1.y1).B(x2.y2)则有
两式作差得 = = = .
又AB的斜率是 =1.
所以4b2=5a2.代入a2+b2=9得a2=4.b2=5.
所以双曲线标准方程是 - =1.
答案:B
5.(全国卷Ⅱ)已知A.B为双曲线E的左.右顶点.点M在E上.△ABM为等腰三角形.且顶角为120°.则E的离心率为( )
A. B.2
C. D.
解析:不妨取点M在第一象限.如图所示.设双曲线方程为 - =1(a>0.b>0).则|BM|=|AB|=2a.∠MBx=180°-120°=60°.
2019-2020学年高中数学课时作业双曲线的简单几何性质新人教A版选修
编 辑:__________________
时 间:__________________
|基础巩固|(25分钟
一、选择题(每小题5分.共25分)
1.双曲线x2- =1的实轴长是( )
A.1 B.4
C.2 D.8
解析:由双曲线的标准方程得a2=1.故a=1.所以实轴长为2a=2.
(2)与双曲线 - =1具有相同的渐近线.且过点M(3.-2);
双曲线的简单几何性质新教材选择性必修人教版选择性必修第一册
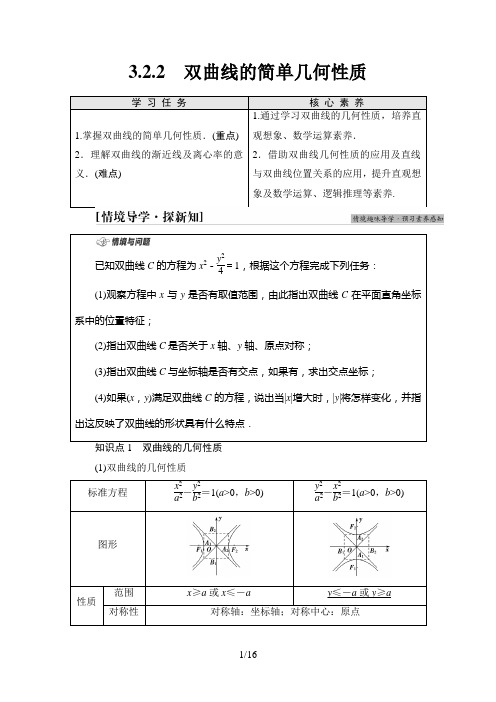
3.2.2双曲线的简单几何性质学习任务核心素养1.掌握双曲线的简单几何性质.(重点) 2.理解双曲线的渐近线及离心率的意义.(难点)1.通过学习双曲线的几何性质,培养直观想象、数学运算素养.2.借助双曲线几何性质的应用及直线与双曲线位置关系的应用,提升直观想象及数学运算、逻辑推理等素养.已知双曲线C的方程为x2-y24=1,根据这个方程完成下列任务:(1)观察方程中x与y是否有取值范围,由此指出双曲线C在平面直角坐标系中的位置特征;(2)指出双曲线C是否关于x轴、y轴、原点对称;(3)指出双曲线C与坐标轴是否有交点,如果有,求出交点坐标;(4)如果(x,y)满足双曲线C的方程,说出当|x|增大时,|y|将怎样变化,并指出这反映了双曲线的形状具有什么特点.知识点1双曲线的几何性质(1)双曲线的几何性质标准方程x2a2-y2b2=1(a>0,b>0)y2a2-x2b2=1(a>0,b>0)图形性质范围x≥a或x≤-a y≤-a或y≥a对称性对称轴:坐标轴;对称中心:原点顶点 顶点坐标:A 1(-a ,0),A 2(a ,0)顶点坐标:A 1(0,-a ),A 2(0,a )轴长实轴长:2a 虚轴长:2b渐近线 y =±baxy =±a b x离心率 e =ca,e ∈(1,+∞),其中c =a 2+b 2a ,b ,c 的关系 c 2=a 2+b 2(c >a >0,c >b >0)(2)双曲线的中心和等轴双曲线 ①双曲线的中心双曲线的对称中心叫做双曲线的中心. ②等轴双曲线实轴和虚轴等长的双曲线叫做等轴双曲线,其渐近线方程为y =±x ,离心率为 2.1.双曲线的离心率对双曲线的形状有何影响? [提示] 以双曲线x 2a 2-y 2b 2=1(a >0,b >0)为例. e =c a =a 2+b 2a=1+b 2a 2,故当b a 的值越大,渐近线y =ba x 的斜率越大,双曲线的开口越大,e 也越大,所以e 反映了双曲线开口的大小,即双曲线的离心率越大,它的开口就越大.1.思考辨析(正确的打“√”,错误的打“×”) (1)双曲线x 2a 2-y 2b 2=1与y 2a 2-x 2b 2=1(a >0,b >0)的形状相同. ( ) (2)双曲线x 2a 2-y 2b 2=1与y 2a 2-x 2b 2=1(a >0,b >0)的渐近线相同. ( ) (3)等轴双曲线的渐近线方程与双曲线方程有关. ( ) (4)离心率是2的双曲线为等轴双曲线.( )[提示] (1)√ 双曲线x 2a 2-y 2b 2=1与y 2a 2-x 2b 2=1(a >0,b >0)的位置不一样,但是形状相同.(2)× 双曲线x 2a 2-y 2b 2=1的渐近线方程为y =±b a x ;双曲线y 2a 2-x 2b 2=1的渐近线方程为y =±ab x .(3)× 等轴双曲线的渐近线方程都是y =±x . (4)√ 等轴双曲线的离心率是 2.2.双曲线x 225-y 29=1的顶点坐标是( ) A .(±5,0) B .(±5,0)或(0,±3) C .(±4,0)D .(±4,0)或(0,±3)A [双曲线顶点在x 轴上,且a =5,故选A .] 知识点2 直线与双曲线的位置关系将y =kx +m 与x 2a 2-y 2b 2=1联立消去y 得一元方程(b 2-a 2k 2)x 2-2a 2kmx -a 2(m 2+b 2)=0.Δ的取值 位置关系交点个数 k =±b a 时(此时m ≠0) 相交只有一个交点k ≠±b a 且Δ>0 有两个交点k ≠±b a 且Δ=0 相切 只有一个交点 k ≠±b a 且Δ<0相离没有公共点2.直线和双曲线只有一个公共点,那么直线和双曲线相切吗? [提示] 不一定.当直线与双曲线的渐近线平行时,直线与双曲线只有一个公共点,但直线与双曲线相交.3.过点(0,b )的直线和双曲线x 2a 2-y 2b 2=1(a >0,b >0)只有一个公共点,这样的直线有几条?[提示] 4条,其中两条切线,两条与渐近线平行的直线.类型1 根据双曲线方程研究其几何性质【例1】 (对接教材P 124例题)(1)双曲线x 29-y 216=1的左顶点到其渐近线的距离为( )A .2B .95C .125 D .3(2)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为43,则双曲线C 的渐近线方程为( )A .y =±43x B .y =±34x C .y =±73xD .y =±377x(3)已知双曲线x 2a 2-y 22=1(a >0)的一条渐近线为y =2x ,则实数a =________. (1)C (2)C (3)1 [(1)由双曲线方程知a 2=9,b 2=16,则a =3,b =4,c =5,从而双曲线左顶点A 1(-3,0),一条渐近线方程为y =43x ,即4x -3y =0, 则左顶点到渐近线的距离d =|4×(-3)|42+(-3)2=125,故选C .(2)由e 2=1+b 2a 2得169=1+b 2a 2,∴b 2a 2=79,即b a =73,又双曲线的焦点在x 轴上,则双曲线渐近线方程为y =±73x ,故选C . (3)由双曲线方程知,双曲线的焦点在x 轴,则2a2=2,即a 2=1,∴a =±1,又a >0,∴a = 1.]由双曲线方程研究几何性质的注意点(1)把双曲线方程化为标准形式,确定a ,b 的值是关键. (2)由方程可以求焦距、实(虚)轴长、离心率、渐近线方程.(3)渐近线是双曲线的重要性质:先画渐近线可使图形更准确,焦点到渐近线距离为虚半轴长.(4)注意双曲线中一些特殊线段(值)的应用.如过双曲线x 2a 2-y 2b 2=1的左焦点F 1(-c ,0)垂直于x 轴的弦AB ,则|AB |=2b 2a . (5)双曲线中c 2=a 2+b 2,易与椭圆中a 2=b 2+c 2混淆.[跟进训练]1.(1)若双曲线x 2a 2-y 2=1(a >0)的离心率为2,则其实轴长为( ) A . 3 B .2 3 C .33 D .233(2)若双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,则m 等于( ) A .-14 B .-4 C .4 D .14(1)D (2)A [(1)由题意得e 2=1+1a 2,即1+1a 2=4, 解得a =33,则实轴长为233,故选D .(2)将双曲线方程化为标准形式为y 2-x 2-1m=1,则有a 2=1,b 2=-1m .由题意知,2=-1m ,∴m =-14.]类型2 由双曲线的几何性质求其标准方程【例2】 求满足下列条件的双曲线的方程:(1)已知双曲线的焦点在x 轴上,离心率为53,且经过点M (-3,23); (2)渐近线方程为y =±12x ,且经过点A (2,-3). [解] (1)设所求双曲线方程为x 2a 2-y 2b 2=1(a >0,b >0).∵e =53,∴e 2=c 2a 2=a 2+b 2a 2=1+b 2a 2=259,∴b 2a 2=169.由题意得⎩⎪⎨⎪⎧b 2a 2=169,9a 2-12b 2=1,解得⎩⎨⎧a 2=94,b 2=4.∴所求双曲线的标准方程为x 294-y 24=1.(2)法一:∵双曲线的渐近线方程为y =±12x .当焦点在x 轴上时,设所求双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0), 则b a =12.①∵点A (2,-3)在双曲线上, ∴4a 2-9b 2=1.②①②联立,无解.当焦点在y 轴上时,设所求方程为y 2a 2-x 2b 2=1(a >0,b >0), 则a b =12.③ ∵点A (2,-3)在双曲线上,∴9a 2-4b 2=1.④联立③④,解得a 2=8,b 2=32. ∴所求双曲线的标准方程为y 28-x 232=1.法二:由双曲线的渐近线方程为y =±12x ,可设双曲线方程为x 222-y 2=λ(λ≠0),∵A (2,-3)在双曲线上,∴2222-(-3)2=λ,即λ=-8. ∴所求双曲线的标准方程为y 28-x 232=1.1.由几何性质求双曲线标准方程的解题思路由双曲线的几何性质求双曲线的标准方程,一般用待定系数法.当双曲线的焦点不明确时,方程可能有两种形式,此时应注意分类讨论,为了避免讨论,也可设双曲线的方程为mx 2-ny 2=1(mn >0).2.常见双曲线方程的设法(1)渐近线为y =±n m x 的双曲线方程可设为x 2m 2-y 2n 2=λ(λ≠0,m >0,n >0);如果两条渐近线的方程为Ax ±By =0,那么双曲线的方程可设为A 2x 2-B 2y 2=m (m ≠0,A >0,B >0).(2)与双曲线x 2a 2-y 2b 2=1或y 2a 2-x 2b 2=1(a >0,b >0)共渐近线的双曲线方程可设为x 2a 2-y 2b 2=λ或y 2a 2-x 2b2=λ(λ≠0). (3)与双曲线x 2a 2-y 2b 2=1(a >0,b >0)离心率相等的双曲线系方程可设为x 2a 2-y 2b 2=λ(λ>0)或y 2a 2-x 2b 2=λ(λ>0),这是因为由离心率不能确定焦点位置.[跟进训练]2.求适合下列条件的双曲线的方程:(1)焦点在x 轴上,虚轴长为8,离心率为53;(2)与双曲线x 29-y 216=1有共同的渐近线,且过点(-3,23).[解] (1)设所求双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0),则2b =8,e =c a =53,从而b =4,c =53a ,代入c 2=a 2+b 2,得a 2=9,故双曲线的标准方程为x 29-y 216=1.(2)法一:当焦点在x 轴上时,设双曲线的方程为x 2a 2-y 2b 2=1. 由题意,得⎩⎪⎨⎪⎧ b a =43,(-3)2a 2-(23)2b 2=1,解得a 2=94,b 2=4,所以双曲线的方程为4x 29-y 24=1.当焦点在y 轴上时,设双曲线的方程为y 2a 2-x 2b 2=1. 由题意,得⎩⎪⎨⎪⎧a b =43,(23)2a 2-(-3)2b 2=1,解得a 2=-4,b 2=-94(舍去).综上所得,双曲线的方程为4x 29-y 24=1. 法二:设所求双曲线方程为x 29-y 216=λ(λ≠0), 将点(-3,23)代入得λ=14,所以双曲线方程为x 29-y 216=14,即4x 29-y 24=1. 类型3 求双曲线的离心率【例3】 (1)设F 为双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的右焦点,O 为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P ,Q 两点.若|PQ |=|OF |,则C 的离心率为( )A . 2B . 3C .2D . 5(2)已知F 为双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的右焦点,A 为C 的右顶点,B 为C 上的点,且BF 垂直于x 轴,若AB 的斜率为3,则C 的离心率为________.(1)A (2)2 [(1)设双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的右焦点F 的坐标为(c ,0).由圆的对称性及条件|PQ |=|OF |可知,PQ 是以OF 为直径的圆的直径,且PQ ⊥OF .设垂足为M ,连接OP ,如图,则|OP |=a , |OM |=|MP |=c2.由|OM |2+|MP |2=|OP |2得⎝ ⎛⎭⎪⎫c 22+⎝ ⎛⎭⎪⎫c 22=a 2,故ca =2,即e =2,故选A . (2)如图,A (a ,0).由BF ⊥x 轴且AB 的斜率为3,知点B 在第一象限,且B ⎝ ⎛⎭⎪⎫c ,b 2a ,则k AB =b 2a -0c -a=3,则b 2=3ac -3a 2.又∵c 2=a 2+b 2,即b 2=c 2-a 2, ∴c 2-3ac +2a 2=0,∴e 2-3e +2=0.解得e =2或e =1(舍去).故e =2.]结合椭圆离心率的求法,试总结双曲线离心率的求解方法. [提示] (1)若可求得a ,c ,则直接利用e =ca 得解. (2)若已知a ,b ,可直接利用e =1+⎝ ⎛⎭⎪⎫b a 2得解.(3)若得到的是关于a ,c 的齐次方程pc 2+qac +ra 2=0(p ,q ,r 为常数,且p ≠0),则转化为关于e 的方程pe 2+qe +r =0求解.[跟进训练]3.(1)已知双曲线的一条渐近线方程为y =2x ,则其离心率为________. (2)在平面直角坐标系xOy 中,若双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点F (c ,0)到一条渐近线的距离为32c ,则其离心率为________.(1)5或52 (2)2 [(1)当焦点在x 轴上时,b a =2,这时离心率e =ca =1+22= 5.当焦点在y 轴上时,a b =2,即b a =12,这时离心率e =ca =1+⎝ ⎛⎭⎪⎫122=52. (2)因为双曲线的右焦点F (c ,0)到渐近线y =±ba x ,即bx ±ay =0的距离为|bc |a 2+b 2=bc c =b ,所以b =32c ,因此a 2=c 2-b 2=c 2-34c 2=14c 2,a =12c ,所以离心率e =ca =2.]类型4 直线与双曲线的位置关系【例4】 已知双曲线C :x 2-y 2=1及直线l :y =kx -1.(1)若直线l 与双曲线C 有两个不同的交点,求实数k 的取值范围; (2)若直线l 与双曲线C 交于A ,B 两点,O 是坐标原点,且△AOB 的面积为2,求实数k 的值.类比直线和椭圆的位置关系的判断方法,你认为如何判断直线和双曲线的位置关系.[解] (1)联立方程⎩⎪⎨⎪⎧y =kx -1,x 2-y 2=1,消去y 并整理得(1-k 2)x 2+2kx -2=0. ∵直线与双曲线有两个不同的交点,则⎩⎪⎨⎪⎧1-k 2≠0,Δ=4k 2+8(1-k 2)>0,解得-2<k <2,且k ≠±1.∴若l 与C 有两个不同交点,实数k 的取值范围为 (-2,-1)∪(-1,1)∪(1,2). (2)设A (x 1,y 1),B (x 2,y 2),对于(1)中的方程(1-k 2)x 2+2kx -2=0, 由根与系数的关系,得x 1+x 2=-2k1-k 2,x 1x 2=-21-k 2, ∴|AB |=1+k 2|x 1-x 2|=1+k 2·⎝ ⎛⎭⎪⎫-2k 1-k 22+81-k2 =(1+k 2)(8-4k 2)(1-k 2)2.又∵点O(0,0)到直线y=kx-1的距离d=11+k2,∴S△AOB =12·|AB|·d=128-4k2(1-k2)2=2,即2k4-3k2=0,解得k=0或k=±62.∴实数k的值为±62或0.直线与双曲线位置关系的判断方法(1)方程思想的应用把直线与双曲线的方程联立成方程组,通过消元后化为ax2+bx+c=0的形式,在a≠0的情况下考察方程的判别式.①Δ>0时,直线与双曲线有两个不同的公共点.②Δ=0时,直线与双曲线只有一个公共点.③Δ<0时,直线与双曲线没有公共点.当a=0时,此时直线与双曲线的渐近线平行,直线与双曲线有一个公共点.(2)数形结合思想的应用①直线过定点时,根据定点的位置和双曲线的渐近线的斜率与直线的斜率的大小关系确定其位置关系.②直线斜率一定时,通过平行移动直线,比较直线斜率与渐近线斜率的关系来确定其位置关系.提醒:利用判别式来判断直线与双曲线的交点个数问题的前提是通过消元化为一元二次方程.[跟进训练]4.已知双曲线x 24-y 2=1,求过点A (3,-1)且被点A 平分的弦MN 所在直线的方程.[解] 法一:由题意知直线的斜率存在,故可设直线方程为y +1=k (x -3),即y =kx -3k -1,由⎩⎨⎧y =kx -3k -1,x 24-y 2=1,消去y ,整理得(1-4k 2)x 2+8k (3k +1)x -36k 2-24k -8=0. 设M (x 1,y 1),N (x 2,y 2), ∴x 1+x 2=8k (3k +1)4k 2-1.∵A (3,-1)为MN 的中点, ∴x 1+x 22=3, 即8k (3k +1)2(4k 2-1)=3,解得k =-34. 当k =-34时,满足Δ>0,符合题意,∴所求直线MN 的方程为y =-34x +54, 即3x +4y -5=0.法二:设M (x 1,y 1),N (x 2,y 2),∵M ,N 均在双曲线上,∴⎩⎪⎨⎪⎧x 214-y 21=1,x 224-y 22=1,两式相减,得x 22-x 214=y 22-y 21,∴y 2-y 1x 2-x 1=x 2+x 14(y 2+y 1). ∵点A 平分弦MN , ∴x 1+x 2=6,y 1+y 2=-2. ∴k MN =y 2-y 1x 2-x 1=x 2+x 14(y 2+y 1)=-34.经验证,该直线MN 存在.∴所求直线MN 的方程为y +1=-34(x -3), 即3x +4y -5=0.1.(多选题)已知双曲线方程为x 2-8y 2=32,则( ) A .实轴长为82 B .虚轴长为4 C .焦距为6D .离心率为324ABD [双曲线方程x 2-8y 2=32化为标准方程为x 232-y 24=1,可得a =42,b =2,c =6,所以双曲线的实轴长为82,虚轴长为4,焦距为12,离心率为324.] 2.若双曲线x 2m -y 2=1的焦距为8,则实数m 的值是( ) A .15 B .17 C .15 D .17C [由题意知:2c =8,c =4,a 2=m ,b 2=1,因为c 2=a 2+b 2,所以16=m +1,解得m =15,故选C .]3.中心在原点,焦点在x 轴上,且一个焦点在直线3x -4y +12=0上的等轴双曲线的方程是( )A .x 2-y 2=8B .x 2-y 2=4C .y 2-x 2=8D .y 2-x 2=4A [令y =0,得x =-4,∴等轴双曲线的一个焦点为(-4,0), ∴c =4,a 2=b 2=12c 2=12×16=8,故选A .]4.已知圆C :x 2+y 2-10y +21=0与双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线相切,则该双曲线的离心率是________.52 [由双曲线x 2a 2-y 2b 2=1(a >0,b >0),可得其一条渐近线的方程为y =b a x ,即bx -ay =0,又由圆C :x 2+y 2-10y +21=0,可得圆心为C (0,5),半径r =2, 则圆心到直线的距离为d =|-5a |b 2+(-a )2=5a c ,则5a c =2,可得e =c a =52.]5.已知直线l :x -y +m =0与双曲线x 2-y 22=1交于不同的两点A ,B ,若线段AB 的中点在圆x 2+y 2=5上,则实数m 的值是________.±1[由⎩⎨⎧x -y +m =0,x 2-y22=1,消去y 得x 2-2mx -m 2-2=0.则Δ=4m 2+4m 2+8=8m 2+8>0. 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=2m ,y 1+y 2=x 1+x 2+2m =4m ,所以线段AB 的中点坐标为(m ,2m ). 又点(m ,2m )在x 2+y 2=5上, 所以m 2+(2m )2=5,得m =±1.]回顾本节知识,自我完成以下问题: (1)如何根据双曲线的方程研究其几何性质? [提示] (1)把双曲线方程化为标准形式; (2)由标准方程确定焦点位置,确定a ,b 的值;(3)由c 2=a 2+b 2求出c 值,从而写出双曲线的几何性质. (2)离心率e 和ba 有怎样的关系? [提示] e 2=1+b 2a 2.(3)如何用待定系数法设出与双曲线x 2a 2-y 2b 2=1有相同渐近线的双曲线方程? [提示] 可设为x 2a 2-y 2b 2=λ(λ≠0).(4)直线与双曲线相交,有两个交点时,其弦长公式与直线与椭圆相交时的弦长公式是否相同,你能写出来吗?[提示] 完全相同.直线y =kx +m 与双曲线x 2a 2-y 2b 2=1相交,其交点为A (x 1,y 1),B (x 2,y 2),则|AB |=1+k2(x 1+x 2)2-4x 1x 2或|AB |=1+1k 2(y 1+y 2)2-4y 1y 2.。
新课标人教A版选修2-1辅导资料—双曲线的简单几何性质(含答案)

双曲线的简单几何性质一、要点精讲1.双曲线的标准方程和几何性质2.等轴双曲线实轴和虚轴等长的双曲线叫做等轴双曲线,其标准方程为()022≠=-λλy x ,离心率2=e ,渐近线方程x y ±=。
3、共渐近线的双曲线系方程:与-22a x 22b y =1有相同渐近线的双曲线系方程可设为-22ax ()022≠=λλb y ,若0>λ,则双曲线的焦点在轴上;若0<λ,则双曲线的焦点在轴上。
4、共焦点的双曲线系方程:与-22ax 22b y =1焦点相同的双曲线系方程可设为()2222221,+x y k b k a a k b k -=<<-二、基础自测1.(15安徽)下列双曲线中,渐近线方程为2y x =±的是( )(A )2214y x -= (B )2214x y -=(C )2212y x -= (D )2212x y -= 2.(2013湖北)已知π04θ<<,则双曲线1C :22221sin cos x y θθ-=与2C :22221cos sin y x θθ-=的 ( ) A .实轴长相等B .虚轴长相等C .离心率相等D .焦距相等3.(2013课标)已知双曲线2222:1x y C a b -=(0,0)a b >>,则C 的渐近线方程为 ( )A .14y x =±B .13y x =±C .12y x =± D .y x =± 4.(15广东)已知双曲线C :12222=-b y a x 的离心率54e =,且其右焦点()25,0F ,则双曲线C 的方程为A .13422=-y x B.191622=-y x C.116922=-y x D. 14322=-y x 5.(2013湖南)设F 1、F 2是双曲线C,22221x y a b-=(a >0,b>0)的两个焦点。
2020-2021学年新教材数学人教A版选择性必修第一册课时分层作业:3.2.2双曲线的简单几何性质

课时分层作业(二十四)(建议用时:40分钟)一、选择题1.若实数k满足0<k<5,则曲线x216-错误!=1与曲线错误!-错误!=1的( )A.实半轴长相等B.虚半轴相等C.离心率相等D.焦距相等D[由于16+(5-k)=(16-k)+5,所以焦距相等.]2.若a>1,则双曲线错误!-y2=1的离心率的取值范围是()A.(错误!,+∞)B.(错误!,2)C.(1,错误!)D.(1,2)C[由题意得双曲线的离心率e=错误!。
即e2=错误!=1+错误!。
∵a>1,∴0<错误!<1,∴1<1+错误!<2,∴1<e<错误!。
故选C。
]3.已知双曲线C:错误!-错误!=1(a>0,b>0)的焦距为10,点P(2,1)在C的渐近线上,则双曲线C的方程为( ) A.错误!-错误!=1 B.错误!-错误!=1C.x280-错误!=1 D.错误!-错误!=1A[双曲线C的渐近线方程为错误!-错误!=0,又点P(2,1)在C 的渐近线上,所以错误!-错误!=0,即a2=4b2①。
又a2+b2=c2=25 ②.由①②,得b2=5,a2=20,所以双曲线C的方程为错误!-错误!=1,故选A。
]4.过双曲线错误!-错误!=1的右焦点F2作垂直于实轴的弦PQ,F1是左焦点,若∠PF1Q=90°,则双曲线的离心率是( ) A.错误!B.1+错误!C.2+错误!D.3-错误!B[因为|PF2|=|F2F1|,P点满足错误!-错误!=1,∴y=错误!错误!,∴2c=错误!错误!,即2ac=b2=c2-a2,∴2=e-错误!,又e>0,故e=1+2。
]5.已知双曲线C:错误!-y2=1,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M,N。
若△OMN为直角三角形,则|MN|=()A.错误!B.3C.2 3 D.4B[根据题意,可知其渐近线的斜率为±错误!,且右焦点为F(2,0),从而得到∠FON=30°,所以直线MN的倾斜角为60°或120°,根据双曲线的对称性,设其倾斜角为60°,可以得出直线MN的方程为y=错误!(x-2),分别与两条渐近线y=错误!x和y=-错误!x联立,求得M(3,3),N错误!,所以|MN|=错误!=3.]二、填空题6.(一题两空)若双曲线x2-错误!=1的离心率为错误!,则实数m =________,渐近线方程是________.2 y=±错误!x[a2=1,b2=m,e2=错误!=错误!=1+m=3,m=2.渐近线方程是y=±错误!x=±错误!x。
3.2.2 双曲线的简单几何性质(第1课时)(分层作业)(人教A版2019选修第一册)(解析版)

3.2.2双曲线的简单几何性质(第1课时)(分层作业)(夯实基础+能力提升)【夯实基础】一、单选题1.(2021·全国·高二课时练习)若直线x t =与双曲线2214xy -=有两个交点,则t 的值可以是()A .4B .2C .1D .-22.(2022·全国·高二课时练习)已知双曲线方程1,169-=下列说法中正确的有()A .焦点坐标()0,5±B .该双曲线的图象过点()1,1C .焦距为10D .双曲线上存在点P ,使得18PF =且20PF =3.(2022·全国·高二课时练习)双曲线2222x y -=的焦点坐标为()A .(1,0)±B.(C .(0,1)±D.(0,A.π4B .π3C .π2D .2π35.(2022·全国·高二课时练习)若双曲线()122:10,0C a b a b-=>>和它的共轭双曲线2C 的离心率分别为1e ,2e ,则1e ,2e 应满足的关系是()A .22121e e +=B .22121e e -=C .2212111e e -=D .2212111e e +=图形,如图2所示,篮球的外轮形状为圆O ,将篮球表面的粘合线看成坐标轴和双曲线,若坐标轴和双曲线与圆O 的交点将圆O 的周长八等分,112AB BC CD ===,则该双曲线的焦距为()AB .2C .D 设双曲线的方程为2222x y a b-则该双曲线过点()2,2,且解得22b =,所以22c a =+所以该双曲线的焦距为2故选:C .7.(2021·全国·高二专题练习)双曲线22a b -=1与()220a bλλ-=≠有相同的()A .实轴B .焦点C .渐近线D .以上都不对【答案】C【分析】根据双曲线的几何性质即可得到答案【详解】当2λ=时,容易判断下面判断渐近线.8.(2022·全国·高二专题练习)已知点P 是双曲线214y x -=上的动点,过原点O 的直线l与双曲线分别相交于M 、N 两点,则PM PN +uuu r uuu r的最小值为()A .4B .3C .2D .19.(2021·广东·佛山一中高二阶段练习)已知双曲线C :195-=的左右焦点为1F ,2F ,点P 在双曲线C 的右支上,点P 关于原点的对称点为Q ,则11PF QF -=()A .4B .C .6D .由22195x y -=可知,3a =,∴111226PF QF PF PF a -=-==.故选:C.10.(2021·福建龙岩·高二期中)关于双曲线221164y x -=,下列说法正确的是()A .实轴长为8B .焦距为C .顶点坐标为(4,0)±D11.(2022·全国·高二课时练习)对于方程214y -=和24y λ-=(0λ>且1λ≠)所表示的双曲线,有相同的()A .顶点B .焦点C .离心率D .渐近线12.(2022·福建厦门·高二期末)曲线:14x C y y +=,则()A .C 上的点(),x y 满足x ∈R ,1y ≤B .C 关于x 轴、y 轴对称C .C 与x 轴、y 轴共有3个公共点D .C 与直线2xy =只有1个公共点双曲线的一条渐近线为2x y =,故选项ACD 正确,选项B 错误.故选:ACD.13.(2022·全国·高二专题练习)已知曲线C :22115x y k k+=--,则下列说法正确的是()A .若曲线C 表示双曲线,则5k >B .若曲线C 表示椭圆,则15k <<且3k ≠C .若曲线C 表示焦点在x7k =D .若曲线C 与椭圆22142x y +=有公共焦点,则4k =14.(2022·山西太原·高二期末)双曲线2214y x -=的顶点坐标为__________.15.(2022·全国·高二课时练习)如果双曲线方程221x my +=焦点在x 轴上,且焦距为则m 的值为___________.【答案】14-##0.25-双曲线虚轴长为______.心率_______.得的线段的中点坐标为______.19.(2022·全国·高二课时练习)与双曲线1164x y -=有公共焦点,且过点()2的双曲线方程为______.,且对称轴都在坐标轴上的等轴双曲线的焦点坐标是______.21.(2022·全国·高二课时练习)点()0,1P 到双曲线214yx -=渐近线的距离是______.22.(2022·全国·高二课时练习)求与双曲线221164x y -=有公共焦点,且过点()的双曲线方程.(1)与双曲线221916x y -=有共同渐近线,且过点(3,-;(2)与双曲线221164x y -=有公共焦点,且过点2)(1)经过点),()3,2;(2)焦点为()0,5-,()0,5,经过点⎝;(3)a b =,经过点()3,1-;(4)经过(3,-和9,54⎫⎛ ⎪⎝⎭两点.(1)焦点()12,0F -,()22,0F ,一个顶点为()1,0;(2)一个焦点为()0,3,离心率为3;(3)一条渐近线为230x y -=,且过点()1,1-;(4)经过点(3,-,9,54⎫⎛ ⎪⎝⎭.(1)一个焦点为()3,0F -,且经过点()2,0;(2)与双曲线221164x y -=有相同的焦点,且经过点()2;(3)经过3M ⎛⎫- ⎪ ⎪⎝⎭和()4,3N -两点.(1)22832x y -=;(2)22981x y -=;(3)224x y -=-;(4)2214925x y -=-.为圆心,1为半径的圆相切,双曲线C的一个顶点A'与点A关于直线y x=对称,设直线l 过点A,斜率为k.(1)求双曲线C的方程;(2)当1k =时,在双曲线C 的上支上求点B ,使其与直线l.(1)焦点在x 轴上,虚轴长为8,离心率为53;(2)过点(2,0),与双曲线2216416y x -=离心率相等.一、单选题1.(2022·安徽省皖西中学高二期末)已知12,F F 是椭圆和双曲线的公共焦点,P 是它们的一个公共点,且122π3F PF ∠=,记椭圆和双曲线的离心率分别为12,e e ,则221231e e +的值为()A .4B .3C .2D .12.(2022·云南·罗平县第一中学高二开学考试)已知曲线22:124x yCm m+=+-,则()A.当2m=时,则C的焦点是)1F,()2FB.当6m=时,则C的渐近线方程为12y x=±C.当C表示双曲线时,则m的取值范围为2m<-D.存在m,使C表示圆3.(2022·全国·高二课时练习)已知双曲线()222210,0x y a ba b-=>>的左、右焦点分别为1F,2F,离心率为3,点(A是双曲线上一点连接2AF,过点1F作12//BF AF交双曲线于点B,且12BF AF<,则21AFBF=______.【详解】)3,2是双曲线上一点和双曲线的离心率为2221113b e =-=,解得2231a b ⎧=⎨=⎩,4,c =2,)2,0,()()22232203AF =-+-=.2AF 的斜率为2,2//AF ,所以直线1BF 的斜率为2.p 1BF 的倾斜角为θ,则tan 2θ=,2θθ=,即sin 2cos θθ=,2cos 1θθ+=,θ为锐角,33θ=.,在12BF F △中,由余弦定理得22BF BF =()212BF a =+,所以135BF =,5=.故答案为:54.(2022·全国·高二课时练习)设A 、B 、C 是双曲线()22210,0y x a b b-=>>上的三个点,AB 经过原点O ,AC 经过右焦点F ,若BF AC ⊥且2AF CF =,则焦距为______.5.(2022·全国·高二课时练习)若过点P (0,1)作直线l ,使l 与双曲线214y x -=有且仅有一个公共点,则直线l 的方程为______.离为4,且该双曲线的虚轴长为8,则该双曲线的标准方程为______.7.(2022·全国·高二课时练习)点P 在双曲线2219y x -=上,若点P 在第一象限,则点P 到直线3y x =的距离的取值范围是______.8.(2022·全国·高二课时练习)已知双曲线C :()222210,0x y a b a b-=>>,以点(),0P b 为圆心,a 为半径作圆P ,圆P 与双曲线C 的一条渐近线交于M 、N 两点,若∠MPN =90°,求C 的离心率.9.(2022·全国·高二课时练习)已知双曲线()222210,0x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A 、B 两点.设A 、B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126d d +=,求双曲线的方程.10.(2022·全国·高二课时练习)若双曲线()22:10,0C a b a b-=>>的一个焦点是()22,0F ,且离心率为2.(1)求双曲线C 的方程;(2)设过焦点2F 的直线l 的一个法向量为(),1m ,当直线l 与双曲线C 的右支相交于,A B 不同的两点时,①求实数m 的取值范围;∠为锐角?若存在,请求出m的取值范围;若不存在,请说②是否存在实数m,使得AOB明理由.11.(2022·全国·高二单元测试)已知点A 、F 分别为双曲线C :()2210,0x y a b a b -=>>的左顶点和右焦点,且点A 、F 到直线2a x c=的距离相等.(1)求双曲线C 的离心率;(2)设M 为双曲线C 上的点,且点M 到双曲线C 的两条渐近线的距离乘积为34.①求双曲线C 的方程;②设过点F 且与坐标轴不垂直的直线l 与双曲线C 相交于点P 、Q ,线段PQ 的垂直平分线与x 轴交于点B ,求PQBF值.近线为0x +=,设过点()A -的直线l 的法向量为(),1k -.(1)求双曲线C 的方程;(2)当k >C 的右支上是否存在点Q ,Q 到直线l ?若存在,求出点Q 的坐标;若不存在,请说明理由.。
高中数学新人教A版选择性必修第一册3.2.2双曲线的简单几何性质课件
C.m ∈R
D.-√2≤m≤√2
【答案】D [ 由
由题意知1—m²=0,
解得一 √2≤m≤√2.]
得(1—m²)x²—2mx—2=0,
4. 如图为一座高100米的双曲线冷却塔外壳的简化三视图(忽略
壁厚),其底面直径大于上底直径,已知其外壳主视图与左视图中 的曲线均为双曲线,高度为100m, 俯视图为三个同心圆,其半径
解:设点M(x,y), 由题知
即 整理得:
请你将例5与椭圆一节中的例6比较,你有什么发现?
例6、 过双曲线 求IABI.
的右焦点F₂, 倾斜角为30度的直线交双曲线于A,B两点,
分析:求弦长问题有两种方法: 法 一:如果交点坐标易求,可直接用两点间距离公 式代入求弦长;
法二:但有时为了简化计算,常设而不求,运用韦达 定理来处理.
A.y²—3x²=36 C.3y²—x²=36
B.x²—3y²=36 D.3x²-y²=36
பைடு நூலகம்
【答案】A [椭圆4
即
则双曲线的焦点在y 轴上,c=4√3,
线的方程为y²-3x²=36.]
焦点为(0,±4 √3),离心率为 从而a=6,b²=12, 故所求双曲
3 .直线y=mx+1 与双曲线x²—y²=1 有公共点,则m 的取值范围是( )
,
即 3x+4y-5=0.
课堂小结
1.掌握双曲线的简单几何性质. 2.双曲线方程的简单应用. 3.理解直线与双曲线的位置关系.
谢谢大家
人教A 版选择性必修第一册
对称性 对称轴:x轴、y轴;对称中心:坐标原点
顶点坐标
性轴 质
新教材高中数学第三章双曲线的简单几何性质分层作业pptx课件新人教A版选择性必修第一册
(1)求点 的轨迹方程;
解 点 和 ,动点 到 , 两点的距离之差的绝对值为 , 点 的轨迹方程是以 和 为焦点的双曲线,且 , , 点 的轨迹方程是 .
(2)点 的轨迹与经过点 且斜率为1的直线交于 , 两点,求线段 的长.
点 的轨迹方程是 ,经过点 且斜率为1的直线方程为 . 联立 得 ,设 , ,则 , , .故线段 的长为 .
5.[探究点三]两个正数 , 的和为5,积为6,且 ,则双曲线 的离心率 _ ___,渐近线方程为_________.
[解析] 由 解 得 或 又 , , , , .渐近线方程为 .
6.[探究点一]已知 为双曲线 的左焦点, , 为 上的点.若 的长等于虚轴长的2倍,点 在线段 上,则 的周长为____.
16.已知 为双曲线 的一条渐近线,其倾斜角为 ,且 的右焦点为 ,则 的右顶点为________; 的方程为_ __________.
[解析] 由题意可得 ,即 ,一条渐近线的斜率为 ,解 得 ,则双曲线的右顶点为 , 的方程为 .
17.已知 为双曲线 的右焦点,过点 向双曲线 的一条渐近线引垂线,垂足为 ,且交另一条渐近线于点 ,若 ,则双曲线 的离心率是_ ___.
C
A. B. C. D.
[解析] 已知双曲线 的离心率为 ,故有 ,所以 ,解 得 .故双曲线 的渐近线方程为 .故选C.
3.[探究点一]如图,双曲线 的左焦点为 ,双曲线上的点 与 关于 轴对称,则 的值是( )
C
A.3 B.4 C.6 D.8
01
分层作业
[精品]新人教A版选修1-1高中数学分层测评10双曲线的简单几何性质和答案
学业分层测评(建议用时:45分钟)[学业达标]一、选择题1.双曲线x 29-y 216=1的渐近线方程是( )A .4x ±3y =0B .16x ±9y =0C .3x ±4y =0D .9x ±16y =0【解析】 由题意知,双曲线焦点在x 轴上,且a =3,b =4,∴渐近线方程为y =±43x ,即4x ±3y =0.【答案】 A2.中心在原点,实轴在x 轴上,一个焦点在直线3x -4y +12=0上的等轴双曲线方程是( )A .x 2-y 2=8B .x 2-y 2=4C .y 2-x 2=8D .y 2-x 2=4【解析】 令y =0,得x =-4, ∴等轴双曲线的一个焦点坐标为(-4,0), ∴c =4,a 2=b 2=12c 2=12×16=8,故选A.【答案】 A3.设双曲线x 2a 2-y 2b2=1(a >0,b >0)的虚轴长为2,焦距为23,则双曲线的渐近线方程为( )A .y =±2xB .y =±2xC .y =±22xD .y =±12x【解析】 由已知,得b =1,c =3,a =c 2-b 2= 2. 因为双曲线的焦点在x 轴上,所以渐近线方程为y =±b a x =±22x .【答案】 C4.(2014·全国卷Ⅰ)已知双曲线x 2a 2-y 23=1(a >0)的离心率为2,则a =( )A .2 B.62C.52D .1【解析】 由题意得e =a 2+3a=2,∴a 2+3=2a ,∴a 2+3=4a 2,∴a 2=1,∴a =1. 【答案】 D5.与曲线x 224+y 249=1共焦点,且与曲线x 236-y 264=1共渐近线的双曲线的方程为( )A.y 216-x 29=1B.x 216-y 29=1 C.y 29-x 216=1 D.x 29-y 216=1 【解析】 根据椭圆方程可知焦点为(0,-5),(0,5).设所求双曲线方程为x 236-y 264=λ(λ<0),即y 2-64λ-x 2-36λ=1.由-64λ+(-36λ)=25,得λ=-14.故所求双曲线的方程为y 216-x 29=1.【答案】 A 二、填空题6.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为________.【解析】 由三角形相似或平行线分线段成比例定理得26=ac,∴ca=3,即e =3. 【答案】 37.直线3x -y +3=0被双曲线x 2-y 2=1截得的弦AB 的长是________.【解析】 联立消去y ,得x 2+3x +2=0,设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=-3,x 1x 2=2,∴|AB |=1+32·-2-4×2=2.【答案】 28.若直线x =2与双曲线x 2-y2b2=1(b >0)的两条渐近线分别交于点A ,B ,且△AOB 的面积为8,则焦距为________.【导学号:26160051】【解析】 由双曲线为x 2-y2b2=1得渐近线为y =±bx ,则交点A (2,2b ),B (2,-2b ).∵S △AOB =12×2×4b =8,∴b =2.又a 2=1,∴c 2=a 2+b 2=5. ∴焦距2c =2 5. 【答案】 2 5 三、解答题9.已知双曲线C 的方程为y 2a 2-x 2b 2=1(a >0,b >0),离心率e =52,顶点到渐近线的距离为255,求双曲线C 的方程.【解】 依题意,双曲线的焦点在y 轴上,顶点坐标为(0,a ),渐近线方程为y =±abx ,即ax ±by =0,所以ab a 2+b 2=ab c =255. 又e =c a =52,所以b =1,即c 2-a 2=1,⎝ ⎛⎭⎪⎪⎫52a 2-a 2=1, 解得a 2=4,故双曲线方程为y 24-x 2=1. 10.双曲线x 2a 2-y 2b2=1(a >0,b >0)的两个焦点为F 1,F 2,若双曲线上存在点P ,使|PF 1|=2|PF 2|,试确定双曲线离心率的取值范围.【解】 由题意知在双曲线上存在一点P ,使得|PF 1|=2|PF 2|,如图所示.又∵|PF 1|-|PF 2|=2a ,∴|PF 2|=2a ,即在双曲线右支上恒存在点P ,使得|PF 2|=2a ,即|AF 2|≤2a .∴|OF 2|-|OA |=c -a ≤2a ,∴c ≤3a .又∵c >a ,∴a <c ≤3a ,∴1<ca≤3,即1<e ≤3.[能力提升]1.双曲线x 24+y 2k=1的离心率e ∈(1,2),则k 的取值范围是( )A .(-10,0)B .(-12,0)C .(-3,0)D .(-60,-12)【解析】 双曲线方程化为x 24-y 2-k=1,则a 2=4,b 2=-k ,c 2=4-k ,e =ca =4-k 2,又∵e ∈(1,2),∴1<4-k2<2,解得-12<k <0. 【答案】 B2.已知双曲线E 的中心为原点,F (3,0)是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为N (-12,-15),则E 的方程为( )A.x 23-y 26=1B.x 24-y 25=1C.x 26-y 23=1 D.x 25-y 24=1 【解析】 设双曲线的标准方程为x 2a 2-y 2b2=1(a >0,b >0),由题意知c =3,a 2+b 2=9,设A (x 1,y 1),B (x 2,y 2),则有⎩⎪⎨⎪⎧x 21a 2-y 21b 2=1,x 22a 2-y22b 2=1,两式作差得y 1-y 2x 1-x 2=b 2x 1+x 2a 2y 1+y 1=-12b 2-15a 2=4b 25a 2,又AB 的斜率是-15-0-12-3=1,所以4b 2=5a 2,代入a 2+b 2=9得a 2=4,b 2=5, 所以双曲线标准方程是x 24-y 25=1.【答案】 B3.已知双曲线x 2-y 23=1的左顶点为A 1,右焦点为F 2,P 为双曲线右支上一点,则PA1→·PF 2→的最小值为________. 【解析】 由题意得A 1(-1,0),F 2(2,0), 设P (x ,y )(x ≥1), 则PA1→=(-1-x ,-y ), PF2→=(2-x ,-y ), ∴PA1→·PF 2→=(x +1)(x -2)+y 2=x 2-x -2+y 2, 由双曲线方程得y 2=3x 2-3, 代入上式得PA1→·PF 2→=4x 2-x -5 =4⎝⎛⎭⎪⎫x -182-8116,又x ≥1,所以当x =1时,PA 1→·PF 2→取得最小值,且最小值为-2.【答案】 -24.(2016·荆州高二检测)双曲线C 的中点在原点,右焦点为F ⎝ ⎛⎭⎪⎫233,0,渐近线方程为y =±3x . (1)求双曲线C 的方程; 【导学号:26160052】(2)设直线L :y =kx +1与双曲线交于A ,B 两点,问:当k 为何值时,以AB 为直径的圆过原点?【解】 (1)设双曲线的方程为x 2a 2-y 2b 2=1,由焦点坐标得c =233,渐近线方程为y =±b a x =±3x ,结合c 2=a 2+b 2得a 2=13,b 2=1,所以双曲线C 的方程为x 213-y 2=1,即3x 2-y 2=1. (2)由⎩⎪⎨⎪⎧y =kx +1,3x 2-y 2=1,得(3-k 2)x 2-2kx -2=0,由Δ>0,且3-k 2≠0,得-6<k <6,且k ≠± 3.设A (x 1,y 1),B (x 2,y 2),因为以AB 为直径的圆过原点,所以OA ⊥OB ,所以x 1x 2+y 1y 2=0.又x 1+x 2=-2k k 2-3,x 1x 2=2k 2-3,所以y 1y 2=(kx 1+1)·(kx 2+1)=k 2x 1x 2+k (x 1+x 2)+1=1,所以2k 2-3+1=0,解得k =±1.。
3.2.2双曲线的简单几何性质2024-2025学年高二上学期数学人教A版(2019)选择性必修一
离
,化简得b²=3a², 因 此 ,c²=4a², 即 c=2a, 从 而
8.设双曲线 是
的左、右焦点分别为F,F₂, 离心率为 √ 5,P
双曲线上一点,且FP⊥F₂P, 若△PFF 的面积为8,则a=
解析;不妨设P 为双曲线左支上的一点,由题意,设PF₂=m,PF₁=n, 则有m-n=2a
,m²+n²=4c²,
,直线y=-b 与 T 交于A,B 两点,直线y=7b
与T 交于C,D 两点,四边形ABCD的两条对角线交于点E,∠AEB=60°, 则双曲
(A 线T 的离心率为(
A
D
B.
C.2
D.4
解析;在
中,令y=-b, 得 x=± √2a,不 妨 设A( √2a,-b),B(- √2a,-b),
同理可得C(-5 √2a,7b),D(5 √2a,7b),由对称性可知,四边形ABCD 的两条对角线
4
设Q(x₂,y₂),因 为Q 是直线l 与直线l₂ 的交点,所以
事
假设x 轴上存在定点M(x₀,0), 使 得MP⊥MQ,
则MP.MQ=(x-x₀,y)·(x₂-xo,y₂)=(x-x,)(x₂-
x₀)+y₁y₂
故存在x₀=2, 使得MP·MQ=0, 即 MP⊥MQ, 所以x 轴上存在定点M(2,0), 使 得MP⊥MQ.
的交点E 在y 轴上,易知直线AC的方程为
令x=0, 得
即
因为∠AEB=60°, 所以△ABE是等边三角形,
所
以 故选A.
,27a²=8b² 因为c²=a²+b², 所以35a²=8c², 所 以
5 . (多选)已知双曲线C:
右顶点为A, 以 A 为圆心, b 为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时分层作业(十) 双曲线的简单几何性质(建议用时:40分钟)[基础达标练]一、选择题1.已知双曲线x 2a 2-y 25=1的右焦点为(3,0),则该双曲线的离心率等于( )A.31414 B.324 C.32 D.43C [由题意知a 2+5=9,解得a =2,故e =32.]2.已知双曲线方程为x 2-y 24=1,过P (1,0)的直线l 与双曲线只有一个公共点,则共有l ( )A .4条B .3条C .2条D .1条B [因为双曲线方程为x 2-y 24=1,所以P (1,0)是双曲线的右顶点,所以过P (1,0)并且和x 轴垂直的直线是双曲线的一条切线,与双曲线只有一个公共点,另外还有两条就是过点P (1,0)分别和两条渐近线平行的直线,所以符合要求的共有3条,故选B.]3.双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的离心率为2,焦点到渐近线的距离为3,则双曲线C 的焦距等于( )A .2B .2 2C .4D .4 2C [由已知得e =c a =2,所以a =12c ,故b =c 2-a 2=32c ,从而双曲线的渐近线方程为y =±ba x =±3x ,由焦点到渐近线的距离为3,得32c =3,解得c =2,故2c =4,故选C.]4.若实数k 满足0<k <5,则曲线x 216-y 25-k =1与曲线x 216-k -y 25=1的( )【导学号:97792092】A .实半轴长相等B .虚半轴长相等C .离心率相等D .焦距相等D [若0<k <5,则5-k >0,16-k >0,故方程x 216-y 25-k=1表示焦点在x 轴上的双曲线,且实半轴的长为4,虚半轴的长为5-k ,焦距2c =221-k ,离心率e =21-k4;同理方程x 216-k -y 25=1也表示焦点在x 轴上的双曲线,实半轴的长为16-k ,虚半轴的长为5,焦距2c =221-k ,离心率e =21-k16-k.可知两曲线的焦距相等,故选D.] 5.设双曲线x 2a 2-y 2b2=1(b >a >0)的半焦距为c ,且直线l 过(a,0)和(0,b )两点,已知原点到直线l 的距离为3c4,则双曲线的离心率为( ) A.233B. 2C. 3D .2D [直线l 的方程为x a +yb=1,即bx +ay -ab =0,原点到直线l 的距离d =ab a 2+b 2=abc=34c 即ab =34c 2,所以a 2(c 2-a 2)=316c 4. 整理得3e 4-16e 2+16=0,解得e 2=4或e 2=43又b >a >0,所以e 2=1+b 2a2>2,故e =2.]二、填空题6.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的焦距为25,且双曲线的一条渐近线与直线2x+y =0垂直,则双曲线方程为________.x 24-y 2=1 [由题意可得⎩⎪⎨⎪⎧b a =12a 2+b 2=5,解得⎩⎪⎨⎪⎧a 2=4b 2=1,故所求双曲线方程为x 24-y 2=1.]7.若a >1,则双曲线x 2a2-y 2=1的离心率的取值范围是________.【导学号:97792093】(1,2) [e 2=1+1a2,由a >1得1<e 2<2.所以1<e < 2.]8.若直线x =2与双曲线x 2-y 2b2=1(b >0)的两条渐近线分别交于点A ,B ,且△AOB 的面积为8,则焦距为________.25 [双曲线的渐近线方程为y =±bx ,则A (2,2b ),B (2,-2b ),|AB |=4b ,从而S △AOB=12×4b ×2=8. 解得b =2,所以c 2=5,从而焦距为2 5.] 三、解答题9.双曲线与椭圆x 216+y 264=1有相同的焦点,它的一条渐近线为y =x ,求双曲线的标准方程和离心率.[解] 由椭圆x 216+y 264=1,知c 2=64-16=48,且焦点在y 轴上,∵双曲线的一条渐近线为y =x ,∴设双曲线方程为y 2a 2-x 2a2=1.又c 2=2a 2=48,∴a 2=24. ∴所求双曲线的方程为y 224-x 224=1.由a 2=24,c 2=48,得e 2=c 2a2=2,又e >0,∴e = 2.10.已知中心在原点的双曲线C 的右焦点为(2,0),右顶点为(3,0). (1)求双曲线C 的方程;(2)若直线l :y =kx +2与双曲线C 恒有两个不同的交点A 和B ,且OA →·OB →>2,其中O 为原点,求k 的取值范围.【导学号:97792094】[解] (1)设双曲线C 的方程为x 2a 2-y 2b2=1(a >0,b >0),由已知得a =3,c =2.又因为a 2+b 2=c 2,所以b 2=1, 故双曲线C 的方程为x 23-y 2=1.(2)将y =kx +2代入x 23-y 2=1中,得(1-3k 2)x 2-62kx -9=0, 由直线l 与双曲线交于不同的两点得:⎩⎨⎧1-3k 2≠0,Δ=-62k2+-3k2,即k 2≠13且k 2<1.①设A (x A ,y A ),B (x B ,y B ), 则x A +x B =62k 1-3k 2,x A x B =-91-3k 2,由OA →·OB →>2得x A x B +y A y B >2,而x A x B +y A y B =x A x B +(kx A +2)(kx B +2) =(k 2+1)x A x B +2k (x A +x B )+2=(k 2+1)·-91-3k 2+2k ·62k 1-3k 2+2=3k 2+73k 2-1, 于是3k 2+73k 2-1>2,解此不等式得13<k 2<3.②由①②得13<k 2<1.故k 的取值范围是⎝ ⎛⎭⎪⎫-1,-33∪⎝ ⎛⎭⎪⎫33,1. [能力提升练]1.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的两条渐近线均与曲线C :x 2+y 2-6x +5=0相切,则该双曲线的离心率等于( )A.355B.62C.32D.55A [曲线C 的标准方程为(x -3)2+y 2=4,所以圆心坐标为C (3,0),半径r =2,双曲线的渐近线为y =±ba x ,不妨取y =b ax ,即bx -ay =0,因为渐近线与圆相切,所以圆心到直线的距离d =|3b |a 2+b 2=2,即9b 2=4(a 2+b 2),所以5b 2=4a 2,b 2=45a 2=c 2-a 2,即95a 2=c 2,所以e 2=95,e =355,选A.]2.设F 1,F 2分别为双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点.若在双曲线右支上存在点P ,满足|PF 2|=|F 1F 2|,且F 2到直线PF 1的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )A .3x ±4y =0B .3x +5y =0C .5x ±4y =0D .4x ±3y =0D [由题意可知|PF 2|=|F 1F 2|=2c ,所以△PF 1F 2为等腰三角形,所以由F 2向直线PF 1作的垂线也是中线,因为F 2到直线PF 1的距离等于双曲线的实轴长2a ,所以|PF 1|=24c 2-4a2=4b ,又|PF 1|-|PF 2|=2a ,所以4b -2c =2a ,所以2b -a =c ,两边平方可得4b 2-4ab +a2=c 2=a 2+b 2,所以3b 2=4ab ,所以4a =3b ,从而b a =43,所以该双曲线的渐近线方程为4x ±3y=0,故选D.]3.设双曲线x 2a 2-y 2b2=1(a >0,b >0)的右焦点是F ,左、右顶点分别是A 1,A 2,过点F 作x轴的垂线与双曲线交于B ,C 两点,若A 1B ⊥A 2C ,则该双曲线的渐近线的斜率为________.±1 [不妨设点B 在第一象限,则A 1(-a,0),B ⎝ ⎛⎭⎪⎫c ,b 2a ,A 2(a,0),C ⎝ ⎛⎭⎪⎫c ,-b 2a ,所以A 1B →=⎝ ⎛⎭⎪⎫a +c ,b 2a ,A 2C →=⎝ ⎛⎭⎪⎫c -a ,-b 2a .因为A 1B ⊥A 2C ,所以A 1B →·A 2C →=0,所以c 2-a 2-b 4a 2=0,整理得,b 2a 2=1,即ba=1,所以渐近线的斜率为±1.]4.已知直线l :x -y +m =0与双曲线x 2-y 22=1交于不同的两点A ,B ,若线段AB 的中点在圆x 2+y 2=5上,则实数m 的值是________.【导学号:97792095】±1 [由⎩⎪⎨⎪⎧x -y +m =0x 2-y 22=1,消去y 得x 2-2mx -m 2-2=0.则Δ=4m 2+4m 2+8=8m 2+8>0.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=2m ,y 1+y 2=x 1+x 2+2m =4m ,所以线段AB 的中点坐标为(m,2m ).又点(m,2m )在圆x 2+y 2=5上,所以m 2+(2m )2=5,得m =±1.]5.直线y =ax +1与双曲线3x 2-y 2=1相交于A ,B 两点. (1)求线段AB 的长;(2)当a 为何值时,以AB 为直径的圆经过坐标原点?新人教部编版初高中精选试题。
