三角形内角和180°证明7种方法
三角形内角和180°证明7种方法
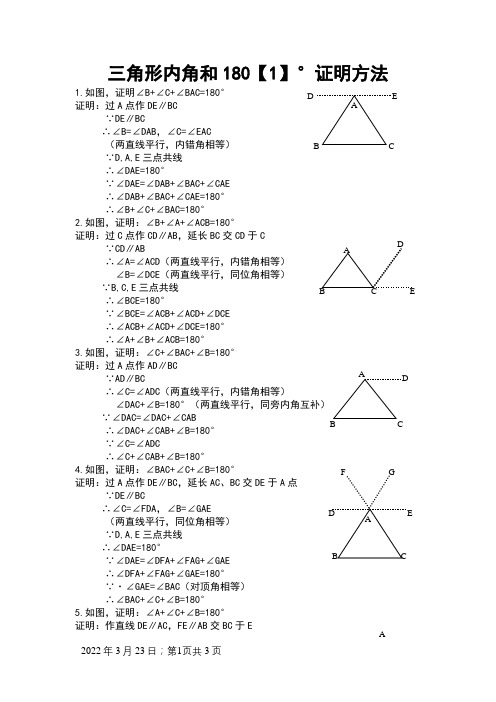
三角形内角和180【1】°证明方法1.如图,证明∠B+∠C+∠BAC=180° 证明:过A 点作DE ∥BC∵DE ∥BC∴∠B=∠DAB ,∠C=∠EAC(两直线平行,内错角相等) ∵D,A,E 三点共线∴∠DAE=180°∵∠DAE=∠DAB+∠BAC+∠CAE∴∠DAB+∠BAC+∠CAE=180°∴∠B+∠C+∠BAC=180°2.如图,证明:∠B+∠A+∠ACB=180°证明:过C 点作CD ∥AB ,延长BC 交CD 于C ∵CD ∥AB ∴∠A=∠ACD (两直线平行,内错角相等)∠B=∠DCE (两直线平行,同位角相等)∵B,C,E 三点共线 ∴∠BCE=180°∵∠BCE=∠ACB+∠ACD+∠DCE∴∠ACB+∠ACD+∠DCE=180°∴∠A+∠B+∠ACB=180°3.如图,证明:∠C+∠BAC+∠B=180°证明:过A 点作AD ∥BC ∵AD ∥BC∴∠C=∠ADC (两直线平行,内错角相等)∠DAC+∠B=180°(两直线平行,同旁内角互补)∵∠DAC=∠DAC+∠CAB ∴∠DAC+∠CAB+∠B=180°∵∠C=∠ADC∴∠C+∠CAB+∠B=180°4.如图,证明:∠BAC+∠C+∠B=180° 证明:过A 点作DE ∥BC ,延长AC 、BC 交DE 于A 点∵DE ∥BC∴∠C=∠FDA ,∠B=∠GAE (两直线平行,同位角相等)∵D,A,E 三点共线∴∠DAE=180° ∵∠DAE=∠DFA+∠FAG+∠GAE∴∠DFA+∠FAG+∠GAE=180°∵·∠GAE=∠BAC (对顶角相等)∴∠BAC+∠C+∠B=180°5.如图,证明:∠A+∠C+∠B=180°证明:作直线DE ∥AC ,FE ∥AB 交BC 于E A∵DE ∥AC∴∠AFE+∠DEF=180°(两直线平行,同旁内角互补) ∠C=∠DEB (两直线平行,同位角相等)∵FE ∥AB∴∠AFE+∠A=180°(两直线平行,同旁内角互补) ∠B=∠FEC (两直线平行,同位角相等)∴∠A=∠DEF∵B,C,E 三点共线∴∠BCE=180°∵∠BCE=∠DEB+∠DEF+∠FEC∴∠DEB+∠DEF+∠FEC =180°∴∠A+∠C+∠B=180°6.如图,证明:∠A+∠B+∠C=180°证明:作DE ∥AC ,FG ∥AB ,MN ∥BC ,都交于点O∵DE ∥AC∴∠AFO+∠FOD=180°(两直线平行,同旁内角互补)∵FG ∥AB ∴∠AFO+∠A=180°(两直线平行,同旁内角互补) ∴∠A=∠FOD∵MN ∥BC ∴∠C=∠FNO ∵DE ∥AC ∴∠FNO=∠DOM ∴∠C=∠DOM∵MN ∥BC∴∠B=∠DMO (两直线平行,同位角相等)∵FG ∥AB∴∠DMO=∠FON (两直线平行,同位角相等)∴∠B=∠FNO∵M,O,N 三点共线∴∠MON=180°∵∠MON=∠DOM+∠DOF+∠FON∴∠DOF+∠DOM+∠FON=180°∴∠A+∠B+∠C=180°7. 如图,证明:∠BAC+∠CBA+∠ACB=180°证明:作DE ∥AC ,FG ∥AB ,MN ∥BC ,都交于点O延长AC 交FG 于点K ,延长AB 到点L ,延长BC 交FG 于点P∵ MN ∥BC∴∠ABC=∠AHN ,∠ACB=∠ANM∴∠ABC=∠FON ∵ DE ∥AC ∴∠ANM=∠DOM (两直线平行,同位角相等) ∠OKA=∠DOF(两直线平行,内错角相等)∴∠ACB=∠DOM∵ FG ∥AB∴∠BAC=∠OKA (两直线平行,同位角相等) ∴∠BAC=∠DOF∵ M,O,N 三点共线∴∠MON=180°∵∠MON=∠DOM+∠DOF+∠FON∴∠DOM+∠DOF+∠FON=180°∴∠BAC+∠CBA+∠ACB=180° CO B E G M N H P。
三角形内角和定理的证明方法

三角形内角和定理的证明方法
三角形内角和定理又被称为三角形内角的性质,它是指任意三角形的三个内角和等于180度。
证明方法如下:
1. 画出任意三角形ABC,并且在三角形的一边AC上取一点D。
2. 连接BD。
3. 分别求解△ABC和△DBC的三角形内角和。
3.1 对于△ABC,我们知道∠ABC+∠BAC+∠CAB=180度。
3.2 对于△DBC,根据三角形内角和定理,我们知道
∠DBC+∠BDC+∠DCB=180度。
4. 观察△ABC和△DBC的两个内角和中的两个角,即∠ABC 和∠BDC,它们是重叠的,即∠ABC=∠BDC。
5. 将等式∠ABC+∠BAC+∠CAB=180度代入等式
∠DBC+∠BDC+∠DCB=180度,得到
∠BDC+∠BAC+∠CAB=180度。
6. 根据等式∠BDC+∠BAC+∠CAB=180度,我们得到△ABC 和△DBC的三个内角和相等。
7. 根据三角形内角和定理,我们可以得知任意三角形的三个内角和等于180度。
综上所述,这是三角形内角和定理的证明方法。
三角形内角和180°证明7种方法

三角形内角和180°证明7种方法三角形是平面几何中的重要概念,它由三条边和三个角组成。
在欧氏几何中,三角形的内角和总是等于180°。
证明三角形内角和等于180°有许多不同的方法。
下面将介绍七种不同的证明方法,以阐述这一重要结论。
方法一:直角三角形的证明考虑一个直角三角形,其中一个角度为90°。
以这个角度为基础,我们可以将其他两个角度表示为α和β。
根据三角形内角和的定义,我们可以得到α+β+90°=180°,因此α+β=90°。
方法二:欧几里得几何法欧几里得几何中,三角形的内角和等于平面中的一直线对应的角。
在直线上,两个互相垂直的角的和是等于90°。
因此,我们可以将直线分为相互垂直的两个角,然后将两个角组合成一个等于90°的角。
这样,我们得到了三角形内角和等于180°的结论。
方法三:外角的证明考虑一个三角形ABC,我们可以在每个顶点处添加一个外角D、E和F。
根据外角定理,我们知道每个外角等于与其不相邻的两个内角之和。
因此,我们可以得到D=C+A,E=A+B和F=B+C。
将D、E和F相加,我们可以得到D+E+F=2(A+B+C)。
由于A+B+C是一个平面中的角的和(即180°),所以我们可以将上述等式重写为D+E+F=360°。
因此,三角形的外角和等于360°,而每个外角等于180°减去与其相邻的内角,即180°-D=180°-(C+A)=B。
因此,我们得出结论:三角形的内角和等于180°。
方法四:平行直线的证明考虑一个三角形ABC,其中一个角度为α。
通过点B,我们可以绘制一条平行于边AC的直线DE。
这样,我们获得了两个平行直线AC和DE,并且角DBC和角BCA为同旁内角,它们的和等于180°。
因此,我们可以得到角DBC+角BCA=180°-α。
“三角形内角和是180°”的验证教学

“三角形内角和是180°”的验证教学几种常见方法的比较验证“三角形的内角和是180°”,常见的有三种方法:(1)用量角器量出三个角的度数,然后加起来看是不是180°(简称“测量求和法”);(2)将三角形三个角剪下来,再将它们拼在一起看能不能组成平角(简称“剪拼法”);(3)将三个角折起来拼在一起,看能不能组成平角(简称“折拼法”)。
这三种方法中,“测量求和法”的优点是:接近学生的思维水平,课堂上学生很容易想到,也很容易理解;缺点是:“测量”存在着误差,因此测得的三个角的度数加起来往往都不是180°。
这使得测量结果非但不能验证结论,相反却易给人造成“三角形内角和不是180°”的错误印象。
“剪拼法”的优点是:操作简单、看起来一目了然;缺点是:破坏了原图形,不能很好地体现原图形与撕下来后图形间的联系与变化。
“折拼法”有效地避免了量、撕的缺陷,可惜操作起来方法不明──学生并不能十分清楚地掌握折的方法。
因此,我们对教材中的“折拼法”方案稍作改进:首先让学生折“高”找到对应的“垂足”,然后将三角形三个“顶点”分别对准“垂足”进行折叠就行了(如图1)。
经改进操作起来简捷多了。
其实,对于三角形内角和的三种常见验证方法,或多或少都存在着误差。
用任何一种方法验证“三角形内角和是180°”,都不足以让人信服。
因此,让尽量多的验证方法出现在课堂上,“让各种方法相互解释、互相佐证”是上好这节课的关键。
然而事实并不随你我所愿。
正常情况下,学生上课时只能想到“量”这一种方法,其他方法的出现,充其量仅仅是一两个“优等生闻道预先”。
如何通过教师艺术的启发,引导出多样的验证方法呢?我们对课堂中可能出现的种种情况进行了预设:学生猜想“三角形内角和是180°”,教师将猜想板书在黑板上追问:三角形内角和真的是180°吗?说说你的依据。
(1)“测量求和法”的引出:采用“一点突破”,紧扣“内角和”逐步逼近。
三角形的内角和证明

三角形的内角和证明
定理:三角形内三个角的和等于180度。
证明:
1. 先取一个平面内的任意直线l,在该直线上取一点P。
2. 在直线l的同侧作一条射线q,使其与直线l的夹角为A。
3. 令q绕点P作旋转,使之与初始位置重合。
4. 在此过程中,q转过了一个平面角。
我们知道,平面角的大小等于360度。
5. 当q旋转时,它与直线l所成的夹角不断变化,从A变为A+B,再变为A+B+C,最后又变回A。
6. 因此,A + B + C = 360度。
7. 由于三角形的三个内角分别为A,B,C,所以三角形的内角和为180度。
结论:任意三角形的内角和都等于180度。
人们常以这种方式来证明三角形内角和等于180度的定理。
该证明基于射线的旋转和平面角的性质,并利用了代数计算。
这种证明不仅清晰简洁,而且富有几何意味,是一种经典的证明方法。
三角形内角和证明方法

三角形内角和证明方法三角形内角和是指三角形的三个内角的度数之和,它是三角形最基本的性质之一。
在本文中,我们将介绍一些关于三角形内角和的证明方法。
1.我们可以使用三角形内角和定理来证明三角形内角和的性质。
根据该定理,三角形的内角和等于180度。
证明方法:假设ABC是一个三角形,我们可以作三角形的外接圆O。
连接AO,BO,CO,以及连接AO与BC的垂线OD。
根据外接圆的性质,AO的长度等于半径R,而R为定值。
又因为AO与OD相交,所以AO的垂足D到外接圆的距离等于OD的长度。
由于OD与BC垂直,并且是BC的中线,所以OD的长度等于BC的一半,即OD=BC/2。
根据三角形ABC的内角和定理,∠A+∠B+∠C=180度,而∠A和∠B是三角形的两个锐角,它们可以理解为AO和BO在三角形内角A和B上的倒影,所以∠A和∠B的和等于AO和BO的倒影两个角之和,即∠A+∠B=∠DOA+∠DOB。
同理,∠B+∠C=∠BOC+∠BOA,∠C+∠A=∠COA+∠COD。
因为∠DOA+∠DOB+∠BOC+∠BOA+∠COA+∠COD=360度,而∠A+∠B+∠C=180度,所以∠DOA+∠DOB+∠BOC+∠BOA+∠COA+∠COD-∠A-∠B-∠C=360度-180度=180度。
同理∠DOA+∠COA=180度-∠A-∠C,∠DOB+∠BOA=180度-∠A-∠B,∠BOC+∠COD=180度-∠B-∠C。
将上述等式代入∠A+∠B+∠C=180度,得到:(180度-∠A-∠C)+(180度-∠A-∠B)+(180度-∠B-∠C)=180度。
化简上述等式,可以得到3*180度-2*(∠A+∠B+∠C)=180度,即3*180度=2*(∠A+∠B+∠C),进一步化简为∠A+∠B+∠C=180度。
证明完毕。
2.另一种证明三角形内角和的方法是使用拓扑学中的欧拉公式。
根据欧拉公式,一个简单多边形的顶点数、边数和面数之间存在着一个关系。
三角形的内角和知识点总结

三角形的内角和知识点总结一、三角形内角和定理。
1. 内容。
- 三角形的内角和等于180°。
2. 证明方法。
- 剪拼法。
- 把三角形的三个角剪下来,然后将它们的顶点拼在一起,可以发现这三个角正好组成一个平角,从而直观地得出三角形内角和为180°。
例如,对于一个锐角三角形,可以分别沿着三角形的三条边剪下三个角,然后将角A、角B、角C的顶点重合拼在一起,就会看到它们拼成了一个180°的角。
- 推理证明法(以平行线的性质为基础)- 已知△ABC,过点A作直线EF∥BC。
- 因为EF∥BC,根据两直线平行,内错角相等,所以∠B = ∠FAB,∠C=∠EAC。
- 又因为∠FAB+∠BAC +∠EAC = 180°(平角的定义),所以∠B+∠BAC+∠C = 180°,从而证明了三角形内角和为180°。
二、三角形内角和定理的应用。
1. 求三角形中未知角的度数。
- 在一个三角形中,如果已知其中两个角的度数,就可以根据三角形内角和为180°求出第三个角的度数。
例如,在△ABC中,∠A = 50°,∠B = 60°,那么∠C=180° - ∠A - ∠B = 180°-50° - 60° = 70°。
2. 判断三角形的类型(按角分类)- 锐角三角形。
- 三个角都是锐角(即每个角都小于90°)的三角形。
如果一个三角形的最大角小于90°,根据三角形内角和为180°,可知另外两个角也必然是锐角,这个三角形就是锐角三角形。
例如,在△ABC中,∠A = 60°,∠B = 70°,∠C = 50°,因为最大角∠B = 70°<90°,所以△ABC是锐角三角形。
- 直角三角形。
- 有一个角是直角(等于90°)的三角形。
三角形的内角和相关知识点

三角形的内角和相关知识点一、三角形内角和定理。
1. 定理内容。
- 三角形的内角和等于180°。
无论是锐角三角形、直角三角形还是钝角三角形,其三个内角的和都是180°。
例如,一个锐角三角形的三个角分别为60°、70°、50°,60°+70° + 50°=180°;直角三角形的一个角是90°,另外两个锐角之和为90°(如30°和60°,30°+60°+90° = 180°);钝角三角形如120°、30°、30°,120°+30°+30° = 180°。
2. 证明方法。
- 剪拼法。
- 把三角形的三个角剪下来,然后将它们的顶点拼在一起,可以发现这三个角刚好组成一个平角,从而直观地证明三角形内角和为180°。
例如,对于一个纸质的三角形,沿角的边剪下三个角,然后把它们的顶点重合在一起,角的边会形成一条直线,即180°。
- 测量法。
- 使用量角器分别测量三角形的三个内角,然后将测量得到的度数相加,多次测量不同的三角形会发现结果接近180°。
由于测量存在误差,所以这种方法只能作为一种初步的验证。
- 推理证明(以平行线的性质证明为例)- 已知三角形ABC,过点A作直线EF平行于BC。
- 因为EF∥BC,根据两直线平行,内错角相等,所以∠B = ∠FAB,∠C=∠EAC。
- 而∠FAB+∠BAC + ∠EAC = 180°(平角的定义),所以∠B+∠BAC+∠C = 180°,从而证明了三角形内角和为180°。
二、三角形内角和定理的应用。
1. 求三角形中未知角的度数。
- 已知三角形的两个内角的度数,根据三角形内角和为180°,用180°减去已知的两个角的度数,就可以求出第三个角的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形内角和180°证明方法
1. 如图,证明/ B+Z C+Z BAC=180 证明:过A点作
DE// BC
••• DE// BC
•••Z B=Z DAB Z C=Z EAC
(两直线平行,内错角相等)
••• D,A,E三点共线
•Z DAE=180
vZ DAE Z DAB Z BAC+Z CAE
•Z DAB Z BAC+Z CAE=180
•Z B+Z C+Z BAC=180
2. 如图,证明:Z B+Z A+Z ACB=180
证明:过C点作CD// AB,延长BC交CD于 C
v CD// AB
•Z A=Z ACD(两直线平行,内错角相等)Z
B=Z DCE(两直线平行,同位角相等)v B,C,E三点共线
•Z BCE=180
vZ BCE Z ACB Z ACD Z DCE
•Z ACB Z ACD Z DCE=180
•Z A+Z B+Z ACB=180
3. 如图,证明:Z C+Z BAC Z B=180°
证明:过A点作AD// BC
v AD// BC
•Z C=Z ADC(两直线平行,内错角相等)
Z DAC Z B=180°(两直线平行,同旁内角互补)
vZ DAC Z DAC Z CAB
• Z DAC Z CAB Z B=180°
vZ C=Z ADC
•Z C+Z CAB Z B=180°
4. 如图,证明:Z BAC Z C+Z B=180°
证明:过A点作DE// BC,延长AC BC交DE于A点
v DE// BC
•Z C=Z FDA Z B=Z GAE
(两直线平行,同位角相等)
v D,A,E三点共线
•Z DAE=180
vZ DAE Z DFA Z FAG Z GAE
•Z DFA+Z FAG Z GAE=180 v・Z GAE Z BAC(对顶角相
等)
•Z BAC Z C+Z B=180°
5. 如图,证明:Z A+Z C+Z B=180°
E
E
A
证明:作直线DE// AC FE// AB交BC于 E
A
•••DE// AC
•••/ AFE+Z DEF=180 (两直线平行,同旁内角互补)
/ C=Z DEB(两直线平行,同位角相等)
•FE// AB
•••/ AFE+/ A=180°(两直线平行,同旁内角互补)
Z B=Z FEC(两直线平行,同位角相等)
•••/ A=Z DEF
•B,C,E三点共线
•••Z BCE=180
•Z BCE Z DEB Z DEF Z FEC
•Z DEB Z DEF Z FEC =180°
•Z A+Z C+Z B=180°
6. 如图,证明:Z A+Z B+Z C=180 证明:作DE// AC, FG// AB MN/ BC,都交于点O
•DE// AC
•Z AFO Z FOD=180 (两直线平行,同旁内角互补)
•FG// AB
•Z AFO Z A=180°
(两直线平行,同旁内角互补)
•Z A=Z FOD
•MN/ BC
•Z C=Z FNO(两直线平行,同位角相等)
•DE// AC
•Z FNO Z DO(两直线平行,同位角相等)
•Z C=Z DOM
•MN/ BC
•Z B=Z DM(两直线平行,同位角相等)
•FG// AB
•Z DMO Z FON(两直线平行,同位角相等)
•Z B=Z FNO
•M,O,N三点共线
•Z MON=180
•Z MON Z DOM Z DOF Z FON
•Z DOF Z DOM Z FON=180
•Z A+Z B+Z C=180
7. 如图,证明:Z BAC Z CBA Z ACB=180
证明:作DE// AC, FG// AB MN/ BC,都交于点O
延长AC交FG于点K,延长AB到点L,延长BC交FG于点P
• MN// BC
•Z ABC Z AHN Z ACB Z ANM
(两直线平行,同位角相等)
•AB // FG
•Z AHN Z FON Z BAC Z AKO
(两直线平行,同位角相等)
•••/ ABC=/ FON
••• DE// AC •••/ ANM N DOM
(两直线平行,同位角相等)
/ OKA N DOF
(两直线平行,内错角相等)
•••N ACB N DOM
••• FG// AB
•/ BAC N OKA(两直线平行,同位角相等)
•N BAC N DOF
••• M,O,N三点共线
•N MON=18°
vZ MON N DOM N DOF N FON
•/ DOM N DOF N FON=180
•N BAC N CBA N ACB=180
A。
