力对点之矩
合集下载
理论力学L4-2空间力矩
力对点的矩矢量在通过该点之轴上的投影,等 于力对该轴之矩。
M z ( F ) M O ( Fxy ) M O ( Fy ) ቤተ መጻሕፍቲ ባይዱ M O ( Fx ) xFy yFx
同理:
2. 力对坐标轴之矩的解析表达式:
M x (F ) yFz zFy M y (F ) zFx xFz
3. 力对点之矩与力对过该点轴之矩的关系 对比力对点的矩在z轴上的投影:
[ MO ( F )]x yFz zFy [ MO ( F )]y zFx xFz [ MO (F )]z xFy yFx
二、力对轴的矩 力对轴的矩是力使刚体产生绕某轴转动效应的度 量。该轴称为力矩的转轴。 1. 力对轴的矩定义 设力 F 作用于可绕z轴转 动的刚体上A点。 过A点作垂直于z轴的平面 π,与z轴交于o点。
( yFz zFy )i ( zFx xFz ) j ( xFy yFx )k
MO (F ) ( yFz zFy )i ( zFx xFz ) j ( xFy yFx )k
若将力矩矢量的解析表达式记为: MO (F ) [ MO (F )]x i [ MO (F )]y j [ MO (F )]z k 单位向量前的每一项就是力对点的矩矢量在 各坐标轴上的投影。 比较两式,力矩矢量在坐标上的投影:
yfxfxfzfzfyf二力对轴的矩力对轴的矩是力使刚体产生绕某轴转动效应的度力对轴的矩定义过a点作垂直于z轴的平面分解为z轴的力和在面上的力力对轴的矩等于力在该轴平面上的分力对该轴与平面交点的矩
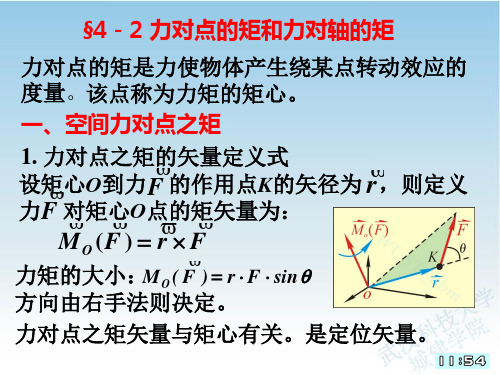
§4-2 力对点的矩和力对轴的矩
力对点的矩是力使物体产生绕某点转动效应的 度量。该点称为力矩的矩心。 一、空间力对点之矩 1. 力对点之矩的矢量定义式 设矩心 O到力 F 的作用点K的矢径为 r ,则定义 力F 对矩心 O 点的矩矢量为:
工程力学 第3章 力偶系
M 2 F2 , F2'
M F1'
r1
F F1 F2 F ' F1' F2'
F2' MR F, F '
F2
F1 F
M2
MR r F ' r (F1'F2 ') r F1'r F2 '
M1 M2
结论:两个力偶的合成仍然为力偶,且
第三章 力偶系
§1 力对点之矩矢 一、 平面力对点之矩(回顾)
力使物体绕某点转动的力学效应,称为力对该点之矩。 例如扳手旋转螺母。
BF
dA L
O
力F对O点之矩定义为: Mo(F)=±Fd
通常规定:力使物体绕矩心逆时针方向转动时,力矩 为正,反之为负。
第三章 力偶系
二、力对点之矩矢量 1、空间力矩三个要素:
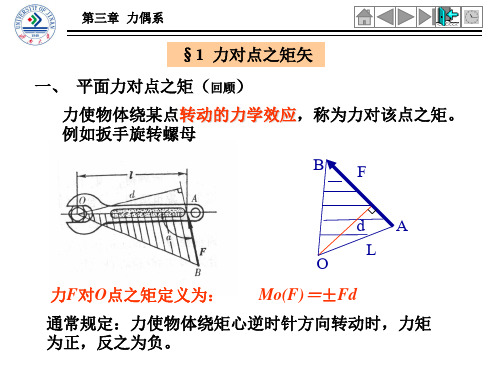
一、力偶 在日常生活和工程实际中经常见到物体受动两个大小相等、 方向相反,但不在同一直线上的两个平行力作用的情况。例如
第三章 力偶系
B d
F’
F A
M
B
F
rBA
F’ d A
1. 定义:在力学中把这样一对等值、反向而不共线的平行力 称为力偶,用符号 ( F , F′)表示。
两个力作用线之间的垂直距离 d 称为力偶臂, 两个力作用线所决定的平面称为力偶的作用面。
x (F ) y (F )
yFz zFx
zFy xFz
M
z
(F
)
xFy
yFx
力对点之矩在各坐标轴上的投影
MO z
O xr
力对点之矩与力对轴之矩

力对轴的矩力对轴的矩是力使刚体绕该轴转动效果的度量是一个代数量其绝对值等于该力在垂直于该轴的平面上的投影对于这个平面与该轴的交点的矩方法一
力对点之矩与力对轴之矩
力对点的矩 对于平面力系,用代数量表示力对点的矩足
以概括它的全部要素。但是在空间情况下,由三个要素 ,这三个因素可以用力矩矢MO(F)来描述。
F x F si,n F y 0 , F z F cos
力作用点D的坐标为
x l, y l a , z 0
(2)代入式(4-12),得
M x ( F ) y z z F y F ( l a ) F ( c) o 0 F s ( l a ) c
M y ( F ) z x F x z F 0 ( l ) F ( c) o F s cl o
力矩矢的大小,即 M O ( F ) 矢量的方位与力矩作用面的法线方向相同;
矢量的指向按右手螺旋法则来确定
|MO( F ) |= F.d =2S∆OAB
z
B
MO ( F )
F
根据矢量的叉乘,我们可以知道: rOA×F= |rOA||F|sinθ=Fd,其方向与力矩失 一致。
A
Or d
y
x
MO( F ) = rOA×F
M z ( F ) x y y F x 0 F ( l a ) F s () i F n ( l a ) si
力对点的矩与力对通过该点的轴的矩的关系
[MO(F)]x Mx(F) [MO(F)]y My (F) [MO(F)]z Mz (F)
MO(F) MO
[Mx
(F)]2
Mz(F)xF yyF x
Mx yFz zFy
My zFx xFz
手柄ABCE在平面Axy内,在D处作用一个力F,如图4-7所 示,它在垂直于y轴的平面内,偏离铅直线的角度为,如果 CD=a,杆BC平行于x轴,杆CE平行于y轴,AB和BC的长度
力对点之矩与力对轴之矩
力对点的矩 对于平面力系,用代数量表示力对点的矩足
以概括它的全部要素。但是在空间情况下,由三个要素 ,这三个因素可以用力矩矢MO(F)来描述。
F x F si,n F y 0 , F z F cos
力作用点D的坐标为
x l, y l a , z 0
(2)代入式(4-12),得
M x ( F ) y z z F y F ( l a ) F ( c) o 0 F s ( l a ) c
M y ( F ) z x F x z F 0 ( l ) F ( c) o F s cl o
力矩矢的大小,即 M O ( F ) 矢量的方位与力矩作用面的法线方向相同;
矢量的指向按右手螺旋法则来确定
|MO( F ) |= F.d =2S∆OAB
z
B
MO ( F )
F
根据矢量的叉乘,我们可以知道: rOA×F= |rOA||F|sinθ=Fd,其方向与力矩失 一致。
A
Or d
y
x
MO( F ) = rOA×F
M z ( F ) x y y F x 0 F ( l a ) F s () i F n ( l a ) si
力对点的矩与力对通过该点的轴的矩的关系
[MO(F)]x Mx(F) [MO(F)]y My (F) [MO(F)]z Mz (F)
MO(F) MO
[Mx
(F)]2
Mz(F)xF yyF x
Mx yFz zFy
My zFx xFz
手柄ABCE在平面Axy内,在D处作用一个力F,如图4-7所 示,它在垂直于y轴的平面内,偏离铅直线的角度为,如果 CD=a,杆BC平行于x轴,杆CE平行于y轴,AB和BC的长度
第三章 力矩

攻丝时为什么要两个手施力,用一个手会有 什么不好之处
?
几个性质
(1) 当力线平移时,力的大小、方向都不改变,但附加力
偶的矩的大小与正负一般要随指定O点的位置的不同而不同。
(2) 力线平移的过程是可逆的,由此可得重要结论:
作用在同一平面内的一个力和一个力偶,总可以归纳为
一个和原力大小相等的平行力。 (3) 力线平移定理是把刚体上平面任意力系分解为一个平 面共点力系和一个平面力偶系的依据。
F'R
MO
FR′≠0,MO≠0,且FR′与 MO 不垂直
力螺旋
O
一个力和一个力偶组成的力系,且这个力垂直
于力偶的作用面。这样的力系称为力螺旋。
FR′ MO FR′
MO
(4) 力系平衡 FR′=0,MO = 0
力螺旋
MO O
FR′
z
O
x d M1 y
A
FR″
M 2 M O sin d FR FR
F′ F′ M F B d B A
A
F′′
M Fd M B ( F )
可以把作用于刚体上点A的力F平行移到同一刚体上 的任意点B,但必须同时附加一个力偶,这个附加 力偶的矩等于原来的力F对新作用点B的矩。 物理含义: 力可使物体移动和转动 力的平移定理说明一个力和一个力偶可 以进一步合成为一个力。
( Fx , Fy , Fz ) (100 14,150 14,50 14)
力F矢量对三个坐标轴的矩为: M x ( F ) yFz zFy 3 50 14 0 100 14
150 14( N m) 同理有:M y ( F ) zFx xFz 100 14( N m) M z ( F ) xFy yFx 0( N m) 力F矢量对O之矩为:
第三章_力对点的矩_平面力偶系

4
平面力偶系的合成和平衡条件
平面力偶系的合成
平面力偶系:作用在同一平面内的一群力偶。 平面力偶系:作用在同一平面内的一群力偶。
=
FR = F1 + F2 + Fn
=
=
′ FR = F1′ + F2′ + Fn′
平面力偶系合成的结果是一个合力偶, 平面力偶系合成的结果是一个合力偶,合力 偶矩等于力偶系中各力偶矩的代数和 中各力偶矩的代数和。 偶矩等于力偶系中各力偶矩的代数和。
力对点的矩
F
h
O
M 0 ( F ) = ± Fh
力对点的矩是一个代数量,它的绝对值 绝对值等于力的大小 力对点的矩是一个代数量,它的绝对值等于力的大小 与力臂的乘积,它的正负可按下法确定, 正负可按下法确定 与力臂的乘积,它的正负可按下法确定,力使物体绕 矩心逆时针转向时为正,反之为负。 矩心逆时针转向时为正,反之为负。 力矩表示力使物体绕某点旋转的量度。 力矩表示力使物体绕某点旋转的量度。 量度
A α M1
OBBiblioteka M2DB 解: 因为杆AB为二力杆,故其反力F 和F 只 因为杆AB为二力杆 故其反力FAB 为二力杆, BA A
α
M1 M2
D
能沿A 能沿A,B的连线方向。 的连线方向。 分别取杆OA和DB为研究对象 分别取杆OA和DB为研究对象。因为力偶只能 为研究对象。 与力偶平衡,所以支座O 与力偶平衡,所以支座O和D的约束力FO 和FD 只 的约束力F ∴ 能分别平行于F 能分别平行于FAB 和FBA ,且与其方向相反。 且与其方向相反。 B 写出杆OA和DB的平衡方程 写出杆OA和DB的平衡方程: ∑M = 0 的平衡方程:
力对点的矩
工程力学第3章(力偶系)

工程力学
Engineering Mechanics
中南大学土木建筑学院力学系
Department of Mechanics of School of Civil Engineering and Architecture of Central South University
第三章 力偶系 §3-1 力对点之矩矢
力偶臂d 力偶臂 1=200mm, ,
,力偶臂d , F2 = F2' = 120N,力偶臂 2=300mm , F3 = F3' = 80 N,
M 1 = 100 × 0.2 = 20
N.m N.m
M 2 = 120 × 0.3 = 36
M 3 = 80 × 0.18 = 14.4 N.m
M Rx M Ry = ∑ M y = M 1 = 20 N.m
二、力对轴之矩的 解析表达式
M x ( F ) = M x ( Fy ) + M x ( Fz ) = -zFy + yFz M y ( F ) = M y ( Fz ) + M y ( Fx ) = -xFz + zFx M z ( F ) = M z ( Fx ) + M z ( Fy ) = -yFx + xFy
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
合力偶矩矢的大小 M R = ( ∑ M x ) 2 + ( ∑ M y )2 + ( ∑ M z )2 合力偶矩矢的方向
R
∑M cos( M ,i ) =
cos( M R,j ) = MR
Engineering Mechanics
中南大学土木建筑学院力学系
Department of Mechanics of School of Civil Engineering and Architecture of Central South University
第三章 力偶系 §3-1 力对点之矩矢
力偶臂d 力偶臂 1=200mm, ,
,力偶臂d , F2 = F2' = 120N,力偶臂 2=300mm , F3 = F3' = 80 N,
M 1 = 100 × 0.2 = 20
N.m N.m
M 2 = 120 × 0.3 = 36
M 3 = 80 × 0.18 = 14.4 N.m
M Rx M Ry = ∑ M y = M 1 = 20 N.m
二、力对轴之矩的 解析表达式
M x ( F ) = M x ( Fy ) + M x ( Fz ) = -zFy + yFz M y ( F ) = M y ( Fz ) + M y ( Fx ) = -xFz + zFx M z ( F ) = M z ( Fx ) + M z ( Fy ) = -yFx + xFy
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
合力偶矩矢的大小 M R = ( ∑ M x ) 2 + ( ∑ M y )2 + ( ∑ M z )2 合力偶矩矢的方向
R
∑M cos( M ,i ) =
cos( M R,j ) = MR
力对点之矩的概念.

解:取工件为研究对象,平面力偶系。
M 0
解出:
FAl M1 M 2 M 3 0
FA
M1
M2 l
M3
FA 200 N
FB FA 200
例2 已知:a、m,杆重不计。 求:铰A、C的反力。
解: AB为二力构件。 对BC构件,由力偶平衡有:
M 0, m NC d 0
MO (F) MO (Ft ) MO (Fr ) MO (Ft ) Fr cosa 78.93N.m
§3-3 力偶矩矢
1.力偶与力偶矩
*大小相等,方向相反, 作用线平行的两个力称 为力偶。
*力偶只能使物体转动。因 此,力偶与一个力不等效, 它既不能合成一个力也不 能与一个力平衡。
例1 如图所示,圆柱直齿轮受啮合力
的 作 用 。 设 F=1400N。 压 力 角 a=20o
齿轮的节圆(啮合圆), 半径 r =60mm , 试计算力对轴的力矩。
解:解法1 按力矩定义求解。
解法2 用合理之矩定理求解。
MO (F) F h Fr cosa
1400 60 cos 20 78.93 N m
(1)平面力偶系的合成: 力偶矩的代数求和。
M
M i
(2)空间力偶系的合成: 力偶矩矢的矢量求和。
M平衡条件
(1)力偶系的合成与平衡
M
M i
0
Mx 0 M y 0 Mz 0
(2)平面力偶系的平衡
Mi 0
例1 工件上作用有三个力偶如图所示。已知:力偶矩分别为 M1=M2=10N·m,M3=20N·m,固定螺柱和的距离l=200mm。求 两光滑螺柱所受的水平力。
M 0
解出:
FAl M1 M 2 M 3 0
FA
M1
M2 l
M3
FA 200 N
FB FA 200
例2 已知:a、m,杆重不计。 求:铰A、C的反力。
解: AB为二力构件。 对BC构件,由力偶平衡有:
M 0, m NC d 0
MO (F) MO (Ft ) MO (Fr ) MO (Ft ) Fr cosa 78.93N.m
§3-3 力偶矩矢
1.力偶与力偶矩
*大小相等,方向相反, 作用线平行的两个力称 为力偶。
*力偶只能使物体转动。因 此,力偶与一个力不等效, 它既不能合成一个力也不 能与一个力平衡。
例1 如图所示,圆柱直齿轮受啮合力
的 作 用 。 设 F=1400N。 压 力 角 a=20o
齿轮的节圆(啮合圆), 半径 r =60mm , 试计算力对轴的力矩。
解:解法1 按力矩定义求解。
解法2 用合理之矩定理求解。
MO (F) F h Fr cosa
1400 60 cos 20 78.93 N m
(1)平面力偶系的合成: 力偶矩的代数求和。
M
M i
(2)空间力偶系的合成: 力偶矩矢的矢量求和。
M平衡条件
(1)力偶系的合成与平衡
M
M i
0
Mx 0 M y 0 Mz 0
(2)平面力偶系的平衡
Mi 0
例1 工件上作用有三个力偶如图所示。已知:力偶矩分别为 M1=M2=10N·m,M3=20N·m,固定螺柱和的距离l=200mm。求 两光滑螺柱所受的水平力。
力对点的矩与力对轴的矩
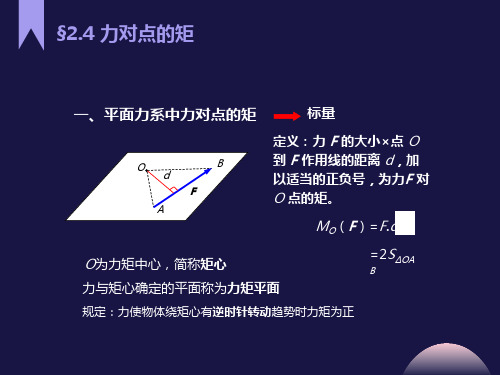
空间力系中,各力作用线与矩心所确定的力矩平面不再重合
F1
F2
F3
F4
F5
O
{ F1、F2、F3、F4 }
{ F1、F2、F4、F5 }
空间力系中,力对矩心的矩取决于三方面(要素)
①力矩的大小(F.d)
②力矩平面在空间中的方位(法线方位)
③力矩平面内,力使物体绕矩心的转向
——需用矢量表示空间力系中力对点的矩
Fv
= MO( Fv ) + MO( Fh )
§2.5 力对轴之矩
一、力对轴之矩的概念
F
xy
z
d
Fz
Fxy
过力 F 的始端做垂直力的平面 xy
将力 F 分解
Fz∥z 轴
Fxy⊥z 轴
定义: Fxy 对 O 点之矩为力 F 对 z 轴之矩:Mz ( F )
即 Mz ( F ) = MO ( Fxy ) =Fxy .d
同理力F 对 ox 轴的矩为
= -Fy.z + Fz .y
力F 对 oy 轴的矩为
= -Fz.x + Fx .z
2.5 力对轴之矩
二、力对点之矩与力对过该点的轴之矩的关系
Fx
Fy
Fz
Fxy
F
O
y
z
x
A
B
y
x
z
O′
A点坐标:x、y、z
F 投影:Fx、Fy、Fz
Mx (F )= yFz – zFy
一、平面力系中力对点的矩
标量
O
F
d
A
B
1. 矩心不一定要选为物体可以绕之转动的固定点。
2. 力为0或力作用线过矩心时,力矩为0。
F1
F2
F3
F4
F5
O
{ F1、F2、F3、F4 }
{ F1、F2、F4、F5 }
空间力系中,力对矩心的矩取决于三方面(要素)
①力矩的大小(F.d)
②力矩平面在空间中的方位(法线方位)
③力矩平面内,力使物体绕矩心的转向
——需用矢量表示空间力系中力对点的矩
Fv
= MO( Fv ) + MO( Fh )
§2.5 力对轴之矩
一、力对轴之矩的概念
F
xy
z
d
Fz
Fxy
过力 F 的始端做垂直力的平面 xy
将力 F 分解
Fz∥z 轴
Fxy⊥z 轴
定义: Fxy 对 O 点之矩为力 F 对 z 轴之矩:Mz ( F )
即 Mz ( F ) = MO ( Fxy ) =Fxy .d
同理力F 对 ox 轴的矩为
= -Fy.z + Fz .y
力F 对 oy 轴的矩为
= -Fz.x + Fx .z
2.5 力对轴之矩
二、力对点之矩与力对过该点的轴之矩的关系
Fx
Fy
Fz
Fxy
F
O
y
z
x
A
B
y
x
z
O′
A点坐标:x、y、z
F 投影:Fx、Fy、Fz
Mx (F )= yFz – zFy
一、平面力系中力对点的矩
标量
O
F
d
A
B
1. 矩心不一定要选为物体可以绕之转动的固定点。
2. 力为0或力作用线过矩心时,力矩为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Qd
h
xqdx
h
x2dx
1
h3
0
0
3
kN·m
Q
h
qdx
h
xdx
1 h2
0
0
2
Qd
h
xqdx
h
x2dx
1
h3
0
0
3
所以
h
d 0 xqdx 2 h
Q
3
m
此d值确定了合力Q
作用线的位置。
A
即
FR = F1+F2+…+ Fn
FR = F1+F2+…+ Fn
• 以 r 对上式两端作矢积,有
• r×FR =r×F1 + r×F2 + … +r×Fn • 由于力F1,F2,…,Fn与点共面, • 上式各矢积平行,因此上式
• 矢量和可按代数和计算。而
• 各矢量积的大小就是力对点
• 之矩,于是证得合力矩定理
MA(F )= MA(F x)+ MA(F y) =- Fx b + Fy a =- F b cosa+ F a sin a = F a sin a- F b cosa
• 例2、设水深为h,水的容重(单位容积的
• 重量)为g,求单位长度的坝面所承受的静水压 • 力的合力。 • 解:作用于坝面的静水压力可简化为沿坝面 • 中心线OA分布的水平荷载,且在水面下x处的的 • 线荷载集度为
矩心到该力作用点的矢径与力矢的矢量积。
2、力对点之矩矢MO (F)的三要素 力矩矢的三要素为大小、方位和指向。
(1)、MO (F)的大小即它的模
MO(F ) = r F Fr sin Fh
式中θ为r和F正方向间 的夹角,h为矩心到力 作用线的垂直距离,称为 力臂。
MO(F)=r×F
θ
• 汇交力系的平衡问题。
• 3、用途
• ①便于找力臂
• ②便于确定合力作用线的位置。
例1、试计算图中力F对A点之矩。 已知F,a、b、a。
解:(1)由定义求MA(F ) 先确定力臂h。而找力臂d 较为麻烦。
(2)由汇交力系合力之矩定理求MA(F ) 现将力F分解为互相垂直的两各分力F x和F y,利用平 面汇交力系合力之矩定理计算力F对A点之矩
yFz
-
zFy
M Oy (F ) = zFx - xFz
M Oz (F ) =
xFy
-
yFx
四、平面汇交力系的合力矩定理
1、定理:
平面汇交力系的合力对于 平面内任一点之矩等于所有各 分力对于该点之矩的代数和。
2、证明:
如图所示, r 为矩心O到汇交点A的矢径,FR为平面汇交力系
F1,F2,…,Fn的合力,
q x(1dx) x
dx
kN/m
A
• 可见荷载集度与水的
• 深度成正比,按此绘出的
• 荷载图为图示的三角形。
• 坝面所受的静水压力的
• 合力Q的大小为
A
Q
h
qdx
0
h
xdx
1
h2
0
2
kN
且此合力Q应与原分布荷载平行。如令Q的作用线到水面的
距离为d,则由合力矩定理,有
第三章 力系的简化
§3-2-1 力对点之矩 §3-2-2 力对轴之矩 §3-3 力偶及其性质 §3-4 力偶系的合成与平衡 §3-5 力的平移定理
一、力对点之矩
1、力对点的矩的概念
作用于刚体的力F对空 间任意一点O的力矩定义 为:
MO(F) = r F
式中O点称为矩心,r为矩心O引向力F的作用点A的矢径, 力对点之矩定义为:
Oxyz,并用i、j、k表示沿
各坐标轴的单位矢量,则
r = xi + yj + zk
F = Fxi Fy j + Fz k
于是
MO(F) r F
i jk
=x y z
Fx Fy Fz
(yFz - zFy )i + (zFx - xFz ) j + (xFy - yFx )k
投影
M Ox (F ) =
• 2、力沿作用线移动,不会改变该力对任一点的力矩。 • 3、当力的作用线通过矩心时,此力对于该矩心的力矩等
于零。
• 4、力对点之矩的单位;
•
N·m 或 kN·m
矩心是可以任意选择的,可以是物体上的固定点, 也可以是物体上不固定之点,甚至是所研究物体以 外的点。
三、 力对点之矩在坐标轴上的投影
为了计算力矩矢在坐 标轴上的投影,以矩心O 为原点引进直角坐标系
O●
hr
MO(F) Fh
F
O●
h
MO(F) = ± Fh
F
正负号通常规定为:
+
逆时针为正
–
顺时针为负
实例
力F对点O的矩记为
MO(F)=-Fh
或
MO(F)=-2A△OAB
式中A△OAB为三角形OAB的面积。
• 二、力矩的性质
• 1、力 F 对点 O 的矩,不仅与力 F 有关,同时还与矩 心O的位置有关,一般力矩将随矩心位置不同而异。因此 必须指明矩心,力对点之矩才有意义。
• MO(F R)= MO(F 1)+ MO(F 2)+…+ MO(F n)
•
=∑MO(F i)
MO(F R)= MO(F 1)+ MO(F 2)+…+ MO(F n) =∑MO(F i)
• 当平面汇交力系平衡时,合力为零。
• 由上式可知,各力对任一点之矩的代数和皆为零。即
•
∑MO(F i)=0
• 上式说明:可用力矩方程代替投影方程求解平面
h
(2)MO (F)的方位: 垂直于r 和F 所确定的 平面,
(3)MO (F)的指向:
指向由右手定则确定。
MO(F)=r×F
θ
h
由于力矩矢的大小和方向都与矩心的位置有关,故 力对点之矩矢的始端必须在力矩中心,不可任意挪 动,这种矢量称为定位矢量。
平面问题
平面问题中,由于矩心与力矢均在同一个特定的 平面内,力矩矢总是垂直于该平面,即力矩的方位 不变,指向可用正、负号区别,故力矩由矢量变成 了代数量,且有
