实验3Matlab绘图操作
Matlab实验报告(三)-MATLAB绘图

实验目的1.掌握MATLAB的基本绘图命令。
2.掌握运用MATLAB绘制一维、二维、三维图形的方法.3.给图形加以修饰。
一、预备知识1.基本绘图命令plotplot绘图命令一共有三种形式:⑴plot(y)是plot命令中最为简单的形式,当y为向量时,以y的元素为纵坐标,元素相应的序列号为横坐标,绘制出连线;若y为实矩阵,则按照列绘出每列元素和其序列号的对应关系,曲线数等于矩阵的列数;当y为复矩阵时,则按列以每列元素的实部为横坐标,以虚部为纵坐标,绘出曲线,曲线数等于列数。
⑵ plot(x,y,[linspec])其中linspec是可选的,用它来说明线型。
当x和y为同维向量时,以x为横坐标,y为纵坐标绘制曲线;当x是向量,y是每行元素数目和x维数相同的矩阵时,将绘出以x为横坐标,以y中每行元素为纵坐标的多条曲线,曲线数等于矩阵行数;当x为矩阵,y为相应向量时,使用该命令也能绘出相应图形。
⑶ plot(x1,y1,x2,y2,x3,y3……)能够绘制多条曲线,每条曲线分别以x和y为横纵坐标,各条曲线互不影响。
线型和颜色MATLAB可以对线型和颜色进行设定,线型和颜色种类如下:线:—实线:点线 -.虚点线——折线点:.圆点 +加号 *星号 x x型 o 空心小圆颜色:y 黄 r 红 g 绿 b 蓝 w 白 k 黑 m 紫 c 青特殊的二维图形函数表5 特殊2维绘图函数[1] 直方图在实际中,常会遇到离散数据,当需要比较数据、分析数据在总量中的比例时,直方图就是一种理想的选择,但要注意该方法适用于数据较少的情况。
直方图的绘图函数有以下两种基本形式。
·bar(x,y) 绘制m*n 矩阵的直方图.其中y 为m *n 矩阵或向量,x 必须单向递增。
·bar(y) 绘制y 向量的直方图,x 向量默认为x=1:m close all; %关闭所有的图形视窗。
x=1:10;y=rand (size(x )); bar(x,y ); %绘制直方图.123456789100.51Bar()函数还有barh ()和errorbar ()两种形式,barh()用来绘制水平方向的直方图,其参数与bar()相同,当知道资料的误差值时,可用errorbar ()绘制出误差范围,其一般语法形式为:errorbar (x,y,l,u)其中x,y 是其绘制曲线的坐标,l ,u 是曲线误差的最小值和最大值,制图时,l 向量在曲线下方,u 向量在曲线上方。
MATLAB 绘图实验报告

实验报告课程名称:MATLAB上机实验实验项目:matlab绘图实验地点:专业班级:学号学生姓名:指导教师:年月日MATLAB绘图一.实验环境计算机 MATLAB软件二.实验目的1.掌握MATLAB的基本绘图命令。
2.掌握运用MATLAB绘制一维,二维,三维图形的方法。
3.绘图形加以修饰。
三.预备知识1.基本图形命令plot2. 线型和颜色3. 特殊的二维图形颜色四.实验内容和步骤1.创建一个5×5魔方矩阵,并画出表示这个矩阵的图形。
>>A=magic(5);>>plot(A)1 1.52 2.53 3.54 4.552.在同一个坐标轴里绘出y=sin(x),z=cos(x)两条曲线。
>> x=linspace(0,2*pi,50); >> y=sin(x); >> plot(x,y); >> hold on; >> z=cos(x); >> plot(x,z) >> hold off1234567-1-0.8-0.6-0.4-0.200.20.40.60.813.画出y=x^2的曲线(x ∈(-5,5))。
在这曲线上加入相同区间里的y=x^(1/3)的曲线,并且要求采用绿色折线标识。
>> close all>> x=linspace(-5,5,100);>> y=x.^2; >> plot(x,y) >> hold on >> z=x.^(1/3); >> plot(x,z,'g--') >> hold off-5-4-3-2-101234505101520254.在同一个窗口,不同坐标系里分别绘出y1=sinx,y2=cosx,y3=sinh(x),y4=cosh(x)4个图形。
实验Matlab三维作图地绘制

实验9 三维绘图一、实验目的学会MATLAB软件中三维绘图的方法。
二、实验内容与要求1.三维曲线图格式一:plot3(X,Y,Z,S).说明:当X,Y,Z均为同维向量时,则plot3描出点X(i),Y(i),Z(i)依次相连的空间曲线.若X,Y均为同维矩阵,X,Y,Z每一组相应列向量为坐标画出一条曲线,S为‘color﹣linestyle﹣marker’控制字符表1.6~表1.10.【例1.79】绘制螺旋线.>>t=0:pi/60:10*pi;>>x=sin(t);>>y=cos(t);>>plot3(x,y,t,’*-b’)>>grid on图形的结果如图1.16所示.格式二:comet3(x,y,z).说明:显示一个彗星通过数据x,y,z确定的三维曲线.【例1.80】>>t=-20*pi:pi/50:20*pi;>>comet3(sin(t),cos(t),t)可见到彗星头(一个小圆圈)沿着数据指定的轨道前进的动画图象,彗星轨道为整个函数所画的螺旋线.格式三:fill3(X,Y,Z,C) ℅填充由参数X,Y,Z确定的多边形,参数C指定颜色.图1.16 例1.79图形结果图1.17 例1.81图形结果【例1.81】>>X=[2,1,2;9,7,1;6,7,0];>>Y=[1,7,0;4,7,9;0,4,3];>>Z=[1,8,6;7,9,6;1,6,1];>>C=[1,0,0;0,1,0;0,0,1]>>fill3(X,Y,Z,C)>>grid on图形的结果如图1.17所示.问题 1.30:图 1.17中每个三角形按什么规律画出的?(用X,Y,Z的对应列元素值为坐标画三角形)每个三角形内填充的颜色又有何规律?(用C 第i列元素值对应的颜色,从第i个三角形对应顶点向中心过渡)若C=[1,5,10;1,5,10;1,5,10],结果如何?2.三维网格图格式:mesh(X,Y,Z,C) ℅画出颜色由C指定的三维网格图.meshc(X,Y,Z,C) ℅画出带有等高线的三维网格图.meshz(X,Y,Z,C) ℅画出带有底座的三维网格图.说明:若X与Y均为向量,n=length(X),m=length(Y), Z必须满足[m,n]=size(Z),则空间中的点(X(j),Y(i),Z(i,j))为所画曲面网线的交点,X 对应于Z的列,Y对应于Z的行;若X,Y,Z均为同维矩阵,则空间中的点(X(i,j),Y(i,j),Z(i,j))为所画曲面的网线的交点;矩阵C指定网线的颜色,MATLAB对矩阵C中的数据进行线性处理,以便从当前色图中获得有用的颜色,若C缺省,网线颜色和曲面的高度Z相匹配.在三维作图常用到命令meshgrid,其功能是生成二元函数z=f(x,y)中x-y平面上的矩形定义域中数据点矩阵X和Y.格式:[X,Y]= meshgrid(x,y).说明:输入向量x为x-y平面上x轴的值,向量y为x-y平面上y轴的值.输出矩阵X为x-y平面上数据点的横坐标值,输出矩阵Y为x-y平面上数据点的纵坐标值.【例1.82】>> x=1:4;>> y=1:5;>> [x,y]=meshgrid(x,y)x =1 2 3 41 2 3 41 2 3 41 2 3 41 2 3 4y =1 1 1 12 2 2 23 3 3 34 4 4 45 5 5 5图1.18所示x-y 平面上的矩形定义域中20个数据点(星号点)的坐标就是有X ,Y 决定的。
matlab实验 绘图

实验三 Matlab 绘图实验目的熟悉MTALAB 中几种常用的绘图命令,掌握几种常用图形的画法。
实验内容1.二维:用 matlab 二维绘图命令 plot 作出函数图形。
形式: plot(x,y) 2.空间三维作图:三维曲线:plot3(x,y,z,s);三维曲面:mesh(X,Y,Z) 网格生成函数:meshgridsurf(X,Y,Z):绘制由矩阵 X,Y,Z 所确定的曲面图,参数含义同 mesh sphere(n): 专用于绘制单位球面实验方法与步骤1.利用 plot 函数在一个坐标系下绘制以下函数的图形,要求采用不同的颜色、线型、点标记。
方程组: sin(),cos(),sin(2),02x t y t z t t π===<< 步骤:t=[0:0.05:2*pi] x=sin(t);y=cos(t);z=sin(2*t)plot(t,x,'r+:',t,y,'bd-.',t,z,'k*-') 2.plot3 绘制类似田螺线的一条三维螺线方程组:步骤:t=[0:0.1:10*pi]x=2.*(cos(t)+t.*sin(t)) y=2.*(cos(t)-t.*sin(t)) z=1.5*tplot3(x,y,z)3.墨西哥帽子方程:z=步骤:[x,y]=meshgrid(-8:.5:8); z=sqrt(x.^2+y.^2)+eps;Z=sin(z)./z;mesh(X,Y,Z)axis square4. 利用 surf 函数绘制马鞍面方程:2294x y z=-步骤:x=[-25:0.5:25];y=[-25:0.5:25] [X,Y]=meshgrid(x,y)Z=(X.^2/9)-(Y.^2/4)surf(X,Y,Z)5.双曲抛物面方程:22222 x yz a b-=步骤:x=[-25:0.5:25];y=[-25:0.5:25] ezsurfc('X.^2./16-Y.^2./12')实验结果1.2.100-100-1010104.-4040-4-224XX 2/16-Y 2/12Y总结与思考matlab 的常见错误分析Inner matrix dimensions must agree因为在matlab 的输入变量是矩阵,参与运算的矩阵维数必须对应,矩阵响应元素的运算必须全部加dot (点)。
MATLAB3+-+MATLAB绘图与程序设计+(2)

(4) 双纵坐标图 语法: plotyy(x1,y1,x2,y2) %以左、右不同纵轴绘制两
条曲线
说明:左纵轴用于(x1,y1)数据,右纵轴用于 (x2,y2)数据来绘制两条曲线。坐标轴的范围、 刻度都自动产生。
例8续 用plotyy函数实现在同一图形窗口绘制两 条曲线。
例5. 绘制三条曲线。
x=0:0.1:2*pi;
plot(x,sin(x),x,cos(x),x,sin(3*x)) %画三条曲线
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0
1
2
3
4
5
6
7
绘制曲线的一般步骤
步骤
内容
1 曲线数据准备:对于二维曲线,横坐标和纵坐标数据变量;对 于三维曲面,矩阵参变量和对应的函数值。
说明:在设置了“hold on”后,如果画多个图 形对象,则在生成新的图形时保留当前坐标系 中已存在的图形对象,MATLAB会根据新图 形的大小,重新改变坐标系的比例。
例8 在同一窗口画出函数sinx在区间[0 2π]的 曲线和cosx在区间[-π π]的曲线。
x1=0:0.1:2*pi; plot(x1,sin(x1)) hold on x2=-pi:.1:pi; plot(x2,cos(x2))
2 指定图形窗口和子图位置:默认时,打开Figure No.1窗口或当 前窗口、当前子图;也可以打开指定的图形窗口和子图。
3 设置曲线的绘制方式:线型、色彩、数据点形。
4 设置坐标轴:坐标的范围、刻度和坐标分格线
MATLAB实验报告绘图
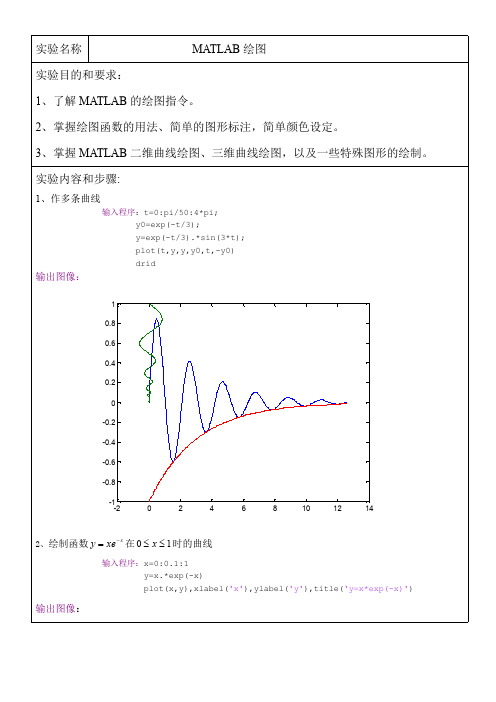
clf;dx=0.1;x=0:dx:4;y=x.*sin(x);s=cumtrapz(y)*dx; sint='{\fontsize{16}\int_{\fontsize{8}0}^{ x}}';
plotyy(x,y,x,s),text(0.5,0,'\fontsize{14}\ity=xsinx') text(2.5,3.5,['\fontsize{14}\its=',sint,'\fontsize{14}\itxsinxdx'])
运行图像:
2/3 exp(-1/2 t) cos(1/2 31/2 t) 0.55 0.5 0.1 0.45 0.4 0.35 0 0.3 0.25 0.2 -0.1 0.15 0 5 10 0 5 10 s = y(t)dt
0.15
0.05
-0.05
t
t
7、编写 MATLAB 程序,画五角星
输入程序:n=1:2:11; x=sin(0.4*n*pi); y=cos(0.4*n*pi); plot(x,y) 输出图像: axis([-1,1,-1,1]),axis square
输出图像
helix
40 30 20 10 0 1 0.5 0 -0.5 -1 -1 -0.5 0
origin 0.5 1
9、用MATLAB绘制饼图
输入程序:function shi h0=figure('toolbar','none', 'position',[200 150 450 250],'name'); t=[54 21 35; 68 54 35; 45 25 12; 48 68 45; 68 54 69]; x=sum(t); h=pie(x); textobjs=findobj(h,'type','text'); str1=get(textobjs,{'string'}); val1=get(textobjs,{'extent'}); oldext=cat(1,val1{:});
MATLAB实验3
实验三函数式M文件和MA TLAB绘图一、实验目的:1、掌握基本的绘图命令2、掌握各种图形注释方法3、掌握三维图形的绘制方法4、了解一些特殊图形的绘制5、了解图形的高级控制技巧二、相关知识1基本的绘图命令1)、常用绘图命令常用的统计图函数:在MA TLAB 7中,使用plot函数进行二维曲线图的绘制>> x=0:0.1:10;>> y1=sin(x);>> y2=cos(x-2.5);>> y3=sqrt(x);>> plot(x,y1,x,y2,x,y3)3)、极坐标图形的绘制MA TLAB提供了polar(x1,x2,s)函数来在极坐标下绘制图形:(参数1角度,参数2极半径,参数3颜色和线性)>> x= 0:0.01:10;>> y1=sin(x);>> y2 = cos(x-2.5);>> polar(y1,y2,'-r+')4)、多个图形的绘制方法subplot函数可以实现多个图形的绘制:>>x = 0:.1:20;>>subplot(2,2,1)>>plot(x,sin(x));>>subplot(2,2,2);>>plot(x,cos(x))5)、曲线的色彩、线型和数据点型基本的绘图命令都支持使用字符串来给不同的曲线定义不同的线型,颜色和数据点型。
plot(x,sin(x),'-rd')图形注释对图形进行注释的方式A 图形注释“工具栏。
B 图形调色板中的注释工具C insert 菜单中的“注释”命令D 直接使用注释命令Annotation 函数Xlabel ,ylabel ,zlabel 函数 Title 函数 Colorbar 函数 Legend 函数实验内容: 一、 基础练习1、跟我练输入x,y 的值,并将它们的值互换后输出 x=input('Input x please:\n');y=input('Input y please:\n'); echo on z=x; x=y; y=z; disp(x); disp(y);echo off2、练习请求键盘输入命令keyboard ,处理完毕后,键入return ,程序将继续运行 求一元二次方程ax2 +bx+c=0的根。
3Matlab高级绘图V2.0

MATLAB语言基础实习指导实习三MATLAB高级绘图目的:通过实习MA TLAB高级绘图指令,能够绘制各种标准图件以及一些特殊图件要求:掌握MATLAB二维绘图指令plot(semilogx、semilogy、loglog),掌握图形加注的各个函数,掌握三维绘图指令mesh、surf,掌握三维图形的加注与修饰,掌握MATLAB绘图颜色控制;熟悉特殊二维图形的绘图函数。
一、二维绘图1.plot(1)单窗口、单曲线绘图>>x=0:0.1:2*pi;y=sin(x);plot(x,y);确定MATLAB绘图的默认线型;把plot(x,y)改为plot(y)看有何异同,为什么?(2)单窗口、多曲线绘图>>x=0:0.1:2*pi;y1=sin(x);y2=cos(x);y3=cos(x)+1;plot(x,y1,x,y2,x,y3);确定MATLAB绘图的默认色序,把plot(x,y1,x,y2,x,y3)改为plot(x,y1);plot(x,y2);plot(x,y3)看有何区别,为什么?(3)开关格式绘图>>x=0:0.1:2*pi;y=sin(x);plot(x,y,’r-’,x,y,’b*’);掌握MATLAB的点型和线型,掌握MATLAB的颜色指定字母。
(4)单窗口分幅绘图subplot的两种调用格式:subplot(nrow,ncol,nfig);subplot(‘position’,[left bottom width height]);第一种格式的调用:t=0:0.1:2*piy=sin(t);y1=sin(t+0.25);y2=sin(t+0.5);subplot(3,1,1);plot(t,y)subplot(3,1,2);plot(t,y3)subplot(3,1,3);plot(t,y2)查看运行结果,为什么?第二种格式的调用:t=0:0.1:2*piy=sin(t);y1=sin(t+0.25);y2=sin(t+0.5);subplot('position',[0.05,0.55,0.4,0.45]);plot(t,y)subplot('position',[0.55,0.55,0.4,0.45]);plot(t,y3)subplot('position',[0.35,0.05,0.4,0.45]);plot(t,y2)查看运行结果,注意MATLAB中对窗口大小的指定可以使用归一化坐标,如果把subplot('position',[0.35,0.05,0.4,0.45]);改成subplot('position',[0.35,0.05,0.4,0.55]);查看运行结果,为什么?(5)多窗口绘图%figure(n) ——创建窗口函数,n为窗口顺序号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验3 Matlab 绘图操作
实验目的:
1、 掌握绘制二维图形的常用函数;
2、 掌握绘制三维图形的常用函数;
3、 掌握绘制图形的辅助操作。
实验内容:
1. 设sin .cos x y x x ⎡⎤
=+⎢⎥+⎣⎦
23051,在x=0~2π区间取101点,绘制函数的曲线。
x=0:2*pi/100:2*pi;
>> y=(0.5+3*sin(x)/(1+x.^2)).*cos(x);
>> plot(x,y,'-r')
2. 已知: y x =21,cos()y x =22,y y y =⨯312,完成下列操作:
(1) 在同一坐标系下用不同的颜色和线性绘制三条曲线;
x=0:2*pi/100:2*pi;
>> y1=x.^2;plot(x,y1,'-g')
>> hold on
>> y2=cos(2*x);
>> plot(x,y2,'-c')
>>
>> hold on
>> y3=y1.*y2;
>> plot(x,y3,'-k')
(2) 以子图形式绘制三条曲线;
x=0:2*pi/100:2*pi;
>> y1=x.^2;plot(x,y1,'-g')
>> hold on
>> y2=cos(2*x);
>> plot(x,y2,'-c')
>>
>> hold on
>> y3=y1.*y2;
>> plot(x,y3,'-k')
(3) 分别用柱形图、阶梯图和杆图绘制三条曲线。
y1=x.^2;
>> y2=cos(2*x);
>> y3=y1.*y2;
>> subplot(2,2,1),bar(x,y1);
>> subplot(2,2,2),stairs(x,y2);
>> subplot(2,2,3),stem(x,y3,'g');
3.
已知:ln(x y x x ≤=⎨⎪+>⎪⎩0102
,在x -≤≤55区间绘制函数曲线。
x=-5:0.01:5;
>> y=(x+sqrt(pi))/exp(2).*(x<=0&x>-5)+1/2*log(x+sqrt(1+x.^2)).*(x>=0&x<5);
>> plot(x,y)
4. 在xy 平面内选择区域[][],,-⨯-8888,
绘制函数z =的三种三维图形(曲
线图、网线图、曲面图)。
x=-8:8;
>> y=x;
>> [x,y]=meshgrid(x,y);
>> z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2);
>> subplot(2,2,1),plot3(x,y,z);
>> subplot(2,2,2),mesh(x,y,z)
>>
subplot(2,2,3),surf(x,y,z)
5. 某工厂2005年度各季度产值(单位:万元)分别为:450.6、395.9、410.2、450.9,试绘制柱形图和饼图(二维)。
x=[1;2;3;4];
>> y=[450.6 395.9 410.2 450.9]; >> b=int8(y==min(y));
>> subplot(1,2,1),bar(x,y,'group'); >> subplot(1,2,2),pie3(x,y)。
