您的位置：360文档中心› 相似三角形A字模型含详细答案-经典

相似三角形A字模型含详细答案-经典

合集下载

相似三角形重难点模型(五大模型)(解析版)

相似三角形重难点模型(五大模型)(解析版)

相似三角形重难点模型(五大模型)【题型01：(双)A字型相似】【题型02：(双)8型相似】【题型03：母子型相似】【题型04：旋转相似】【题型05：K字型相似】【题型01：(双)A字型相似】1.如图，在△ABC中，BC=12，高AD=6，正方形EFGH一边在BC上，点E,F分别在AB,AC上，AD交EF于点N，求AN的长．【答案】2【分析】设正方形EFGH的边长EF=EH=x，易证四边形EHDN是矩形，则DN=x，根据正方形的性质得出EF∥BC，推出△AEF∽△ABC，根据相似三角形的性质计算即可得解．【详解】解：设正方形EFGH的边长EF=EH=x，∵四边形EFGH是正方形，∴∠HEF=∠EHG=90°,EF∥BC，∴△AEF∽△ABC，∵AD是△ABC的高，∴∠HDN=90°，∴四边形EHDN是矩形，∴DN=EH=x，∵△AEF∽△ABC，∴AN AD =EFBC(相似三角形对应边上的高的比等于相似比)，∵BC=12,AD=6，∴AN=6-x，∴6-x6=x 12，解得：x=4，∴AN=6-x=6-4=2．【点睛】本题考查了相似三角形的判定和性质，矩形的判定和性质．解题的关键是掌握相似三角形的判定和性质，矩形的判定和性质的运用，注意：矩形的对边相等且平行，相似三角形的对应高的比等于相似比．2.如图，光源P 在水平横杆AB 的上方，照射横杆AB 得到它在平地上的影子为CD (点P 、A 、C 在一条直线上，点P 、B 、D 在一条直线上)，不难发现AB ⎳CD ．已知AB =1.5m ，CD =4.5m ，点P 到横杆AB 的距离是1m ，则点P 到地面的距离等于m ．【答案】3【分析】作PF ⊥CD 于点F ，利用AB ∥CD ，推导△P AB ∽△PCD ，再利用相似三角形对应高之比是相似比求解即可．【详解】解：如图，过点P 作PF ⊥CD 于点F ，交AB 于点E ，∵AB ∥CD ，∴△P AB ∽△PCD ，PE ⊥AB ，∵△P AB ∽△PCD ，∴AB CD =PE PF ，(相似三角形对应高之比是相似比)即：1.54.5=1PF，解得PF =3．故答案为：3．【点睛】本题考查相似三角形的判定与性质，掌握相似三角形对应高之比是相似比是解题的关键．3.如图，在Rt △ABC 中，∠ACB =90°，∠BAC =60°，AC =6，AD 平分∠BAC ，交边BC 于点D ，过点D 作CA 的平行线，交边AB 于点E ．(1)求线段DE 的长；(2)取线段AD 的中点M ，连接BM ，交线段DE 于点F ，延长线段BM 交边AC 于点G ，求EF DF的值．【答案】(1)4(2)23【分析】(1)根据平行线分线段成比例定理，列出比例式求解即可；(2)根据平行线分线段成比例定理，列出比例式求解即可．【详解】(1)解：∵AD 平分∠BAC ，∠BAC =60°，∴∠DAC =30°，在Rt △ACD 中，∠ACD =90°，∠DAC =30°，AC =6，∴CD =23，在Rt △ACB 中，∠ACB =90°，∠BAC =60°，AC =6，∴BC =63，∴BD =BC -CD =43，∵DE ∥CA ，∴DE CA=BD BC =23，∴DE =4；(2)解：如图．∵点M 是线段AD 的中点，∴DM =AM ，∵DE ∥CA ，∴DF AG =DM AM．∴DF =AG ．∵DE ∥CA ，∴EF AG =BF BG ，BF BG =BD BC ．∴EF AG=BD BC ．∵BD =43，BC =63，DF =AG ，∴EF DF=23．【点睛】考查了平行线分线段成比例定理，注意线段之间的对应关系．4.如图，△ABD 中，∠A =90°，AB =6cm ，AD =12cm ．某一时刻，动点M 从点A 出发沿AB 方向以1cm/s 的速度向点B 匀速运动；同时，动点N 从点D 出发沿DA 方向以2cm/s 的速度向点A 匀速运动，运动的时间为ts ．(1)求t 为何值时，△AMN 的面积是△ABD 面积的29；(2)当以点A ，M ，N 为顶点的三角形与△ABD 相似时，求t 值．【答案】(1)t 1=4，t 2=2；(2)t =3或245【分析】(1)由题意得DN =2t (cm )，AN =(12-2t )cm ，AM =tcm ，根据三角形的面积公式列出方程可求出答案；(2)分两种情况，由相似三角形的判定列出方程可求出t的值．【详解】解：(1)由题意得DN=2t(cm)，AN=(12-2t)cm，AM=tcm，∴△AMN的面积=12AN•AM=12×(12-2t)×t=6t-t2，∵∠A=90°，AB=6cm，AD=12cm∴△ABD的面积为12AB•AD=12×6×12=36，∵△AMN的面积是△ABD面积的29，∴6t-t2=29×36，∴t2-6t+8=0，解得t1=4，t2=2，答：经过4秒或2秒，△AMN的面积是△ABD面积的2 9；(2)由题意得DN=2t(cm)，AN=(12-2t)cm，AM=tcm，若△AMN∽△ABD，则有AMAB=ANAD，即t6=12-2t12，解得t=3，若△AMN∽△ADB，则有AMAD=ANAB，即t12=12-2t6，解得t=24 5，答：当t=3或245时，以A、M、N为顶点的三角形与△ABD相似．【点睛】本题考查了相似三角形的判定，直角三角形的性质和一元二次方程的应用，正确进行分类讨论是解题的关键．【题型02：(双)8型相似】5.已知：如图，四边形ABCD是平行四边形，在边AB的延长线上截取BE=AB，点F在AE的延长线上，CE和DF交于点M，BC和DF交于点N，联结BD．(1)求证：△BND∽△CNM；(2)如果AD2=AB•AF，求证：CM•AB=DM•CN．【答案】(1)见解析；(2)见解析【分析】(1)利用平行四边形的性质得AB=CD，AB∥CD，再证明四边形BECD为平行四边形得到BD∥CE，根据相似三角形的判定方法，由CM∥DB可判断△BND∽△CNM；(2)先利用AD 2=AB •AF 可证明△ADB ∽△AFD ，则∠1=∠F ，再根据平行线的性质得∠F =∠4，∠2=∠3，所以∠3=∠4，加上∠NMC =∠CMD ，于是可判断△MNC ∽△MCD ，所以MC ：MD =CN ：CD ，然后利用CD =AB 和比例的性质即可得到结论．【详解】证明：(1)∵四边形ABCD 是平行四边形，∴AB =CD ，AB ∥CD ，而BE =AB ，∴BE =CD ，而BE ∥CD ，∴四边形BECD 为平行四边形，∴BD ∥CE ，∵CM ∥DB ，∴△BND ∽△CNM ；(2)∵AD 2=AB •AF ，∴AD ：AB =AF ：AD ，而∠DAB =∠FAD ，∴△ADB ∽△AFD ，∴∠1=∠F ，∵CD ∥AF ，BD ∥CE ，∴∠F =∠4，∠2=∠3，∴∠3=∠4，而∠NMC =∠CMD ，∴△MNC ∽△MCD ，∴MC ：MD =CN ：CD ，∴MC •CD =MD •CN ，而CD =AB ，∴CM •AB =DM •CN ．【点睛】本题考查了三角形相似的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．在运用相似三角形的性质时主要利用相似比计算线段的长．也考查了平行四边形的判定与性质．6.如图，在平行四边形ABCD 中，点E 是AD 上一点，AE =2ED ，连接BE 交AC 于点G ，延长BE 交CD 的延长线于点F ，则BG GF 的值为()A.23B.12C.13D.34【答案】A【分析】本题考查了相似三角形的判定与性质，平行四边形的性质，解决本题的关键是利用平行四边形的性质对边平行而构建相似三角形．先根据平行四边形的性质得到AB ∥CD ，则可判断△ABG ∽△CFG ，△ABE ∽△DFE ，于是根据相似三角形的性质和AE =2ED 即可得结果．【详解】解：∵四边形ABCD 为平行四边形，∴AB ∥CD ，∴△ABG ∽△CFG ，∴BG GF =AB CF∵△ABE ∽△DFE ，∴AE DE =AB DF，∵AE =2ED ，∴AB =2DF ，∴AB CF =23，∴BG GF=23．故选：A ．7.如图1，在四边形ABDE 中，∠ABC =∠BDE ，点C 在边BD 上，且AC ∥DE ，AB ∥CE ，点F 在边AC 上，且AF =CE ，连接BF ,DF ，DF 交CE 于点G ．(1)求证：BF =DF ；(2)如图2，若∠ACE =∠CDF ，求证：CE ⋅CF =BF ⋅DG ；(3)如图3，若延长BF 恰好经过点E ，求BC CD的值．【答案】(1)见解析(2)见解析(3)1+52【分析】(1)证明△ABF ≌△CAE ，得出BF =AE ，证明四边形AFDE 为平行四边形，得出AE =DF ，则可得出结论；(2)证明△FCG ∽△FDC ，得出CF DF =GF CF ，证明△FCG ∽△DEG ，得GF DG =CF DE ，则得出结论；(3)证明△ABF ∽△CEF ，得出AB CE =AF CF，设AB =x ,AF =CE =m ，解方程求出x ，则可得出答案．【详解】(1)∵AC∥DE,AB∥CE∴∠BDE=∠ACB,∠ABC=∠DCE,∠BAC=∠ACE ∵∠ABC=∠BDE∴∠ABC=∠BDE=∠ACB=∠DCE∴AB=AC,CE=DE在△ABF和△CAE中，又∵AF=CE∠BAC=∠ACE AB=AC∴△ABF≌△CAE(SAS)∴BF=AE∵CE=DE,AF=CE∴AF=DE∵AF=DE,AC∥DE∴四边形AFDE为平行四边形∴AE=DF∴BF=DF(2)∵∠CFG=∠CFD ∠ACE=∠CDF∴△FCG∽△FDC∴CF DF =GF CF又∵AC∥DE∴△FCG∽△DEG∴GF DG =CFDE，即GFCF=DGDE∴CF DF =DGDE．又∵DE=CE,DF=BF∴CF BF =DGCE，即CE⋅CF=BF⋅DG(3)∵∠ABC=∠DCE ∠ACB=∠EDC∴△ABC∽△ECD∴BC CD =AB CE∵AB∥CE，∴△ABF∽△CEF∴AB CE =AF CF∴AB⋅CF=AF⋅CE．设AB=x,AF=CE=m，则有x(x-m)=m2解得x=1+52m(负值舍去)∴BC CD =ABCE=1+52【点睛】本题考查了相似三角形的判定和性质、全等三角形的判定和性质、平行四边形的性质，利用相似三角形的判定和性质是本题解题的关键．8.如图1，在矩形ABCO 中，OA =8，OC =6，D ，E 分别是AB ，BC 上一点，AD =2，CE =3，OE 与CD 相交于点F ．(1)求证：OE ⊥CD ；(2)如图2，点G 是CD 的中点，延长OG 交BC 于H ，求CH 的长．【答案】(1)见解析；(2)CH 的长为6．【分析】(1)根据四边形ABCO 是矩形，可得OA =BC =8，OC =AB =6，根据勾股定理可得OE 和CP 的长，进而得EF 和CF 的长，再根据勾股定理的逆定理即可得OE ⊥CD ；(2)在Rt △CBD 中，CB =8，BD =AB -AD =6-2=4，根据勾股定理可得CD =45，根据点G 是CD 的中点，可得CG =DG =25，所以得点G 是CP 的三等分点，根据OA ∥BC ，对应边成比例即可求出CH 的长．【详解】(1)∵四边形ABCO 是矩形，∴OA =BC =8，OC =AB =6，在Rt △OCE 中，CE =3，∴OE =OC 2+CE 2=62+32=35，∵AB ∥OC ，即AD ∥OC ，且AD =2，∴AD OC =P A PO ，∴26=P A P A +8，∴P A =4，∴PO =P A +OA =12，∴在Rt △OPC 中，OC =6，∴CP =OC 2+PO 2=62+122=65，∵OA ∥BC ，即OP ∥CE ，∴CE OP =EF OF =CF PF ，∴EF OF=CF PF =312=14，∴EF =15OE =355，CF =15CP =655，∵355 2+655 2=95+365=9，∴EF 2+CF 2=CE 2，∴△CEF 是直角三角形，∴∠CFE=90°，∴OE⊥CD；(2)在Rt△CBD中，CB=8，BD=AB-AD=6-2=4，根据勾股定理，得CD=CB2+BD2=82+42=45，∵点G是CD的中点，∴CG=DG=25，由(1)知：CP=65，∴DP=CP-CD=25，∴点G是CP的三等分点，∵OA∥BC，即OP∥CH，∴CH OP =CG GP，∴CH12=12，∴CH=6．答：CH的长为6．【点睛】本题考查了矩形的性质、勾股定理及其逆定理的应用、相似三角形的判定与性质以及平行线分线段成比例定理，解决本题的关键是掌握矩形的性质．【题型03：母子型相似】9.【典例3】如图1，∠C=90，BC=6，tan B=43，点M从点B出发以每秒1个单位长度的速度向点C运动，点N同时从点C出发以每秒2个单位长度的速度向点A运动，当一点到达终点时，另一点也停止运动．(1)求AB的长．(2)当以点M、C、N为顶点的三角形与△ABC相似时，求t的值．(3)如图2，将本题改为点M从点B出发以每秒3个单位长度的速度在BA上向点A运动，点N同时从点A出发向点C运动，其速度是每秒2个单位长度，其它条件不变，求当t为何值时，△MNA为等腰三角形．【答案】(1)10(2)t=125或t=1811时，以点M、C、N为顶点的三角形与△ABC相似(3)t=2或t=4017或t=5031时，△MNA为等腰三角形【分析】(1)根据三角函数解得即可；(2)分①当△MCN ∽△BCA 时和②当△MCN ∽△ACB 时，两种情况利用相似三角形的性质解答即可；(3)分①当AM =AN 时，②当AM =MN 时，③当MN =AN 时，三种情况，利用等腰三角形的性质得出比例解答即可．【详解】(1)解：∵∠C =90°,BC =6,tan B =43∴AC =8∴AB =BC 2+AC 2=62+82=10(2)解：解：①当△MCN ∽△BCA 时，∴MC BC =CN CA ，即6-t 6=2t 8，解得：t =125，②当△MCN ∽△ACB 时，∵MC AC =CN BC ，即6-t 8=2t 6，解得：t =1811，综上所述，t =125或t =1811时，以点M 、C 、N 为顶点的三角形与△ABC 相似，(3)解：①如图3，当AM =AN 时，10-3t =2t ，解得：t =2，②如图4，当AM =MN 时，过点M 作MD ⊥AC 于D ，则∠ADM =90°，AM =MN =10-3t ，AD =12AN =t ，∵∠ACB =90°，∴MD ∥BC ，∴△AMD ∽△ABC ，∴AM AB =AD AC ，即10-3t 10=t 8，解得：t =4017，③如图5，当MN =AN 时，过点N 作ND ⊥AB 于D ，则∠ADN =∠ACB =90°，AD =DM =12AM =12(10-3t )，∵∠A =∠A ，∴△ADN ∽△ACB ，∴AD AC =AN AB ，即12(10-3t )8=2t 10，解得：t =5031，综上所述，t =2或t =4017或t =5031时，△MNA 为等腰三角形【点睛】本题考查考查了相似三角形的判定与性质、等腰三角形的性质，已知正切求边长，解题的关键是掌握辅助线的作法，数形结合，分类讨论思想的应用．10.如图，在△ABC 中，D 是BC 上的点，E 是AD 上一点，且AB AC=AD CE ，∠BAD =∠ECA ．(1)求证：AC 2=BC •CD ；(2)若AD 是△ABC 的中线，求CE AC 的值．【答案】(1)证明见解析；(2)22【分析】(1)首先利用相似三角形的判定得出△BAD ∽△ACE △，得∠B =∠EAC ，进而求出△ABC ∽△DAC ，再利用相似三角形的性质得出答案即可；(2)由△BAD ∽△ACE 可证∠CDE =∠CED ，进而得出CD =CE ，再由(1)可证AC =2CD ，由此即可得出线段之间关系．【详解】(1)证明：∵AB AC =AD CE ，∠BAD =∠ECA ，∴ΔBAD ∽ΔACE ，∴∠B =∠EAC ，∵∠ACB =∠DCA ，∴△ABC ∽△DAC ，∴AC CD =BC AC，∴AC 2=BC ·CD ．(2)解：∵△BAD ∽△ACE ，∴∠BDA =∠AEC ，∴∠CDE =∠CED ，∴CD =CE ，∵AD 是△ABC 的中线，∴BC =2BD =2CD ，∴AC 2=BC ·CD =2CD 2，即：AC =2CD ，∴CE AC =CD 2CD=22．【点睛】此题主要考查了相似三角形的判定与性质以及重心的性质等知识，根据已知得出△BAD ∽△ACE 是解题关键．11.如果两个相似三角形的对应边存在2倍关系，则称这两个相似三角形互为母子三角形．(1)如果△DEF 与△ABC 互为母子三角形，则DE AB 的值可能为()A.2B.12C.2或12(2)已知：如图1，△ABC 中，AD 是∠BAC 的角平分线，AB =2AD , ∠ADE =∠B ．求证：△ABD 与△ADE 互为母子三角形．(3)如图2，△ABC 中，AD 是中线，过射线CA 上点E 作EG ⎳BC ，交射线DA 于点G ，连结BE ，射线BE 与射线DA 交于点F ，若△AGE 与△ADC 互为母子三角形．求AG GF的值．【答案】(1)C ；(2)见解析；(3)AG GF=13或3．【分析】(1)根据互为母子三角形的定义即可得出结论；(2)根据两角对应相等两三角形相似得出△ABD ∽△ADE ，再根据AB =2AD 从而得出结论；(3)根据题意画出图形，分当G ,E 分别在线段AD ,AC 上时和当G ,E 分别在射线DA ,CA 上时两种情况加以讨论；【详解】(1)∵△DEF 与△ABC 互为母子三角形，∴DEAB=12或2故选：C(2)∵AD 是∠BAC 的角平分线，∴∠BAD =∠CAD ，∵∠ADE =∠B ，∴△ABD ∽△ADE ．又∵AB =2AD ，∴△ABD 与△ADE 互为母子三角形．(3)如图，当G ,E 分别在线段AD ,AC 上时，∵△AGE 与△ADC 互为母子三角形，∴CD GE =AD AG=2，∴AG =DG ，∵AD 是中线，∴BD =CD ，又∵GE ⎳BC ，∴△GEF ∽△DBF ．∴DF GF =DB GE =CD GE=2，∴DG =3GF ，∴AG GF=3．如图，当G ,E 分别在射线DA ,CA 上时，∵△AGE 与△ADC 互为母子三角形，∴CD GE =AD AG =2，∴AG =12AD =13DG ，∵AD 是中线，∴BD =CD ，又∵GE ⎳BC ，∴△GEF ∽△DBF ．∴DF GF =DB GE =CD GE=2，∴DG =GF ，∴AG GF =13．综上所述，AG GF =13或3【点睛】本题主要考查了相似三角形的判定与性质、分类讨论的数学思想以及接受与理解新生事物的能力．准确理解题设条件中互为母子三角形的定义是正确解题的先决条件，在分析与解决问题的过程中，要考虑全面，进行分类讨论，避免漏解．12.如图1，AB =AC =2CD ，DC ∥AB ，将△ACD 绕点C 逆时针旋转得到△FCE ，使点D 落在AC 的点E 处，AB 与CF 相交于点O ，AB 与EF 相交于点G ，连接BF ．(1)求证：△ABE ≌△CAD ；(2)求证：AC ∥FB ；(3)若点D，E，F在同一条直线上，如图2，求ABBC的值．(温馨提示：请用简洁的方式表示角)【答案】(1)见解析(2)见解析(3)2【分析】(1)根据旋转变换的性质得到旋转前后两个三角形全等，从而得到CE=CD，根据AC=2CD，就能得到AE=CD，然后利用平行可以得到内错角相等，最后加上AB=AC，就可以通过边角边证明两个三角形全等．(2)根据旋转和第一小题的结论，可以得到BE=FE，然后用等角对等边即可得到∠EFB=∠EBF，又可以从前面的两个全等中得到∠EFC=∠EBA，∠OAC=∠OCA从而得到∠OFB=∠OBF，那么△ACO和△BOF就是顶角互为对顶角的一组等腰三角形，所以就能得到底角相等，即∠CAO=∠FOB，那么内错角相等，两直线平行即可证结论．(3)根据D，E，F在同一条直线上，可以证明△AEG和△CED全等，即可得到AG=12AB，那么EG就是中位线，则EG∥CB，加上第二小题结论就能得到四边形BCEF是平行四边形，那么BC=AD，然后通过三角形外角的性质，可以证得∠ADE=∠ACD，就能证△ACD和△ADE是一组子母型相似，然后根据相似比可得最终答案．【详解】(1)解：∵将△ACD绕点C逆时针旋转得到△FCE，∴△FCE≌△ACD，∴CE=CD，∵AC=2CD，∴AC=2CE，∴AE=AC-CE=2CE-CE=CE=CD，∵DC∥AB∴∠DCA=∠EAB，在△ABE和△CAD中，∵AE=CD∠EAB=∠DCA AB=CA，∴△ABE≌△CAD SAS．(2)解：由(1)得BE=AD，∠ABE=∠CAD，∵△CEF≌△CDA，∴FE=AD，∠EFC=∠DAC，∴BE=FE，∠EFC=∠EBA，∴∠EFB=∠EBF，∵∠OFB=∠EFB-∠EFC，∠OBF=∠EBF-∠EBA，∴∠OFB=∠OBF，∵∠ECF=∠DCA，∴∠OAC=∠OCA，∵∠OCA+∠OAC+∠AOC=180°，∠OBF+∠OFB+∠BOF=180°，又∠AOC=∠BOF，∴∠OCA+∠OAC=∠OBF+∠OFB，即2∠CAO=2∠FOB，∴∠CAO=∠FOB，∴AC∥FB(3)解：在△AEG和△CED中，∵∠GAE=∠DCE AE=CE∠AEG=∠CED ，∴△AEG≌△CED ASA∴AG=CD=12AB，∵AE=CE，∴EG∥CB，∵AC∥FB，∴四边形BCEF是平行四边形，∴BC=FE=AD，∵∠AEG=∠ACD+∠CAD=∠DAE+∠ADE，∴∠ADE=∠ACD，∵∠CAD=∠DAE，∴△ACD∽△ADE，∴EA DA =DA CA，即DA2=EA⋅CA=2EA2，∴DA=2EA，∵AB=AC=2EA，∴AB BC =ABDA=2EA2EA=22=2．【点睛】本题考查了三角形全等的证明，平行线的判定以及利用相似三角形求线段长之比，解题时需要学会将多个小题的结论联系起来，把前面小题的结论用到后面小题的思路中，熟练寻找证明三角形全等或相似所需要的条件是解题的关键．【题型04：旋转相似】13.【典例4】某校数学活动小组探究了如下数学问题：(1)问题发现：如图1，△ABC中，∠BAC=90°，AB=AC．点P是底边BC上一点，连接AP，以AP为腰作等腰Rt△APQ，且∠P AQ=90°，连接CQ、则BP和CQ的数量关系是______；(2)变式探究：如图2，△ABC中，∠BAC=90°，AB=AC．点P是腰AB上一点，连接CP，以CP为底边作等腰Rt△CPQ，连接AQ，判断BP和AQ的数量关系，并说明理由；(3)问题解决：如图3，在正方形ABCD中，点P是边BC上一点，以DP为边作正方形DPEF，点Q是正方形DPEF两条对角线的交点，连接CQ．若正方形DPEF的边长为210，CQ=22，请直接写出正方形ABCD的边长．【答案】(1)BP=CQ(2)BP=2AQ(3)6【分析】(1)根据已知条件利用边角边证明△ABP≌△ACQ，再利用全等三角形的性质即可得到BP和CQ 的数量关系；(2)根据任意等腰直角三角形的直角边与斜边的比是相等的，利用两边长比例且夹角相等的判定定理证明△CBP∽△CAQ，之后再由相似三角形对应边成比例即可得到BP和AQ的数量关系；(3)连接BD，先由正方形的性质判断出△BCD和△PQD都是等腰直角三角形，再利用与第二问同样的方法证出△BDP∽△CDQ，由对应边成比例，依据相似比求出线段BP的长，接着设正方形ABCD的边长为x，运用勾股定理列出方程即可求得答案．【详解】(1)解：∵△APQ是等腰直角三角形，∠P AQ=90°，在△ABC中，∠BAC=90°，AB=AC，∴AP=AQ，∠BAP+∠P AC=∠CAQ+∠P AC，∴∠BAP=∠CAQ．在△ABP和△ACQ中，AB=AC∠BAP=∠CAQ AP=AQ，∴△ABP≌△ACQ(SAS)，∴BP=CQ；(2)解：结论：BP=2AQ，理由如下：∵△CPQ是等腰直角三角形，△ABC中，∠BAC=90°，AB=AC，∴QCPC=ACBC=22，∠ACB=∠QCP=45°．∵∠BCP+∠ACP=∠ACQ+∠ACP=45°，∴∠BCP=∠ACQ，∴△CBP∽△CAQ，∴QCPC=ACBC=AQBP=22，∴BP=2AQ；(3)解：连接BD，如图所示，∵四边形ABCD与四边形DPEF是正方形，DE与PF交于点Q，∴△BCD和△PQD都是等腰直角三角形，∴QDPD=CDBD=22，∠BDC=∠PDQ=45°．∵∠BDP+∠PDC=∠CDQ+∠PDC=45°，∴∠BDP=∠CDQ，∴△BDP∽△CDQ，∴QDPD=CDBD=CQBP=22．∵CQ=22，∴BP=2CQ=4．在Rt△PCD中，CD2+CP2=DP2，设CD=x，则CP=x-4，又∵正方形DPEF的边长为210，∴DP=210，∴x2+(x-4)2=(210)2，解得x1=-2(舍去)，x2=6．∴正方形ABCD的边长为6．【点睛】本题是一道几何综合题，考查了全等三角形，相似三角形的判定和性质，以及正方形和等腰三角形的性质，正确识图并能熟练地掌握几何图形的性质与判定定理进行证明是解题的关键．14.如图1，已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．(1)证明：四边形CEGF是正方形；(2)探究与证明：将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°)，如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；(3)拓展与运用：正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°)，如图3所示，当B，E，F三点在一条直线上时，延长CG交AD于点H，若AG=9，GH=32，求BC的长．【答案】(1)答案见解析；(2)AG=2BE；理由见解析；(3)BC=95 2．【分析】(1)先说明GE⊥BC、GF⊥CD，再结合∠BCD=90°可证四边形CEGF是矩形，再由∠ECG= 45°即可证明；(2)连接CG，证明△ACG∽△BCE，再应用相似三角形的性质解答即可；(3)先证△AHG∽△CHA可得AGAC =GHAH=AHCH，设BC=CD=AD=a，则AC=a，求出AH=23a，DH=13a，CH=103a最后代入即可求得a的值．【详解】(1)∵四边形ABCD是正方形，∴∠BCD=90°，∠BCA=45°，∵GE⊥BC、GF⊥CD，∴∠CEG=∠CFG=∠ECF=90°，∴四边形CEGF是矩形，∠CGE=∠ECG=45°，∴EG=EC，∴四边形CEGF是正方形．(2)结论：AG=2BE；理由：连接CG，由旋转性质知∠BCE=∠ACG=α，在Rt △CEG 和Rt △CBA 中，CE CG=cos45°=22，CB CA =cos45°=22，∴CG CE =CA CB=2，∴△ACG ∽△BCE ，∴AG BE =CA CB=2∴线段AG 与BE 之间的数量关系为AG =2BE ；(3)∵∠CEF =45°，点B 、E 、F 三点共线，∴∠BEC =135°，∵△ACG ∽△BCE ，∴∠AGC =∠BEC =135°，∴∠AGH =∠CAH =45°，∵∠CHA =∠AHG ，∴△AHG ∽△CHA ，∴AG AC =GH AH=AH CH ，设BC =CD =AD =a ，则AC =2a ，由AG AC =GH AH ，得92a =32AH ，∴AH =23a ，则DH =AD -AH =13a ，CH =CD 2+DH 2=103a ，∴AG AC =AH CH ，得 92a =23a 103a ,解得：a =952，即BC =952．【点睛】本题属于四边形综合题，主要考查相似形的判定和性质、正方形的性质等知识点，解题的关键是正确寻找相似三角形解决问题并利用参数构建方程解决问题．【题型05：K 字型相似】15.综合探究如图，在平面直角坐标系中，点O 为原点，□ABCD 的顶点B 、C 在x 轴上，A 在y 轴上，OA =OC =2OB =4，直线y =x +t (-2≤t ≤4)分别与x 轴、y 轴、线段AD 、直线AB 交于点E 、F 、P 、Q ．(1)当t =1时，求证：AP =DP ．(2)探究线段AP 、PQ 之间的数量关系，并说明理由．(3)在x 轴上是否存在点M ，使得∠PMQ =90°，且以点M 、P 、Q 为顶点的三角形与△AOB 相似，若存在，请求出此时t 的值以及点M 的坐标；若不存在，请说明理由．【答案】(1)见解析(2)PQ =22AP(3)t =73时，M 13,0 ；t =23时，M 143,0 ；t =-1时，M -7，0 ．【分析】(1)根据t =1，求出t =1与AD 交点P 的坐标，即可求解；(2)先求出直线AB 的表达式为y =2x +4，再联立直线AB 与直线y =x +t 求出Q (t -4,2t -4)，再求出点P (4-t ,4)，利用坐标系中两点距离公式求出即可PQ =22(t -4)，结合AP =4-t 即可求解；(3)证明△PHM ∽△MIQ ，得到PM QM =AO BO =2或PM QM =BO AO=12，分四种情况画图求解．【详解】(1)证明：由OA =OC =2OB =4知，OC =4，OB =2，则AD =BC =6，则点A 、B 的坐标分别为：(0,4)、(-2,0)，当y =4时，y =x +1=4，则x =3=12AD ，即点P (3,4)，∴AP =DP =3；(2)解：PQ =22AP ，理由：设直线AB 的表达式为：y =kx +b ，将A 0，4 、B -2，0 代入得：4=b 0=-2k +b ，解得：k =2b =4 ．∴直线AB 的表达式为：y =2x +4，联立上式和y =x +t 得y =x +t y =2x +4 ，解得x =t -4y =2t -4 ，即点Q (t -4,2t -4)，同理(1)可得，点P (4-t ,4)，∴PQ =t -4 -4-t 2+2t -4 -4 2=224-t∵AP =4-t ，∴PQ =22AP ；(3)分别过点P 、Q 作PH ⊥x 轴，QI ⊥x 轴，∴∠PHM =∠MIQ =90°，∵∠PMQ =90°，∴∠PMH +∠QMI =90°，∵∠MQI +∠QMI =90°，∴∠PMH =∠MQI ，∴△PHM ∽△MIQ ，∴PH MI =MH QI =PM QM，设点M (x ,0)，由(2)知，点P 、Q 的坐标分别为：(4-t ,4)、(t -4,2t -4)，①若m >0，如图2，则MI =m -(t -4)，MH =4-t -m ，QI =2t -4，当△PMQ ∽△AOB 时，∴PM QM =AO BO=42=2，∴PH MI =MH QI=2．∴PH =2MI ，MH =2QI ，联立方程组：4=2m -(t -4) 4-t -m =2(2t -4) ，解得：m =13t =73∴t =73时，M 13,0 ，②若m >0，MI =m -(t -4)，MH =m -(4-t )，QI =4-2t ，如图3，当△QMP ∽△AOB 时，∴PM QM =BO AO=24=12∴PH MI =MH QI =12∴2PH =MI ，2MH =QI ，联立方程组：2×4=m -(t -4)2m -(4-t ) =4-2t ，解得m =143t =23．∴t =23时，M 143,0 ③若m <0，当△PMQ ∽△AOB 时，如图4，MI =(t -4)-m ，MH =(4-t )-m ，QI =4-2t ，∴PM AO =QM BO ，∴PM QM =AO BO=42=2，∴PH MI =MH QI =2∴PH =2MI ，MH =2QI ，联立方程组：4=2(t -4)-m 4-t -m =2(4-2t )，解得：m =-7t =-1 ∴t =-1，M -7，0④m <0，△QMP ∽△AOB 的情况不存在，综上，t =73时，M 13,0 ；t =23时，M 143,0 ；t =-1时，M -7，0 ．【点睛】本题考查的是一次函数综合运用，涉及到三角形相似、平行四边形的性质等，分类求解是解题的关键．16.如图，边长为10的等边△ABC 中，点D 在边AC 上，且AD =3，将含30°角的直角三角板(∠F =30°)绕直角顶点D 旋转，DE 、DF 分别交边AB 、BC 于P 、Q ，连接PQ ．当EF ∥PQ 时，DQ 长为()A.6B.39C.10D.63【答案】B【分析】证明△ADP ∽△BPQ ，由相似三角形的性质得出AD BP =AP BQ =DP PQ ，求出BP =6，CQ =2，过点Q 作QM ⊥AC 于点M ，由勾股定理可求出答案．【详解】解：∵∠F =30°，∴∠E =60°，∵EF ∥PQ ，∴∠DPQ =∠E =60°，∠DQP =∠F =30°，∴∠APD +∠BPQ =120°，∵△ABC 为等边三角形，∴∠A =∠B =60°，AC =BC =AB =10，∴∠APD +∠ADP =120°，∴∠BPQ =∠ADP ，∴△ADP ∽△BPQ ，∴AD BP =AP BQ =DP PQ，∵∠PDQ =90°，∠DQP =30°，∴PD =12PQ ，∴3 BP =APBQ=12，∴BP=6，∴AP=4，BQ=8，∴CQ=2，过点Q作QM⊥AC于点M，∴CM=12CQ=1，QM=3，∵CD=AC-AD=10-3=7，∴DM=CD-CM=7-1=6，∴DQ=DM2+QM2=62+(3)2=29．故选：B．【点睛】本题考查了勾股定理，等边三角形的性质，相似三角形的判定与性质，直角三角形的性质．先证明△ADP∽△BPQ是解题的关键．17.(1)问题如图1，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=90°时，求证：AD⋅BC=AP ⋅BP．(2)探究若将90°角改为锐角(如图2)，其他条件不变，上述结论还成立吗？说明理由．(3)应用如图3，在△ABC中，AB=22，∠B=45°，以点A为直角顶点作等腰Rt△ADE．点D在BC上，点E在AC上，点F在BC上，且∠EFD=45°，若CE=5，求CD的长．【答案】(1)见解析；(2)成立；理由见解析；(3)5【分析】(1)由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC,即可证到△ADP∽△BPC，然后运用相似三角形的性质即可解决问题；(2)由∠DPC=∠A=∠B=α可得∠ADP=∠BPC,即可证到△ADP∽△BPC，然后运用相似三角形的性质即可解决问题；(3)证明△ABD∽△DFE,求出DF=4，再证△EFC∽△DEC,可求FC=1,进而解答即可．【详解】解：(1)证明：如图1，∵∠DPC=90°∴∠BPC+∠APD=90°，∵∠A=90°，∴∠ADP+∠APD=90°∴∠APD=∠BPC，又∵∠A=∠B=90°∴△ADP∽△BPC，∴AD:BP=AP:BC∴AD⋅BC=AP⋅BP；(2)结论AD⋅BC=AP⋅BP仍成立；理由：如图2，∵∠BPD=∠DPC+∠BPC，又∵∠BPD=∠A+∠APD，∴∠DPC+∠BPC=∠A+∠APD，∵∠DPC=∠A=α，∴∠BPC=∠APD，又∵∠A=∠B=α，∴△ADP∽△BPC，∴AD:BP=AP:BC∴AD⋅BC=AP⋅BP；(3)∵∠EFD=45°,∴∠B=∠ADE=45°,∴∠BAD=∠EDF,∴△ABD∽△DFE∴AB:DF=AD:DE∵Rt△ADE是等腰直角三角形∴AD:DE=1:2∴AB:DF=1:2∵AB=22∴DF=4∵Rt△ADE是等腰直角三角形∴∠AED=45°∵∠EFD=45°∴∠DEC=∠EFC=180°-45°=135°又∵∠C=∠C∴△DEC∽△EFC∴DC:EC=EC:CF即EC2=FC⋅(4+FC)∵EC=5∴5=FC(4+FC)∴FC=1解得CD=5．【点睛】本题考查相似三角形的综合题，三角形的相似，正切值的求法，能够通过构造45°角将问题转化为一线三角是解题的关键．18.如图，在Rt△ABC中，∠ACB=90°，BCAC =mn，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．(1)探究发现：如图1，若m =n ，点E 在线段AC 上，则DE DF =；(2)数学思考：①如图2，若点E 在线段AC 上，则DE DF =(用含m ，n 的代数式表示)；②当点E 在直线AC 上运动时，①中的结论是否仍然成立？请仅就图3的情形给出证明；(3)拓展应用：若AC =5，BC =25，DF =42，请直接写出CE 的长．【答案】(1)1；n m ；(2)①n m ；②n m ；(3)CE =25或CE =255【分析】(1)先用等量代换判断出∠ADE =∠CDF ，∠A =∠DCB ，得到△ADE ∽△CDF ，再判断出△ADC ∽△CDB 即可；(2)方法和1 一样，先用等量代换判断出∠ADE =∠CDF ，∠A =∠DCB ，得到△ADE ∽△CDF ，再判断出△ADC ∽△CDB 即可；(3)由2 的结论得出△ADE ∽△CDF ，判断出CF =2AE ，求出DE ，再利用勾股定理，计算出即可．【详解】解：1 当m =n 时，即：BC =AC ，∵∠ACB =90°，∴∠A +∠ABC =90°，∵CD ⊥AB ，∴∠DCB +∠ABC =90°，∴∠A =∠DCB ，∵∠FDE =∠ADC =90°，∴∠FDE -∠CDE =∠ADC -∠CDE ，即∠ADE =∠CDF ，∴△ADE ∽△CDF ，∴DE DF =AD DC，∵∠A =∠DCB ，∠ADC =∠BDC =90°，∴△ADC ∽△CDB ，∴AD DC =AC BC=1，∴DE DF =12 ①∵∠ACB =90°，∴∠A +∠ABC =90°，∵CD ⊥AB ，∴∠DCB +∠ABC =90°，∴∠A =∠DCB ，∵∠FDE=∠ADC=90°，∴∠FDE-∠CDE=∠ADC-∠CDE，即∠ADE=∠CDF，∴△ADE∽△CDF，∴DE DF =AD DC，∵∠A=∠DCB，∠ADC=∠BDC=90°，∴△ADC∽△CDB，∴AD DC =ACBC=nm，∴DEDF=nm②成立.如图3，∵∠ACB=90°，∴∠A+∠ABC=90°，又∵CD⊥AB，∴∠DCB+∠ABC=90°，∴∠A=∠DCB，∵∠FDE=∠ADC=90°，∴∠FDE+∠CDE=∠ADC+∠CDE，即∠ADE=∠CDF，∴△ADE∽△CDF，∴DE DF =AD DC，∵∠A=∠DCB，∠ADC=∠BDC=90°，∴△ADC∽△CDB，∴AD DC =ACBC=nm，∴DE DF =n m．3 由2 有，△ADE∽△CDF，∵DE DF =ACBC=12，∴AD CD =AECF=DEDF=12，∴CF=2AE，如图4图5图6，连接EF．在Rt△DEF中，DE=22，DF=42，∴EF=210，①如图4，当E在线段AC上时，在Rt△CEF中，CF=2AE=2AC-CE=25-CE，EF=210，根据勾股定理得，CE2+CF2=EF2，∴CE2+25-CE2=40∴CE=25，或CE=-255(舍)②如图5，当E在AC延长线上时，在Rt△CEF中，CF=2AE=2AC+CE=25+CE，EF=210，根据勾股定理得，CE2+CF2=EF2，∴CE2+25+CE2=40，∴CE=255，或CE=-25(舍)，③如图6，当E在CA延长线上时，在Rt△CEF中，CF=2AE=2CE-AC=2CE-5，EF=210，根据勾股定理得，CE2+CF2=EF2，∴CE2+2CE-52=40，∴CE=25，或CE=-255(舍)，综上：CE=25或CE=25 5．【点睛】本题是三角形综合题，主要考查了三角形相似的性质和判定，勾股定理，判断相似是解决本题的关键，求CE是本题的难点．。

相似的基本模型教师版带答案

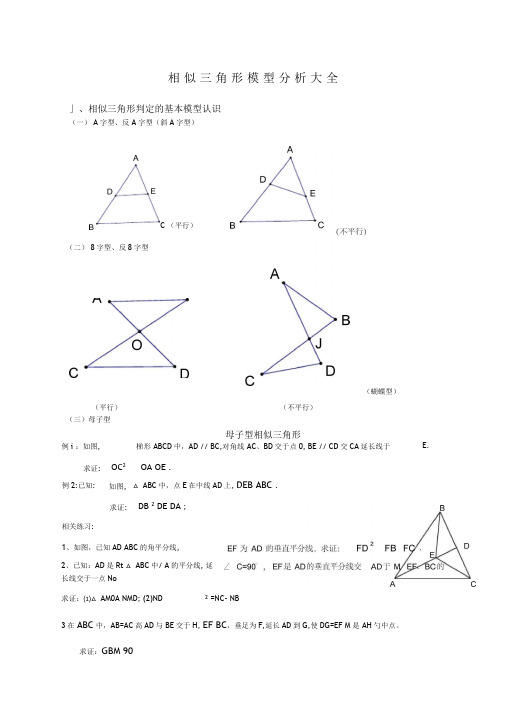
相似的基本模型教师版带答案

C （平行）（二） 8字型、反8字型（蝴蝶型）（平行）（三）母子型 （不平行）例i ：如图,母子型相似三角形梯形 ABCD 中，AD // BC ,对角线 AC 、BD 交于点0, BE // CD 交CA 延长线于 E . 求证:OC 2 OA OE . 例2:已知: 如图, △ ABC 中，点E 在中线AD 上, DEB ABC .求证: DB 2 DE DA ;相关练习:1、如图，已知AD ABC 的角平分线,2、已知：AD 是Rt △ ABC 中/ A 的平分线, 延长线交于一点No求证：⑴△ AM0A NMD; (2)ND 2 =NC- NB3在 ABC 中，AB=AC 高AD 与 BE 交于H, EF BC ，垂足为F ,延长AD 到G,使DG=EF M 是 AH 勺中点。

求证：GBM 90相 似 三 角 形 模 型 分 析 大 全」、相似三角形判定的基本模型认识（一） A 字型、反 A 字型（斜A 字型）4(四) 一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五) 一线三直角型:例1:如图，等边△ ABC 中，边长为6, D 是BC 上动点，/ EDF=60 °(1) 求证：△ BDE CFD(2) 当 BD=1 , FC=3 时，求 BE例 2:已知在梯形 ABCD 中，AD // BC , AD < BC ,且 AD = 5, AB = DC = 2.(1)如图8, P 为AD 上的一点，满足/ BPC =Z A .①求证；△ ABP ^A DPC②求AP 的长. A PD (2)如果点P 在AD 边上移动(点 P 与点A 、D 不重合)，且满足/ BPE =Z A , PE 交直线 BC 于点E ,同时交直线DC 于点Q ,那么当点Q 在线段DC 的延长线上时，设 AP = x , CQ = y , B C求y 关于x 的函数解析式，并写出函数的定义域； 相关练习:1、如图，已知在厶 ABC 中， AB=AC=6, BC=5, D 是AB 上一点，BD=2, E 是BC 上一动点，联 结DE ,并作 DEF B ，射线EF 交线段AC 于F .(1)求证：△ DBE ECF ; ( 2)当F 是线段AC 中点时，求线段 BE 的长；(3)联结DF ，如果△ DEF 与厶DBE 相似，求FC 的长.2、已知在梯形 ABCD 中，AD // BC , AD < BC ,且 BC =6 , AB=DC=4,点 E 是 AB 的中点.(1) 如图，P 为BC 上的一点，且 BP=2 .求证：△ BEPCPD ；(2) 如果点 P 在BC 边上移动(点 P 与点B 、C 不重合)，且满足/ EPF= / C , PF 交直线 CD 于点F ，同时交直线AD 于点M ，那么当点F 在线段CD 的延长线上时，设 BP=x , DF= y , 求y 关于X 的函数解析式，并写出函数的定义域；一线三等角型相似三角形A D4 D A一线三直角型相似三角形D=3 ,点P 是AD 上的一个动点，交边AB/于点E,设y ，求_y 关于x 的函数关系式P CA 例1、已知矩形 且和点 A,D ABCD 中，CD=2 , 重合，过点 P 作 PE CP , PD x, EB 【练习1】 (第25题图) 在直角 ABC 中，C 90o , AB 5,tanB 3 (备用图)-，点D 是BC 的D P D中点，点E是AB边上的动点，DF DE交射线AC于点F(1)、求AC和BC的长(2)、当EF //BC时，求BE的长。

相似三角形”A“字模型(含详细答案解析)~经典

相似三角形”A“字模型(含详细答案解析)~经典

教师辅导教案授课日期：年月日授课课时：课时ABC △与A B C '''△相似，AD 是ABC △中BAC ∠的角平分线，A D ''是A B C '''△中B A C '''∠的角平分线，则有AB BC AC AD k A B B C A C A D ====''''''''（k 为相似比）． 4．相似三角形周长的比等于相似比． ABC △与A B C '''△相似，则有AB BC ACk A B B C A C ===''''''（k 为相似比）．应用比例的等比性质有AB BC AC AB BC ACk A B B C A C A B B C A C++====''''''''''''++． 5．相似三角形面积的比等于相似比的平方．ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有AB BC AC AH k A B B C A C A H ====''''''''（k 为相似比）．进而可得21212ABC A B C BC AHS BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△．二、相似三角形的判定1．平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似． 2．如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．可简单说成：两角对应相等，两个三角形相似．3．如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似． 4．如果一个三角形的三条边与另一个三角形的你对应成比例，那么这两个三角形相似．可简单地说成：三边对应成比例，两个三角形相似．5．如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．6．直角三角形被斜边上的高分成的两个直角三角形相似（常用但要证明）7．如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等，那么这两个等腰三角形相似；如果它们的腰和底对应成比例，那么这两个等腰三角形也相似． 三、相似证明中的基本模型A 字形图①A 字型，DE//BC ;结论：AD AE DEAB AC BC==， 【例1】李老师在编写下面这个题目的答案时，不小心打乱了解答过程的顺序，你能帮他调整过来吗？证明步骤正确的顺序是（ ）已知：如图，在△ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，且DE ∥BC ，DF ∥AC ，求证：△ADE∽△DBF．证明：①又∵DF∥AC，②∵DE∥BC，③∴∠A=∠BDF，④∴∠ADE=∠B，∴△ADE∽△DBF．A．③②④① B．②④①③ C．③①④② D．②③④①【解答】证明：②∵DE∥BC，④∴∠ADE=∠B，①又∵DF∥AC，③∴∠A=∠BDF，∴△ADE∽△DBF．故选：B．【练1】如图，在△ABC中，∠ACB=90°，BC=16cm，AC=12cm，点P从点B出发，以2cm/秒的速度向点C移动，同时点Q从点C出发，以1cm/秒的速度向点A移动，设运动时间为t秒，当t=秒时，△CPQ与△ABC相似．【解答】解：CP和CB是对应边时，△CPQ∽△CBA，所以，，即，解得t=4.8；CP和CA是对应边时，△CPQ∽△CAB，所以，，即，解得t=．时，△CPQ与△CBA相似．．图②反A字型，∠ADE=∠ B或∠1=∠B结论：AE AD DE==AC AB BC【例2】如同，在△ABC中，点D，E分别在边AB，AC上，下列条件中不能判断△ABC∽△AED的是（）A．=B．=C．∠ADE=∠C D．∠AED=∠B【解答】解：∵∠DAE=∠CAB，∴当∠AED=∠B或∠ADE=∠C时，△ABC∽△AED；当=即=时，△ABC∽△AED．故选：A．【例3】如图，P是△ABC的边AB上的一点．（不与A、B重合）当∠ACP=∠ B 时，△APC与△ABC是否相似；当AC、AP、AB满足时，△ACP与△ABC相似．【解答】解：∵∠A=∠A，∠ACP=∠B，∴△ACP∽△ABC；∵，∠A=∠A，∴△ACP与△ABC；故答案为：B；．【练习1】如图，D、E为△ABC的边AC、AB上的点，当∠ADE=∠B 时，△ADE∽△ABC．其中D、E分别对应B、C．（填一个条件）．【解答】解：当∠ADE=∠B，∵∠EAD=∠CAB，相似三角形全章节教案和练习比例线段一，线段的比 定义：在同一长度单位下，两条线段的长度的比叫做这两条线段的比。

中考数学难点突破与经典模型精讲练相似三角形中的“A”字型相似模型(解析版)

中考数学难点突破与经典模型精讲练相似三角形中的“A”字型相似模型(解析版)

专题09 相似三角形中的“A”字型相似模型【模型展示】非平行A字型∠AED＝∠B∠∠ADE∠∠ACB∠ADAC＝AEAB＝DEBC.非平行A字型∥ACD＝∥B∥∥ADC∥∥ACB∥ADAC＝ACAB＝CDBC.【题型演练】一、单选题1．如图，已知,ADE ABC若:1:3,AD AB ABC的面积为9，则ADE的面积为（）A．1B．2C．3D．9【答案】A 【分析】根据相似三角形的性质得出21=3ADEABC S S ⎛⎫ ⎪⎝⎭，代入求出即可． 【详解】解：∥∥ADE∥∥ABC ，AD ：AB ＝1：3，∥21=3ADEABC S S ⎛⎫ ⎪⎝⎭， ∥∥ABC 的面积为9，∥1=99ADES ， ∥S ∥ADE ＝1，故选：A ．【点睛】本题考查了相似三角形的性质定理，能熟记相似三角形的面积比等于相似比的平方是解此题的关键．2．如图，在∥ABC 中，DE ∥BC ，若AE ＝2，EC ＝3，则∥ADE 与∥ABC 的面积之比为（ ）A ．4：25B ．2：3C ．4：9D ．2：5【答案】A【分析】根据相似三角形的判定定理得到∥ADE ∥∥ABC ，根据相似三角形的面积比等于相似比的平方计算，得到答案．【详解】解：∥AE =2，EC =3，∥AC =AE +EC =5，∥DE ∥BC ，∥∥ADE ∥∥ABC ， ∥2224525ADE ABC S AE S AC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， 故选：A ．【点睛】本题考查的是相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．3．如图，在∥ABC 中，∥C=90°，BC=3，D ，E 分别在AB、AC 上，将∥ADE 沿DE 翻折后，点A 落在点A′处，若A′为CE 的中点，则折痕DE 的长为（ ）A．12B．3C．2D．1【答案】D【详解】试题解析：由题意得：DE∥AC，∥∥DEA=90°，∥∥C=∥DEA，∥∥A=∥A，∥∥AED∥∥ACB,∥DEBC=AEAC,∥A′为CE的中点，∥C A′=E A′，∥C A′=E A′=AE，∥AEAC=DEBC=13，∥DE=1.故选D.4．如图．在∥ABC中，DE∥BC，∥B=∥ACD，则图中相似三角形有（）A．2对B．3对C．4对D．5对【答案】C【分析】根据相似三角形的判定定理即可得到结论．【详解】∥∥B=∥ACD，∥A=∥A，∥∥ACD∥∥ABC，∥DE∥BC，∥∥ADE∥∥ABC，∥∥ACD∥∥ADE，∥DE∥BC，∥∥EDC=∥DCB，∥∥B=∥DCE，∥∥CDE ∥∥BCD ，故共4对，故选：C ．【点睛】本题考查了相似三角形的判定．注意掌握数形结合思想的应用，注意平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似．5．如图，ABC ∆中，8AB =，6AC =，90A ∠=︒，点D 在ABC ∆内，且DB 平分ABC ∠，DC 平分ACB ∠，过点D 作直线PQ ，分别交AB 、AC 于点P 、Q ，若APQ ∆与ABC ∆相似，则线段PQ 的长为（ ）A ．5B ．356C ．5或356D ．6【答案】B 【分析】分∥APQ∥∥ABC ，∥APQ∥∥ACB 两种情况，结合相似三角形的性质和三角形内切圆求解即可.【详解】解：若∥APQ∥∥ABC ，∥∥APQ=∥ABC ，∥PQ∥BC ，AP AQ PQ AB AC BC==， ∥∥PDB=∥DBC ，∥BD 平分∥ABC ，∥∥PBD=∥CBD ，∥∥PBD =∥PDB ，∥PB=PD ，同理，DQ=CQ ，∥8AB =，6AC =，90A ∠=︒，，设AP=x ，根据AP AQ AB AC=得43AP AB AQ AC ==, ∥AQ=34x ， ∥PB=PD=8-x ，CQ=DQ=6-34x ，∥PQ=PD+QD=7144x-，∥AP PQAB BC，即7144810xx-=，解得：x=143，∥PQ=356；若∥APQ∥∥ACB，则AP AQ PQ AC AB BC==，由题意知：D为∥ABC的内心，设∥ABC的内切圆交AB于M，交AC于N，可知四边形AMDN为正方形，∥∥A=∥AMD=∥AND=∥MDN=90°，∥AM∥DN，AN∥DM，∥∥MPD=∥NDQ，∥MDP=∥NQD，∥∥MPD∥∥NDQ，∥MP MD ND NQ=，∥AB=8，AC=6，BC=10，∥DM=DN=68102+-=2，∥AM=AN=2，设PM=x，则22xNQ =，∥NQ=4x，∥AP AQAC AB=，即42268x x++=，解得：x=32或-2（舍），∥AP=32+2=72， ∥PQ=AP×BC÷AC=72×10÷6=356.综上：PQ 的值为356. 故选B.【点睛】本题考查了相似三角形的判定和性质，三角形内切圆，角平分线的定义，有一定难度，解题的关键是将三角形相似分两种情况讨论.6．如图，在Rt ABC ∆中，90ACB ∠=︒，取AC 的中点D ，连接BD ，点C 关于线段BD 的对称点为点E ，点F 为线段CD 上的一个动点，连接AE 、BD 、BE 、DE ，已知AC =2BC =，103AE =，//BD AE ，当EF BF +的值最小时，则EF BF的值为（ ）A B C ．109 D ．32【答案】C【分析】设点M 和点B 关于AC 对称，F 为EM 与AC 交点，过点E 作EG∥AC 于G ，过点E 作EN∥BC ，交BC 延长线于点N ，根据题意得出当EF+BF 最小时点F 的位置，再通过平行线的性质得到∥EAG=∥BDC ，从而求出EG 的长，再判定四边形EGCN 为矩形，得到CN ，最后利用∥MFC∥MEN 将EF BF 转化为NC CM求值即可. 【详解】解：当EF+BF 最小时，如图，点M 和点B 关于AC 对称，F 为EM 与AC 交点，过点E 作EG∥AC 于G ，过点E 作EN∥BC ，交BC 延长线于点N ，此时EF+BF 的最小值即为EF+FM ，即EM ，∥AC=D 为AC 中点，BC=2，∥tan∥BDC=BC DC =， ∥AE∥BD ，∥∥EAG=∥BDC ，∥tan∥EAG=EG AG EG=x ，x ，而AE=103，在∥AEG 中，222103x x ⎫⎛⎫+=⎪ ⎪⎪⎝⎭⎝⎭， 解之得：x=209或209-（舍）， 由题意可得：∥N=∥ACB=∥EGC=90°，∥四边形EGCN 为矩形， ∥EG=NC=209， ∥AC∥BC ，EN∥BC ，∥AC∥EN ，∥∥MFC∥MEN ， ∥MC MF CN EF =，则2010299EF EF NC BF FM CM ===÷=， 故选C.【点睛】本题考查了平行线的性质，解直角三角形，相似三角形的判定和性质，最短路径问题，矩形的判定和性质，解题的关键是根据平行利用三角函数得到FG 的长.二、填空题7．如图，光源P 在水平横杆AB 的上方，照射横杆AB 得到它在平地上的影子为CD （点P 、A 、C 在一条直线上，点P 、B 、D 在一条直线上），不难发现//AB CD ．已知 1.5AB m =，4.5CD m =，点P 到横杆AB 的距离是1m ，则点P 到地面的距离等于______m ．【答案】3【分析】易得∥P AB ∥∥PCD ，利用相似三角形对应边的比等于对应高的比可得AB 与CD 间的距离．【详解】解：如图，作PF ∥CD 于点F ，∥AB ∥CD ，∥∥P AB ∥∥PCD ，PE ∥AB ，∥∥P AB ∥∥PCD ， ∥AB PE CD PF=， 即：1.514.5PF =， 解得：PF =3．故答案为：3．【点睛】考查相似三角形的应用；用到的知识点为：相似三角形对应边的比等于对应高的比． 8．如图，矩形 ABCD 中，2AD =，4AB =，AC 为对角线，E 、F 分别为边 AB 、CD 上的动点，且 EF AC ⊥ 于点 M ，连接 AF 、CE ，求AF CE +的最小值是_____．【答案】5【分析】AF 与EC 两条线段不在同一条直线上，只需将两条线段转换在同一条直线上即可，作//CG EF ，且CG EF =，连接AG ，又因点F 是DC 上是一动点，由三角形的边与边关系AF FG AG +≥，只有当点F 在直线AG 上时，AF FG +最小，由平行四边形CEFG 可知FG EC =时，可求AF CE +的最小值【详解】解：如图所示：过点C 作//CG EF ，且CG EF =，连接FG ，设DF x =，则4FC x =-,当点A 、F 、G 三点共线时，AF FG +的最值小，∥//CG EF ，且CG EF =，∥四边形CEFG 是平行四边形；∥//EC FG ，EC FG =，又∥点A 、F 、G 三点共线，∥//AF EC ，又∥四边形ABCD 是矩形，∥//AE DC ，90D ∠=︒，∥四边形AECF 是平行四边形，又∥EF AC ⊥，∥四边形AECF 是菱形，∥4AF FC x ==-，在Rt ADF 中，由勾股定理得：222AD DF AF +=，又∥2AD =，DF x =，则4AF x =-，∥2222(4)x x +=-， 解得：32x =， ∥52AF =， 在Rt ADC 中，由勾股定理得，2222224AC AD DC =+=+，所以AC =∥AM =又∥//MF CG ，∥AMF ACG ∠=∠，AFM AGC ∠=∠，∥A AMF CG ∽， ∥AM AF AC AG=，52AG=，∥5AG =，又∥AG AF FG =+，FG EC =，∥5AF EC +=，即最小值是5，故答案为：5．【点睛】本题考查了矩形的性质，平行四边形的判定与性质，三角形相似的判定与性质，勾股定理和最短距离问题等知识点，解题的关键是掌握辅助线的作法以及相似三角形的性质与判定．9．如图，正方形ABCD 边长为3，点E 是AD 上一点，且1AE =，连接BE ，过C 作CF BE ⊥，垂足为F ，CF 交对角线BD 于G ，将BCG 沿CG 翻折得到HCG △，CH 交对角线BD 于M ，则HGM S =______．【答案】928【分析】过点G 作GR ∥BC 于R ，过点H 作HN ∥BC 交BD 于N ，由正方形性质可证明：∥ABE ∥∥FCB ，由勾股定理可求BF ，由翻折性质可得∥HGC ∥∥BGC ，进而可证明：∥BHN ∥∥BED ，可求得HN ，再由∥HNM ∥∥CBM ，可求得HGM HGC S S ，再由∥CGR ∥∥CBF 即可求得结论． 【详解】解：如图，过点G 作GR BC ⊥于R ，过点H 作HN BC ∥交BD 于N则90BRG CRG ∠=∠=︒，∥CF BE ⊥90BFC ∴∠=︒90CBF BCF ∴∠+∠=︒正方形ABCD90A ABC ∴∠=∠=︒，3AB AD BC ===90ABE CBF ∴∠+∠=︒ABE BCF ∴∠=∠ABE ∴∥FCB在Rt ABE 中，BE ==BF AE BC BE ∴=，即3BF =BF ∴=由翻折知：FH BF =BH =3HC BC ==，HGC ∥BGC //HN BC BHN ∴∥BEDHN BH DE BE ∴=，即2HN = 65HN ∴= HNM ∥CBM 25HM HN MC BC ∴== 27HM HC ∴=， 27HGM HGC SHMS HC ∴==，GR BC ⊥，45CBG ∠=︒BGR ∴是等腰直角三角形，设BR GR x ==，则3CR x =-， CGR ∥CBF13GR BF CR CF ∴==，即133x x =-，解得34x = 34GR ∴= 113932248BCG S BC GR ∴=⨯⨯=⨯⨯= 98HGC S ∴= 229977828HGM HGC S S ∴==⨯=， 故答案为：928． 【点睛】本题考查了正方形性质，翻折变换的性质，等腰直角三角形性质，勾股定理，全等三角形判定和性质，相似三角形判定和性质，三角形面积等知识点；解题关键是利用平行线证明相似三角形进行转化，有一定难度，属于中考填空压轴题类型．10．如图，在三角形ABC 中，点D 为边BC 的中点，连接AD ，将三角形ABD 沿直线AD 翻折至三角形ABC 平面内，使得B 点与E 点重合，连接CE 、BE ，分别与边AC 交于点H ，与AD 交于点O ，若AH CH =，AB =4OB =，则点A 到线段BC 的距离为__________．【答案】365【分析】如图，过点A 作AT CB ⊥交CB 的延长线于T ．利用勾股定理求出AO ，利用三角形重心的性质求出OD ，再利用勾股定理求出BD ，利用相似三角形的性质求出AT 即可．【详解】解：如图，过点A 作AT CB ⊥交CB 的延长线于T ．由翻折的性质可知，AD 垂直平分线段BE ，90AOB ∠=︒∴，∥AB =4OB =，∥6OA ，∥AH CH =，点D 为边BC 的中点，∴点O 是ABC 的重心，2OA OD ∴=，3OD ∴=，5BD ∴=，BDO ADT ∠=∠，90BOD T ∠=∠=︒，DOB DTA ∴△∽△， ∴OB DB AT AD =， ∴459AT =， 365AT ∴=， 故答案为：365． 【点睛】本题考查翻折变换，勾股定理的应用，相似三角形的判定和性质以及重心的性质等知识，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．11．如图，在矩形ABCD 中，AB =2，BC =3，点E 是边AB 的中点，连接CE ，将∥BCE 沿CE 折叠得到∥FCE ，CF 与BD 交于点P ，则DP 的长为 ___．【分析】由勾股定理可求出BD 、EC 的长，连接BF 交CE 于点G ，作FH ∥BC 于点H ，PQ ∥BC 于点Q ，根据相似三角形的性质求出BG 的长，再根据面积等式列方程求出FH 的长，再根据相似三角形的性质求出BQ 与CQ 的比，进而求出DP 的长．【详解】解：如图，连接BF 交CE 于点G ，作FH ∥BC 于点H ，PQ ∥BC 于点Q ，∥四边形ABCD 是矩形，∥AB =DC =2，∥ABC =∥BCD =90°，∥BC =3，∥.BD =∥AE =BE =12AB =12×2=1，∥EC =由折叠得，CE 垂直平分BF ，∥∥BGC =∥EBC =90°，∥∥GCB =∥BCE ，∥∥BGC ∥∥EBC ， ∥GB BC BE EC=，∥BC BE GB EC ⋅===∥22BF GB ===CG ==由12BC •FH =12BF •CG 得，12×3FH =12 解得，FH =95； ∥∥CHF =90°，FC =BC =3，∥125CH==；∥PQ∥FH，∥∥CPQ∥∥CFH，∥CQ PQCH FH=，∥1245935CQ CHPQ FH===，∥CQ=43PQ，∥∥BQP=∥BCD=90°，∥PQ∥DC，∥∥BPQ∥∥BDC，∥BQ PQBC DC=，∥32BQ BCPQ DC==，∥BQ=32PQ，∥392483PQBP BQDP CQ PQ===，∥881717DP BD==，．【点睛】本题重点考查矩形的性质、轴对称的性质、相似三角形的判定与性质、勾股定理、二次根式的化简以及用面积等式列方程等知识与方法，解题的关键是正确地作出所需要的辅助线，此题难度较大，计算烦琐，应注意检验所求的结果是否正确．三、解答题12．如图，∥ABD中，∥A＝90°，AB＝6cm，AD＝12cm．某一时刻，动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动；同时，动点N从点D出发沿DA方向以2cm/s的速度向点A匀速运动，运动的时间为ts．（1）求t为何值时，∥AMN的面积是∥ABD面积的29；（2）当以点A ，M ，N 为顶点的三角形与∥ABD 相似时，求t 值．【答案】（1）14t =，22t =；（2）t ＝3或245【分析】（1）由题意得DN ＝2t （cm ），AN ＝（12﹣2t ）cm ，AM ＝t cm ，根据三角形的面积公式列出方程可求出答案；（2）分两种情况，由相似三角形的判定列出方程可求出t 的值．【详解】解：（1）由题意得DN ＝2t （cm ），AN ＝（12﹣2t ）cm ，AM ＝t cm ，∥∥AMN 的面积＝12AN •AM ＝12×（12﹣2t ）×t ＝6t ﹣t 2， ∥∥A ＝90°，AB ＝6cm ，AD ＝12cm∥∥ABD 的面积为12AB •AD ＝12×6×12＝36， ∥∥AMN 的面积是∥ABD 面积的29， ∥6t ﹣t 2＝2369⨯， ∥t 2﹣6t +8＝0，解得t 1＝4，t 2＝2，答：经过4秒或2秒，∥AMN 的面积是∥ABD 面积的29； （2）由题意得DN ＝2t （cm ），AN ＝（12﹣2t ）cm ，AM ＝t cm ，若∥AMN ∥∥ABD ， 则有AM AN AB AD =，即122612t t -=， 解得t ＝3，若∥AMN ∥∥ADB ， 则有AM AN AD AB=，即122126t t -=， 解得t ＝245， 答：当t ＝3或245时，以A 、M 、N 为顶点的三角形与∥ABD 相似． 【点睛】本题考查了相似三角形的判定，直角三角形的性质和一元二次方程的应用，正确进行分类讨论是解题的关键．13．在ABC 中，()0AB m m =>，D 为AB 上一点，过D 作DE ∥BC 交AC 于点E ，连接CD ．设21,DCE ABC S S S S ==，求21S S 的取值范围． 【答案】21104S S <≤ 【分析】作AG ∥BC 于F 点，交DE 于G 点，设AD =x ，首先结合相似三角形的判定与性质推出DE BC 和GF AF的值，然后结合面积公式进行列式，得出二次函数解析式，最后结合二次函数的性质以及自变量的取值范围进行判断即可．【详解】解：如图所示，作AG ∥BC 于F 点，交DE 于G 点，设AD =x ，∥DE ∥BC ，∥∥ADE ∥∥ABC ， ∥DE AD AG AE x BC AB AF AC m ====， ∥GF m x AF m-=， ∥()2211212DE GF x m x S DE GF x m x S BC AF m m m BC AF --==⨯=⨯=， 整理得：22222111124S x m x x S m m m ⎛⎫=-+=--+ ⎪⎝⎭， ∥点D 在AB 上，0m >，∥0x m <<，210m -<， ∥抛物线21S S 的开口向下，且当2m x =时，21S S 取得最大值为14， 当0x =和x m =时，均有210S S =，综上分析，21S S 的取值范围是21104S S <≤．【点睛】本题考查相似三角形的判定与性质，二次函数的性质运用等，掌握相似三角形的判定与性质推出相关线段的比例，以及熟练运用二次函数的性质分析是解题关键． 14．Rt ABC 中，90C ∠=︒，20cm AC =，15cm BC =，现有动点P 从点A 出发，沿AC 向点C 方向运动，动点Q 从点C 出发，沿线段CB 也向点B 方向运动，如果点P 的速度是4cm/s ，点Q 的速度是2cm/s ，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动时间为t 秒．（1）求运动时间为多少秒时，P 、Q 两点之间的距离为10cm?（2）若CPQ 的面积为S ，求S 关于t 的函数关系式．（3）当t 为多少时，以点C ，P ，Q 为顶点的三角形与ABC 相似?【答案】（1）3秒或5秒；（2）()22204cm S t t =-；（3）3t =或4011t = 【分析】（1）根据题意得到AP =4t cm ，CQ =2t cm ，AC =20cm ，CP =（20-4t ）cm ，根据三角形的面积公式列方程即可得答案；（2）若运动的时间为t s ，则CP =（20-4t ）cm ，CQ =2t cm ，利用三角形的面积计算公式，即可得出S =20t -4t 2，再结合各线段长度非负，即可得出t 的取值范围；（3）分∥Rt CPQ Rt CAB ∽△△和∥Rt CPQ Rt CBA ∽△△，利用相似三角形得出比例式，建立方程求解，即可得出结论．【详解】（1）解：由运动知，AP =4tcm ，CQ =2t cm ，∥AC =20cm ，∥CP =（20-4t ）cm ，在Rt ∥CPQ 中，222CP CQ PQ +=，即()()222204210t t -+=；∥3t =秒或5t =秒（2）由题意得4AP t =，2CQ t =，则204CP t =-，因此Rt CPQ 的面积为()()2212042204cm 2S t t t t =⨯-⨯=-； （3）分两种情况：∥当Rt CPQ Rt CAB ∽△△时，CP CQ CA CB =，即20422015t t -=，解得3t =； ∥当Rt CPQ Rt CBA ∽△△时，CP CQ CB CA =，即20421520t t -=，解得4011t =． 因此3t =或4011t =时，以点C 、P 、Q 为顶点的三角形与ABC 相似． 【点睛】本题考查了勾股定理，相似三角形的性质，用方程的思想解决问题是解本题的关键． 15．如图，在∥ABC 中，点D 在边AB 上，点E 、点F 在边AC 上，且DE ∥BC ，AF AE FE EC=． （1）求证：DF ∥BE ；（2）如且AF ＝2，EF ＝4，AB ＝∥ADE ∥∥AEB ．【答案】（1）见详解；（2）见详解【分析】（1）由题意易得AD AE BD EC =，则有AF AD FE BD =，进而问题可求证；（2）由（1）及题意可知12AD AF BD EF ==，然后可得AD =AE AD AB AE ==后问题可求证．【详解】解：（1）∥DE ∥BC ， ∥AD AE BD EC =， ∥AF AE FE EC =， ∥AF AD FE BD =， ∥DF ∥BE ；（2）∥AF ＝2，EF ＝4，∥由（1）可知，12AD AF BD EF ==，AE =6， ∥AB ＝∥13AD AB ==∥AE AD AB AE ==，∥AE AD AB AE == ∥∥A =∥A ，∥∥ADE ∥∥AEB ．【点睛】本题主要考查相似三角形的判定，熟练掌握相似三角形的判定方法是解题的关键．16．矩形ABCD 中，AB ＝CD ＝3cm ，AD ＝BC ＝4cm ，AC 是对角线，动点P 从点A 出发沿AC 方向向点C 匀速运动，速度为1cm/s ；动点Q 从点C 出发沿CD 方向向点D 匀速运动，速度为2cm/s ．过点P 作BC 的垂线段PH ，运动过程中始终保持PH 与BC 互相垂直，连接HQ 交AC 于点O ．若点P 和点Q 同时出发，设运动的时间为t （s ）（0＜t ＜1.5），解答下列问题：（1）求当t 为何值时，四边形PHCQ 为矩形；（2）是否存在一个时刻，使HQ 与AC 互相垂直？如果存在请求出t 值；如果不存在请说明理由；（3）是否存在一个时刻，使矩形ABCD 的面积是四边形PHCQ 面积的7544，如果存在请求出t 值；如果不存在请说明理由．【答案】（1）1513t =；（2）存在，4023t =；（3）存在，1t = 【分析】（1）当四边形PHCQ 为矩形时，PH CQ =，利用相似三角形的性质求出PH ，CH ，构建方程求解即可；（2）证明HCQ ABC ，由相似的性质得出，CH CQAB BC=，由此构建方程求解即可； （3）根据矩形ABCD 的面积是四边形PHCQ 面积的7544，构建方程求解即可． 【详解】解：（1）3AB =，4BC =，5AC ∴，由题可得：AP t =，5CP t =-，2CQ t =， 四边形ABCD 是矩形，90B ∴∠=︒，PH BC ⊥，90CHP B ∴∠=∠=︒， PCH ACB ∠=∠， PCHACB ∴，PH CH PC AB CB AC ∴==，即5345PH CH t-==， 3(5)5PH t ∴=-，4(5)5CH t =-，当四边形PHCQ 为矩形时，PH CQ =，3(5)25t t ∴-=， 解得：1513t =， ∴当1513t =时，四边形PHCQ 为矩形； （2）存在一个时刻，使HQ AC ⊥， 当HQ AC ⊥时，90QHC ACB ∠+∠=︒，90BAC ACB ∠+∠=︒，QHC BAC ∴∠=∠，90HCQ B ∠=∠=︒，HCQ ABC ∴，CH CQAB BC∴=，即CH BC AB CQ ⋅=⋅， 4(5)4325t t ∴-⨯=⨯， 解得：4023t =，∴当4023t =时，HQ AC ⊥； （3）存在， 由题意得：7513434[2(5)](5)44255t t t ⨯=⨯⨯+-⨯-， 解得：1t =或137t =（舍去）， ∴当1t =时，矩形ABCD 的面积是四边形PHCQ 面积的7544． 【点睛】本题属于四边形综合问题，考查了矩形的性质，相似三角形的判定与性质，掌握相关的知识点是解决本题的关键．17．图，AB GH CD ∥∥，点H 在BC 上，AC 与BD 交于点G ，AB ＝2，CD ＝3，求GH 的长．【答案】65【分析】根据平行线分线段成比例定理，由AB GH ∥，可证∥CGH ∥∥CAB ，由性质得出GH CH AB BC =，由GH CD ∥，可证∥BGH ∥∥BDC ，由性质得出GH BHCD BC=，将两个式子相加，即可求出GH 的长． 【详解】解：∥AB CH ∥， ∥∥A =∥HGC ，∥ABC =∥GHC ， ∥∥CGH ∥∥CAB ， ∥GH CHAB BC=， ∥GH CD ∥，∥∥D =∥HGB ，∥DCB =∥GHB ， ∥BGH ∥∥BDC ， ∥GH BHCD BC=， ∥1GH GH CH BHAB CD BC BC+=+=， ∥AB =2，CD =3，∥123GH GH+=， 解得：GH =65．【点睛】本题考查了相似三角形的判定和性质，平行线性质，熟练掌握相似三角形的判定和性质是解题的关键．18．一块直角三角形木板的面积为21.5m ，一条直角边AB 为1.5m ，怎样才能把它加工成一个面积最大的正方形桌面？甲、乙两位木匠的加工方法如图所示，请你用学过的知识说明哪位木匠的方法符合要求（加工损耗忽略不计，计算结果中的分数可保留）．【答案】乙木匠的加工方法符合要求．说明见解析．【分析】要求哪位木匠的加工方法符合要求，需要先求出两种加工方式中正方形的边长，边长最大就符合要求；由已知三角形的面积和一条直角边的边长可求出其余两边的边长，根据乙加工方案中的平行关系得到相似三角形，根据相似三角形对应变成比例，可求出正方形的边长；根据甲加工方案中，根据相似三角形的高的比等于边长比，可求出正方形的边长，对比两方案的边长即可知谁符合要求．【详解】解：作BH ∥AC 于H ，交DE 于M ，如图∥1=2ABC S AB BC ⋅△∥2 1.521.5BC ⨯==∥52AC =∥1=2ABC S AC BH ⋅△∥65 BH=又∥DE∥AC∥DE BM AC BH=∥655625xx-=，解得3037x=设正方形的边长为x米，如图乙∥DE∥AB∥DE CD AB CB∥21.52x x-=，解得67x=∥630 737 >∥乙木匠的加工方法符合要求．【点睛】本题考查了相似三角形的判定与性质的实际应用及分析、解决问题的能力，正确理解题意，建立数学模型，把实际问题转化为数学问题是解决本题的关键．19．如图，已知D是BC的中点，M是AD的中点．求:AN NC的值．【答案】12【分析】解法1：过点D作AC的平行线交BN于点H，构造“A”型和“8”型，得出BDH BCN∽和DHM ANM∽，再结合相似三角形的性质和中点的定义即可得出答案；解法2：过点C作AD的平行线交BN的延长线于点H，构造“A”型和“8”型，得出BDM BCH△∽和AMN CHN△∽△，再结合相似三角形的性质和中点的定义即可得出答案；解法3：过点A作BC的平行线交BN的延长线于点H，构造“A”型和“8”型，得出AHM DBM△∽△和AHN CBN△∽△，再结合相似三角形的性质和中点的定义即可得出答案；解法4：过点D作BN的平行线交AC于点H，根据三角形中位线定理得出AN NH CH==，即可得出答案；【详解】解法1：如图2，过点D 作AC 的平行线交BN 于点H ．因为//DH AC ． 所以BDH BCN ∽， 所以DH BDCN BC=． 因为D 为BC 的中点，所以12DH BD CN BC ==． 因为//DH AN ，所以DHM ANM ∽， 所以DH DMAN AM=． 因为M 为AD 的中点，所以1DH DMAN AM==． 所以DH AN =， 所以12AN CN =． 解法2：如图3，过点C 作AD 的平行线交BN 的延长线于点H ．因为//DM CH ，所以BDM BCH △∽， 所以DM BDCH BC=． 因为D 为BC 的中点，所以12DM BD CH BC ==．因为M 为AD 的中点，所以AM DM =， 所以12AM CH =． 因为//DM CH ， 所以AMN CHN △∽△， 所以12AN AM CN CH ==． 解法3：如图4，过点A 作BC 的平行线交BN 的延长线于点H ．因为//AH BD ，所以AHM DBM △∽△， 所以AH AMBD DM=． 因为M 为AD 的中点，所以AM DM =，所以AH BD =． 因为//AH BD ，所以AHN CBN △∽△， 所以AN AHCN BC=． 因为D 为BC 的中点，且AH BD =， 所以12AN BD CN BC ==． 解法4：如图5，过点D 作BN 的平行线交AC 于点H ．在ADH 中，因为M 为AD 的中点，//MN DH ，所以N 为AH 的中点，即AN NH =．在CBN △中，因为D 为BC 的中点，//DH BN ，所以H 为CN 的中点，即CN HN =， 所以AN NH CH ==． 所以12AN CN =． 20．如图， ABC 中，中线AD ，BE 交于点F ，//EG BC 交AD 于点G ．（1）求AGGF的值．（2）如果BD =4DF =，请找出与BDA △相似的三角形，并挑出一个进行证明．【答案】（1）3；（2）BDA FGE ∽△△，证明见解析 【分析】（1）先证明AGE ADC △∽△，再证明GEF DBF ∽△△，得到2DF GF =，则问题可解； （2）根据题意分别证明BDA FDB ∽△△，BDA FGE ∽△△问题可证． 【详解】解：（1）D 是BC 的中点，E 是AC 的中点， BD CD ∴=，AE CE =，//GE BC ， AGE ADC ∴∽△△，12AG GE AE AD CD AC ∴===， AG GD ∴=，2GE CD BD ==， //GE BC ， GEF DBF ∴∽△△，12GE GF BD DF ∴==， 2DF GF ∴=， 3AG DG GF ∴==，3AGGF∴=．（2）当BD =4DF =时， 由（1）可得 122GF DF ==，36AG DG GF ===，212AD AG ==，12GE BD == 44BD DF ==AD BD == AD BDBD DF∴=， 又BDG ADB ∠=∠，BDA FDB ∴∽△△，3GEGF =AD BD == AD GEBD GF∴=， //GE BC ， ADB EGF ∴∠=∠， BDA FGE ∴∽△△．【点睛】本题考查了相似三角形的性质和判定，解答关键是根据题意选择适当方法证明三角形相似．21．如图，在ABC ∆中，点,E F 分别在,AB AC 上，且AE ABAF AC=．（1）求证：AEFABC ∆∆；（2）若点D 在BC 上，AD 与EF 交于点G ，求证：EG FGBD CD=． 【答案】（1）见解析；（2）见解析【分析】（1）直接利用两边成比例且夹角相等的两个三角形相似即可证得结论； （2）根据相似三角形的性质和平行线的判定方法可得EF ∥BC ，于是可得∥AEG ∥∥ABD ，∥AGF ∥∥ADC ，再根据相似三角形的性质即可推出结论． 【详解】解：（1）在∥AEF 和∥ABC 中， ∥EAF BAC ∠=∠，AE ABAF AC=， ∥∥AEF ∥∥ABC ；（2）∥∥AEF∥∥ABC，∥∥AEF=∥ABC，∥EF∥BC，∥∥AEG∥∥ABD，∥AGF∥∥ADC，∥EG AGBD AD=,FG AGCD AD=，∥EG FG BD CD=．【点睛】本题考查了相似三角形的判定和性质，属于常考题型，熟练掌握相似三角形的判定和性质是解题关键．22．如图，在平行四边形ABCD中，AD＝AC，∥ADC＝α，点E为射线BA上一动点，且AE＜AB，连接DE，将线段DE所在直线绕点D顺时针旋转α交BA延长线于点H，DE所在直线与射线CA交于点G．（1）如图1，当α＝60°时，求证：∥ADH∥∥CDG；（2）当α≠60°时，∥如图2，连接HG，求证：∥ADC∥∥HDG；∥若AB＝9，BC＝12，AE＝3，请直接写出EG的长．【答案】（1）证明见详解；（2）∥证明见详解；∥EG．【分析】（1）AD＝AC，∥ADC＝60°，可证∥ACD为等边三角形，根据四边形ABCD为平行四边形，可得AB=CD=BC=AD，∥B=∥ADC=60°，AD∥BC，可得∥HAD=∥B=60°=∥GCD，由∥GDH=∥CDA=60°，可证∥HAD =∥CDG，即可证∥ADH∥∥CDG（ASA）；（2）∥根据AD＝AC，∥ADC＝α，可得∥ACD=∥ADC＝α，根据四边形ABCD为平行四边形，可得AD∥BC，可得∥HAD=∥ADC=α=∥GCD，由∥GDH=α=∥ADC，可得∥ADH =∥CDG 即可；∥根据点E的位置分两种情况，当点E在AB上时，过C作CN∥AB于N，过G作GM∥AE于M，根据四边形ABCD为平行四边形，AB∥DC，AB=DC=9，AD=BC=12，可证∥AGE∥∥CGD，得出AG=3，CG=AC-AG=12-3=9，根据等腰三角形三线合一性质可得AN=BN=1922AB=，根据勾股定理CN==GM∥CN，再证∥AMG∥∥ANC，可求1948AM AN==,14GM CN==EM=AE-AM=915388-=，根据勾股定理EG==，当点E在BA延长线上，过C作CN∥AB于N，过G作GM∥AE于M，由AE∥CD，∥GAE∥∥GCD，可求GA=6，由GM∥CN，可证∥GMA∥∥CNA，可得1122GM CN===，11992224AM AN==⨯=，EM=AE-AM=3-9344=，根据勾股定理EG=．【详解】（1）证明：∥AD＝AC，∥ADC＝60°，∥∥ACD为等边三角形，∥四边形ABCD为平行四边形，∥AB=CD=BC=AD，∥B=∥ADC=60°，AD∥BC，∥∥HAD=∥B=60°=∥GCD，∥∥GDH=∥CDA=60°，∥∥HDA+∥ADG=∥CDG+∥ADG=60°，∥∥HDA =∥CDG，在∥ADH和∥CDG中ADH CDGAD CDHAD GCD∠=∠⎧⎪=⎨⎪∠=∠⎩∥ADH∥∥CDG（ASA）；（2）∥证明：∥AD＝AC，∥ADC＝α，∥∥ACD=∥ADC＝α，∥四边形ABCD为平行四边形，∥AD∥BC，∥∥HAD=∥ADC=α=∥GCD，∥∥GDH=α=∥ADC，∥∥ADH+∥ADG=∥CDG+∥ADG=α，∥∥ADH =∥CDG，∥∥ADH∥∥CDG；∥解：当点E在AB上时，过C作CN∥AB于N，过G作GM∥AE于M，∥四边形ABCD为平行四边形，AB∥DC，AB=DC=9，AD=BC=12，∥∥EAG=∥DCG，∥AEG=∥CDG，∥∥AGE∥∥CGD，∥3193 AG AECG CD===，∥3CG AG=，∥AD=AC=12，∥AG+CG=AG+3AG=4AG=12，∥AG=3，∥CG=AC-AG=12-3=9，∥AC=AD=BC，CN∥AB，∥AN=BN=19 22 AB=，在Rt∥BCN中，根据勾股定理CN=∥GM∥CN，∥∥AMG∥∥ANC，∥31124 AM AG GMAN AC CN====，∥1948AM AN==,14GM CN==∥EM=AE-AM=915388-=，在Rt∥MGE中，根据勾股定理EG==，当点E在BA延长线上，过C作CN∥AB于N，过G作GM∥AE于M，∥AE∥CD，∥∥GAE=∥GCD，∥GEA=∥GDC，∥∥GAE∥∥GCD，∥3193 GA EAGC DC===，∥3GC GA=，∥AC=GC-GA=3GA-GA=2GA=12,∥GA=6，∥AC=AD=BC，CN∥AB，∥AN=BN=19 22 AB=，在Rt∥BCN 中，根据勾股定理CN =∥CN ∥AB ， GM ∥AE ， ∥GM∥CN ， ∥∥GMA ∥∥CNA ， ∥61122GA GM AM CA CN AN ====，∥1122GM CN ===11992224AM AN ==⨯=， ∥EM =AE -AM =3-9344=，在Rt∥GME 中，根据勾股定理EG∥综合EG ． 【点睛】本题考查图形旋转性质，平行四边形性质，等边三角形判定与性质，三角形全等判定，三角形相似判定与性质，勾股定理，本题难度角度，利用辅助线画出准确图形，掌握以上知识是解题关键．23．已知：矩形ABCD 中，AB ＝9，AD ＝6，点E 在对角线AC 上，且满足AE ＝2EC ，点F 在线段CD 上，作直线FE ，交线段AB 于点M ，交直线BC 于点N ． （1）当CF ＝2时，求线段BN 的长；（2）若设CF ＝x ，∥BNE 的面积为y ，求y 关于x 的函数解析式，并写出自变量的取值范围； （3）试判断∥BME 能不能成为等腰三角形，若能，请直接写出x 的值．【答案】（1）BN＝10；（2）6273xyx-=-，0＜x＜3；2763xyx-=-，3＜x＜4.5；（3）x＝2或32或29 12【分析】（1）由AB CD∥得∥CFE∥∥AME，∥NCF∥∥NBM，进而求得；（2）分为0＜x＜3和3＜x＜4.5两种情形，作EG∥BC于G，根据三角形相似求出EG和BN；（3）分为BM＝BE，EM＝BE，EN＝BM三种，可根据BM＝9﹣2CF求得．【详解】解：（1）如图1，在矩形ABCD中，BC＝AD＝6，AB CD∥，∥∥CFE∥∥AME，∥NCF∥∥NBM，∥1,2CF EC CF NC AM AE BM NB ===,∥AM＝2CF＝4，∥BM＝AB﹣AM＝5，∥265BNBN-=，∥BN＝10；（2）当CF＝BM时，MF BC∥，此时∥BEN不存在，∥CF＝9﹣2CF，∥CF＝3，当点M和B点重合时，AB＝2CF，∥CF＝4.5，∥分为0＜x＜3和3＜x＜4.5，如图2，当0＜x＜3时，作EG∥BC于G，由（1）知，EG＝3，AM＝2CF＝2x，∥BM＝9﹣2x，由CF NCBM NB=得，692x BNx BN-=-，∥1843x BNx-=-，∥y＝12BN EG⋅＝11843 23xx-⋅⨯-＝6273xx--；如图3，当3＜x ＜4.5时， 由BN BMCN CF=得， 926BN xBN x-=+∥CN ＝2(92)3x x --， ∥y ＝12(92)323x x -⋅⨯- ＝2763xx --； （3）如图4，∥EG AB ∥， ∥13CG EG CB AB ==， ∥CG ＝13CB ＝2，∥GB ＝CB ﹣CG ＝4， ∥BE ＝5，当BM ＝BE ＝5时， 9﹣2x ＝5， ∥x ＝2， 如图5，当EM ＝EB ＝5时， 作EH ∥AB 于H ， ∥BM ＝2BH ＝2EG ＝6， ∥9﹣2x ＝6， ∥x =32，如图6，当EM ＝BM 时， 作MH ∥BE 于H ，在Rt ∥BMH 中，BH ＝1522BE =，∥MBH ＝cos ∥BEG ＝35EG BE =， ∥BM ＝355252cos 6BH MBH ==∠，∥9﹣2x ＝256， ∥x ＝2912， 综上所述：x ＝2或32或2912．【点睛】此题考查相似三角形的判定及性质，锐角三角函数，勾股定理解直角三角形，矩形的性质，正确引出辅助线及掌握分类思想解决问题是解题的关键．24．如图，在平行四边形ABCD 中，90ADB ∠=︒，10cm AB =，8cm AD =，点P 从点D 出发，沿DA 方向匀速运动，速度为2cm/s ；同时，点Q 从点B 出发，沿BC 方向匀速运动，速度为1cm/s .当一个点停止运动，另一个点也停止运动.过点P 作//PE BD 交AB 于点E，连接PQ ，交BD 于点F .设运动时间为()()s 04t t <<.解答下列问题：（1）当t 为___________时，//PQ AB ？（2）连接EQ ，设四边形APQE 的面积为()2cm y ，求y 与t 的函数关系式.（3）当t 为何值时，点E 在线段PQ 的垂直平分线上？（4）若点F 关于AB 的对称点为F'，是否存在某一时刻t ，使得点P ，E ，F'三点共线？若存在，求出t 的值；若不存在，请说明理由.【答案】（1）83；（2）233244y t t =--+；（31；（4）2425．【分析】（1）由题意得，PQ ∥AB ，则四边形P ABQ 是平行四边形，根据平行四边形的性质可得AP =BQ ，即8-2t =t ，解方程即可求解；（2）过点Q 作QH ∥AB 交AB 的延长线于点H ，由勾股定理求出BD =6，证明∥ADB ∥∥BHQ ，根据相似三角形的性质可得QH =35t ，根据平行线分线段成比例定理可得DP BEAD AB =，可得出BE =52t ，根据y =S 四边形APQB -S ∥BEQ 即可求解；（3）先证出∥APE ∥∥ABD ，根据相似三角形的性质可得PE AP DB AD=，可得PE =6-32t ，根据线段垂直平分线的性质得EQ =PE ，由（2）得QH =35t ，可得出BH =45t ，根据勾股定理得出EH 2+HQ 2=EQ 2，列出方程即可求解；（4）连接FF ′交AB 于点N ，由对称及平行线的性质可得∥FEB =∥ABD ，由等角对等边得EF =FB ，则1524BN EN BE t ===，再证∥DPF ∥∥BQF ，可得DF =2BF ，可求出BF =2，然后证明∥BNF ∥∥BDA ，根据相似三角形的性质即可得t 的值． 【详解】解：（1）∥四边形ABCD 是平行四边形， ∥AD ∥BC ， 若PQ ∥AB ，∥四边形P ABQ 是平行四边形， ∥AP =BQ ，∥8-2t =t ， ∥t =83，∥当t =83时，PQ ∥AB ；故答案为：83；（2）如图，过点Q 作QH ∥AB 交AB 的延长线于点H ，∥∥ADB =90°，∥BD 2=AB 2-AD 2=100-64=36，即BD =6， ∥四边形ABCD 是平行四边形， ∥AD ∥BC ， ∥∥A =∥QBH ，又∥∥ADB =∥BHQ =90°， ∥∥ADB ∥∥BHQ ， ∥BD AB QH BQ =，即610QH t=， ∥35QH t =，∥PE ∥BD ， ∥DP BE AD AB =，即2810t BE=， ∥52BE t =，∥y =S 四边形APQB -S ∥BEQ =211533(82)632422254t t t t t t -+⨯-⨯⨯=--+；（3）如图：∥PE ∥BD ， ∥∥APE =∥ADB ， ∥∥A =∥A ， ∥∥APE ∥∥ADB ， ∥PE AP DB AD =，即8268PE t-=， ∥362PE t =-，∥点E 在线段PQ 的垂直平分线上， ∥EQ =362PE t =-，由（2）得35,52QH t BE t ==，∥BH =∥45335210EH BH BE t t t =+=+=Rt ∥EQH 中，EH 2+HQ 2=EQ 2， ∥2223333()()(6)1052t t t +=-，即t 2+2t -4=0，解得：121,10t t =<（舍去），∥当t 1时，点E 在PQ 的垂直平分线上； （4）连接FF '交AB 于点N ，∥点F 关于AB 的对称点为F ′，∥∥FEB =∥F ′EB ，FN ∥EB ，∥点P ，E ，F ′三点共线，PE ∥AB ，∥∥F ′EB =∥ABD ，∥∥FEB =∥ABD ，∥EF =FB ， ∥15,24BN EN BE t ===， ∥四边形ABCD 是平行四边形，∥AD ∥BC ，∥∥DPF =∥FQB ，∥DFP =∥BFQ ，∥∥DPF ∥∥BQF ， ∥2DF DP BF BQ==， ∥DF =2BF ，∥2BF +BF =6，∥BF =2，∥∥FBN =∥ABD ，∥FNB =∥ADB ，∥∥BNF ∥∥BDA ， ∥BN BD BF AB=， ∥564210t =，解得：t =2425， ∥存在某一时刻t ，使得点P ，E ，F ′三点共线，t 的值为2425． 【点睛】本题属于四边形综合题，考查了解直角三角形，相似三角形的判定和性质，平行四边形的性质，多边形的面积等知识，解题的关键是学会利用参数构建方程解决问题． 25．如图1，平行四边形ABCD 的对角线AC ，BD 相交于点O ，CD 边的垂直平分线EH 交BD 于点E ，连接AE ，CE ．（1）过点A 作//AF EC 交BD 于点F ，求证：AF BF =；（2）如图2，将ABE △沿AB 翻折得到'ABE △．∥求证：'//BE CE ；∥若'//AE BC ，1OE =，求CE 的长度．【答案】（1）见解析；（2）∥见解析；∥1【分析】（1）根据题意证明()COE AOF AAS △≌△，即可证明ED BF =，在根据EH 垂直平分CD 可得EC ED =，即可证的结果；（2）∥过点A 作//AF EC 交BD 于点F ，根据（1）中结论，然后证明'//BE AF 即可； ∥求证AEF BCE ∽，则AF EF BE CE=，据此解答即可． 【详解】证明：（1）∥四边形ABCD 是平行四边形，∥OA OC =，OB OD =．∥//AF EC ，∥CEO AFO ∠=∠，FAO ECO ∠=∠，∥()COE AOF AAS △≌△，∥CE AF =，OE OF =，∥ED BF =．∥EH 垂直平分CD ，∥EC ED =．∥AF BF =；（2）如图2，过点A 作//AF EC 交BD 于点F ．∥证明：由（1）可知AOF COE ≌，AF BF =，∥ABF BAF ∠=∠，∥将ABE △沿AB 翻折得到'ABE △，∥'ABE ABF ∠=∠，∥'ABE BAF ∠=∠，∥'//BE AF ，又∥//AF CE ，∥'//BE CE ；。

初中几何模型 专题07相似三角形模型

初中几何模型 专题07相似三角形模型

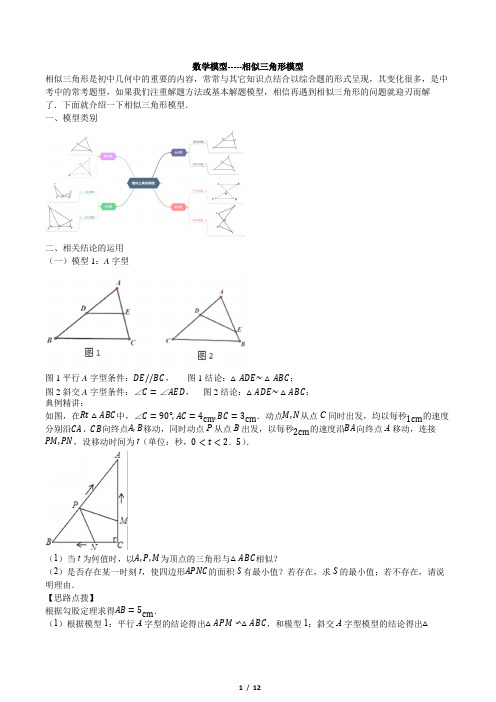
数学模型-----相似三角形模型相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考中的常考题型，如果我们注重解题方法或基本解题模型，相信再遇到相似三角形的问题就迎刃而解了．下面就介绍一下相似三角形模型．一、模型类别二、相关结论的运用（一）模型1：A字型图1平行A字型条件：DE//BC，图1结论：△ADE~△ABC；图2斜交A字型条件：∠C=∠AED，图2结论：△ADE~△ABC；典例精讲：如图，在Rt△ABC中，∠C=90°,AC=4cm,BC=3cm．动点M,N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A,B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM,PN，设移动时间为t（单位：秒，0<t<2．5）．（1）当t为何值时，以A,P,M为顶点的三角形与△ABC相似？（2）是否存在某一时刻t，使四边形APNC的面积S有最小值？若存在，求S的最小值；若不存在，请说明理由．【思路点拨】根据勾股定理求得AB=5cm．（1）根据模型1：平行A字型的结论得出△APM∽△ABC，和模型1：斜交A字型模型的结论得出△AMP∽△ABC两种情况讨论：利用相似三角形的对应边成比例来求t的值．（2）过点P作PH⊥BC于点H，构造平行线PH//AC，根据模型1：平行A字型的结论得出△PBH∽△ABC，从而求得以t表示的PH的值；然后根据“S=S△ABC−S△BPH”列出S与t的关系式S=45(t−32)2+215(0<t<2.5)，则由二次函数最值的求法即可得到S的最小值．【详解】解：∵如图，在Rt△ABC中，∠C=90°,AC=4cm,BC=3cm．∴根据勾股定理，得AB=√AC2+BC2=5cm．（1）以A,P,M为顶点的三角形与△ABC相似，分两种情况：①当△APM∽△ABC时，AMAC =APAB，即4−t4=5−2t5，解得t=0（不合题意，舍去）．②当△AMP∽△ABC时，APAC =AMAB，即5−2t4=4−t5，解得t=32；综上所述，当t=32时，以A、P、M为顶点的三角形与△ABC相似．（2）存在某一时刻t，使四边形APNC的面积S有最小值．理由如下：假设存在某一时刻t，使四边形APNC的面积S有最小值．如图，过点P作PH⊥BC于点H．则PH//AC，∴△PBH∽△ABC∴PHAC =BPBA，即PH4=2t5．∴PH=8t5．∴S=S△ABC−S△BPN=12×3×4−12×(3−t)⋅85t=45(t−32)2+215(0<t<2.5)．∵45>0，∴S有最小值．当t=32时，S最小值=215．答：当t=32时，四边形A P NC的面积S有最小值，其最小值是215．【解题技法】作平行线构造A字型相似，是解题中常用的一种作辅助线的方法实战演练：1．如图，AD经过△ABC的重心，点E是AC的中点，过点E作EG//BC交AD于点G，若BC=12，则线段GE 的长为（）A．6 B．4 C．5 D．32．如图，在△ABC中，DE//BC，EF//AB，则下列结论正确的是（）A．ADDB =DEBCB．BFBC=EFADC．EFAB=BFBCD．AEEC=DEFC3．如图，在△ABC中，D、E分别在AB边和AC边上，DE//BC，M为BC边上一点（不与B、C重合），连结AM交DE于点N，则（）A．ADAN =ANAEB．BDMN=MNCEC．DNBM=NEMCD．DNMC=NEBM（二）模型2：8字型图1平行8字型条件：AB//CD，图1结论：△AOB∽△DOC；图2斜交8字型条件：∠A=∠D，，图2结论：△AOB∽△DOC；典例精讲：如图1，在矩形ABCO中，OA=8,OC=6,D,E分别是AB,BC上一点，AD=2,CE=3,OE与CD相交于点F．（1）求证：OE⊥CD；（2）如图2，点G是CD的中点，延长OG交BC于H，求CH的长．【思路点拨】（1）根据四边形ABCO是矩形，可得OA=BC=8,OC=AB=6，根据模型1中的图1结论得出△ADP∽△OCP，从而求出PA和PO，再根据模型2中的图1结论得出△OPF∽△ECF，求出EF和CF的长，再根据勾股定理的逆定理即可得OE⊥CD；（2）在Rt△CBD中，CB=8,BD=AB−AD=6−2=4，根据勾股定理可得CD=4√5，根据点G是CD 的中点，可得CG=DG=2√5，所以得点G是CP的三等分点，根据模型2中的图1结论得出△OPG∽△HCG即可求出CH的长．【详解】（1）∵四边形ABCO是矩形，∴OA=BC=8,OC=AB=6，在Rt△OCE中，CE=3，∴OE=√OC2+CE2=√62+32=3√5，∵AB//OC，即AD//OC，且AD=2，∴△ADP∽△OCP∴ADOC =PAPO，∴26=PAPA+8，∴PA=4，∴PO=PA+OA=12，∴在Rt△OPC中，OC=6，∴CP=√OC2+PO2=√62+122=6√5，∵OA//BC ，即OP//CE ， ∴△OPF ∽△ECF ∴CEOP =EFOF =CFPF ， ∴EFOF =CFPF =312=14， ∴EF =15OE =3√55， CF =15CP =6√55，∵(3√55)2+(6√55)2=95+365=9，∴EF 2+CF 2=CE 2， ∴△CEF 是直角三角形， ∴∠CFE =90°， ∴OE ⊥CD ；（2）在Rt △CBD 中，CB =8,BD =AB −AD =6−2=4， 根据勾股定理，得CD =√CB 2+BD 2=√82+42=4√5， ∵点G 是CD 的中点， ∴CG =DG =2√5， 由（1）知：CP =6√5， ∴DP =CP −CD =2√5， ∴点G 是CP 的三等分点， ∵OA//BC ，即OP//CH ， ∴△APG ∽△HCG ∴CHOP =CGGP ， ∴CH12=12，∴CH =6．答：CH 的长为6．【解题技法】利用A 字型和8字型混合模型得出三角形相似，再利用相似三角形的对应边成比例得出线段的长或比值，解决本题的关键 实战演练：1、已知，如图，在平行四边形ABCD 中，M 是BC 边的中点，E 是边BA 延长线上的一点，连接EM ，分别交线段AD 于点F 、AC 于点G ． （1）求证：△AFG ∽△CMG ； （2）求证：GF EFGM EM．2、如图，在平行四边形ABCD中，点E在边BC上，连结AE并延长，交对角线BD于点F、DC的延长线于点G．如果CEBE =23，求FEEG的值．3、如图，BD,AC相交于点P，连结AB,BC,CD,DA,∠DAP=∠CBP．（1）求证：△ADP∽△BCP；（2）直接回答△ADP与△BCP是不是位似图形？（3）若AB=8,CD=4,DP=3，求AP的长．4、在△ABC中，∠ACB=90∘，BE是AC边上的中线，点D在射线BC上．（1）如图1，点D在BC边上，CD:BD=1:2，AD与BE相交于点P，过点A作AF//BC，交BE的延长线于点F，易得APPD的值为_______；（2）如图2，在△ABC中，∠ACB=90∘，点D在BC的延长线上，AD与AC边上的中线BE的延长线交于点P，DC:BC=1:2，求APPD的值；（3）在（2）的条件下，若CD=2,AC=6，则BP=_____．（三）模型3：k字型图1一线三垂直条件：AB ⊥BD,DE ⊥BD,AC ⊥CE ，图1结论：△ABC ∽△CDE ； 图2一线三等角条件：∠B =∠ACE =∠D ，图2结论：△ABC ∽△CDE ； 典例精讲：如图，点P 是线段BD 上一个动点，∠B =∠D =90°,AB =6,CD =4,BD =a ． （1）当∠APC =90°,a =14时，求BP 的长度；（2）若∠APC =90°时，点P 有两个符合要求即P 1,P 2，且P 1P 2=2，求a 的值； （3）若∠APC =120°时，点P 有且只有一个点符合要求，求a 的值．【思路点拨】（1）根据模型3：k 字型的一线三垂直，证得△ABP ∽△PDC ，根据相似三角形的性质即可求得；（2）设BP =x ，则PD =a −x ，根据模型3：k 字型的一线三垂直证得△ABP ∽△PDC ，由相似三角形的性质得到x 2−ax +24=0，设方程的两个根为x 1,x 2，根据根与系数的关系可知x 1+x 2=a,x 1⋅x 2=24，根据题意即可得到=(x 1+x 2)2−4x 1x 2=4，即可得到a 2−4×24=4，解得即可； （3）作∠AEP =∠CFP =120°，解直角三角形求得BE =2√3,DF =4√33,AE =4√3,CF =8√33，根据模型3：k 字型的一线三等角证得△EPA ∽△FCP ，由相似三角形的性质得到x 2−(a −10√33)x +32=0，根据题意Δ=(a −10√33)2−4×1×32=0，即可即可．【详解】 解：（1）∵∠B =∠D =90°,∠APC =90°， ∴∠A +∠APB =∠CPD +∠APB =90°， ∴∠A =∠CPD ， ∴△ABP ∽△PDC ， ∴BP CD=AB PD，即BP 4=614−BP，解得BP =2或12；（2）设BP =x ，则PD =a −x ， 由（1）可知△ABP ∽△PDC ， ∴ABPD =BPDC ，即6a−x =x4，∴x2−ax+24=0，设方程的两个根为x1,x2，根据根与系数的关系可知x1+x2=a,x1⋅x2=24，∵P1P2=2，∴|x1−x2|=2，∴(x1−x2)2=(x1+x2)2−4x1x2=4，∴a2−4×24=4，解得a=±10（负数舍去），∴a=10；（3）作∠AEP=∠CFP=120°，∴∠AEB=∠CFD=60°，∵AB=6,CD=4，∴BE=√33AB=2√3,DF=√33CD=4√33，∴AE=2BE=4√3,CF=2DF=8√33∵∠AEP=∠CFP=∠APC=120°，∴∠EAP=∠CPF，∴△EPA∽△FCP，∴AEPF =EPFC，设EP=x，则PF=a−10√33−x，∴√3a−10√33−x=x8√33，∴x2−(a−10√33)x+32=0，∵△=0，∴(a−10√33)2−4×1×32=0，∵a>0，∴a=10√33+8√2．【解题技法】通过运用模型3：k字型中从特殊到一般的方法，证明出两组对应角相等，从而得出相似三角形，利用对应边成比例是解题的关键．实战演练：1、如图1和图2，在△ABC中，AB=AC，BC=8，tan C=34．点K在AC边上，点M，N分别在AB,BC 上，且AM=CN=2．点P从点M出发沿折线MB−BN匀速移动，到达点N时停止；而点Q在AC边上随P 移动，且始终保持∠APQ =∠B ．（1）当点P 在BC 上时，求点P 与点A 的最短距离；（2）若点P 在MB 上，且PQ 将△ABC 的面积分成上下4:5两部分时，求MP 的长；（3）设点P 移动的路程为x ，当0≤x ≤3及3≤x ≤9时，分别求点P 到直线AC 的距离（用含x 的式子表示）；（4）在点P 处设计并安装一扫描器，按定角∠APQ 扫描△APQ 区域（含边界），扫描器随点P 从M 到B 再到N 共用时36秒．若AK =94，请直接．．写出点K 被扫描到的总时长 2、如图，△AOB 是直角三角形，∠AOB =90°,OB =2OA ，点A 在反比例函数y =1x 的图象上．若点B 在反比例函数y =kx 的图象上，则k 的值为_____．3、如图，在△ABC 中，点D 、E 分别在边BC 、AC 上，连接AD 、DE ，且∠B =∠ADE =∠C ． （1）证明：△BDA ∽△CED ；（2）若∠B =45°,BC =2，当点D 在BC 上运动时（点D 不与B 、C 重合），且△ADE 是等腰三角形，求此时BD 的长．4、感知：如图①，在四边形ABCD 中，AB//CD,∠B =90°，点P 在BC 边上，当∠APD =90°时，可知△ABP ∽△PCD ．（不要求证明）探究：如图②，在四边形ABCD 中，点P 在BC 边上，当∠B =∠C =∠APD 时，求证：△ABP ∽△PCD ．拓展：如图③，在△ABC中，点P是边BC的中点，点D、E分别在边AB、AC上．若∠B=∠C=∠DPE= 45°，BC=6√2，BD=4，则DE的长为______．（四）模型4：母子型图1垂直母子型条件：AC⊥BC,AB⊥CD，图1结论：△ABC∽△ACD∽△CBD；图2斜交母子字型条件：∠C=∠ABD，图2结论：△ABC∽△ABD；典例精讲：1、在Rt△ABC中，∠ACB=90°,CD⊥AB，垂足为D,AD=8,DB=2，求CD的长【思路点拨】根据垂直母子型模型4证得△ADC∽△CDB，再根据对应边成比例，即可求出CD的值．【详解】∵CD⊥AB，∴∠ADC=∠CDB=90°，∴∠ACD+∠A=90°，∵∠ACB=90°，∴∠ACD+∠BCD=90°，∴∠A=∠BCD，∴△ADC∽△CDB，∴CDBD =ADCD，∴CD2=AD⋅BD=8×2=16，∴CD=4．2、如图，在△ABC中，AB=AC，点P、D分别是BC、AC边上的点，且∠APD=∠B．（1）求证：AC⋅CD=CP⋅BP；（2）若AB=10,BC=12，当PD//AB时，求BP的长．【思路点拨】（1）根据已知得出∠APD=∠B=∠C，再根据斜交母子型模型4得出△ABP∽△PCD，根据相似三角形的性质得到AB⋅CD=CP⋅BP，由AB=AC即可得到AC⋅CD=CP⋅BP；（2）由PD//AB根据斜交母子型模型4得出△BAP∽△BCA，然后运用相似三角形的性质即可求出BP的长．【详解】（1）∵AB=AC，∴∠B=∠C．∵∠APD=∠B，∴∠APD=∠B=∠C．∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC，∴∠BAP=∠DPC，∴△ABP∽△PCD，∴BPCD =ABCP，∴AB⋅CD=CP⋅BP．∵AB=AC，∴AC⋅CD=CP⋅BP；（2）如图，∵PD//AB，∴∠APD=∠BAP．∵∠APD=∠C，∴∠BAP=∠C．∵∠B=∠B，∴△BAP∽△BCA，∴BABC =BPBA．∵AB=10,BC=12，∴1012=BP10，∴BP=253．【解题技法】利用母子型模型4中有一组隐含的等角，此时需要通过已知得出判定三角形相似的条件，把证明AC⋅CD=CP⋅BP转化为证明AB⋅CD=CP⋅BP是解题的关键．实战演练：1、如图，已知BC是⊙O的直径，AC切⊙O于点C，AB交O于点D,E为AC的中点，连接CD，DE．（1）求证：DE是⊙O的切线；（2）若BD=4,CD=3，求AC的长．2、如图，在△ABC中，AC=2,BC=4,D为BC边上的一点，∠CAD=∠B．若△ADC的面积为a，则△ABD 的面积为（）A．2a B．52a C．3a D．72a3、如图，点D是△ABC的边BC的中点，且∠CAD=∠B，若△ABC的周长为10，则△ACD的周长是（）A．5 B．5√2C．52D．5√22。

专题13 A字型和反A字型相似模型(解析版)

专题13 A字型和反A字型相似模型(解析版)

专题13A 字型和反A 字型相似模型【模型1】A 字型相似模型如图13-1，A A ∠=∠，要证ADE ∆∽ABC ∆，只要知道BC DE //即可。

【模型2】反A 字型相似模型如图13-2，A A ∠=∠，要证ADE ∆∽ACB ∆，只要再知道一组对应角相等即可，即只需知道ACB ADE ∠=∠或ABC AED ∠=∠。

【例1】如图，在△ABC 中，DE ∥BC ，若AE ＝2，EC ＝3，则△ADE 与△ABC 的面积之比为（）A．4：25B．2：3C．4：9D．2：5【答案】A【分析】根据相似三角形的判定定理得到△ADE∽△ABC，根据相似三角形的面积比等于相似比的平方计算，得到答案．【解析】解：∵AE=2，EC=3，∴AC=AE+EC=5，∵DE∥BC，∴△ADE∽△ABC，∴2224525 ADEABCS AES AC⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭，故选：A．【例2】如图，已知D是BC的中点，M是AD的中点．求:AN NC的值．【答案】1 2【分析】解法1：过点D作AC的平行线交BN于点H，构造“A”型和“8”型，得出BDH BCN∽和DHM ANM∽，再结合相似三角形的性质和中点的定义即可得出答案；解法2：过点C作AD的平行线交BN的延长线于点H，构造“A”型和“8”型，得出BDM BCH△∽和AMN CHN△∽△，再结合相似三角形的性质和中点的定义即可得出答案；解法3：过点A作BC的平行线交BN的延长线于点H，构造“A”型和“8”型，得出AHM DBM△∽△和AHN CBN△∽△，再结合相似三角形的性质和中点的定义即可得出答案；解法4：过点D作BN的平行线交AC于点H，根据三角形中位线定理得出AN NH CH==，即可得出答案；【解析】解法1：如图2，过点D 作AC 的平行线交BN 于点H ．因为//DH AC ．所以BDH BCN ∽，所以DH BD CN BC=．因为D 为BC 的中点，所以12DH BD CN BC ==．因为//DH AN ，所以DHM ANM ∽，所以DH DM AN AM=．因为M 为AD 的中点，所以1DH DM AN AM ==．所以DH AN =，所以12AN CN =．解法2：如图3，过点C 作AD 的平行线交BN 的延长线于点H ．因为//DM CH ，所以BDM BCH △∽，所以DM BD CH BC=．因为D 为BC 的中点，所以12DM BD CH BC ==．因为M 为AD 的中点，所以AM DM =，所以12AM CH =．因为//DM CH ，所以AMN CHN △∽△，所以12AN AM CN CH ==．解法3：如图4，过点A 作BC 的平行线交BN 的延长线于点H ．因为//AH BD ，所以AHM DBM △∽△，所以AH AM BD DM=．因为M 为AD 的中点，所以AM DM =，所以AH BD =．因为//AH BD ，所以AHN CBN △∽△，所以AN AH CN BC=．因为D 为BC 的中点，且AH BD =，所以12AN BD CN BC ==．解法4：如图5，过点D 作BN 的平行线交AC 于点H ．在ADH 中，因为M 为AD 的中点，//MN DH ，所以N 为AH 的中点，即AN NH =．在CBN 中，因为D 为BC 的中点，//DH BN ，所以H 为CN 的中点，即CN HN =，所以AN NH CH ==．所以12AN CN =．【例3】【教材呈现】下图是华师版九年级上册数学教材第77页的部分内容．【定理证明】请根据教材内容，结合图①，写出证明过程．【定理应用】如图②，在矩形ABCD 中，AC 为矩形ABCD 的对角线，点E 在边AB 上，且AE =2BE ，点F 在边CB 上，CF =2BF ．O 为AC 的中点，连结EF 、OE 、OF ．（1）EF 与AC 的数量关系为__________．（2）OEF 与ABC 的面积比为___________．【答案】【定理证明】证明见解析；【定理应用】（1）EF 与AC 的数量关系为13EF AC =；（2）OEF 与ABC 的面积比为2:9．【分析】定理证明：先根据相似三角形的判定与性质可得1,2DE AD ADE ABC BC AB ==∠=∠，再根据平行线的判定即可得证；定理应用：（1）先根据线段的比例关系可得13BE BF BA BC ==，再根据相似三角形的判定与性质即可得；（2）如图（见解析），先根据三角形中位线定理可得11,22OM BC ON AB ==，设,BE a BF b ==，再根据三角形的面积公式分别求出OEF 与ABC 的面积，由此即可得出答案．【解析】定理证明：点D 、E 分别是AB 、AC 的中点，12AE AD AC AB ∴==，在ADE 和ABC 中，12AE AD AC AB A A⎧==⎪⎨⎪∠=∠⎩，ADEABC ∴，1,2DE AD ADE ABC BC AB ∴==∠=∠，//DE BC ∴，且12DE BC =；定理应用：（1）2,2AE BE CF BF ==，13BE BF BA BC ∴==，在BEF 和BAC 中，BE BF BA BC B B⎧=⎪⎨⎪∠=∠⎩，BEF BAC ∴~，13EF BF AC BC ∴==，即13EF AC =；（2）如图，过点O 作OM AB ⊥于点M ，作ON BC ⊥于点N ，四边形ABCD 是矩形，90B ∴∠=︒，即AB BC ⊥，//,//OM BC ON AB ∴，点O 是AC 的中点，OM ∴、ON 是ABC 的两条中位线，11,22OM BC ON AB ∴==，设,BE a BF b ==，则332,3,2,3,,22AE a AB a CF b BC b OM b ON a ======，1122BEF SBE BF ab ∴=⋅=，1322AOE SAE OM ab =⋅=，1322COF SCF ON ab =⋅=，1922ABC S AB BC ab =⋅=，OEF ABC BEF AOE COF S SS S S ab ∴=---=，2992OEFABC Sab S ab ∴==，即OEF 与ABC 的面积比2:9．一、单选题1．如图．在△ABC 中，DE ∥BC ，∠B =∠ACD ，则图中相似三角形有（）A ．2对B ．3对C ．4对D ．5对【答案】C 【分析】根据相似三角形的判定定理即可得到结论．【解析】∵∠B =∠ACD ，∠A =∠A ，∴△ACD ∽△ABC ，∵DE ∥BC ，∴△ADE ∽△ABC ，∴△ACD ∽△ADE ，∵DE ∥BC ，∴∠EDC =∠DCB ，∵∠B =∠DCE ，∴△CDE ∽△BCD ，故共4对，故选：C ．2．如图，已知,ADE ABC V :V 若:1:3,AD AB ABC =V 的面积为9，则ADE 的面积为（）A ．1B ．2C ．3D ．9【答案】A 【分析】根据相似三角形的性质得出21=3ADEABC S S ⎛⎫ ⎪⎝⎭，代入求出即可．【解析】解：∵△ADE ∽△ABC ，AD ：AB ＝1：3，∴21=3ADEABC S S ⎛⎫ ⎪⎝⎭，∵△ABC 的面积为9，∴1=99ADE S，∴S △ADE ＝1，故选：A ．3．如图，在△ABC 中，∠C=90°，BC=3，D ，E 分别在AB 、AC 上，将△ADE 沿DE 翻折后，点A 落在点A′处，若A′为CE 的中点，则折痕DE 的长为（）A ．12B ．3C ．2D ．1【答案】D 【解析】试题解析：由题意得：DE ⊥AC ，∴∠DEA =90°，∵∠C =∠DEA ，∵∠A =∠A ，∴△AED ∽△ACB ,∴DE BC =AE AC,∵A ′为CE 的中点，∴C A ′=E A ′，∴C A ′=E A ′=AE ，∴AE AC =DE BC =13，∴DE =1.故选D.二、填空题4．如图，P 是ABC ∆内一点，过点P 分别作直线平行于ABC ∆各边，形成三个小三角形面积分别为1233,12,27S S S ===，则ABC S ∆=__________【答案】108【分析】根据平行可得三个三角形相似，再由它们的面积比得出相似比，再求出最小三角形的边与最大三角形边的比，从而得到它们的面积的比，求出结果即可．【解析】解：过P 作BC 的平行线交AB 、AC 于点D 、E ，过P 作AB 的平行线交AB 于点I 、G ，过P 作AC 的平行线交AC 于点F 、H ，∵DE//BC ，IG//AB ，FH//AC ，∴四边形AFPI 、四边形PHCE 、四边形DBGP 均为平行四边形，△FDP ∽△IPE ∽△PGH ∽△ABC ，∵12331227S S S ===，，，∴FP ：IE ：PH=1：2：3，∴AI ：IE ：EC=1：2：3，∴AI ：IE ：EC ：AB=1：2：3：6，S △ABC ：S △FDP =36：1，∴S △ABC =36×3=108．故答案为:108．5．如图，在ABC 中，点D 、E 分别在AB 、AC 上，ADE C ∠=∠，如果3AD =，ADE 的面积为9，四边形BDEC 的面积为16，则AC 的长为________．【答案】5【分析】由∠ADE=∠C ，∠DAE=∠CAB ，根据相似三角形的判定得到△DAE ∽△CAB ，根据相似的性质得S △DAE ：S △CAB =2AD AC ⎛⎫ ⎪⎝⎭，然后把三角形面积代入计算即可．【解析】解：∵∠ADE=∠C ，而∠DAE=∠CAB ，∴△DAE ∽△CAB ，∴S △DAE ：S △CAB =2AD AC ⎛⎫ ⎪⎝⎭，∵△ADE 的面积为9，四边形BDEC 的面积为16，∴△ABC 的面积=9+16=25，∴2925AD AC ⎛⎫= ⎪⎝⎭，∴AC=5．故答案为5．三、解答题6．如图，△ABD 中，∠A ＝90°，AB ＝6cm ，AD ＝12cm ．某一时刻，动点M 从点A 出发沿AB 方向以1cm/s 的速度向点B 匀速运动；同时，动点N 从点D 出发沿DA 方向以2cm/s 的速度向点A 匀速运动，运动的时间为ts ．（1）求t 为何值时，△AMN 的面积是△ABD 面积的29；（2）当以点A ，M ，N 为顶点的三角形与△ABD 相似时，求t 值．【答案】（1）14t =，22t =；（2）t ＝3或245【分析】（1）由题意得DN ＝2t （cm ），AN ＝（12﹣2t ）cm ，AM ＝t cm ，根据三角形的面积公式列出方程可求出答案；（2）分两种情况，由相似三角形的判定列出方程可求出t 的值．【解析】解：（1）由题意得DN ＝2t （cm ），AN ＝（12﹣2t ）cm ，AM ＝t cm ，∴△AMN 的面积＝12AN •AM ＝12×（12﹣2t ）×t ＝6t ﹣t 2，∵∠A ＝90°，AB ＝6cm ，AD ＝12cm∴△ABD 的面积为12AB •AD ＝12×6×12＝36，∵△AMN 的面积是△ABD 面积的29，∴6t ﹣t 2＝2369⨯，∴t 2﹣6t +8＝0，解得t 1＝4，t 2＝2，答：经过4秒或2秒，△AMN 的面积是△ABD 面积的29；（2）由题意得DN ＝2t （cm ），AN ＝（12﹣2t ）cm ，AM ＝t cm ，若△AMN ∽△ABD ，则有AM AN AB AD =，即122612t t -=，解得t ＝3，若△AMN ∽△ADB ，则有AM AN AD AB =，即122126t t -=，解得t ＝245，答：当t ＝3或245时，以A 、M 、N 为顶点的三角形与△ABD 相似．7．在ABC 中，()0AB m m =>，D 为AB 上一点，过D 作DE ∥BC 交AC 于点E ，连接CD ．设21,DCE ABC S S S S ==，求21S S的取值范围．【答案】21104S S <≤【分析】作AG ⊥BC 于F 点，交DE 于G 点，设AD =x ，首先结合相似三角形的判定与性质推出DE BC 和GF AF的值，然后结合面积公式进行列式，得出二次函数解析式，最后结合二次函数的性质以及自变量的取值范围进行判断即可．【解析】解：如图所示，作AG ⊥BC 于F 点，交DE 于G 点，设AD =x ，∵DE ∥BC ，∴△ADE ∽△ABC ，∴DE AD AG AE x BC AB AF AC m ====，∴GF m x AF m-=，∴()2211212DE GF x m x S DE GF x m x S BC AF m m m BC AF --==⨯=⨯=，整理得：22222111124S x m x x S m m m ⎛⎫=-+=--+ ⎪⎝⎭，∵点D 在AB 上，0m >，∴0x m <<，210m -<，∴抛物线21S S 的开口向下，且当2m x =时，21S S 取得最大值为14，当0x =和x m =时，均有210S S =，综上分析，21S S 的取值范围是21104S S <≤．8．Rt ABC 中，90C ∠=︒，20cm AC =，15cm BC =，现有动点P 从点A 出发，沿AC 向点C 方向运动，动点Q 从点C 出发，沿线段CB 也向点B 方向运动，如果点P 的速度是4cm/s ，点Q 的速度是2cm/s ，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动时间为t 秒．（1）求运动时间为多少秒时，P 、Q 两点之间的距离为10cm?（2）若CPQ 的面积为S ，求S 关于t 的函数关系式．（3）当t 为多少时，以点C ，P ，Q 为顶点的三角形与ABC 相似?【答案】（1）3秒或5秒；（2）()22204cm S t t =-；（3）3t =或4011t =【分析】（1）根据题意得到AP =4t cm ，CQ =2t cm ，AC =20cm ，CP =（20-4t ）cm ，根据三角形的面积公式列方程即可得答案；（2）若运动的时间为t s ，则CP =（20-4t ）cm ，CQ =2t cm ，利用三角形的面积计算公式，即可得出S =20t -4t 2，再结合各线段长度非负，即可得出t 的取值范围；（3）分①Rt CPQ Rt CAB ∽△△和②Rt CPQ Rt CBA ∽△△，利用相似三角形得出比例式，建立方程求解，即可得出结论．【解析】（1）解：由运动知，AP =4tcm ，CQ =2t cm ，∵AC =20cm ，∴CP =（20-4t ）cm ，在Rt △CPQ 中，222CP CQ PQ +=，即()()222204210t t -+=；∴3t =秒或5t =秒（2）由题意得4AP t =，2CQ t =，则204CP t =-，因此Rt CPQ 的面积为()()2212042204cm 2S t t t t =⨯-⨯=-；（3）分两种情况：①当Rt CPQ Rt CAB ∽△△时，CP CQ CA CB =，即20422015t t -=，解得3t =；②当Rt CPQ Rt CBA ∽△△时，CP CQ CB CA =，即20421520t t -=，解得4011t =．因此3t =或4011t =时，以点C 、P 、Q 为顶点的三角形与ABC 相似．9．如图，在△ABC 中，点D 在边AB 上，点E 、点F 在边AC 上，且DE ∥BC ，AF AE FE EC =．（1）求证：DF ∥BE ；（2）如且AF ＝2，EF ＝4，AB ＝ADE ∽△AEB ．【答案】（1）见详解；（2）见详解【分析】（1）由题意易得AD AE BD EC =，则有AF AD FE BD =，进而问题可求证；（2）由（1）及题意可知12AD AF BD EF ==，然后可得AD =AE AD AB AE ==，最后问题可求证．【解析】解：（1）∵DE ∥BC ，∴AD AE BD EC =，∵AF AE FE EC =，∴AF AD FE BD =，∴DF ∥BE ；（2）∵AF ＝2，EF ＝4，∴由（1）可知，12AD AF BD EF ==，AE =6，∵AB ＝∴13AD AB ==∴363AE AD AB AE ====，∴3AE AD AB AE ==，∵∠A =∠A ，∴△ADE ∽△AEB ．10．如图，AB 为⊙O 的直径，C 为BA 延长线上一点，点D 为圆上一点且∠ADC =∠AOF ，OF ⊥AD 于点E ，交CD 于点F ．（1）判断CD 与⊙O 的位置关系；（2）若sin C =13，BD =8，求EF 的长．【答案】（1）CD 与⊙O 相切；（2）2EF =．【分析】（1）要判断CD 与⊙O 的位置关系，可连接OD ，判断OD 与CD 能否垂直即可；（2）观察图形可知：EF =OF -OE ，所以要求EF ，只需设法分别求出OF 和OE 的长度即可；由于AB 是⊙O 的直径，可以判断出OF 与BD 平行的位置关系，从而利用OAE BAD △∽△和OCF BCD △∽△，即可分别求出OF 和OE 的长度．【解析】（1）CD 与⊙O 相切．证明：连接OD ．∵AB 为⊙O 的直径，∴∠ADO +∠BDO =∠DAO +∠B =90°，∵OF ⊥AD ，OD =OA ，∴∠AOD =2∠AOF ，∠DAO =∠ODA ．∵∠AOD =2∠B ，∴∠ADC =∠B ．∴∠ADC +∠ADO =90°．∴OD ⊥CD ．∴CD 是⊙O 的切线．∴CD 与⊙O 相切．（2）设⊙O 的半径为r ．在Rt △OCD 中，∵1sin 3C =，∴13OD OC =，∴3OD r OC r ==，．∵OA =r ，∴AC =OC -OA =2r ．∵AB 为⊙O 的直径，∴∠ADB =90°．又∵OF ⊥AD ，∴OF ∥BD ．∴OAE BAD △∽△且OCF BCD △∽△．由OAE BAD △∽△，得，12OE OA BD AB ==．∴118422OE BD ==⨯=．由OCF BCD △∽△，得，34OF OC BD BC ==．∴338644OF BD ==⨯=．∴642EF OF OE =-=-=．11．如图，在ABC ∆中，点,E F 分别在,AB AC 上，且AE AB AF AC=．（1）求证：AEF ABC ∆∆；（2）若点D 在BC 上，AD 与EF 交于点G ，求证：EG FG BD CD=．【答案】（1）见解析；（2）见解析【分析】（1）直接利用两边成比例且夹角相等的两个三角形相似即可证得结论；（2）根据相似三角形的性质和平行线的判定方法可得EF ∥BC ，于是可得△AEG ∽△ABD ，△AGF ∽△ADC ，再根据相似三角形的性质即可推出结论．【解析】解：（1）在△AEF 和△ABC 中，∵EAF BAC ∠=∠，AE AB AF AC =，∴△AEF ∽△ABC ；（2）∵△AEF ∽△ABC ，∴∠AEF =∠ABC ，∴EF ∥BC ，∴△AEG ∽△ABD ，△AGF ∽△ADC ，∴EG AG BD AD =,FG AG CD AD =，∴EG FG BD CD=．12．如图，已知，⊙O 为△ABC 的外接圆，BC 为直径，点E 在AB 上，过点E 作EF ⊥BC ，点G 在FE 的延长线上，且GA=GE ．（1）求证：AG 与⊙O 相切．（2）若AC=6，AB=8，BE=3，求线段OE 的长．【答案】（1）证明见解析；（2【分析】（1）连接OA ，由OA=OB ，GA=GE 得出∠ABO=∠BAO ，∠GEA=∠GAE ；再由EF ⊥BC ，得出∠BFE=90°，进一步由∠ABO+∠BEF=90°，∠BEF=∠GEA ，最后得出∠GAO=90°求得答案；（2）BC 为直径得出∠BAC=90°，利用勾股定理得出BC=10，由△BEF ∽△BCA ，求得EF 、BF 的长，进一步在△OEF 中利用勾股定理得出OE 的长即可．【解析】（1）连接OA ，∵OA=OB，GA=GE∴∠ABO=∠BAO，∠GEA=∠GAE ∵EF⊥BC，∴∠BFE=90°，∴∠ABO+∠BEF=90°，又∵∠BEF=∠GEA，∴∠GAE=∠BEF，∴∠BAO+∠GAE=90°，即AG与⊙O相切．（2）解：∵BC为直径，∴∠BAC=90°，AC=6，AB=8，∴BC=10，∵∠EBF=∠CBA，∠BFE=∠BAC，∴△BEF∽△BCA，∴BF BE EF BA BC AC==∴EF=1.8，BF=2.4，∴OF=OB-BF=5.2．4=2.6，∴=．13．已知：矩形ABCD中，AB＝9，AD＝6，点E在对角线AC上，且满足AE＝2EC，点F 在线段CD上，作直线FE，交线段AB于点M，交直线BC于点N．（1）当CF＝2时，求线段BN的长；（2）若设CF＝x，△BNE的面积为y，求y关于x的函数解析式，并写出自变量的取值范围；（3）试判断△BME能不能成为等腰三角形，若能，请直接写出x的值．【答案】（1）BN＝10；（2）6273xyx-=-，0＜x＜3；2763xyx-=-，3＜x＜4.5；（3）x＝2或32或29 12【分析】（1）由AB CD∥得△CFE∽△AME，△NCF∽△NBM，进而求得；（2）分为0＜x＜3和3＜x＜4.5两种情形，作EG⊥BC于G，根据三角形相似求出EG和BN；（3）分为BM＝BE，EM＝BE，EN＝BM三种，可根据BM＝9﹣2CF求得．【解析】解：（1）如图1，在矩形ABCD中，BC＝AD＝6，AB CD∥，∴△CFE∽△AME，△NCF∽△NBM，∴1,2CF EC CF NC AM AE BM NB ===,∴AM＝2CF＝4，∴BM＝AB﹣AM＝5，∴26 5BNBN-=，∴BN＝10；（2）当CF＝BM时，MF BC∥，此时△BEN不存在，∴CF＝9﹣2CF，∴CF＝3，当点M和B点重合时，AB＝2CF，∴CF＝4.5，∴分为0＜x＜3和3＜x＜4.5，如图2，当0＜x＜3时，作EG⊥BC于G，由（1）知，EG＝3，AM＝2CF＝2x，∴BM＝9﹣2x，由CF NCBM NB=得，692x BNx BN-=-，∴1843x BNx-=-，∴y＝12BN EG⋅＝11843 23xx-⋅⨯-＝6273xx--；如图3，当3＜x ＜4.5时，由BN BM CN CF=得，926BN x BN x-=+∴CN ＝2(92)3x x --，∴y ＝12(92)323x x -⋅⨯-＝2763x x --；（3）如图4，∵EG AB ∥，∴13CG EG CB AB ==，∴CG ＝13CB ＝2，∴GB ＝CB ﹣CG ＝4，∴BE ＝5，当BM ＝BE ＝5时，9﹣2x ＝5，∴x ＝2，如图5，当EM ＝EB ＝5时，作EH ⊥AB 于H ，∴BM ＝2BH ＝2EG ＝6，∴9﹣2x ＝6，∴x =32，如图6，当EM ＝BM 时，作MH ⊥BE 于H ，在Rt △BMH 中，BH ＝1522BE =，cos ∠MBH ＝cos ∠BEG ＝35EG BE =，∴BM ＝355252cos 6BH MBH ==∠，∴9﹣2x ＝256，∴x ＝2912，综上所述：x ＝2或32或2912．14．如图，在平行四边形ABCD 中，90ADB ∠=︒，10cm AB =，8cm AD =，点P 从点D 出发，沿DA 方向匀速运动，速度为2cm/s ；同时，点Q 从点B 出发，沿BC 方向匀速运动，速度为1cm/s .当一个点停止运动，另一个点也停止运动.过点P 作//PE BD 交AB 于点E ，连接PQ ，交BD 于点F .设运动时间为()()s 04t t <<.解答下列问题：（1）当t为___________时，//PQ AB？（2）连接EQ，设四边形APQE的面积为()2cmy，求y与t的函数关系式.（3）当t为何值时，点E在线段PQ的垂直平分线上？（4）若点F关于AB的对称点为'F，是否存在某一时刻t，使得点P，E，'F三点共线？若存在，求出t的值；若不存在，请说明理由.【答案】（1）83；（2）233244y t t=--+；（351；（4）2425．【分析】（1）由题意得，PQ∥AB，则四边形PABQ是平行四边形，根据平行四边形的性质可得AP=BQ，即8-2t=t，解方程即可求解；（2）过点Q作QH⊥AB交AB的延长线于点H，由勾股定理求出BD=6，证明△ADB∽△BHQ，根据相似三角形的性质可得QH=35t，根据平行线分线段成比例定理可得DP BEAD AB=，可得出BE=52t，根据y=S四边形APQB-S△BEQ即可求解；（3）先证出△APE∽△ABD，根据相似三角形的性质可得PE APDB AD=，可得PE=6-32t，根据线段垂直平分线的性质得EQ=PE，由（2）得QH=35t，可得出BH=45t，根据勾股定理得出EH2+HQ2=EQ2，列出方程即可求解；（4）连接FF′交AB于点N，由对称及平行线的性质可得∠FEB=∠ABD，由等角对等边得EF=FB，则1524BN EN BE t===，再证△DPF∽△BQF，可得DF=2BF，可求出BF=2，然后证明△BNF∽△BDA，根据相似三角形的性质即可得t的值．【解析】解：（1）∵四边形ABCD是平行四边形，∴AD∥BC，若PQ∥AB，∴四边形PABQ是平行四边形，∴AP=BQ，∴8-2t=t，∴t =83，∴当t =83时，PQ ∥AB ；故答案为：83；（2）如图，过点Q 作QH ⊥AB 交AB 的延长线于点H ，∵∠ADB =90°，∴BD 2=AB 2-AD 2=100-64=36，即BD =6，∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠A =∠QBH ，又∵∠ADB =∠BHQ =90°，∴△ADB ∽△BHQ ，∴BD AB QH BQ =，即610QH t=，∴35QH t =，∵PE ∥BD ，∴DP BE AD AB =，即2810t BE =，∴52BE t =，∴y =S 四边形APQB -S △BEQ =211533(82)632422254t t t t t t -+⨯-⨯⨯=--+；（3）如图：∵PE ∥BD ，∴∠APE =∠ADB ，∵∠A =∠A ，∴△APE ∽△ADB ，∴PE AP DB AD =，即8268PE t -=，∴362PE t =-，∵点E 在线段PQ 的垂直平分线上，∴EQ =362PE t =-，由（2）得35,52QH t BE t ==，∴222234()55BH BQ QH t t =-=-=∴45335210EH BH BE t t t =+=+=，Rt △EQH 中，EH 2+HQ 2=EQ 2，∴2223333()()(6)1052t t t +=-，即t 2+2t -4=0，解得：1251,510t t =-=-<（舍去），∴当t 51时，点E 在PQ 的垂直平分线上；（4）连接FF '交AB 于点N ，∵点F 关于AB 的对称点为F ′，∴∠FEB =∠F ′EB ，FN ⊥EB ，∵点P ，E ，F ′三点共线，PE ∥AB ，∴∠F ′EB =∠ABD ，∴∠FEB =∠ABD ，∴EF =FB ，∴15,24BN EN BE t ===，∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠DPF =∠FQB ，∵DFP =∠BFQ ，∴△DPF ∽△BQF ，∴2DF DP BF BQ==，∴DF =2BF ，∴2BF +BF =6，∴BF =2，∵∠FBN =∠ABD ，∠FNB =∠ADB ，∴△BNF ∽△BDA ，∴BN BD BF AB=，∴564210t =，解得：t =2425，∴存在某一时刻t ，使得点P ，E ，F ′三点共线，t 的值为2425．15．如图，在矩形ABCD 的边AB 上取一点E ，连接CE 并延长和DA 的延长线交于点G ，过点E 作CG 的垂线与CD 的延长线交于点H ，与DG 交于点F ，连接GH．（1）当tan 2BEC ∠=且4BC =时，求CH 的长；（2）求证：DF FG HF EF ⋅=⋅；（3）连接DE ，求证：CDE CGH ∠=∠．【答案】（1）10CH =；（2）见解析；（3）见解析【分析】（1）根据已知条件先求出CE 的长，再证明∠=∠BEC ECH ，在Rt △CHE 中解三角形可求得EH 的长，最后利用勾股定理求CH 的长；（2）证明∽∆∆GFE HFD ，进而得出结果；（3）由（2）∽∆∆GFE HFD 得∠=∠EGF FHD ，进而sin sin ∠=∠EGF FHD ，即=CD CE CG CH，再结合∠=∠ECD DCE ，可得出∽∆∆CDE CGH ，进一步得出结果.【解析】（1）解：∵矩形ABCD ，EH CG ⊥，∴90∠=︒=∠=∠BCD CEH B .而90BEC BCE ∠+∠=︒，90∠+∠=︒BCE ECH ，∴∠=∠BEC ECH ，又∵4BC =，tan 2BEC ∠=，∴2BE =，易得CE ==∴tan 2∠==EH ECH CE ，∴EH =∴10CH ==.（2）证明：∵矩形ABCD ，EH CG ⊥，∴∠=∠CEH HDG ，而∠=∠GFE DFH ，∴∽∆∆GFE HFD ，∴=DF FH EF FG，∴⋅=⋅DF FG EF FH ；（3）证明：由（2）∽∆∆GFE HFD 得∠=∠EGF FHD ，∴sin sin ∠=∠EGF FHD ，即=CD CE CG CH，而∠=∠ECD DCE ，∴∽∆∆CDE CGH ，∴CDE CGH ∠=∠．。

相似三角形”A“字模型(含详细答案)-经典.docx

相似三角形”A“字模型(含详细答案)-经典.docx

教师辅导教案授课日期：年月日授课课时：课时△ ABC与厶AB C ■相似，AH是厶ABC中BC边上的高线，AH ■是△ ABC ■中BC ■边上的高线，则有AB _ BC AB^BCAC AHk =AC AH（k为相似比）.进而可得S∆ ABCS∆ ABC1BC AH211BC AH2BC AH 2kBC AH、相似三角形的判定1.平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似.2•如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似•可简单说成：两角对应相等，两个三角形相似.3•如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似.4. 如果一个三角形的三条边与另一个三角形的你对应成比例，那么这两个三角形相似.可简单地说成：三边对应成比例，两个三角形相似.5. 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似.6•直角三角形被斜边上的高分成的两个直角三角形相似（常用但要证明）7.如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等，那么这两个等腰三角形相似；如果它们的腰和底三、相似证明中的基本模型A字形图①A字型，DE//BC ;结论: AD _ AE _ DE AB 一AC 一BC，【例1】李老师在编写下面这个题目的答案时，不小心打乱了解答过程的顺序，你能帮他调整过来吗？证明步骤正确的顺序是（）已知：如图，在∆ABC中，点D, E, F分别在边AB, AC, BC上，且DE// BC, DF// AC, 求证：∆ADEs∆ DBF.证明：①又∙∙∙DF//AC,②∙∙∙DE// BC,③∙∙∙∠ A= ∠ BDF,④∙∙∙∠ ADE=∠ B,A.③②④①B.②④①③C.③①④②D.②③④①【解答】证明：②I DE// BC,④∙∠ADE=∠ B,①又∙∙∙DF// AC,③∙∠A= ∠ BDF,•••△ ADE^∆DBF.故选：B.故选：A .【练1】如图，在△ ABC 中，∠ ACB=90, BC=16cm, AC=12cm ,点P 从点B 出发，以2cm∕秒的速度向点 C 移 动，同时点Q 从点C 出发，以1cm∕秒的速度向点 A 移动，设运动时间为与厶ABC 相似.【解答】 解：CP 和CB 是对应边时，△ CPQ^△ CBA 所以，C e ICB CA即-■ -I --t1512解得t=4.8;CP 和CA 是对应边时，△ CPQ^△ CAB, 所以，丄二二，CA CBIMtt 12^16 解得t=-综上所述，当t=4.8或斤一时，△ CPQ 与厶CBA 相似. 故答案为4.8或〒二.AE AD DE 图②反A 字型，∠ ADE ∠ B 或∠仁∠B 结论：==AC AB BCt 秒，当t= 4.8或空秒时，△ CPQ---------- 11-【例2】如同，在△ ABC 中，点D , E 分别在边AB , AC 上，下列条件中不能判断厶 ABC^△ AED 的是（ ）AD AE AB =AC AD AC-'AB【解答】 解：τ∠ DAE=∠ CAB,•••当∠ AED=∠ B 或∠ ADE=∠ C 时，△ ABC ^△ AED; AD .AC'AE∙≠∙件二 ι∙WA . B.C.∠ ADE=∠ C D .∠ AED=∠ B时，△ ABC ^△ AED. 当—昱L 二一―即【例3】如图，P 是厶ABC 的边AB 上的一点.（不与A 、B 重合）当∠ ACP=∠ B 时，△ APC 与厶ABC 是否相 似；当 AC AP 、AB 满足 丄二丄 时，△ ACP 与厶ABC 相似.— AC AB-【解答】解：τ∠ A= ∠ A ,∠ ACP=∠ B ,故答案为：B ；寺二二【练习1】如图，D 、EABC 的边AC 、AB 上的点，当 ∠ ADE=∠ B 时，△ ADE ^△ ABC.其 中D 、E 分别对应B 、C.（填一个条件）. 【解答】解：当∠ ADE=∠ B ,∙∠ EAD=∠ CAB,• △ ADE ^△ ABC. 故答案为∠ ADE=∠ B .【练习2】如图，在△ ABC 中，D E 分别在AB 与AC 上，且AD=5, DB=7, AE=6, EC=4 求证：△ ADE ^△ ACB.【解答】证明：• AD=5, DB=7, AE=6, EC=4, • AB=5+7=12, AC=6+4=10,.AD = 5 _1 AE = 6 _1 • AC 10 T r AB 12 = 2， .AP =Ag• AC AB ， 又∙∠ A= ∠ A , • △ ADE ^△ ACB.【练习3】如图，AB=AC, ∠ A=36° , BD 是∠ ABC 的角平分线，求证：△ ABC^△ BCD. 【解答】证明：• AB=AC, ∠ A=36°, ∙∠ ABC=∠ C=72 , • BD 是角平分线，∙∠ ABD=∠ DBC=36 , ∙∠ A= ∠ CBD, 又∙∠ C=∠ C, • △ ABC^△ BCD.•丄二丄''[I∠ A= ∠ A ,【练习4】已知：如图，△ ABC 中，∠ ACD=∠ B ,求证：△ ABC^△ ACD. 【解答】 证明：τ∠ ACD=∠ B ,∠ A= ∠ A ,【例4】如图，在△ ABC 中，D ，E 分别是AB ，AC 上的点，∠ AED=∠ ABC,∠ BAC 的平分线 AF 交DE 于点G ,• △ ABC^△ AED.τ∠ AED=∠ ABC,∠ EAG=∠ BAF,• △ AEG^△ ABF.【练习5】如图，已知 AD?AC=AB?AE 求证：△ ADE^△ ABC. 【解答】证明：I AD?AC=AE?AB— =AEAB AC在厶ABC 与厶ADE 中 ■: 一.AEAB AC• △ ABC^△ ADE.【练习6】已知：如图，在厶ABC 中，D , E 分别为AB 、AC 边上的点，且AD 匚AE,连接DE.若AC=4, AB=5.求 证：△ ADE ^△ ACB【解答】证明：∙∙∙ AC=3, AB=5, ADjL 匕,5.AC _ AB厂-Λ,τ∠ A= ∠ A ,• △ ADE ^△ ACB.图③双A 字型交BC 于点F .(1)试写出图中所有的相似三角形，并说明理由.3'2BC的值. 【解答】 解：(1 )∙∙∙∠ AED=∠ ABC,∠ EAD=∠ BAC,,∠ A= ∠ A , R3(2)若,求小τ∠ EDG=∠ ACF, ∠ DAG=∠ CAF , •••△ ADG sA ACF.•••△ ADG sA ACF,」丄 .A.-. 3GF 5【练习1】如图，在△ ABC 中，D 、E 分别是 AB 、AC 上的点，AE=4, AB=6, AD : AC=2: 3,A ABC 的角平分线AF 交DE 于点G ，交BC 于点F .(1) 请你直接写出图中所有的相似三角形； (2) 求AG 与GF 的比.【解答】 解：(1 )△ ADG sA ACF △ AGE^A AFB,A ADE sA ACB;(2).• AE _4」2 AD _2(∙ TiTE =可，疋=可胚. -AE)AB '又 τ∠ DAE=∠ CAB,• △ ADE sA ACB,∙∠ ADG=∠ C ,∙∙∙ AF 为角平分线，∙∠ DAG=∠ FAE• △ ADG sA ACF,AG. 3GF 2(2)AG . Ar 2 ^^' AC 3 =2.AG GF图④内含正方形 A 字形，结论AH a=_^ ( a 为正方形边长) AH BC【例5】如图，△ ABC ,是一张锐角三角形的硬纸片， AD 是边BC 上的高，BC=40cm,AD=30cm ,从这张硬纸片上剪下一个长 HG 是宽HE 的2倍的矩形EFGH 使它的一边EF 在BC 上，顶点 G 、H 分别在 AC, AB 上，AD 与HG 的交点为 M .(2)的周长;(3)是否存在一个实数 a ,当HEFa 时从三角形硬纸片上剪下的矩形面积最大？若存在,请说明理由.【解答】(1)证明：•••四边形 HEFG 为矩形, ∙∙∙ HG // EF, 而 AD ⊥ BC,∙ AM 丄 BC, •••△ AHGsA ABC,AJfl HGAD - S BC(2)解：设 HE=X HG=2X,•这个矩形 EFGH 的周长=2x+4x=6x=72 (Cm );(3) 存在.AD BC(1)求证:30-x i 2x30 - _40,解得x=12,则30-a . .HG 30当HE=a,则• HG=- 430_ 2X 〔申 即当HEF Cm 时从三角形硬纸片上剪下的矩形面积最大.4• S 矩形 HEFG Fa (- a+30) F -a 2+30a ,当a=- 454时，S 矩形HEFG 最大, 试求出a ；若不存在,【练习1】如图，△ ABC ,是一张锐角三角形的硬纸片， AD 是边BC 上的高，BC=80cm , AD=60cm ,从这张硬纸片上剪下一个长 HG 是宽HE 的2倍的矩形EFGH 使它的一边 EF 在BC 上，顶点G 、H 分别在AC, AB 上,AD 与HG 的交点为M .(2)求这个矩形 EFG H 的面积.∙∙∙ EF// GH, ∙∙∙∠ AHG=∠ ABC,又 τ∠ HAG=∠ BAC,AJI L L … ADBC(2)解：设 HE=XCm, MD=HE=xcm , ■/ AD=60cm ,• AM= (60 - x ) Cm , ∙∙∙ HG=2HE, • HG=2xcm,AD ~BC'解得，x=24, 故 HE=24, HG=2x=48, 则矩形 EFGH 的面积=24 × 12=1152cm 2.【例6】如图，在△ ABC 中，D 为AC 上一点，E 为CB 延长线上一点，且 求证：AD=EB【解答】证明：过D 点作DH / BC 交AB 于H,如图, ∙/ DH // BC, • △ AHD ^△ ABC,∙/ DH // BE ,M L .HG AD BC的理由;(1)试说明:&0-x. -2x60 ' SO可得【解答】(1)证明：I 四边形 EFG H 为矩形,AD DH AC CS B CAD ACBC,即GH5DED-2.-EF HD DP , AC EFBC ' -Il =■> DF ADHD DH,∙∙∙ AD=EB.【例7】如图，在△ ABC中，∠ BAC=90, BC的垂直平分线交BC于点E,交CA的延长线于D,交AB于点F,求证：AE=EF?ED【解答】解：τ∠BAC=90 ,∙∠B+∠ C=90, ∠ D+∠ C=90 ,∙∠B=∠ D,∙∙∙ BC的垂直平分线交BC于点E,∠ BAC=90 .• BE=EA∙∠B=∠ BAE∙∠D=∠ BAEτ∠FEA=∠AED,• △ FEA^△ AED,.恆=DE•EP =AE•AE=EF?ED旋转型”相似三角形，如图•若图中∠仁∠ 2,∠ B=∠ D（或∠ C=∠ £）,则厶ADE∞^ABC,该图可看成把第一个图中的△ADE绕点A旋转某一角度而形成的.【例8】如图，在厶ABC与厶ADE中，∠ BAC=∠ D,要使△ ABC与厶ADE相似，还需满足下列条件中的（）AC AB AD=AE AC BC AD==DE【解答】解：τ∠BAC=∠D, • △ ABC^△ ADE.AC ABAD=DEAC ABADAC BCAE ==AEA. B.C D.E故选：C.【练习1】如图所示，在厶ABC 与厶ADE 中，AB?ED=AE?BC 要使△ ABC 与厶ADE 相似，还需要添加一个条件, 这个条件是∠ B=∠ E （答案不唯一）（只加一个即可）并证明.【解答】解：条件①，∠ B=∠ E 证明：∙∙∙ AB?ED=AE?BCAEECAD•••△ ABC^△ AED.故答案为：∠ B=∠ E （答案不唯一）【练习 2】如图，已知：∠ BAC=∠ EAD, AB=20.4, AC=48, AE=17, AD=40. 求证：△ ABC^△ AED.【解答】证明：I AB=20.4, AC=48, AE=17, AD=40. • AB =20. 4 =1 2 AC 座=1 2• AE .,而 40 .， •塑座'二=「，∙∙∙∠ BAC=∠ EAD,• △ ABC^△ AED.【练习3】如图，在△ ABC 和厶ADE 中，已知∠ABC^△ ADE.【解答】 解：如图，τ∠ BAD=∠ CAE, ∙∠ BAD+ ∠ BAE=∠ CAE+ ∠ BAE , 即 ∠ DAE=∠ BAC. 又τ∠ B= ∠ D ,• AB - BCAE F.C∙∙∙∠ B= ∠ E ,• △ ABC^△ AED.条件②, AD==AEAC证明：•• • AB? ED=AE?BC• AB = BCAE EC-AE --- ,AC AB AB =BC = AC B= ∠ D ,∠ BAD=∠ CAE 求证：△C• △ABC^△ADE.【练习4】如图，△ ABC △ DEP是两个全等的等腰直角三角形，∠BAC=∠ PDE=90 .(1)若将△ DEP的顶点P放在BC上(如图1) , PD PE分别与AC、AB相交于点F、G.求证:(2)若使△ DEP的顶点P与顶点A重合(如图2), PD、PE与BC相交于点F、似吗？为什么？【解答】(1)证明：如图1,•••△ ABC △ DEP是两个全等的等腰直角三角形,∙∙∙∠B=∠ C=∠ DPE=45 ,∙∙∙∠BPG+∠ CPF=135,在厶BPG 中，τ∠B=45,∙∠BPG+∠ BGP=135 ,∙∠BGP=∠ CPF,τ∠B=∠C,•••△ PBG∞^ FCP(2)解：△ PBG与厶FCP相似.理由如下：如图2, •••△ ABC △ DEP是两个全等的等腰直角三角形,∙∠B=∠C=∠DPE=45 ,∙∙∙∠ BGP=∠C+∠CPG=45 + ∠CAG,∠CPF=Z FPGF ∠CAG=45 + ∠CAG,∙∠AGP=∠CPF,τ∠B=∠C,•••△ PBG∞^ FCP.课堂小结: △ PBG∞^ FCPG.试问△ PBG与厶FCP还相。

自学初中数学资料-相似三角形的概念-(资料附答案)

自学初中数学资料-相似三角形的概念-(资料附答案)

自学资料一、相似三角形的概念【知识探索】1．相似用符号“∽”表示，读作“相似于”．【说明】用符号表示两个相似三角形时，通常把对应顶点的字母分别写在三角形记号“△”后相应的位置上．【错题精练】例1．如图所示，△ABC中若DE∥BC，EF∥AB，则下列比例式正确的是（）A. ADDB =DEBC；B. FBBC =EFAD；C. AEEC =BFCF；第1页共30页自学七招之日计划护体神功：每日计划安排好，自学规划效率高非学科培训D. FEAB =DEBC．【答案】C例2．如图，在□ABCD中，E在AB上，CE、BD交于F，若AE：BE＝4：3，且BF＝2，则DF＝_____．【答案】143【举一反三】1．如图所示，点E是平行四边形ABCD的边CB延长线上的点，AB与DE相交于点F，则图中相似三角形共有（）对．A. 5B. 4C. 3D. 2【答案】B2．如图，在△ABC中，DE∥BC，AD=1，AB=3，DE=2，则BC=__________ .第2页共30页自学七招之错题本锁骨术：巧用智能错题本，错题定期反复练非学科培训【解答】解：∵DE∥BC，∴△ADE∽△ABC，∴= ，即=解得：BC=6【答案】6二、相似三角形的性质【知识探索】1．（1）相似三角形性质定理1：相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比；（2）相似三角形性质定理2：相似三角形的周长比等于相似比；（3）相似三角形性质定理3：相似三角形的面积比等于相似比的平方．【说明】（1）研究和运用相似比的性质时，要注意相似比与表述这两个三角形相似的顺序有关；（2）性质定理1和性质定理2可以概括为：相似三角形中对应线段（高线、中线、角平分线）及周长的比都等于相似比．【错题精练】例1．如图，在△ABC中，∠A=36∘，AC=AB=2，将△ABC绕点B逆时针方向旋转得到△DBE，使点E在边AC上，DE交AB于点F，则△AFE与△DBF的面积之比等于（）；A. √5−12；B. √5−14；C. 3−√52D. 3−√5．4【答案】C第3页共30页自学七招之提前完卷飞刀：考场控时莫紧张，跳跃答卷心不慌非学科培训例2．如图，四边形ABCD是平行四边形，点E在BA的延长线上，点F在BC的延长线上，连接EF，分别交AD，CD于点G，H，则下列结论错误的是（）A. EAEB =EGEFB. EGGH =AGGDC. ABAE =BCCFD. FHEH =CFAD【答案】C例3．如图，已知△ABC∽△ADE，AB=30cm，AD=18cm，BC=20cm，∠BAC=75°，∠ABC=40°．（1）求∠ADE和∠AED的度数；（2）求DE的长．【答案】解：（1）∵∠BAC=75°，∠ABC=40°，∴∠C=180°-∠BAC-∠ABC=180°-75°-40°=65°，∵△ABC∽△ADE，∴∠ADE=∠ABC=40°，∠AED=∠C=65°；（2）∵△ABC∽△ADE，∴ABAD第4页共30页自学七招之错题本锁骨术：巧用智能错题本，错题定期反复练非学科培训=BCDE，即3018=20DE，解得DE=12cm．例4．如图，在△ABC中，AB=8cm，BC=16cm，点P从点A开始沿边AB向点B以2cm/s的速度移动，点Q从点B开始沿边BC向点C以4cm/s的速度移动，如果点P、Q 分别从点A、B同时出发，经几秒钟△PBQ与△ABC相似？试说明理由．【答案】解：设经x秒钟△PBQ与△ABC相似，则AP=2xcm，BQ=4xcm，∵AB=8cm，BC=16cm，∴BP=AB-AP=（8-2x）cm，∵∠B是公共角，∵①当BPBA=BQBC，即第5页共30页自学七招之提前完卷飞刀：考场控时莫紧张，跳跃答卷心不慌非学科培训8-2x8=4x16时，△PBQ∽△ABC，解得：x=2；②当BPBC=BQBA，即8-2x16=4x8时，△QBP∽△ABC，解得：x=0.8，∴经2或0.8秒钟△PBQ与△ABC相似．例5．在⊙O的内接△ABC中，AB+AC=12，AD⊥BC，垂足为D，且AD=3，设⊙O的半径为y，AB 的长为x。

模型05 相似三角形中的常见五种基本模型(解析版)

模型05 相似三角形中的常见五种基本模型(解析版)

模型探究相似三角形考查范围广，综合性强，其模型种类多，其中有关一线三垂直模型在前面的专题已经很详细的讲解，这里就不在重复.模型一、A字型相似模型A字型（平行）反A字型（不平行）模型二、8字型与反8字型相似模型模型三、AX型相似模型（A字型及X字型两者相结合）模型四、共边角相似模型（子母型）模型五、手拉手相似模型例题精讲考点一、A字相似模型【例1】．如图，在△ABC中，∠A＝78°，AB＝4，AC＝6，将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）A．B．C．D．解：A、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；B、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；C、两三角形的对应边不成比例，故两三角形不相似，故本选项正确．D、两三角形对应边成比例且夹角相等，故两三角形相似，故本选项错误；故选：C．变式训练【变式1-1】．如图，在△ABC中，DE∥BC，AH⊥BC于点H，与DE交于点G．若，则＝．解：∵，∴，∵DE∥BC，∴△ADE∽△ABC，∴，故答案为．【变式1-2】.如图，在△ABC中，M是AC的中点，E是AB上一点，AE＝AB，连接EM并延长，交BC的延长线于D，则＝__________.解：如图，过C点作CP∥AB，交DE于P，∵PC∥AE，∴△AEM∽△CPM，∴＝，∵M是AC的中点，∴AM＝CM，∴PC＝AE，∵AE＝AB，∴CP＝AB，∴CP＝BE，∵CP∥BE，∴△DCP∽△DBE，∴＝＝，∴BD＝3CD，∴BC＝2CD，即＝2．【变式1-3】．如图，在△ABC中，点D在边AB上，AD＝9，BD＝7．AC＝12．△ABC的角平分线AE交CD于点F．（1）求证：△ACD∽△ABC；（2）若AF＝8，求AE的长度．解：（1）∵AD＝9，BD＝7，AC＝12，∴AB＝AD+BD＝16，∵＝＝，＝＝，∴＝，∵∠BAC＝∠CAD，∴△ACD∽△ABC；（2）由（1）可知，△ACD∽△ABC，∴∠ABE＝∠ACF，∵AE平分∠BAC，∴∠BAE＝∠CAF，∴△ABE∽△ACF，∴＝，即＝，∴AE＝＝．考点二、8字与反8字相似模型【例2】．如图，AG∥BD，AF：FB＝1：2，BC：CD＝2：1，求的值解：∵AG∥BD，∴△AFG∽△BFD，∴＝，∵，∴CD＝BD，∴，∵AG∥BD，∴△AEG∽△CED，∴．变式训练【变式2-1】．如图，AB∥CD，AE∥FD，AE、FD分别交BC于点G、H，则下列结论中错误的是（）A．B．C．D．解：A、∵AB∥CD，∴＝，故本选项不符合题目要求；B、∵AE∥DF，∴△CEG∞△CDH，∴＝，∴＝，∵AB∥CD，∴＝，∴＝，∴＝，∴＝，故本选项不符合题目要求；∵AB∥CD，AE∥DF，∴四边形AEDF是平行四边形，∴AF＝DE，∵AE∥DF，∴，∴＝，故本选项不符合题目要求；D、∵AE∥DF，∴△BFH∞△BAG，∴，故本选项符合题目要求；故选：D．【变式2-2】．如图，在平行四边形ABCD中，E为边AD的中点，连接AC，BE交于点F．若△AEF的面积为2，则△ABC的面积为（）A．8B．10C．12D．14解：如图，∵四边形ABCD是平行四边形，∵EA∥BC，∴△AEF∽△CBF，∵AE＝DE＝AD，CB＝AD，∴＝＝＝＝，∴AF＝AC，EF＝BF，＝S△ABC，∴S△ABF＝S△ABF＝×S△ABC＝S△ABC，∴S△AEF＝2，∵S△AEF＝6S△AEF＝6×2＝12，故选：C．∴S△ABC【变式2-3】.如图，锐角三角形ABC中，∠A＝60°，BE⊥AC于E，CD⊥AB于D，则DE：BC＝1：2．解：如图，∵在△ADC中，∠A＝60°，CD⊥AB于点D，∴∠ACD＝30°，∴＝．又∵在△ABE中，∠A＝60°，BE⊥AC于E，∴∠ABE＝30°，∴＝，∴＝．又∵∠A＝∠A，∴△ADE∽△ACB，∴DE：BC＝AD：AC＝1：2．故答案是：1：2．考点三、AX型相似模型（A字型及X字型两者相结合）【例3】.如图，在△ABC中，点D和E分别是边AB和AC的中点，连接DE，DC与BE交于点O，若△DOE的面积为1，则△ABC的面积为（）A．6B．9C．12D．13.5解：∵点D和E分别是边AB和AC的中点，∴O点为△ABC的重心，∴OB＝2OE，＝2S△DOE＝2×1＝2，∴S△BOD＝3，∴S△BDE∵AD＝BD，＝2S△BDE＝6，∴S△ABE∵AE＝CE，＝2S△ABE＝2×6＝12．故选C．∴S△ABC变式训练【变式3-1】.如图，DE是△ABC的中位线，F为DE中点，连接AF并延长交BC于点G，＝1，则S△ABC＝24．若S△EFG解：方法一：∵DE是△ABC的中位线，∴D、E分别为AB、BC的中点，如图过D作DM∥BC交AG于点M，∵DM∥BC，∴∠DMF＝∠EGF，∵点F为DE的中点，∴DF＝EF，在△DMF和△EGF中，，∴△DMF≌△EGF（AAS），＝S△EGF＝1，GF＝FM，DM＝GE，∴S△DMF∵点D为AB的中点，且DM∥BC，∴AM＝MG，∴FM＝AM，＝2S△DMF＝2，∴S△ADM∵DM为△ABG的中位线，∴＝，＝4S△ADM＝4×2＝8，∴S△ABG＝S△ABG﹣S△ADM＝8﹣2＝6，∴S梯形DMGB＝S梯形DMGB＝6，∴S△BDE∵DE是△ABC的中位线，＝4S△BDE＝4×6＝24，∴S△ABC方法二：连接AE，∵DE是△ABC的中位线，∴DE∥AC，DE＝AC，∵F是DE的中点，∴＝，∴＝＝，＝1，∵S△EFG＝16，∴S△ACG∵EF∥AC，∴＝＝，∴＝＝，＝S△ACG＝4，∴S△AEG＝S△ACG﹣S△AEG＝12，∴S△ACE＝2S△ACE＝24，故答案为：24．∴S△ABC【变式3-2】．如图：AD∥EG∥BC，EG交DB于点F，已知AD＝6，BC＝8，AE＝6，EF ＝2．（1）求EB的长；（2）求FG的长．解：（1）∵EG∥AD，∴△BAD∽△BEF，∴＝，即＝，∴EB＝3．（2）∵EG∥∥BC，∴△AEG∽△ABC，∴＝，即＝，∴EG＝，∴FG＝EG﹣EF＝．【变式3-3】.如图，已知AB∥CD，AC与BD相交于点E，点F在线段BC上，，．（1）求证：AB∥EF；：S△EBC：S△ECD．（2）求S△ABE（1）证明：∵AB∥CD，∴＝＝，∵，∴＝，∴EF∥CD，∴AB∥EF．（2）解：设△ABE的面积为m．∵AB∥CD，∴△ABE∽△CDE，∴＝（）2＝，＝4m，∴S△CDE∵＝＝，＝2m，∴S△BEC：S△EBC：S△ECD＝m：2m：4m＝1：2：4．∴S△ABE模型四、子母型相似模型【例4】.如图，点C，D在线段AB上，△PCD是等边三角形，且∠APB＝120°，求证：（1）△ACP∽△PDB，（2）CD2＝AC•BD．证明：（1）∵△PCD是等边三角形，∴∠PCD＝∠PDC＝∠CPD＝60°，∴∠ACP＝∠PDB＝120°，∵∠APB＝120°，∴∠APC+∠BPD＝60°，∵∠CAP+∠APC＝60°∴∠BPD＝∠CAP，∴△ACP∽△PDB；（2）由（1）得△ACP∽△PDB，∴，∵△PCD是等边三角形，∴PC＝PD＝CD，∴，∴CD2＝AC•BD．变式训练【变式4-1】.如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（）A．∠ABP＝∠C B．∠APB＝∠ABC C．D．解：在△ABP和△ACB中，∠BAP＝∠CAB，∴当∠ABP＝∠C时，满足两组角对应相等，可判断△ABP∽△ACB，故A正确；当∠APB＝∠ABC时，满足两组角对应相等，可判断△ABP∽△ACB，故B正确；当时，满足两边对应成比例且夹角相等，可判断△ABP∽△ACB，故C正确；当时，其夹角不相等，则不能判断△ABP∽△ACB，故D不正确；故选：D．【变式4-2】.如图，在△ABC中，点D在AC边上，连接BD，若∠ABC+∠BDC＝180°，AD＝2，CD＝4，则AB的长为（）A．3B．4C．D．2解：∵∠ABC+∠BDC＝180°，∠ADB+∠BDC＝180°，∴∠ADB＝∠ABC，∵∠A＝∠A，∴△ABC∽△ADB，∴，∵AD＝2，CD＝4，∴，∴AB2＝12，∴AB＝2或﹣2（不合题意，舍去），故选：D．【变式4-3】．如图，边长为4的正方形，内切圆记为圆O，P为圆O上一动点，则PA+PB的最小值为2．解：设⊙O半径为r，OP＝r＝BC＝2，OB＝r＝2，取OB的中点I，连接PI，∴OI＝IB＝，∵，，∴，∠O是公共角，∴△BOP∽△POI，∴，∴PI＝PB，∴AP+PB＝AP+PI，∴当A、P、I在一条直线上时，AP+PB最小，作IE⊥AB于E，∵∠ABO＝45°，∴IE＝BE＝BI＝1，∴AE＝AB﹣BE＝3，∴AI＝＝，∴AP+PB最小值＝AI＝，∵PA+PB＝（PA+PB），∴PA+PB的最小值是AI＝＝2．故答案是2．模型五、手拉手相似模型【例5】.如图，△ABC与△DEF均为等边三角形，O为BC、EF的中点，则AD：BE的值为．解：连接OA、OD，∵△ABC与△DEF均为等边三角形，O为BC、EF的中点，∴AO⊥BC，DO⊥EF，∠EDO＝30°，∠BAO＝30°，∴OD：OE＝OA：OB＝：1，∵∠DOE+∠EOA＝∠BOA+∠EOA即∠DOA＝∠EOB，∴△DOA∽△EOB，∴OD：OE＝OA：OB＝AD：BE＝：1＝，故答案为：．变式训练【变式5-1】.如图，在△ABC与△ADE中，∠BAC＝∠DAE，∠ABC＝∠ADE．求证：（1）△BAC∽△DAE；（2）△BAD∽△CAE．证明：（1）∵∠BAC＝∠DAE，∠ABC＝∠ADE．∴△BAC∽△DAE；（2）∵△BAC∽△DAE，∴，∴，∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，∴△BAD∽△CAE．【变式5-2】.如图，点D是△ABC内一点，且∠BDC＝90°，AB＝2，AC＝，∠BAD＝∠CBD＝30°，AD＝．解：如图，过点A作AB的垂线，过点D作AD的垂线，两垂线交于点M，连接BM，∵∠BAD＝30°，∴∠DAM＝60°，∴∠AMD＝30°，∴∠AMD＝∠DBC，又∵∠ADM＝∠BDC＝90°，∴△BDC∽△MDA，∴，又∠BDC＝∠MDA，∴∠BDC+∠CDM＝∠ADM+∠CDM，即∠BDM＝∠CDA，∴△BDM∽△CDA，∴＝，∵AC＝，∴BM＝3，在Rt△ABM中，AM＝＝＝，∴AD＝AM＝．【变式5-3】．如图，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD＝5，AD＝kAB（k为常数），则BD的长为．（用含k的式子表示）解：如图中，∵AE⊥BC，BE＝EC，∴AB＝AC，将△ABD绕点A逆时针旋转得到△ACG，连接DG．则BD＝CG，∵∠BAD＝∠CAG，∴∠BAC＝∠DAG，∵AB＝AC，AD＝AG，∴∠ABC＝∠ACB＝∠ADG＝∠AGD，∴△ABC∽△ADG，∵AD＝kAB，∴DG＝kBC＝4k，∵∠BAE+∠ABC＝90°，∠BAE＝∠ADC，∴∠ADG+∠ADC＝90°，∴∠GDC＝90°，∴CG＝＝．∴BD＝CG＝，故答案为：．实战演练1．如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（）A．＝B．C．D．解：A、∵EF∥AB，∴＝，∵DE∥BC，∴＝，∴＝，故A正确，B、易知△ADE∽△EFC，∴＝，∴＝，故B正确．C、∵△CEF∽△CAB，∴＝，∴＝，故C正确．D、∵DE∥BC，∴＝，显然DE≠CF，故D错误．故选：D．2．如图，梯形ABCD中，AD∥BC，∠B＝∠ACD＝90°，AB＝2，DC＝3，则△ABC与△DCA的面积比为（）A．2：3B．2：5C．4：9D．：解：∵AD∥BC，∴∠ACB＝∠DAC又∵∠B＝∠ACD＝90°，∴△CBA∽△ACD＝＝＝，∵＝（）2＝∴△ABC与△DCA的面积比为4：9．故选：C．3．如图，菱形ABCD中，E点在BC上，F点在CD上，G点、H点在AD上，且AE∥HC ∥GF．若AH＝8，HG＝5，GD＝4，则下列选项中的线段，何者长度最长？（）A．CF B．FD C．BE D．EC解：∵AH＝8，HG＝5，GD＝4，∴AD＝8+5+4＝17，∵四边形ABCD为菱形，∴BC＝CD＝AD＝17，∵AE∥HC，AD∥BC，∴四边形AECH为平行四边形，∴CE＝AH＝8，∴BE＝BC﹣CE＝17﹣8＝9，∵HC∥GF，∴＝，即＝，解得：DF＝，∴FC＝17﹣＝，∵＞9＞8＞，∴CF长度最长，故选：A．4．如图，在△ABC中，BC＝6，E，F分别是AB，AC的中点，动点P在射线EF上，BP 交CE于点D，∠CBP的平分线交CE于点Q，当CQ＝CE时，EP+BP的值为（）A．6B．9C．12D．18解：如图，延长BQ交射线EF于M，∵E、F分别是AB、AC的中点，∴EF∥BC，∴∠M＝∠CBM，∵BQ是∠CBP的平分线，∴∠PBM＝∠CBM，∴∠M＝∠PBM，∴BP＝PM，∴EP+BP＝EP+PM＝EM，∵CQ＝CE，∴EQ＝2CQ，由EF∥BC得，△MEQ∽△BCQ，∴＝2，∴EM＝2BC＝2×6＝12，即EP+BP＝12．故选：C．5．如图，在四边形ABCD中，AD∥BC，∠ABC＝90°，AB＝2，AD＝2，将△ABC绕点C顺时针方向旋转后得△A′B′C，当A′B′恰好经过点D时，△B′CD为等腰三角形，若BB′＝2，则AA′等于（）A．B．2C．D．解：过D作DE⊥BC于E，则BE＝AD＝2，DE＝2，设B′C＝BC＝x，则DC＝x，∴DC2＝DE2+EC2，即2x2＝28+（x﹣2）2，解得：x＝4（负值舍去），∴BC＝4，AC＝，∵将△ABC绕点C顺时针方向旋转后得△A′B′C，∴∠DB′C＝∠ABC＝90°，B′C＝BC，A′C＝AC，∠A′CA＝∠B′CB，∴∴△A′CA∽△B′CB，∴，即∴AA′＝，故选：A．6．如图，已知，△ABC中边AB上一点P，且∠ACP＝∠B，AC＝4，AP＝2，则BP＝6．解：∵∠A＝∠A，∠ACP＝∠B，∴△ACP∽△ABC，∴AC2＝AP•AB，即AB＝AC2÷AP＝16÷2＝8，∴BP＝AB﹣AP＝6．7．如图，在▱ABCD中，AC、BD相交于点O，点E是OA的中点，联结BE并延长交AD 于点F，如果△AEF的面积是4，那么△BCE的面积是36．解：∵在▱ABCD中，AO＝AC，∵点E是OA的中点，∴AE＝CE，∵AD∥BC，∴△AFE∽△CBE，∴＝＝，＝4，＝（）2＝，∵S△AEF＝36，故答案为36．∴S△BCE8．如图，在△ABC中，点G为ABC的重心，过点G作DE∥AC分别交边AB、BC于点D、E，过点D作DF∥BC交AC于点F，如果DF＝4，那么BE的长为8．解：连接BG并延长交AC于H，∵G为ABC的重心，∴＝2，∵DE∥AC，DF∥BC，∴四边形DECF是平行四边形，∴CE＝DF＝4，∵GE∥CH，∴△BEG∽△CBH，∴＝2，∴BE＝8，故答案为：8．9．如图，已知Rt△ABC中，两条直角边AB＝3，BC＝4，将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE，并且点A落在DE边上，则sin∠ABE＝．解：∵将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE，∴BD＝AB，BC＝BE，∠ABD＝∠CBE，∠DEB＝∠ACB，∴∠D＝∠BAC＝∠BAD＝（180°﹣∠ABD），∴∠BEC＝（180°﹣∠CBE），∴∠D＝∠BEC，∵∠ABC＝∠DBE＝90°，∴∠DEB+∠BEC＝90°，∴∠AEC＝90°，∵∠AGB＝∠EGC，∴∠ACE＝∠ABE，∵在Rt△ABC中，AB＝3，BC＝4，∴AC＝DE＝5，过B作BH⊥DE于H，则DH＝AH，BD2＝DH•DE，∴DH＝＝，∴AD＝，∴AE＝DE﹣AD＝，∴sin∠ABE＝sin∠ACE＝＝＝，故答案为：．10．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AC＝6，AD平分∠BAC，交边BC于点D，过点D作CA的平行线，交边AB于点E．（1）求线段DE的长；（2）取线段AD的中点M，联结BM，交线段DE于点F，延长线段BM交边AC于点G，求的值．解：（1）∵AD平分∠BAC，∠BAC＝60°，∴∠DAC＝30°，在Rt△ACD中，∠ACD＝90°，∠DAC＝30°，AC＝6，∴CD＝2，在Rt△ACB中，∠ACB＝90°，∠BAC＝60°，AC＝6，∴BC＝6，∴BD＝BC﹣CD＝4，∵DE∥CA，∴，∴DE＝4；（2）如图，∵点M是线段AD的中点，∴DM＝AM，∵DE∥CA，∴，∴DF＝AG，∵DE∥CA，∴，∴，∵BD＝4，BC＝6，DF＝AG，∴．11．如图，在菱形ABCD中，∠ADE、∠CDF分别交BC、AB于点E、F，DF交对角线AC 于点M，且∠ADE＝∠CDF．（1）求证：CE＝AF；（2）连接ME，若＝，AF＝2，求ME的长．解：（1）∵四边形ABCD是菱形，∴AD＝CD，∠DAF＝∠DCE，又∵∠ADE＝∠CDF，∴∠ADE﹣∠EDF＝∠CDF﹣∠EDF，∴∠ADF＝∠CDE，在△ADF和△CDE中，，∴△ADF≌△CDE，∴CE＝AF．（2）∵四边形ABCD是菱形，∴AB＝BC，由（1）得：CE＝AF＝2，∴BE＝BF，设BE＝BF＝x，∵＝，AF＝2，∴，解得x＝，∴BE＝BF＝，∵＝，且CE＝AF，∴＝＝，∵∠CMD＝∠AMF，∠DCM＝∠AMF，∴△AMF∽△CMD，∴，∴＝，且∠ACB＝∠ACB∴△ABC∽△MEC∴∠CAB＝∠CME＝∠ACB∴ME＝CE＝212．[问题背景]（1）如图①，已知△ABC∽△ADE，求证：△ABD∽△ACE．[尝试应用]（2）如图②，在△ABC和△ADE中，∠BAC＝∠DAE＝90°∠ABC＝∠ADE＝30°，AC与DE相交于点F，点D在BC边上，＝，①填空：＝1；②求的值．（1）证明：如图①，∵△ABC∽△ADE，∴∠BAC＝∠DAE，＝，∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，＝，∴∠BAD＝∠CAE，∴△ABD∽△ACE．（2）解：①如图②，∵∠DAE＝90°，∠ADE＝30°，∴DE＝2AE，∴AD＝＝＝AE，∵＝，∴AD＝BD，∴AE＝BD，∴＝1，故答案为：1．②如图②，连接CE，∵∠BAC＝∠DAE＝90°，∠ABC＝∠ADE，∴△BAC∽△CAE，∴＝，∴＝，∵∠BAD＝∠CAE＝90°﹣∠CAD，∴△BAD∽△CAE，∴∠ABC＝∠ACE，∴∠ADE＝∠ACE，∵∠AFD＝∠EFC，∴△AFD∽△EFC，∴＝，由①得AD＝AE，AD＝BD，∴＝＝，∴BD＝CE，∴AD＝×CE＝3CE，∴＝3，∴＝3，∴的值是3．13．如图，在正方形ABCD中，AB＝4，E、F分别是BC、CD上的点，且∠EAF＝45°，AE、AF分别交BD于点M、N，连接EN、EF．（1）求证：△ABN∽△MBE；（2）求证：BM2+ND2＝MN2；（3）①求△CEF的周长；②若点G、F分别是EF、CD的中点，连接NG，则NG的长为．（1）证明：如图1，∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝∠ABC＝90°，∴∠ABD＝∠ADB＝45°，∴∠ABN＝∠MBE＝45°，∠BME＝∠ABD+∠BAM＝45°+∠BAM，∵∠EAF＝45°，∴∠BAN＝∠EAF+∠BAM＝45°+∠BAM，∴∠BAN＝∠BME，∴△ABN∽△MBE．（2）证明：如图1，将△ADN绕点A顺时针旋转90°得到△ABH，连接MH，∴∠BAH＝∠DAN，AH＝AN，HB＝ND，∵∠MAN＝∠EAF＝45°，∴∠MAH＝∠BAH+∠BAM＝∠DAN+∠BAM＝45°，∴∠MAH＝∠MAN，∵AM＝AM，∴△MAH≌△MAN（SAS），∴MH＝MN，∵∠ABH＝∠ADN＝45°，∴∠MBH＝∠ABD+∠ABH＝90°，∴BM2+HB2＝MH2，∴BM2+ND2＝MN2．（3）解：①如图2，将△ADF绕点A顺时针旋转90°得到△ABK，∴AK＝AF，∠BAK＝∠DAF，BK＝DF，∠ABK＝∠ADF＝90°，∴∠ABK+∠ABE＝180°，∴点K、点B、点E在同一条直线上，∵∠EAK＝∠BAE+∠BAK＝∠BAE+∠DAF＝45°，∴∠EAK＝∠EAFM，∵AE＝AE，∴△EAK≌△EAF（SAS），∴EK＝EF，∴BE+DF＝BE+BK＝EK＝EF，∵CB＝CD＝AB＝4，∴CE+EF+CF＝CE+BE+DF+CF＝CB+CD＝4+4＝8，∴△CEF的周长是8．②如图2，∵F是CD的中点，∴CF＝DF＝CD＝2，∵∠C＝90°，∴CF2+EF2＝CE2，∵EF＝BE+DF＝BE+2，CE＝CB﹣BE＝4﹣BE，∴22+（4﹣BE）2＝（BE+2）2，解得BE＝，∴EF＝+2＝，∵∠MBE＝∠MAN＝45°，∠BME＝∠AMN，∴△BME∽△AMN，∴＝，∴＝，∴∠AMB＝∠NME，∴△AMB∽△NME，∴∠NEM＝∠ABM＝45°，∴∠ENF＝∠MAN+∠NEM＝90°，∵G是EF的中点，∴NG＝EF＝×＝，故答案为：．14．问题背景如图（1），已知△ABC∽△ADE，求证：△ABD∽△ACE；尝试应用如图（2），在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝30°，AC与DE相交于点F，点D在BC边上，＝，求的值；拓展创新如图（3），D是△ABC内一点，∠BAD＝∠CBD＝30°，∠BDC＝90°，AB ＝4，AC＝2，直接写出AD的长．问题背景证明：∵△ABC∽△ADE，∴，∠BAC＝∠DAE，∴∠BAD＝∠CAE，，∴△ABD∽△ACE；尝试应用解：如图1，连接EC，∵∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝30°，∴△ABC∽△ADE，由（1）知△ABD∽△ACE，∴，∠ACE＝∠ABD＝∠ADE，在Rt△ADE中，∠ADE＝30°，∴，∴＝3．∵∠ADF＝∠ECF，∠AFD＝∠EFC，∴△ADF∽△ECF，∴＝3．拓展创新解：如图2，过点A作AB的垂线，过点D作AD的垂线，两垂线交于点M，连接BM，∵∠BAD＝30°，∴∠DAM＝60°，∴∠AMD＝30°，∴∠AMD＝∠DBC，又∵∠ADM＝∠BDC＝90°，∴△BDC∽△MDA，∴，又∠BDC＝∠MDA，∴∠BDC+∠CDM＝∠ADM+∠CDM，即∠BDM＝∠CDA，∴△BDM∽△CDA，∴，∵AC＝2，∴BM＝2＝6，∴在Rt△ABM中，AM＝＝＝2，∴AD＝．15．如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG、线段DE的数量关系BG＝DE及所在直线的位置关系BG⊥DE；②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断；（2）将原题中正方形改为矩形（如图4﹣6），且AB＝a，BC＝b，CE＝ka，CG＝kb（a≠b，k＞0），则线段BG、线段DE的数量关系＝及所在直线的位置关系BG ⊥DE；（3）在第（2）题图5中，连接DG、BE，且a＝4，b＝3，k＝，直接写出BE2+DG2的值为．解：（1）①猜想：BG ⊥DE ，BG ＝DE ；故答案为：BG ＝DE ，BG ⊥DE ；②结论成立．理由：如图2中，∵四边形ABCD 和四边形CEFG 是正方形，∴BC ＝DC ，CG ＝CE ，∠BCD ＝∠ECG ＝90°，∴∠BCG ＝∠DCE ，∴△BCG ≌△DCE （SAS ），∴BG ＝DE ，∠CBG ＝∠CDE ，又∵∠CBG +∠BHC ＝90°，∴∠CDE +∠DHG ＝90°，∴BG ⊥DE ．（2）∵AB ＝a ，BC ＝b ，CE ＝ka ，CG ＝kb ，∴＝＝，又∵∠BCG ＝∠DCE ，∴△BCG ∽△DCE ，∴∠CBG ＝∠CDE ，＝＝，又∵∠CBG +∠BHC ＝90°，∴∠CDE +∠DHG ＝90°，∴BG⊥DE．故答案为：＝，BG⊥DE．（3）连接BE、DG．根据题意，得AB＝4，BC＝3，CE＝2，CG＝1.5，∵BG⊥DE，∠BCD＝∠ECG＝90°∴BE2+DG2＝BO2+OE2+DO2+OG2＝BC2+CD2+CE2+CG2＝9+16+2.25+4＝．。

相似三角形”A“字模型(含详细问题详解)-经典

相似三角形”A“字模型(含详细问题详解)-经典

教师辅导教案授课日期：年月日授课课时：课时ABC △与A B C '''△相似，AD 是ABC △中BAC ∠的角平分线，A D ''是A B C '''△中B A C '''∠的角平分线，则有AB BC AC AD k A B B C A C A D ====''''''''（k 为相似比）． 4．相似三角形周长的比等于相似比． ABC △与A B C '''△相似，则有AB BC ACk A B B C A C ===''''''（k 为相似比）．应用比例的等比性质有AB BC AC AB BC ACk A B B C A C A B B C A C++====''''''''''''++． 5．相似三角形面积的比等于相似比的平方．ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有AB BC AC AH k A B B C A C A H ====''''''''（k 为相似比）．进而可得21212ABC A B C BC AHS BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△．二、相似三角形的判定1．平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似． 2．如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．可简单说成：两角对应相等，两个三角形相似．3．如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似． 4．如果一个三角形的三条边与另一个三角形的你对应成比例，那么这两个三角形相似．可简单地说成：三边对应成比例，两个三角形相似．5．如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．6．直角三角形被斜边上的高分成的两个直角三角形相似（常用但要证明）7．如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等，那么这两个等腰三角形相似；如果它们的腰和底对应成比例，那么这两个等腰三角形也相似． 三、相似证明中的基本模型A 字形图①A 字型，DE//BC ;结论：AD AE DEAB AC BC==， 【例1】李老师在编写下面这个题目的答案时，不小心打乱了解答过程的顺序，你能帮他调整过来吗？证明步骤正确的顺序是（ ）已知：如图，在△ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，且DE ∥BC ，DF ∥AC ，求证：△ADE∽△DBF．证明：①又∵DF∥AC，②∵DE∥BC，③∴∠A=∠BDF，④∴∠ADE=∠B，∴△ADE∽△DBF．A．③②④① B．②④①③ C．③①④② D．②③④①【解答】证明：②∵DE∥BC，④∴∠ADE=∠B，①又∵DF∥AC，③∴∠A=∠BDF，∴△ADE∽△DBF．故选：B．【练1】如图，在△ABC中，∠ACB=90°，BC=16cm，AC=12cm，点P从点B出发，以2cm/秒的速度向点C移动，同时点Q从点C出发，以1cm/秒的速度向点A移动，设运动时间为t秒，当t= 4.8或秒时，△CPQ与△ABC相似．【解答】解：CP和CB是对应边时，△CPQ∽△CBA，所以，，即，解得t=4.8；CP和CA是对应边时，△CPQ∽△CAB，所以，，即，解得t=．综上所述，当t=4.8或时，△CPQ与△CBA相似．故答案为4.8或．图②反A字型，∠ADE=∠B或∠1=∠B结论：AE AD DE==AC AB BC【例2】如同，在△ABC中，点D，E分别在边AB，AC上，下列条件中不能判断△ABC∽△AED的是（）A．=B．=C．∠ADE=∠C D．∠AED=∠B【解答】解：∵∠DAE=∠CAB，∴当∠AED=∠B或∠ADE=∠C时，△ABC∽△AED；当=即=时，△ABC∽△AED．故选：A．【例3】如图，P是△ABC的边AB上的一点．（不与A、B重合）当∠ACP=∠ B 时，△APC与△ABC是否相似；当AC、AP、AB满足时，△ACP与△ABC相似．【解答】解：∵∠A=∠A，∠ACP=∠B，∴△ACP∽△ABC；∵，∠A=∠A，∴△ACP与△ABC；故答案为：B；．【练习1】如图，D、E为△ABC的边AC、AB上的点，当∠ADE=∠B 时，△ADE∽△ABC．其中D、E分别对应B、C．（填一个条件）．【解答】解：当∠ADE=∠B，∵∠EAD=∠CAB，∴△ADE∽△ABC．故答案为∠ADE=∠B．【练习2】如图，在△ABC中，D、E分别在AB与AC上，且AD=5，DB=7，AE=6，EC=4．求证：△ADE∽△ACB．【解答】证明：∵AD=5，DB=7，AE=6，EC=4，∴AB=5+7=12，AC=6+4=10，∴====，∴=，又∵∠A=∠A，∴△ADE∽△ACB．【练习3】如图，AB=AC，∠A=36°，BD是∠ABC的角平分线，求证：△ABC∽△BCD．【解答】证明：∵AB=AC，∠A=36°，∴∠ABC=∠C=72°，∵BD是角平分线，∴∠ABD=∠DBC=36°，∴∠A=∠CBD，又∵∠C=∠C，∴△ABC∽△BCD．【练习4】已知：如图，△ABC中，∠ACD=∠B，求证：△ABC∽△ACD．【解答】证明：∵∠ACD=∠B，∠A=∠A，∴△ABC∽△ACD．【练习5】如图，已知AD•AC=AB•AE．求证：△ADE∽△ABC．【解答】证明：∵AD•AC=AE•AB，∴=在△ABC与△ADE 中∵=，∠A=∠A，∴△ABC∽△ADE．【练习6】已知：如图，在△ABC中，D，E分别为AB、AC边上的点，且AD=AE，连接DE．若AC=4，AB=5．求证：△ADE∽△ACB．【解答】证明：∵AC=3，AB=5，AD=，∴，∵∠A=∠A，∴△ADE∽△ACB．图③双A字型【例4】如图，在△ABC中，D，E分别是AB，AC上的点，∠AED=∠ABC，∠BAC 的平分线AF交DE于点G，交BC于点F．（1）试写出图中所有的相似三角形，并说明理由（2）若=，求的值．【解答】解：（1）∵∠AED=∠ABC，∠EAD=∠BAC，∴△ABC∽△AED．∵∠AED=∠ABC，∠EAG=∠BAF，∴△AEG∽△ABF．∵∠EDG=∠ACF，∠DAG=∠CAF，∴△ADG∽△ACF．（2）∵=，∴=，∵△ADG∽△ACF，∴==．【练习1】如图，在△ABC中，D、E分别是AB、AC上的点，AE=4，AB=6，AD：AC=2：3，△ABC的角平分线AF交DE于点G，交BC于点F．（1）请你直接写出图中所有的相似三角形；（2）求AG与GF的比．【解答】解：（1）△ADG∽△ACF，△AGE∽△AFB，△ADE∽△ACB；（2）∵==，=，∴=，又∵∠DAE=∠CAB，∴△ADE∽△ACB，∴∠ADG=∠C，∵AF为角平分线，∴∠DAG=∠FAE∴△ADG ∽△ACF ， ∴==，∴=2．图④内含正方形A 字形，结论AH a aAH BC-=（a 为正方形边长）【例5】如图，△ABC ，是一张锐角三角形的硬纸片，AD 是边BC 上的高，BC=40cm ，AD=30cm ，从这张硬纸片上剪下一个长HG 是宽HE 的2倍的矩形EFGH ，使它的一边EF 在BC 上，顶点G 、H 分别在AC ，AB 上，AD 与HG 的交点为M ． （1）求证：=；（2）求这个矩形EFGH 的周长；（3）是否存在一个实数a ，当HE=a 时从三角形硬纸片上剪下的矩形面积最大？若存在，试求出a ；若不存在，请说明理由．【解答】（1）证明：∵四边形HEFG 为矩形， ∴HG ∥EF ， 而AD ⊥BC ， ∴AM ⊥BC ，。

三角形 数学建模 四大常考相似模型

三角形 数学建模 四大常考相似模型
为BC上一点,MN⊥AM,MN交CD 于点N. (1)求证:△ABM∽△MCN; (2)若AB=6,BM=2,求DN的长.
(1)证明:∵∠B=∠C=∠AMN=90°,
∴∠AMB+∠CMN=90°,∠CMN+∠MNC=90°,
∴∠AMB=∠MNC,
∴△ABM∽△MCN.
2.结论: (1)
一线三垂直型 已知:∠B=∠ACE=∠D=90° 结论:(1)△ABC∽△CDE (2)AB·DE=BC·CD (3)当C为BD中点时,△ABC∽△CDE∽△ACE
(2)
一线三等角型 已知:∠B=∠ACE=∠D=α 结论:(1)△ABC∽△CDE (2) AB·DE=BC·CD (3)当C为BD中点时,△ABC∽△CDE∽△ACE
BC
1 3
.
2.如图,在△ABC中,P为边AB上一点,且∠ACP=∠B,若 AP=2,BP=3,则AC的长为 10.
3.如图,在△ABC中,AB=8,AC=6,点D在边AC上,AD=2,若点E在
边AB上,以A,D,E为顶点的三角形与△ABC相似,则AE的长
为
8或3
32
.
模型解读
模型二 8字型 特征:有一组隐含的等角(即对顶角相等). (1)
第四章 三角形
数学建模 四大常考相似模型
模型解读
特征:有一个公共角. (1)
模型一 A字型
A 字型 已知:DE∥BC 结论:AD = AE = DE
AB AC BC
反 A 字型 (2)
已知:∠AED=∠C 结论:AD = AE = DE
AB AC BC
(3)
反 A 字型(共边共角)
已知:∠ABD=∠C
8 字型 已知:AB∥CD 结论:AO = BO = AB

相似三角形重要模型—(双)A字型与(双)8字型—2023-2024学年九年级数学上册(解析版)

相似三角形重要模型—(双)A字型与(双)8字型—2023-2024学年九年级数学上册(解析版)

相似三角形重要模型-（双）A 字型与（双）8字型相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考的常考题型。

本专题重点讲解相似三角形的（双）A 字模型和（双）8（X ）字模型．A 字型和8 (X )字型的应用难点在于过分割点(将线段分割的点)作平行线构造模型，有的是直接作平行线，有的是间接作平行线(倍长中线就可以理解为一种间接作平行线) ， 这一点在模考中无论小题还是大题都是屡见不鲜的。

模型1. “A ”字模型 【模型解读与图示】“A ”字模型图形（通常只有一个公共顶点）的两个三角形有一个“公共角”（是对应角），再有一个角相等或夹这个公共角的两边对应成比例，就可以判定这两个三角形相似．图1 图2 图31）“A ”字模型 条件：如图1，DE ∥BC ；结论：△ADE ∽△ABC ⇔AD AB ＝AE AC ＝DEBC. 2）反“A ”字模型 条件：如图2，∠AE D ＝∠B ；结论：△ADE ∽△ACB ⇔AD AC ＝AE AB ＝DEBC .3）同向双“A ”字模型条件：如图3，EF ∥BC ；结论：△AEF ∽△ABC ，△AEG ∽△ABD ，△AGF ∽△ADC ⇔EG FG AGBD CD AD== 例1．（2022·浙江杭州·中考真题）如图，在ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，连接DE ，EF ，已知四边形BFED 是平行四边形，DE 1BC 4=．(1)若8AB =，求线段AD 的长．(2)若ADE 的面积为1，求平行四边形BFED 的面积．【答案】(1)2(2)6【分析】（1）利用平行四边形对边平行证明ADE ABC △△∽，得到DE ADBC AB=即可求出； （2）利用平行条件证明ADE EFC ∽，分别求出ADE EFC 与、ADE ABC 与的相似比，通过相似三角形的面积比等于相似比的平方分别求出EFC S V 、ABCS，最后通过BFEDABCEFCADESSSS=−−求出．(1)∵四边形BFED 是平行四边形，∴∥DE BC ，∴ADE ABC △△∽，∴DE ADBC AB=， ∵DE 1BC 4=，∴AD 1AB 4=，∴118244AD AB ==⨯=； (2)∵四边形BFED 是平行四边形，∴∥DE BC ，EF AB ∥，DE =BF ，∴,AED ECF EAD CEF ∠=∠∠=∠，∴ADE EFC ∽∴2ADE EFCSDE SFC ⎛⎫= ⎪⎝⎭， ∵DE 1BC 4=，DE =BF ，∴43FC BC DE DE DE DE =−=−=， ∴133DE DE FC DE ==，∴221139ADE EFCS DE SFC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， ∵ADE ABC △△∽，DE 1BC 4=，2211416ADE ABCS DE SBC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， ∵1ADE S =△，∴9,16EFCABCSS==，∴16916BFEDABCEFCADES SSS=−−=−−=．【点睛】本题考查了相似三角形，熟练掌握相似三角形的面积比等于相似比的平方、灵活运用平行条件证明三角形相似并求出相似比是解题关键．例2．（2023秋·安徽六安·九年级校考期末）如图，在ABC 中，BD 、CE 分别是AC 、AB 边上的高．求证：ACB AED ∽V V ．【答案】见详解【分析】先证明ACE ABD ∽，即有AE ACAD AB =，再结合A A ∠=∠，即可证明ACB AED ∽V V ．【详解】∵BD 、CE 分别是AC 、AB 边上的高，∴90AEC ADB ∠=∠=︒， ∵A A ∠=∠，∴ACE ABD ∽，∴AE ACAD AB =，又∵A A ∠=∠，∴ACB AED ∽V V ． 【点睛】本题主要考查了相似三角形的判定与性质，掌握三角形的判定与性质是解答本题的关键． 例3．（2022·山东东营·中考真题）如图，在ABC 中，点F 、G 在BC 上，点E 、H 分别在AB 、AC 上，四边形EFGH 是矩形，2,EH EF AD =是ABC 的高．8,6BC AD ==，那么EH 的长为____________．【答案】245##4.8【分析】通过四边形EFGH 为矩形推出E H B C ∥，因此△AEH 与△ABC 两个三角形相似，将AM 视为△AEH 的高，可得出AM EHAD BC =，再将数据代入即可得出答案． 【详解】∵四边形EFGH 是矩形，∴E H B C ∥，∴AEF ABC ∽， ∵AM 和AD 分别是△AEH 和△ABC 的高，∴,AM EH DM EF AD BC ==，∴6AM AD DM AD EF EF =−=−=−，∵=2EH EF ，代入可得：6268EF EF −=，解得12=5EF ， ∴1224=255EH ⨯=，故答案为：245．【点睛】本题考查了相似三角形的判定和性质及矩形的性质，灵活运用相似三角形的性质是本题的关键． 例4．（2022·浙江宁波·中考真题）(1)如图1，在ABC 中，D ，E ，F 分别为,,AB AC BC 上的点，,,DE BC BF CF AF =∥交DE 于点G ，求证：DG EG =．(2)如图2，在（1）的条件下，连接,CD CG ．若,6,3⊥==CG DE CD AE ，求DEBC的值． (3)如图3，在ABCD 中，45,︒∠=ADC AC 与BD 交于点O ，E 为AO 上一点，EG BD ∥交AD 于点G ，⊥EF EG交BC 于点F ．若40,︒∠=EGF FG 平分,10∠=EFC FG ，求BF 的长．【答案】(1)证明见详解(2)13(3)5+【分析】（1）利用∥DE BC ，证明,ADG ABF AEG ACF △△△△，利用相似比即可证明此问； （2）由（1）得DG EG =，CG DE ⊥，得出DCE 是等腰三角形，利用三角形相似即可求出DEBC的值； （3）遵循第（1）、（2）小问的思路，延长GE 交AB 于点M ，连接FM ，作MN BC ⊥，垂足为N ．构造出等腰三角形、含30°、45°角的特殊直角三角形，求出BN 、FN 的值，即可得出BF 的长． (1)解：∵DE BC ∥，∴,ADG ABF AEG ACF △△△△， ∴,==DG AG EG AG BF AF CF AF ，∴DG EGBF CF=．∵BF CF =，∴DG EG =． (2)解：由（1）得DG EG =，∵CG DE ⊥，∴6CE CD ==． ∵3AE =，∴9AC AE CE =+=．∵DE BC ∥，∴ADEABC ．∴13DE AE BC AC ==． (3)解：如图，延长GE 交AB 于点M ，连接FM ，作MN BC ⊥，垂足为N ．在ABCD 中，,45=∠=∠=︒BO DO ABC ADC ． ∵EG BD ∥，∴由（1）得=ME GE ，∵⊥EF EG ，∴10==FM FG ，∴∠=∠EFM EFG ． ∵40∠︒=EGF ，∴40EMF ∠=︒，∴50EFG ∠=︒． ∵FG 平分EFC ∠，∴50∠=∠=︒EFG CFG ， ∴18030∠=︒−∠−∠−∠=︒BFM EFM EFG CFG ．∴．在Rt FMN 中，sin 305,cos30=︒==︒=MN FM FN FM∵45,∠=︒⊥MBN MN BN ，∴5==BN MN ，∴5=+=+BF BN FN【点睛】本题考查了相似三角形的性质及判定、等腰三角形的性质及判定、解特殊的直角三角形等知识，遵循构第（1）、（2）小问的思路，构造出等腰三角形和特殊的直角三角形是解决本题的关键．例5. （2022•安庆一模）如图，在△ABC 中，点D 、E 、F 分别在边BC 、AB 、CA 上，且DE ∥CA ，DF ∥AB ．（1）若点D 是边BC 的中点，且BE ＝CF ，求证：DE ＝DF ；（2）若AD ⊥BC 于D ，且BD ＝CD ，求证：四边形AEDF 是菱形；（3）若AE ＝AF ＝1，求+的值．【分析】（1）根据中点和平行两个条件可得中点，从而可得DE 是△ABC 的中位线，进而可得DE ＝FC ，同理可得DF ＝BE ，即可解答；（2）根据已知易证四边形AEDF 是平行四边形，再利用等腰三角形的三线合一性质可得∠BAD ＝∠CAD ，然后利用平行线的性质可得∠＝∠CAD ，从而可得∠BAD ＝∠EDA ，进而可得EA ＝ED ，即可解答； （3）根据A 字模型相似三角形可知△BED ∽△BAC ，△CDF ∽△CBA ，从而可得＝，＝，然后把两个式子相加进行计算，即可解答．【解答】（1）证明：∵点D 是边BC 的中点，DE ∥CA ，∴点E 是AB 的中点，∴DE 是△ABC 的中位线，∴DE ＝AC ，∵点D 是边BC 的中点，DF ∥AB ，∴点F 是AC 的中点， ∴FC ＝AC ，∴DE ＝FC ，同理可得：DF ＝BE ，∵BE ＝FC ，∴DE ＝DF ；（2）证明：∵DE ∥CA ，DF ∥AB ，∴四边形AEDF 是平行四边形， ∵AD ⊥BC ，BD ＝CD ，∴AD 是BC 的垂直平分线，∴AB ＝AC ，∴∠BAD ＝∠CAD ，∵DE ∥AC ，∴∠EDA ＝∠CAD ，∴∠BAD＝∠EDA，∴EA＝ED，∴四边形AEDF是菱形；（3）∵DE∥CA，∴∠EDB＝∠C，∵∠B＝∠B，∴△BED∽△BAC，∴＝，∵DF∥AB，∴∠B＝∠FDC，∵∠C＝∠C，∴△CDF∽△CBA，∴＝，∴+＝+＝＝1，∵四边形AEDF是平行四边形，∴DE＝AF，DF＝AE，∵AE＝AF＝1，∴DE＝DF＝1，∴+＝1，∴+的值为1．【点评】本题考查了相似三角形的判定与性质，全等三角形的判定与性质，线段垂直平分线的性质，分式的化简求值，菱形的判定与性质，熟练掌握菱形的判定与性质，以及A字模型相似三角形的关键．模型2. “X”字模型（“8”模型）【模型解读与图示】“8”字模型图形的两个三角形有“对顶角”，再有一个角相等或夹对顶角的两边对应成比例就可以判定这两个三角形相似．图1 图2 图3 图41）“8”字模型条件：如图1，AB∥CD；结论：△AOB∽△COD⇔ABCD＝OAOC＝OBOD.2）反“8”字模型条件：如图2，∠A＝∠D；结论：△AOB∽△DOC⇔ABCD＝OAOD＝OBOC.3）平行双“8”字模型条件：如图3，AB∥C D；结论：AE BE ABDF CF CD==4）斜双“8”字模型条件：如图4，∠1＝∠2；结论：△AOD∽△B O C，△AOB∽△DOC⇔∠3＝∠4.例1．（2022·河北·中考真题）如图是钉板示意图，每相邻4个钉点是边长为1个单位长的小正方形顶点，钉点A ，B 的连线与钉点C ，D 的连线交于点E ，则（1）AB 与CD 是否垂直？______（填“是”或“否”）；（2）AE ＝______．【答案】 是【分析】（1）证明△ACG ≌△CFD ，推出∠CAG =∠FCD ，证明∠CEA =90°，即可得到结论；（2）利用勾股定理求得AB 的长，证明△AEC ∽△BED ，利用相似三角形的性质列式计算即可求解． 【详解】解：（1）如图：AC =CF =2，CG =DF =1，∠ACG =∠CFD =90°， ∴△ACG ≌△CFD ， ∴∠CAG =∠FCD ， ∵∠ACE +∠FCD =90°，∴∠ACE +∠CAG =90°，∴∠CEA =90°，∴AB 与CD 是垂直的，故答案为：是；（2）AB ∵AC ∥BD ，∴△AEC ∽△BED ，∴AC AEBD BE =，即23AE BE =，∴2AE BE =∴AE =25BE【点睛】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，解答本题的关键是明确题意，找出所求问题需要的条件．例2.（2022·广西·中考模拟）如图，已知在△ABC 中，BE 平分∠ABC 交AC 于E ，点D 在BE 延长线上，且BA •BC ＝BD •BE ．（1）求证：△ABD ∽△EBC ；（2）求证：AD 2＝BD •DE ．【答案】见解析【解答】证明：（1）∵BE 平分∠ABC ，∴∠ABD ＝∠EBC ， ∵BA •BC ＝BD •BE ．即AB BC=BD BE，∴△ABD ∽△EBC ；（2）∵△ABD ∽△EBC ，∴∠BAD ＝∠BEC ，∠ADB ＝∠BCE ， ∵∠AED ＝∠BEC ，∴∠BAD ＝∠AED ，∴△ADE ∽△BEC ， ∴△AED ∽△ABD ，∴AD BD=DE AD，即AD 2＝BD •DE ．例3.（2023·浙江九年级期中）如图，AD 与BC 交于点O ，EF 过点O ，交AB 与点E ，交CD 与点F ，BO ＝1，CO ＝3，AO =32，DO =92．（1）求证：∠A ＝∠D ．（2）若AE ＝BE ，求证：CF ＝DF ．【答案】【解析】证明：（1）∵BO ＝1，CO ＝3，AO =32，DO =92．∴OB OC =AO DO，∵∠AOB ＝∠COD ，∴△OAB ∽△ODC ，∴∠A ＝∠D ． （2）∵∠A ＝∠D ，∴AB ∥CD ， ∴AE DF =OE OF ，BE CF =OE OF ，∴AE DF =BECF． ∵AE ＝BE ，∴CF ＝DF ．例4．（2022·广西贵港·中考真题）已知：点C ，D 均在直线l 的上方，AC 与BD 都是直线l 的垂线段，且BD 在AC 的右侧，2BD AC =，AD 与BC 相交于点O ． (1)如图1，若连接CD ，则BCD △的形状为______，AOAD的值为______； (2)若将BD 沿直线l 平移，并以AD 为一边在直线l 的上方作等边ADE ． ①如图2，当AE 与AC 重合时，连接OE ，若32AC =，求OE 的长；②如图3，当60ACB ∠=︒时，连接EC 并延长交直线l 于点F ，连接OF ．求证：OF AB ⊥．【答案】(1)等腰三角形，13(2)①OE =②见解析【分析】（1）过点C 作CH ⊥BD 于H ，可得四边形ABHC 是矩形，即可求得AC =BH ，进而可判断△BCD 的形状，AC 、BD 都垂直于l ，可得△AOC ∽△BOD ，根据三角形相似的性质即可求解．（2）①过点E 作EF AD ⊥于点H ，AC ，BD 均是直线l 的垂线段，可得//AC BD ，根据等边三角形的性质可得30BAD ∠=︒，再利用勾股定理即可求解．②连接CD ，根据//AC BD ，得60CBD ACB ∠=∠=︒，即BCD △是等边三角形，把ABD △旋转得90ECD ABD ∠=∠=︒，根据30°角所对的直角边等于斜边的一般得到13AF AO AB AD ==，则可得AOF ADB △∽△，根据三角形相似的性质即可求证结论． (1)解：过点C 作CH ⊥BD 于H ，如图所示：∵AC ⊥l ，DB ⊥l ，CH ⊥BD ，∴∠CAB =∠ABD =∠CHB =90°，∴四边形ABHC 是矩形，∴AC =BH ， 又∵BD =2AC ，∴AC=BH=DH ，且CH ⊥BD ，∴BCD △的形状为等腰三角形， ∵AC 、BD 都垂直于l ，∴△AOC ∽△BOD ，122AO AC AC DO DB AC ∴===，即2DO AO =， 133AO AO AD AO DO A AO O ∴===+，故答案为：等腰三角形，13．(2)①过点E 作EF AD ⊥于点H ，如图所示：∵AC ，BD 均是直线l 的垂线段，∴//AC BD ，∵ADE 是等边三角形，且AE 与AC 重合，∴∠EAD =60°，∴60ADB EAD ∠=∠=︒，∴30BAD ∠=︒，∴在Rt ADB 中，2AD BD =，=AB ，又∵2BD AC =，32AC =，∴6,AD AB ==∴132AH DH AD ===，又Rt ADB ，∴EH =又由（1）知13AO AD =，∴123AO AD ==，则1OH =，∴在Rt EOH △中，由勾股定理得：OE =②连接CD ，如图3所示：∵//AC BD ，∴60CBD ACB ∠=∠=︒，∵BCD △是等腰三角形，∴BCD △是等边三角形，又∵ADE 是等边三角形， ∴ABD △绕点D 顺时针旋转60︒后与ECD 重合，∴90ECD ABD ∠=∠=︒， 又∵60BCD ACB ∠=∠=︒，∴30ACF FCB FBC ∠=∠=∠=︒， ∴2FC FB AF ==，∴13AF AO AB AD ==，又OAF DAB ∠=∠，∴AOF ADB △∽△， ∴90AFO ABD ∠=∠=︒，∴OF AB ⊥．【点睛】本题考查了矩形的判定及性质、三角形相似的判定及性质、等边三角形的判定及性质、勾股定理的应用，熟练掌握三角形相似的判定及性质和勾股定理的应用，巧妙借助辅助线是解题的关键．模型3. “AX ”字模型（“A 8”模型） 【模型解读与图示】图1 图2 图3 1）一“A ”一“8”模型条件：如图1，DE ∥BC ；结论：△ADE ∽△ABC ，△DEF ∽△CBF ⇔AD AE DE DF FEAB AC BC FC BF====2）两“A ”一“8”模型条件：如图2，DE ∥AF ∥BC ；结论：111BC DE AF+=. 3）四“A ”一“8”模型 条件：如图3，DE ∥AF ∥BC,1111BC DE AF AG+==；结论：AF =AG 例1．（2022·山东东营·中考真题）如图，点D 为ABC 边AB 上任一点，DE BC ∥交AC 于点E ，连接BE CD 、相交于点F ，则下列等式中不成立．．．的是（ ）A ．AD AEDB EC= B ．DE DFBC FC= C ．DE AEBC EC= D ．EF AEBF AC= 【答案】C【分析】根据平行线分线段成比例定理即可判断A ，根据相似三角形的性质即可判断B 、C 、D ． 【详解】解：∵∥DE BC ，∴AD AEBD EC =，△DEF ∽△CBF ，△ADE ∽△ABC ，故A 不符合题意； ∴DE DF EF CB CF BF ==，DE AECB AC =，故B 不符合题意，C 符合题意； ∴EF AEBF AC =，故D 不符合题意；故选C ． 【点睛】本题主要考查了相似三角形的性质与判定，平行线分线段成比例定理，熟知相似三角形的性质与判定，平行线分线段成比例定理是解题的关键．例2．（2023·浙江·杭州九年级期中）如图， ABC 中，中线AD ，BE 交于点F ，//EG BC 交AD 于点G ．（1）求AGGF的值．（2）如果BD =4DF =，请找出与BDA V 相似的三角形，并挑出一个进行证明．【答案】（1）3；（2）BDA FGE ∽△△，证明见解析 【分析】（1）先证明AGE ADC △∽△，再证明GEF DBF ∽△△，得到2DF GF =，则问题可解； （2）根据题意分别证明BDA FDB ∽△△，BDA FGE ∽△△问题可证． 【详解】解：（1）D Q 是BC 的中点，E 是AC 的中点，BD CD ∴=，AE CE =，//GE BC ，AGE ADC ∴∽△△，12AG GE AE AD CD AC ∴===，AG GD ∴=，2GE CD BD ==，//GE BC ，GEF DBF ∴∽△△，12GE GF BD DF ∴==，2DF GF ∴=，3AG DG GF ∴==，3AGGF ∴=．（2）当BD =4DF =时，由（1）可得 122GF DF ==，36AG DG GF ===，212AD AG ==，12GE BD ==44BD DF ==AD BD ==，AD BD BD DF ∴=，又BDG ADB ∠=∠，BDA FDB ∴∽△△，3GEGF =AD BD ==，AD GE BD GF ∴=，//GE BC ，ADB EGF ∴∠=∠，BDA FGE ∴∽△△．【点睛】本题考查了相似三角形的性质和判定，解答关键是根据题意选择适当方法证明三角形相似． 例2.（2023·广东九年级期中）如图，在菱形ABCD 中，∠ADE 、∠CDF 分别交BC 、AB 于点E 、F ，DF 交对角线AC 于点M ，且∠ADE ＝∠CDF ．（1）求证：CE ＝AF ；（2）连接ME ，若CE BE ＝CDCE，AF ＝2，求ME 的长．【解析】解：（1）∵四边形ABCD 是菱形，∴AD ＝CD ，∠DAF ＝∠DCE ， 又∵∠ADE ＝∠CDF ，∴∠ADE ﹣∠EDF ＝∠CDF ﹣∠EDF ，∴∠ADF ＝∠CDE ，在△ADF 和△CDE 中，ADF CDFAD CD DAF DCE ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ADF ≌△CDE ，∴CE ＝AF ．（2）∵四边形ABCD 是菱形，∴AB ＝BC ，由（1）得：CE ＝AF ＝2，∴BE ＝BF ，设BE ＝BF ＝x ，∵CE BE ＝CDCE，AF ＝2，∴222x x +=，解得x1，∴BE ＝BF1，∵CE BE ＝CD CE ，且CE ＝AF ，∴CE BE ＝CD CE ＝CD AF， ∵∠CMD ＝∠AMF ，∠DCM ＝∠AMF ，∴△AMF ∽△CMD ，∴CD CMAF AM=， ∴CD CM CEAF AM BE==，且∠ACB ＝∠ACB,∴△ABC ～△MEC, ∴∠CAB ＝∠CME=∠ACB ，∴ME=CE=2．例3. （2022·浙江九年级期中）如图，已知AB ∥CD ，AC 与BD 相交于点E ，点F 在线段BC 上，AB CD =12，BFCF =12．（1）求证：AB ∥EF ；（2）求S △ABE ：S △EBC ：S △ECD ．【答案】见解析【解析】（1）证明：∵AB ∥CD ，∴AB CD =BE ED =12，∵BF CF =12，∴BE ED =BFFC，∴EF ∥CD ，∴AB ∥EF ． （2）设△ABE 的面积为m ．∵AB ∥CD ，∴△ABE ∽△CDE ，∴S △ABE S △EDC =（AB CD ）2=14，∴S △CDE ＝4m ，∵AE CE =AB CD =12，∴S △BEC ＝2m ， ∴S △ABE ：S △EBC ：S △ECD ＝m ：2m ：4m ＝1：2：4．例4．（2022•安庆模拟）在四边形ABCD 中，对角线AC 、BD 相交于点O ． （1）如图①，若四边形ABCD 为矩形，过点O 作OE ⊥BC ，求证：OE ＝CD ．（2）如图②，若AB ∥CD ，过点O 作EF ∥AB 分别交BC 、AD 于点E 、F ．求证：＝2．（3）如图③，若OC 平分∠AOB ，D 、E 分别为OA 、OB 上的点，DE 交OC 于点M ，作MN ∥OB 交OA 于一点N ，若OD ＝8，OE ＝6，直接写出线段MN 长度．【分析】（1）由OE ⊥BC ，DC ⊥BC ，可知EO ∥CD ，且OB ＝OD ，可得结论； （2）由△DFO ∽△DAB ，得，同理，，，利用等式的性质将比例式相加，从而得出结论；（3）作DF ∥OB 交OC 于点F ，连接EF ，可知△ODF 是等腰三角形，得DO ＝DF ＝8，由△DMF ∽△EMO ，可得EM ＝，由△DMN ∽△DOE ，得，从而得出答案．【解答】（1）证明：∵四边形ABCD 是矩形，∴O 是AC 中点，AB ⊥BC ， ∵OE ⊥BC ，∴OE ∥AB ，∴E 是BC 中点，∴OE ＝； （2）证明：∵EF ∥AB ，∴△DFO ∽△DAB ，∴， 同理，，，∴＝，∴，即； （3）解：作DF ∥OB 交OC 于点F ，连接EF ，∵OC 平分∠AOB ，∴∠AOC ＝∠BOC ，∵DF ∥OB ，∴∠DFO ＝∠BOC ＝∠AOC ， ∴△ODF 是等腰三角形，∴DO ＝DF ＝8，∵DF ∥OE ，∴△DMF ∽△EMO ，∴，∴EM ＝，∴，∵MN ∥OE ，∴△DMN ∽△DOE ，∴，∴，∴MN ＝．【点评】本题是相似形综合题，主要考查了矩形的性质，相似三角形的判定与性质，等腰三角形的性质，对比例式进行恒等变形是解题的关键．课后专项训练1. （2021·山东淄博·中考真题）如图，,AB CD 相交于点E ，且////AC EF DB ，点,,C F B 在同一条直线上．已知,,AC P EF r DB q ===，则,,p q r 之间满足的数量关系式是（ ）A ．111r q p+=B ．112p r q+= C ．111p q r += D ．112q r p+=【答案】C【分析】由题意易得BEF BAC ∽△△，CEF CDB ∽，则有EF BF AC BC =，EF CF BD BC =，然后可得1EF EFAC BD +=，进而问题可求解．【详解】解：∵////AC EF DB ，∴BEF BAC ∽△△，CEF CDB ∽， ∴EF BFAC BC =，EF CF BD BC =，∴1EF EF BF CFAC BD BC BC +=+=，∵,,AC P EF r DB q ===， ∴1r r p q +=，即111p q r +=； 故选C ．【点睛】本题主要考查相似三角形的性质与判定，熟练掌握相似三角形的性质与判定是解题的关键． 九年级校考期末）如图，ABC 中，:PEDPDGS S=（ 【答案】A【分析】根据角平分线的定义及平行线的性质可知PEH △是等腰三角形，再根据相似三角形的判定与性质可知12ED EH FD PF ==，进而解答即可． 【详解】解：过点E 作PF EH ∥AD 的延长线于点H ， ∵AD 是ABC 的角平分线， ∴BAD CAD ∠=∠， ∵PE AB ∥，PF AC ∥，∴BAC EPD ∠=∠，CAD DPF ∠=∠， ∴EPD FPD ∠=∠， ∵EH PF ∥， ∴H DPF ∠=∠， ∴EPD H ∠=∠， ∴PEH △是等腰三角形， ∴PE EH =， ∵3PE =，∴3PE EH ==， ∵EH PF ∥， ∴PFD HED ∠=∠， ∴EDH FDP ∽， ∴ED EHFD PF =， ∵6PF =，∴3162ED EH FD PF ===， ∴2FD ED =，∴设ED a =，2FD a =， ∴3EF ED FD a =+=， ∵G 是EF 的中点，∴1322EG EF a ==， ∴3122DG EG ED a a a=−=−=， 过P 作PM ED ⊥，垂足为M ， ∴12PEDSED PM=⋅⋅，12PDGS DG PM =⋅⋅，∴122:11122PED PDGED PMSaS DG PM a ⋅⋅===⋅⋅，故选：A ．【点睛】本题考查了平行线的性质，相似三角形的判定与性质，角平分线的定义，中点的定义，等腰三角形的判定与性质，掌握相似三角形的判定与性质是解题的关键．3．（2022秋·九年级单元测试）如图，在平行四边形ABCD 中，E 为边AD 的中点，连接AC，BE 交于点F ．若△AEF 的面积为2，则△ABC 的面积为( )A ．8B ．10C ．12D ．14【答案】C【分析】先利用平行四边形的性质得AD BC ∥，AD=BC ，由AE BC ∥可判断△AEF ∽△CBF ，根据相似三角形的性质得12EF AF AE BF CF BC ===，然后根据三角形面积公式得16AEF ABC S S ∆∆=，则=6=12ABC AEF S S ∆∆．【详解】∵平行四边形ABCD ∴AD BC ∥，AD=BC ∵E 为边AD 的中点 ∴BC=2AE ∵AE BC ∥ ∴∠EAC=∠BCA 又∵∠EFA=∠BFC ∴△AEF ∽△CBF如图，过点F 作FH ⊥AD 于点H ，FG ⊥BC 于点G ， 则12EF AF AE HF BF CF BC FG ====，∴111221362AEF ABC AE FH BC FHS S BC FH BC HG ∆∆⋅⋅⋅===⋅⋅⋅，∵△AEF 的面积为2 ∴66212ABC AEF S S ∆∆==⨯=故选C ．【点睛】本题考查了相似三角形的性质，属于同步基础题．A ．43AC =，123BD = C ．6AC =，83BD = 【答案】D【分析】过点B 作BO AD ∥交AC 于点O ，证明AED OEB ∽，可求得OE AO =理求出BO 的长，进而可求出AC 的长，再根据勾股定理求出BE 的长，进而求出BD 的长． 【详解】过点B 作BO AD ∥交AC 于点O ，如图所示：∵AC AD ⊥，BO AD ∥， ∴90DAC BOA ︒∠=∠=． ∵AED OEB ∠=∠， ∴AED OEB ∽， ∴BE EO BODE AE DA ==． ∵3DE BE =，∴13EO BO AE DA ==．∵AE =，∴OE∴AO =∵AB AC =，75ACB ∠=︒， ∵75ABC ACB ∠=∠=︒， ∴30BAC ∠=︒， ∴2AB BO =．在Rt AOB △中，222BO AO AB +=，即(()2222BO BO +=，解得：4BO =，∴8AB AC ==．∵OE 4BO =，∴BE ==∴3DE BE ==∴BD BE DE =+= 故选D ．【点睛】本题考查了相似三角形的判定与性质，等腰三角形的性质，含30度角的直角三角形的性质，勾股定理以及平行线的性质，解题的关键是利用勾股定理求出BE 的长度．A ．45B ．54【答案】C【分析】先由平行四边形性质得到AB CD ∥，AB CD =，证明AOB COE ∽△△得到249AOB COE S AB CE S æöç÷==ç÷èø△△，进而得到221AB DE ==，再证明AFB DFE ∽求解即可．【详解】解：∵四边形ABCD 是平行四边形， ∴AB CD ∥，AB CD =， ∴ABO E ∠=∠，BAO ECO ∠=∠，∴AOB COE ∽△△， ∴249AOB COE S AB CE S æöç÷==ç÷èø△△， ∴23AB CE =，则221AB DE ==，∵AFB DFE ∠=∠，ABF E ∠=∠， ∴AFB DFE ∽， ∴2AF ABDF DE ==，故选：C ．【点睛】本题考查平行四边形的性质、相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解答的关键．6．（2023·福建福州·校考二模）在数学综合实践课上，某学习小组计划制作一个款式如图所示的风筝．在骨架设计中，两条侧翼的长度设计50cm AB AC ==，风筝顶角BAC ∠的度数为110︒，在AB AC ，上取D ，E 两处，使得AD AE =，并作一条骨架AF DE ⊥．在制作风筝面时，需覆盖整个骨架，根据以上数据，B ，C 两点间的距离大约是（ ）（参考数据：sin550.82cos550.57tan55 1.43︒≈︒≈︒≈，，）A ．41cmB ．57cmC ．82cmD ．143cm【答案】C【分析】设AF 与DE 交于点G ，连接BC ，交AF 于点H ，根据已知易证ADE ABC △△∽，然后利用相似三角形的性质可得ADE ABC =∠∠，从而可得DE BC ∥，进而可得BC AF ⊥，再利用等腰三角形的三线合一性质可得2BC BH =，1552BAH BAC ∠=∠=︒，最后在Rt BAH 中，利用锐角三角函数的定义求出BH 的长，即可解答．【详解】解：设AF 与DE 交于点G ，连接BC ，交AF 于点H ，AD AE =，AB AC =，∴AD AEAB AC =， DAE BAC ∠=∠， ADE ABC ∴△△∽， ADE ABC ∴∠=∠， DE BC ∴∥，AF DE ⊥，BC AF ∴⊥，AB AC =，AF BC ⊥，2BC BH ∴=，1552BAH BAC ∠=∠=︒，在Rt BAH 中，50cm AB =，sin 55500.8241cm BH AB ∴=⋅︒≈⨯=， 282cm BC BH ∴==，B ∴，C 两点间的距离大约是82cm ，故选：C ．【点睛】本题考查了解直角三角形的应用，相似三角形的判定与性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．7．（2023·广东深圳·校考三模）如图，在Rt ABC 中，906ACB AC BC ∠=︒==，，D 是AB 上一点，点E 在BC上，连接CD AE ，交于点F ，若452CFE BD AD ∠=︒=，，则CE ＝ ．【答案】2【分析】过D 作DH 垂直AC 于H 点，过D 作DG AE ∥交BC 于G 点，先利用解直角三角形求出CD 的长，其次利用CDG CBD ∽，求出CG 的长，得出BG 的长，最后利用BDG BAE ∽，求出BE 的长，最后得出答案．【详解】解：如图：过D 作DH 垂直AC 于H 点，过D 作DG AE ∥交BC 于G 点，∵在Rt ABC 中，6AC BC ==，∴AB =又∵2BD AD =，∴AD =，∴在等腰直角三角形AHD 中，2AH DH ==， ∴624CH =−=，在Rt CHD 中，CD =∵DG AE ∥，∴45CFE CDG ∠=∠=︒，45B ∠=︒， ∴CDG B ∠=∠， 又∵DCG BCD ∠=∠，∴CDG CBD ∽， ∴CD CGCB CD =， ∴ 2CD CG CB =⋅，即206CG =， ∴CG =103 ，∴BG BC CG =−=108633−=，又∵DG AE ∥，∴BDG BAE ∽， 又∵2BD AD ＝， ∴23BD BG BA BE ==，又83BG =，∴342BE BG =⨯=，∴642CE =−=， 故答案为：2．【点睛】本题考查勾股定理，等腰直角三角形性质及相似三角形的判定与性质综合，解题关键在于正确做出辅助线，利用相似三角形的性质得出对应边成比例求出答案．8．（2023春·山东东营·八年级统考期末）如图，在ABC 中，D ，E ，F 分别是AB ，AC ，BC 上的点，且DE BC ∥，EF AB ∥，:2:3AD DB =，20cm BC =，则BF = cm ．【答案】8【分析】首先根据平行四边形的判定证明四边形BDEF 是平行四边形，则BF DE =，然后根据相似三角形的性质即可求解．【详解】解：∵DE BC ∥，EF AB ∥， ∴四边形BDEF 是平行四边形， ∴BF DE =． ∵:2:3AD DB =， ∴:2:5AD AB =． ∵DE BC ∥， ∴ADE ABC △△∽，∴::2:5DE BC AD AB ==，即:202:5DE =， ∴8DE =， ∴8BF =． 故BF 的长为8cm ． 故答案为：8【点睛】本题主要考查平行四边形的判定及性质，相似三角形的判定与性质，掌握这些性质及判定是解题的关键．九年级校考阶段练习）如图，在ABC 中，【答案】【分析】如图所示，取AC 中点H ，连接DH ，先求出5BC =，再由线段垂直平分线的性质得到DE DB ⊥，点D 为AB 中点，证明BD DE =得到DE BD ===AD BD ==得到12.52DH BC DH BC ==∥，，进而证明DFH EFC △∽△，得到57DF DE ==，利用勾股定理可得AF ==．【详解】解：如图所示，取AC 中点H ，连接DH ， ∵61BE CE CE ==，， ∴6BE =， ∴5BC =，∵DE 垂直平分线段AB ， ∴DE DB ⊥，点D 为AB 中点， 又∵=45ABC ∠︒，∴9045E DBE =︒−=︒∠∠， ∴E DBE =∠， ∴BD DE =，∴2DE BD ===∴AD BD ==∵点H 为AC 中点，点D 为AB 中点， ∴DH 为ABC 中位线， ∴12.52DH BC DH BC ==∥，，∴DFH EFC △∽△， ∴2.5512DF DH EF CE ===，∴577DF DE ==，∴AF ==，故答案为：．【点睛】本题主要考查了相似三角形的性质与判定，三角形中位线定理，勾股定理，线段垂直平分线的性质，等腰直角三角形的性质与判定等等，正确作出辅助线构造相似三角形是解题的关键．【答案】45【分析】如图所示，延长CD 交各格线于点D ，证明AOC BOD ∽，即可得到45OA AC OB BE ==． 【详解】解：如图所示，延长CD 交网格线于点D ， 由网格的特点可知点E 在格点处， ∵AC BE ， ∴AOC BOD ∽， ∴45OA AC OB BE ==， 故答案为：45．【点睛】本题主要考查了相似三角形的性质与判定，正确作出辅助线构造相似三角形是解题的关键．11.已知：如图，点D ，F 在△ABC 边AC 上，点E 在边BC 上，且DE ∥AB ，CD 2＝CF •CA ． （1）求证：EF ∥BD ；（2）如果AC •CF ＝BC •CE ，求证：BD 2＝DE •BA ．【答案】见解析【解析】证明：（1）∵DE ∥AB ，∴CD AC =CE CB，∵CD 2＝CF •CA ．∴CD AC=CF CD，∴CF CD=CE CB，∴EF ∥BD ；（2）∵EF ∥BD ，∴∠CEF ＝∠CBD ，∵AC •CF ＝BC •CE ，∴AC BC =CECF ，且∠C ＝∠C ，∴△CEF ∽△CAB ，∴∠CEF ＝∠A ，∴∠DBE ＝∠A ，∵DE ∥AB ，∴∠EDB ＝∠DBA ，且∠DBE ＝∠A ，∴△BAD ∽△DBE ，∴BA BD =BDDE∴BD 2＝BA •DE12．[阅读理解]构造“平行八字型”全等三角形模型是证明线段相等的一种方法，我们常用这种方法证明线段的中点问题．例如：如图，D 是△ABC 边AB 上一点，E 是AC 的中点，过点C 作CF ∥AB ，交DE 的延长线于点F ，则易证E 是线段DF 的中点．[经验运用]请运用上述阅读材料中所积累的经验和方法解决下列问题．（1）如图1，在正方形ABCD 中，点E 在AB 上，点F 在BC 的延长线上，且满足AE ＝CF ，连接EF 交AC 于点G ．求证：①G 是EF 的中点；②CG ＝2BE ； [拓展延伸]（2）如图2，在矩形ABCD 中，AB ＝2BC ，点E 在AB 上，点F 在BC 的延长线上，且满足AE ＝2CF ，连接EF 交AC 于点G ．探究BE 和CG 之间的数量关系，并说明理由；（3）如图3，若点E 在BA 的延长线上，点F 在线段BC 上，DF 交AC 于点H ，BF ＝2，CF ＝1，（ 2）中的其它条件不变，请直接写出GH 的长．【答案】（1）①详见解析；②详见解析；（2）BE ，理由详见解析；（3．【分析】（1）①过点E 作EI ∥BC 交AC 于点I ，证明△EIG ≌△FCG （ASA ），得出EG ＝FG 即可；②由等腰直角三角形的性质得出 AI ，由平行线得出AIAE＝IC EB IC ，由全等三角形的性质得出IG ＝CG ＝12IC ，即可得出结论；（2）作EI ∥BC 交AC 于点I ，由三角函数证出AE ＝2IE ，得出IE ＝CF ，证△EIG ≌△FCG （ASA ），得出EG ＝FG ，IG ＝CG ，设IE ＝a ，则AE ＝2a ，求出AE AI，则IC EB ＝AI AE ，得出IC EB ，即可得出结果；（3）作FP ∥AB 交AC 于P ，则FP ∥CD ，∠CFP ＝∠ABC ＝90°，∠CPF ＝∠CAB ，则tan ∠CPF ＝CF PF＝tan ∠CAB ＝BCAB＝12，求出AE ＝PF ＝2，BC ＝3，CD ＝AB ＝2BC ＝6，AC ＝△CPF ∽△CAB ，得出PCAC ＝CF BC ＝13，求出PC ＝13AC PA ＝AG ＝PG △PFH ∽△CDH ，得出PH CH ＝PF CD ＝13，得出PH ＝14PC 【详解】（1）证明：①过点E 作EI ∥BC 交AC 于点I ，如图1所示：∵四边形ABCD 是正方形， ∴AB ＝BC ，∠AEI ＝∠ABC ＝90°， ∴∠BAC ＝45°， ∴∠AIE ＝∠BAC ＝45°，∴AE＝EI，∵AE＝CF，∴CF＝EI，∵EI∥BC，∴∠EIG＝∠FCG，∠IEG＝∠CFG，在△EIG和△FCG中，EIG FCG EI FCIEG CFG ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△EIG≌△FCG（ASA），∴EG＝FG，∴G是EF的中点；②在Rt△AEI中，∠AEI＝90°，AE＝EI，∴△AEI是等腰直角三角形，∴AI，∴AI AE∵EI∥BC，∴AIAE＝ICEB∴IC，∵△EIG≌△FCG，∴IG＝CG＝12IC，∴CG＝12＝2BE；（2）解：BE和CG之间的数量关系为：BE；理由如下：过点E作EI∥BC交AC于点I，如图2所示：∵四边形ABCD是矩形，∴∠AEI＝∠ABC＝90°，AB∥CD，AB＝CD，在Rt△AEI和Rt△ABC中，∠ABC＝∠AEI＝90°，AB＝2BC，∴tan∠IAE＝IEAE＝BCAB＝12，∴AE＝2IE，∵AE＝2CF，∴IE＝CF，∵EI∥BC，∴∠EIG＝∠FCG，∠IEG＝∠CFG，在△EIG和△FCG中，EIG FCG EI CFIEG CFG ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△EIG≌△FCG（ASA），∴EG＝FG，IG＝CG，设IE＝a，则AE＝2a，在Rt△AEI中，∠AEI＝90°，∴AI，cos∠IAE＝AEAI，即AEAI，∵EI∥BC，∴ICEB＝AIAE，∴ICEB，∵IG＝CG＝12IC，∴CG，∴BE；（3）解：作FP∥AB交AC于P，如图3所示：则FP∥CD，∠CFP＝∠ABC＝90°，∠CPF＝∠CAB，在Rt△CFP和Rt△ABC中，AB＝2BC，∴tan∠CPF＝CFPF＝tan∠CAB＝BCAB＝12，∴PF＝2CF，∵AE＝2CF，∴AE＝PF＝2，同（2）得：△AEG≌△PFG（AAS），∴AG＝PG，∵BF＝2，CF＝1，∴BC＝3，CD＝AB＝2BC＝6，∴AC∵FP∥AB，∴△CPF∽△CAB，∴PCAC＝CFBC＝13，∴PC＝13AC PA＝AC﹣PC＝∴AG＝PG＝12PA ∵FP∥CD，∴△PFH∽△CDH，∴PHCH＝PFCD＝26＝13，∴PH＝14 PC∴GH＝PG+PH＝【点睛】本题是四边形综合题，主要考查了正方形的性质、矩形的性质、勾股定理、三角函数、全等三角形的判定与性质、平行线的性质、相似三角形的判定与性质等知识；作辅助线构建全等三角形与相似三角形是解题的关键．13．（2022·湖南常德·九年级校考期中）如图1，ΔABC中，AB=AC，点D在BA的延长线上，点E在BC上，DE=DC，点F是DE与AC的交点．（1）求证：∠BDE=∠ACD；（2）若DE=2DF，过点E作EG//AC交AB于点G，求证：AB=2AG；（3）将“点D在BA的延长线上，点E在BC上”改为“点D在AB上，点E在CB的延长线上”，“点F是DE 与AC的交点”改为“点F是ED的延长线与AC的交点”，其它条件不变，如图2．①求证：AB·BE=AD·BC；②若DE=4DF，请直接写出SΔABC:SΔDEC的值．【答案】（1）见解析；（2）见解析；（3）①见解析；②16:15．【分析】（1）运用等腰三角形的性质及三角形的外角性质就可解决问题．（2）如图1，证明△DCA≌△EDG（AAS），得AD=EG，根据等腰三角形的判定得：DG=AB，由平行线分线段成比例定理得：2DE DGDF AD==，由此可得结论；（3）①如图2△DCA≌△EDG（AAS），得DA=EG，再证明△ACB∽△GEB，列比例式可得结论；②如图3，作辅助线，构建△ABC和△DCE的高线，先得14AF ADEG DG==，设AF=a，则EG=AD=4a，DG=16a，根据AH∥PD，得123164PD BD aAH AB a===，设PD=3h，AH=4h，根据EG∥AC，同理得41164BG BE aAB BC a===，设BE=y，BC=4y，利用三角形面积公式代入可得结论．【详解】（1）证明：∵AC=AB，∴∠ACB=∠B，∵DC=DE，∴∠DCE=∠DEC，∴∠ACD+∠ACB=∠B+∠BDE，∴∠BDE=∠ACD；（2）证明：如图1，∵EG∥AC，∴∠DAC=∠DGE，∠BEG=∠ACB，由（1）知：∠DCA=∠BDE，∵DC=DE，∴△DCA≌△EDG（AAS），∴AD=EG，∵∠B=∠ACB=∠BEG，∴EG=BG=AD，∴DG=AB，∵DE=2DF，AF∥EG，∴2 DE DGDF AD==，∴DG=2AD=2AG，∴AB=DG=2AG；（3）解：①如图2，过点E作EG∥AC，交AB的延长线于点G，则有∠A=∠G，∵AB=AC，CD=DE，∴∠ACB=∠ABC，∠DCE=∠DEC，∴∠ACD+∠DCE=∠EDG+∠DEC，∴∠ACD=∠EDG，在△DCA和△EDG中，∵ACD EDGA GCD DE∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DCA≌△EDG（AAS）．∴DA=EG，∵AC∥EG，∴△ACB∽△GEB，∴AC BC EG BE=，∵EG=AD，AC=AB，∴AB•BE=AD•BC；②如图3，过A作AH⊥BC于H，过D作DP⊥BC于P，则AH∥PD，∵AF∥EG，∴AF AD DF EG DG DE==，∵DE=4DF，∴14 AF ADEG DG==，设AF=a，则EG=AD=4a，DG=16a，∵∠ACB=∠ABC，∴∠GBE=∠BEG，∴BG=EG=4a，∴BD=12a，∵AH∥PD，∴123164 PD BD aAH AB a===，设PD=3h，AH=4h，∵EG∥AC，∴41164 BG BE aAB BC a===，设BE=y，BC=4y，∴S△ABC=12BC•AH=4•42y h=162yh=8yh，S△DCE=12CE•PD=5•32y h=152yh，∴S△ABC：S△DEC=8yh：152yh=16：15．【点睛】本题是三角形的综合题，考查了相似三角形的判定与性质、全等三角形的判定与性质、平行线分线段成比例、等腰三角形的性质和判定等知识，第三问有难度，利用参数表示各线段的长是本题的关键，综合性较强．，将BCP沿直线【答案】(1)见解析(2)或2 5(3)13或3或555【分析】（1）由四边形ABCD 是平行四边形得到AD BC ∥，则E CBE =∠∠，由折叠可知，EBF CBE ∠=∠，则E EBF ∠=∠，即可得到结论；（2）过点B 作BM AE ⊥于点M ，分点F 在点D 的右侧和点F 在点D 的左侧两种情况进行求解即可；（3）分五种情况，分别画出图形，分别进行求解即可．【详解】（1）证明：∵四边形ABCD 是平行四边形，∴AD BC ∥，∴E CBE =∠∠，由折叠可知，EBF CBE ∠=∠，∴E EBF ∠=∠，∴BF EF =；（2）过点B 作BM AE ⊥于点M ，则3tan 4BM A AM ==，设3,4BM x AM x ==，且0x >，∵10AB =，四边形ABCD 为菱形，∴10AB BC CD AD ====，在Rt ABM 中，222AM BM AB +=，即()()2224310x x +=，解得2x =，∴6,8BM AM ==，∴1082DM AD AM =−=−=，当点F 在点D 的右侧时，如图，。

相似三角形中的“A”字模型(4种题型)-2023新九年级数学核心知识点与常见题型(沪教版)(解析版)

相似三角形中的“A”字模型(4种题型)-2023新九年级数学核心知识点与常见题型(沪教版)(解析版)

重难点专项突破：相似三角形中的“A”字模型（4种题型）【知识梳理】【考点剖析】题型一：直接利用“A”字模型解题例1.如图，E是▱ABCD的边BA延长线上一点，CE与AD相交于点F，AE＝1，AB＝2，BC＝3，那么AF＝．【分析】利用A字模型相似三角形进行计算即可解答．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠EAF＝∠B，∠EFA＝∠ECB，∴△EAF∽△EBC，∴EAEB =AFBC，∴13=AF3，∴AF＝1，故答案为：1．【点评】本题考查了平行四边形的性质，相似三角形的判定与性质，熟练掌握A字模型相似三角形是解题的关键．例2．（2022秋•静安区期末）在△ABC中，AB＝6，AC＝5，点D、E分别在边AB、AC上，当AD＝4，∠ADE＝∠C时，＝．【分析】首先判定△ADE∽△ACB，然后利用该相似三角形的对应边成比例解答．【解答】解：∵∠ADE＝∠C，∠A＝∠A，∴△ADE∽△ACB．∴＝．∵AC＝5，AD＝4，∴＝．故答案为：．【点评】本题考查的是相似三角形的判定与性质，相似三角形是相似多边形的特殊情形，它沿袭相似多边形的定义，从对应边的比相等和对应角相等两方面下定义；反过来，两个三角形相似也有对应角相等，对应边的比相等．题型二：添加辅助线构造“A”字模型解题例3.如图，在△ABC中，∠C＝90°，BC＝2，AB=2√5，点D在边AC上，CD：AD＝1：3，联结BD，点E 在线段BD上，如果∠BCE＝∠A，那么CE＝．【分析】根据已知∠BCE＝∠A，想到构造这两个角所在的三角形相似，所以过点E作EF⊥BC，垂足为F，可得△ABC∽△CEF，进而可得CF＝2EF，然后设EF为a，则CF为2a，BF为2﹣2a，最后再证明A字模型相似△BFE∽△BCD，从而解答即可．【解答】解：过点E作EF⊥BC，垂足为F，∵∠ACB ＝90°，BC ＝2，AB =2√5，∴AC =√AC 2−BC 2=√(2√5)2−22=4，∵CD ：AD ＝1：3，∴CD ＝1，∵∠BCE ＝∠A ，∠ACB ＝∠CFE ＝90°，∴△ABC ∽△CEF ，∴AC BC =CF EF =42=2，∴设EF 为a ，则CF 为2a ，BF 为2﹣2a ，∵∠ACB ＝∠BFE ＝90°，∠CBD ＝∠FBE ，∴△BFE ∽△BCD ，∴BF BC =EF CD ，∴2−2a 2=a 1， ∴a =12，∴EF =12，CF ＝1，∴CE =√EF 2+CF 2=√(12)2+12=√52， 故答案为：√52．【点评】本题考查了相似三角形的判定与性质，勾股定理，熟练掌握A 字模型相似是解题的关键． 例4． 如图，已知ABC ∆中，AD 、BE 相交于G ，:3:1BD DC =，:1:2AG GD =．求:BG GE 的值．【答案】11．【解析】点G 作//GM BC 交AC 于点M ．//GM BC ∴AG GM AD CD =，EG GM EB CB =；:1:2AG GD =， ∴13AG GM AD CD ==，:3:1BD DC =，∴14DC BC =，∴112GM BC =， ∴112GE EB =，∴:BG GE 的值为11．【总结】本题考查了三角形一边的平行线知识，要学会构造平行基本模型．例5．如图，在ABC ∆中，点D 在线段BC 上，75BAD ∠=︒，30CAD ∠=︒，AD = 2，BD = 2DC ，求AC 的长．【答案】3．【解析】过点D 作//DM AB 交AC 于点M ．//DM AB， ∴75BAD ADM ∠=∠=；又180ADM AMD DAM ∠+∠+∠=，30CAD ∠=∴75AMD∠=，∴AMD ADM∠=∠，∴2AD AM==．//DM AB，∴AM BDAC BC=．又2BD DC=，∴23BD AMBC AC==．∴3AC=．【总结】本题考查了三角形一边的平行线及等腰三角形的相关知识．题型三：“AX”字型解题例6.如图，ABC∆中，//DE BC，3AE=，4DE=，2DF=，5CF=，求EC的长．【答案】92EC=．【解析】//DE BC，25DE DF AEBC CF AC∴===，即3235EC=+，求得：92EC=．【总结】相似三角形中“A”字型和“X”字型的综合应用，可得到相等比例关系式．例7.如图，在梯形ABCD中，//AD BC，对角线AC、BD交于点O，点E在AB上，且//EO BC，已知3AD=，6BC=．求EO的长．【答案】2． 【解析】由//AD BC ，可得：3162AO AD CO BC ===，故13AO AC =，由//EO BC ，13EO AO BC AC ==，求得2EO =．【总结】相似三角形中“A ”字型和“X ”字型的综合应用，可得到相等比例关系式．题型四：双A 字模型例8.如图，AB ⊥BD ，CD ⊥BD ，垂足分别为B 、D ，AC 和BD 相交于点E ，EF ⊥BD ， 垂足为F ．求证：111AB CD EF+=．【解析】AB ⊥BD ，CD ⊥BD ，EF ⊥BD ，∴////AB CD EF∴EF DF AB DB =，EF BF CD DB = ∴1EF EF AB DC +=，即111AB CD EF +=．【总结】本题考查了三角形一边的平行线知识的应用．【过关检测】一．选择题（共3小题）1．（2023•嘉定区二模）如图，已知点D 、E 分别在△ABC 的边AB 、AC 上，DE ∥BC ，AD ：DB ＝1：3，那么S △DEC ：S △DBC 等于（ ）AB CDEFA．1：2B．1：3C．2：3D．1：4【分析】根据题意可得AD：AB＝1：4，再证明△ADE∽△ABC，得，即BC＝4DE，根据平行线间的距离处处相等可得C到DE的距离为等于点D到BC的距离，以此即可求解．【解答】解：∵AD：DB＝1：3，∴AD：AB＝1：4，∵DE∥BC，∴△ADE∽△ABC，∴，∴BC＝4DE，设点C到DE的距离为h1，点D到BC的距离为h2，∵DE∥BC，∴h1＝h2，∴，即S△DEC：S△DBC＝1：4．故选：D．【点评】本题主要考查平行线的性质、相似三角形的判定与性质，灵活运用相关知识解决问题是解题关键．2．（2022秋•徐汇区期末）如图，在△ABC中，DE∥FG∥BC，AD：AF：AB＝1：2：5，则S△ADE：S四边形DEGF：S四边形FGCB＝（）A．1：2：5B．1：4：25C．1：3：25D．1：3：21【分析】由DE∥FG∥BC，可得△ADE∽△AFG∽△ABC，又由AD：AF：AB＝1：2：5，利用相似三角形的面积比等于相似比的平方，即可求得S△ADE：S△AFG：S△ABC＝1：4：25，然后设△ADE的面积是a，则△AFG和△ABC的面积分别是3a，21a，即可求两个梯形的面积，继而求得答案．【解答】解：∵DE∥FG∥BC，∴△ADE∽△AFG∽△ABC，∴AD：AF：AB＝1：2：5，∴S△ADE：S△AFG：S△ABC＝1：4：25，设△ADE的面积是a，则△AFG和△ABC的面积分别是4a，25a，则S四边形DFGE＝S△AFG﹣S△ADE＝3a，S四边形FBCG＝S△ABC﹣S△AFG＝21a，∴S△ADE：S四边形DFGE：S四边形FBCG＝1：3：21．故选：D．【点评】此题考查了相似三角形的判定与性质．此题难度适中，解题的关键是掌握相似三角形面积的比等于相似比的平方．3．（2022秋•奉贤区期中）在△ABC中，点D、E在边AB、AC上，，要使DE∥BC，可添加下列条件中的（）A．B．C．D．【分析】先求出比例式，再根据相似三角形的判定得出△ADE∽△ABC，根据相似推出∠ADE＝∠B，根据平行线的判定得出即可【解答】解：只有选项D正确，理由是：∵AD：BD＝3：2，∴AD：AB＝3：5，∴AE：AC＝3：5，∵∠DAE＝∠BAC，∴△ADE∽△ABC，∴∠ADE＝∠B，∴DE∥BC，根据选项A、B、C的条件都不能推出DE∥BC，故选：D．【点评】本题考查了平行线分线段成比例定理，相似三角形的性质和判定的应用，能灵活运用定理进行推理是解此题的关键．二．填空题（共13小题）4．（2023春•普陀区期中）如图，在梯形ABCD中，AD∥BC，E、F分别是AB、DC上的点，EF∥BC，如果，AD＝4，BC＝9，那么EF的长为．【分析】延长BA，与CD的延长线交于点G，易证明△GAD∽△GBC，得到，进而得到，再证明△GEF∽△GBC，利用相似三角形的性质即可解答．【解答】解：延长BA，与CD的延长线交于点G，如图，∵AD∥BC，AD＝4，BC＝9，∴△GAD∽△GBC，∴，∵，∴，，∵EF∥BC，∴△GEF∽△GBC，∴，∵BC＝9，∴EF＝6．故答案为：6．【点评】本题主要考查相似三角形的判定与性质，熟知相似三角形的对应边成比例是解题关键．5．（2023•普陀区一模）如图，△ABC中的一边BC与双边平行且单位相同的刻度尺的一边重合，边AB、AC 分别与刻度尺的另一边交于点D、E，点B、C、D、E在刻度尺上的读数分别为0、5、1、3，如果刻度尺的宽度为3，那么△ABC的面积是．【分析】过点A作AF⊥DE，垂足为G，并延长AG交BC于点H，根据题意得：DE＝2，BC＝5，GH＝3，DE ∥BC，从而可得∠ADE＝∠ABC，∠AED＝∠ACB，然后证明A字模型相似三角形△ADE∽△ABC，从而利用相似三角形的性质求出AH的长，最后利用三角形的面积公式进行计算，即可解答．【解答】解：过点A作AF⊥DE，垂足为G，并延长AG交BC于点H，由题意得：DE＝2，BC＝5，GH＝3，DE∥BC，∴∠ADE＝∠ABC，∠AED＝∠ACB，∴△ADE∽△ABC，∴＝，∴＝，解得：AH＝5，∴△ABC的面积＝BC•AH＝×5×5＝，故答案为：．【点评】本题考查了相似三角形的判定与性质，三角形的面积，平行线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．6．（2023•静安区校级一模）在△ABC中，AB＝6，AC＝5，点D、E分别在边AB、AC上，当AD＝4，∠ADE＝∠C时，＝．【分析】首先判定△ADE∽△ACB，然后利用该相似三角形的对应边成比例解答．【解答】解：∵∠ADE＝∠C，∠A＝∠A，∴△ADE∽△ACB．∴＝．∵AC＝5，AD＝4，∴＝．故答案为：．【点评】本题考查的是相似三角形的判定与性质，相似三角形是相似多边形的特殊情形，它沿袭相似多边形的定义，从对应边的比相等和对应角相等两方面下定义；反过来，两个三角形相似也有对应角相等，对应边的比相等．7．（2023•青浦区一模）如图，在△ABC中，点D、E、F分别在边AB、AC、BC上，DE∥BC，EF∥AB，CF＝3BF．如果S△ADE＝1，那么S四边形DBCE＝．【分析】根据题意可得，四边形DEFB为平行四边形，则，易证明△ADE∽△ABC，根据相似三角形的性质得，以此求出S△ABC＝16，由S四边形DBCE＝S△ABC﹣S△ADE 即可解答．【解答】解：∵CF＝3BF，∴，∵DE∥BC，EF∥AB，∴四边形DEFB为平行四边形，∴DE＝BF，△ADE∽△ABC，∴，∴，∵S△ADE＝1，∴S△ABC＝16，∴S四边形DBCE＝S△ABC﹣S△ADE＝15．故答案为：15．【点评】本题主要考查平行四边形的判定与性质、相似三角形的判定与性质，熟练掌握相似三角形的面积比等于相似比的平方是解题关键．8．（2022秋•黄浦区期中）如图，DE是△ABC的中位线，M是DE的中点，CM的延长线交AB于点N，则S△DMN：S四边形DBCM＝．【分析】由DE为三角形ABC的中位线，利用中位线定理得到DE平行于BC，且DE等于BC的一半，再由M 为DE的中点，得到DM为DE的一半，可得出DM为BC的四分之一，由DM与BC平行，得到两对同位角相等，进而确定出三角形DMN与三角形NBC相似，由相似三角形面积之比等于相似比的平方，求出三角形DMN与三角形NBC面积之比，即可求出四边形DBCM与三角形DMN的面积之比．【解答】解：∵DE为△ABC的中位线，∴DE∥BC，DE＝BC，∴∠NDM＝∠B，∠NMD＝∠NCB，∴△NDM∽△NBC，∵M为DE的中点，∴DM＝DE＝BC，即相似比为1：4，∴S△NDM：S△NBC＝1：16，则S△DMN：S四边形DBCM＝1：15．故答案为：1：15．【点评】此题考查了相似三角形的判定与性质，以及三角形的中位线定理，熟练掌握相似三角形的判定与性质是解本题的关键．9．（2022秋•宝山区期中）在梯形ABCD中，AD∥BC，AD＝2，BC＝5，点E、F分别在边AB、CD上，且EF∥BC，如果AE：EB＝2：1，那么EF的长为．【分析】连接AC交EF于点P，先利用平行线分线段成比例定理求出、，再利用相似三角形的性质求出EP、FP EF．【解答】解：如图，连接AC交EF于点P．∵AD∥BC，EF∥BC，∴AD∥EF∥BC．∴＝＝．∴＝，＝．∵AD∥EF∥BC，∴△AEP∽△ABC，△CFP∽△CDA．∴＝＝，＝＝．∵AD＝2，BC＝5，∴EP＝，PF＝．∵EF＝EP+PF＝+＝4．故答案为：4．【点评】本题主要考查了相似三角形的性质和判定，掌握“平行线分线段成比例定理”、相似三角形的判定和性质是解决本题的关键．10．（2022秋•嘉定区期中）如图，AD∥BC∥EF，AE：AB＝2：3，AD＝8，BC＝14则EF＝．【分析】过点A作AH∥DC，交EF于点G，利用平行四边形的判定可得四边形AGFD和四边形AHCD都是平行四边形，从而可得AD＝GF＝8，AD＝CH＝8，进而可得BH＝6，然后证明A字模型相似三角形△AEG∽△ABH，从而利用相似三角形的性质可得EG＝4，最后进行计算即可解答．【解答】解：过点A作AH∥DC，交EF于点G，∵AD∥BC∥EF，∴四边形AGFD是平行四边形，四边形AHCD是平行四边形，∴AD＝GF＝8，AD＝CH＝8，∵BC＝14，∴BH＝BC﹣CH＝6，∵EG∥BH，∴∠AEG＝∠B，∠AGE＝∠AHB，∴△AEG∽△ABH，∴＝，∴＝，∴EG＝4，∴EF＝EG+FG＝4+8＝12，故答案为：12．【点评】本题考查了相似三角形的判定与性质，平行四边形的判定与性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．11．（2022秋•浦东新区期中）如图、在△ABC，CD平分∠ACB，DE∥BC，AD＝2，BD＝3，BC＝5，则CE ＝．【分析】根据平行线的性质可得∠ADE＝∠B，∠AED＝∠C，从而可得△ADE∽△ABC，然后利用相似三角形的性质进行计算可得DE＝2，最后再根据角平分线的定义和平行线的性质可得△EDC是等腰三角形，即可解答．【解答】解：∵DE∥BC，∴∠ADE＝∠B，∠AED＝∠C，∴△ADE∽△ABC，∴＝，∴＝，∴DE＝2，∵DE∥BC，∴∠EDC＝∠DCB，∵CD平分∠ACB，∴∠DCB＝∠ACD，∴∠EDC＝∠ACD，∴ED＝EC＝2，故答案为：2．【点评】本题考查了相似三角形的判定与性质，等腰三角形的判定与性质，平行线的性质，熟练掌握根据角平分线的定义和平行线的性质可得等腰三角形是解题的关键．12．（2022秋•徐汇区校级月考）如图，AM：MB＝AN：NC＝1：3，则MN：BC＝．【分析】首先根据已知条件可以证明MN∥BC，然后证明△AMN∽△ABC即可求解．【解答】解：∵AM：MB＝AN：NC＝1：3，∴MN∥BC，AM：AB＝1：4，∴△AMN∽△ABC，∴MN：BC＝AM：AB＝1：4．故答案为：1：4．【点评】此题主要考查了相似三角形的性质与判定，熟练掌握相似三角形的性质是解题的关键．13．（2022秋•虹口区校级月考）如图，矩形DEFG为△ABC的内接矩形，点G，F分别在AB，AC上，AH 是BC边上的高，BC＝10，AH＝6，EF：GF＝2：5，则矩形DEFG的面积为．【分析】据矩形的性质可得出GF∥BC，进而可得出△AGF∽△ABC，设EF＝2x，则GF＝5x，根据相似三角形的性质即可得出关于x的一元一次方程，解之即可得出x的值，再利用矩形的面积公式即可求出矩形DEFG 的面积．【解答】解：设EF＝2x，则GF＝5x．∵GF∥BC，AH⊥BC，∴AK⊥GF．∵GF∥BC，∴△AGF∽△ABC，∴＝．∵AH＝6，BC＝12，∴＝．解得x＝．∴EF＝，GF＝6，∴矩形DEFG的面积为．故答案为：．【点评】本题考查了相似三角形的判定与性质、矩形的性质以及解一元一次方程，根据相似三角形的性质列出关于x的一元一次方程是解题的关键．14．（2022春•青浦区校级期末）已知：如图，在△ABC中，AC＝6，BC＝8，AB＝10，点D位于边AB上，过点D作边BC的平行线交边AC于点E，过点D作边AC的平行线交边BC于点F，设AE＝x，四边形CEDF的面积为y，则y关于x的函数关系式是．（不必写定义域）【分析】根据已知可证四边形DECF是平行四边形，然后利用勾股定理的逆定理证明△ABC是直角三角形，从而可得∠C＝90°，进而可得四边形DECF是矩形，再证明A字模型相似三角形△AED∽△ABC，从而利用相似三角形的性质可得DE＝x，最后根据矩形的面积公式进行计算即可解答．【解答】解：∵DE∥BC，DF∥AC，∴四边形DECF是平行四边形，在△ABC中，AC＝6，BC＝8，AB＝10，∵AC2+BC2＝62+82＝100，AB2＝102＝100，∴AC2+BC2＝AB2，∴△ABC是直角三角形，∴∠C＝90°，∴四边形DECF是矩形，∵DE∥BC，∴∠AED＝∠C＝90°，∵∠A＝∠A，∴△AED∽△ABC，∴＝，∴＝，∴DE＝x，∴矩形CEDF的面积＝DE•CE，∴y＝x（6﹣x）＝﹣x2+8x，故答案为：y＝﹣x2+8x．【点评】本题考查了相似三角形的判定与性质，勾股定理的逆定理，函数关系式，熟练掌握A字模型相似三角形是解题的关键．15．（2021秋•金山区期末）如图，E是▱ABCD的边BA延长线上一点，CE与AD相交于点F，AE＝1，AB ＝2，BC＝3，那么AF＝．【分析】利用A字模型相似三角形进行计算即可解答．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠EAF＝∠B，∠EFA＝∠ECB，∴△EAF∽△EBC，∴＝，∴＝，∴AF＝1，故答案为：1．【点评】本题考查了平行四边形的性质，相似三角形的判定与性质，熟练掌握A字模型相似三角形是解题的关键．16．（2021秋•嘉定区期末）如图，在△ABC中，∠C＝90°，BC＝2，，点D在边AC上，CD：AD＝1：3，联结BD，点E在线段BD上，如果∠BCE＝∠A，那么CE＝．【分析】根据已知∠BCE＝∠A，想到构造这两个角所在的三角形相似，所以过点E作EF⊥BC，垂足为F，可得△ABC∽△CEF，进而可得CF＝2EF，然后设EF为a，则CF为2a，BF为2﹣2a，最后再证明A字模型相似△BFE∽△BCD，从而解答即可．【解答】解：过点E作EF⊥BC，垂足为F，∵∠ACB＝90°，BC＝2，，∴AC＝＝＝4，∵CD：AD＝1：3，∴CD＝1，∵∠BCE＝∠A，∠ACB＝∠CFE＝90°，∴△ABC∽△CEF，∴＝＝＝2，∴设EF为a，则CF为2a，BF为2﹣2a，∵∠ACB＝∠BFE＝90°，∠CBD＝∠FBE，∴△BFE∽△BCD，∴＝，∴＝，∴a＝，∴EF＝，CF＝1，∴CE＝＝＝，故答案为：．【点评】本题考查了相似三角形的判定与性质，勾股定理，熟练掌握A字模型相似是解题的关键．三．解答题（共5小题）17．（2022秋•奉贤区期中）如图，已知在四边形ABCD中，AD∥BC．E为边CB延长线上一点，联结DE 交边AB于点F，联结AC交DE于点G，且＝．（1）求证：AB∥CD；（2）如果AE2＝AG•AC，求证：＝．【分析】（1）由AD∥BC，得到△ADG∽△CEG，根据相似三角形的性质即可得到结论；（2）由AE2＝AG•AC易得△AEG∽△ACE，所以∠AEG＝∠ACE＝∠DAG，可得△ADG∽△EDA，再根据相似三角形的性质可得结论．【解答】证明：（1）∵AD∥BC，∴△ADG∽△CEG，∴＝，∵＝，∴＝，∴AB∥CD；（2）∵AE2＝AG•AC，∴＝，∵∠EAG＝∠CAE，∴△AEG∽△ACE，∴∠AEG＝∠ACE，∵AD∥BC，∴∠ACE＝∠DAG，∴∠DAG＝∠AEG，∵∠ADG＝∠EDA，∴△ADG∽△EDA，∴，即＝．【点评】本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．18．（2022秋•杨浦区期中）如图，点D、E分别在△ABC的边AB、AC上，DE∥BC．如果S△ADE＝2，S△BCE＝7.5．求S△BDE．【分析】设S△BDE＝x，则可得出△ABE△BCE的面积之比，再将x的值代入即可得出答案；【解答】解：（1）设S△BDE＝x．∴＝，∴＝．∵DE∥BC，∴＝，∵S△ADE＝2，S△BCE＝7.5，∴＝，解得：x1＝﹣5（舍），x2＝3．∴S△BDE＝3．【点评】本题考查了平行线分线段成比例定理以及分式方程的应用，难度较大．19．（2022秋•奉贤区期中）如图，在△ABC中，点D在边AB上，点F、E在边AC上，且DF∥BE，．（1）求证：DE∥BC；（2）如果＝，S△ABC＝12，求S△ADE的值．【分析】（1）由DF∥BE得比例，结合已知比例，利用过渡比得出＝，证明结论；（2）首先可以证明＝，然后证明△ADE∽△ABC，最后利用相似三角形的面积比等于相似比的平方求解．【解答】（1）证明：∵DF∥BE，∴＝，∵＝，∴＝，∴DE∥BC；（2）解：∵＝，∴＝，∴＝，∵DE∥BC，∴△ADE∽△ABC，∴＝＝（）2＝，∵S△ABC＝12，∴S△ADE＝．【点评】本题考查了相似三角形的判定与性质，平行线的性质，平行线分线段成比例．关键是利用平行线得出相似三角形及比例，利用相似三角形的面积比等于相似比的平方解题．20．（2023•青浦区一模）如图，在平行四边形ABCD中，点F在边AD上，射线BA、CF相交于点E，DF＝2AF．（1）求EA：AB的值；（2）如果，，试用、表示向量．【分析】（1）根据平行四边形的性质可得AB∥CD，AB＝CD，易证△AEF∽△DCF，则＝，由DF ＝2AF即可求解；（2）先算出，再根据即可求解．【解答】解：（1）∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∴△AEF∽△DCF，∴，∴，∵DF＝2AF，∴，∴；（2）∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵DF＝2AF，∴，∵，，∴，，∴．【点评】本题主要考查相似三角形的判定与性质、平行四边形的性质、平面向量，熟练掌握平面向量的运算法则是解题关键．21．（2021秋•普陀区期末）如图，在△ABC中，边BC上的高AD＝2，tan B＝2，直线l平行于BC，分别交线段AB，AC，AD于点E、F、G，直线l与直线BC之间的距离为m．（1）当EF＝CD＝3时，求m的值；（2）将△AEF沿着EF翻折，点A落在两平行直线l与BC之间的点P处，延长EP交线段CD于点Q．①当点P恰好为△ABC的重心时，求此时CQ的长；②联结BP，在∠CBP＞∠BAD的条件下，如果△BPQ与△AEF相似，试用m的代数式表示线段CD的长．【分析】（1）根据＝tanB＝2，可得：BD＝1，再由EF＝CD＝3，DG＝m，可得：BC＝4，AG＝2﹣m，利用EF∥BC，可得＝，建立方程求解即可；（2）①由翻折可得：BD＝CD＝1，AP＝2PD，即PD＝AD＝，AP＝AD＝，进而得出：AG＝，推出DP＝GP，再由EF∥BC，可得出EG＝，利用ASA证明△PQD≌△PEG，即可求得答案；②分两种情况：Ⅰ．当△BPQ∽△FAE时，由△FAE∽△CAB，推出△BPQ∽△CAB，建立方程求解即可；Ⅱ．当△BPQ∽△AFE时，由△AFE∽△ACB，推出△BPQ∽△ACB，建立方程求解即可．【解答】解：（1）如图1，在△ABC中，边BC上的高AD＝2，tanB＝2，∴＝tanB＝2，∴BD＝1，∵EF＝CD＝3，DG＝m，∴BC＝BD+CD＝4，AG＝AD﹣DG＝2﹣m，∵EF∥BC，∴＝，即＝，解得：m＝，∴m的值为；（2）①如图2，∵将△AEF沿着EF翻折，点A落在△ABC的重心点P处，∴BD＝CD＝1，AP＝2PD，即PD＝AD＝，AP＝AD＝，∴AG＝GP＝AP＝，∴DP＝GP，∵EF∥BC，∴∠PGE＝∠PDQ＝90°，△AEG∽△ABD，∴＝，即＝，∴EG＝，在△PQD和△PEG中，，∴△PQD≌△PEG（ASA），∴DQ＝EG＝，∴CQ＝CD﹣DQ＝1﹣＝，∴此时CQ的长为；②在Rt△ABD中，AB＝＝，∵将△AEF沿着EF翻折，点A落在两平行直线l与BC之间的点P处，∴∠PBQ＜∠ABD，∵EF∥BC，∴∠AEF＝∠ABD，∴∠PBQ＜∠AEF，∵∠CBP＞∠BAD，∴∠BAD＜∠PBQ＜∠AEF，∵GP＝AG＝2﹣m，DG＝m，∴DP＝DG﹣GP＝m﹣（2﹣m）＝2m﹣2，∴m＞1，∴1＜m＜2，∵∠AEF＝∠ABD，∴＝tan∠AEF＝tan∠ABD＝2，∴＝2，∴EG＝，∵EF∥BC，∴△PEG∽△PQD，∴＝，即＝，∴DQ＝m﹣1，∴BQ＝BD+DQ＝m，∵∠AEF＝∠PEG＝∠BQP，∠PBQ＜∠AEF，∴△BPQ与△AEF相似，则△BPQ∽△FAE或△BPQ∽△AFE，Ⅰ．当△BPQ∽△FAE时，∵△FAE∽△CAB，∴△BPQ∽△CAB，∴＝，即＝，∴BC＝，∴CD＝BC﹣BD＝﹣1＝；Ⅱ．当△BPQ∽△AFE时，∵△AFE∽△ACB，∴△BPQ∽△ACB，∴＝，即＝，∴BC＝，∴CD＝BC﹣BD＝﹣1＝，综上，线段CD的长为或．【点评】本题考查了全等三角形判定和性质，相似三角形的判定和性质，勾股定理，三角函数，翻转变换的性质等，熟练掌握全等三角形判定和性质、相似三角形的判定和性质等相关知识，运用分类讨论思想和方程思想思考解决问题是解题关键．22．（2023•奉贤区一模）已知：如图，在梯形ABCD中，AD∥BC，点E在对角线BD上，∠EAD＝∠BDC．（1）求证：AE•BD＝AD•DC；（2）如果点F在边DC上，且，求证：EF∥BC．【分析】（1）利用平行线的性质证明∠ADB ＝∠DBC ，然后利用已知条件可以证明△ADE ∽△DBC ，由此即可解决问题；（2）利用（1）的结论和已知条件可以证明△DEF ∽△DBC ，接着利用相似三角形的在即可求解．【解答】证明：（1）∵AD ∥BC ，∴∠ADB ＝∠DBC ，又∵∠EAD ＝∠BDC ，∴△ADE ∽△DBC ，∴AE ：AD ＝DC ：BD ，∴AE •BD ＝AD •DC ；（2）∵AE ：AD ＝DC ：BD ，且，∴＝， 而∠EDF ＝∠BDC ，∴△DEF ∽△DBC ，∴∠DEF ＝∠DBC ，∴EF ∥BC ．【点评】此题主要考查了相似三角形的性质与判定，同时也利用了平行线的性质，比例的基本性质，有一定的综合性．23.如图，在平行四边形ABCD 中，E 是AD 上一点，CE 与BD 相交于点O ，CE 与BA 的延长线相交于点G ，已知2DE AE =，10CE =，求GE 和CO 的长．【答案】56GE CO ==，． 【解析】四边形ABCD 是平行四边形，//AD BC AD BC ∴=，．又2DE AE =，13GE AE AE GC BC AD ∴===，23EO DE OC BC ==， 即13GE GE EC =+，23EC CO CO −=， 代入即可求得56GE CO ==，．【总结】考查利用三角形一边平行线的性质构造“A ”字型和“X ”字型，进行比例线段的综合应用．24.如图，在ABC ∆中，设D 、E 是AB 、AC 上的两点，且BD CE =，延长DE 交BC 的延长线于点F ，:3:5AB AC =，12cm EF =，求DF 的长．【答案】20cm ．【解析】过点D 作//DH AC 交BC 于H ，则有35BD AB DH AC ==，又BD CE =， 则有35CE DH =，由//CE DH ， 得35EF CE DF DH ==，代入计算得：125320DF cm =⨯÷=． 【总结】作平行线，构造出与所求线段相关的“A ”字型或“X ”字型，比例转化．25.如图，已知ABC ∆中，点D 、E 分别在边AB 、AC 上，且:3:2AD DB =，:1:2AE EC =，直线ED和CB 的延长线交于点F ，求:FB FC ． FE DC B A【答案】1:3．【解析】过点B 作//BG FE 交AC 于G ．根据三角形一边平行线的性质定理，可得：32AE AD EG DB ==，又:1:2AE EC =，故13EG EC =， 由//BG FE ，可得：::1:3FB FC EG EC ==．【总结】作平行线，构造出与所求线段相关的“A ”字型或“X ”字型，比例转化． G F EDCB A。

考点19 相似三角形模型-备战2023届中考数学一轮复习考点梳理(解析版)

考点19 相似三角形模型-备战2023届中考数学一轮复习考点梳理(解析版)

考点19 相似三角形基本模型相似三角形在初中数学中因为不同类型的规律比较明显，所以被总结了很多的模型，比如：A 字图、8字图、母子三角形、一线三等角、手拉手相似等。

而掌握了这类模型的套路后，可以更快的应对相似三角形类的应用。

所以考生需要对该考点完全掌握。

一、A 字图及其变型二、8字图及其变型三、一般母子型四、一线三等角五、手拉手模型考向一、A 字图及其变型“斜A 型”型在圆中的应用：如图可得：△PAB ∽△PCD1．如图，在△ABC中，DE∥BC，DE＝2，BC＝6，则的值为（ ）A．B．C．D．【分析】利用平行线的性质和相似三角形的判定与性质解答即可．【解答】解：∵DE∥BC，∴△ADE∽△ABC，∴＝＝＝，故选：C．2．如图，在△ABC中，DE∥FG∥BC，AD：AF：AB＝1：2：5，则S△ADE：S四边形DEGF：S四边形FGCB＝（ ）A．1：2：5B．1：4：25C．1：3：25D．1：3：21【分析】由DE∥FG∥BC，可得△ADE∽△AFG∽△ABC，又由AD：AF：AB＝1：2：5，利用相似三角形的面积比等于相似比的平方，即可求得S△ADE：S△AFG：S△ABC＝1：4：25，然后设△ADE的面积是a，则△AFG和△ABC的面积分别是3a，21a，即可求两个梯形的面积，继而求得答案．【解答】解：∵DE∥FG∥BC，∴△ADE∽△AFG∽△ABC，∴AD：AF：AB＝1：2：5，∴S△ADE：S△AFG：S△ABC＝1：4：25，设△ADE的面积是a，则△AFG和△ABC的面积分别是4a，25a，则S四边形DFGE＝S△AFG﹣S△ADE＝3a，S四边形FBCG＝S△ABC﹣S△AFG＝21a，∴S△ADE：S四边形DFGE：S四边形FBCG＝1：3：21．故选：D．3．将一张直角三角形纸片沿一条直线剪开，将其分成一张三角形纸片与一张四边形纸片，如果所得四边形纸片ABCD如图5所示，其中∠A＝∠C＝90°，AB＝7厘米，BC＝9厘米，CD＝2厘米，那么原来的直角三角形纸片的面积是　54或　平方厘米．【分析】分两种情况讨论，由勾股定理求出AD长，由三角形面积公式求出四边形ABCD的面积，由相似三角形的性质，即可解决问题．【解答】解：（1）分别延长CD，BA交于M，连接BD，设△MBC的面积是S（cm2），∵∠C＝∠DAB＝90°，∴DC2+BC2＝AB2+AD2＝BD2，∴22+92＝72+AD2，∴AD＝6（cm），∴△ADB的面积＝AD•AB＝×6×7＝21（cm2），△DCB的面积＝DC•BC＝×2×9＝9（cm2），∴四边形ABCD的面积＝21+9＝30（cm2），∴△DMA的面积＝（S﹣30）（cm2），∵∠M＝∠M，∠MAD＝∠MCB，∴△MDA∽△MBC，∴＝＝＝，∴＝，∴S＝54（cm2）．（2）分别延长AD，BC交于N，设△NAB的面积是S′（cm2），由（1）知四边形ABCD的面积＝30（cm2），∵∠N＝∠N，∠NCD＝∠A＝90°，∴△NCD∽△NAB，∴＝＝＝，∴＝，∴S′＝（cm2），∴原来的直角三角形纸片的面积是54cm2或cm2．故答案为：54或．4．如图，矩形DEFG的边DE在△ABC的边BC上，顶点G、F分别在边AB、AC上．已知BC＝6cm，DE ＝3cm，EF＝2cm，那么△ABC的面积是　12　cm2．【分析】过点A作AN⊥BC，先利用相似三角形的判定说明△AGF∽△ABC，再利用相似三角形的性质求出△ABC的高，最后利用三角形的面积得结论．【解答】解：过点A作AN⊥BC，垂足为N，交GF于点M．∵四边形DEFG是矩形，∴GF∥DE，GF＝DE＝3cm，EF＝MN＝2cm．设AM＝acm，则AN＝（a+2）cm．∵GF∥DE，∴△AGF∽△ABC．∴＝．∴＝．∴a＝2．∴AN＝4cm．S△ABC＝BC•AN＝6×4＝12（cm）2．故答案为：12．5．如图▱ABCD中，点E在BA的延长线上，连接EC、BD交于点G，EC交AD于F，已知EA：AB＝1：2．（1）求EF：EC；（2）求FG：GC．【分析】（1）利用平行线分线段成比例定理和比例的性质求解即可；（2）利用相似三角形的判定，先说明△EAF∽△CDF，再利用相似三角形的性质和比例的性质求出BC：FD，最后通过说明△FDG∽△CBG，利用相似三角形的性质得结论．【解答】解：∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，AD∥BC，AD＝BC．（1）∵EA：AB＝1：2，∴＝．∵AD∥BC，∴＝＝．（2）∵AB ∥CD ，∴△EAF ∽△CDF ．∴＝＝＝．∴＝＝．∵AD ∥BC ，∴△FDG ∽△CBG ．∴＝＝．考向二、8字图及其变型“蝴蝶型”变型1．如图，在△ABC 中，中线AD 与中线BE 相交于点G ，联结DE ．下列结论成立的是（ ）A ．B ．C ．D ．【分析】由AD ，BE 是△ABC 的中线，得到DE 是△ABC 的中位线，推出△DEG ∽△ABG ，△CDE ∽△CBA ，由相似三角形的性质即可解决问题．【解答】解：AD ，BE 是△ABC 的中线，∴DE是△ABC的中位线，∴DE∥AB，DE＝AB，∴△DEG∽△ABG，∴DG：AG＝DE：AB＝1：2，BG：EG＝AB：DE，＝＝，∴DG＝AG，∵BG：EG＝AB：DE＝2：1，∴GB：BE＝2：3，∴S△AGB：S△AEB＝2：3，∵AE＝EC，∴S△AEB＝S△ABC，∴S△AGB＝S△ABC，∵△CDE∽△CBA，∴＝＝，∴S△CDE＝S△ABC，∴＝，结论成立的是＝，故选：C．2．如图，在平行四边形ABCD中，F为BC的中点，延长AD至点E，使DE：AD＝1：3，连接EF交DC 于点G，则S△CFG：S△DEG等于（ ）A．9：4B．2：3C．4：9D．3：2【分析】利用平行四边形的性质可得AD∥BC，AD＝BC，，再根据线段中点的定义可得CF＝BC＝AD，然后证明8字模型相似三角形△EDG∽△FCG，利用相似三角形的性质进行计算即可解答．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵F为BC的中点，∴CF＝BC，∴CF＝AD，∵AE∥CF，∴∠E＝∠GCF，∠EDG＝∠C，∴△EDG∽△FCG，∵DE：AD＝1：3，∴DE＝AD，∴S△CFG：S△DEG＝（）2＝（）2＝（）2＝，故选：A．3．如图，在正方形ABCD中，E为AD上的点，连接CE．以点E为圆心，以任意长为半径作弧分别交EC，ED于点N，M，再分别以M，N为圆心，以大于MN长为半径作弧，两弧在∠CED内交于点P，连接EP并延长交DC于点H，交BC的延长线于点G．若AB＝16，AE：AD＝1：4，则EH的长为　6　．【分析】根据题中作图判断EP是∠DEC的角平分线，利用线段比和勾股定理求出EC，再利用角平分线的性质和平行线的性质得到CG，利用相似三角形的判定和性质求出DH，最后利用勾股定理得结论．【解答】解：∵以点E为圆心，以任意长为半径作弧分别交EC，ED于点N，M，再分别以M，N为圆心，以大于MN长为半径作弧，两弧在∠CED内交于点P，连接EP，∴EP是∠DEC的角平分线，∴∠DEG＝∠CEG．∵四边形ABCD是正方形，∴AD＝DC＝AB＝16，∠D＝90°，AD∥BC．∵AE：AD＝1：4，AE+ED＝16，∴AE＝4，ED＝12．在Rt△EDC中，EC＝＝＝20．∵AD∥BC，∴∠G＝∠DEG＝∠CEG．∴EC＝CG＝20．∵AD∥BC，∴△EDH∽△GCH．∴＝＝＝．∵DH+HC＝CD＝16，∴DH＝6．在Rt△EDH中，EH＝＝＝＝6．故答案为：6．4．如图，在▱ABCD中，G是CD延长线上一点，连接BG交AC，AD于E，F．（1）求证：△ABE∽△CGE；（2）若AF＝2FD，求的值．【分析】（1）根据平行四边形对边平行，得到∠ABE＝∠CGE，再利用对顶角相等，可得△ABE∽△CGE；（2）利用平行四边形对边平行，证明△AEF∽△CEB，得到，再由（1）得，，从而求解．【解答】（1）证明：∵四边形ABCD为平行四边形，∴AB∥CD，∴∠ABE＝∠CGE，又∵∠AEB＝∠CGE，∴△ABE∽△CGE．（2）解：设FD＝m，则AF＝2m，∴AD＝3m，∵四边形ABCD为平行四边形，∴AD∥BC，BC＝AD＝3m，∴∠EAF＝∠ECB，∠AFE＝∠CBE，∴△AEF∽△CEB∴＝＝，又∵△ABE∽△CGE，∴＝＝．即的值为．5．以下各图均是由边长为1的小正方形组成的网格，A，B，C，D均在格点上．（1）在图①中，的值为　1：3　；（2）利用网格和无刻度的直尺作图，保留痕迹，不写作法．①如图②，在AB上找一点P，使AP＝3；②如图③，在BD上找一点P，使△APB∽△CPD．【分析】（1）如图①中，利用平行线的性质求解即可．（2）①根据勾股定理得AB的长为5，再根据相似三角形的判定方法即可找到点P；②作点A的对称点A′，连接A′C与BD的交点即为要找的点P，使△APB∽△CPD．【解答】解：（1）如图①中，∵AB∥CD，∴△PCD∽△PBA．∴＝＝，故答案为：1：3；（2）①取格点E，F，连接EF交AB于点P，点P即为所求的点．由勾股定理知：AB＝＝5．∵AP＝3，∴BP＝2．∵BE∥FA，∴△EPB∽△FPA．∵AP：BP＝AF：BE＝3：2．∴取格点E，F，连接EF交AB于点P，点P即为所求的点；②如图③所示，作点A的对称点A′，连接A′C，交BD于点P，点P即为所要找的点，∵AB ∥CD ，∴△APB ∽△CPD ．考向三、一般母子型：联系应用：切割线定理：如图，PB 为圆O 切线，B 为切点，则：△PAB ∽△PBC得：1．如图，在△ABC 中，CD ⊥AB 于点D ，有下列条件：①∠A ＝∠BCD ；②∠A +∠BCD ＝∠ADC ；③；④BC 2＝BD •BA ．其中能判断△ABC 是直角三角形的有（ ）A ．0个B ．1个C ．2个D ．3个【分析】根据题目中①②③④给出的条件分别判定△BCD ∽△BAC 或△ABC ∽△ACD 即可求得∠ACB ＝90°，计算能求证△BCD ∽△BAC 或△ABC ∽△ACD 的个数即可解题．【解答】解：①∵∠A ＝∠BCD ，∠A +∠ACD ＝90°，∴∠BCD +∠ACD ＝90°，故本命题成立；②条件不足，无法求证∠ACB ＝90°，故本命题错误；③∵BD ：CD ＝BC ：AC ，∠ADC ＝∠CDB ＝90°，∴Rt △ADC ∽Rt △CDB ，（因为都有一个直角，斜边直角边成比例）∴∠ACD ＝∠B ；∵∠B +∠BCD ＝90°，其中：∠A 是公共角AB 是公共边BD 与BC 是对应边∴∠ACD+∠BCD＝90°，∵∠ACB＝∠ACD+∠BCD，∴∠ACB＝90°；故本命题正确；④∵BC2＝BD×BA，∴＝，∵∠B＝∠B，∴△ABC∽△CBD，∴∠ACB＝90°，故本命题成立，故选：D．2．如图，Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，∠ACD＝3∠BCD，E为斜边AB的中点，则＝（ ）A．B．C．D．【分析】利用相似三角形的判定与性质得到∠BCD＝∠A＝22.5°，利用三角形的外角的性质得到∠CED＝45°，利用直角三角形斜边上的中线等于斜边的一半，得到AE＝CE＝BE＝AB，设CD＝DE＝x，则CE＝，AD＝（+1）x，代入化简即可得出结论．【解答】解：∵∠ACB＝90°，∠ACD＝3∠BCD，∴∠BCD＝22.5°，∠ACD＝67.5°．∵∠ACB＝90°，CD⊥AB，∴△BCD∽△BAC，∴∠BCD＝∠A＝22.5°．∵∠ACB＝90°，E为斜边AB的中点，∴AE＝CE＝BE＝AB．∴∠ECA＝∠A＝22.5°，∴∠CED＝∠A+∠ECA＝45°，∵CD⊥AB，∴CD＝DE．设CD＝DE＝x，则CE＝，∴AE＝x，∴AD＝AE+DE＝（+1）x，∴＝+1．故选：B．3．如图，在△ABC中，∠A＝90°，点D、E分别在AC、BC边上，BD＝CD＝2DE，且∠C+∠CDE＝45°，若AD＝6，则BC的长为　8　．【分析】首先根据等腰三角形的性质和已知条件证出∠BDE＝90°，作DF⊥BC于F，则BF＝CF，△DEF ∽△BED∽△BDF，得出＝＝＝，设EF＝x，则DF＝2x，BF＝CF＝4x，得出BC＝8x，DE＝x，得出CD＝BD＝2x，AC＝6+2x，证明△CDF∽△CBA，得出＝，代入计算即可得出结果．【解答】解：∵∠A＝90°，∴∠ABD+∠ADB＝90°，∵BD＝CD，∴∠DBC＝∠C，∴∠ADB＝∠DBC+∠C＝2∠C，∵∠C+∠CDE＝45°∴2∠C+∠CDE＝90°，∴∠ADB+∠CDE＝90°，∴∠BDE＝90°，作DF⊥BC于F，如图所示：则BF＝CF，△DEF∽△BED∽△BDF，∴＝＝＝，设EF＝x，则DF＝2x，BF＝CF＝4x，∴BC＝8x，DE＝x，∴CD＝BD＝2x，AC＝6+2x，∵∠DFC＝∠A＝90°，∠C＝∠C，∴△CDF∽△CBA，∴＝，即＝，解得：x＝，∴BC＝8；故答案为：8．4．如图，在Rt△ABC中，∠ABC＝90°，点D是斜边AC的中点，连接DB，线段AE⊥线段BD交BC于点E，交DB于点G，垂足为点G．（1）求证：EB2＝EG•EA；（2）联结CG，若∠CGE＝∠DBC，求证：BE＝CE．【分析】（1）根据相似三角形的判定与性质可得结论；（2）由直角三角形的性质得BD＝AC＝CD，再由相似三角形的判定与性质可得EC2＝GE•EA，结合（1）的结论可得答案．【解答】证明：（1）∵AE⊥BD，∴∠BGE＝90°，∵∠ABC＝90°，∴∠BGE＝∠ABE，∵∠BEG＝∠AEB，∴△ABE∽△BGE，∴＝，即EB2＝EG•EA；（2）在Rt△ABC中，点D是斜边AC的中点，∴BD＝AC＝CD，∴∠DBC＝∠DCB，∵∠CGE＝∠DBC，∴∠CGE＝∠DCB，∵∠GEC＝∠GEC，∴△GEC∽△CEA，∴＝，∴EC2＝GE•EA，由（1）知EB2＝EG•EA，∴EC2＝EB2，∴BE＝CE．考向四、一线三等角：同侧型（通常以等腰三角形或者等边三角形为背景）异侧型1．如图，AB⊥BD于点B，ED⊥BD于点D．AB＝2，DE＝4，BD＝6．点C为BD上一点，连接AC、CE．当BC＝（ ）时，可使AC⊥CE．A．3B．2或4C．D．2或3【分析】根据垂直定义可得∠B＝∠D＝∠ACE＝90°，从而利用直角三角形的两个锐角互余可得∠A+∠ACB＝90°，再利用平角定义可得∠ACB+∠ECD＝90°，然后利用同角的余角相等可得∠ECD＝∠A，从而证明△ABC∽△CDE，最后利用相似三角形的性质进行计算即可解答．【解答】解：∵AB⊥BD，ED⊥BD，∴∠B＝∠D＝90°，∴∠A+∠ACB＝90°，∵AC⊥CE，∴∠ACE＝90°，∴∠ACB+∠ECD＝180°﹣∠ACE＝90°，∴∠ECD＝∠A，∴△ABC∽△CDE，∴＝，∴＝，解得：BC＝2或BC＝4，∴当BC＝2或4时，可使AC⊥CE，故选：B．2．如图，点A，B，C在同一直线上，∠A＝∠DBE＝∠C，则下列结论：①∠D＝∠CBE，②△ABD∽△CEB，③＝，其中正确的结论有（ ）个．A．0B．1C．2D．3【分析】根据三角形内角和和平角的定义可得①正确，进行可得△ABD∽△CEB，得出②正确；由相似三角形的性质可知，相似三角形的对应线段成比例，得出结论．【解答】解：由图可知，∠A+∠D+∠ABD＝180°，∠ABD+∠DBE+∠CBE＝180°，∵∠A＝∠DBE，∴∠D＝∠CBE，故①正确；∵∠A＝∠C，∴△ABD∽△CEB，故②正确；∴＝，故③正确；故选：D．3．如图，在矩形ABCD中，点E是对角线上一点，连接AE并延长交CD于点F，过点E作EG⊥AE交BC 于点G，若AB＝8，AD＝6，BG＝2，则AE＝（ ）A．B．C．D．【分析】过点E作EN⊥BC，垂足为N，延长NE交AD于点M，根据矩形的性质可得AD＝BC＝6，∠DAB ＝∠ABC＝90°，从而可得四边形AMNB是矩形，进而可得∠AMN＝90°，AB＝MN＝8，AM＝BN，MN ∥AB，然后设ME＝x，则EN＝MN﹣EM＝8﹣x，再证明A字模型相似三角形△DME∽△DAB，并利用相似三角形的性质求出DM，从而求出AM，GN的长，最后证明一线三等角模型相似三角形△AME∽△ENG，利用相似三角形的性质列出关于x的方程，进行计算即可求出ME，AM的长，从而在Rt△AME 中，利用勾股定理进行计算即可解答．【解答】解：过点E作EN⊥BC，垂足为N，延长NE交AD于点M，∴∠ENB＝90°，∵四边形ABCD是矩形，∴AD＝BC＝6，∠DAB＝∠ABC＝90°，∴四边形AMNB是矩形，∴∠AMN＝90°，AB＝MN＝8，AM＝BN，MN∥AB，∴∠DME＝∠DAB＝90°，∠DEM＝∠DBA，∴△DME∽△DAB，∴＝，设ME＝x，则EN＝MN﹣EM＝8﹣x，∴＝，∴DM＝x，∴BN＝AM＝AD﹣DM＝6﹣x，∵BG＝2，∴GN＝BN﹣BG＝4﹣x，∵EG⊥AE，∴∠AEG＝90°，∴∠AEM+∠GEN＝90°，∵∠AEM+∠MAE＝90°，∴∠MAE＝∠GEN，∵∠AME＝∠ENG＝90°，∴△AME∽△ENG，∴＝，∴＝，∴x1＝，x2＝8，经检验：x1＝，x2＝8都是原方程的根，x2＝8（舍去），∴ME＝，AM＝6﹣x＝，∴AE＝＝＝，故选：B．4．如图，在△ABC中，AB＝10，BC＝34，cos∠ABC＝，射线CM∥AB，D为线段BC上的一动点且和B，C不重合，联结DA，过点D作DE⊥DA交射线CM于点E，联结AE，作EF＝EC，交BC的延长线于点F，设BD＝x．（1）如图1，当AD∥EF，求BD的长；（2）若CE＝y，求y关于x的函数解析式，并写出定义域；（3）如图2，点G在线段AE上，作∠AGD＝∠F，若△DGE与△CDE相似，求BD的长．【分析】（1）可推出△ABD是等腰三角形，从而求得BD；（2）作AK⊥BC于K，EH⊥CF于H，可证得△AKD∽△DHE，可求得AK＝8，DK＝x﹣6，EH＝y，DH＝34﹣x+y，进一步求得结果；（3）推出可以是△GDE∽△CDE或△GDE∽△CED，当△GDE∽△CDE时，可推出△GDE≌△CDE及△ABD≌△AGD，进而求得此时BD的值；当△GDE∽△CED时，推出四边形ADFED是平行四边形，再根据△AKD∽△DTE，进而求得此时BD．【解答】解：（1）如图1，作AK⊥BC于K，∴BK＝AB•cos∠ABC＝10×＝6，∴AK＝＝＝8，∵EF＝EC，∴∠ECF＝∠F，∵CM∥AB，AD∥EF，∴∠B＝∠ECF，∠ADB＝∠F，∴∠B＝∠ADB，∴AB＝AD，∴BD＝2BK＝12；（2）如图2，作AK⊥BC于K，EH⊥CF于H，∴∠ADK＝∠CHE＝90°，∴∠ADK+∠DAK＝90°，∵AD⊥DE，∴∠ADE＝90°，∴∠ADK+∠EDH＝90°，∴∠DAK＝∠EDH，∴△AKD∽△DHE，∴＝，∵BD＝x，BK＝6，BC＝34，∴DK＝x﹣6，DC＝34﹣x，∵∠ECF＝∠ABD，∴CH＝CE•cos∠ECF＝y•cos∠ABD＝，∴EH＝y，∴DH＝DC+CH＝34﹣x+，∴＝，化简，得，y＝，当∠HDE＝∠ECF时，DE∥CE，∴∠DAK＝∠ECH＝∠ABD，∴DK＝AK•tan∠DAK＝8•tan∠ABK＝8×＝，此时，BD＝BK+DK＝6+＝，∴6＜x＜；（3）如图3，∵∠AGD＝∠F，∠AGD+∠DGE＝180°，∴∠DGE+∠F＝180°，∵∠ECF+∠DCE＝180°，∠F＝∠ECF，∴∠DGE＝∠DCE，∴△GDE∽△CDE或△GDE∽△CED，当△GDE∽△CDE时，∠GDE＝∠CDE，∵DE＝DE，∴△CDE≌△GDE（AAS），∴DG＝DC，∵∠ADE＝90°，∴∠ADB+∠EDC＝∠ADG+∠GDE＝90°，∴∠ADB＝∠ADG，∵∠ABD＝∠ECF＝∠F，∴∠ABD＝∠AGD，∵AD＝AD，∴△ABD≌△AGD（AAS），\∴DB＝DG，∴BD＝CD＝BC＝17，∵6＜BD＜，∴BD＝17不符合题意，舍去；当△GDE∽△CED时，如图4，∠GDE＝∠DEC，∠GED＝∠CDE，∴DG∥CE，CD∥GE，∴四边形CDGE是平行四边形，由（1）（2）知，AK＝8，DK＝x﹣6，CD＝34﹣x，△AKD∽△DTE，∴ET＝AK＝8，CT＝BK＝6，DT＝40﹣x，∴＝，∴＝，∴x＝8，综上所述：BD＝8．考向五、手拉手相似模型：模型名称几何模型图形特点具有性质相似型手拉手△ABC ∽△ADEA 、D 、E 逆时针A 、B 、C 逆时针连结BD 、CE ①△ABD ∽△ACE ②△AOB ∽△HOC③旋转角相等④A 、B 、C 、H 四点共圆“反向”相似型手拉手△ABC ∽△ADE A 、D 、E 顺时针A 、B 、C 逆时针A 、D 、E`逆时针作△ADE 关于AD 对称的△ADE`性质同上①②③1．如图，△ABC 中，∠BAC ＝30°，∠ACB ＝90°，且△ABC ∽△AB 'C '，连接CC '，将CC ′沿C ′B ′方向平移至EB '，连接BE ，若CC '＝，则BE 的长为（ ）A ．1B ．C ．D ．2【分析】连接BB′，在Rt△ABC中，利用锐角三角函数的定义可得＝，再利用相似三角形的性质可得＝，∠ACB ＝∠AC ′B′＝90°，∠BAC ＝∠B ′AC ′＝30°，从而利用等式的性质可得∠BAB ′＝∠CAC ′，进而可证△BAB ′∽△CAC ′，然后利用相似三角形的性质可得∠BB ′A ＝∠CC ′A ，＝＝，再利用平移的性质可得CC ′∥B ′E ，＝＝，从而利用平行线的性质可得∠BB ′E ＝30°，最后证明△BCA ∽△BEB ′，从而可得∠BEB ′＝90°，进而在Rt △BEB ′中，利用锐角三角函数的定义进行计算即可解答．【解答】解：连接BB ′，∵∠BAC＝30°，∠ACB＝90°，∴cos30°＝＝，∵△ABC∽△AB'C'，∴＝，∠ACB＝∠AC′B′＝90°，∠BAC＝∠B′AC′＝30°，∴∠BAC+∠CAB′＝∠B′AC′+∠CAB′，∴∠BAB′＝∠CAC′，∴△BAB′∽△CAC′，∴∠BB′A＝∠CC′A，＝＝，由平移得：CC′＝B′E＝，CC′∥B′E，∴＝＝，∵CC′∥B′E，∴∠CC′B′+∠AB′C′+∠BB′A+∠BB′E＝180°，∴∠CC′B′+∠AB′C′+∠CC′A+∠BB′E＝180°，∴∠AC′B′+∠AB′C′+∠BB′E＝180°，∵∠AC′B′＝90°，∠B′AC′＝30°，∴∠AB′C′＝90°﹣∠B′AC′＝60°，∴∠BB′E＝30°，∴∠BB′E＝∠CAB＝30°，∴△BCA∽△BEB′，∴∠BEB′＝∠ACB＝90°，∴BE＝B′E•tan30°＝×＝，故选：B．2．如图，在△ABC中，AB＝AC＝3，BC＝6，点P在边AC上运动（可与点A，C重合），将线段BP 绕点P逆时针旋转120°，得到线段DP，连接BD，CD，则CD长的最小值为 ．【分析】以BC为边构建出和△BPD相似的三角形，通过将CD边转化为其他边来求值．【解答】解：如图所示，以BC为底边向上作等腰△BQC，使∠BQC＝120°，连接PQ．由题意可得△BQC和△BPD均为顶角为120°的等腰三角形，可得，∠QBC＝∠PBD＝30°，∴∠QBC﹣∠QBD＝∠PBD﹣∠QBD，∴∠PBQ＝∠DBC，∴△PBQ∽△DBC，∴，∴当PQ⊥AC时，有PQ最小，即此时CD最小，如图所示，设OP′⊥AC，延长AQ与BC交K，此时QP'为QP的最小值，可得AK⊥BC，∵△BQC中，∠BQC＝120°，BC＝6，∴BK＝3，∠QBK＝30°，∴QK＝，∵AB＝AC＝3，KC＝3，∴AK＝＝6，∴AQ＝AK﹣QK＝5，∵∠AP'Q＝∠AKC＝90°，∠QAP'＝∠CAK，∴△AQP'∽△ACK，∴，∴，∴QP'＝，∴CD＝P′＝．3．已知在Rt△ABC中，CD⊥AB于点D．（1）在图1中，写出其中两对相似三角形．（2）已知BD＝1，DC＝2，将△CBD绕着点D按顺时针方向进行旋转得到△C'BD，连接AC'，BC．①如图2，判断AC'与BC之间的位置及数量关系，并证明；②在旋转过程中，当点A，B，C'在同一直线时，求BC的长．【分析】（1）利用两个角相等可得△ABC∽△ACD，△BCD∽△BAC；（2）①利用两边成比例且夹角相等证明△DBC∽△DC'A，得，∠DC'A＝∠DBC，可得结论；②分点C'在线段AB或AB的延长线两种情形，分别画出图形，利用勾股定理列方程可得答案．【解答】解：（1）∵CD⊥AB，∴∠ADC＝∠BDC＝∠ACB＝90°，∴△ABC∽△ACD，△BCD∽△BAC；（2）①，AC'⊥BC，理由如下：由（1）知，在图1中，△ABC∽△CBD∽△ACD，∴，如图2，∵∠BDC'＝∠CDA＝90°，∴∠BDC＝∠C'DA，∴△DBC∽△DC'A，∴，∠DC'A＝∠DBC，∵∠DEB＝∠CEC'，∴∠C'FE＝∠BDC'＝90°，∴AC'⊥BC，∴，AC'⊥BC；②如图，当点A、B、C'在同一直线上时，由①知，，AC'⊥BC，设BC＝x，AC'＝2x，在Rt△ACB中，由勾股定理得，x2+（2x﹣）2＝（2）2，解得x＝（负值舍去），如图，当A、C'、B在同一直线上时，同理可得，x2+（2x+）2＝（2）2，解得x＝（负值舍去），综上：BC＝或．1．（2022秋•泗阳县期末）如图，利用标杆BE测量建筑物的高度，已知标杆BE高2m，测得AB＝3m，BC ＝6m．则建筑物CD的高是（ ）A．4m B．9m C．8m D．6m【分析】利用相似三角形的性质求解即可．【解答】解：∵EB∥CD，∴△AEB∽△ADC，∴＝，∴＝，∴CD＝6（m），故选：D．2．（2022秋•成华区期末）如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，连接DE，EF，已知四边形BDEF是平行四边形，．若△ADE的面积为1，则平行四边形BDEF的面积为（ ）A．3B．4C．5D．6【分析】利用平行四边形的性质先说明△ADE∽△ABC、△CEF∽△CBA，再利用相似三角形的性质求出△ADE、△ABC、△CEF的面积，最后利用面积的和差关系得结论．【解答】解：∵四边形BDEF是平行四边形，∴DE∥BC，EF∥AB．∴△ADE∽△ABC，△CEF∽△CBA．∵，∴＝．∴＝．∴＝（）2＝，＝（）2＝．∵S△ADE＝1，∴S△ABC＝9，S△CEF＝4．∵S△ADE+S△CEF+S平行四边形BDEF＝S△ABC，∴S平行四边形BDEF＝9﹣1﹣4＝4．故选：B．3．（2022秋•海淀区校级月考）如图，在等腰△ABC中，AB＝AC＝9，BP＝BC＝2，D在AC上，且∠APD ＝∠B，则CD＝ ．【分析】根据已知易得BC＝6，从而可得CP＝4，再利用等腰三角形的性质可得∠B＝∠C，从而利用三角形内角和定理可得∠BAP+∠APB＝180°﹣∠B，然后利用平角定义可得∠APB+∠DPC＝180°﹣∠B，从而可得∠DPC＝∠BAP，进而可得△ABP∽△PCD，最后利用相似三角形的性质进行计算即可解答．【解答】解：∵BP＝BC＝2，∴BC＝3BP＝6，∴CP＝BC﹣BP＝6﹣2＝4，∵AB＝AC＝9，∴∠B＝∠C，∴∠BAP+∠APB＝180°﹣∠B，∵∠APD＝∠B，∴∠APB+∠DPC＝180°﹣∠APD＝180°﹣∠B，∴∠DPC＝∠BAP，∴△ABP∽△PCD，∴＝，∴＝，∴CD＝，故答案为：．4．（2022秋•万州区期末）如图，矩形ABCD中，AB＝6，BC＝9，E为CD的中点，F为BC上一点，BF＜FC，且AF⊥FE．对角线AC与EF交于点G，则GC的长为 ．【分析】根据矩形的性质可得∠B＝∠FCE＝90°，由∠AFB+∠EFC＝∠AFB+∠BAF可得∠EFC＝∠BAF，以此证明△ABF∽△FCE，根据相似三角形的性质得，设BF＝x，则CF＝9﹣x，以此列出方程解得BF＝3，CF＝6，过点G作GH⊥BC于点H，再证明△CHG∽△CBA，△FHG∽△FCE，得到，，联立两式子，算出CH、GH，最后根据勾股定理即可求解．【解答】解：∵四边形ABCD为矩形，∴∠B＝∠FCE＝90°，∵AF⊥FE，∴∠AFB+∠EFC＝90°，∵∠AFB+∠BAF＝90°，∴∠EFC＝∠BAF，∴△ABF∽△FCE，∴，设BF＝x，则CF＝9﹣x，∵四边形ABCD为矩形，AB＝6，E为CD的中点，∴CE＝3，∴，整理得：x2﹣9x+18＝0，解得：x1＝3，x2＝6，∵BF＜FC，∴BF＝3，CF＝6，过点G作GH⊥BC于点H，如图，∵AB⊥BC，DC⊥BC，∴GH∥AB，GH∥CD，∴△CHG∽△CBA，△FHG∽△FCE，∴，，∴①，②，联立①②得：，解得：，在Rt△CHG中，由勾股定理得GC＝．故答案为：．5．（2022•安徽模拟）在数学探究活动中，小明进行了如下操作：如图，将两张等腰直角三角形纸片ABC 和CDE如图放置（其中∠ACB＝∠E＝90°，AC＝BC，CE＝DE）．CD、CE分别与AB边相交于M、N 两点．请完成下列探究：（1）若AC＝2，则AN•BM的值为　4　；（2）过M作MF⊥AC于F，若＝，则的值为 ．【分析】（1）由等腰直角三角形的性质可得∠A＝∠B＝45°，∠MCN＝45°，可得∠ACN＝∠ACM+∠MCN＝∠ACM+45°，∠BMC＝∠ACM+∠A＝∠ACM+45°，即可证明△ACN∽△BMC，可得＝，即可求解；（2）过点C作CG⊥AB于点G，可得∠CGN＝∠CFM＝90°，由等腰直角三角形的性质可得∠NCG+∠MCG＝45°，∠ACM+∠MCG＝45°，从而可得∠NCG＝∠MCF，可证得△GCN∽△FCM，可得＝＝，设CG＝4k，则CF＝5k，AC＝4k，即可求解＝．【解答】解：（1）∵△ABC和△CDE为等腰直角三角形，∴∠A＝∠B＝45°，∠MCN＝45°，BC＝AC＝2，∵∠ACN＝∠ACM+∠MCN＝∠ACM+45°，∠BMC＝∠ACM+∠A＝∠ACM+45°，∴∠ACN＝∠BMC，∴△ACN∽△BMC，∴＝，∵BC＝AC＝2，∴AN•BM＝AC•BC＝4，故答案为：4；（2）如图，过点C作CG⊥AB于点G，∵MF⊥AC，∴∠CGN＝∠CFM＝90°，∵∠NCG+∠MCG＝45°，∠ACM+∠MCG＝45°，∴∠NCG＝∠MCF，∴△GCN∽△FCM，∵＝，∴＝＝，设CG＝4k，则CF＝5k，AC＝4k，∴＝，故答案为：．6．（2022秋•驻马店期末）如图，AD是Rt△ABC斜边上的高，若AB＝4cm，BC＝10cm，求BD的长．【分析】根据射影定理列出算式，代入数据计算即可．【解答】解：由射影定理得，AB2＝BD•BC，则BD＝＝1.6．7．（2022秋•开化县期中）如图，在△ABC和△DEC中，∠A＝∠D，∠BCE＝∠ACD．（1）求证：△ABC∽△DEC；（2）若AC：DC＝2：3，BC＝6，求EC的长．【分析】（1）由∠BCE＝∠ACD，可得出∠BCA＝∠ECD，结合∠A＝∠D，可证出△ABC∽△DEC；（2）由△ABC∽△DEC，利用相似三角形的性质可得出AC：DC＝BC：CE，结合已知条件，可求出EC 的长．【解答】（1）证明：∵∠BCE＝∠ACD，∴∠BCE+∠ECA＝∠ACD+∠ACE，即∠BCA＝∠ECD．又∵∠A＝∠D，∴△ABC∽△DEC．（2）解：∵△ABC∽△DEC，AC：DC＝2：3，∴AC：DC＝BC：CE＝2：3，而BC＝6，∴EC＝9，∴EC的长为9．8．（2022秋•奉贤区期中）如图，已知在四边形ABCD中，AD∥BC．E为边CB延长线上一点，联结DE 交边AB于点F，联结AC交DE于点G，且＝．（1）求证：AB∥CD；（2）如果AE2＝AG•AC，求证：＝．【分析】（1）由AD∥BC，得到△ADG∽△CEG，根据相似三角形的性质即可得到结论；（2）由AE2＝AG•AC易得△AEG∽△ACE，所以∠AEG＝∠ACE＝∠DAG，可得△ADG∽△EDA，再根据相似三角形的性质可得结论．【解答】证明：（1）∵AD∥BC，∴△ADG∽△CEG，∴＝，∵＝，∴＝，∴AB∥CD；（2）∵AE2＝AG•AC，∴＝，∵∠EAG＝∠CAE，∴△AEG∽△ACE，∴∠AEG＝∠ACE，∵AD∥BC，∴∠ACE＝∠DAG，∴∠DAG＝∠AEG，∵∠ADG＝∠EDA，∴△ADG∽△EDA，∴，即＝．9．（2022秋•长安区校级月考）如图，已知AB∥EF∥CD，AC，BD相交于点E，EF：AB＝2：3．（1）若CE＝4，求AE的长；（2）若CD＝6，求AB的长；（3）若四边形ABFE的面积为8，直接写出△CEF的面积．【分析】（1）根据AB∥EF得到△CEF∽△CAB，接着利用相似三角形的性质得到EF：AB＝2：3＝CE：CA，由此求出CA＝6即可求解；（2）根据AB∥EF∥CD，得到△ABE∽△CDE，接着得到AB：CD＝AE：CE，利用比例的性质最后得到EFAE：CE＝AB：CD＝1：2即可求出AB＝3；（3）由于△CEF∽△CAB得到S△CEF：S△CAB＝＝＝，由此即可求解．【解答】解：（1）∵AB∥EF，∴△CEF∽△CAB，∴EF：AB＝2：3＝CE：CA，∵CE＝4，∴2：3＝4：CA，∴CA＝6，∴AE＝CA﹣CE＝6﹣4＝2；（2）∵AB∥EF∥CD，∴△ABE∽△CDE，∴AB：CD＝AE：CE，∵EF：AB＝2：3＝CE：CA，∴CE：EA＝2：1，∴AE：CE＝AB：CD＝1：2，而CD＝6，∴AB＝3；（3）∵△CEF∽△CAB，∴S△CEF：S△CAB＝＝＝，∴＝，∴＝，∴S△CEF＝．10．（2022•文山州模拟）如图，在△ABC中，∠A＝90°，D、E分别是AB、BC上的点，过B、D、E三点作⨀O，交CD延长线于点F，AC＝3，BC＝5，AD＝1．（1）求证：△CDE∽△CBF；（2）当⨀O与CD相切于点D时，求⨀O的半径；（3）若S△CDE＝3S△BDF，求DF的值．【分析】（1）根据圆内接四边形的性质可得∠BED+∠BFD＝180°，再根据同角的补角相等可得∠CED ＝∠BFD，然后根据两角相等的两个三角形相似进行证明即可解答；（2）连接OD，过点O作OM⊥BD，垂足为M，可得DM＝BM＝DB，∠OMD＝90°，从而可得∠ODM+∠MOD＝90°，再在Rt△ABC中利用勾股定理求出AB的长，从而求出BD，DM的长，然后在Rt△ACD 中，利用勾股定理求出CD的长，再利用切线的性质可得∠ODC＝90°，最后利用一线三等角相似模型证明△DMO∽△CAD，从而利用相似三角形的性质进行计算即可解答；（3）过点D作DH⊥BC，垂足为H，过点B作BG⊥CF，垂足为G，根据△BDC的面积＝BC•DH＝BD•AC＝BG•CD，可求出DH＝，BG＝，再根据已知S△CDE＝3S△BDF，可得＝，然后设DF＝x，则CE＝15x，从而利用（1）的结论，进行计算即可解答．【解答】（1）证明：∵四边形BEDF是⊙O的内接四边形，∴∠BED+∠BFD＝180°，∵∠BED+∠CED＝180°，∴∠CED＝∠BFD，∵∠DCE＝∠BCF，∴△CDE∽△CBF；（2）连接OD，过点O作OM⊥BD，垂足为M，∴DM＝BM＝DB，∠OMD＝90°，∴∠ODM+∠MOD＝90°，∵∠A＝90°，BC＝5，AC＝3，∴AB＝＝＝4，∵AD＝1，∴BD＝AB﹣AD＝4﹣1＝3，∴DM＝BD＝，在Rt△ADC中，CD＝＝＝，∵⨀O与CD相切于点D，∴∠ODC＝90°，∴∠ODM+∠ADC＝180°﹣∠ODC＝90°，∴∠MOD＝∠ADC，∵∠OMD＝∠A＝90°，∴△DMO∽△CAD，∴＝，∴＝，∴DO＝，∴⨀O的半径为；（3）过点D作DH⊥BC，垂足为H，过点B作BG⊥CF，垂足为G，∵△BDC的面积＝BC•DH＝BD•AC＝BG•CD，∴BC•DH＝BD•AC＝BG•CD，∴5DH＝3×3＝BG，∴DH＝，BG＝，∵S△CDE＝3S△BDF，∴CE•DH＝3×DF•BG，∴CE•DH＝3DF•BG，∴CE＝3DF•，∴＝＝，∴设DF＝x，则CE＝15x，由（1）得：△CDE∽△CBF，∴＝，∴＝，解得：x＝，经检验：x＝是原方程的根，∴DF＝x＝，∴DF的长为．1．（2022•巴中）如图，在平面直角坐标系中，C为△AOB的OA边上一点，AC：OC＝1：2，过C作CD∥OB交AB于点D，C、D两点纵坐标分别为1、3，则B点的纵坐标为（ ）A．4B．5C．6D．7【分析】根据CD∥OB得出，根据AC：OC＝1：2，得出，根据C、D两点纵坐标分别为1、3，得出OB＝6，即可得出答案．【解答】解：∵CD∥OB，∴，∵AC：OC＝1：2，∴，∵C、D两点纵坐标分别为1、3，∴CD＝3﹣1＝2，∴，解得：OB＝6，∴B点的纵坐标为6，故选：C．2．（2022•凉山州）如图，在△ABC中，点D、E分别在边AB、AC上，若DE∥BC，，DE＝6cm，则BC的长为（ ）A．9cm B．12cm C．15cm D．18cm【分析】根据＝，得到＝，根据DE∥BC，得到∠ADE＝∠B，∠AED＝∠C，得到△ADE∽△ABC，根据相似三角形对应边成比例即可得出答案．【解答】解：∵＝，∴＝，∵DE∥BC，∴∠ADE＝∠B，∠AED＝∠C，∴△ADE∽△ABC，∴＝，∴＝，∴BC＝15（cm），故选：C．3．（2022•哈尔滨）如图，AB∥CD，AC，BD相交于点E，AE＝1，EC＝2，DE＝3，则BD的长为（ ）A．B．4C．D．6【分析】利用平行线证明判定三角形相似，得到线段成比例求解．【解答】解：∵AB∥CD，∴△ABE∽△CDE，∴＝，即＝，∴BE＝1.5，∴BD＝BE+DE＝4.5．故选：C．4．（2022•雅安）如图，在△ABC中，D，E分别是AB和AC上的点，DE∥BC，若＝，那么＝（ ）A．B．C．D．【分析】根据相似三角形的判定定理和性质定理解答即可．【解答】解：∵DE∥BC，∴△ADE∽△ABC，∴＝，∵＝，∴＝，∴＝＝．故选：D．5．（2022•扬州）如图，在△ABC中，AB＜AC，将△ABC以点A为中心逆时针旋转得到△ADE，点D在BC 边上，DE交AC于点F．下列结论：①△AFE∽△DFC；②DA平分∠BDE；③∠CDF＝∠BAD，其中所有正确结论的序号是（ ）A．①②B．②③C．①③D．①②③【分析】由旋转的性质得出∠BAC＝∠DAE，∠B＝∠ADE，AB＝AD，∠E＝∠C，进而得出∠B＝∠ADB，得出∠ADE＝∠ADB，得出DA平分∠BDE，可判断结论②符合题意；由∠AFE＝∠DFC，∠E＝∠C，得出△AFE∽△DFC，可判断结论①符合题意；由∠BAC＝∠DAE，得出∠BAD＝∠FAE，由相似三角形的性质得出∠FAE＝∠CDF，进而得出∠BAD＝∠CDF，可判断结论③符合题意；即可得出答案．【解答】解：∵将△ABC以点A为中心逆时针旋转得到△ADE，∴∠BAC＝∠DAE，∠B＝∠ADE，AB＝AD，∠E＝∠C，∴∠B＝∠ADB，∴∠ADE＝∠ADB，∴DA平分∠BDE，∴②符合题意；∵∠AFE＝∠DFC，∠E＝∠C，∴△AFE∽△DFC，∴①符合题意；∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠BAD＝∠FAE，∵△AFE∽△DFC，∴∠FAE＝∠CDF，∴∠BAD＝∠CDF，∴③符合题意；故选：D．6．（2022•达州）如图，点E在矩形ABCD的AB边上，将△ADE沿DE翻折，点A恰好落在BC边上的点F 处，若CD＝3BF，BE＝4，则AD的长为（ ）A．9B．12C．15D．18【分析】证明△BEF∽△CFD，求得CF，设BF＝x，用x表示DF、CD，由勾股定理列出方程即可求解．【解答】解：∵四边形ABCD是矩形，∴AD＝BC，∠A＝∠EBF＝∠BCD＝90°，∵将矩形ABCD沿直线DE折叠，∴AD＝DF＝BC，∠A＝∠DFE＝90°，∴∠BFE+∠DFC＝∠BFE+∠BEF＝90°，∴∠BEF＝∠CFD，∴△BEF∽△CFD，∴，∵CD＝3BF，∴CF＝3BE＝12，设BF＝x，则CD＝3x，DF＝BC＝x+12，∵∠C＝90°，∴Rt△CDF中，CD2+CF2＝DF2，∴（3x）2+122＝（x+12）2，解得x＝3（舍去0根），∴AD＝DF＝3+12＝15，故选：C．7．（2022•云南）如图，在△ABC中，D、E分别为线段BC、BA的中点，设△ABC的面积为S1，△EBD的面积为S2，则＝（ ）A ．B ．C ．D ．【分析】根据三角形的中位线定理，相似三角形的面积比等于相似比的平方解答即可．【解答】解：在△ABC 中，D 、E 分别为线段BC 、BA 的中点，∴DE 为△ABC 的中位线，∴DE ∥AC ，DE ＝AC ，∴△BED ∽△BAC ，∵＝，∴＝，即＝，故选：B ．8．（2022•锦州）如图，在正方形ABCD 中，E 为AD 的中点，连接BE 交AC 于点F ．若AB ＝6，则△AEF 的面积为 3　．【分析】由正方形的性质可知AE ＝3，AD //BC ，则可判断△AEF ∽△CBF ，利用相似三角形的性质得到，然后根据三角形面积公式得到S △AEF ＝S △ABE ．【解答】解：∵四边形ABCD 是正方形，∴AD ＝BC ＝AB ＝6，AD ∥BC ，∵E 为AD 的中点，∴AE ＝AB ＝3，∵AE ∥BC ，∴△AEF ∽△CBF ，∴＝＝，∴S △AEF ：S △ABF ＝1：2，∴S△AEF＝S△ABE＝××3×6＝3．故答案为：3．9．（2022•牡丹江）如图，在等腰直角三角形ABC和等腰直角三角形ADE中，∠BAC＝∠DAE＝90°，点D 在BC边上，DE与AC相交于点F，AH⊥DE，垂足是G，交BC于点H．下列结论中：①AC＝CD；②AD2＝BC•AF；③若AD＝3，DH＝5，则BD＝3；④AH2＝DH•AC，正确的是　②③　．【分析】①根据等腰直角三角形可知∠B＝∠ACB＝45°，若AC＝CD，则∠ADC＝∠CAD＝67.5°，这个根据已知得不出来，所以①错误；②证明△AEF∽△ABD，列比例式可作判断；④证明△ADH∽△BAH，列比例式可作判断；③先计算AH的长，由④中得到的比列式计算可作判断．【解答】解：①∵△ABC是等腰直角三角形，∴∠B＝∠ACB＝45°，∵∠ADC＝∠B+∠BAD，而∠BAD的度数不确定，∴∠ADC与∠CAD不一定相等，∴AC与CD不一定相等，故①错误；②∵∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，∵∠B＝∠AED＝45°，∴△AEF∽△ABD，∴＝，∵AE＝AD，AB＝BC，∴AD2＝AF•AB＝AF•BC，∴AD2＝AF•BC，故②正确；④∵∠DAH＝∠B＝45°，∠AHD＝∠AHD，∴△ADH∽△BAH，∴＝，∴AH2＝DH•BH，而BH与AC不一定相等，故④不一定正确；③∵△ADE是等腰直角三角形，∴∠ADG＝45°，∵AH⊥DE，∴∠AGD＝90°，∵AD＝3，∴AG＝DG＝，∵DH＝5，∴GH＝＝＝，∴AH＝AG+GH＝2，由④知：AH2＝DH•BH，∴（2）2＝5BH，∴BH＝8，∴BD＝BH﹣DH＝8﹣5＝3，故③正确；本题正确的结论有：②③故答案为：②③．10．（2022•东营）如图，在△ABC中，点F、G在BC上，点E、H分别在AB、AC上，四边形EFGH是矩形，EH＝2EF，AD是△ABC的高，BC＝8，AD＝6，那么EH的长为 ．【分析】设AD交EH于点R，由矩形EFGH的边FG在BC上证明EH∥BC，∠EFC＝90°，则△AEH∽△ABC，得＝，其中BC＝8，AD＝6，AR＝6﹣EH，可以列出方程＝，解方程求出EH 的值即可．【解答】解：设AD交EH于点R，∵矩形EFGH的边FG在BC上，∴EH∥BC，∠EFC＝90°，∴△AEH∽△ABC，∵AD⊥BC于点D，∴∠ARE＝∠ADB＝90°，∴AR⊥EH，∴＝，∵EF⊥BC，RD⊥BC，EH＝2EF，∴RD＝EF＝EH，∵BC＝8，AD＝6，AR＝6﹣EH，∴＝，解得EH＝，∴EH的长为，故答案为：．11．（2022•上海）我们经常会采用不同方法对某物体进行测量，请测量下列灯杆AB的长．（1）如图（1）所示，将一个测角仪放置在距离灯杆AB底部a米的点D处，测角仪高为b米，从C点测得A点的仰角为α，求灯杆AB的高度．（用含a，b，α的代数式表示）（2）我国古代数学家赵爽利用影子对物体进行测量的方法，在至今仍有借鉴意义．如图（2）所示，现将一高度为2米的木杆CG放在灯杆AB前，测得其影长CH为1米，再将木杆沿着BC方向移动1.8米至DE的位置，此时测得其影长DF为3米，求灯杆AB的高度．【分析】（1）根据题意可得BE＝CD＝b米，EC＝BD＝a米，∠AEC＝90°，∠ACE＝α，然后在Rt△AEC 中，利用锐角三角函数的定义求出AE的长，进行计算即可解答；（2）根据题意得：GC＝DE＝2米，CD＝1.8米，∠ABC＝∠GCD＝∠EDF＝90°，然后证明A字模型相似三角形△ABH∽△GCH，从而可得＝，再证明A字模型相似三角形△ABF∽△EDF，从而可得＝，进而可得＝，最后求出BC的长，从而求出AB的长．【解答】解：（1）如图：由题意得：BE＝CD＝b米，EC＝BD＝a米，∠AEC＝90°，∠ACE＝α，在Rt△AEC中，AE＝CE•tanα＝a tanα（米），∴AB＝AE+BE＝（b+a tanα）米，∴灯杆AB的高度为（a tanα+b）米；（2）由题意得：GC＝DE＝2米，CD＝1.8米，∠ABC＝∠GCD＝∠EDF＝90°，∵∠AHB＝∠GHC，∴△ABH∽△GCH，∴＝，∴＝，∵∠F＝∠F，∴△ABF∽△EDF，∴＝，∴＝，∴＝，∴BC＝0.9米，∴＝，∴AB＝3.8米，∴灯杆AB的高度为3.8米．1．（2022•贺州）如图，在△ABC中，DE∥BC，DE＝2，BC＝5，则S△ADE：S△ABC的值是（ ）A．B．C．D．【分析】根据相似三角形的面积比等于相似比的平方计算即可．【解答】解：∵DE∥BC，∴△ADE∽△ABC，∵DE＝2，BC＝5，∴S△ADE：S△ABC的值为，故选：B．2．（2022•南岗区三模）如图，点E在菱形ABCD的边CD的延长线上，连接BE交AD于点F，则下列式子一定正确的是（ ）A．B．C．D．。

相关主题
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

教师辅导教案
授课日期：年月日授课课时：课时
4．相似三角形周长的比等于相似比．
ABC △与A B C '''△相似，则有AB BC AC k A B B C A C
===''''''（k 为相似比）．应用比例的等比性质有AB BC AC AB BC AC k A B B C A C A B B C A C ++====''''''''''''
++． 5．相似三角形面积的比等于相似比的平方．
ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有
AB BC AC AH k A B B C A C A H ====''''''''
（k 为相似比）．进而可得21212ABC A B C BC AH S BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△．
二、相似三角形的判定
1．平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似．
2．如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．可简单说成：两角对应相等，两个三角形相似．
3．如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．
4．如果一个三角形的三条边与另一个三角形的你对应成比例，那么这两个三角形相似．可简单地说成：三边对应成比例，两个三角形相似．
5．如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．
6．直角三角形被斜边上的高分成的两个直角三角形相似（常用但要证明）
7．如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等，那么这两个等腰三角形相似；如果它们的腰和底对应成比例，那么这两个等腰三角形也相似．
三、相似证明中的基本模型
A 字形
图①A 字型，DE//BC ;结论：AD AE DE AB AC BC
==， 【例1】老师在编写下面这个题目的答案时，不小心打乱了解答过程的顺序，你能帮他调
整过来吗？证明步骤正确的顺序是（ ）
已知：如图，在△ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，且DE ∥BC ，DF ∥AC ，
求证：△ADE ∽△DBF ．
证明：①又∵DF ∥AC ，
②∵DE ∥BC ，
③∴∠A=∠BDF ，
④∴∠ADE=∠B ，
∴△ADE ∽△DBF ．
A．③②④① B．②④①③C．③①④② D．②③④①
【解答】证明：②∵DE∥BC，
④∴∠ADE=∠B，
①又∵DF∥AC，
③∴∠A=∠BDF，
∴△ADE∽△DBF．故选：B．
【练1】如图，在△ABC中，∠ACB=90°，BC=16cm，AC=12cm，点P从点B出发，以2cm/秒的速度向点C移动，同时点Q从点C出发，以1cm/秒的速度向点A移动，设运动时间为t秒，当t= 4.8或秒时，△CPQ与△ABC相似．
【解答】解：CP和CB是对应边时，△CPQ∽△CBA，
所以，，
即，
解得t=4.8；
CP和CA是对应边时，△CPQ∽△CAB，
所以，，
即，
解得t=．
综上所述，当t=4.8或时，△CPQ与△CBA相似．
故答案为4.8或．
图②反A字型，∠ADE=∠B或∠1=∠B结论：AE AD DE
==
AC AB BC
【例2】如同，在△ABC中，点D，E分别在边AB，AC上，下列条件中不能判断△ABC∽△AED的是（）A．=B．=C．∠ADE=∠C D．∠AED=∠B
【解答】解：∵∠DAE=∠CAB，
∴当∠AED=∠B或∠ADE=∠C时，△ABC∽△AED；
当=即=时，△ABC∽△AED．
故选：A．
【例3】如图，P是△ABC的边AB上的一点．（不与A、B重合）当∠ACP=∠ B 时，△APC与△ABC 是否相似；当AC、AP、AB满足时，△ACP与△ABC相似．
【解答】解：∵∠A=∠A，∠ACP=∠B，
∴△ACP∽△ABC；
∵，∠A=∠A，
∴△ACP与△ABC；
故答案为：B；．
【练习1】如图，D、E为△ABC的边AC、AB上的点，当∠ADE=∠B 时，△ADE∽
△ABC．其中D、E分别对应B、C．（填一个条件）．
【解答】解：当∠ADE=∠B，
∵∠EAD=∠CAB，
∴△ADE∽△ABC．
故答案为∠ADE=∠B．
【练习2】如图，在△ABC中，D、E分别在AB与AC上，且AD=5，DB=7，AE=6，EC=4．
求证：△ADE∽△ACB．
【解答】证明：∵AD=5，DB=7，AE=6，EC=4，
∴AB=5+7=12，AC=6+4=10，
∴====，
∴=，
又∵∠A=∠A，
∴△ADE∽△ACB．
【练习3】如图，AB=AC，∠A=36°，BD是∠ABC的角平分线，求证：△ABC∽△
BCD．
. I
【解答】证明：∵AB=AC ，∠A=36°，
∴∠ABC=∠C=72°，
∵BD 是角平分线，
∴∠ABD=∠DBC=36°，
∴∠A=∠CBD ，
又∵∠C=∠C ，
∴△ABC ∽△BCD ．
【练习4】已知：如图，△ABC 中，∠ACD=∠B ，求证：△ABC ∽△ACD ．
【解答】证明：∵∠ACD=∠B ，∠A=∠A ，
∴△ABC ∽△ACD ．
【练习5】如图，已知AD•AC=AB•AE． 求证：△ADE ∽△ABC ．
【解答】证明：∵AD•AC=AE•AB，
∴= 在△ABC 与△ADE 中
∵=，∠A=∠A ，
∴△ABC ∽△ADE ．
【练习6】已知：如图，在△ABC 中，D ，E 分别为AB 、AC 边上的点，且AD=AE ，连接DE ．若AC=4，AB=5．求证：△ADE ∽△ACB ．
【解答】证明：∵AC=3，AB=5，AD=
，
∴， ∵∠A=∠A ，
∴△ADE ∽△ACB ．
图③双A 字型
【例4】如图，在△ABC 中，D ，E 分别是AB ，AC 上的点，∠AED=∠ABC ，∠BAC 的平分线AF 交DE 于点G ，交BC 于点F ．
（1）试写出图中所有的相似三角形，并说明理由
（2）若=，求的值．
. I。

相关文档
最新文档