工程流体力学-单元4解析
工程流体力学课后习题答案

第1章 绪论【1-1】500cm 3的某种液体,在天平上称得其质量为0.453kg ,试求其密度和相对密度。
【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 相对密度330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水,在温度不变的条件下,当压强从98000Pa 增加到4.9×105Pa 时,体积减少1L 。
求水的压缩系数和弹性系数。
【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃,流量为60m 3/h 的水流入加热器,如果水的体积膨胀系数βt =0.00055K -1,问加热到80℃后从加热器中流出时的体积流量变为多少? 【解】根据膨胀系数1t dV V dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。
罐装时液面上压强为98000Pa 。
封闭后由于温度变化升高了20℃,此时汽油的蒸汽压力为17640Pa 。
若汽油的膨胀系数为0.0006K -1,弹性系数为13.72×106Pa ,(1)试计算由于压力温度变化所增加的体积,(2)问灌装时汽油的体积最多不应超过桶体积的百分之多少?【解】(1)由1β=-=P pdV Vdp E可得,由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积,可由1β=tt dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT(2)因为∆∆tp V V ,相比之下可以忽略由压力变化引起的体积改变,则由 200L β+=t V V dT得1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板,其水平运动速度为u =1m/s ,δ=10mm ,油品的粘度μ=0.9807Pa ·s ,求作用在平板单位面积上的阻力。
工程流体力学习题课1-第2-3-4章-部分习题解答

2 2 d2
习题3-14解题示意图1
Dr W-X Huang, School of Chemical Engineering, Sichuan University, Chengdu 610065, P.R. China
工程流体力学——习题课(1)——第 2-3-4 章部分习题解答
Fx1 =
y x
H1
D
H2
图 3-26 习题 3-11 附图
1 1 ρ gH1 × ( DL) = × 1000 × 9.8 × 4 × (4 × 10) = 784000 N=784kN 2 2 1 D 1 4 Fx 2 = ρ gH 2 × ( L) = × 1000 × 9.8 × 2 × × 10 = 196000 N=196kN 2 2 2 2
H
h
由此得: H ≥ 122mm + h ≥ 244mm (2) 结合以上正负压操作时结果有:
p / ρ g ≤ h ≤ H − | p| / ρ g
图 3-23 习题 3-8 附图
→ 122mm ≤ h ≤ 178mm
Dr W-X Huang, School of Chemical Engineering, Sichuan University, Chengdu 610065, P.R. China
工程流体力学——习题课(1)——第 2-3-4 章部分习题解答
F1-6
习题 3-8 旋风除尘器如图 3-23 所示,其下端出灰口管段长 H,部分插入 水中,使旋风除尘器内部与外界大气隔开,称为水封;同时要求出灰管内液面 不得高于出灰管上部法兰位置。设除尘器内操作压力 ( 表 压 ) p = −1.2 kPa~ 1.2kPa。 净化空气 (1) 试问管段长 H 至少为多少 mm? (2) 若H=300mm,问其中插入水中的部分h应在 什么范围?(取水的密度 ρ =1000kg/m3) 含尘 解:(1) 正压操作时,出灰管内液面低于管外液 面,高差为 h′ = p / ρ g ;为实现水封,出灰管插入深 度 h 必须大于此高差,即
工程流体水力学第四章习题答案
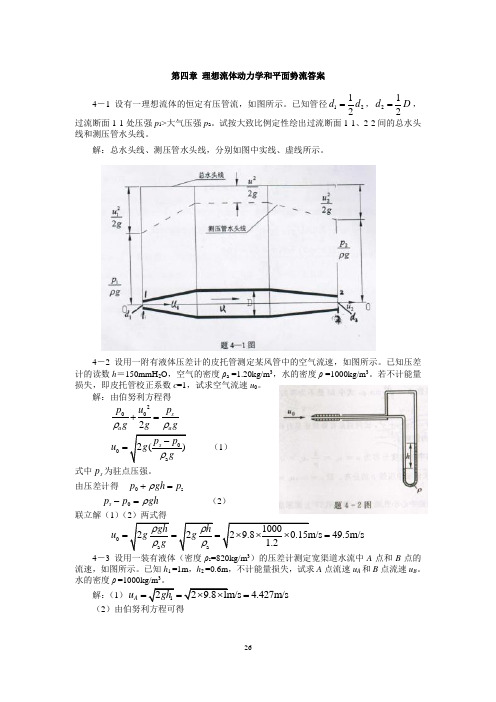
第四章 理想流体动力学和平面势流答案4-1 设有一理想流体的恒定有压管流,如图所示。
已知管径1212d d =,212d D =,过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解:总水头线、测压管水头线,分别如图中实线、虚线所示。
4-2 设用一附有液体压差计的皮托管测定某风管中的空气流速,如图所示。
已知压差计的读数h =150mmH 2O ,空气的密度ρa =1.20kg/m 3,水的密度ρ =1000kg/m 3。
若不计能量损失,即皮托管校正系数c =1,试求空气流速u 0。
解:由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=(1) 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= (2)联立解(1)(2)两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4-3 设用一装有液体(密度ρs =820kg/m 3)的压差计测定宽渠道水流中A 点和B 点的流速,如图所示。
已知h 1 =1m ,h 2 =0.6m ,不计能量损失,试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解:(1)1229.81m/s 4.427m/s A u gh ==⨯⨯= (2)由伯努利方程可得22A AA u p h g gρ+= (1)22B BB u p h g gρ+= (2)式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由(1)、(2)式可得2222A B A BA B p p u u h h g g gρ-=+-- (3) 由压差计得,22ρρρρ--++=A A s B B p gh gh gh gh p ,所以220.82A BA B p p h h h h gρ-=+-- (4) 由(3)式、(4)式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。
工程流体力学答案详解

第一章 流体及其物理性质1-1 已知油的重度为7800N/m 3,求它的密度和比重。
又,0.2m 3此种油的质量和重量各为多少?已已知知::γ=7800N/m 3;V =0.2m 3。
解解析析::(1) 油的密度为 3kg/m 79581.97800===gγρ; 油的比重为 795.01000795OH 2===ρρS (2) 0.2m 3的油的质量和重量分别为 kg 1592.0795=⨯==V M ρ N 15602.07800=⨯==V G γ1-2 已知300L(升)水银的质量为4080kg ,求其密度、重度和比容。
已已知知::V =300L ,m =4080kg 。
解解析析::水银的密度为 33kg/m 13600103004080=⨯==-V m ρ 水银的重度为3N/m 13341681.913600=⨯==g ργ水银的比容为 kg /m 10353.7136001135-⨯===ρv1-3 某封闭容器内空气的压力从101325Pa 提高到607950Pa ,温度由20℃升高到78℃,空气的气体常数为287.06J/k g ·K 。
问每kg 空气的体积将比原有体积减少多少?减少的百分比又为多少?已已知知::p 1=101325Pa ,p 2=607950Pa ,t 1=20℃,t 2=78℃,R =287.06J/k g ·K 。
解解析析::由理想气体状态方程(1-12)式,得 kg /m 83.0101325)27320(06.2873111=+⨯==p RT v kg /m 166.0607950)27378(06.2873222=+⨯==p RT v kg /m 664.0166.083.0321=-=-v v%80%10083.0166.083.0%100121=⨯-=⨯-v v v每kg 空气的体积比原有体积减少了0.664m 3;减少的百分比为80%。
工程流体力学教学课件ppt作者闻建龙工程流体力学习题+答案(部分)

闻建龙主编的《工程流体力学》习题参考答案第一章 绪论1-1 物质是按什么原则分为固体和液体两大类的? 解:从物质受力和运动的特性将物质分成两大类:不能抵抗切向力,在切向力作用下可以无限的变形(流动),这类物质称为流体。
如空气、水等。
而在同等条件下,固体则产生有限的变形。
因此,可以说:流体不管是液体还是气体,在无论多么小的剪应力(切向)作用下都能发生连续不断的变形。
与此相反,固体的变形与作用的应力成比例,经一段时间变形后将达到平衡,而不会无限增加。
1-2 何谓连续介质假设?引入连续介质模型的目的是什么?在解决流动问题时,应用连续介质模型的条件是什么?解:1753年,欧拉首次采用连续介质作为流体宏观流动模型,即不考虑流体分子的存在,把真实的流体看成是由无限多流体质点组成的稠密而无间隙的连续介质,甚至在流体与固体边壁距离接近零的极限情况也认为如此,这个假设叫流体连续介质假设或稠密性假设。
流体连续性假设是流体力学中第一个根本性假设,将真实流体看成为连续介质,意味着流体的一切宏观物理量,如密度、压力、速度等,都可看成时间和空间位置的连续函数,使我们有可能用数学分析来讨论和解决流体力学问题。
在一些特定情况下,连续介质假设是不成立的,例如:航天器在高空稀薄气体中飞行,超声速气流中激波前后,血液在微血管(1μm )内的流动。
1-3 底面积为25.1m 的薄板在液面上水平移动(图1-3),其移动速度为s m 16,液层厚度为mm 4,当液体分别为C 020的水和C 020时密度为3856m kg 的原油时,移动平板所需的力各为多大?题1-3图解:20℃ 水:s Pa ⋅⨯=-3101μ20℃,3/856m kg =ρ, 原油:s Pa ⋅⨯='-3102.7μ水: 233/410416101m N u=⨯⨯=⋅=--δμτ 油: 233/8.2810416102.7m N u =⨯⨯=⋅'=--δμτ 1-4 在相距mm 40=δ的两平行平板间充满动力粘度s Pa ⋅=7.0μ液体(图1-4),液体中有一边长为mm a 60=的正方形薄板以s m u 15=的速度水平移动,由于粘性带动液体运动,假设沿垂直方向速度大小的分布规律是直线。
[工程流体力学(水力学)]1-4章习题解答
![[工程流体力学(水力学)]1-4章习题解答](https://img.taocdn.com/s3/m/e2ca2551ad02de80d4d84087.png)
第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]第二章 流体静力学2-1.一密闭盛水容器如图所示,U 形测压计液面高于容器内液面h=1.5m ,求容器液面的相对压强。
工程流体力学第二版习题答案解析-[杜广生]
![工程流体力学第二版习题答案解析-[杜广生]](https://img.taocdn.com/s3/m/69030e8165ce0508763213b5.png)
《工程流体力学》习题答案(杜广生主编)第一章 习题1. 解:依据相对密度的定义:1360013.61000f w d ρρ===。
式中,w ρ 表示4摄氏度时水的密度。
2. 解:查表可知,标准状态下:231.976/CO kg m ρ=,232.927/SO kg m ρ=,231.429/O kg m ρ=,231.251/N kg m ρ=,230.804/H O kg m ρ= ,因此烟气在标准状态下的密度为:112231.9760.1352.9270.003 1.4290.052 1.2510.760.8040.051.341/n nkg m ρραραρα=++=⨯+⨯+⨯+⨯+⨯=3. 解:(1)气体等温压缩时,气体的体积弹性模量等于作用在气体上的压强,因此,绝对压强为4atm的空气的等温体积模量:34101325405.310T K Pa =⨯=⨯ ;(2)气体等熵压缩时,其体积弹性模量等于等熵指数和压强的乘积,因此,绝对压强为4atm 的空气的等熵体积模量:31.44101325567.410S K p Pa κ==⨯⨯=⨯式中,对于空气,其等熵指数为1.4。
4. 解:根据流体膨胀系数表达式可知:30.0058502V dV V dT m α=⋅⋅=⨯⨯=因此,膨胀水箱至少应有的体积为2立方米。
5. 解:由流体压缩系数计算公式可知:392511050.5110/(4.90.98)10dV V k m N dp -⨯÷=-=-=⨯-⨯ 6. 解:根据动力粘度计算关系式:74678 4.2810 2.910Pa S μρν--==⨯⨯=⨯⋅7. 解:根据运动粘度计算公式:3621.310 1.310/999.4m s μνρ--⨯===⨯8. 解:查表可知,15摄氏度时空气的动力粘度617.8310Pa s μ-=⨯⋅,因此,由牛顿内摩擦定律可知:630.317.83100.2 3.36100.001U F AN h μπ--==⨯⨯⨯⨯=⨯ 9. 解:如图所示,高度为h 处的圆锥半径:tan r h α=,则在微元高度dh 范围内的圆锥表面积:2=2=tan cos cos dh h dA rdh παπαα由于间隙很小,所以间隙内润滑油的流速分布可看作线性分布,则有:===tan d r h υυωωαυδδδ则在微元dh 高度内的力矩为:332===2tan tan tan tan cos cos h h dM dA r dh h h dh ωαπαωατμαπμδαδα⋅⋅因此,圆锥旋转所需的总力矩为:33430==2=24tan tan cos cos H H M dM h dh ωαωαπμπμδαδα⎰⎰10. 解:润滑油与轴承接触处的速度为0,与轴接触处的速度为轴的旋转周速度,即:=60n Dπυ 由于间隙很小,所以油层在间隙中沿着径向的速度分布可看作线性分布,即:=d dy υυδ则轴与轴承之间的总切应力为:==T A Db υτμπδ克服轴承摩擦所消耗的功率为:2==P T Db υυμπδ因此,轴的转速可以计算得到:60=r/min n D υπ11.解:根据转速n 可以求得圆盘的旋转角速度:2290===36060n ππωπ⨯ 如图所示,圆盘上半径为r 处的速度:=r υω,由于间隙很小,所以油层在间隙中沿着轴向的速度分布可看作线性分布,即:=d dy υυδ则微元宽度dr 上的微元力矩:3233==2=2=6r dM dA r rdr r r dr r dr ωπμτμππμπδδδ⋅⋅ 因此,转动圆盘所需力矩为:4422322-30(2)0.40.23==6=6=6 3.14=71.98N m 40.23104DD M dM r dr μμππδδ⨯⨯⨯⋅⨯⎰⎰12. 解:摩擦应力即为单位面积上的牛顿内摩擦力。
(完整版)工程流体力学第二版习题答案解析-[杜广生]
![(完整版)工程流体力学第二版习题答案解析-[杜广生]](https://img.taocdn.com/s3/m/8f982c7e19e8b8f67c1cb9b1.png)
《工程流体力学》习题答案(杜广生主编)第一章 习题1. 解:依据相对密度的定义:1360013.61000f w d ρρ===。
式中,w ρ 表示4摄氏度时水的密度。
2. 解:查表可知,标准状态下:231.976/CO kg m ρ=,232.927/SO kg m ρ=,231.429/O kg m ρ=,231.251/N kg m ρ=,230.804/H O kg m ρ= ,因此烟气在标准状态下的密度为:112231.9760.1352.9270.003 1.4290.052 1.2510.760.8040.051.341/n nkg m ρραραρα=++=⨯+⨯+⨯+⨯+⨯=3. 解:(1)气体等温压缩时,气体的体积弹性模量等于作用在气体上的压强,因此,绝对压强为4atm的空气的等温体积模量:34101325405.310T K Pa =⨯=⨯ ;(2)气体等熵压缩时,其体积弹性模量等于等熵指数和压强的乘积,因此,绝对压强为4atm 的空气的等熵体积模量:31.44101325567.410S K p Pa κ==⨯⨯=⨯式中,对于空气,其等熵指数为1.4。
4. 解:根据流体膨胀系数表达式可知:30.0058502V dV V dT m α=⋅⋅=⨯⨯=因此,膨胀水箱至少应有的体积为2立方米。
5. 解:由流体压缩系数计算公式可知:392511050.5110/(4.90.98)10dV V k m N dp -⨯÷=-=-=⨯-⨯ 6. 解:根据动力粘度计算关系式:74678 4.2810 2.910Pa S μρν--==⨯⨯=⨯⋅7. 解:根据运动粘度计算公式:3621.310 1.310/999.4m s μνρ--⨯===⨯8. 解:查表可知,15摄氏度时空气的动力粘度617.8310Pa s μ-=⨯⋅,因此,由牛顿内摩擦定律可知:630.317.83100.2 3.36100.001U F AN h μπ--==⨯⨯⨯⨯=⨯ 9. 解:如图所示,高度为h 处的圆锥半径:tan r h α=,则在微元高度dh 范围内的圆锥表面积: 2=2=tan cos cos dh h dA rdh παπαα由于间隙很小,所以间隙内润滑油的流速分布可看作线性分布,则有:===tan d r h υυωωαυδδδ则在微元dh 高度内的力矩为:332===2tan tan tan tan cos cos h h dM dA r dh h h dh ωαπαωατμαπμδαδα⋅⋅因此,圆锥旋转所需的总力矩为:33430==2=24tan tan cos cos H H M dM h dh ωαωαπμπμδαδα⎰⎰10. 解:润滑油与轴承接触处的速度为0,与轴接触处的速度为轴的旋转周速度,即:=60n Dπυ 由于间隙很小,所以油层在间隙中沿着径向的速度分布可看作线性分布,即:=d dy υυδ则轴与轴承之间的总切应力为:==T A Db υτμπδ克服轴承摩擦所消耗的功率为:2==P T Db υυμπδ因此,轴的转速可以计算得到:3-360606050.7100.810====2832.16r/min 3.140.20.245 3.140.20.3P n D D Db υδππμπ⨯⨯⨯⨯⨯⨯⨯11.解:根据转速n 可以求得圆盘的旋转角速度:2290===36060n ππωπ⨯ 如图所示,圆盘上半径为r 处的速度:=r υω,由于间隙很小,所以油层在间隙中沿着轴向的速度分布可看作线性分布,即:=d dy υυδ则微元宽度dr 上的微元力矩:3233==2=2=6r dM dA r rdr r r dr r dr ωπμτμππμπδδδ⋅⋅ 因此,转动圆盘所需力矩为:4422322-30(2)0.40.23==6=6=6 3.14=71.98N m 40.23104DD M dM r dr μμππδδ⨯⨯⨯⋅⨯⎰⎰12. 解:摩擦应力即为单位面积上的牛顿内摩擦力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆能源职业学院教案课程名称:流体力学授课时间2013 年 3 月日重 庆 能 源 职 业 学 院 教 案教学内容第四章 流动阻力和水头损失主要内容阻力产生的原因及分类 两种流态实际流体运动微分方程式(N -S 方程) 因次分析方法、相似原理 水头损失的计算方法第一节 流动阻力产生的原因及分类一、基本概念1、 湿周:管子断面上流体与固体壁接触的边界周长。
以 χ 表示。
单位:米2、水力半径:断面面积和湿周之比。
χAR =单位:米例: 圆管:442dd d R ==ππ正方:442a a a R == 圆环流: 明渠流:()()()4422d D d D d DR -=+-=ππ42212aa aR ==3、绝对粗糙度:壁面上粗糙突起的高度。
4、平均粗糙度:壁面上粗糙颗粒的平均高度或突起高度的平均值。
以Δ表示。
5、相对粗糙度:Δ/D (D——管径)。
二、阻力产生的原因1、外因:(a)管子的几何形状与几何尺寸。
面积:A1=a2 A2=a2 A3=3a2/4湿周:a41=χa52=χa43=χ水力半径:R1=0.25a > R2=0.2a > R3=0.1875a实验结论:阻力1 < 阻力2 < 阻力3水力半径R,与阻力成反比。
R↑,阻力↓(b)管壁的粗糙度。
Δ↑,阻力↑(c)管长。
与h f 成正比。
L↑,阻力↑2、内因:流体在流动中永远存在质点的摩擦和撞击现象,流体质点由于相互摩擦所表现出的粘性,以及质点撞击引起速度变化所表现出的惯性,才是流动阻力产生的根本原因。
沿程阻力:粘性造成的摩擦阻力和惯性造成的能量消耗。
局部阻力:液流中流速重新分布,旋涡中粘性力做功和质点碰撞产生动量交换。
三、阻力的分类1、沿程阻力与沿程水头损失(1)沿程阻力:沿着管路直管段所产生的阻力(管路直径不变,计算公式不变)(2)沿程水头损失:克服沿程阻力所消耗的能量∑h f=h f1+ h f2+ h f32、局部阻力与局部阻力损失(1)局部阻力:液流流经局部装置时所产生的阻力。
(2)局部水头损失:∑h j=h j1+ h j2+ h j33、总水头损失:h w=∑h f+∑h j第二节两种流态及转化标准一、流动状态——流态转化演示实验:雷诺实验结果:(a)速度小时,色液直线前进,质点做直线运动——层流(b)速度较大时,色液颤动,质点做曲线运动——过渡区(c)速度大时,色液不连续,向四周紊乱扩散,质点做无规则运动——紊流(湍流)由此得出以下三个概念:层流、紊流、过渡状态(1). 层流:流体质点平行向前推进,各层之间无掺混。
主要以粘性力为主,表现为质点的摩擦和变形。
为第一种流动状态。
(2). 过渡状态:层流、紊流之间有短暂的过渡状态。
为第二种流动状态。
(3). 紊流:单个流体质点无规则的运动,不断掺混、碰撞,整体以平均速度向前推进。
主要以惯性力为主,表现为质点的撞击和混掺,为第三种流动状态。
二、沿程水头损失与流速的关系实验方法:在实验管路A、B两点装测压管测压降,用实测流量求流速。
()γ21p p h f -=A Q V VA Q =⇒=实验数据处理:把实验点描在双对数坐标纸上回归方程式:Vm K h f lg lg lg +=(1). 层流时,45,1==θm(2). 紊流时,m =1.75~2,θ=60°(3). 实验还证明,不能用临界速度作为判别流态的标准,因为由层流到紊流变化时的V cup 和由紊流到层流转化时的V cdown 不同,且有V cup > V cdown(4). 流动介质变化时,V c 也不同,由此得出,V c 不能作为判别流态的标准。
三、判别流动状态的标准 Re1、 雷诺实验中所发生的现象与下列因素有关,流体密度ρ,粘性系数μ,平均流速V ,管径D ,即 流动现象=f (ρ,μ,V ,D ) 利用π定理可得:流动现象=f ( ρVD/μ )=f (Re ) 即流动现象只与雷诺数Re 有关。
对于圆管,雷诺数 νμρVdVd ==ReV ——管内流速切向应力τ=0 τ≠0变形不变形变形微小六面体表面受力个数法向力6个切向力0个法向力6个切向力12个二、Navier-Stokes方程式——粘性不可压缩流体运动微分方程式1、方程推导:(1)取研究对象:微元体从运动着的流体中取出一块微小的长方体ABCDEFGH边长:dx,dy,dz质量力:ρdxdydz设长方体:中心点压强:p;粘性应力:τ(2)受力分析A、质量力单位质量流体所受的质量力在三个坐标轴方向的分量为:X,Y,Z.B、表面力:表面力有两部分。
①由压强形成的压力,单位质量流体所受的压力在三个坐标方向的分量分别zpypxp∂∂-∂∂-∂∂-ρρρ1;1;1②流体的粘滞力而引起的流体间的相互作用力,此粘滞力在每个面上有三个分量。
则得2)主要内容:流速分布流量计算公式切应力分布规律沿程水头损失的计算一、流速分布由实际不可压流体的运动微分方程求出。
Navier—Stokes方程:dtduzuyuxuxpX xxxx=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂+∂∂-2222221νρdtduzuyuxuypY yyyy=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂+∂∂-2222221νρdtduzuyuxuzpZ zzzz=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂+∂∂-2222221νρ以下根据圆管层流的运动特点对N-S方程进行简化(1). 液流沿水平等径管运动:u x=u,u y=u z=0 (2). 水平运动且为稳定流:X=Y=0,Z=-g(3). C=ρ:=∂∂+∂∂+∂∂zuyuxuzyx=∂∂xux,22=∂∂xux(4). 对于稳定流动=∂∂tux=∂∂tuy结论:有效断面上,切应力随 r 成线性关系。
六、水头损失对于水平等径管γph f ∆=又 l pD V μ322∆= 232D lV p γμγ=∆ 则V g V D L D D lV ph f 22323222⋅⋅⋅==∆=ρμγμγ 结论:层流状态,水头损失与速度呈线性关系。
所以g V D L g V D L h f 22Re 6422λ== ——达西公式 其中Re 64=λ为层流沿程水力摩阻系数。
说明:结论与管路的放置位置无关。
第六节 紊流理论分析一、紊流的产生由于粘性的存在,限制了流体质点的扰动,从而在一定雷诺数限度内能维持层流状态。
1. 粘滞性对漩涡的产生、存在和发展具有决定性的作用。
惯性力(升力)使涡体脱离本层,粘滞力阻止涡体运动。
因此,当Re 较小时,粘滞力起主要作用,涡体不能发展运动(上移);当Re 很大时,粘性力起次要作用,惯性力占主导地位,漩涡随时间的进程而增强,发展成为紊流。
2. 两层流体有速度差别亦是造成不稳定的主要原因。
3.在剪切流动中,横向压力梯度的存在导致漩涡的产生。
二、紊流的基本特征和研究方法1.紊流的特征——紊流的随机性紊流状况下,流体质点运动非常紊乱,其运动速度的大小和方向随时改变。
表现为各点速度和压力的脉动现象——紊流的随机性。
2.紊流流动的基本性质(1). 紊流能量的输运性。
紊流动量输运表现为紊流的粘性;紊流内能输运表现为紊流的热传导。
(2). 紊流流动的耗散性(能量损失)。
它有两项,平均粘性耗散项;脉动耗散项。
(3). 紊流流动的有旋性。
紊流流场中的输运是通过漩涡来传递的。
从理论上讲,没有旋涡就不能维持紊流。
3、研究方法——统计平均方法虽然在某一瞬时,紊流运动仍然服从N—S方程,但由于紊流的随机性,求解N-S方程是困难的。
实验证明,虽然紊流具有随机性,但是,在条件相同时,进行无数次实验,其运动参数的算术平均值还是趋于一致,即,虽然个别的实验结果无规律性,但大量实验结果的算术平均值具有一定的规律性。
所以,只有大量实验的统计平均才能给出具有决定性的结果。
因此,统计方法在紊流问题的研究中具有重要的意义。
在紊流理论中,有三种统计平均方法:时均法,体均法,统计平均法(1)时均法——在紊流流场中某一固定点上,于不同时刻测量该处的速度。
图中两条曲线为两次实验结果,由图,每次实验的速度变化都极不规则,在相当长的时段内的平均却是相同的。
●定义:()()dtt zyxuTut Ttt⎰+=0,,,1()ut——随机速度用时均法算出的平均值T ——理论上应为无穷大时段()t z yxu,,,——随机速度(真实速度)●时均法的适用范围:只能用来描述对时均值而言的定常流动。
●应用时均法的条件:()ut与t0及T(只要足够长)无关,即()ut不再是时间的函数——稳定紊流。
(2). 体均法湍流的随机性不仅表现在时间上,在空间分布上也具有随机性。
若在管流轴线L 段上同时测量各点轴向速度分布。
在不同时刻可以测到不同的速度分布,但在L 内求速度的平均值,则任意两次试验的平均值相同。
●一维体均法的定义:⎰+=Lx x d t u L u x 00),(1)(ξξu x )(——沿x 轴向L 段上的平均速度L ——足够长的距离),(t u ξ——在相同条件下,任一次实验的速度分布适用范围:积分与x 0、L 无关 空间体均法定义:ςηξςηξd d d t u V u V V i i ⎰⎰⎰=),,,(1)(i u V )( ——(x ,y ,z)点处的体均值V ——包含某空间点(x ,y ,z )在内的足够大的体积),,,(t u i ςηξ——在相同条件下,任一次实验的速度分布适用范围:均匀的紊流流场。
(3). 统计平均法因为时均法适用于定常流场,体均法适用于均匀流场,而对于一般不定常非均匀流场只有采用统计平均法。
将重复多次的试验结果作算术平均。
()()t z y x u Nt z y x u N K K iN p i ,,,1lim,,,1)()(∑=∞→=()t z y x u p i ,,,)(——用概率平均法算得的平均值N ——重复次数()t z y x u K i ,,,)(——第k 次实验的流场分布函数三、脉动值与平均值的性质由于脉动而产生的附加法向应力:222,,zyxuuu'''ρρρ由于脉动而产生的切向应力:xzzyyxuuuuuu''''''ρρρ,,统称为:雷诺应力四、紊流切应力与附加切应力1、附加切应力——雷诺应力,产生的原因流体质点混杂,产生动量交换和能量消耗,从而引起附加阻力。
2、简单平行流动附加切应力Ox 轴取在物面上,时均流速为xu则有:()0,===zyxxuuyuu现在考虑面y=y i上的雷诺应力异号附yxyxuuuu''''-=,,ρτ()⎪⎪⎭⎫⎝⎛''⇒=⋅⋅'+⋅⋅'异号据质量守恒,yxyxuubuau,11ρ3、紊流中总的摩擦应力τ对于简单平行流动(如水平圆管),总的摩擦应力应等于粘性摩擦应力与附加切应力之和。
