线性代数清考复习题
《线性代数》复习要点及练习

第一章 行列式复习要点:1. 会计算逆序数,余子式,代数余子式2. 熟练掌握行列式的性质,并能利用性质计算行列式3. 掌握克莱姆法则练习题:1. 排列1 6 5 3 4 2的逆序数是( ).A. 8 B .9 C .7 D . 62122.431235-的代数余子式12A 是( ).A 2143-- B2143- C 4125--D4125-3. 排列32514的逆序数是( ).A. 3B. 4C. 5D. 64.关于行列式,下列命题错误的是( ).A. 行列式第一行乘以2,同时第二列除以2,行列式的值不变 B .互换行列式的第一行和第三行,行列式的值不变 C .互换行列式的任意两列,行列式仅仅改变符号 D . 行列式可以按任意一行展开 5. 关于行列式,下列命题正确的是( ).A. 任何一个行列式都与它的转置行列式相等B .互换行列式的任意两行所得到的行列式一定与原行列式相等C .如果行列式有一行的所有元素都是1,则这个行列式等于零D . 以上命题都不对6. 关于行列式,下列正确的是( ).A. 如果行列式有一行的所有元素都是1,则这个行列式等于零.B. 互换行列式的任意两行所得到的行列式一定与原行列式相等.C. 行列式中有两行对应成比例,则此行列式为零.D. 行列式与它的转置行列式互为相反数.7. 下列命题错误的是( ).A. 如果线性方程组的系数行列式不等于零,则该方程组有唯一解 B .如果线性方程组的系数行列式不等于零,则该方程组无解 C .如果齐次线性方程组的系数行列式等于零,则该方程组有非零解 D .如果齐次线性方程组的系数行列式不等于零,则该方程组只有零解8212431235-的余子式32M =————,代数余子式32A =—————— 9. 已知k341k 000k 1-=,则k =__________.10. 若52k 74356=,则k =__________.11. 计算行列式|12345006|=_________ 12. 计算行列式|1111123413610141020| 13.计算行列式53-120172520-23100-4-14002350D =14. 计算行列式1234248737124088D =15.计算行列式x yyxx x y y yx x y+++第二章 矩阵复习要点:1. 掌握矩阵的线性运算,矩阵乘法运算律,转置矩阵的运算律,2. 掌握矩阵的初等变换3. 掌握方阵行列式的性质,转置矩阵的性质,逆矩阵的性质4. 会求逆矩阵.了解待定系数法和伴随矩阵法,掌握用初等变换求解逆矩阵相关问题.能够证明矩阵的可逆性.5. 会用初等行变换求矩阵的秩6. 会求解矩阵方程练习题:1. 设A ,B 均为n 阶可逆阵,则下列公式成立的是( ). A T T T B A AB =)( B T T T B A B A +=+)( C 111)(---=B A AB D 111)(---+=+B A B A2. A,B 均为n 阶方阵,若要22(A B)(A B)A B +-=-不成立,需满足( ).A. A=E B .B=O C .A=B D . AB ≠BA 3. 若方阵2A A,=A 不是单位方阵,则( ).A. A 0= B . A 0≠ C .A O = D .A O ≠4.若矩阵111A 121231⎛⎫ ⎪= ⎪ ⎪λ+⎝⎭的秩为2,则λ=( ). A. 0 B . 2 C .1 D . -15.矩阵⎪⎪⎭⎫⎝⎛=32015431A 的秩是( ) 6. 110201211344⎛⎫⎪-- ⎪ ⎪-⎝⎭ 的秩是( )7. 设矩阵⎪⎪⎪⎭⎫ ⎝⎛=321212113A ,⎪⎪⎪⎭⎫ ⎝⎛---=111012111B 求AB 和BA8. 设矩阵,⎪⎪⎭⎫ ⎝⎛=1021A 求32A A ,. 9. 设矩阵521320A ,B 341201--⎛⎫⎛⎫== ⎪ ⎪--⎝⎭⎝⎭,求T T T(1)AB ;(2)B A;(3)A A.10.⎪⎪⎪⎭⎫⎝⎛--=210111121A ,求逆矩阵11. 223110121⎛⎫ ⎪- ⎪ ⎪-⎝⎭.,求逆矩阵 12. 求矩阵X , 使B AX =, 其中.341352,343122321⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=B A13. 求解矩阵方程,X A AX += 其中.010312022⎪⎪⎪⎭⎫⎝⎛=A.B AX X ,B ,A . 132231 11312221414=⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫⎝⎛--=使求设15. 已知n 阶方阵A 满足矩阵方程2A 3A 2E O --=,其中A 给定,E 为n 阶单位矩阵,证明A 可逆,并求1A -. 16. 设A 、B 为n 阶矩阵,2A B AB E --=,2A A =,其中E 为n 阶单位矩阵.证明:A B -为可逆矩阵,并求()1A B --.17. 设方阵A 满足22A A E O --=,证明A 及2A E +都可逆.第三章 线性方程组复习要点:1. 熟练掌握方程组解无解/有解/有唯一解/有无穷多解的充要条件2. 会求向量组的秩;能够验证向量组的线性相关性;会求向量组的极大线性无关组,并可以将其他向量用极大无关组线性表示.3. 熟练掌握基础解系的求解3. 会求解齐次线性方程组的通解,会求非齐次线性方程组的通解和特解练习题:1. 若线性方程组Ax b =的增广矩阵为B 23124010012⎛⎫ ⎪→λλ ⎪ ⎪λ-λ-⎝⎭,当常数λ=( )时,此线性方程组有唯一解.A. -1 B .0 C .1 D . 22. 已知n 元线性方程组b Ax =,其增广矩阵为B ,当( )时,线性方程组有解.A. ()n B r =B. ()n B r ≠C. ()()B r A r =D. ()()B r A r ≠3. 若线性方程组Ax b =的增广矩阵为B 23124010012⎛⎫ ⎪→λλ ⎪ ⎪λ-λ-⎝⎭,当常数λ=( )时,此线性方程组有唯一解.A. -1 B .0 C .1 D . 24. 设A 为m×n 矩阵,齐次线性方程组Ax =0仅有零解的充分必要条件是 系数矩阵的秩r (A )( )A. 小于mB. 小于nC. 等于mD. 等于n5. 已知向量组1,,m αα线性相关,则( ).A 、该向量组的任何部分组必线性相关.B 、该向量组的任何部分组必线性无关.C 、该向量组的秩小于m .D 、该向量组的最大线性无关组是唯一的.6. 如果齐次线性方程组有非零解,则它的系数行列式D _____0. ( = 或 ≠)7. 已知线性方程组Ax b =有解,若系数矩阵A 的秩r(A)=4,则增广矩阵B 的r(B)=__________.8. 若线性方程组Ax b =的增广矩阵为B 312400120012⎛⎫⎪→ ⎪ ⎪λ⎝⎭,则当常数λ=__________时,此线性方程组有无穷多解.9. 若线性方程组Ax b =的增广矩阵为B 300200a 11⎛⎫→ ⎪+⎝⎭,则当常数a =__________时,此线性方程组无解.10.λ取何值时,非齐次线性方程组 1231232123+1++x x x x x x x x x λλλλλ⎧+=⎪+=⎨⎪+=⎩(1)有唯一解(2)无解(3)有无穷多解? 取何值时,线性方程组当 11..λ ()()()()⎪⎩⎪⎨⎧=++++=+-+=+++3313123321321321x λλx x λλx x λλx λx x x λ 有唯一解、无解、无穷多解?当方程组有无穷多解时求出它的解.12.求下列方程组的通解.236222323754325432154321⎪⎩⎪⎨⎧=+++-=-+++=++++x x x x x x x x x x x x x x13. 判断下列向量组的线性相关性:(1)1234=-1,3,2,5=3-1,0-4=2,2,2,2=1,5,4,6αααα(),(,,),(),()(2)1234=1,1,3,1=10,00=2,2,7,-1=3,-1,2,4αααα(),(,,),(),() 14. 已知向量组()()()()T4T3T2T13 2 10 0 10 1 11 1 1α-====,,α,,,α,,,α,,,,求向量组的一个极大无关组,并将其余向量用此极大无关组线性表示.15. 求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛---140113*********12211的列向量组()54321α,α,α,α,α的一个极大无关组,并把不属于极大无关组的列向量用极大无关组线性表示.16. 试证若向量组γβα,,线性无关, 则向量组,βα+,γβ+αγ+亦线性无关. 17. 已知向量321ααα,,线性无关,证明向量11232βααα=+-,2123312βαααβαα=--=+,也是线性无关的。
线性代数考前必做50题

2 1 0 * * * 27、(公式考查)设矩阵 A 1 2 0 ,矩阵 B 满足 ABA 2 BA E ,其中 A 为 A 的伴随矩阵, E 是单位矩阵, 0 0 1
则B 28、 (概念考查)设 A, B 为满足 AB 0 的任意两个非零矩阵,则必有 ( )
线性代数考前必做 50 题
一、解答题部分:
1 2 3 1、设矩阵 A 1 4 3 的特征方程有一个二重根,求 a 的值,并讨论 A 是否可相似对角化. 1 a 5
2、已知二次型 f ( x1 , x 2 , x3 ) (1 a ) x1 (1 a ) x 2 2 x3 2(1 a ) x1 x 2 的秩为 2. (I) 求 a 的值; (II) 求正交变换 x Qy ,把 f ( x1 , x 2 , x3 ) 化成标准形; (III) 求方程 f ( x1 , x 2 , x3 ) =0 的解.
(A) A 的列向量组线性相关, B 的行向量组线性相关.(B) A 的列向量组线性相关, B 的列向量组线性相关. (C) A 的行向量组线性相关, B 的行向量组线性相关. (D) A 的行向量组线性相关, B 的列向量组线性相关. 29、(向量组与行列式考查) 设 1 , 2 , 3 均为 3 维列向量,记矩阵 A ( 1 , 2 , 3 ) , B ( 1 2 3 , 1 2 2 4 3 , 1 3 2 9 3 ) , 如果 A 1 ,那么 B . )
20、设行列式|A|=
唯一解 、无
解 时时求其通解
2 2 1 1
2 2 3 1 3 4 1 5 M 31 M 32 M 33 M 34 2
清华大学线性代数考试真题3

清华大学线性代数考试真题3几何与代数讨论课(三)(向量组的线性相关性)1.下列命题是否正确(1)若向量组α1,α2,···,αm线性相关,则α1,α2,···,αm中任意一个向量都可由其余m?1个向量线性表出.(2)若α可由向量组α1,α2,···,αm线性表示,则存在不全为零的数k1,k2,···,k m使α=mi=1k iαi.(3)若向量组α1,α2,···,αm线性相关,则它的任意一个部分组也线性相关.(4)若向量组α1,α2,···,αm线性无关,则它的任意一个部分组也线性无关.(5)若向量组α1,α2,···,αm线性无关,且向量组β1,β2,···,βm也线性无关,则向量组α1,α2,···,αm,β1,β2,···,βm线性无关.(6)向量组α1,α2,···,αm线性无关?α1,α2,···,αm中任意两个向量都线性无关.(7)若n维向量组α1,α2,···,αm及β1,β2,···,βm都线性无关,则向量组α1+β1,α2+β2,···,αm+βm也线性无关.(8)若n维向量组α1,α2,···,αm及β1,β2,···,βm都线性相关,则向量组α1+β1,α2+β2,···,αm+βm也线性相关.(9)若n维列向量组α1,α2,···,αm与n维列向量组β1,β2,···,βm等价,则矩阵A=(α1,α2,···,αm)与矩阵B=(β1,β2,···,βm)相抵.(10)若矩阵A,B,C满足A=BC,则A的列向量组可由B的列向量组线性表示.(11)若|A|=0,则A必有一列向量是其余列向量的线性组合.(12)αm不能由α1,α2,···,αm?1线性表出?α1,α2,···,αm线性无关.2.已知:α1+α2,α2+α3,α3+α1线性无关,(1)求证:α1,α2,α3线性无关.(2)试判断下面的证法是否正确?为什么?证:因α1+α2,α2+α3,α3+α1线性无关,故k1(α1+α2)+k2(α2+α3)+k3(α3+α1)=0?k1=k2=k3=0因而(k1+k3)α1+(k2+k1)α2+(k2+k3)α3=0有k1+k3=k2+k1=k2+k3=0,故α1,α2,α3线性无关.3.设向量组α,β,γ线性无关,α,β,δ线性相关,下列说法是否正确?为什么?(1)α必可被β,γ,δ线性表出.(2)β必不可由α,γ,δ线性表出.(3)δ必可由α,β,γ线性表出.4.设向量β可由向量组α1,α2,···,αm线性表出,但不能由向量组(I)α1,α2,···,αm?1线性表出,记向量组(II)为α1,α2,···,αm?1,β,试判断αm能不能由(I)线性表出?能不能由(II)线性表出?5.已知:A∈M n×m,B∈M m×n且n< p="">6.α1,α2,···,αn是n个线性无关的n维向量,αn+1=k1α1+k2α2+···+k nαn,且k i(i= 1,2,···,n)全不为零.求证:α1,α2,···,αn,αn+1中任意n个n维向量均线性无关.7.证明α1,α2,···,αm(其中α1=0)线性相关的充要条件是至少有一个αi(1<i≤m)可被α1,α2,···,αi?1线性表出,且表出系数惟一.< p="">11(1) α1,α2,···,αm α1,α2,···,αm m ?1m =3 α1=(1,0)T ,α2=(2,0)T ,α3=(0,1)T α3(2) α α1,α2,···,αm k 1,k 2,···,k m α=m i =1k i αi α 0 α1,α2,···,αm k 1,k 2,···,k m 0(3) α1,α2,···,αmm =3 α1=(1,0)T ,α2=(2,0)T ,α3=(0,1)T α1,α3(4) α1,α2,···,αm(5) α1,α2,···,αm β1,β2,···,βm α1,α2,···,αm ,β1,β2,···,βmα1=β1 α1,α2,···,αm ,β1,β2,···,βm(6) α1,α2,···,αm ?α1,α2,···,αmm =3 α1=(1,1,0)T ,α2=(1,0,0)T ,α3=(0,1,0)T(7) n α1,α2,···,αm β1,β2,···,βm α1+β1,α2+β2,···,αm +βmi =1,2,···,m αi =?βi α1+β1,α2+β2,···,αm +βm 0(8) n α1,α2,···,αm β1,β2,···,βm α1+β1,α2+β2,···,αm +βm1m=n=3α1=(0,?1,1)T,α2=(1,2,?1)T,α3=(1,1,0)Tβ1=(1,1,?1)T,β2=(?1,?1,1)T,β3=(?1,?1,1)Tα1+β1=(1,0,0)T,α2+β2=(0,1,0)T,α3+β3=(0,0,1)T(9) n α1,α2,···,αm n β1,β2,···,βm A=(α1,α2,···,αm) B=(β1,β2,···,βm)(10) A,B,C A=BC A B(11) |A|=0 A(12)αm α1,α2,···,αm?1 ?α1,α2,···,αmm=3 α1=(1,0)T,α2=(2,0)T,α3=(0,1)T α32. α1+α2,α2+α3,α3+α1 α1,α2,α3α1+α2,α2+α3,α3+α1k1(α1+α2)+k2(α2+α3)+k3(α3+α1)=0?k1=k2=k3=0(k1+k3)α1+(k2+k1)α2+(k2+k3)α3=0 k1+k3=k2+k1= k2+k3=0α1,α2,α3α1,α2,α3 0 λ1,λ2,λ3 λ1α1+λ2α2+λ3α3=01 2(λ1+λ2?λ3)(α1+α2)+12(?λ1+λ2+λ3)(α2+α3)+12(λ1?λ2+λ3)(α3+α1)=0α1+α2,α2+α3,α3+α1 12(λ1+λ2?λ3)=12(?λ1+λ2+λ3)=12(λ1?λ2+λ3)=0 λ1=λ2=λ3=0 α1,α2,α30 λ1,λ2,λ3 λ1α1+λ2α2+λ3α3=03. α,β,γ α,β,δ(1)α β,γ,δ(2)β α,γ,δ2(3)δ α,β,γ(1) α=(1,0,0)T,β=(0,1,0)T,γ=(0,0,1)T,δ=(0,0,1)T(2) α=(1,0,0)T,β=(0,1,0)T,γ=(0,0,1)T,δ=(0,0,1)T(3) k1,k2,k3 k1α+k2β+k3δ=0 k1,k2,k3δ α,β,γ k3=0 k1α+k2β=0 k2,k3α,β,γ δ α,β,γ4. β α1,α2,···,αm I α1,α2,···,αm?1 II α1,α2,···,αm?1,β αm III ?β 0 β α1,α2,···,αm β=k1α1+k2α2+···+k m?1αm?1+k mαm k m=0 αm IIαm I αm=l1α1+l2α2+···+l m?1αm?1β=(k1+k m l1)α1+(k2+k m l2)α2+···+(k m?1+k m l m?1)αm?1 βI α1,α2,···,αm?1 αm I5. A∈M n×m,B∈M m×n n<="" p="">B B=(α1,α2,···,αn)αi,i=1,2,···,n m 0 k1,k2,···,k nk1α1+k2α2+···+k nαn=0 B·k=0 k=(k1,k2,···,k n)T ABk=Ik=A·0=0 k1,k2,···,k n 0B6.α1,α2,···,αn n n αn+1=k1α1+k2α2+···+k nαn k i(i=1,2,···,n) α1,α2,···,αn,αn+1n nα1,α2,···,αn n nα1 n n α2,···,αn,αn+1 α2,···,αnλ2,···,λn αn+1=λ2α2+···+λnαnα2+ k1α1+k2α2+···+k nαn=λ2α2+···+λnαn α1=λ2?k2k1αn α1,α2,···,αn n n···+λn?k nk1α1,α2,···,αn,αn+1 n n7. α1,α2,···,αm α1=0αi(1<="">(1)α1,α2,···,αm α1=0α1=0 {α1} {α1,α2,···,αm}p∈{2,···,m} {α1,α2,···,αp?1} {α1,α2,···,αp}αp α1,α2,···,αp?1 0 k1,k2,···,k p3k1α1+k2α2+···+k pαp=0 k p=0 {α1,α2,···,αp?1}k p=0 αp α1,α2,···,αp?1k1,k2,···,k p?1 k 1,k 2,···,k p?1 αp=k1α1+k2α2+···+kp?1αp?1=k 1α1+k 2α2+···+k p?1αp?1(k1?k 1)α1+(k2?k 2)α2+···+(k p?1?k p?1)αp?1=0 k1?k 1,k2?k 2,···,k p?1?k p?1 0 {α1,α2,···,αp?1}(2)αi(1<="">αi=k1α1+k2α2+···+k i?1αi?1 {α1,α2,···,αi}α1,α2,···,αm4</i≤m)可被α1,α2,···,αi?1线性表出,且表出系数惟一.<><>。
线性代数-多套复习试题简洁版(含答案)
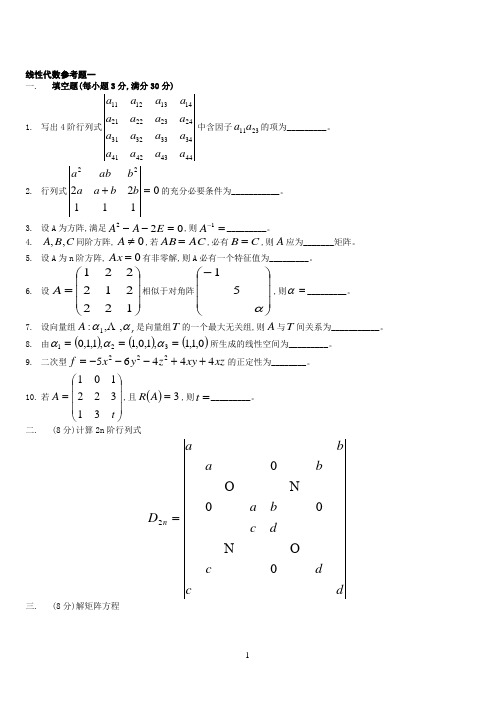
线性代数参考题一一. 填空题(每小题3分,满分30分)1. 写出4阶行列式44434241343332312423222114131211a a a a a a a a a a a a a a a a 中含因子2311a a 的项为_________。
2. 行列式01112222=+b b a a b ab a 的充分必要条件为___________。
3. 设A 为方阵,满足022=--E A A ,则=-1A _________。
4. C B A ,,同阶方阵,0≠A ,若AC AB =,必有C B =,则A 应为_______矩阵。
5.设A 为n 阶方阵,0=Ax 有非零解,则A 必有一个特征值为_________。
6.设⎪⎪⎪⎭⎫ ⎝⎛=122212221A 相似于对角阵⎪⎪⎪⎭⎫ ⎝⎛-α51,则=α_________。
7. 设向量组r A αα,,:1 是向量组T 的一个最大无关组,则A 与T 间关系为___________。
8.由()()()0,1,1,1,0,1,1,1,0321===ααα所生成的线性空间为_________。
9. 二次型xz xy z y x f 44465222++---=的正定性为________。
10. 若⎪⎪⎪⎭⎫ ⎝⎛=t A 31322101,且()3=A R ,则=t _________。
二. (8分)计算2n 阶行列式d cdc dc b a ba ba D n 0002=三. (8分)解矩阵方程⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛1302313512343122321X求?=X四. (10分)设向量组A:()()()()3,6,2,0,1,3,0,1,3,1,1,2,0,1,4,14321-=--=--==αααα求向量组A 的秩及一个最大无关组. 五. 12分)讨论方程组的解的情况⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x六. (16分)求正交变换PY X =,将二次型323121232221222222x x x x x x x x x f ---++=化为标准形,并写出其标准形. 七. (8分)设n n ααβααβαβ++=+== 121211,,,且n αα,,1 线性无关,证明:n ββ,,1 线性无关.八. (8分)A 为n 阶方阵,且A 与())1,,2,1(1-=-+n i iE A i均不可逆.则A 可否对角化? 线性代数参考题二填空题(每小题3分,满分30分) 1. 设B A ,都是5阶矩阵,且2,31=-=-B A ,则=A B2. 已知0222=++I A A ,则=+-1)(I A (其中I 是n 阶单位阵)3.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=12241031xA 设,已知矩阵A 的秩r(A)=2,则=x4.()814370122222632144-==⨯ij a A 设,又ij A 是ij a 的代数余子式,则=+++44434241A A A A5.若一向量组只有唯一的极大无关组,则该向量组6.设3221232221321222),,(x tx x x x x x x x x f ++++=是正定二次型,则t 的取值区间为7.设A 是n阶正交矩阵,1-=A ,则()=*TA8.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=20002121x A 相似于对角阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--211,则=x9.设非齐次线性方程组b AX =的两个解为)(,,2121ξξξξ≠A 的秩为1-n ,则 b AX =的一般解=ξ .10.已知向量组[][][]1,4,2,1,0,,0,2,1,1,2,1321--==-=αααt 的 秩为2,则=t二.(8分)计算n 阶行列式ba a a ab a a a a b a D n nn n ---=212121三.(8分)求矩阵X 满足⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎦⎤⎢⎣⎡1041120112201117241X四.(10分)设[][][][]10,2,1,2,4,1,5,1,3,6,3,11,5,5,10,2,3,2,1,24321-==-=-=αααα求向量组的秩及其一个极大无关组. 五. (12分)问常数b a ,各取何值时, 方程组()()⎪⎪⎩⎪⎪⎨⎧=+++++=++++=+-=+++,5853,34232,12,1432143214324321x a x x x b x x a x x x x x x x x x 无解,有唯一解,或有无穷多解,并在有无穷多解时写出其一般解. 六. (16分)求正交变换PY X =,将二次型()323121232221321222222,,x x x x x x x x x x x x f ---++=化为标准形,并写出其标准形.七. (8分)设向量432,,,1αααα线性无关,且43214432134321243211,,,ββββαββββαββββαββββα+---=-+--=--+-=---=证明向量组4321,,,ββββ线性无关.八. (8分)A 为n 阶方阵,且A 与())1,,2,1(1-=-+n i iI A i均不可逆。
线代清考试卷(本科)

武汉科技大学2009-2010-2线性代数清考试卷(本科)一、单项选择(15分=3分⨯5)1.10020120()034034=(A )-20, (B ) 4, (C ) -4, (D ) 20.2. 设,A B 为同阶方阵,则( )成立(A )A B A B +=+ , (B ) AB BA =, (C ) AB BA =, (D ) ()111A B AB---+=+.3. 设A 是n 阶可逆矩阵,*A 是A 的伴随矩阵,则( )成立;(A )*A A =; (B )1*n A A-=; (C )*nA A =; (D )*1A A -=.4. 初等矩阵();(A ) 都可以经过初等变换化为单位矩阵;(B ) 所对应的行列式的值都等于1;(C ) 相乘仍为初等矩阵; (D ) 相加仍为初等矩阵; 5. 已知三阶矩阵A 的特征值为1,1,2,-则矩阵2A A E ++的特征值为( )(A ) 1,1,2--; (B ) 1,3,7; (C ) 1,1,2-; (D )1,0,3--.二、填空题(15分=3分5⨯) 6. 设(,1,2)ij A i j = 为行列式2131D =中元素ij a 的代数余子式,则11122122A A A A = .7.设()()()123325αααααα-++=+,其中12(2,5,1,3),(10,1,5,10),T T αα==3(4,1,1,1)Tα=-, 则α=________. 8. 设300140003A ⎛⎫⎪= ⎪ ⎪⎝⎭,则()12A E --=_______. 9. 设1234(1,2,3,4),(2,3,4,5),(3,4,5,6),(4,5,6,7)αααα====,则该向量组的秩为_______;10.设21101000A k k ⎛⎫⎪= ⎪ ⎪⎝⎭为正定矩阵,则k _______. 三、计算题(50分=10分5⨯)11. 计算行列式210121012, 12. 解矩阵方程X B AX +=,其中⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=021531201,201301012B A , 13. 求线性方程组⎪⎩⎪⎨⎧=+++=+++=++-543265421432143214321x x x x x x x x x x x x 的通解,14. 求向量组()()()1231,2,3,2,2,2,3,0,5T T Tααα===的秩, 15. 求矩阵211210111A -⎛⎫⎪= ⎪ ⎪-⎝⎭的逆. 四、解答题题(14分)16.将二次型22212312323(,,)4332f x x x x x x x x =+++化成标准型。
线代复习题

线代复习题
1. 矩阵的基本概念
- 定义矩阵及其元素
- 矩阵的阶数
- 矩阵的表示方法
2. 矩阵的运算
- 矩阵的加法和减法
- 矩阵的数乘
- 矩阵的乘法
- 矩阵的转置
- 矩阵的逆
3. 特殊矩阵
- 零矩阵
- 单位矩阵
- 对角矩阵
- 斜对角矩阵
- 正交矩阵
4. 行列式
- 行列式的定义
- 行列式的计算方法
- 行列式的性质
5. 线性方程组
- 线性方程组的表示
- 高斯消元法
- 线性方程组的解的存在性
- 齐次线性方程组的解
6. 向量空间
- 向量空间的定义
- 基和维数
- 向量的线性组合
- 向量的线性相关性
7. 特征值和特征向量
- 特征值和特征向量的定义
- 特征值和特征向量的计算方法 - 特征多项式
8. 二次型
- 二次型的定义
- 二次型的矩阵表示
- 正定二次型
9. 线性变换
- 线性变换的定义
- 线性变换的矩阵表示
- 线性变换的性质
10. 矩阵分解
- 矩阵的对角化
- 矩阵的谱分解
- 矩阵的QR分解
11. 应用题
- 利用矩阵解决实际问题
- 矩阵在不同领域的应用案例分析
请根据以上复习题进行复习,确保掌握线性代数的基本概念和运算法则。
线性代数考试题

线性代数考试题
1. 矩阵的定义与基本运算
a) 什么是矩阵?矩阵的定义是什么?
b) 如何进行矩阵的加法和减法运算?
c) 如何进行矩阵的数乘运算?
2. 矩阵的转置与乘法
a) 如何进行矩阵的转置运算?
b) 如何进行矩阵的乘法运算?
c) 矩阵乘法的性质有哪些?
3. 矩阵的逆与行列式
a) 什么是矩阵的逆?
b) 如何求解矩阵的逆?
c) 什么是行列式?
d) 如何计算矩阵的行列式?
4. 向量的线性相关性与线性无关性
a) 什么是线性相关性与线性无关性?
b) 如何判断一组向量是否线性相关?
c) 如何判断一组向量是否线性无关?
d) 线性相关与线性无关的定理有哪些?
5. 向量空间与子空间
a) 什么是向量空间?
b) 向量空间的性质有哪些?
c) 什么是子空间?
d) 如何判断一个子集是否为向量空间的子空间?
6. 特征值与特征向量
a) 什么是特征值和特征向量?
b) 如何求解特征值和特征向量?
c) 特征值和特征向量的性质有哪些?
7. 相似矩阵与对角化
a) 什么是相似矩阵?
b) 如何判断两个矩阵是否相似?
c) 什么是对角化?
d) 如何对角化一个矩阵?
8. 线性变换与矩阵的应用
a) 什么是线性变换?
b) 线性变换与矩阵的关系是什么?
c) 线性变换的应用有哪些?
以上是关于线性代数的考试题目,通过回答这些问题,你可以对线性代数的基本概念和运算有一个全面的了解。
希望你能够认真准备,并取得优异的成绩!。
线性代数复习题(附简答)

总复习题一、求逆序数:1、排列32514的逆序总数为_____;2、在5阶行列式中,项前的符号是.二、行列式的计算:1、计算:,,,;2、设行列式,求;3、设3阶行列式,则.三、伴随阵和逆矩阵的行列式、余子式:1、若是阶可逆方阵,且;2、设为3阶矩阵,,是的伴随矩阵,则=______;3、设其中元素的代数余子式的值是 .四、矩阵的运算:1、已知,,则______;2、已知,,则;3、设向量,求(1)(2);4、已知,则;5、设, 求;6、设,求;7、若是可逆方阵,则.五、解矩阵方程:1、设,求解矩阵方程:.2、已知方阵A满足试证:可逆,并求其逆矩阵3、设矩阵,矩阵B满足方程,为二阶单位阵,试求.六、向量组的相关性、秩、最大无关组:1、设向量组,,,(1)为何值时向量组线性相关;(2)为何值时向量组线性无关.2、设,,,问为何值时线性相关.3、设,,,问为何值时线性相关.4、设,线性无关,试证:,也线性无关.5、设,,线性无关,试证:,,也线性无关.6、设向量组,且求向量组的秩.7、设向量组,,,,求该向量组的秩和一个最大无关组.8、设向量组,,,,求该向量组的秩和一个最大无关组.七、方程组之解的基本概念、性质:1、线性方程组有解的充分必要条件是;2、方程组的基础解系是 .八、方程组的解:1、试问当为何值时下列方程组无解?有无穷多解?唯一解?并在有无穷多解时求出通解.⑴; ⑵ ;⑶ .2、求如下线性方程组的通解:⑴;⑵九、解的性质:1、设四元非齐次线性方程组的系数矩阵的秩为3,已知是它的两个解向量,且,求该方程组的通解.2、设四元非齐次线性方程组的系数矩阵的秩为3,已知是它的三个解向量,且,求该方程组的通解.参考答案一、5;“”. 二、1、0,48, 160,; 2、; 3、.三、1、; 2、; 3、.四、1、14;2、;3、(1) ,(2),4、;5、;6、;7、.五、1、;2、;3、.六、1、时,线性相关;时,线性无关;2、;3、; 6、2;7、3,、都可为其一个最大无关组;8、3,、、都可为其一个最大无关组.七、1、;2、.八、1、⑴ 当时,方程组有唯一解用法求之(略);当时,方程组无解;当时方程组有无穷多解,且通解为..⑵ 当时,方程组无解;当时方程组有无穷多解(略);当时,方程组有唯一解(略).⑶ 当时,方程组有唯一解;当时,方程组无解;当时方程组有无穷多解,且通解为2、⑴ ;⑵ .九、1、或; 2、.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 单项选择
题 1.设行列式==1
111034222,1111304z
y x z y x 则行列式( A ) A.32
B.1
C.2
D.38
2.已知2阶行列式22
11b a b a =m ,2211c b c b =n
,则2
22
111c a b c a b ++=( B )
A.m-n
B.n-m
C.m+n
D.-(m+n )
3.设A ,B ,C 为同阶可逆方阵,则(ABC )-1=( B )
A. A -1B -1C -1
B. C -1B -1A -1
C. C -1A -1B -1
D. A -1C -1B -1
4.设A , B , C 均为n 阶方阵,AB=BA ,AC=CA ,则ABC=( D )
A.ACB
B.CAB
C.CBA
D.BCA
5.设α1,α2,α3,α4是4维列向量,矩阵A =(α1,α2,α3,α4).如果|A |=2,则|-2A |=(
D ) A.-32 B.-4
C.4
D.32
6.设A 为3阶方阵,B 为4阶方阵,且行列式|A |=1,|B |=-2,则行列式||B |A |之值为( A )
A.-8
B.-2
C.2
D.8
7.已知A=⎪⎪⎪⎭⎫ ⎝⎛333231232221131211a a a a a a a a a ,B =⎪⎪⎪
⎭⎫ ⎝⎛333231232221131211333a a a a a a a a a ,P =⎪⎪⎪⎪⎭⎫ ⎝⎛100030001,Q =⎪⎪
⎪⎪
⎭
⎫
⎝⎛100013001,则B =( B )
A.PA
B.AP
C.QA
D.AQ
8.设α1,α2,α3,α4 是三维实向量,则( C )
A. α1,α2,α3,α4一定线性无关
B. α1一定可由α2,α3,α4线性表出
C. α1,α2,α3,α4一定线性相关
D. α1,α2,α3一定线性无关
9.向量组α1=(1,0,0),α2=(1,1,0),α3=(1,1,1)的秩为( C )
A.1
B.2
C.3
D.4
10.已知A 是一个3×4矩阵,下列命题中正确的是( C )
A.若矩阵A 中所有3阶子式都为0,则秩(A )=2
B.若A 中存在2阶子式不为0,则秩(A )=2
C.若秩(A )=2,则A 中所有3阶子式都为0
D.若秩(A )=2,则A 中所有2阶子式都不为0
11.下列命题中错误..
的是( C ) A.只含有一个零向量的向量组线性相关
B.由3个2维向量组成的向量组线性相关
C.由一个非零向量组成的向量组线性相关
D.两个成比例的向量组成的向量组线性相关
12.已知向量组α1,α2,α3线性无关,α1,α2,α3,β线性相关,则( D )
A.α1必能由α2,α3,β线性表出
B.α2必能由α1,α3,β线性表出
C.α3必能由α1,α2,β线性表出
D.β必能由α1,α2,α3线性表出
13.设A 是4×6矩阵,r (A )=2,则齐次线性方程组Ax =0的基础解系中所含向量的个数是( D )
A.1
B.2
C.3
D.4
14.设A 是m ×n 矩阵,已知Ax =0只有零解,则以下结论正确的是( A )
A.m ≥n
B.Ax =b (其中b 是m 维实向量)必有唯一解
C.r (A )=m
D.Ax =0存在基础解系
15.设A 为m ×n 矩阵,m ≠n ,则齐次线性方程组Ax =0只有零解的充分必要条件是A 的秩
( D ) A.小于m B.等于m
C.小于n
D.等于n
16.设矩阵A =⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡---49637525
4,则以下向量中是A 的特征向量的是( A )
A.(1,1,1)T
B.(1,1,3)T
C.(1,1,0)T
D.(1,0,-3)T
17.设矩阵A =⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡--1111311
11的三个特征值分别为λ1,λ2,λ3,则λ1+λ2+λ 3 = ( B )
A.4
B.5
C.6
D.7
18.设A 为可逆矩阵,则与A 必有相同特征值的矩阵为( A )
A.A T
B.A 2
C.A -1
D.A *
19.三元二次型f (x 1,x 2,x 3)=233222312121912464x x x x x x x x x +++++的矩阵为( A )
A.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡963642321
B.⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡
963640341
C.⎥⎥⎥⎦⎤
⎢⎢⎢⎣⎡960642621 D.⎥⎥⎥⎦
⎤
⎢⎢⎢
⎣⎡9123042321
二、 填空题
1.行列式13
769543
21=____0_____.
2.行列式20102008
20092007的值为__________-2_______________.
3.设A =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1100120000120025,则A -1=1200250
000110012-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦. 4.设方阵A 满足A 3-2A +E =0,则(A 2-2E )-1=__-A_______.
5.设矩阵A=⎪⎪⎭⎫ ⎝⎛-102311,B=⎪⎪⎭⎫ ⎝⎛1002,则A T B=___222061⎛⎫ ⎪- ⎪ ⎪⎝⎭
____. 6.设4维向量=α(3,-1,0,2)T ,β=(3,1,-1,4)T ,若向量γ满足2+αγ=3β,则γ=(3,5,-3,8)T .
7.设A 为n 阶可逆矩阵,且|A |=n
1-,则|A -1|=_____-n__. 8.设A 为n 阶矩阵,B 为n 阶非零矩阵,若B 的每一个列向量都是齐次线性方程组Ax =0的解,则|A |=_____0_____________.
9.设α1,α2是非齐次线性方程组Ax =b 的解.则A (5α2-4α1)=___b______.
10.设A 是m ×n 实矩阵,若r (A T A )=5,则r (A )=_____5____.
11.齐次线性方程组⎩⎨⎧=+-=++0320321
321x x x x x x 的基础解系所含解向量的个数为_____1___________. 12.设线性方程组⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡211111111321x x x a a a 有无穷多个解,则a =___-2______.
13.设n 阶可逆矩阵A 的一个特征值是-3,则矩阵1
231-⎪⎭
⎫ ⎝⎛A 必有一个特征值为__13___. 14.设n 阶矩阵A 有一个特征值3,则|-3E +A |=_0________.
15.设向量α=(1,2,-2),β=(2,a ,3),且α与β正交,则a =__2_______.
16.设矩阵A=⎪⎪⎪⎪⎪
⎪⎭
⎫ ⎝⎛----00202221x 的特征值为4,1,-2,则数x=_________2_______________. 17.已知A =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛100021021b a 是正交矩阵,则a +b =________0_______。
18.二次型f (x 1, x 2, x 3)=-4x 1x 2+2x 1x 3+6x 2x 3的矩阵是__021203130-⎛⎫ ⎪- ⎪ ⎪⎝⎭
____。
三、 计算题
1. 计算4阶行列式D =87657
6546
5435
432.
2. 计算行列式3
11251
3420
111
533D =------的值 3. A =⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡---375254132,判断A 是否可逆,若可逆,求其逆矩阵A -1. 4. 已知矩阵A =⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛100210
321,B=⎪⎪⎪⎪⎪⎪⎪⎭
⎫ ⎝⎛--315241.(1)求A -1;(2)解矩阵方程AX =B 。
5. 设向量组α1=(1,2,3,6),α2=(1,-1,2,4),α3=(-1,1,-2,-8),α4=(1,2,3,2).
(1)求该向量组的一个极大线性无关组;
(2)将其余向量表示为该极大线性无关组的线性组合.
6. 设向量组,,,,T 4T 3T 2T 1(1,1,1,1))(-1,1,-3,0(1,2,0,1)(2,1,3,1)=α=α=α=α求向量组的秩及一个极大线性无关组,并用该极大线性无关组表示向量组中的其余向量。
7. 求齐次线性方程组⎪⎩
⎪⎨⎧=--=---=-+0304023214321421x x x x x x x x x x 的基础解系及其通解.
8. 问a 为何值时,线性方程组⎪⎪⎩⎪⎪⎨⎧=++=+=++632222432321
32321x x x ax x x x x 有惟一解?有无穷多解?并在有解时求出其解(在有无穷多解时,要求用一个特解和导出组的基础解系表示全部解)。
9. 设矩阵A =⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡---324010223,求可逆方阵P ,使P -1AP 为对角矩阵.
10. 设矩阵A =⎪⎪⎪⎪⎪⎪⎭⎫
⎝
⎛3030002
a a 的三个特征值分别为1,2,5,求正的常数a 的值及可逆矩阵P , 使P -1AP =⎪⎪⎪⎪⎪⎪⎭⎫
⎝⎛500020001。
