热工基础第三章
合集下载
热工基础课后答案第三章
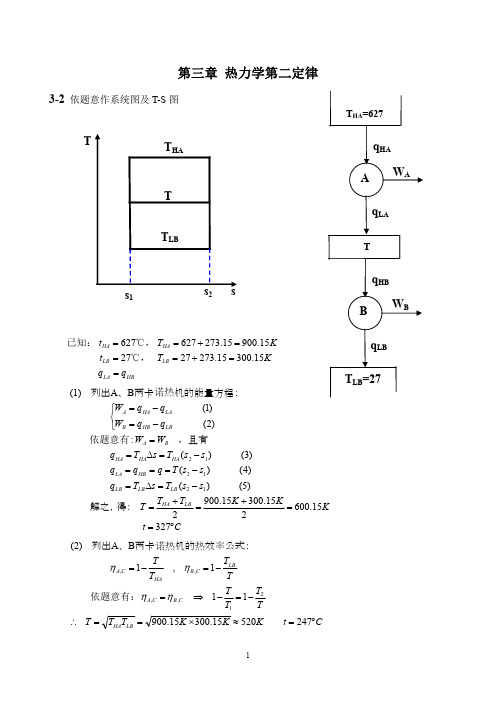
第三章 习 题3-1 解：设定熵压缩过程的终态参数为222S T p 和、，而定温压缩过程的终态参数为222S T p '''和、,根据给定的条件可知： 1222T T p p ='='； 又因为两个终态的熵差为S ∆，固有：21222222lnlnlnT T Mcp p mRT T mc S S S pgp='-'=-'=∆所以有：)exp(12pmCS T T ∆-=对于定熵压缩过程有：kkkkT p T p 212111--=所以：)exp()exp(])1(exp[()(11112112gpk kmR S p mRS M p mck S k p T T p p ∆-=∆-=-∆==-3-2解：设气体的初态参数为1111m T V p 和、、，阀门开启时气体的参数为2222m T V p 和、、，阀门重新关闭时气体的参数为3333m T V p 和、、，考虑到刚性容器有：321V V V ==，且21m m =。
⑴当阀门开启时，贮气筒内压力达到51075.8⨯Pa ，所以此时筒内温度和气体质量分别为：K 25366.78.752931212=⨯==p p T Tkg T R V p m m 0.2252932870.02710751g 1121=⨯⨯⨯===⑵阀门重新关闭时，筒内气体压力降为 5104.8⨯Pa ，且筒内空气温度在排气过程中保持不变，所以此时筒内气体质量为： kg T R V p T R V p m g g 216.025.366287027.0104.852333333=⨯⨯⨯==所以，因加热失掉的空气质量为：kg m 0.0090.2160.225m m Δ32=-=-=3-3 解：⑴气体可以看作是理想气体，理想气体的内能是温度的单值函数，选取绝热气缸内的两部分气体共同作为热力学系统，在过程中，由于气缸绝热，系统和外界没有热量交换，同时气缸是刚性的，系统对外作功为零，故过程中系统的内能不变，而系统的初温为30℃，所以平衡时系统的温度仍为30℃。
热工基础 第三章.理想气体的性质与热力过程
CV ,m McV xi M i cV ,i xi CV ,m,i
i 1 i 1
29
k
i 1 k
i 1 k
3-4 理想气体的热力过程
1．热力过程的研究目的与方法
（1）目的： 了解外部条件对热能与机械 能之间相互转换的影响，以便合理地安排 热力过程，提高热能和机械能转换效率。
V V1 V2 Vk Vi
i 1
k
25
3. 理想混合气体的成分 成分：各组元在混合气体中所占的数量份额。 （1） 成分的分类 1）质量分数 ：某组元的质量与混合气体总质量
的比值称为该组元的质量分数。
k k mi wi , m mi wi 1 m i 1 i 1 2）摩尔分数 ： 某组元物质的量与混合气体总物
22
3-3
理想混合气体
1. 理想混合气体的定义 由相互不发生化学反应的理想气体组成混合 气体，其中每一组元的性质如同它们单独存在一 样，因此整个混合气体也具有理想气体的性质。 混合气体的性质取决于各组元的性质与份额。 2. 理想混合气体的基本定律 （1）分压力与道尔顿定律 分压力： 某组元i单独占有混合气体体积V并处于 混合气体温度T 时的压力称为该组元的 分压力。用 pi 表示。
10
由比定容热容定义式可得
qV u cV dT T V
（4）比定压热容
cp
q p dT
据热力学第一定律，对微元可逆过程，
q dh vdp
11
焓也是状态参数， h h(T ,
p)
h h dh dT dp T p p T 对定压过程，dp 0 ,由上两式可得 h q p dT T p
i 1 i 1
29
k
i 1 k
i 1 k
3-4 理想气体的热力过程
1．热力过程的研究目的与方法
（1）目的： 了解外部条件对热能与机械 能之间相互转换的影响，以便合理地安排 热力过程，提高热能和机械能转换效率。
V V1 V2 Vk Vi
i 1
k
25
3. 理想混合气体的成分 成分：各组元在混合气体中所占的数量份额。 （1） 成分的分类 1）质量分数 ：某组元的质量与混合气体总质量
的比值称为该组元的质量分数。
k k mi wi , m mi wi 1 m i 1 i 1 2）摩尔分数 ： 某组元物质的量与混合气体总物
22
3-3
理想混合气体
1. 理想混合气体的定义 由相互不发生化学反应的理想气体组成混合 气体，其中每一组元的性质如同它们单独存在一 样，因此整个混合气体也具有理想气体的性质。 混合气体的性质取决于各组元的性质与份额。 2. 理想混合气体的基本定律 （1）分压力与道尔顿定律 分压力： 某组元i单独占有混合气体体积V并处于 混合气体温度T 时的压力称为该组元的 分压力。用 pi 表示。
10
由比定容热容定义式可得
qV u cV dT T V
（4）比定压热容
cp
q p dT
据热力学第一定律，对微元可逆过程，
q dh vdp
11
焓也是状态参数， h h(T ,
p)
h h dh dT dp T p p T 对定压过程，dp 0 ,由上两式可得 h q p dT T p
热工基础3_答案_
(1) QH 1500 J , QL 800 J S iso QH QL 0 TH TL 1500 J 800 J 0 1.93( J / K ) 0 2000 K 300 K
QL TL = 300K
根据孤立系熵增原理判定：该循环可行，且不可 逆。 (2) QH 2000 J , W0 1800 J , QL QH W0 2000 J 1800 J 200 J S iso QH QL 0 TH TL
Tav
Q
5
1） 当冷源0℃的冰变的0℃的水时，可将冷、热源视为恒温
3-17
依题意有：TH 298K (t H 25℃） , TL 273K (t L 0℃） QL mrice 其中：m 1000kg ， rice 333kJ / kg 且为可逆热机，故有 t C 1 QH TH T QL H mrice TL TL QL T 1 L QH TH
TH TH mrice mrice mrice 1 TL TL 298K 1000kg 333kJ / kg 1 30 103 kJ 273K 2） 当冷源0℃的水变为25℃的水时，可将热源视为恒温， 冷源为变温 W1 QH QL 热机工作循环视为无数个微元卡诺循环 故有
4
I
Sg
3-16
依题意有：mt 50℃ 8kg , t m 8kg 50℃ , Tm 8 kg 323.15 K mt 100℃ 5kg , t m5kg 100℃ , Tm 5 kg 373.15 K cw 4.187 kJ /(kg K ) 设8kg 50℃的水与5kg100℃的水混合后的混合水质量为m，温度为Tav m mt 50℃ mt 100℃ 则有 cw mt 50℃ (Tav 323.15 K ) cw mt 100℃ (373.15 K Tav ) 解得 Tav 373.15 Kmt 100℃ 323.15 Kmt 50℃ mt 50℃ mt 100℃
西安交通大学本科课程-热工基础-03第三章 热能转换物质的热力性和热力过程
比定容热容 比定压热容 cv ( cp ( δq dT δq dT )v )p
2、理想气体的定压比热容和定容比热容 应用第一定律，并假定过程可逆则有： q du pdv q dh vdp
cv ( cp ( δq dT δq dT )v ( )p ( du pdv dT dh vdp dT )( )( u T h T )v )p ( 3 10 ) ( 3 11 )
一 研究热力过程的目的及一般方法
1、目的 揭示过程中工质状态参数的变化规律以及能量转换情 况，进而找出影响转化的主要因素。 2、一般方法 (1)、对实际热力过程进行分析，将各种过程近似地概括 为几种典型过程，即定容、定压、定温和绝热过程。为 使问题，暂不考虑实际过程中的不可逆的耗损而作为可 逆过程。
i
Δh i (T )
(3)、混合气体的熵
S
S
i
s
s
i i
s i f (T , p i )
d si c pi dT T R g ,i d pi pi dp i pi
ds
( c
i
dT
pi
T
) ( i R g ,i
)
(3 51)
请看思考题
第二节
理想气体的热力过程
(2)、用简单的热力学方法对四种基本热力过程进行分析计算。 (3)、考虑不可逆耗损再借助一些经验系数进行修正。
本章分析理想气体热力过程的具体方法 1)、根据过程特点确定过程方程式，得到 p=f (v). 2)、用过程方程和状态方程，计算初、终态参数。 3)、在p-v、T-s图上画出过程曲线。 4)、确定工质的初、终态比热学能、比焓、比熵的变化。 5)、计算过程中膨胀功、技术功和过程热量。 本节研究理想气体的可逆过程。
2、理想气体的定压比热容和定容比热容 应用第一定律，并假定过程可逆则有： q du pdv q dh vdp
cv ( cp ( δq dT δq dT )v ( )p ( du pdv dT dh vdp dT )( )( u T h T )v )p ( 3 10 ) ( 3 11 )
一 研究热力过程的目的及一般方法
1、目的 揭示过程中工质状态参数的变化规律以及能量转换情 况，进而找出影响转化的主要因素。 2、一般方法 (1)、对实际热力过程进行分析，将各种过程近似地概括 为几种典型过程，即定容、定压、定温和绝热过程。为 使问题，暂不考虑实际过程中的不可逆的耗损而作为可 逆过程。
i
Δh i (T )
(3)、混合气体的熵
S
S
i
s
s
i i
s i f (T , p i )
d si c pi dT T R g ,i d pi pi dp i pi
ds
( c
i
dT
pi
T
) ( i R g ,i
)
(3 51)
请看思考题
第二节
理想气体的热力过程
(2)、用简单的热力学方法对四种基本热力过程进行分析计算。 (3)、考虑不可逆耗损再借助一些经验系数进行修正。
本章分析理想气体热力过程的具体方法 1)、根据过程特点确定过程方程式，得到 p=f (v). 2)、用过程方程和状态方程，计算初、终态参数。 3)、在p-v、T-s图上画出过程曲线。 4)、确定工质的初、终态比热学能、比焓、比熵的变化。 5)、计算过程中膨胀功、技术功和过程热量。 本节研究理想气体的可逆过程。
热工基础(2.1.3)--第三章习题及答案
热工基础第三章作业题及答案3-3 体积为0.03m 3的某刚性储气瓶内盛有700kPa 、20℃的氮气。
瓶上装有一排气阀，压力达到880kPa 时阀门开启，压力降到850kPa 时关闭。
若由于外界加热的原因造成阀门开启，问：(1)阀开启时瓶内气体温度为多少？(2)因加热，阀门开闭一次期间瓶内气体失去多少？设瓶内氮气温度在排气过程中保持不变。
答案：（1）t 2=93.3℃; (2)∆m =0.0097kg3-4 氧气瓶的容积V =0.30m 3，瓶中氧气的表压力p gl =1.4MPa ，温度t 1=30℃。
问瓶中盛有多少氧气？若气焊时用去一半氧气，温度降为t 2=20℃，试问此时氧气瓶的表压力为多少？(当地大气压力p b =0. 098MPa)答案： m =5.72kg; p g2=0.625MPa.3-6 某理想气体等熵指数κ=1.4，定压比热容c p =1.042kJ/(kg.K)，求该气体的摩尔质量M 。
答案：M =27.93 g/mol3-8 摩尔质量为0.03kg/mol 的某理想气体，在定容下由275℃加热到845 ℃，若比热力学能变化为400kJ/kg ，问焓变化了多少？热求其热力学能、焓和熵的变化。
答案：∆ℎ=557.9kJ/kg3-11 在体积V =1.5m 3的刚性容器内装有氮气。
初态表压力p gl =2.0MPa ，温度t =230℃，问应加入多少热量才可使氮气的温度上升到750℃？其焓值变化是多少？大气压力为0.1MPa 。
(1)按定值比热容计算；(2) 按平均比热容的直线关系式计算；(3)按平均比热容表计算；(4) 按真实比热容的多项式表达式计算。
答案：(1) Q =8137 kJ, ΔH =11410 kJ (2) Q =9005 kJ, ΔH =12260 kJ(3) Q =8962 kJ, ΔH =1200 kJ (4) Q =9025 kJ, ΔH =12280 kJ3-15 由氧气、氮气和二氧化碳组成的混合气体，各组元的摩尔数为2O 0.08mol n =，2N 0.65mol n =，2CO 0.3mol n =试求混合气体的体积分数，质量分数和在p = 400kPa 、t =27℃时的比体积。
热工基础-3-完整-第三章 理想气体ppt课件
始压力p1＝7×105Pa，温度t1=20℃。因泄漏，后 压力降至p2＝4.9×105Pa ，温度未变。问漏去多少
氧气？
解：取钢瓶的容积为系统（控制容积），泄漏过 程看成是一个缓慢的过程。初终态均已知。假定 瓶内氧气为理想气体。根据状态方程:
精选ppt
8
二. 理想气体的比热容
物体温度升高1K所吸收的热量称为热容； 一单位质量的物体温度升高（或降低）１℃所吸 收（或放出）的热量称为（质量）比热容。
2) 理想气体： pvRgT cpcv Rg
uf(T) hf(T)
kcp cv
ucv T; hcp T
s c vln T T 1 2 R lnv v 1 2; s cpln T T 1 2 R lnp p 1 2
3)可逆过程：
w pdv 精选ppt
w t vdp
q
Tds
37
分析热力过程的步骤：
讨论：
1、比较教材P75例3-4的解法，上面是利用基本 定义来解的，显然要容易得多，不需记忆相关换算公 式；
2、若本题不要求折合摩尔质量，仅要求折合气 体常数，则也可用：
Rg,eq wiRg,i
i
精选ppt
34
作业：P103-104
3-10 3-15
思考题: P102
10
精选ppt
35
五. 理想气体的基本热力过程
1.热力学能的变化量： u cvdT
若比热容取定值或平均值，有： u cvT
2.焓的变化量： hcpdT
u cV
T T2
T1
若比热容取定值或平均值，有： h cpT
h cp
T2 T1
T
精选ppt
21
3. 理想气体熵变化量的计算：
氧气？
解：取钢瓶的容积为系统（控制容积），泄漏过 程看成是一个缓慢的过程。初终态均已知。假定 瓶内氧气为理想气体。根据状态方程:
精选ppt
8
二. 理想气体的比热容
物体温度升高1K所吸收的热量称为热容； 一单位质量的物体温度升高（或降低）１℃所吸 收（或放出）的热量称为（质量）比热容。
2) 理想气体： pvRgT cpcv Rg
uf(T) hf(T)
kcp cv
ucv T; hcp T
s c vln T T 1 2 R lnv v 1 2; s cpln T T 1 2 R lnp p 1 2
3)可逆过程：
w pdv 精选ppt
w t vdp
q
Tds
37
分析热力过程的步骤：
讨论：
1、比较教材P75例3-4的解法，上面是利用基本 定义来解的，显然要容易得多，不需记忆相关换算公 式；
2、若本题不要求折合摩尔质量，仅要求折合气 体常数，则也可用：
Rg,eq wiRg,i
i
精选ppt
34
作业：P103-104
3-10 3-15
思考题: P102
10
精选ppt
35
五. 理想气体的基本热力过程
1.热力学能的变化量： u cvdT
若比热容取定值或平均值，有： u cvT
2.焓的变化量： hcpdT
u cV
T T2
T1
若比热容取定值或平均值，有： h cpT
h cp
T2 T1
T
精选ppt
21
3. 理想气体熵变化量的计算：
理想气体
∆h = ∫ c p dT
T1
T2
平均比热容 平均比热容（ 平均比热容（表） 定值比热容 热力性质表
∆u = cV ∆u = cV
t2
t1
⋅ (t 2 − t 1 ) ⋅ t 2 − cV
t1
∆h = c p
∆h = c p
t2 t1
⋅ (t 2 − t1 )
⋅ t2 − c p
t1 0° C
t2
0° C
热力学能 焓和熵
T p ∆s = c p ln 2 − Rg ln 2 T1 p1
∆h = c p ∆T = c p ∆t
ct =
t2
1
c 02°C ⋅t2 −c 01°C ⋅t1
t t
t2 −t1
定值比热容表
单原子气体
cV (C ,m) V
c p (Cp,m)
3 3 Rg ( R ) 2 2
双原子气体
0° C
⋅ t1
t2 0° C
⋅ t1
∆u = cV ∆T = cV ∆t
∆u = u 2 (T2 ) − u1 (T1 )
∆h = c p ∆T = c p ∆t
∆h = h2 (T2 ) − h1 (T1 )
西安交通大学热流中心
热工基础与应用 第三章
2、 理想气体的熵
ds =
δqre
T
=
du + pdv cV dT + pdv dT dv p / T = Rg / v = ds = cV + Rg → T T T v
混合气体 组成气体
1、分压力定律 ： 分压力 ：各组元在混合物温度
下单独占据混合物所占体积时 所产生的压力。
热工基础
1 2 1 0
∫
2
1
cdt = ∫ cdt − ∫ cdt = cm 0 (t 2 − 0) − cm 0 (t1 − 0)
2
cm 1
∫ =
2
1
cdt
t2 − t1
=
cm 0 ·t2 − cm 0 ·t1
2 1
t2 − t1
平均比热容也有定压比热容和定容比热容之分，附表 列 平均比热容也有定压比热容和定容比热容之分，附表2列 出了几种理想气体的平均定压质量比热容， 出了几种理想气体的平均定压质量比热容，平均定容质量 比热容可由迈耶公式求得。 比热容可由迈耶公式求得。
3－4 理想气体混合物 －
2种或 种以上理想气体的机械混合物，称为理想 种或2种以上理想气体的机械混合物 种或 种以上理想气体的机械混合物， 气体混合物（理想气体的定律均适用）。 气体混合物（理想气体的定律均适用）。 一、混合气体的分压力和分容积 1、分压力与道尔顿定律 、 在与混合气体具有相同的T 分压力 pi ：在与混合气体具有相同的 、V 下， 某组分气体单独具有的压力。 某组分气体单独具有的压力。
分压力的确定： 分压力的确定： 由 piV=ni RT PVi=ni RT
〉→
pi Vi = = ϕi , pi = ϕ i p = xi p p V
三、混合气体的折合分子量和折合气体常数 折合分子量 折合气体常数
Rg , = R M eq = R m ∑ ni = R ∑ ni m mi R∑ = m Mi = Σωi R g
U = ΣU i H = ΣH i
u = Σω i u i h = Σω i hi s = Σ ω i si
S = ΣS i
注意:计算 时应代入分压力p 注意:计算si 时应代入分压力 i
∫
2
1
cdt = ∫ cdt − ∫ cdt = cm 0 (t 2 − 0) − cm 0 (t1 − 0)
2
cm 1
∫ =
2
1
cdt
t2 − t1
=
cm 0 ·t2 − cm 0 ·t1
2 1
t2 − t1
平均比热容也有定压比热容和定容比热容之分，附表 列 平均比热容也有定压比热容和定容比热容之分，附表2列 出了几种理想气体的平均定压质量比热容， 出了几种理想气体的平均定压质量比热容，平均定容质量 比热容可由迈耶公式求得。 比热容可由迈耶公式求得。
3－4 理想气体混合物 －
2种或 种以上理想气体的机械混合物，称为理想 种或2种以上理想气体的机械混合物 种或 种以上理想气体的机械混合物， 气体混合物（理想气体的定律均适用）。 气体混合物（理想气体的定律均适用）。 一、混合气体的分压力和分容积 1、分压力与道尔顿定律 、 在与混合气体具有相同的T 分压力 pi ：在与混合气体具有相同的 、V 下， 某组分气体单独具有的压力。 某组分气体单独具有的压力。
分压力的确定： 分压力的确定： 由 piV=ni RT PVi=ni RT
〉→
pi Vi = = ϕi , pi = ϕ i p = xi p p V
三、混合气体的折合分子量和折合气体常数 折合分子量 折合气体常数
Rg , = R M eq = R m ∑ ni = R ∑ ni m mi R∑ = m Mi = Σωi R g
U = ΣU i H = ΣH i
u = Σω i u i h = Σω i hi s = Σ ω i si
S = ΣS i
注意:计算 时应代入分压力p 注意:计算si 时应代入分压力 i
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例3-2
三. 分子扩散系数
由： J A， Z
DAB -
dC A DAB dz J A,z
dC A / dz
DAB意义：沿扩散方向 ，在单位时间每下降单位 z 1
浓度梯度时，单位表面 积所扩散的物质的量。
DAB表示了 物质的扩散能力
DAB大小取决于扩散系统的 压力、温度、组成 等。 其数值主要依赖 试验测定
气体----y 固体\液体----x
混合物中某组分的摩尔浓度与混合物总 i 摩尔浓度的比， i y
固体 \ 液体： Ci Ci i 1 xi n C Ci 由理想气体状态方程又 有：
i 1
Ci Pi / RT Pi yi C P / RT P yi 1
i 1 n
u iui / w iu i
i 1 i 1
n
n
其 中 ： i — 组 分i的 质 量 浓 度 kg/m3 ， ui — 组 分i相 对 于 固 定 坐 标 系 的 度 速
— 总质量浓度
(2)而多元混合物的 平均速度 mol 定义式为：
um Ci ui / C y i ui
扩散速度存在的前提 存在浓度梯度。 —
质量平均速度或mol平均速度侧重于整体
扩散速度则侧重于个体
4.扩散通量
定义：单位时间通过垂直于浓度梯度的单位
面积的 物质数量。
分为 质量扩散通量 （kg/m 2s） m mol 扩散通量N kmol/m s） （
2
因为传质中伴随混合物的整体流动，所以 通量可以 以相对于空间的固定坐标确定； 也可以以相对于随混合物整体平均速度 （u或uM ）移动的动坐标来确定， 所以有两种
i 1 n
其中： i — 组分i相对于固定坐标系的速 u 度
( 3)组 i相 于 量 均 度 u或 分 对 质 平 速 者 mol平 速 uM的 度 为 扩 速 。 均 度 速 称 散 度
ui u — 组分i相对于质量平均速度的 扩散速度。
ui uM — 组分i相对于 平均速度的扩散速度。 mol
dC A dz
其中，J A，Z — 组分A沿z方向相对于摩尔平均速 uM 的 度 分子扩散摩尔通量 (kmol/m 2s)
dC A / dz — 组分A在z方向上的浓度梯度（ kmol/m 4 ） D AB — 比例系数，称 分子扩散系数 下标AB 表示：A组分在B中的扩散（m 2 / s） 负号表示：通量方向与 浓度梯度方向相反。
（1）相对于固定坐标所确定的通量，为净质
量通量或净mol通量
（2）相对于以平均速度u或uM移动的动坐标所 确定的通量，为分子扩散质量通量或分子扩
散摩尔通量
二元混合物中A、B两组分的相互扩散过程，及组 分A、B的浓度沿y方向的分布状况。 因为浓度分布不均，所以A、B两组分均从各自 高浓度区域向低浓度区域扩散，方向相反。 若A、B两组分互扩散速度不等，则混合物会产生 整体流动，以某一平均速度u或uM通过某一指定 截面。
组分A相对于固定坐标的净扩 散通量 组分A的分子扩散通量 组分A随混合物整体流动而传 递的通量
等摩尔扩散时： N A N B 则： N A N B 0 N J A J B 0, NA J A
（ ）同理： 6 dw A m A A DAB w A (m A m B ) dw
0.15×10-5
0.11×10-5 2.59×10-9 1.30×10-30
（2）多孔材料中的扩散
气体或液体通过含大量孔隙的固体材料的扩散现象 矿石的还原和焙烧 粉末冶金制品的脱气 多孔材料吸附气体、液体 ①孔隙直径 〉气体分子平均自由行程
特点：扩散不受孔隙壁面影响，Fick定律仍适用
Dolton 分压定律
例3-1 对于浓度恒定均匀的系统，无传质推动力， 无传质或扩散发生 当系统中各处浓度不等，存在浓度梯度时， 扩散发生，传质发生。此时由扩散引起物 质的流动。流动快慢怎样描述？
3.扩散速度
多元混合物中各组分具 有不同速度 多元混合物的速度应为 各组分速度的平均值。
(1)多元混合物的 质量平均速度 定义式为
2.液体
液体的D AB，即与物质种类和温度 有关，还与 浓度 变化有关。
液体DAB的理论计算和试验测定 都很困难
若已知温度T1、溶剂粘度B1下的液体扩散系数 1，AB， D 则温度T2、溶剂粘度B2下有：
D2, AB D1, AB
B1 T2 (m 2 /s) B2 T1
表3-4 二元溶液的扩散系数DAB× 109（ m2/S）
3.固体
两类： 与固体结构无关的、能遵循Fick定律的扩散 与结构有关的在多孔材料中扩散
（1）遵循Fick定律的在固体中的扩散
此时，溶质溶解于固体中形成均匀的固溶体
锌水通过铜的扩散 H2或O2通过橡皮的扩散 粮食内水分的扩散
物质在固体中无扩散整 体流动， 摩尔通量为：
N A J A DAB dCA 2 o (kmol/m C) dz
1.气体
气体混合物（气体分子运动理论建立的半经验公式）：
3 2
DAB
435.7T
1 3 A
P (v v )
P : 混合气体总压力， Pa T：混合气体温度， K
1 3 2 B
1 1 MA MB
v A、v B : 气体A、B在正常沸点下的液态摩 尔容积，cm 3 / mol M A、M B：气体A、B 的分子量
表3-1 二元混合物浓度、速度和扩散通量的表示方法
二. 斐克（fick）定律
描述分子扩散过程中传质通量与浓度梯度之间关 系的定律。
（1） 定温、定压、稳定温度 下，相对于混合物的 场 摩尔平均速度 M，Z移动的坐标系，斐克定 u 律为 J A ,Z dC A D AB dz
J A, Z DAB
D2, AB D1, AB
P1 T2 1.75 2 ( ) (cm /s) P2 T1
表3-3 常见气体在空气中的扩散系数DO,AB（m2/S）
气体 HCl H2 H2 O CO2 N2 NH3 O2 SO2
D0,AB 0.130 0.611 0.220 0.138 0.132 0.170 0.178 0.103 ×104
第三章 传质原理
1.传质：物质由高浓度向低浓度方向传递的过程。
也称质量传递。
2.传质推动力：浓度差 传热推动力：温度差
3.其它传质推动力：
温度差 总压力差 热扩散 压力扩散
在温度差及总压力 差较大时，由明显 作用
4.传质方式：
分子扩散 紊流（涡流）扩散 包含分子扩散
静止流体 层流 固体
湍流脉动
（）物质的量浓度（摩尔 2 浓度） i C
单位体积混合物中，某 一组分i的摩尔数, kmol / m 3 ni Ci V
对 n组 分 的 混 合 物 ， 质 的 量 浓 度 总物 C Ci
i 1 n
n
V
i
n V
显然，有 i C C
i
Mi
M
③对于混合气体，由理 想状态方程 nRT可得: PV
**适用范围：无经验值的混合物的初步估算
表3-2 常见气体的液态摩尔容积（cm3/mol）
气体 空气 H2 H 2O CO2 N2 NH3 O2 SO2
摩尔 22.9 14.3 18.9 34.0 31.1 25.8 25.6 44.8 容积
试验研究：
已知T1、P1下的D1，AB，则T2、P2 下有：
jA jB Au A Au Bu B Bu Au A Bu B u( A B )
u u
i
i
A uA B uB A B
A uA B uB j A jB A uA B uB ( A B ) 0 A B
（1）流体流动过程（动量传递）
三传理论： （2）传热过程（热量传递）
（3）传质过程（质量传递）
对传质（质量传递）的理解 质量传递过程又称扩散过程。因物质的传递过程 凭借扩散作用（分子扩散和涡流扩散）实现的。 质量传递可以在一相内进行，也可以在相际进行。 质量传递的起因是系统内存在化学势的差异。化 学势的差异由浓度、温度、压力或外加电磁场引起。 质量传递是均相混合物分离的物理基础，也是反 应过程中几种反应物互相接触及反应产物分离的基 本依据。
二元混合物中组分 和B的分子扩散质量通量 A 大小相等方向相反
（ ）同理， A C A u A u M） 4 J （ J B C（u B u M） B 则J A J B 0
则二元混合物中组分 和B的分子扩散摩尔通量 A 大小相等方向相反
工程场合下常采用相对于固定坐标的净扩散通量m或N 试验研究时多采用分子扩散通量j或J
2
DAB — A在B中的扩散系数， /s m
表3-5 某些物质在固体中的扩散系数DAB× 104（ m2/S） 溶质A
H2 O2
固体B
硫化橡胶 硫化橡胶
温度（K）
298 298
扩散系数
0.85×10-5 0.21×10-5
N2
CO2 He Al
硫化橡胶
硫化橡胶 Fe Cu
298
298 293 293
（3）若组分A、B的分子扩散质量通量 分别为jA，jB 流体流动带动组分 、B传替的质量通量分别为 A u、 Bu A 则组分A、B的净质量通量 为： m A jA A u m B jB B u
代入 m A AuA，mB B uB得 jA A u A u） （ jB （u B u） B
采用图中固定坐标，则此时净扩散通量包括两部 分（1）浓度梯度产生的相对于平均速度的分子 扩散通量（2）混合物沿扩散方向的整体流动而 带动组分从一处向另一处传递的通量。