(完整版)北京课改版五年级(下)数学复习提纲
北京课改版五年级下册小学数学全册期末复习单元知识清单
第一单元 长方体和正方体一、长方体和正方体的认识1.长方体和正方体的特征。
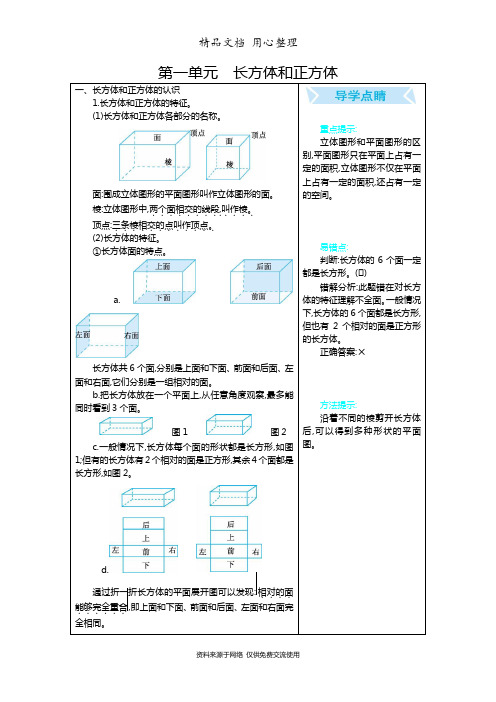
(1)长方体和正方体各部分的名称。
面:围成立体图形的平面图形叫作立体图形的面。
棱:立体图形中,两个面相交的线段．．．．．．．．,．叫作棱。
．．．． 顶点:三条棱相交的点叫作顶点。
．．．．．．．．．．．． (2)长方体的特征。
①长方体面的特点。
a.长方体共6个面,分别是上面和下面、前面和后面、左面和右面,它们分别是一组相对的面。
b.把长方体放在一个平面上,从任意角度观察,最多能同时看到3个面。
图1图2c.一般情况下,长方体每个面的形状都是长方形,如图1;但有的长方体有2个相对的面是正方形,其余4个面都是长方形,如图2。
d.通过折一折长方体的平面展开图可以发现:相对的面．．．．能够完全重合．．．．．．,即上面和下面、前面和后面、左面和右面完全相同。
重点提示:立体图形和平面图形的区别,平面图形只在平面上占有一定的面积,立体图形不仅在平面上占有一定的面积,还占有一定的空间。
易错点:判断:长方体的6个面一定都是长方形。
( )错解分析:此题错在对长方体的特征理解不全面。
一般情况下,长方体的6个面都是长方形,但也有2个相对的面是正方形的长方体。
正确答案:✕方法提示:沿着不同的棱剪开长方体后,可以得到多种形状的平面图。
②长方体棱的特征。
长方体有．．．．12．．条棱．．;．相对的棱互相平行．．．．．．．．,．相邻的棱互相．．．．．．垂直．．;．相对的棱的长度相等．．．．．．．．．,．即．4．条相对的棱的长度相等。
．．．．．．．．．．． ③长方体顶点的数量:长方体共有8个顶点。
(3)正方体的特征。
①正方体的面:一个正方体有6个面,每个面都是正方形,并且6个面完全相同。
②正方体的棱:正方体有．．．．12．．条棱．．,．12．．条棱的长度都相．．．．．．．等．,．相对的棱互相平行．．．．．．．．,．相邻的棱互相垂直。
．．．．．．．．．③正方体的顶点:正方体有8个顶点。
最新北师大版本数学小学五年级的下册的学习知识点及对应练习全面总结复习
( 最新 ) 北师大版数学五年级下册知识点及对应练习( 全面复习 )知识点： 1、同分母的分数加减法计算方法：分母不变，直接用分子相加减。
2、异分母的分数加减法计算方法（1）找到这几个分母的最小公倍数。
（2）通分（马上分母化为同一个数）（3）相加减（4）不是最简分数的一定约分。
3、分数加减混淆运算的运算次序和整数加减混淆运算的运算次序相同．没有括号的分数加减混淆运算次序是从左往右挨次计算；有括号的分数加减混淆运算的运算次序是先算括号里面的，后算括号外面的。
4、分数加减法的简易运算加法运算定律有哪些：（1）加法互换律： a+b=b+a（2）加法联合律： a+b+c=a+(b+c)减法运算定律有哪些：连减的性质： (1)a-b-c=a-(b+c) (2)a-(b+c)=a-b-c其余： (1)a-b+c=a+c-b (2)a-(b-c)=a-b+c(3)a-b+c-d=(a+c)-(b+d)5、把一个分数化成小数的方法：分子除以分母6、小数化成分数的方法：小数化分数时，小数位数上有几位数字，分母上就有几个07、分数、小数加减混淆运算：能够把分数化成小数（能化成有限小数的分数），也能够把小数化成分数，有时还可以直接约分。
北师大版数学五年级下册期末复习题分数加减法姓名：一、填一填1. 分母是 12 的最简真分数有（）个，他们的和是（）。
2.一根铁丝长错误 !米，另一根比它短错误 !米，另一根长（）米。
3.一根铁丝长错误 !米，比另一根短错误 !米，两根铁丝共（）米。
4. 一批化肥，第一天运走它的错误!，次日运走它的错误!，还剩这批化肥的（）没有运。
5.把下边的分数和小数互化。
0.75= （）错误 !=（） 0.125=（）错误 !=（） 2.4=（） 4错误 !=（）8316. 2 ，3.41 从大到小摆列起来：（） >（） >（） >把 3 ，3.14，（）二、计算。
1. 算一算。
(完整版)北师大版小学数学五年级下册知识点整理
北师大版小学数学五年级（下册）知识点分数的加法和减法知识要点一、分数的意义1、分数的意义：把单位“1”平均分成若干份，表示这样的一份或几份的数，叫做分数。
2、分数单位：把单位“1”平均分成若干份，表示这样的一份的数叫做分数单位。
二、分数与除法的关系，真分数和假分数1、分数与除法的关系：除法中的被除数相当于分数的分子，除数相等于分母。
2、真分数和假分数：①分子比分母小的分数叫做真分数，真分数小于1。
②分子比分母大或分子和分母相等的分数叫做假分数，假分数大于1或等于1。
③由整数部分和分数部分组成的分数叫做带分数。
2、假分数与带分数的互化：①把假分数化成带分数，用分子除以分母，所得商作整数部分，余数作分子，分母不变。
②把带分数化成假分数，用整数部分乘以分母加上分子作分子，分母不变。
三、分数的基本性质分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变，这叫做分数的基本性质。
2、分数的大小比较：③ 同分母分数，分子大的分数就大，分子小的分数就小；②同分子分数，分母大的分数反而小，分母小的分数反而大。
③异分母分数，先化成同分母分数（分数单位相同），再进行比较。
（依据分数的基本性质进行变化）四、约分（最简分数）1、最简分数：分子和分母只有公因数1的分数叫做最简分数。
2、约分：把一个分数化成和它相等，但分子和分母都比较小的分数，叫做约分。
（并不是一定要把分数化成与它相等的最简分数才叫约分；但一般要约到最简分数为止）注意：分数加减法中，计算结果能约分的，一般要约分成最简分数。
五、分数和小数的互化：1、小数化分数：一位小数表示十分之几，两位小数表示百分之几，三位小数表示千分之几……，能约分的必须约成最简分数；2、分数化小数：用分子除以分母，除不尽的按要求保留几位小数。
（一般保留三位小数。
）3、分数和小数比较大小：一般把分数变成小数后比较更简便。
六、分数的加法和减法1、真分数加减法（1）同分母分数加、减法（分母不变，分子相加减）（2）异分母分数加、减法（通分后再加减）（3）分数加减混合运算：同整数。
北师大版小学数学五年级下册分类复习提纲
北师大版小学数学五年级下册分类复习提纲知识点1、长度单位有：千米、米、分米、厘米、毫米等。
1千米=1000米1米=10分米=100厘米=1000毫米1分米=10厘米=100毫米1厘米=10毫米2、面积单位有：平方米、平方分米、平方厘米、平方毫米等。
1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米3、地积单位有平方千米、公顷。
1平方千米=100公顷=1000000平方米1公顷=10000平方米4、体积单位有：立方米、立方分米、立方厘米、立方毫米等。
相邻单位之间的进率是1000。
1立方米=1000立方分米1立方分米=1000立方厘米1立方厘米=1000立方毫米5、容积单位有：升、毫升。
1升=1000毫升1升=1立方分米1毫升=1立方厘米7、质量单位有：吨、千克、克等。
相邻单位之间的进率是1000。
1吨=1000千xx1千xx=1000xx练习题1、在括号里填上适当的单位名称旗杆高15（）教室面积80（）油箱容积16（）一瓶墨水60（）2、3.5立方米=（）立方分米470立方厘米=（）立方分米0.8立方米=（）立方厘米60立方分米=（）立方米4300毫升=（）升35立方分米=（）升1200平方厘米=（）平方分米=（）平方米8.25立方米=（）立方分米=（）立方厘米4.8升=（）立方分米=（）立方厘米3.8公顷=（）平方米4080克＝()千克1.3吨=（）吨（）千克3.4小时＝()小时()分50.06公顷＝()公顷()平方米4小时15分＝()小时1010千克＝()吨198厘米＝()分米＝()米120米＝()千米4.15立方米=（）立方分米=（）立方米（）立方分米4小时15分＝()小时7千米70米＝()千米4．15小时＝()小时()分2.07千米＝()千米()米小时＝()小时()分8.5吨＝()吨()千克北师大五年级五年级下册复习（2）表面积北师大五年级五年级下册复习（4）分数计算知识点：分数混合运算的运算顺序：分数混合运算的运算顺序和整数是一样的，都是先算乘除，再算加减，有括号的先算括号里的。
北师大版五年级数学下册知识点总结(分版块总结,复习更高效)
五年级数学下册知识点总结第一单元分数加减法【考点一】同分母分数加减法。
【方法点拨】1.分数加法的含义：分数加法和整数加法的含义相同，都是把两个数合成一个数的运算。
2.分数减法的含义：分数减法和整数减法的含义相同，都是已知两个数的和与其中一个加数，求另一个加数的运算。
3.同分母分数加、减法的计算方法：分母不变，把分子相加、减。
注意：分数加减法的结果要约分成最简分数。
4.含有带分数的分数加减法：直接分数部分相加减，所得结果再加上带分数的整数部分。
【考点二】异分母分数加减法。
【方法点拨】异分母分数相加、减，先通分，然后按照同分母分数加、减法的计算方法进行计算。
【考点三】分数加减混合运算。
【方法点拨】1.分数加减法混合运算同整数加减法混合运算顺序一样：有括号先算括号里面的，没有括号从左往右算，注意最后结果要写成最简分数形式。
2.在计算时，有时会出现分数和小数的混合运算，如果分数能转化为有限小数，可以把分数转化为小数计算；如果分数不能转化为有限小数，就把小数转化为分数计算。
注意：分数加减法的结果要约分成最简分数。
【考点四】分数加法简便计算。
【方法点拨】1.整数加法的运算定律在分数加法中依然适用；2.交换律：a+b=b+a；3.结合律：a+b+c=a+（b+c）【考点五】分数减法简便计算。
【方法点拨】1.减法的性质：连续减去两个数，等于减去这两个数的和。
3.去括号时，括号外面是减号，括号里面的符号要变号。
【考点六】解分数加减法的方程。
【方法点拨】解方程以等式的性质为基础，应用在分数加减法中，方法不变。
【考点七】有带分数的分数加减法简便计算。
【方法点拨】有带分数的分数加减法简便计算，需要把带分数拆分成整数+分数的形式，再进行简便计算。
【典型例题】计算：77779999998888+++=【对应练习】77779+99+999+99998888【考点八】拓展：裂项相消法。
【方法点拨】“裂项相消法：()n a a 1+⨯=n1n a 1-a 1⨯⎪⎭⎫ ⎝⎛+”。
北师大五年级下册数学复习提纲
北师大五年级下册复习提纲复习时按照整册教材的知识体系分数与代数、空间与图形、统计图表、实践与综合运用这四大块来进行知识的梳理。
复习目标：1．通过整理和复习，使学生掌握分数加减乘除法运算的方法，并能正确的进行计算。
2．通过整理和复习，使学生掌握正方体、长方体的表面积计算方法，灵活运用知识解决生活中的实际问题。
3．通过整理和复习，使学生能在方格纸上根据给出的轴对称图形的一半画出另一半；能在方格纸上将简单图形旋转。
4．通过整理和复习，使学生知道复式折线统计图的作用，会用折线统计图来表示数据。
能根据需要选择条形统计图或折线统计图表示数据；能根据统计结果作出简单的分析和判断。
具体安排：周次内容16-17 分单元复习基础知识18 综合复习及检测19 查缺补漏阶段复习措施：（1）教会学生复习方法，先全面复习每一单元，再重点复习有关重点内容。
然后引导学生进行单元训练，对于出错多的知识点再次进行讲评和训练。
（2）采用多种方法，比如学生出题，抢答，抽查，学生互批等方法，提高学习兴趣。
（3）加强补差，让优等生帮助后进生。
（4）课堂上教会学生抓住每单元的知识要点，重点突破，加强解决问题能力的培养，并相互进行口算能力的培养。
（5）多采取独立思考、相互协作的复习方式。
给学生留有较多的自主空间，充分利用小组互助的形式，通过多种复习活动发挥每个学生的特点和优势。
对各类学生给予充分的信任和鼓励，师生共同努力，使不同层次的学生都有较大提高和发展。
（6）重抓双基，分层推进。
复习中以巩固、强化基础为核心，借用具体的课堂活动帮助学生对所学知识进行再现、梳理，进一步巩固、强化双基。
针对不同层次的学生提出不同的知识与技能目标，（学困生：帮助他们查缺补漏，让其掌握最基本的知识点，能进行简单运用即可；中等生：掌握基础的知识与技能，并能正确在解决常见、典型的数学问题，加强他们分析、解决问题能力及计算能力的培养；优生：掌握基础知识与技能，正确在解决常见、典型的数学问题，注意他们数学思维和方法的培养）。
(完整版)北京课改版五年级(下)数学复习提纲
.北京课改版五年级（下）数学复习纲要一长方体和正方体【观点】1、由 6 个长方形（特别状况有两个相对的面是正方形）围成的立体图形叫做长方体。
在一个长方体中，相对面完整相同，相对的棱长度相等。
2、两个面订交的边叫做棱。
三条棱订交的点叫做极点。
订交于一个极点的三条棱的长度分别叫做长方体的长、宽、高。
3、由 6 个完整相同的正方形围成的立体图形叫做正方体（也叫做立方体）。
正方体有12条棱，它们的长度都相等，所有的面都完整相同。
4、长方体和正方体的面、棱和极点的数目都相同，不过正方体的棱长都相等，正方体能够说是长、宽、高都相等的长方体，它是一种特别的长方体。
5、长方体有 6 个面， 8 个极点， 12 条棱，相对的面的面积相等，相对的棱的长度相等。
一个长方体最多有 6 个面是长方形，最罕有 4 个面是长方形，最多有 2 个面是正方形。
正方体有 6 个面，每个面都是正方形，每个面的面积都相等，有12 条棱，每条的棱的长度都相等。
长方体的棱长总和 = （长 +宽 + 高）×4L= （a＋ b＋h）×4长 = 棱长总和÷4－宽－高a=L÷4－b －h宽 = 棱长总和÷4－长－高b=L ÷4－a－h高 = 棱长总和÷4－长－宽h=L ÷4－a－b正方体的棱长总和 = 棱长×12L=a×12正方体的棱长 = 棱长总和÷12a=L÷126、长方体或正方体 6 个面和总面积叫做它的表面积。
长方体的表面积 = （长×宽＋长×高＋宽×高）×2S=2（ab ＋ah＋ bh ）无底（或无盖）长方体表面积= 长×宽＋（长×高＋宽×高）×2S=2（ab＋ah＋ bh）－ ab S=2（ah＋ bh ）＋ ab无底又无盖长方体表面积=（长×高＋宽×高）×2S=2（ah＋bh）正方体的表面积 = 棱长×棱长×6S=a×a×67、物体所占空间的大小叫做物体的体积。
最新北师大版数学五年级下册知识点及对应练习全面复习
最新北师大版数学五年级下册知识点及对应练习全面复习北师大版五年级数学下册概念与公式整理版一、分数乘法、分数除法1. 分数乘法的意义：求几个相同分数的和的简便运算2. 分数除法的意义：已知两个乘数的积和其中一个乘数，求另一个乘数的运算。
如：25÷5=? 已知两个乘数（因数）的积是25，其中的一个因数是5，求另一因数是多少？3. 分数乘法的运算法则：1）分数与整数相乘：分子和整数相乘，分母不变；2）分数与分数相乘：分子与分子相乘，分母与分母相乘，能约分的可以先约分。
4. 分数除法的运算法则：1）一个数除以一个整数（0除外）等于这个数乘以这个整数的倒数；2）一个数除以一个分数等于这个数乘以这个分数的倒数；3）除以一个数（0除外）等于乘这个数的倒数；4）当除数<1时，商大于被除数；（商就是得数）5）当除数=1时，商等于被除数；6）当除数>1时，商小于被除数。
5. 分数除法的意义：如果两个数的乘积是1，那么这两个数叫做互为倒数，其中一个数叫做另一个数的倒数。
6. 注意：1的倒数是1，而0没有倒数。
7. 分数乘整数的意义：与整数乘法的意义相同，就是求几个相同加数的和的简便运算。
如：12×5表示求5个12的和是多少，或者表示12的5倍是多少。
8. 一个数乘分数的意义：就是求这个数的几分之几是多少。
如：4×13表示求4的13是多少。
3×13表示3的13是多少。
9. 分数乘、除法的实际问题1）求一个数的几分之几是多少，用乘法。
2）已知一个数的几分之几是多少，求这个数，用除法，也可以用解方程。
10. 原价×折扣=现价；现价÷原价=折扣；现价÷折扣=原价。
11. 找单位“1”的方法：①总数量是单位“1”；例如：小红看完整本书的12，那么单位“1”是整本书的页码。
②原价就是单位“1”；例如：笔记本电脑原价是3000元，现在降价了12，那么单位“1”是原价3000元。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
北京课改版五年级（下）数学复习提纲一长方体和正方体【概念】1、由6个长方形（特殊情况有两个相对的面是正方形）围成的立体图形叫做长方体。
在一个长方体中，相对面完全相同，相对的棱长度相等。
2、两个面相交的边叫做棱。
三条棱相交的点叫做顶点。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
3、由6个完全相同的正方形围成的立体图形叫做正方体（也叫做立方体）。
正方体有12条棱，它们的长度都相等，所有的面都完全相同。
4、长方体和正方体的面、棱和顶点的数目都一样，只是正方体的棱长都相等，正方体可以说是长、宽、高都相等的长方体，它是一种特殊的长方体。
5、长方体有6个面，8个顶点，12条棱，相对的面的面积相等，相对的棱的长度相等。
一个长方体最多有6个面是长方形，最少有4个面是长方形，最多有2个面是正方形。
正方体有6个面，每个面都是正方形，每个面的面积都相等，有12条棱，每条的棱的长度都相等。
长方体的棱长总和=（长+宽+高）×4 L=（a＋b＋h）×4长=棱长总和÷4－宽－高a=L÷4－b－h宽=棱长总和÷4－长－高b=L÷4－a－h高=棱长总和÷4－长－宽h=L÷4－a－b正方体的棱长总和=棱长×12 L=a×12正方体的棱长=棱长总和÷12 a=L÷126、长方体或正方体6个面和总面积叫做它的表面积。
长方体的表面积=（长×宽＋长×高＋宽×高）×2 S=2（ab ＋ah ＋bh ） 无底（或无盖）长方体表面积= 长×宽＋（长×高＋宽×高）×2S=2（ab ＋ah ＋bh ）－ab S=2（ah ＋bh ）＋ab无底又无盖长方体表面积=（长×高＋宽×高）×2 S=2（ah ＋bh ） 正方体的表面积=棱长×棱长×6S=a ×a ×67、物体所占空间的大小叫做物体的体积。
常用的体积单位有立方厘米，立方分米和立方米，可以写成cm3，dm3 ，m3。
长方体的体积=长×宽×高 V=abh 长=体积÷宽÷高 a=V ÷b ÷h宽=体积÷长÷高 b=V ÷a ÷h 高=体积÷长÷宽h= V ÷a ÷b正方体的体积=棱长×棱长×棱长 V=a ×a ×a8、箱子、油桶、仓库等所能容纳物体的体积，通常叫做他们的容积。
常用的容积单位有升和毫升，也可以写成L 和ml 。
1升=1立方分米 1毫升=1立方厘米 1升=1000毫升9、a 3读作“a 的立方”表示3个a 相乘，（即a x a x a ）【体积单位换算】 高级单位 低级单位低级单位 高级单位体积单位进率： 1立方米＝1000立方分米＝1000000立方厘米1立方分米＝1000立方厘米＝1升＝1000毫升1立方厘米＝1毫升×进率÷进率面积单位进率：1平方米=100平方分米=10000平方厘米1平方千米=100公顷=1000000平方米重量单位进率：时间单位进率：长度单位进率：二因数和倍数1、整除：被除数、除数和商都是自然数，并且没有余数。
大数能被小数整除时，大数是小数的倍数，小数是大数的因数。
找因数的方法：一个数的因数的个数是有限的，其中最小的因数是1，最大的因数是它本身。
一个数的倍数的个数是无限的，最小的倍数是它本身。
2、自然数按能不能被2整除来分：奇数偶数奇数：不能被2整除的数偶数：能被2整除的数。
最小的奇数是1，最小的偶数是0.个位上是0，2，4，6，8的数都是2的倍数。
个位上是0或5的数，是5的倍数。
一个数各位上的数的和是3的倍数，这个数就是3的倍数。
能同时被2、3、5整除的最大的两位数是90，最小的三位数是120。
奇数+偶数=奇数奇数+奇数=偶数偶数+偶数=偶数偶数±偶数＝偶数奇数±奇数＝偶数奇数±偶数＝奇数偶数个偶数相加是偶数，奇数个奇数相加是奇数。
偶数×偶数＝偶数奇数×奇数＝奇数奇数×偶数＝偶数相临两个自然数之和为奇数，相邻自然数之积为偶数。
如果乘式中有一个数为偶数，那么乘积一定是偶数。
3、自然数按因数的个数来分：质数、合数、1.质数：有且只有两个因数，1和它本身合数：至少有三个因数，1、它本身、别的因数1：只有1个因数。
“1”既不是质数，也不是合数。
最小的质数是2，最小的合数是4。
20以内的质数：有8个（2、3、5、7、11、13、17、19）100以内的质数：2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、974、质因数质因数：如果一个质数是某个数的因数，那么这个质数就是这个数的质因数。
分解质因数：把一个合数用质因数相成的方式表示出来叫做分解质因数。
用短除法分解质因数（一个合数写成几个质数相乘的形式）如：4=2×2 ，6=2×3，8=2×2×2。
5、公因数、最大公因数几个数公有的因数叫这些数的公因数。
其中最大的那个就叫它们的最大公因数。
求最大公因数的方法：（1）列举法：就是把几个数的所有因数都写出来，通过对比、观察、找出最大公因数。
12的因数有：1、2、3、4、6、12。
18的因数有：1、2、3、6、9、18。
12和18的公因数有：1、2、3、6。
12和18的最大公因数是6（2）分解质因数法：就是将几个数各自分解成质因数的形式，把公有的质因数相乘得到的就是最大公因数。
如：12=2×2×318=2×3×312和18的最大公因数是2×3=6。
（3）短除法：除到互质为止，把所有的除数连乘起来如：12和18的最大公因数是2×3=632 3几个数的公因数只有1，就说这几个数互质。
两数互质的特殊情况：⑴1和任何自然数互质；⑵2和所有奇数互质；⑶相邻两个自然数互质；⑷两个连续奇数一定互质⑸两个质数一定互质；⑹质数与比它小的合数互质；如果两数是倍数关系时，那么较小的数就是它们的最大公因数。
如果两数互质时，那么1就是它们的最大公因数。
两个数分别除以他们的最大公因数，所得商互质。
6、公倍数、最小公倍数几个数公有的倍数叫这些数的公倍数。
其中最小的那个就叫它们的最小公倍数。
公倍数是最小公倍数的倍数，最小公倍数是公倍数的因数。
最小公倍数是最大公因数的倍数。
最大公因数是最小公倍数的因数。
求最小公倍数的方法：（1）列举法：就是把几个数的所有因数都写出来，通过对比、观察、找出最小公倍数。
12的倍数有：12、24、36、48、60、72……18的倍数有：18、36、54、72……12和18的公倍数有36、72等12和18的最小公倍数是36（2）分解质因数法：就是将几个数各自分解成质因数的形式，全部公因数和全部商的乘积即为最小公倍数。
如：12=2×2×318=2×3×312和18的最小公倍数是2×3×2×3 =36。
（3）短除法：用短除法求两个数的最小公倍数（除到互质为止，把所有的除数和商连乘起来）；用短除法求三个数的最小公倍数（除到两两互质为止，把所有的除数和商连乘起来）如：12和18的最大公因数是2×3×2×3 = 3632 3如果两数是倍数关系时，那么较大的数就是它们的最小公倍数。
如果两数互质时，那么它们的积就是它们的最小公倍数。
两个数的最大公因数与最小公倍数的乘积等于这两个数的乘积。
7、完全数（完美数）6的因数有1，2，3，6，这几个因数的关系是：1+2+3=6，像6这样的数叫完全数，也叫完美数。
完全数较小的有6，28，496，8128……三分数的意义和性质1、分数的意义在进行测量、分物或计算时，往往不能正好得到整数的结果，这时常用分数来表示。
分数的意义：一些物体﹑一些物体等都可以看作一个整体，把这个整体平均分成若干份，这样的一份或几份都可以用分数来表示。
一个整体可以用自然数1来表示，通常把它叫做单位“1”。
把单位“1”平均分为若干份，表示其中的一份的数叫分数单位。
如：2/3的分数单位是1/3。
分数与除法的关系：分子相当于被除数，分母相当于除数，分数线相当于除号，分数值相当于商，分母不能等于零。
如a÷b＝a/b （b≠0）2、真分数与假分数真分数：分子比分母小的分数叫真分数。
真分数小于1。
假分数：分子比分母大或分子和分母相等的分数叫做假分数。
假分数大于1或等于1。
4带分数：带分数由整数和真分数两部分组成。
如15假分数化成整数或带分数：用分子除以分母，要是能够整除，那么整除后的商就是你所要化简的整数，要是不能整除，那么商就是带分数的整数部分，余数就是分数的分子，分母不变。
3、分数的基本性质分数的基本性质：分数的分子和分母同时乘或者除以相同的数（0除外，分数的分子、分母同时扩大或缩小相同的倍数，），分数大小不变。
根据分数的基本性质可以进行约分和通分。
4、约分约分：把一个分数化成和它相等，但分子和分母都比较小的分数，叫做约分。
最简分数：分子分母互质的分数（最简真分数、最简假分数）约分的方法：（1）分子分母同时除以它们的公因数，一直除到是最简分数为止。
（2）分子分母同时除以它们的最大公因数。
5、通分通分：把异分母分数分别化成和原来分数相等的同分母分数，叫做通分。
通分的方法：通常把两个分数化成以分母的最小公倍数为公分母的分数。
注意根据分数的基本性质，分母乘几，分子也乘几。
6、分数大小的比较：分母相同，分子大的分数大；分子相同，分母大的反而小。
异分母的分数相比较，先通分然后再比较。
7、分数和小数的互化：分数化小数：用分子除以分母，除不尽时，要根据需要按“四舍五入”法保留几位小数。
小数化分数：把小数先化成以10、100、1000……为分母的分数，如0.7=7/10，如果不是最简分数必须化成最简分数。
最简分数的分母只含有质因数2和5,这个分数一定能化成有限小数。
如果含有2和5以外的质因数，就不能化成有限小数。
分数化简包括两步：一是约分；二是把假分数化成整数或带分数。
21=0.5 41=0.25 43=0.75 51=0.2 52=0.4 53=0.6 54=0.8 81=0.125 83=0.375 85=0.625 87=0.875 201=0.05 251=0.04。