电磁场与电磁波课后习题答案(杨儒贵编着)(第二版)第5章

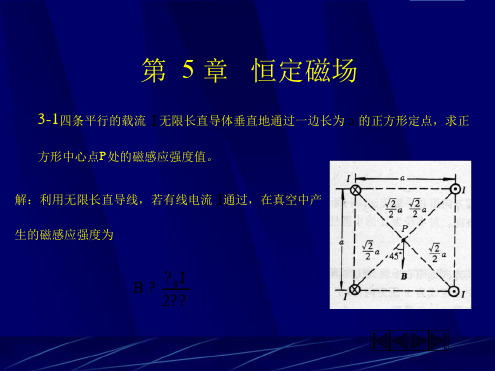
1 第五章 恒定磁场 5-1 在均匀线性各向同性的非磁性导电媒质（即0）中，当存在恒定电流时，试证磁感应强度应满足拉普拉斯方程，即02B。

证 在均匀线性各向同性的非磁性导电媒质中，由HB0及JH，得 JB0 对等式两边同时取旋度，得 JΒ0 JΒ0

但是0J，考虑到恒等式AAA2，得 0BB

又知0B，由上式求得 02B。 5-2 设两个半径相等的同轴电流环沿x轴放置，如习题图5-2所示。试证在中点P处，磁感应强度沿x轴的变 化率等于零，即

0dddd22xx

BB

P a a a

z

习题图5-2

x

y ① ②

o 2

解 设电流环的半径为a，为了求解方便，将原题中坐标轴x换为坐标轴z，如图示。那么，中点P的坐标为（z，

0，0），电流环①位于2az处，电流环②位于2az处。根据毕奥—沙伐定律，求得电流环①在P点产生的磁感应强度为 13101d4lIrr

rrlB



取圆柱坐标系，则 dd1IaIel，zzer，2rzrzreer，

因此



20302030122d4 22d4rrrrIrrzrzrzrzIrzrzrzrzzrzeeeeeeee

eeeeB

同理可得，电流环②在P点产生的磁感应强度为 2030222d4rrrrIrrzrzee

eeeB

那么，P点合成磁感应强度为 21BBB 由于1B和2B均与坐标变量z无关，因此P点的磁感应强度沿z轴的变化率为零，即 3

0dddd22zz

BB

5-3 已知边长为a的等边三角 形回路电流为I，周围媒质为 真空，如习题图5-3所示。试求 回路中心点的磁感应强度。 解 取直角坐标系，令三角形的AB边沿x 轴，中心点P位于y轴上，电流方向如图示。 由毕奥—沙伐定律，求得AB段线电流在P点产生的磁感应强度为 lI301d4rr

rrlB



式中xIIxddel，ay63er，xxer，即

aIxaxaxIzaaxyxyx2336363d4022301eeeeeeB





由于轴对称关系，可知BC段及AC段电流在P点产生的磁感应强度与AB段产生的磁感应强度相等。因此，P点的磁感应强度为

aIz239301eBB

5-4 已知无限长导体圆柱半径为a，通过的电流为I，且电流均匀分布，试求柱内外的磁感应强度。 解 建立圆柱坐标系，令圆柱的轴线为Z轴。那么，由安培环路定律得知，在圆柱内线积分仅包围的部分电流为

IarI221，又ddrel，则

a o a a P

a x

y A C

B 习题图5-3 4 Iarl22dlH22a

rIH

即 202arIeB 在圆柱外，线积分包围全部电流I，那么 IllHdrIH2

即 rI20eB 5-5 已知无限长导体圆柱的半径为a，其内部存在的圆柱空腔半径为b，导体圆柱的轴线与空腔圆柱的轴线之间的间距为c，如习题图5-5（a）所示。若导体中均匀分布的电流密度为0JzeJ，试求空腔中的磁感应强度。

解 柱内空腔可以认为存在一个均匀分布的等值反向电流，抵消了原有的电流而形成的。那么，利用叠加原理和安培环路定律即可求解。已知半径为a，电流密度为0J

的载流圆柱在柱内半径r处产生的磁场强度H1为 021dJrllH

求得 201rJH，或写为矢量形式 21rJH

Y X c

a b

J

Y

习题图5-5(a) 习题图5-5(b)

Y X r r

rr 5

对应的磁感应强度为 201rJB 同理可得半径为b，电流密度为J的载流圆柱在柱内产生的磁场强度为

22rJH

对应的磁感应强度为 202rJB 上式中rr,的方向及位置如习题图5-5（b）示。因此，空腔内总的磁感应强度为

21BBBrrJ

20



200cJxzee200cJ

y

e

5-6 两条半无限长直导线与一个半圆环导线形成一个电流回路，如习题图5-6所示。若圆环半径r =10cm，电流I = 5A，试求半圆环圆心处的磁感应强度。

解 根据毕奥—沙伐定律，载流导线产生的磁场强度为 lI3d41rr

rrlH

设半圆环圆心为坐标原点，两直导线平行于X轴，如图所示。那么，对于半无限长线段① xIIxddel，0r，rxyxeer

因此，在圆心处产生的磁场强度为 

rIrxrxxIzyxx4d410

23221

eeeeH



同理线段③在圆心处产生的磁场强度为

r I

① ②

③ 0 X

习题图5-6

Y r r 6

rIz43eH 对于半圆形线段② ddIrIel, 0r, rrer

因此，它在半圆心处产生的磁场强度为 rIrrIrzr40d41

2

232eeeH







那么，半圆中心处总的磁感应强度为 3210HHHB)T(107.2512460rIze

5-7 若在ay处放置一根无限长线电流Ize，在y = a处放置另一根无限长线电流Ixe，如习题图5-7所示。试 求坐标原点处的磁感应强度。

解 根据无限长电流产生的磁场强度公式，求得位于ay处的无限长线电流Ize在原点产生的磁场为

aIx21eH 位于ay处的无限长线电流Ixe产生的磁场为

aIz22eH 因此，坐标原点处总磁感应强度为 210HHBxzaIee20

Y Z -a a I

0 I X

习题图5-7 7

5-8 已知宽度为W的带形电流的面密度sxJeJs，位于z = 0平面内，如习题图5-8所示。试求),0,0(dP处的磁感应强度。

习题图5-8(a) 习题图5-8(b) 解 宽度为yd，面密度为sJ的面电流可看作为线电流yJsd，其在P点产生的磁场为

yddyyJzyseeH222dd



由对称性可知，z方向的分量相互抵消，如习题图5-8（b） 所示，则

y

wsdyydJeH20222

d2dwJsy2

arctane

因此，在dP,0,0处的磁感应强度为

dwJsy2arctan00eHB 5-9 已知电流环半径为a， 电流为I，电流环位于z = 0 平面，如习题图5-9所示。 试求),0,0(hP处的磁感应强度。 解 由毕奥—沙伐定律得

y z -w/2 w/2

I

o d

x Jx

P

dy y z

y o

B

Y Z P

a h

0 I X

习题图5-9