同底数幂的除法(2)PPT课件
合集下载
4.同底数幂的除法PPT课件(华师大版)

2.计算:
随堂演练
3.计算: 3(x2)3·x3-(x3)3+(-x)2·x9÷x2
4.计算:(1)(a8)2÷a8; (2)(a-b)2(b-a)2n÷(a-b)2n-1
5.已知am=3,an=4,求a2m-n的值.
6.若(xm÷x2n)3÷xm-n与4x2为同类项,且 2m+5n=7,求4m2-25n2的值.
课堂小结
通过这节课的学习活动, 你有什么收获?
课后作业
1.从教材习题中选取, 2.完成练习册本课时的习题.
现在,我怕的并不是那艰苦严峻的生活, 而是不能再学习和认识我迫切想了解的世 界。对我来说,不学习,毋宁死。
—— 罗蒙诺索夫
推动新课
1.计算下列各式
2
2
2
2
2
2
2
2
5-3
53
a
a
a
a
a
3-2
32
2.探究:am÷an=? 由幂的定义可知:
你能从中归纳出同底数幂除法的法则吗?
【归纳结论】
同底数幂相除,底数不变,指 数相减. am÷an=am-n(a≠0,m,n是 正整数,且m>n)
逆用:
am-n= am÷an (a≠0,m, n是正整数,且m>n)
(3)积的乘方等于积中各因数乘方的积.(ab)n= anbn (n是正整数)
2.一个2GB的便携式U盘可以存储的数码照片张 数与数码照片文件的大小有关,文件越大,存 储的张数越少,若每张数码照片的大小为 211KB,则这个U盘能存储多少张照片?
解:2G=2048M=2097125KB U盘能存储照片的张数2097125÷211≈9938(张) 答:这个U盘能存储9938张照片.
同底数幂除法ppt课件二

作业:
习题 1.7
1, 2, 3, 4,
n
的形式: (1)120000;
(2)0.000021;
(3)0.00005001.
例5 计算 3.6 10
-3
3 a 10
0
4 3
5
3
6
回顾交流:
本节课我们学习了那些内容? 同底数幂的除法性质:
a ÷ a =a
m n m-n
(m,n都是正整数,a≠0)
底数 不变
,指数 相减
幂的意义:
n个a
同底幂的除法运算法则:
a· … · a· a
=
an
am÷an=am–n
规定 :
a0 =1
p
同底数幂的乘法运算法则:
am · n =am+n a
n 个0
n
a
1 p a
n ; 10 0.0001 10 1000 (n为正整数) n 个0
∴ 规定 :
a
1 p 。 a
阅读 体验
☞
1.6 104 (3)
【例2】用小数或分数表示下列各数: 例题解析
70 82; (2)
103; (1)
解: (1) 10 3 1 3 1 0.001
10
1000 (2) 70 8 2 1 12 1 64 8 (3) 1.6 10 4 1.6 1 4 1.6 0.0001 0.00016 。。 。 。 。 10
不变 相减 同底数幂相除,底数_____,指数______. 由幂的定义,
m个a
a a
m
n
aaa a aaa a
n个a
同底数幂的除法(第2课时)同步课件

0.000 000 001 295 =1.295×10 – 9
归纳总结
表示小于1的正数科学记数法.
一般地,一个小于1的正数可以表示成a×10n,其中1≤a <10,n为负整数.
0.000 8.61= 8.61×10-4
0.000 861= 8.61×10-4
0.00…01 1
10n
10n
a=8.61
新知探究
用科学记数法表示下列各数:
0.000 000 000 1, 0.000 000 000 002 9, 0.000 000 001 295.
0.000 000 000 1= 1×10–10 0.000 000 000 002 9=2.9×10–12
再看看这些数在计算 器上是怎样表示的, 它们相同吗?
(2)原式=(a-b)3÷(a-b)2-(a+b)5÷(a+b)4 =(a -b)-(a+b)=a-b-a-b=-2b.
巩固练习
1. 数据 0.000 031 4 用科学记数法表示为( )
A. 31.4×10–4
B. 3.14×10–5
C. 3.14×10–6
D. 0.314×10–6
巩固练习
2.把0.081 3写成a×10n(1≤a<10,n为整数)的情势,则a为( )
22
(4) (-8)0÷ (-8)-2 .
只要m,n都是整数,就 有am ÷an=am-n成立!
新知探究
在引进了零指数幂和负整数指数幂后,指数的范围已 经扩充到了全体整数,幂的运算性质仍然成立.即有: (1)am·an=am+n;(2)(am)n=amn;(3)(ab)n=anbn; (4)am÷an=am-n;(5)a-1=1/a ; (6)a0=1. (这里m,n为整数,a≠0,b≠0)
同底数幂的除法(2)
• [6-2
1997 0 × ] 1988
-2
说说零指数和负整数幂的意义
P61
练一练1,2,3
P63 3、4 本 子 上 百分百:P78 2
代数作业格式 P79 3
评价手册:P28 第2课时
0
用文字概括为: 任何一个非零数的0次幂等于1.
你2 222 1 4 2 2222 2
2 2 2
3 4
2 5
34
2
3
1
1 2 2
1
请计算 10 10 , 3 3
1 规定:a -n= a n
为正整数)
( a≠0, n
即: 任何非零数的- n ( n 为正整数)次幂等于这个数n次幂 的倒数
1 -3 ;(π-3.14) 0 2
(-0.1)0×10-2;
3、把下列各数写成负整数指数幂的形式:
1 1 ;0.0001; 64 8
(5 5 5 ) 5
2 0
2
3
2 (2)
0
3
1 -5 1 3 1 2 • × × 2 2 2
1 10
(
0
)
0.1 10
( -1 ) (
-2
0.01 10
)
)
-3
0.001 10
(
)
8.3 同底数幂的除法(2)
零指数幂与负指数幂
2 2
3 3
10 10
2 2
3 3
5 5
1 1 1
2 3
33
2 3
0
10
2 2
10 0
0
同底数幂的除法ppt课件

A.-9 B.-3 C.9
D.3
2.已知m,n为正整数,且xn=4,xm=8,
(1)求xm-n的值;
(2)求x3m-2n的值.
解:当xn=4,xm=8时,
(1)xm-n=xm÷xn=8÷4=2.
(2)x3m-2n=x3m÷x2n=(xm)3÷(xn)2=83÷42=32.
零指数幂和负整数指数幂
0
1.规定:a = 1
解:(1)6-1÷6-1=6-1-(-1)=60=1.
-5
-4
(2)(- ) ÷(- ) =(- )
解:(3)(-8)0÷(-8)-2
=(-8)0-(-2)
=(-8)2
=64.
-5-(-4)
-1
=(- ) =-2.
(1)任何非零数的零次幂都等于1;
(2)负整数指数幂是正整数指数幂的倒数,不是正整数指数幂的相反数;
=(-x)4
=x4.
(3)(ab)5÷ab;
(4)am+1÷a2(m>1);
(5)(x-y)5÷(x-y)2.
解:(3)(ab)5÷ab=(ab)5-1
=(ab)4
=a4b4.
(4)am+1÷a2
=am+1-2
=am-1.
(5)(x-y)5÷(x-y)2
=(x-y)5-2
=(x-y)3.
运用同底数幂的除法法则注意
-p
(a≠0),即任何不等于零的数的 0 次幂都等于 1 .
2.a = (a≠0,p 为正整数),即任何不为零的数的-p(p 为正整数)次幂
等于这个数的 p 次幂的 倒数 .
苏科版数学七年级下册同底数幂的除法课件(共16张)

课后回顾
课堂小结
∵ an×a( m–n ) =am,
∴ am÷an= am–n .
(法二) 用幂的定义:
m个a
am÷an
=
a ·a a ·a
·…·a ·…·a
n个a
(m-n)个a
n个a
=
a ·a ·…·a ·a ·a ·…·a a ·a ·…·a
= am-n
n个a
同底数幂的除法法则
am ÷ an = a m-n (m、n为正整数)
2、(1)已知2x=3,2y=5,求: 2x-2y的值. (2)x-2y+1=0,求:2x÷4y×8的 值.
例4、计算: (1)(m4)2+m5•m3+(-m)4•m4 (2)x6÷x3•x2+x3•(-x)2.
练习:计算: (1)(-3a4)2-a•a3•a4-a10÷a2 (2)(-x3)5÷[(x2)2·(-x)2]2·x2 (3)(a+b)3·(b+a)2÷(a+b)4 (4)(a-b)5÷(b-a)3·(a-b)4
②底数中系数不能为负;
③ 幂的底数是积的情势时,要再用一次
(ab)n=anbn.
练一练
计算: (1)315÷313 (3)y14÷y2
(2) 4 7 4 4
3 3
(4)(-a)5÷(-a)
(5)(-xy)5÷(-xy) 2
(6)a10n÷a2n (n是正整数)
(7)32m÷3÷32 (8)(-x2y3z)4÷(-x2y3z)2 (9)(-x-y)4 ÷(x+y)2
am÷an÷ap=am-n-p(a≠0,m、n、p都是正整数, 且m>n+p)
同底数幂的除法法则的应用
北师大版数学七年级下册第1课时同底数幂的除法课件(共18张)

(3) (-3 )m÷( -3 )n.
(1) 1012÷109 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
=1000=103
合作探究
m 个 10
(m-n)个10
(2) 10m÷10n 10 10
10 10
10 =10×10×···×10
归纳总结
n个a
运算法则:
am÷an = am-n (a≠0,m,n 是正整数,且 m>n).
文字说明:同底数幂相除,底数_不__变__,指数_相__减__.
典例精析
例1 计算: (1) a7÷a4 ;
(2) (-x)6÷(-x)3;
(3) (xy)4÷(xy);
(4) b2m+2÷b2.
解:(1) a7÷a4 = a7-4 = a3.
=0.001.
(2)70×8-2
=1
1 82
=
1. 64
注意:
a0 =1
(3)1.6×10-4
1 =1.6
104
=
1.6×0.0001
=
0.00016.
议一议
计算下列各式,你有什么发现?与同伴进行交流.
(1) 7-3÷7-5;
(2) 3-1÷36;
3 15
12
2
解:(1)
2
7-3÷7-5
=
1 73
(4) (-8)0÷(-8)-2.
1 75
1 73
75
72= 7-3-(-5).
(2)
3-1÷36
=
1 3
1 36
=
1 3 36
七年级数学下册《同底数幂的除法》ppt课件

(1)105÷103 =102
(2)27 ÷ 23 =24 (3)a9÷ a4 =a5
学习目标1: 通过同底数幂乘法的运算性质, 自己得出同底数幂除法的运算
(4)(-a)10 ÷(-a)2=(-a)8 性质。
由前面的习题猜想:
am an am-n
同底数幂相除, 底数不变,指
数相减
(其中a≠0, m,n都是正整数,且m>n)
(6)(- x)4÷(- x);-x3 (7)(-a)4÷ (-a)2;a2
(8)( -t )11÷( -t )2;-t9 (9)(ab)6÷ (ab)2 ;a4b4
(10)(xy)8 ÷(xy)3;x5y5 (11)(a+b)6÷(a+b)4; (a+b)2 (12)(a-b)6÷(a-b)4 (a-b)2
学习目标
1.通过同底数幂乘法的运算性质,自己得出同底数幂 除法的运算性质。
2.会利用同底数幂除法的运算性质进行计算。 3.会利用同底数指数幂的运算性质进行计算。
温故知新
练习1: 1、计算: (1)(-2)3•(-2)2;(-2)5 (3)(-2)4•22 ;26 (5)(-a)2•a3;a5
(2) a5•a2 ;a7 (4)-a2•a3; -a5 (6)(a-b)•(a-b)2 ;(a-b)3
m (3) m3 3 m3 2
3
4a3 3 • a4 3 a2 3 a3 2
a9 • a12 a6 a6
a21 a6 a6 a9
思考●探索●交流
若ax= 3 , ay= 5, 求:
(1) ax-y的值? a xy a x a y 3
5
(2) a3x-2y的值? a3x2 y a3x a 2 y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 5.6
2020年10月2日
1
温故而知新
1、计算(1)a m+2÷a m+1×a m (2) (-x)5 ÷x3 ÷(-x)
2、已知:am=5,an=4,求a 3m-2n的值。
2020年10月2日
2
探索与合作学习
(1)53÷53=5(3 )-(3)=5(0 )
又53 ÷53=1
得到______5_0_=__1_______
3、计算下列各式中的x:
(1)—31—2 =2x
(3)(-0.3)x=- —1207—00
4、已知(a-1)a 2-1=1,求整数a的值。
2020年10月2日
9
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
2020年10月2日
5
例1 用分数或整数表示下列各负整数指 数幂的值:
(1)10-3 (2)(-0.5)-3 (3)(-3)-4
例2 把下列各数表示成a×10n(1≤a<10,n为整数 )的形式:
(1)12000 (2)0.0021 (3)0.0000501
注意:我们可以用科学记数法表示绝对值较小的数。
(n为正整数)
10n0.0 001 n 个0
7
例3 计算:
(1)950×(-5)-1
(2)3.6×10Βιβλιοθήκη 3(3)a3÷(-10)0
(4) (-3)5÷36
注意
1、结果都要化成正整数幂
22、020年通10过月2知日 识的学习,幂的法则使用于整个整数范围
8
自我挑战
1、若(2x-5)0=1,则x满足____________ 2、已知︱a︱=2,且(a-2)0=1,则2a=____
汇报人:XXX 汇报日期:20XX年10月10日
10
2020年10月2日
6
归纳拓展
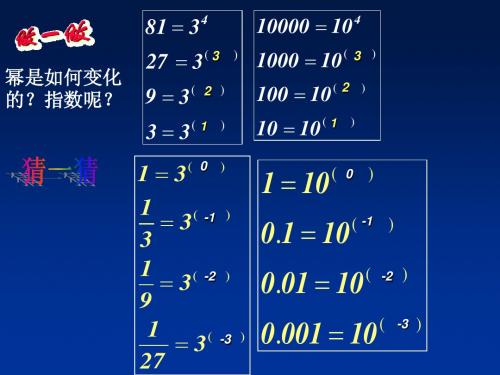
10 4 10000 10 3 1000 10 2 100 10 1 10 10 0 1 10 1 0 . 1 10 2 0 . 01 10 3 0 . 001 10 4 0 . 0001
找规律
2020年10月2日
n 个0 1n 010 00
a = ? 得到______3_(__-_2_)_=__—_3_1_2—______ 问:一般地
-p
规定 任何不等于零的数的-p(p是正整数)次幂,
等于这个数的p次幂的倒数。
a20-20p年1=0月2日—1a—p (a≠0,p是正整数)
4
判断:下列计算对吗?为什么?错 的请改正。
(1)(-7)0=-1 (2 )(-1)-1=1 (3) 8-1=-8 (4) ap×a-p=1(a≠0)
更一般地,a0= ?(a≠0)
规定 a0=1(a≠0)
任何不等于零的数的零次幂都等于1。
2020年10月2日
3
(2)33 ÷35=——(—3)—×—(—3)—×—(—3)———
(3)×(3)(3) × (3)×(3)
1
1
=(—3)—×—(—3)=—3(—2)
又33÷35=3( 3)-(5)=3( -2)
2020年10月2日
1
温故而知新
1、计算(1)a m+2÷a m+1×a m (2) (-x)5 ÷x3 ÷(-x)
2、已知:am=5,an=4,求a 3m-2n的值。
2020年10月2日
2
探索与合作学习
(1)53÷53=5(3 )-(3)=5(0 )
又53 ÷53=1
得到______5_0_=__1_______
3、计算下列各式中的x:
(1)—31—2 =2x
(3)(-0.3)x=- —1207—00
4、已知(a-1)a 2-1=1,求整数a的值。
2020年10月2日
9
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
2020年10月2日
5
例1 用分数或整数表示下列各负整数指 数幂的值:
(1)10-3 (2)(-0.5)-3 (3)(-3)-4
例2 把下列各数表示成a×10n(1≤a<10,n为整数 )的形式:
(1)12000 (2)0.0021 (3)0.0000501
注意:我们可以用科学记数法表示绝对值较小的数。
(n为正整数)
10n0.0 001 n 个0
7
例3 计算:
(1)950×(-5)-1
(2)3.6×10Βιβλιοθήκη 3(3)a3÷(-10)0
(4) (-3)5÷36
注意
1、结果都要化成正整数幂
22、020年通10过月2知日 识的学习,幂的法则使用于整个整数范围
8
自我挑战
1、若(2x-5)0=1,则x满足____________ 2、已知︱a︱=2,且(a-2)0=1,则2a=____
汇报人:XXX 汇报日期:20XX年10月10日
10
2020年10月2日
6
归纳拓展
10 4 10000 10 3 1000 10 2 100 10 1 10 10 0 1 10 1 0 . 1 10 2 0 . 01 10 3 0 . 001 10 4 0 . 0001
找规律
2020年10月2日
n 个0 1n 010 00
a = ? 得到______3_(__-_2_)_=__—_3_1_2—______ 问:一般地
-p
规定 任何不等于零的数的-p(p是正整数)次幂,
等于这个数的p次幂的倒数。
a20-20p年1=0月2日—1a—p (a≠0,p是正整数)
4
判断:下列计算对吗?为什么?错 的请改正。
(1)(-7)0=-1 (2 )(-1)-1=1 (3) 8-1=-8 (4) ap×a-p=1(a≠0)
更一般地,a0= ?(a≠0)
规定 a0=1(a≠0)
任何不等于零的数的零次幂都等于1。
2020年10月2日
3
(2)33 ÷35=——(—3)—×—(—3)—×—(—3)———
(3)×(3)(3) × (3)×(3)
1
1
=(—3)—×—(—3)=—3(—2)
又33÷35=3( 3)-(5)=3( -2)
