高中数学新课程精品限时训练(31)
高中数学新课程精品限时训练(34)

限时训练(三十四)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)已知集合{}2|30M x x x =+<,{}2|1N x x =…,则图中阴影部分表示的集合为( ). (A )[1,1)- (B )(31)--, (C )(3][1,-∞--+∞U ,)(D )(3,1]-(2)复数1i1i-+(i 是虚数单位)的虚部为(). (A )1- (B )1 (C )i - (D )i(3)如果实数x ,y 满足10201x y x y x -+⎧⎪+-⎨⎪+⎩≤≤≥0,则目标函数4z x y =+的最大值为( ).(A )2 (B )3 (C )72(D )4 (4)执行如图所示的程序框图,当输入1a =,9n =时输出的结果等于( ). (A )253 (B )1024 (C )2045 (D )4093(5)表达式22ππlog sinlog cos 1212+的值为( ). (A )2- (B )1- (C ) 12(D )1(6)设数列{}n a 是以2为首次,1d =的等差数列,而数列{}n b 是一个首次为1,2q =的等比数列,则1210b b b a a a +++=L ( ).(A )1033 (B )1034 (C )2057 (D )2058 (7)函数5()|21|xx =-的图像为( ).(A ) (B ) (C ) (D )(8)如图所示,ABC △中,90BCA =︒∠且4AC BC ==,点M 满足3BM MA =u u u u r u u u r ,则CM CB ⋅=u u u u r u u u r( ).(A )2 (B )3 (C )4 (D )6(9)一个几何体的三视图如下图所示,其正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为( ).(A )12π (B )3π (C )43π (D )123π(10)函数()f x 是定义在R 上的可导函数,若()(2)f x f x =-,且当(1)x ∈-∞,时(1)0x f x -⋅'<().设(0)a f =,12b f ⎛⎫= ⎪⎝⎭,(3)c f =,则( ).(A )a b c << (B )c b a << (C )c a b << (D )b c a <<(11)已知点P 是双曲线22221x y a b-=(0,0a b >>)右支上一点,1F ,2F 分别是双曲线的左右焦点,I 为12PF F △的内心,若存在关系,12122IF F IPF IPF S S S =+△△△成立,则双曲线的离心率为( ).(A )5 (B )4 (C )3 (D )2(12)在等差数列{}n a 中,0n a >且21384a a a a ++=则310a S ⋅的最大值( ).(A )3754 (B )2754 (C )4254 (D )4758二、填空题:本题共4小题,每小题5分. (13)函数25()10(0)f x x x x=++<的最大值为________. (14)函数2()lg f x x x x =-+-的零点个数为________个. (15)已知函数()2sin()(0)f x x ωϕω=+>的图像关于直线π3x =对称.且π012f ⎛⎫= ⎪⎝⎭,则ω的最小值是________. (16)吴敬,字信民,号主一翁,浙江仁和人.曾任浙江布政使司幕府,中国明代景泰年是数学家,著有《九算算法比类大全》一书,书中有这样的一道题目:远望巍巍塔七层,红灯向下成倍增,共灯三百八十一.请问塔顶几盏灯?塔顶灯数为________.限时训练(三十四)答案部分一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 BACCAABCBCDA二、填空题13. 0 14. 1 15.2 16. 3解析部分(1)解析 对于M :(3)030x x x +<⇒-<<,对于N :2111x x ⇒-剟?.阴影部分表示集合M 中除M N I 的部分,画数轴分析,即31x -<<-.故选B评注 本题应注意,阴影中没有1x =-,容易出现D 这个错误选项.(2)解析 解法一:2221i (1i)12i i 2ii 1i (1i)(1i)1i 2---+-====-++--.故选A. 解法二:21i i i i(1i)i 1i 1i 1i----+===-+++.故选A. (3)解析 由约束条件得可行域如图所示,经分析易知:当取点A 时,目标函数取最大值.1013,2022x y A x y -+=⎧⎛⎫⇒⎨ ⎪+-=⎝⎭⎩,所以13744222z x y =+=⨯+=.故选C. (4)解析 1k =,1a =;2k =,5a =; 3k =,13a =; 4k =,29a =; 5k =,61a =; 6k =,125a =;7k =,253a =; 8k =,509a =; 9k =,1021a =;10k =,2045a =, 109n >=,所以输出结果为2045.故选C.(5)解析 原式222ππ1π1log sincos log sin log 21212264⎛⎫⎛⎫=⋅===- ⎪ ⎪⎝⎭⎝⎭.故选A. (6)解析 由题意得112(1)11122n n n n a n n b --=+-⋅=+=⋅=,, 所以11221n n n b a a --==+.所以原式101(21)10103321⋅-=+=-.故选A. (7)解析 1221|21|x xxxx y y y =−−−−→=-−−−−−−−−→=-向下平移保留轴上方的图像个单位把轴下方的图像翻折上去. .故选B.(8)解析 ()CM CB CB BM CB ⋅=+⋅u u u u r u u u r u u u r u u u u r u u u r .解法一:易知33||||423244BM BA =⋅=⋅=u u u u r u u u r ,3π4BM CB ⋅=u u u u r u u u r 〈〉.所以223||||||cos π=4CM CB CB BM CB CB BM CB ⋅=+⋅=+⋅⋅u u u u r u u u r u u u r u u u u r u u u r u u u r u u u u r u u u r21632416124⎛⎫+⋅⋅-=-= ⎪ ⎪⎝⎭.故选C.解法二:如图所示建立平面直角坐标系.则(0,0)C ,(4,0)A ,(0,4)B ,设点M 的坐标为(,)x y .则(,4)BM x y =-u u u u r ,(4,)MA x y =--u u u r ,所以3(4)3(3,1)43()1x x x M y y y =-=⎧⎧⇒⇒⎨⎨-=-=⎩⎩.所以(3,1)CM =u u u u r ,(0,4)CB =u u u r.所以30144CM CB ⋅=⨯+⨯=u u u u r u u u r .故选C.(9)解析 由题意得,几何体的立体图如图所示.其中PA ⊥底面ABCD ,设外接球半径为R .则2||3||3R PCPA ===,所以32R =,所以223443π2S R ⎛⎫=π=π= ⎪ ⎪⎝⎭球.故选B. (10)解析 由()(2)f x f x =-可知()f x 是关于1x =对称的图形.而(1)-∞,时(1))00()x f x f x f x -'<⇒'>⇒(()在(1)-∞,上单调递增,本题可类想成 一个二次函数2()(1)f x x =--,则离对称轴1x =越近值越大,反之越小.则易知c a b <<.故选C. (11)解析 如图所示,设内切圆半径为r ,则由题意得,12121||112||||222F F rPF r PF r ⋅⋅=⋅+,所以12121||||||222cPF PF F F a c e a-=⇒=⇒==.故选D.(12)解析 由题意得,设公差为d ,则213844443334333()a a a a d a d a d a a d a d ++=-+-++==+=+,所以3433a d a +=⇒=,所以31044()(1015)a S a d a d ⋅=-⋅+(3)(3015)d d =-+2151590d d =-++.所以当15122152b d a =-=-=⨯-()时,()310max 151537590424a S ⋅=-++=.故选A. (13)解析 解法一:2525()10()100f x x x x x-=-+--⋅=--≥. 所以()0f x ≤ 所以max ()0f x =.解法二:25()10f x x x -=-+--222()20x x x x x x =-+--=----…, 所以()0f x „,所以max ()0f x =.(14)解析 本题实际在问函数21y x x =-+和2lg y x =的两个图像的交点个数,如图所示,故只有一个交点,即()f x 只有一个零点.(15)解析 由题意可知π,012⎛⎫⎪⎝⎭是函数()f x 的一个对称中心. 由于相邻对称轴与对称中心之间间隔14个周期,设周期为T , 则max πππ2ππ243124T T ωω⎛⎫=-=⇒π⇒⇒⎪⎝⎭剟?,所以min 2ω=. (16)解析 本题即一个首项为1a ,公比为2的等比数列,前7项和381,求1a .则()71112381312a a -=⇒=-.。
高中数学新课程精品限时训练(30))

因此 ,因此 . 故选C.
解法二:如图所示,取 的中点 ,连接 ,则 , , ,所以 ,
则 .
5.解析这个正三棱柱的直观图如图所示,设 ,过 作 交 于 ,过 作 交 于 点,连接 ,则 .
, .
所以 .故选B.
6.解析因为 ,所以 , , ,则 .故选B.
评注解决这类比较大小的问题常常借助于中间量来进行比较,常用的中间量是“0”和“1”.
7.解析由实数 满足的约束条件知,可行域如图所示.
在点 处取最大值,且 ,
代入 ,得 . 故选C.
8.解析① 有两个相等实根,因此曲线 不具有“可平行性”;
② , 总有两个不同的实根与之对应,因此曲线 是具有“可平行性”的曲线;
③ ,则 至少有两个不同的实根与之对应,因此曲线 是具有“可平行性”的曲线;
④ ,当 时,只有一个实根 ,因此曲线 不具有“可平行性”.
综上,②③是具有“可平行性”的曲线.故选B.
评注本题将“可平行性”这一抽象的概念转化为曲线对应函数的导函数是否存在2个不同的零点的问题,使解答变得易于操作.
9.解析 ,又 ,所以 ,得 .
10.解析因为 ,故 ,又数列 为等差数列,所以
所以 ,由 ,得 .
已知下列曲线:① ;② ;③ ;④ ,其中具有“可平行性”的曲线是( ).
A.①②B.②③C.①②③D.①③④
二、填空题:本大题共 小题,每小题 分,共 分.
9.已知向量 , , .若 与 共线,则 ________.
10.已知等差数列 的前 项和为 ,且 ,若 ,则 .
11.若 , , 是直角 的三边的边长( 为斜边),则圆 : 被直线 :
一、选择题
1
2
高中数学新课程精品限时训练(34)

限时训练(三十四)
答案部分
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
B
D
B
A
B
A
A
C
C
二、填空题
13. 14. 15. 16.
解析部分
(1)解析因为 ,又因为 ,所以 ,所以 .故选D.
(2)解析解法一: ,所以实部为1,虚部为1,实部与虚部之和为2.
(A) (B) (C) (D)
(4)在“双11”促销活动中,某网店对11月11日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知12时到14时的销售额为42万元,则9时到11时的销售额为( ).
(A)9万元(B)18万元(C)24万元(D)30万元
(5)运行如图所示的程序框图,输出的 值为().
(11)解析取 的中点 ,联结 , ,因为在四面体 中, 平面 ,
是边长为3的等边三角形.
所以 , 是等腰三角形,
的中心为 ,作 交 的中垂线 于 , 为外接球的中心,
, , .
四面体 外接球的表面积为: .故选C.
(12)解析记 ,则
,记 ,则 在 上为增函数,且 ,所以当 时, ,此时 ,为增函数;当 时, ,此时 ,此时函数为减函数.所以 ,B错; ,C错; ,A对.故选C.
故选C.
解法二:设 ,
,所以 .故选C.
(3)解析因为 ,所以 .
故选B.
(4)解析12时 14时对应的频率为: ,总销售数为 .
高中数学新课程精品限时训练(27)

a=结束是输出ai 开始限时训练(二十七)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合{}0,1,2,4A =,集合{}04B x x =∈<R …,集合C A B =I ,则集合C 表示为 ( ) . A.{}0,1,2,4B.{}1,2,3,4C.{}1,2,4D.{}04x x ∈<R …2.复数z 满足()1i 1z -=(其中i 为虚数单位),则z = ( ) . A .11i22- B.11i 22+ C .11i 22-+ D.11i 22-- 3.下列函数中,为奇函数的是 ( ) . A .122x xy += B .{},0,1y x x =∈C .sin y x x ⋅=D .1,00,01,0x y x x ⎧⎪⎨⎪⎩<->==4.“1ω=”是“函数()cos f x x ω=在区间[]0,π上单调递减”的 ( ) . A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件 5.执行如图所示的程序框图,则输出的a 的值为 ( ) .A .2B .13C .12- D .3-6.已知直线1:4360l x y -+=和直线2:1l x =-,抛物线24y x =上一动点P 到直线1l 和直线2l 的距离之和的最小值为( ) . A.2 B.3 C.115 D. 37167. 如图所示,1F ,2F 是双曲线1:C 2213y x -=与椭圆2C 的公共焦点,点A 是1C ,2C 在第一象限的公共点.若121F F F A =,则2C 的离心率是( ) .A .13B .23 C.2235或 D .25(第7题图)8.在平面直角坐标系中,定义两点()11,P x y 与()22,Q x y 之间的“直角距离”为()1212,d P Q x x y y =-+-.给出下列命题:(1)若()1,2P ,()()sin ,2cos Q ααα∈R ,则(),d P Q的最大值为3(2)若,P Q 是圆221x y +=上的任意两点,则(),d P Q的最大值为(3)若()1,3P ,点Q 为直线2y x =上的动点,则(),d P Q 的最小值为12. 其中为真命题的是( ) .A .(1)(2)(3)B .(1)(2)C .(1)(3)D .(2)(3)二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中的横线上. 9.设α为锐角,若π4cos 65α⎛⎫+= ⎪⎝⎭,则πsin 23α⎛⎫+= ⎪⎝⎭ .10.已知向量()2,1x =-m ,()1,x =n ,若⊥m n ,则实数x 的值为 . 11.函数()x f 的定义域为 .12.某几何体的三视图如图所示,其正视图是边长为2的正方形,侧视图和俯视图都是等腰直角三角形,则此几何体的体积是 .13.以抛物线24y x =的焦点为圆心且与双曲线222214x y a a-=的渐近线相切的圆的方程是 .14.已知奇函数()f x 是定义在R 上的增函数,数列{}n x 是一个公差为2的等差数列,且满足()()()()8910110f x f x f x f x +++=,则2014_______x =.限时训练(二十七)答案部分一、选择题二、填空题 9.242510. 1 11. [)2,+∞ 12.83 13.()22415x y -+= 14. 4009 解析部分1. 解析 因为{}{}0,1,2,4,04A B x x ==<…,所以{}1,2,4C A B ==I .故选C. 2. 解析 由题可得()()11i 1i1i 1i 1i 2z ++===--+.故选B. 3. 解析 A 选项中令()122xx f x =+,则()()112222x xx xf x f x ---=+=+=,所以()f x 为偶函数, 故选项A 中的函数不是奇函数;B 选项中的函数的定义域为{}0,1,不关于原点对称,所以B 中函数不是奇函数;C 选项中令()sin f x x x =,则()()()()sin sin f x x x x x f x -=--==,所以()f x 为偶函数,故C 中函数不是奇函数;D 选项中的函数的定义域及图像都是关于原点对称的,所以D 中函数是奇函数.故选D.4. 解析 当1ω=时,()cos f x x =,它在区间[]0,π上是单调递减的;若()cos f x x ω=在区间[]0,π上是单调递减的,则12ππ2ω⋅…,即01ω<…,所以()1cos f x x ωω=⇒=在[]0,π上单调递减,()cos f x x ω=在区间[]0,π上单调递减1ω⇒=/,所以1ω=是()cos f x x ω=在区间[]0,π上单调递减的充分不必要条件.故选A. 5. 解析 该程序框图的模拟分析如下表.根据上表得输出的a 的值为3-.故选D.6. 解析 如图所示,设点P 到直线1l 的距离为1d ,到直线2l 的距离为2d ,点F 为抛物线的焦点.因为抛物线方程为24y x =,所以直线2l 为抛物线的准线,所以2d PF =,即距离之和等于1d PF +.过点F 作1FH l ⊥与点H ,FH 与抛物线交于点0P ,则点P 位于点0P 的位置时,1d PF +最小,此时()1min d PF FH +==4130625⨯-⨯+=.故选A.7. 解析 设焦半径为c ,椭圆的长半轴长为a .由双曲线方程2213yx -=可得2c =,所以11224AF F F c ===.由双曲线的定义及点A 在第一象限可得122AF AF -=,所以212422AF AF =-=-=.由椭圆定义知,12422AF AF a +=+=,则3a =,所以椭圆2C 的离心率23c e a ==.故选B. 8. 解析(1)由“直角距离”的定义知(),1sin 22cos 1sin 22cos d P Q αααα=-+-=-+-=()()3sin 2cos 3αααϕ-+=+(其中tan 2α=).又因为sin()1,αϕ+-…所以()33αϕ+…,即(),3d P Q …(),d P Q 的最大值为3,故(1)正确.(2)过点P 作x 轴的垂线,过点Q 作y 轴的垂线,两垂线交于点R,如图所示,设,QR a PR b ==,根据“直角距离”的定义有()1212,d P Q x x y y ab =-+-=+.因为2224a b PQ +=…,所以2a b +a b +…(),d P Q …,(),d P Q的最大值为,故(2)正确.(3)因为点Q 在直线2y x =上运动,所以可设点Q 的坐标为(),2x x .由“直角距离”的定义得()43,13,1322,12334,2x x d P Q x x x x x x ⎧⎪-<⎪⎪=-+-=-<⎨⎪⎪-⎪⎩……,画出这个函数的图像如图所示.当32x =时函数有最小值为313422⨯-=,即(),d P Q 的最小值为12,故(3)正确.综上可知(1),(2),(3)均为真命题.故选A. 9. 解析 因为π0,2α⎛⎫∈ ⎪⎝⎭,所以ππ2π,663α⎛⎫+∈ ⎪⎝⎭.又由已知π4cos ,65α⎛⎫+= ⎪⎝⎭得πππ,662α⎛⎫+∈ ⎪⎝⎭, 所以π3sin ,65α⎛⎫+= ⎪⎝⎭故πππ3424sin 22sin cos 23665525ααα⎛⎫⎛⎫⎛⎫+=++=⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 10. 解析 因为⊥m n ,所以20x x ⋅-+=m n =,可得1x =. 11. 解析 若使函数()f x =240x -…,所以2x …,即()f x 的定义域为[)2,+∞. 12. 解析 符合条件中的三视图的几何体如图所示,图中ABCD 为正方形,边长为2,BE ⊥平面ABCD ,且2BE =,所以11824333E ABCD ABCD V BE S -=⋅=⨯⨯=.13. 解析 抛物线24y x =的焦点为()1,0F ,双曲线222214x y a a-=的渐近线为2y x =±.设点F 到其中一条渐近线2y x =的距离为d ,因为以点F 为圆心的圆与2y x =相切,所以r d ===, 所以所求圆的方程为()22415x y -+=. 14. 解析 因为数列{}n x 为等差数列,所以811910x x x x +=+.若8119100x x x x +=+>,则()()8110f x f x +>,()()9100f x f x +>,所以()()()()8910110f x f x f x f x +++>与已知矛盾;若8119100x x x x +=+<,则()()()()8119100,0f x f x f x f x +<+<,所以()()89f x f x ++()()10110f x f x +<也与已知矛盾,故8119100x x x x +=+=.又因为数列{}n x 的公差为2,即1092x x -=,由91010902x x x x +=⎧⎨-=⎩,得101x =, 所以2014102004=1+20042=4009x x d =+⨯.E222DCBA。
高中数学新课程精品限时训练(38)

限时训练(三十八)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)已知集合413A x x ⎧⎫=-⎨⎬-⎩⎭…,(){}2log 21B x x =-<,则A B =I ( ).(A )()1,4- (B )()1,3- (C ) ()2,3 (D )()3,4(2)复数z 满足()12i 3i z +=+,则复数z =( ).(A )1i + (B )1i - (C )1i -+ (D )1i -- (3)已知函数()22f x x mx =+-,在区间[]2,4-上随机取一个实数x ,若事件“()0f x '<”发生的概率为23,则m 的值为( ). (A )2(B )2-(C )4(D )4-(4)在ABC △中,三个内角A ,B ,C 所对的边为a ,b ,c ,若cos cos 2cos a B b A c C +=,6a b +=且ABC S =△,则c =( ). (A) (B) (C )3 (D)(5)数列{}n a 满足11=a ,且11n n a a n +=++,对任意的*n ∈N 恒成立,则122017111a a a +++=L ( ). (A )20151008 (B )20171009 (C )40342017 (D )20152018(6)下列命题正确的个数是( ). ①“1x ≠”是“0232≠+-x x”的充分不必要条件② 若()()sin 2f x x θ=+,则“()f x 的图像关于π3x =对称”是“π6θ=-”的必要不充分条件 ③()0,0x ∃∈-∞,使0034xx <成立④命题“角α的终边在第一象限,则α是锐角”的逆否命题为真命题 (A )4 (B )3 (C )2 (D )1(7)过双曲线()222210,0x y a b a b -=>>的右焦点F 作直线by x a=-的垂线,垂足为A 交双曲线左支于B 点,若12OAF OBF S S =△△,则该双曲线的离心率为( ). (A(B )2 (C )(D(8)已知Rt AOB △的面积为1,O 为直角顶点.设向量OAOA=uu r uu r a ,OB OB=uuruur b ,2OP =+uura b ,则PA PB -uu r uu r 的最小值为( ). (A )1(B )2(C)(D )4(9)某三棱锥的三视图如图所示,该三棱锥的外接球半径是( ). (A(B(C(D(10)阅读如图所示的程序框图,运行相应的程序,输出的结果S =( ).(A )20172018 (B )20162017 (C )40332018 (D )40332017俯视图(11)已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示,则π6y f x ⎛⎫=- ⎪⎝⎭图的单调递增区间为( ).(A )πππ,π,44k k k ⎡⎤-+∈⎢⎥⎣⎦Z (B )ππ2π,2π,44k k k ⎡⎤-+∈⎢⎥⎣⎦Z (C )πππ,π,36k k k ⎡⎤-+∈⎢⎥⎣⎦Z (D ) ππ2π,2π,36k k k ⎡⎤-+∈⎢⎥⎣⎦Z (12)设函数()e xxf x =,关于的方程()()210f x mf x +-=⎡⎤⎣⎦有三个不同的实数解,则实数m 的取值范围是( ).(A )1,e e ⎛⎫-∞- ⎪⎝⎭ (B )1e ,e⎛⎫-+∞ ⎪⎝⎭(C )()0,e (D )()1,e 二、填空题:本题共4小题,每小题5分.(13)若变量x ,y 满足约束条件200220x y x y x y +⎧⎪-⎨⎪-+⎩…„…,则2z x y =-的取值范围是________.(14)已知cos 212sin 2αα+=,()tan 2αβ+=,则tan =β .(15)设定义在R 的偶函数()y f x =,满足对任意x R ∈都有()()2f t f t +=-,且(]0,1x ∈时,()1xf x x =+.若20153a f ⎛⎫= ⎪⎝⎭,20165b f ⎛⎫= ⎪⎝⎭,20177c f ⎛⎫= ⎪⎝⎭,则 .(16)过抛物线22y x =的焦点F 的直线分别交抛物线于,A B 两点,交直线12x =-于点P ,若PA mAF =u u u r u u u r ,(),PB nBF m n =∈R u u u r u u u r,则m n +=____________.限时训练(三十八)答案部分一、选择题二、填空题13. []1,2- 14.3415. c b a << 16. 0 解析部分(1)解析 因为{}13A x x =-<„,()()2log 21022242,4x x x B -<⇒<-<⇒<<⇒=, 所以()2,3A B =I.故选C .(2)解析 根据题意可知()()3i 12i 3i 55i1i12i 55z +-+-====-+,所以1i z =+.故选A. (3)解析()20f x x m '=+<,2m x <-,22m -=,4m =-.故选D.(4)解析 由正弦定理得sin cos sin cos 2sin cos A B B A C C +=,()sin 2sin cos A B C C +=⋅,sin 2sin cos C C C =⋅, 因为sin 0C ≠,所以1cos 2C =. ()0,πC ∈,π3C =,又ABC S =△,则1sin 2ab C = 所以8ab =,又因为6a b +=,所以()()2222222cos 2363812c a b ab C a b ab ab a b ab =+-=+--=+-=-⨯=. 所以c =.故选B.(5)解析 因为11n n a a n +=++,所以1n n a a n -=+,即1nn a a n --=,121n n a a n ---=-,…,()2122a a n -=….以上1n -个等式分别相加得()()()11222n n n a a n -+-=….所以()()212122nn n n na -++=+=,所以2121121n a n n n n ⎛⎫==- ⎪++⎝⎭. 所以12201711111111201721223201720181009a a a ⎛⎫+++=-+-++-= ⎪⎝⎭L L .故选B.(6)解析 对于①1x ≠推不出2320x x -+≠,因为22320x x x =⇒-+=,但2320x x -+≠,可得1x ≠且2x ≠,故为必要不充分条件,①为假命题.对于②充分性明显不成立,对于π6θ=-时, ()sin 26f x x π⎛⎫=- ⎪⎝⎭,又sin 21336f πππ⎛⎫⎛⎫=⨯-= ⎪ ⎪⎝⎭⎝⎭,故π3x =是()f x 的对称轴,必要性成立,故②为真命题.对于③()003,0,14x x ⎛⎫∀∈-∞> ⎪⎝⎭,故③为假命题.对于④第一象限角不一定是锐角,原名题为假命题,则其逆否命题为假命题,故选D.(7)解析 设(),0F c ,则直线AB 的方程为()a y x c b =-代入双曲线渐近线方程by x a =-得2,a ab M cc ⎛⎫- ⎪⎝⎭,由2FB FA =u u u r u u u r ,可得2222,33c a ab B c c ⎛⎫+-- ⎪⎝⎭,把B 点坐标代入双曲线方程22221x y a b -=,即()222222224199c a a c a c +-=,整理可得c =即离心率ce a==.故选C. (8)解析 以O 为原点,直线OA 为x 轴建立直角坐标系.由已知2OA OB ⋅=,设()0OA t t =>,则点(),0A t ,20,B t ⎛⎫⎪⎝⎭,()1,0=a ,()0,1=b ,()1,2OP =u u u r . 从而()1,2PA t =--u u u r ,21,2PB t ⎛⎫=-- ⎪⎝⎭u u u r .2,PA PB t t ⎛⎫-=- ⎪⎝⎭u uu r u u u r所以PA PB -u u u r u u u r =2t =时取等号;所以PA PB ⋅u u u r u u u r的最小值为故选A . (9)解析 根据题意,可得出如图所示的三棱锥A BCD -,底面Rt BCD △中,BC CD ⊥,且5BC =,4CD =,侧面ABC △中,高AE BC ⊥于E ,且4AE =,2BE =,3CE =,侧面ACD △中,5AC =.因为平面ABC ⊥平面BCD ,平面ABC I 平面BCD BC =,AE BC ⊥,所以AE ⊥平面BCD ,结合CD ⊆平面BCD ,得AE CD ⊥,因为BC CD ⊥,AE BC E =I , 所以CD ⊥平面ABC ,结合AC ⊆平面ABC ,得AC CD ⊥,所以在ADB △中,AB ==BD ==AD ==设ABC △外心为O ,如图设G 为AB 中点, H 为BC 中点.过1O 的垂线与过CD 中点F 且平行1C C 的直线相交于O ,则O 为外接球球心.则1Rt RtCHO AEB△△:,故1O C HCAB AE=,故14O C=.所以R==.故选D.(10)解析由程序框图知,S可看成一个数列{}n a的前2017项和,其中()()*1,12017nannnn∈=+N„,所以1111111112017112122017201822320172018201820118 S⎛⎫⎛⎫++⋯+++⋯+-⎪ ⎪⎝⎛⎫==---==⎭⎪⎝⎭⎭⨯⨯⨯⎝.故输出的是20172018.故选A.(11)解析由图可知2A=,ππ4π312T⎛⎫=-=⎪⎝⎭,所以2π2πω==.因为由图可得点π,212⎛⎫⎪⎝⎭在函数图像上,可得:π2sin2212ϕ⎛⎫⨯+=⎪⎝⎭,解得ππ22π,122k kϕ⨯+=+∈Z,所以由π2ϕ<,可得π3ϕ=.所以()π2sin23f x x⎛⎫=+⎪⎝⎭.因为若将()y f x=的图像向右平移π6个单位后,得到的函数解析式为()ππ2sin22sin263g x x x⎡⎤⎛⎫=-+=⎪⎢⎥⎝⎭⎣⎦.所以由ππ2π22π,22k x k k-+∈Z剟,可得ππππ,44k x k k-+∈Z剟,所以函数()g x的单调增区间为πππ,π,44k k k⎡⎤-+∈⎢⎥⎣⎦Z.故选A.(12)解析11()()01e ex xx xf x f x x--'=⇒==⇒=,因此当1x„时,()1ef x„;当1x>时()1ef x<<,因此2()10g t t mt=+-=有两个根,其中110,et⎛⎫∈ ⎪⎝⎭,(]21,0et⎧⎫∈-∞⎨⎬⎩⎭U,因为()01g=-,所以110ee eg m⎛⎫>⇒>-⎪⎝⎭.故选B.(13)解析如图所示,2y x z=-,当2y x z=-过()0,1A时,z-取得最大值,此时z取得最小值;当2y x z=-过点()2,2B时,z-取得最小值,此时z取得最大值.故min max1,2z z=-=,故z的范围是[]1,2-.=0评注 2z x y =-的范围呢?这是基本类型,希望同学们滚瓜烂熟!(14)解析 依题意22cos 22sin cos ααα=,故1tan 2α=,故()()()tan tan 3tan tan 1tan tan 4αβαβαβααβα+-=+-==⎡⎤⎣⎦++.(15)解析 ()()()2f t f t f t +=-=,故()y f x =是周期为2的偶函数.()y f x =在(]0,1上为增函数,20151116723333a f f f f ⎛⎫⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,201644140515555b f f f f ⎛⎫⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,201711288777c f f f ⎛⎫⎛⎫⎛⎫==+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,因为111753<<,所以c b a <<. 评注 在研究函数性质特别是奇偶性、周期、对称性、单调性、最值、零点时,要注意用好条件的相互关系,结合特征进行等价转化研究.如奇偶性可实现自变量正负转化,周期可实现自变量大小转化,单调性可实现去“f ”,把函数值的大小转化自变量大小关系.(16)解析 直线1x =-是抛物线的准线,如图设,A B 在直线上的射影分别是,M N ,AM AF =,BN BF =,PA PA AF AM =,PB PB BF BN=,因为//AM BN ,所以PA PBAF BF =,m n =, 又0,0m n <>,所以0m n +=.评注 抛物线问题中抛物线的定义在解题中常常用到.抛物线上点到焦点距离与点到准线的距离常用定义相互转化.利用定义还可得出与焦点弦有关的一些常用结论:(以下图为依据)(1)212y y p =-,1224x x p =;(2)1222sin AB x x p pθ=++=(θ为AB 的倾斜角); (3)11AF BF +为定值2p; (4)以AB 为直径的圆与准线相切; (5)以AF 或BF 为直径的圆与y 轴相切.。
高中数学新课程精品限时训练(20)
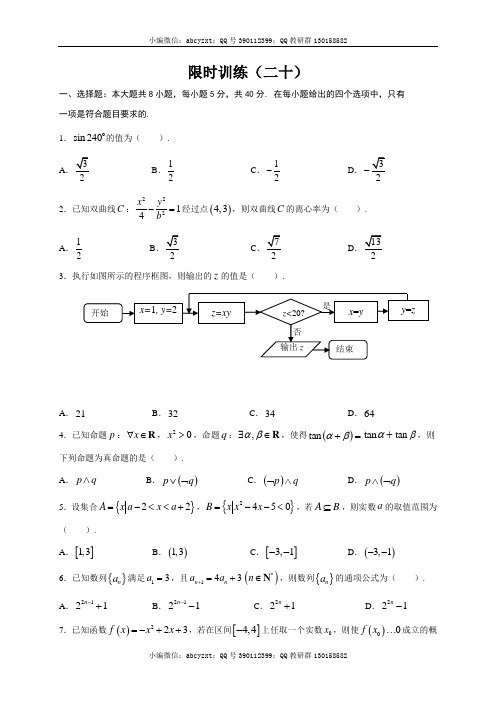
限时训练(二十)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有 一项是符合题目要求的. 1.sin 240o的值为( ).AB .12C .12- D.- 2.已知双曲线C :22214x y b -=经过点()4,3,则双曲线C 的离心率为( ). A .12B.2 C.2 D.23.执行如图所示的程序框图,则输出的z 的值是( ).A .21B .32C .34D .644.已知命题p :x ∀∈R ,20x >,命题q :,αβ∃∈R ,使得()tan αβ+=tan α+tan β,则下列命题为真命题的是( ). A .p q ∧ B .()p q ∨⌝ C .()p q ⌝∧ D .()p q ∧⌝5.设集合{}22A x a x a =-<<+,{}2450B x x x =--<,若A B ⊆,则实数a 的取值范围为( ).A .[]1,3B .()1,3C .[]3,1--D .()3,1-- 6.已知数列{}n a 满足13a =,且143n n a a +=+()*n ∈N ,则数列{}na 的通项公式为( ).A .2121n -+ B .2121n -- C .221n + D .221n -7.已知函数()223f x x x =-++,若在区间[]4,4-上任取一个实数0x ,则使()00f x …成立的概率为( ). A .425B .12C .23D .18.设函数()3233f x x ax bx =++有两个极值点1x ,2x ,且[]11,0x ∈-,[]21,2x ∈,则点(),a b 在平面aOb 上所构成区域的面积为( ). A .14 B .12 C .34D .1二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中的横线上. 9.已知i 为虚数单位,复数1iiz -=,则z = . 10.已知向量(),1x =a ,()2,y =b ,若()1,1=-a +b ,则x y += .11.某种型号的汽车紧急刹车后滑行的距离y km 与刹车时的速度x km /h 的关系可以 用2y ax =来描述,已知这种型号的汽车在速度为60km/h 时,紧急刹车后滑行的距离 为b km .一辆这种型号的汽车紧急刹车后滑行的距离为3b km ,则这辆车的行驶速度12.在平面直角坐标系中,已知曲线1C 和2C 的方程分别为3212x ty t =-⎧⎨=-⎩(t 为参数)和242x ty t=⎧⎨=⎩(t 为参数),则曲线1C 和2C 的交点有 个. 13. 一个几何体的三视图如图所示,图中直角三角形的直角边长均为1,则该几何体体积为 .14.设点()0,1M x ,若在圆O :221x y +=上存在点N ,使得45OMN ∠=o,则0x 的取值范围是 .限时训练(二十)答案部分一、选择题二、填空题9.10. 3- 11.12. 1 13.1614. []1,1- 解析部分1. 解析 ()sin 240sin 18060sin 602=+=-=-o o o o .故选D. 2. 解析 由题可得216914b -=,解得23b =,所以2227c a b =+=,所以2c e a ==. 故选C.3. 解析 1x =,2y =,220z =<→2x =,2y =,420z =<→2x =,4y =,820z =<→4x =,8y =,3220z =>→输出32z =.故选B.4. 解析 因为x ∈R 时,20x …,所以命题p 是假命题;当tan 0α=或tan 0β=时,都有()tan tan tan αβαβ+=+,所以命题q 是真命题,所以()p q ⌝∧是真命题.故选C.5. 解析 由题可得{}15B x x =-<< ,若A B ⊆,则有2125a a --⎧⎨+⎩……,解得13a剟.故选A.6. 解析 因为143n n a a +=+,所以()1141n n a a ++=+.又因为14n a +=,所以{}1n a +是以4为首项,4为公比的等比数列,所以1214442n n n n a -+=⨯==,所以221n n a =-.故选D.7. 解析 令()0f x …,得2230x x -++…,解得1x -…或13x-剟,所以当[]01,3x ∈-时,()00f x …,根据几何概型知成立的概率()()311442P --==--. 故选B.8. 解析 由()3233f x x ax bx =++可得()2363f x x ax b '=++.因为()f x 有两个极值点1x ,2x ,所以()0f x '=有两个根1x ,2x ,且[]11,0x ∈-,[]21,2x ∈.又因为()f x '的图像开口向上,所以有()()()()10001020f f f f '-⎧⎪'⎪⎨'⎪⎪'⎩…………,即2102144a b b a b a b -⎧⎪⎪⎨+-⎪⎪+-⎩…………,对应的可行域如图阴影部分所示,所以点(),a b 在平面aOb 上所构成区域的面积111111121121222222S =⨯-⨯⨯-⨯⨯-⨯⨯=.故选D.9. 解析 221i i i 1i i iz --===--,所以z 10. 解析 ()()2,11,1x y +=++=-a b ,所以2111x y +=⎧⎨+=-⎩,解得12x y =-⎧⎨=-⎩,所以3x y +=-.11. 解析 由题意可得3600b a =,所以33360010800b a a =⨯=,所以这辆车的行驶速度/h x ==.12. 解析 曲线1C 和2C 的直角坐标系方程分别为20x y --=和28x y =,联立方程2208x y x y--=⎧⎨=⎩,消去y ,整理得28160x x -+=,解得4x =,所以1C 和2C 的交点只有1个. 13. 解析 由三视图可知该几何体是底面为直角三角形,高为1的倒置的三棱锥,将其放入正方体中如图所示,所以111111326V ⎛⎫=⨯⨯⨯⨯= ⎪⎝⎭.414. 解析 解法一:如图所示,在圆O 上任取一点N ,连接ON ,在OMN △中,由正弦定理得sin sin ON OMOMN ONM =∠∠,即sin sin ON ONM OM ONM OMN∠==∠∠.又因为3π0,4ONM ⎛⎫∠∈ ⎪⎝⎭,所以(]sin 0,1ONM ∠∈,故(OM ∈,即2012x +…,得011x -剟,所以0x 的取值范围是[]1,1-.解法二:过点M 作圆O 的切线,切点为Q ,连接OQ ,如图所示,则)45,90OMQ ⎡∠∈⎣o o,所以sin sin 452OMQ ∠=o…又在Rt OMQ △中,1sin OQ OMQ OM OM ∠==,所以12OM …,即OM …11x -剟,即0x 的取值范围是[]1,1-.1CA。
高中数学新课程精品限时训练(3)

y x 1
14.设
x,
y
满足约束条件:
y
2
,则 z x y 的最大值_______.
2x y 7
15.已知 a (1,1),OA a b,OB a b .若 △OAB 是以 O 为直角顶点的等腰直角三角形,则
△OAB 的面积是_______.
16.椭圆
x2 a2
y2 b2
1a Βιβλιοθήκη S△PAC1 1 2
5
5 2
, S△PBC
1 2 2
5
5,
因此三棱锥的表面积为 S△PAB S△PAC S△ABC S△PBC
5 2
5 2 2
52 52.
故选 C.
9. 解析 依题意,从10 个球中任取一球,已知它不是白球的情形下,
3 则它是黑球的概率为 .故选 D.
5
10. 解析 依题意,当 i 6 时输出 S的值.
A.若 // , m , n ,则 m//n
B.若 m, n , m// , n// ,则 //
C. m, n 是异面直线,若 m// , m// , n// , n// ,则 //
D. 若 // , m// ,则 m//
6.过点 2, 3 的直线 l 与圆 C : x2 y2 4x 3 0 交于 A, B 两点,当弦 AB 取最大值时,直线
F1Q//l
,
所以直线
F1Q
的斜率为
b c
,可得直角顶点
Q
0,
b
,
且 FQO π ,故 b c . 4
所以椭圆的离心率 e c
c
2
.
a b2 c2 2
b
0 的右焦点
高中数学新课程精品限时训练(33)

限时训练(三十三)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{}1,0,1,2,3A =-,2{|30}B x x x =-<,则()A B =R I ð( ).A . {1}-B .{0,1,2}C .{1,2,3}D .{0,1,2,3} (2)已知复数2iia +-(其中a ∈R ,i 为虚数单位)是纯虚数,则i a +的模为( ). A.52B. C. 5D.(3)某产品在某销售点的零售价x (单位:元)与每天的销售量y (单位:个)的统计数据如下表所示( ).由表可得回归直线方程ˆˆˆybx a =+中的ˆ5b =-,根据模型预测零售价为20元时,每天的销售量约为( ). A. 30 B. 29C. 27.5D. 26.5(4)若非零向量,a b ,满足且()2-⊥a b a ,则a 与b 的夹角为( ). A.B. C.D. (5)ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,若ABC △的面积22()S b c a =+-,则sin A =( ).A.517 B. 5C. 817D. 5(6)已知()f x 是定义在R 上的奇函数,且在()0,+∞上是增函数,若12log 3a f ⎛⎫=- ⎪⎝⎭,()4log 5b f =,(c f =,则a ,b ,c 之间的大小关系为( ).A. a b c <<B. a c b <<C. ba c << D. c ab <<(7).中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器﹣商鞅铜方升,其三视图(单位:寸)如图所示,若π取3 ,其体积为12.6(立方寸),则图中x 的为( )俯视图A. 2.5B. 3C. 3.2D. 4(8)将函数()22sin cos f x x x x =-(0)t t >个单位,所得图像对应的函数为奇函数,则t 的最小值为( ).A.B.D. (9)已知双曲线C : 2213y x -=的右顶点为A ,过右焦点F 的直线l 与C 的一条渐近线平行,交另一条渐近线于点B ,则ABF S ∆=( )A.B.4C. 8D. 2(10)斐波拉契数列0,1,1,2,3,5,8,L 是数学史上一个著名的数列,定义如下:()00F =,()11F =,()()()()122,F n F n F n n n =-+-∈N …,某同学设计了—个求解斐波拉契数列前15项和的程序框图,那么在空白矩形框和判断框内应分别填入的语句是( ).A. 14c a i =,…B. 14b c i =,…C. 15c a i =,…D. 15b c i =,…(11)如图所示,已知棱长为4的正方体ABCD A B C D -'''',M 是正方形BB C C ''的中心,P 是A C D ''△内(包括边界)的动点.满足PM PD =,则点P 的轨迹长度是( ).A1AA.2B.2CD (12)已知函数22,0()ln(1),0x x x f x x x ⎧-+=⎨+>⎩…,若a 的取值范围是( ).A.(,0]-∞B.(,1]-∞C.[2,1]-D.[2,0]-(13)若,x y 满足约束条件1020220x y x y x y -+⎧⎪-⎨⎪+-⎩………,则z x y =+的最大值为_____________.(14)若02απ<<,02βπ<<,3sin 35απ⎛⎫-= ⎪⎝⎭,cos 23βπ⎛⎫-= ⎪⎝⎭,则cos 2βα⎛⎫- ⎪⎝⎭的值为 .(15)已知抛物线2:8C y x =,点()0,4P ,点A 在抛物线上,当点A 到抛物线准线l 的距离与点A 到点P 的距离之和最小时,延长AF 交抛物线于点B ,则AOB △的面积为__________.(16)给出下列四个命题:①“若5x y +≠,则2x ≠或3y ≠”是假命题;②已知在ABC △中,“A B <”是“sin sin A B <”成立的充要条件;③若函数()()()()3141log 1a a x a x f x x x ⎧-+<⎪=⎨⎪⎩…,对任意的12x x ≠都有()()2121f x f x x x --<0,则实数a 的取值范围是1,17⎛⎫⎪⎝⎭;④若实数x , []1,1y ∈-,则满足221x y +…的概率为其中正确的命题的序号是__________(请把正确命题的序号填在横线上).限时训练(三十三)答案部分一、选择题二、填空题13.3214. 25 15. 16. ②④解析部分(1)分析 A 集合是具体的整数, B 集合是一元二次不等式,先求解,然后求出集合B 的补集,然后求交集. 解析 对于集合B ,由230x x -<,得230x x ->,解不等式得30x x ><或{|03}B x x =R 剟ð,所以(){}0123A B =R I ,,,ð.故选D.(2)分析 由已知条件利用复数代数形式的除法运算法则,再由纯虚数的概念,求出12a =,由此能求出i a +.再求模.解析 ()()()()()()22i i 212i2i i i i 1a a a a a a a ++-+++==--++是纯虚数,则21020a a -=⎧⎨+≠⎩,解得12a =,所以1i i 2a +=+==.故选B .(3)分析 由统计中回归直线方程的意义,先计算平均数,代入回归方程可求得ˆa,然后可以将20直接代入求解.解析 17.5,39x y == ,所以()39517.51.ˆ265a=--⨯=, 因此520126.526.5y =-⨯+=.故选D.(4)分析 . 解析 由()2-⊥a b a 得()20-⋅=a b a ,()2220-⋅=-⋅=a b a a a b ,即22a ab ⋅=r r r ,故选B.(5)分析 根据题意画出三角形,考虑用正弦定理和余弦定理求解,由于本题条件22()S b c a =+-可以用余弦定理化为2(cos 1)S bc A =+,因此选用1sin 2S bc A =,可进一步解出sin A 的值. 解析 由余弦定理222cos 2b c a A bc+-=,所以2222cos b c a bc A +-=,又因为22222()2S b c a b c a bc =+-=+-+2(cos 1)bc A =+,又由1sin 2S bc A =,12(cos 1)sin 2bc A bc A +=得,1cos 1sin 4A A +=所以,即1cos sin 14A A =-,221sin sin 114A A ⎛⎫+-= ⎪⎝⎭所以,8sin 17A =所以.故选C.(6)分析 根据函数的奇偶性,由于()f x 是定义在R 上的奇函数,且在()0,+∞上是增函数,则在(),0-∞上也是增函数,画出图像,再根据自变量的取值来判断.解析 因为()122log 3log 3a f f ⎛⎫=-= ⎪⎝⎭,()(42log 5log b f f ==,(c f =,所以由题设可得22log log 3<<b a c <<.故选C .(7)分析 根据三视图可得商鞅铜方升由一圆柱和一长方体组合而成.由此画出大致的立体图形来求解.解析 由三视图知,商鞅铜方升由一圆柱和一长方体组合而成,由题意得:()215.4 1.61 1.612.62x ⎛⎫-⋅⋅+π⋅⋅= ⎪⎝⎭,π=3,解得x =3.故选B.(8)分析为奇函数可得t .解析,平移后函数,0k = 时, t .故选D. (9)分析 根据双曲线方程可以求出右顶点F 为和焦点A ,再根据渐近线的特征,可求B 点,从而可要求面积.解析 因为()()2,1,0,2,0c A F ==0y ±=,所以直线l 的方程为)2y x =-,与0y +=联立可得(1,B ;又因为1AF =,所以112ABF S ∆=⨯=.应选答案D. (10)分析 根据算法的程序框图,准确进行循环代入计算解析 依题意知,程序框图中变量S 为累加变量,变量a b c ,,(其中c a b =+)为数列连续三项,在每一次循环中,计算出S 的值后,变量b 的值变为下一个连续三项的第一项a ,即a b =,变量c 的值为下一个连续三项的第二项b ,即b c =,所以矩形框应填入b c =,又程序进行循环体前第一次计算S 的值时已计算出数列的前两项,因此只需要循环12次就完成,所以判断框中应填入14i ….故选B.(11)分析 满足PM PD =的点P 的轨迹是过MD 的中点,且与MD 垂直的平面,根据P 是A C D ''△内(包括边界)的动点,可得点P 的轨迹是两平面的交线ST .T 在中点,S 在4等分点,利用余弦定理,求出ST 即可. 解析 满足PM PD =的点P 的轨迹是过MD 的中点,且与MD 垂直的平面,因为P 是A C D ''△内(包括边界)的动点,所以点P 的轨迹是两平面的交线ST .T 在中点,S 在4等分点时,SD =SM ==满足SD SM =所以SD =TD =,所以ST ==D .A 1A(12)分析 在直角坐标系内作出函数()y f x =的图像与直线y ax =的图像,结合导数的几何意义求解,充分体现图形的作用.解析 在直角坐标系内作出函数()y f x =的图像与直线y ax =的图像,因为当0x …时,2()2y f x x x ==-,22y x '=-,02x y ='=-,即当直线y ax =与2()2y f x x x ==-相切时,2a =-,a的取值范围是[2,0]-.故选D .(13)分析 根据题意在直角坐标系中作出可行域,再根据目标函数来求解. 解析 如图所示可得在11,2A ⎛⎫⎪⎝⎭处取得最大值,即max 13122z =+=.(14)分析 本题的解题关键在于根据已知条件进行拆分和揍角,注意角的范围.据题设条件,观察出角之间的关系,将cos 2βα⎛⎫-⎪⎝⎭表示cos cos 2323ββαα⎡ππ⎤⎛⎫⎛⎫⎛⎫-=-+-= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦43555525⨯+⨯= ,从而将问题进行等价转化,从而使得问题巧妙获解. 解析43cos cos 232355ββαα⎡ππ⎤⎛⎫⎛⎫⎛⎫-=-+-==⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦故填25. (15)分析 由题可知:当点A 到抛物线准线l 的距离与点A 到点P 的距离之和最小时,根据抛物线性质抛物线上一点到准线的距离等于到焦点的距离,所以当P A F 、、三点共线时达到最小值.解析 由0,42,0P F ()、(),可得:240AB l x y +-=,联立抛物线方程可得: 2640x x -+=,设点()()1122,,,A x y B x y ,故126410AB x x p =++=+=,原点到直线:240AB l x y +-=的距离为d ==AOB ∆的面积为11052⨯=,因此填:(16)分析 根据命题进行逐一判断.解析 因为 “若5x y +≠,则2x ≠或3y ≠”的逆否命题“若2x =且3y =,则5x y +=”是真命题,所以①是错误;因为sin sin a b A B A B <⇔<⇔<,所以②正确;若函数()()()()3141log 1a a x a x f x x x ⎧-+<⎪=⎨⎪⎩…,对任意的12x x ≠都有()()21210f x f x x x -<-可得函数为减函数,即310013140a a a a -><<+⎪-⎧⎪⎨⎩…,式可得实数x , []1,1y ∈-,则满足221x y +…的概率为.故答案为②④.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(A) (B) (C) 或 (D)
(4)已知等差数列 中, , ,则 ().
(A) (B) (C) (D)
(5)宋代诗词大师欧阳修的《卖油翁》中有一段关于卖油翁的精湛技艺的细节描写:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.”如果铜钱是直径为 的圆,钱中间的正方形孔的边长为 ,则卖油翁向葫芦内注油,油正好进入孔中的概率是().
(A) (B)
(C) (D)
(6)某一算法框图如图所示,输出的 值为( ).
(A) (B) (C) (D)
(7)将4个不同的小球装入4个不同的盒子,则在至少一个盒子为空的条件下,恰好有两个盒子为空的概率是().
(A) (B) (C) (D)
(8)若 , , 分别是方程 , , 的根,则 , , 的大小关系为().
(9)解析① ,所以 ,故①正确;又因为 ,所以 .又因为 , ,所以 错误.故②错;
.故③错误;对于④由 知 在 上单调递增, 是 的一条对称轴,且在 取最大值,
所以 .故④正确;对于⑤由 ,所以对称中心为 .故⑤错误.故选D.
(10)解析由题知三视图还原为 .正方体棱长为2,所以几何体外球为正方体外接球,所以外接球直径为 .故选D.
(A)2 (B) (C) (D)
(11)设 , 是椭圆 上长轴的两个端点,若椭圆上恒存在一点 ,使得 ,则椭圆离心率的取值范围是().
(A) (B) (C) (D)
(12)已知函数 ,若 ,且 对任意的 恒成立,则 的最大值为().
(A)2 (B) 3 (C) 4 (D) 5
二、填空题:本题共4小题,每小题5分.
(5)解析由题 , .所以 .故选D.
(6)解析由题 , ; , ; , ; , ; , .可知周期为4.又因为 ,所以 .故选D.
(7)解析依题:设至少一个盒子为空的事件为 ,则 .
恰有两个为空的概率为 ,
所以至少一个为空、恰好2个为空的概率为: .故选A.
(8)解析方程 , 的根转化为函数图像交点问题,如图所示,可得方程 的根在 之间,利用零点定理可以验证,如图易知方程 的根在 上,而 的零点为1即 .故选B.
(14)解析由 知 ,两边平方得 .
即 .
(15)解析当 ,即 时, 即 ,即 或 (舍).
当 ,即 时, 即 ,即 .
综合可得
(16)解析
.
即 ,
.
限时训练(三十一)
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)已知集合 , ,则 ().
(A) (B) (C) (D)
(2)已知 ( 为虚数单位),则复数 的共轭复数在复平面内对应的点位于().
(A)第一象限(B)第二象限(C)第三象限(D)第四象限
(12)解析由题 .又因为 , 在 单调递增.又因为 恒过 点,若要 即 在 下方,即当 与 相切时是临界值.设切点为 ,则 ,即 .令 , ,得到 单调递增, , ,所以 ,即 ,又因为 ,所以 .
故选B.
(13)解析画出图如图所示:
通过平移 知,当 过点 时, 取最小值 .
评注本题的关键是求出不等式组表示的可行域,理解代数式是表示直线的意义,然后在进行求解,此类问题先画出不等式组表示的(C) (D)
(9)函数 的部分图像如图所示,其中 , ,给出下列结论:
①最小正周期为 ;② ;③函数 是偶函数;
④ ;⑤ .
其中正确结论的个数是( ).
(A)5(B)4(C)3(D)2
(10)如图是某个几何体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体外接球的直径为().
(11)解析由题可知当 为上顶点或下顶点时 为最大,依题意得 ,可得 ,即 ,若椭圆上恒存在一点 满足 ,则 ,即 ,所以 ,即 .
故选D.
评注求解离心率的方法有:(1)依据公式 ;(2)若 未知,则一般建立一个关于 的方程,通过这个方程以及 与 的关系消掉 ,建立 之间的方程,通过这个方程求出 即可;(3)离心率范围问题其关键就是确立 之间的不等式,再根据 与 的关系消掉 ,建立 之间的不等式,最后确立 关系.
C
A
C
B
D
D
A
D
B
D
C
B
二、填空题
13. 14. 15. 16.
解析部分
(1)解析由题分别求出 , 集合,然后通过数轴求出区间.
, .故选C.
(2)解析 . 坐标为 .故选A.
(3)解析由 得 , ,所以 .故选C.
(4)解析一:由 , , , , , .故选B.
解法二:根据题可得奇数项成等差数列,即 ,故选B.
(13)若 , 满足约束条件 ,则 的最小值为.
(14)已知 ,则 __________________.
(15)设函数 ,则满足 的 取值范围为.
(16)已知数列 , 的前 项和分别为 ,记 ,若 , ,则数列 的前 项和为.
限时训练(三十一)
答案部分
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
