[东北大学]19秋学期《离散数学》在线平时作业1[参考答案]
国家开放大学《离散数学(本)》形考任务1-3参考答案
）。
A.f°g={<a，5>, <b，4>}
B.g° f ={<a，5>, <b，4>}
C.f°g={<5，a >, <4，b >}
D.g° f ={<5，a >, <4，b >}
19.设集合 A={1,2,3}上的函数分别为：f={<1,2>，<2,1>，<3,3>}，g={<1,3>，<2,2>，
（
）个。
A.0
B.2
C.1
D.3
13.设集合 A={1,2,3,4}上的二元关系 R={<1,1>，<2,2>，<2,3>，<4,4>}，S={<1,1>，
<2,2>，<2,3>，<3,2>，<4,4>}，则 S 是 R 的（
）闭包。
A.自反
B.传递
C.对称
D.自反和传递
14.设 A={1,2,3,4,5,6,7,8}，R 是 A 上的整除关系，B={2,4,6}，则集合 B 的最大元、
（
）。
A.自反的
B.对称的
C.传递且对称的
D.反自反且传递的
11.集合 A={1,2,3,4}上的关系 R={<x，y>|x=y 且 x,y∈A}，则 R 的性质为（
A.不是自反的
）。
B.不是对称的
C.传递的
D.反自反
12.如果 R1 和 R2 是 A 上的自反关系，则 R1∪R2，R1∩R2，R1-R2 中自反关系有
离散数学答案版(全)
则称 G1，G2，…，Gn 蕴涵 H，又称 H 是 G1，G2，…，Gn 的逻辑结果，记作（G1 ∧G2∧…∧Gn） H 或（G1，G2，…，Gn） H。 1.6.2 基本蕴涵式 （1）P∧Q P； （3）P P∨Q； （5） P （P→Q） ； （7） （P→Q） P； （9）P，P→Q Q； （11） P，P∨Q Q； （13）P∨Q，P→R，Q→R R； （15）P，Q P∧Q。 （2）P∧Q Q； (4) Q P∨Q； （6）Q （P→Q） ； （8） （P→Q） Q； （10） Q，P→Q P； （12）P→Q，Q→R P→R； （14）P→Q，R→S （P∧R）→（Q∧S） ；
变元，若将 A 和 A*写成 n 元函数形式，则 （1） A（P1，P2，…，Pn） A*（ P1， P2，…， Pn） （2）A（ P1， P2，…， Pn） A*（P1，P2，…，Pn） 定理（对偶原理）设 A、B 是两个命题公式，若 AÛB，则 A* B*，其中 A*、 B*分别为 A、B 的对偶式。 1.5.2 范式 定义 仅由有限个命题变元及其否定构成的析取式称为简单析取式，仅由有 限个命题变元及其否定构成的合取式称为简单合取式。 定义 仅由有限个简单合取式构成的析取式称为析取范式。仅由有限个简单 析取式构成的合取式称为合取范式。 定理（范式存在定理）任何命题公式都存在着与之等价的析取范式和合取范式。 1.5.3 主范式 定义 在含有 n 个命题变元 P1，P2，…，Pn 的简单合取范式中，若每个命
P
Q
PQ
1 0 0 0
0 0 1 1
0 1 0 1
性质： （1）P↓P ﹁（P∨Q） ﹁P； （2） （P↓Q）↓（P↓Q） ﹁（P↓Q） P∨Q； （3） （P↓P）↓（Q↓Q） ﹁P↓﹁Q ﹁（﹁P∨﹁Q） P∧Q。
离散数学大作业答案
一、简要回答下列问题：（每小题3分，共30分）1．请给出集合的结合率。
答：结合律(AUB)UC=AU(BUC)x∈(AUB)UC，即 x∈AUB 或 x∈C即 x∈A 或 x∈B 或 x∈C 即 x∈A 或 x∈B∪C即 x∈AU(BUC)说明 (AUB)UC包含于AU(BUC)同理可证AU(BUC)包含于(AUB)UC所以(AUB)UC=AU(BUC)2．请给出一个集合A，并给出A上既不具有自反性，又不具有反自反性的关系。
3．设A={1，2}，问A上共有多少个不同的对称关系？答：不同的对称关系有：8种R = ΦR = {<1,1>}R = {<2,2>}R = {<1,1>,<2,2>}R = {<1,2>,<2,1>}R = {<1,1>,<1,2>,<2,1>}R = {<1,2>,<2,1>,<2,2>}R = {<1,1>,<1,2>,<2,1>,<2,2>}4．设A={1，2，3，4，5，6}，R是A上的整除关系，M={2,3}，求M的上界，下界。
5．关于P，Q，R请给出使极小项m0，m4为真的解释。
答：m0= ┐p∧┐q∧┐r m4= p∧┐q∧┐r6．什么是图中的简单路？请举一例。
答：图的通路中，所有边e1,e2,…,ek互不相同，称为简单通路。
7．什么是交换群，请举一例。
答：如果群〈G，*〉中的运算*是可以交换的，则称该群为可交换群，或称阿贝尔群。
如〈I，+〉是交换群。
8．什么是群中右模H合同关系？答：设G是群，H是G的子群，a,b∈G，若有h∈H，使得a =bh，则称a合同于b（右模H），记为a≡b（右mod H）。
9．什么是有壹环？请举一例。
答：幺元：如果A中的一个元素e，它既是左幺元又是右幺元，则称e为A中关于运算☆的幺元。
国开形成性考核50501《离散数学(本)》形考任务(1-3)试题及答案
国开形成性考核《离散数学(本)》形考任务(1-3)试题及答案（课程ID：50501，整套相同，如遇顺序不同，Ctrl+F查找，祝同学们取得优异成绩！）形考任务1 集合论部分概念及性质一、单项选择题题目：1、设A={a，b}，B={1，2}，C={4，5}，从A到B的函数f={<a，1>, <b，2>}，从B到C的函数g={<1，5>, <2，4>}，则下列表述正确的是（）。
【A】：f°g ={<5，a >, <4，b >}【B】：g°f ={<a，5>, <b，4>}【C】：f°g ={<a，5>, <b，4>}【D】：g°f ={<5，a >, <4，b >}答案：g°f ={<a，5>, <b，4>}题目：2、设A={1, 2, 3, 4, 5, 6, 7, 8}，R是A上的整除关系，B={2, 4, 6}，则集合B的最大元、最小元、上界、下界依次为（）。
【A】：8、1、6、1【B】：无、2、无、2【C】：8、2、8、2【D】：6、2、6、2答案：无、2、无、2题目：3、设集合A={2, 4, 6, 8}，B={1, 3, 5, 7｝，A到B的关系R={<x, y>| y = x +1｝，则R= （）。
【A】：{<2, 1>, <4, 3>, <6, 5>}【B】：{<2, 1>, <3, 2>, <4, 3>}【C】：{<2, 3>, <4, 5>, <6, 7>}【D】：{<2, 2>, <3, 3>, <4, 6>}答案：{<2, 3>, <4, 5>, <6, 7>}题目：4、设集合A ={1 , 2, 3}上的函数分别为：（）。
离散数学作业标准答案
离散数学作业标准答案离散数学作业⼀、选择题1、下列语句中哪个是真命题（C ）。
A ．我正在说谎。
B ．如果1+2=3，那么雪是⿊⾊的。
C ．如果1+2=5，那么雪是⽩⾊的。
D ．严禁吸烟！2、设命题公式))((r q p p G →∧→=，则G 是（ C ）。
A. 恒假的B. 恒真的C. 可满⾜的D. 析取范式 3、谓词公式),,(),,(z y x yG x z y x F ??→中的变元x （ C ）。
A ．是⾃由变元但不是约束变元 B ．既不是⾃由变元⼜不是约束变元 C ．既是⾃由变元⼜是约束变元 D ．是约束变元但不是⾃由变元4、设A={1，2，3}，则下列关系R 不是等价关系的是（C ）A ．R={<1，1>，<2，2>，<3，3>}B ．R={<1，1>，<2，2>，<3，3>，<2，3>，<3，2>}C ．R={<1，1>，<2，2>，<3，3>，<1，4>}D ．R={<1，1>，<2，2>，<3，3>，<1，2>，<1，3>，<2，3>，<2，1>，<3，1>，<3，2>} 5、设R 为实数集，映射σ=R →R ，σ（x ）= -x 2+2x-1，则σ是（ D ）。
A ．单射⽽⾮满射 B ．满射⽽⾮单射 C ．双射 D ．既不是单射，也不是满射 6、下列⼆元运算在所给的集合上不封闭的是（ D ） A. S={2x-1|x ∈Z +}，S 关于普通的乘法运算 B. S={0，1}，S 关于普通的乘法运算 C. 整数集合Z 和普通的减法运算D. S={x | x=2n ，n ∈Z +}，S 关于普通的加法运算7、*运算如下表所⽰，哪个能使（{a,b}，*）成为含⼳元半群（ D ）b a b b a a b a * b b b a a a b a * a a b a a a b a * a b b b a a b a *A B C D8、下列图中是欧拉图的是（ A ）。
东北大学15秋学期《离散数学》在线作业1 答案
15秋学期《离散数学》在线作业1单选题判断题多选题一、单选题（共 10 道试题，共 50 分。
）1.....-----------------选择：2.单选填空题：设G是有向简单图，其结点度数序列为(2,2,3,3)，入度序列为(0,0,2,3)。
则结点的出度序列为( )。
. (2,2,3,3). (1,1,0,0). (2,2,1,0). (2,2,0,0)-----------------选择：3.令命题P表示“没有大学生不懂外语。
”下面命题( )与P等价。
.有些大学生懂一些外语。
. 所有大学生都懂一些外语。
. 有些大学生懂所有外语。
. 没有大学生懂所有外语。
-----------------选择：4.X,Y 是有限集合，|X|=m，|Y|=n。
若可构成从X到Y的入射的函数，则可构成从X到Y的入射的函数有（）个。
.nm. n!. 2mn. n(n-1)(n-2)…(n-m+1)-----------------选择：5.单选填空题。
E是全集，E={,}，E的幂集P(E)上的并运算?的幺元是（）。
.Φ；. {} ；. {}；. {,}；E. 不存在。
-----------------选择：6.....-----------------选择：7.选择填空。
下面给定的集合中 ( ) 与－相等。
. ＝{1,2,3,4,5,6,7,8,9}，. ＝{2,4,6,8}，. ＝{1,3,5,7,9}，. ＝{3,4,5}，E. E＝Ф，F. F＝{1,4,7,9}，G. G＝{1,7,9}。
-----------------选择：G8.选择填空题。
R是上关系，如果R是反对称的，当且仅当（）。
. 所有中元素x,y，如果有<x,y>∈R ，就没有< y, z >∈R ；.没有中元素x,y，使得有<x,y>∈R ，也有< y, x>∈R ；.所有中元素x,y，如果有<x,y>∈R ，也有< y, x >∈R，则x=y 。
最新电大《离散数学》形考作业任务01-07网考试题及答案-
最新电大《离散数学》形考作业任务01-07网考试题及答案:最新电大《离散数学》形考作业任务01-07网考试题及答案 100%通过考试说明：《离散数学》形考共有7个任务。
任务3、任务5、任务7是主观题，任务2、任务4、任务6是客观题，任务2、任务4、任务6需在考试中多次抽取试卷，直到出现02任务_0001或02任务_0009、04任务_0001或04任务_0009、06任务_0001或06任务_0009试卷，就可以按照该套试卷答案答题。
做考题时，利用本文档中的查找工具，把考题中的关键字输到查找工具的查找内容框内，就可迅速查找到该题答案。
本文库还有其他教学考一体化答案，敬请查看。
01任务一、单项选择题（共 8 道试题，共 80 分。
）1. 本课程的教学内容分为三个单元，其中第三单元的名称是（）． A. 数理逻辑 B. 集合论 C. 图论 D. 谓词逻辑 2. 本课程的教学内容按知识点将各种学习资源和学习环节进行了有机组合，其中第2章关系与函数中的第3个知识点的名称是（）． A. 函数 B. 关系的概念及其运算 C. 关系的性质与闭包运算 D. 几个重要关系 3. 本课程所有教学内容的电视视频讲解集中在VOD点播版块中，VOD点播版块中共有（）讲． A. 18 B. 20 C. 19 D. 17 4. 本课程安排了7次形成性考核作业，第3次形成性考核作业的名称是（）． A. 集合恒等式与等价关系的判定 B. 图论部分书面作业 C. 集合论部分书面作业 D. 网上学习问答 5. 课程学习平台左侧第1个版块名称是：（）． A. 课程导学 B. 课程公告 C. 课程信息 D. 使用帮助 6. 课程学习平台右侧第5个版块名称是：（）． A. 典型例题 B. 视频课堂 C. VOD点播 D. 常见问题7. “教学活动资料”版块是课程学习平台右侧的第（）个版块． A. 6 B. 7 C. 8 D. 9 8. 课程学习平台中“课程复习”版块下，放有本课程历年考试试卷的栏目名称是：（）． A. 复习指导 B. 视频 C. 课件 D. 自测二、作品题（共 1 道试题，共 20 分。
离散数学习题集(十五套含答案)
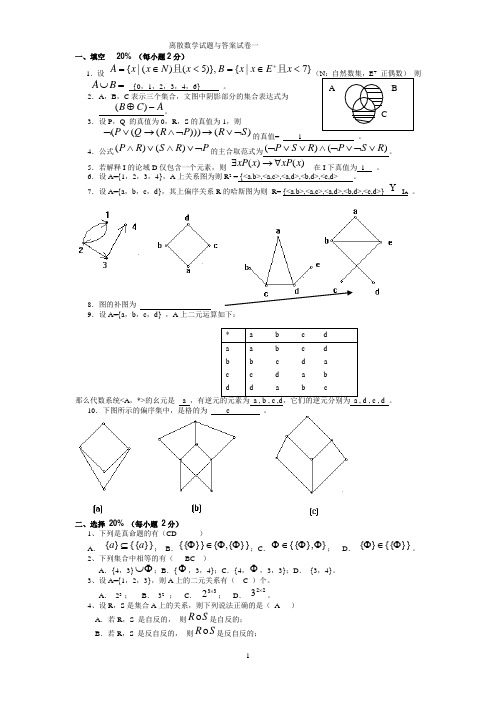
离散数学试题与答案试卷一一、填空20% （每小题2分）1．设}7|{)},5()(|{<∈=<∈=+xExxBxNxxA且且（+=⋃BA{0，1，2，3，4，6} 。
2．A，B，C表示三个集合，文图中阴影部分的集合表达式为。
3R，S的真值为1，则)()))(((SRPRQP⌝∨→⌝∧→∨⌝的真值= 1 。
4．公式PRSRP⌝∨∧∨∧)()(的主合取范式为)()(RSPRSP∨⌝∨⌝∧∨∨⌝。
5．若解释I的论域D仅包含一个元素，则)()(xxPxxP∀→∃在I下真值为1 。
6．设A={1，2，3，4}，A上关系图为则R2 = {<a.b>,<a,c>,<a,d>,<b,d>,<c,d> 。
7．设A={a，b，c，d}，其上偏序关系R的哈斯图为则R= {<a.b>,<a,c>,<a,d>,<b,d>,<c,d>} I A。
8．图的补图为9．设A={a，b，c，d} ，A上二元运算如下：那么代数系统<A，*>的幺元是 a ，有逆元的元素为a , b , c ,d，它们的逆元分别为 a , d , c , d 。
10．下图所示的偏序集中，是格的为 c 。
二、选择20% （每小题2分）1、下列是真命题的有（CD）A．}}{{}{aa⊆；B．}}{,{}}{{ΦΦ∈Φ；C．}},{{ΦΦ∈Φ；D．}}{{}{Φ∈Φ。
2、下列集合中相等的有（BC ）A．{4，3}Φ⋃；B．{Φ，3，4}；C．{4，Φ，3，3}；D．{3，4}。
3、设A={1，2，3}，则A上的二元关系有（ C ）个。
A．23 ；B．32 ；C．332⨯；D．223⨯。
4、设R，S是集合A上的关系，则下列说法正确的是（A ）A．若R，S 是自反的，则SR 是自反的；B．若R，S 是反自反的，则SR 是反自反的；C ．若R ，S 是对称的， 则S R是对称的；D ．若R ，S 是传递的， 则S R 是传递的。
东北大学智慧树知到“计算机科学与技术”《离散数学X》网课测试题答案卷5
长风破浪会有时，直挂云帆济沧海。
住在富人区的她东北大学智慧树知到“计算机科学与技术”《离散数学X》网课测试题答案（图片大小可自由调整）第1卷一.综合考核(共10题)1.设A={a，{a}，{a，b}，{{a，b}，c}}，则{a}∈A。
判断该命题的真值。
()A.正确B.错误2.命题公式 (P ® Q) ®Q 的主合取范式是()。
A.P∨QB.P∨ØQC.(P∨Q )∧(Ø P∨ØQ )D.(ØP∨Q)∧(P∨ØQ )3.判断下面的说法是否正确。
R和S都是A上任何传递关系，则R∩S也传递。
()A.正确B.错误4.下面是"xC(x)， $x(A(x)ÚB(x))， "x(B(x)®ØC(x)) Þ$xA(x)的谓词推理过程。
在这个过程中每一步中的()处是此步所用的推理规则。
请写出这些推理规则。
⑴$x(A(x)ÚB(x))， ()⑵A(a)ÚB(a) ()⑴⑶"xC(x) ()⑷C(a) ()⑶⑸"x(B(x)→ØC(x)) ()⑹B(a)→ØC(a) ()⑸⑺ØB(a) ()⑷⑹I12⑻A(a) ()⑵⑺I10⑼$xA(x)) ()⑻A.⑴P；⑵US；⑶T；⑷UG；⑸P；⑹UG；⑺P；⑻T；⑼UG。
B.⑴P；⑵T；⑶T；⑷UG；⑸P；⑹US；⑺P；⑻T；⑼ES。
C.⑴P；⑵ES；⑶P；⑷US；⑸P；⑹US；⑺T；⑻T；⑼EG。
D.⑴P；⑵EG；⑶T；⑷UG；⑸P；⑹UG；⑺P；⑻T；⑼EG。
5.不是谓词公式的前束范式为()。
A.B.C.D.6.令P(E)是全集E的幂集；Ç是集合的交运算；È是集合的并运算；Å是集合的对称差运算。
下面所列代数系统哪些是独异点?()A.B.C.7.给定集合A={1，2，3}，定义A上的等价关系如下：T=A×A(完全关系(全域关系))，等价关系T中含有等价类()。
(完整word版)离散数学课后答案(word文档良心出品)
离散数学课后答案习题一6.将下列命题符号化。
（1）小丽只能从框里那一个苹果或一个梨.（2）这学期，刘晓月只能选学英语或日语中的一门外语课.答：（1）（p Λ¬q ）ν（¬pΛq）其中p:小丽拿一个苹果，q:小丽拿一个梨（2）（p Λ¬q ）ν（¬pΛq）其中p:刘晓月选学英语，q:刘晓月选学日语14.将下列命题符号化.(1) 刘晓月跑得快, 跳得高.(2)老王是山东人或河北人.(3)因为天气冷, 所以我穿了羽绒服.(4)王欢与李乐组成一个小组.(5)李辛与李末是兄弟.(6)王强与刘威都学过法语.(7)他一面吃饭, 一面听音乐.(8)如果天下大雨, 他就乘班车上班.(9)只有天下大雨, 他才乘班车上班.(10)除非天下大雨, 他才乘班车上班.(11)下雪路滑, 他迟到了.(12)2与4都是素数, 这是不对的.(13)“2或4是素数, 这是不对的”是不对的.答：(1)p∧q, 其中, p: 刘晓月跑得快, q: 刘晓月跳得高.(2)p∨q, 其中, p: 老王是山东人, q: 老王是河北人.(3)p→q, 其中, p: 天气冷, q: 我穿了羽绒服.(4)p, 其中, p: 王欢与李乐组成一个小组, 是简单命题.(5)p, 其中, p: 李辛与李末是兄弟.(6)p∧q, 其中, p: 王强学过法语, q: 刘威学过法语.(7)p∧q, 其中, p: 他吃饭, q: 他听音乐.(8)p→q, 其中, p: 天下大雨, q: 他乘班车上班.(9)p→q, 其中, p: 他乘班车上班, q: 天下大雨.(10)p→q, 其中, p: 他乘班车上班, q: 天下大雨.(11)p→q, 其中, p: 下雪路滑, q: 他迟到了.(12) ¬ (p∧q)或¬p∨¬q, 其中, p: 2是素数, q: 4是素数.(13) ¬ ¬ (p∨q)或p∨q, 其中, p: 2是素数, q: 4是素数.16.19.用真值表判断下列公式的类型:(1)p→ (p∨q∨r) (2)(p→¬q) →¬q(3) ¬ (q→r) ∧r(4)(p→q) →(¬q→¬p)(5)(p∧r) ↔( ¬p∧¬q)(6)((p→q) ∧ (q→r)) → (p→r)(7)(p→q) ↔ (r↔s)答：(1), (4), (6)为重言式.(3)为矛盾式.(2), (5), (7)为可满足式习题二9.用真值表求下面公式的主析取范式.(1) (pνq)ν(¬pΛr)(2) (p→q) →(¬p↔q)答：(1)(2)p q (p → q) →(¬p ↔ q)0 0 1 0 0 10 1 1 1 1 01 0 0 1 1 11 1 1 0 0 0从真值表可见成真赋值为01, 10.于是(p → q) →(¬p ↔ q) ⇔ m1 ∨ m211.用真值表求下面公式的主析取范式和主合取范式；(1) (pνq)Λr(2) p→(pνqνr)(3) ¬(q→¬p)Λ¬p15.用主析取范式判断下列公式是否等值:(1) (p→q) →r与q→ (p→r)(2) ¬(pΛq)与(¬pνq)答：(1)(p→q) →r ⇔¬(¬p∨q) ∨ r ⇔¬(¬p∨q) ∨ r ⇔ p¬∧q ∨ r ⇔p¬∧q∧(r¬∨r) ∨(p¬∨p) ∧(q¬∨q)∧r ⇔p¬∧q∧r ∨p¬∧q∧¬r ∨ p ∧q∧r ∨ p∧¬q∧r ∨¬p∧q∧r ∨¬p∧¬q∧r = m101 ∨ m100 ∨ m111 ∨m101 ∨ m011 ∨ m001 ⇔m1 ∨ m3 ∨ m4 ∨ m5 ∨ m7 = ∑(1, 3, 4, 5, 7).而 q→(p→r) ⇔¬q ∨(¬p∨r) ⇔¬q ∨¬p ∨r ⇔(¬p∨p)¬∧q∧(¬r∨r) ∨¬p∧(¬q∨q)∧(¬r∨r) ∨(¬p∨p)∧(¬q∨q)∧r ⇔(¬p¬∧q∧¬r)∨(¬p¬∧q∧r)∨(p¬∧q∧¬r)∨(p¬∧q∧r) ∨(¬p∧¬q∧¬r)∨(¬p∧¬q∧r)∨(¬p ∧q∧¬r)∨(¬p∧q∧r) ∨(¬p∧¬q∧r)∨(¬p∧q∧r)∨(p∧¬q∧r)∨(p∧q∧r) = m0 ∨ m1 ∨ m4 ∨ m5 ∨ m0 ∨ m1 ∨ m2 ∨ m3 ∨ m1 ∨ m3 ∨ m5 ∨m7 ⇔ m0 ∨ m1 ∨ m2 ∨ m3 ∨ m4 ∨ m5 ∨ m7 ⇔∑(0, 1, 2, 3, 4, 5, 7). 两个公式的主吸取范式不同, 所以(p→q) →rk q→ (p→r).16. 用主析取范式判断下列公式是否等值:(1)(p→q) →r与q→ (p→r)(2) ¬ (p∧q)与¬ (p∨q)答：(1)(p→q) →r) ⇔m1∨m3∨m4∨m5∨m7q→ (p→r) ⇔m0∨m1∨m2∨m3∨m4∨m5∨m7所以(p→q) →r) k q→ (p→r)(2)¬ (p∧q) ⇔m0∨m1∨m2¬ (p∨q) ⇔m0所以¬ (p∧q) k ¬ (p∨q)习题三15.在自然推理系统P中用附加前提法证明下面各推理:(1)前提: p→ (q→r), s→p, q 结论: s→r(2)前提: (p∨q) → (r∧s), (s∨t) →u 结论: p→u答：(1)证明: ① s 附加前提引入② s→p 前提引入③ p ①②假言推理④ p→(q→r) 前提引入⑤ q→r ③④假言推理⑥ q 前提引入⑦ r ⑤⑥假言推理(2)证明: ① P 附加前提引入② p∨q ①附加③ (p∨q) → (r∧s) 前提引入④ r∧s ②③假言推理⑤④化简⑥ s∨t ⑤附加⑦ (s∨t) →u 前提引入⑧ u ⑥⑦假言推理16.在自然推理系统P中用归谬法证明下面推理:(1)前提: p→¬q, ¬r∨q, r∧¬s 结论: ¬p(2)前提: p∨q, p→r, q→s 结论: r∨s答：(1)证明: ① P 结论否定引入② p→¬q 前提引入③¬q ①②假言推理④¬r∨q 前提引入⑤¬r ③④析取三段论⑥ r∧¬s 前提引入⑦ r ⑥化简⑧¬r∧r ⑤⑦合取⑧ 为矛盾式, 由归谬法可知, 推理正确.(2)证明: ①¬ (r∨s) 结论否定引入② p∨q 前提引入③ p→r 前提引入④ q→s 前提引入⑤ r∨s ②③④构造性二难⑥¬ (r∨s) ∧ (r∨s) ①⑤合取⑥为矛盾式, 所以推理正确.18.在自然推理系统P中构造下面推理的证明.(1)如果今天是星期六, 我们就要到颐和园或圆明园去玩. 如果颐和园游人太多, 我们就不去颐和园玩. 今天是星期六. 颐和园游人太多. 所以我们去圆明园玩.(2)如果小王是理科学生, 他的数学成绩一定很好. 如果小王不是文科生, 他必是理科生. 小王的数学成绩不好. 所以小王是文科学生.(1)令 p: 今天是星期六;q: 我们要到颐和园玩;r: 我们要到圆明园玩;s:颐和园游人太多.前提: p→ (q∨r), s →¬q, p, s. 结论: r.证明① p 前提引入② p→q∨r前提引入③q∨r①②假言推理④s前提引入⑤ s →¬q前提引入⑥¬q ④⑤假言推理⑦ r ③⑥析取三段论r ¬q s →¬q sq∨r p→q∨r p(2)令p: 小王是理科生,q: 小王是文科生,r: 小王的数学成绩很好.前提: p→r, ¬q→p, ¬r 结论: q证明：① p→r 前提引入②¬r 前提引入③¬p ①②拒取式④¬q→p 前提引入⑤ q ③④拒取式习题四在一阶逻辑中将下列命题符号化:(1)没有不能表示成分数的有理数.(2)在北京卖菜的人不全是外地人.(3)乌鸦都是黑色的.(4)有的人天天锻炼身体. 没指定个体域, 因而使用全总个体域.答：(1) ¬∃x(F(x) ∧¬G(x))或∀x(F(x) →G(x)), 其中, F(x): x为有理数, G(x): x能表示成分数.(2) ¬∀x(F(x) →G(x))或∃x(F(x) ∧¬G(x)), 其中, F(x): x在北京卖菜,G(x): x是外地人.(3) ∀x(F(x) →G(x)), 其中, F(x): x是乌鸦, G(x): x是黑色的.(4) ∃x(F(x) ∧G(x)), 其中, F(x): x是人, G(x): x天天锻炼身体.5. 在一阶逻辑中将下列命题符号化:(1)火车都比轮船快.(2)有的火车比有的汽车快.(3)不存在比所有火车都快的汽车.(4)“凡是汽车就比火车慢”是不对的.答：因为没指明个体域, 因而使用全总个体域(1) ∀x∀y(F(x) ∧G(y) →H(x,y)), 其中, F(x): x是火车, G(y): y是轮船, H(x,y):x比y快.(2) ∃x∃y(F(x) ∧G(y) ∧H(x,y)), 其中, F(x): x是火车, G(y): y是汽车, H(x,y):x比y快.(3) ¬∃x(F(x) ∧∀y(G(y) →H(x,y))) 或∀x(F(x) →∃y(G(y) ∧¬H(x,y))), 其中, F(x): x是汽车, G(y): y是火车, H(x,y):x比y快.(4) ¬∀x∀y(F(x) ∧G(y) →H(x,y)) 或∃x∃y(F(x) ∧G(y) ∧¬H(x,y) ), 其中, F(x): x是汽车, G(y): y是火车, H(x,y):x比y慢.9.给定解释I如下:(a)个体域DI为实数集合\.(b)DI中特定元素⎯a =0.(c)特定函数⎯f (x,y)=x−y, x,y∈DI.(d)特定谓词⎯F(x,y): x=y,⎯G(x,y): x<y, x,y∈DI.说明下列公式在I下的含义, 并指出各公式的真值:(1) ∀x∀y(G(x,y) →¬F(x,y))(2) ∀x∀y(F(f(x,y),a) →G(x,y))(3) ∀x∀y(G(x,y) →¬F(f(x,y),a))(4) ∀x∀y(G(f(x,y),a) →F(x,y))答：(1) ∀x∀y(x<y→x≠y), 真值为1.(2) ∀x∀y((x−y=0) →x<y), 真值为0.(3) ∀x∀y((x<y) → (x−y≠0)), 真值为1.(4) ∀x∀y((x−y<0) → (x=y)), 真值为0.习题五5.给定解释I如下:(a) 个体域D={3,4}.(b)⎯f (x)为⎯f (3)=4,⎯f (4)=3.(c)⎯F(x,y)为⎯F(3,3)=⎯F(4,4)=0,⎯F(3,4)=⎯F(4,3)=1.试求下列公式在I下的真值:(1) ∀x∃yF(x,y)(2) ∃x∀yF(x,y)(3) ∀x∀y(F(x,y) →F(f(x),f(y)))答：(1) ∀x∃yF(x,y)⇔(F(3,3)∨F(3,4))∧(F(4,3)∨F(4,4))⇔(0∨1)∧(1∨0) ⇔1(2)∃x∀yF(x,y)⇔(F(3,3)∧F(3,4))∨(F(4,3)∧F(4,4))⇔(0∧1)∨(1∧0)⇔0(3)∀x∀y(F(x,y)→F(f(x),f(y)))⇔(F(3,3)→F(f(3),f(3)))∧(F(4,3)→F(f(4),f(3)))∧(F(3,4)→F(f(3),f(4)))∧(F(4,4)→F(f(4),f(4))) ⇔ (0→0)∧(1→1)∧(1→1)∧(0→0)⇔112.求下列各式的前束范式.(1) ∀xF(x) →∀yG(x, y);(3) ∀xF(x, y) ↔∃xG(x, y);答：前束范式不是唯一的.(1) ∀xF(x) →∀yG(x, y) ⇔∃x(F(x) →∀yG(x, y))⇔∃x∀y(F(x) → G(x, y)).(3) ∀xF(x, y) ↔∃xG(x, y) ⇔ (∀xF(x, y) →∃xG(x, y)) ∧ (∃xG(x, y) →∀xF(x, y)) ⇔ (∀x1F(x1, y) →∃x2G(x2, y)) ∧ (∃x3G(x3, y) →∀x4F(x4, y)) ⇔∃x1∃x2(F(x1, y) → G(x2, y)) ∧∀x3∀x4(G(x3, y) → F(x4, y)) ⇔∃x1∃x2∀x3∀x4((F(x1, y) → G(x2, y)) ∧ (G(x3, y) → F(x4, y))).13.将下列命题符号化, 要求符号化的公式全为前束范式:(1) 有的汽车比有的火车跑得快.(2) 有的火车比所有的汽车跑得快.(3) 说所有的火车比所有的汽车跑得快是不对的.(4) 说有的飞机比有的汽车慢是不对的.答：(1)令F(x):x是汽车,G(y):y是火车,H(x,y):x比y跑得快.∃x(F(x)∧∃y(G(y)∧H(x,y))⇔∃x∃y(F(x)∧G(y)∧H(x, y)).(2)令F(x):x是火车, G( y): y 是汽车,H(x,y):x比y跑得快.∃x(F(x)∧∀y(G(y)→ H(x,y)))⇔∃x∀y(F(x)∧(G y)→H(x,y))).;错误的答案:∃x∀y(F(x)∧G(y)→H(x,y)).(3)令F(x):x是火车,G(y):y是汽车,H(x,y):x比y跑得快.¬∀x(F(x)→∀y(G(y)→H(x,y)))⇔¬∀x∀y(F(x)→(G(y)→H(x,y)))⇔¬∀x∀y(F(x)∧G(y)→H(x,y))(不是前束范式)⇔∃x∃y(F(x)∧G(y)∧H(x,y)).(4)令F(x):x是飞机,G(y):y是汽车,H(x,y):x比y跑得慢.¬∃x(F(x)∧∃y(G(y)∧H(x,y)))⇔¬∃x∃y(F(x)∧G(y)∧H(x,y))(不是前束范式)⇔∀x∀y¬(F(x)∧G(y)∧H(x,y))⇔∀x∀y(F(x)∧G(y)→¬H(x,y)).21.24.在自然推理系统F中, 构造下面推理的证明:每个喜欢步行的人都不喜欢骑自行车. 每个人或者喜欢骑自行车或者喜欢乘汽车. 有的人不喜欢乘汽车, 所以有的人不喜欢步行. (个体域为人类集合) 答：令 F(x): x 喜欢步行, G( x): x喜欢骑自行车, H(x): x 喜欢乘汽车.前提:∀x(F(x)→¬G(x)), ∀x(G(x)∨H(y)),∃x¬H(x).结论:∃x¬F(x).② ∀x(G(x) ∨ H(y)) 前提引入② G(c) ∨ H(c) ①UI③∃x¬H(x) 前提引入④¬H(c) ③UI⑤ G(c) ②④析取三段⑥∀x(F(x) →¬G(x)) 前提引入⑦ F(c) →¬G(c) ⑥UI⑧¬F(c) ⑤⑦拒取⑨∃x¬F(x) ⑧EG习题七12.设A={0, 1, 2, 3}, R是A上的关系, 且R={〈0, 0〉, 〈0, 3〉, 〈2, 0〉, 〈2,1〉, 〈2, 3〉, 〈3, 2〉} 给出R的关系矩阵和关系图.16.设A={a,b,c,d}, R1,R2为A上的关系, 其中R1={〈a,a〉,〈a,b〉,〈b,d〉}R2={〈a,d〉,〈b,c〉,〈b,d〉,〈c,b〉} 求R1·R2, R2·R1,R1²,R2³. R1·R2={〈a,a〉,〈a,c〉,〈a,d〉},R2·R1={〈c,d〉}, R1²={〈a,a〉,〈a,b〉,〈a,d〉},R2³={〈b,c〉,〈b,d〉,〈c,b〉}20.设R1和R2为A上的关系,证明: (1)(R1∪R2) −1=R1−1∪R2−1(2)(R1∩R2) −1=R1−1∩R2−1答：(1)(R1∪R2)−1=R1−1∪R2−1任取〈x,y〉〈x,y〉(∈R1∪R2)−1⇔〈y,x〉(∈R1∪R2)⇔〈y,x〉∈R1∨ (y,x)∈R2)⇔〈x,y〉∈R1−1∨〈x,y〉∈R2−1⇔〈x,y〉∈R1−1∨R2−1所以(R1∪R2) −1=R1−1∪R2−1(2)(R1∩R2) −1=R1−1∩R2−1 任取〈x,y〉〈x,y〉(∈R1∩R2) −1⇔〈y,x〉(∈R1∩R2)⇔〈y,x〉∈R1∧ (y,x)∈R2)⇔〈x,y〉∈R1−1∧〈x,y〉∈R2−1⇔〈x,y〉∈R1−1∧R2−1所以(R1∪R2) −1=R1−1∩R2−126.33.43.16.47.。
东北大学2021年秋学期《离散数学》在线作业
东北大学2021年秋学期《离散数学》在线作业东北大学17秋学期《离散数学》在线作业2东大100分 1/d 2/d 3/d一、单选题（共 10 道试题，共 50 分。
）1. 下面的命题公式中不是永真式的是（）。
A. (P∧Q)→Q B.(P∧(P→Q))→Q C. P→(P∨Q) D. (P∨Q)→P 正确答案：D2. 一个有向图是根树，当且仅当该图（ A. 有树根，也有树叶；B. 忽略边的方向时，是连通无回路的无向图；C. 有一个结点可以到达任何其余结点；D. 恰有一个结点入度为0：其余结点入度为1。
正确答案：D3. 一棵树有7片树叶，3个3度结点，其余都是4度结点，该树有（ A. 4； B. 3； C. 2； D. 1；E. 不在给定的选择的范围内。
正确答案：D14度结点。
）个东北大学17秋学期《离散数学》在线作业24. 下面是\的谓词推理过程。
在这个过程中每一步中的（）处是此步所用的推理规则。
请写出这些推理规则。
⑴ $x(A(x)úB(x)), ( ) ⑵ A(a)úB(a) ( ) ⑴ ⑶ \ ⑷ C(a) ( ) ⑶ ⑸ \ ⑹ B(a)→?C(a)( ) ⑸ ⑺ ?B(a) ( ) ⑷ ⑹ I12 ⑻ A(a)( ) ⑵ ⑺ I10 ⑼ $xA(x)) ( ) ⑻A. ⑴ P；⑵ T；⑶ T；⑷ UG；⑸ P；⑹ US；⑺ P；⑻ T；⑼ ES。
B. ⑴ P；⑵ EG；⑶ T；⑷ UG；⑸ P；⑹ UG；⑺ P；⑻ T；⑼ EG。
C. ⑴ P；⑵ ES；⑶ P；⑷ US；⑸ P；⑹ US；⑺ T；⑻ T；⑼ EG。
D. ⑴ P；⑵ US；⑶ T；⑷ UG；⑸ P；⑹ UG；⑺ P；⑻ T；⑼ UG。
正确答案：C 5.A. B:①：⑵⑶⑺⑻B. B:②：⑶⑷⑻C. B:③：⑶⑹⑺⑻D. B:④：⑶⑺ 正确答案：D 6.给定集合A={1,2,3},定义A上的关系如下：2东北大学17秋学期《离散数学》在线作业2R={<1,1>,<1,2>,<1,3>,<2,2><3,3>} S={<1,1>,<1,2>,<2,1>,<2,2>,<3,3>}T={<1,1>,<1,3>,<2,1>,<2,2>,<2,3>,<3,3>} M=Ф(空关系) N=A×A(完全关系（全域关系）) 上述关系中，是偏序关系的有( )。
东大18秋学期《离散数学》在线作业1答案
B正确
正确答案是：B
5、
判断题，判断下面说法是否正确。
“对于整数集合I上的减法运算“－”来说， 0是幺元。”
A错误
B正确
正确答案是：A
三、多选题共5题，25分
1、
AA：⑴⑵⑶
BB：⑴⑵⑷
CC：⑵⑶⑷
DD：⑴⑵⑶⑷
正确答案是：AD
2、
多选题。下面哪些序列可能是汉米尔顿图的结点度数序列
A (1,2,3,4,5)
C无法确定
D不知道
正确答案是：B
7、
单选题。一棵根树是m叉树，当且仅当 该图（ ）。
A每个结点的度数是m；
B 每个结点的出度都是m；
C每个结点的出度小于或等于m；
D恰有一个结点入度为0：其余结点入度为1。
正确答案是：C
8、
单选填空题。E是全集，E={a,b}，E的幂集P(E)上的交运算Ç，的零元是
（）。
3、
单选题。结点是树的叶结点，当且仅当该结点（ ）。
A度数不为0；
B度数大于1；
C度是等于1。
正确答案是：C
4、
A等价
B不等价
C无法确定
D不知道
正确答案是：A
5、
单选题。有n个结点的无向完全图有( )条边。
A2n；
B (n(n-1))÷2；
Cn(；
D n2。
正确答案是：B
6、
A矛盾式
B重言式
AΦ；
B{a} ；
C {b}；
D {a,b}；
E不存在。
正确答案是：A
9、
单选题。一棵根树是完全m叉树，当且仅当 该图（ ）。
A每个结点的度数是m；
B每个结点的出度都是m；
离散数学第一章作业答案
第一章作业答案3. 将下列命题符号化：(2) 我去新华书店，仅当我有时间。
(4) 除非天不下雨，我将去新华书店。
(6)“2或4是素数，这是不对的”是不对的。
(8) 只要努力学习，成绩就会好的。
(10) 小张是山东人或河北人。
解(2) 符号化为Q→R，其中，R：我有时间，Q：我去新华书店。
除非的含义：①只有。
表示唯一的条件，常与“才，否则，不然”搭配：若要人不知，除非己莫为。
②除了。
表示不计算在内：除非临时有事，我一定去。
(4) 符号化为P→Q，其中，P：天下雨，Q：我去新华书店。
(6) 符号化为⌝(⌝(P∨Q))，“2或4是素数，这是不对的”是不对的，其中，P：2是素数，Q：4是素数。
(8) 符号化为P→Q，其中，P：努力学习，Q：成绩就会好的。
(10) 符号化为(⌝P∧Q)∨(P∧⌝Q)，其中，P：小张是山东人，Q：小张是河北人。
4. 构造下列命题公式的真值表，并据此说明哪些是其成真赋值，哪些是其成假赋值？(1) ⌝(P∨⌝Q)。
(2) P∧(Q∨R)。
(3) ⌝(P∨Q)↔(⌝P∧⌝Q)。
(4) ⌝P→(Q→P)。
解(1)由真值表可知，公式⌝(P∨⌝Q)的成真赋值为：FT，成假赋值为FF、TF、TT。
(2)由真值表可知，公式P∧(Q∨R)的成真赋值为：TFT、TTF、TTT，成假赋值为FFF、FFT、FTF、FTT、TFF。
(3)由真值表可知，公式⌝(P ∨Q)↔(⌝P ∧⌝Q)的成真赋值为：FF 、FT 、TF 、TT ，没有成假赋值。
(4)由真值表可知，公式⌝P →(Q →P)的成真赋值为：FF 、TF 、TT ，成假赋值为：FT 。
5. 分别用真值表法和公式法判断下列命题公式的类型：(2) (P∧Q)→(P∨Q)。
(4) (P∧Q→R)→(P∧⌝R∧Q)。
(6) (⌝P↔Q)↔⌝(P↔Q)。
解(2) 真值表法：由真值表可知，公式(P∧Q)→(P∨Q)为重言式。
公式法：因为(P∧Q)→(P∨Q) ⇔⌝(P∧Q)∨(P∨Q) ⇔⌝P∨⌝Q∨P∨Q ⇔ T，所以，公式(P∧Q)→(P∨Q)为重言式。
东大20秋学期《离散数学X》在线平时作业2【标准答案】
东大20秋学期《离散数学X》在线平时作业2【标准答案】A.所有有理数都是整数。
B.存在一个自然数n，使得n+1>n。
C.对于任意实数x，都有x+0=x。
D.所有图形都具有对称性。
答案: B为假，其他为真。
19.判断题。
对于任意两个自然数a和b，一定存在两个整数q和r，满足a=bq+r且0≤r<b。
答案:正确20.判断题。
对于一个有限集合A和它的子集B，B的补集一定是A的子集。
答案:正确离散数学X在线平时作业2试卷一、单选题（共10道试题，共40分）1.X,Y是有限集合，|X|=m，|Y|=n。
可以构成多少个从X 到Y的函数？A。
mnB。
mnC。
2mnD。
nm答案：D2.设集合S={Ф,{1},{1,2}}，下面给定的四个选择答案中哪个是S的子集？A。
Ф；B。
{1}；C。
{2}；D。
{1,2}。
答案：A3.如果两个关系是等价关系，则它们是什么关系？A。
等价关系B。
不等价关系C。
无法确定D。
不知道答案：A4.在无向图中，度数是奇数的结点有多少个？A。
奇数；B。
非负整数C。
偶数。
答案：C5.有n个结点的无向完全图有多少条边？A。
2n；B。
(n(n-1))/2；C。
n(n-1)；D。
n2.答案：B6.如果一个命题公式在所有情况下都为真，则它是什么？A。
矛盾式B。
重言式C。
无法确定D。
不知道答案：B7.在集合A上给定了两个二元关系R和S，下列哪个选项是R和S的交集？A.B.C.D.答案：D8.一个有向图中，每个结点的入度都等于出度，则这个有向图是什么？A。
有向树B。
有向图C。
有向___图D。
无向图答案：C9.在一个n元集合上，有多少个二元关系？A。
nB。
2nC。
n^2D。
2^n答案：2^(n^2)10.在下列选项中，哪个选项列出了4个逻辑运算符号？A。
⑷⑸⑺⑻B。
⑴⑵⑷⑹C。
⑴⑷⑸⑹D。
⑴⑷⑸⑺答案：C二、多选题（共5道试题，共20分）11.下面哪些代数系统是独异点？A。
B。
C。
D。
E。
答案：ABCDE12.下面的命题公式中哪些是永真式？A。
(完整版)《离散数学》试题及答案解析,推荐文档
4. 设 I 是如下一个解释：D = {2, 3},
a
b
f (2) f (3)
3
2
3
2
试求 (1) P(a, f (a))∧P(b, f (b));
WORD 整理版
一、填空题 1 设集合 A,B，其中 A＝{1,2,3}, B= {1,2}, 则 A - B＝____________________;
(A)
- (B)＝ __________________________ . 2. 设有限集合 A, |A| = n, 则 |(A×A)| = __________________________. 3. 设集合 A = {a, b}, B = {1, 2}, 则从 A 到 B 的所有映射是 __________________________ _____________, 其中双射的是
专业资料学习参考
WORD 整理版
0 1 1 1 1
15. 设图 G 的相邻矩阵为 1 0 1 0 0 ，则 G 的顶点数与边数分别为(
).
1 1 0 1 1
1 0 1 0 1
1 0 1 1 0
(A)4, 5 (B)5, 6 三、计算证明题
(C)4, 10
(D)5, 8.
1.设集合 A＝{1, 2, 3, 4, 6, 8, 9, 12}，R 为整除关系。
则在解释 I 下取真值为 1 的公式是( ).
(A)xyP(x,y) (B)xyP(x,y) (C)xP(x,x) (D)xyP(x,y). 6. 若供选择答案中的数值表示一个简单图中各个顶点的度，能画出图的是( ).
东大22春《离散数学》在线平时作业1【参考答案】
《离散数学》在线平时作业1【参考答案】试卷总分:100 得分:100一、单选题 (共 10 道试题,共 50 分)1.单选题。
无向图是连通的，当且仅当（）。
A.任何两个结点之间都有通路；B.任何两个结点之间都有唯一路；C.任何两个结点之间都有路；D.任何两个结点之间都有迹。
标准答案:C2.单选题。
一个有向图是根树，当且仅当该图（）。
A.有树根，也有树叶；B.忽略边的方向时，是连通无回路的无向图；C.有一个结点可以到达任何其余结点；D.恰有一个结点入度为0：其余结点入度为1。
标准答案:D3.单选择题：在一次集会中，与奇数个人握手的人数共有( )个。
A.奇数；B.非负整数；C.偶数；D.不能确定。
标准答案:C4.单选题。
一棵树有7片树叶，3个3度结点，其余都是4度结点，该树有（）个4度结点。
A.4；B.3；C.2；D.1；E.不在给定的选择的范围内。
标准答案:D5.{图}A.f是满射，g是入射。
B.f是双射，g是双射C.f是入射，g是满射。
D.f是入射，g是入射。
标准答案:C6.选择填空题。
R是A上关系，如果R是自反的，当且仅当（）。
A.A中有些元素x，有<x,x>∈R ；B.所有A中元素x，都有<x,x>∈R ；C.所有A中元素x,y，如果有<x,y>∈R ，也有< y, x >∈R；则x=y 。
标准答案:B7.单选题。
无向图G中有21条边，3个4度结点，其余都是3度结点。
问G中有（）个结点？A.12；B.13；C.16；D.18。
标准答案:B8.选择填空题。
如果A、B都是有限集，且|A|=m, |B|=n，则 |A′B |=( ) 。
A.m+n ；B.mn ；C.mn ；D.nm 。
标准答案:B9.设.X、Y 是有限集合，|X|=3，|Y|=2，可以构成( )个是从X到Y的入射函数。
东大19春学期《离散数学》在线作业1
(单选题)1:A: ⑷⑸⑺⑻B: ⑴⑵⑷⑹C: ⑴⑷⑸⑹D: ⑴⑷⑸⑺正确答案:(单选题)2: 具有两个命题变元P、Q情况下，在P指派为T，Q指派为F时，真值为假的大项是( )。
A: P∨ØQ； B: P∧ØQ；C: ØP∨Q；D: Ø P∧Q 。
正确答案:(单选题)3: 单选题。
结点是树的叶结点，当且仅当该结点（ ）。
A: 度数不为0；B: 度数大于1；C: 度是等于1。
正确答案:(单选题)4:A: 等价B: 不等价C: 无法确定D: 不知道正确答案:(单选题)5: 单选题。
有n个结点的无向完全图有( )条边。
A: 2n； B: (n(n-1))÷2； C: n(n-1)； D: n2。
正确答案:(单选题)6:A: 矛盾式B: 重言式C: 无法确定D: 不知道正确答案:(单选题)7: 单选题。
一棵根树是m叉树，当且仅当该图（ ）。
东大19春学期《离散数学》在线作业2
------------------------------------------------------------------------------------------------------------------------------ (单选题)1: 单选题。
一棵树有7片树叶，3个3度结点，其余都是4度结点，该树有（）个4度结点。
A: 4；B: 3；C: 2；D: 1；E: 不在给定的选择的范围内。
正确答案:(单选题)2:A: B:①：⑵⑶⑺⑻B: B:②：⑶⑷⑻C: B:③：⑶⑹⑺⑻D: B:④：⑶⑺正确答案:(单选题)3: 单选题。
一棵根树是完全m叉树，当且仅当该图（）。
A: 每个结点的度数是m；B: 每个结点的出度都是m；C: 每个结点的出度不是0就是m；D: 恰有一个结点入度为0：其余结点入度为1。
正确答案:(单选题)4: 令命题P表示没有大学生不懂外语。
下面命题( )与P等价。
A: 有些大学生懂一些外语。
B: 所有大学生都懂一些外语。
C: 有些大学生懂所有外语。
D: 没有大学生懂所有外语。
正确答案:(单选题)5:A: 矛盾式B: 重言式C: 无法确定D: 不知道正确答案:(单选题)6: 7.选择题：在一次集会中，与奇数个人握手的人数共有()个。
A: 奇数B: 不能确定C: 偶数D: 不知道正确答案:(单选题)7: 下面是"xC(x), $x(A(x)ÚB(x)), "x(B(x)®ØC(x)) Þ $xA(x)的谓词推理过程。
在这个过程中每一步中的（）处是此步所用的推理规则。
请写出这些推理规则。
⑴ $x(A(x)ÚB(x)), ( )⑵ A(a)ÚB(a) ( ) ⑴⑶ "xC(x) ( )⑷C(a) ( ) ⑶ ⑸ "x(B(x)&rarrØC(x)) ( ) ⑹ B(a)&rarrØC(a) ( ) ⑸⑺ ØB(a) ( ) ⑷ ⑹ I12⑻ A(a) ( ) ⑵ ⑺ I10⑼------------------------------------------------------------------------------------------------------------------------------ $xA(x)) ( ) ⑻A: ⑴ P；⑵ T；⑶ T；⑷ UG；⑸ P；⑹ US；⑺ P；⑻ T；⑼ ES。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
19秋学期《离散数学》在线平时作业1
试卷总分:100 得分:100
一、单选题 (共 10 道试题,共 50 分)
1.单选填空题：设G是有向简单图，其结点度数序列为(2,2,3,3)，入度序列为(0,0,2,3)。
则结点的出度序列为( )。
A.(2,2,3,3)
B.(1,1,0,0)
C.(2,2,1,0)
D.(2,2,0,0)
答案:C
2.{图}
A.{图}
B.{图}
C.{图}
D.{图}
答案:A
3.单选择题：在一次集会中，与奇数个人握手的人数共有( )个。
A.奇数；
B.非负整数；
C.偶数；
D.不能确定。
答案:C
4.设命题P、Q所代表的意义如下：
P：天气好。
Q：我去旅游。
命题“只有天气好，我才去旅游。
”的符号表达式为：（）
A.P?Q，
B.Q? P，
C.Ø P ? Q，
D.Ø Q ? P
答案:B
5.命题公式(P?Q)?Q的主合取范式是（）。
A.P∨ØQ；
B.P∨Q；
C.(ØP∨Q)∧(P∨ØQ )；
D.(P∨Q )∧(Ø P∨ØQ ) 。
答案:B
6.{图}
A.重言式。