高等数学-曲率
同济大学 高等数学 课件 2.11

.
例3 求 y ln x 在任意点处的曲率. 解 因
1 1 y , y 2 , x x
由计算公式得曲线在任一点处的曲率为
K
y
1 y
x 0
2 3/ 2
1/ x 2
1 1/ x
2 3/ 2
x
1 x
2 3/ 2
,
注意到, lim K
y f x M M0 s M +
o a b
x
而线段 MM 的长度为
MM
并注意到
x 0
x
s MM
2
y ,
2
lim
1,
(此式将在定积分中证明) 因
s MM lim lim lim x 0 x x 0 MM x x 0 s
K
2a
3/ 2
,
曲率圆与曲率半径 设曲线 C 在点 M 点 D, 使
x, y 处的曲率为K K 0 , 作出
y
D
1 K
点 M 处曲线 C 的法线,并且在曲线凹向一侧的法线上取
1 MD . K 以 D为圆心, 为半径作圆,
称该圆为曲线 C 在点 M 的曲率 圆, 为曲线 C 在 M 处的率的极限存在,则称此极限为 曲线 C 在点 M 处的曲率,记为K ,即
K lim . M M s
⑴
例1 对直线而言,动点从 M 到 M 相应的切线的转角 为 0, 则
K 0, s
从而曲率
K lim 0. M M s
x3 , 并设OA 的方程为 y aRl
的长度,a是待定常数.
《高等数学曲率》课件

曲率与生物形态
在自然界中,许多生物形态都呈现出 曲率的特点。例如,鸟类的飞行轨迹 、河流的流向、植物的生长方式等都 与曲率密切相关。通过研究这些生物 形态的曲率特点,可以更好地理解自 然界的规律和原理。
VS
曲率在生物形态中的应用还体现在仿 生学领域。通过模仿自然界中生物的 形态和运动方式,可以创造出更加高 效、环保和可持续的交通工具、建筑 材料等。例如,仿生学中的“蜂巢” 结构就是利用了曲率的特点,具有很 好的抗压和抗震性能。
曲率与建筑设计
在建筑设计中,曲率也被广泛应用。通过合理利用曲率,可以创造出更加美观、舒适和功能性的建筑。例如,在建筑设计时 可以利用曲率来优化建筑的外观和结构,提高建筑的稳定性和安全性。
曲率还可以用于建筑内部的布局和空间设计。例如,利用曲率可以将建筑的内部空间划分为不同的区域,提高建筑的实用性 和舒适性。
曲率研究展望
曲率与几何拓扑关系
未来研究可以探索曲率与几何拓扑之间的关系,例如研究 曲率在曲面分类中的作用,以及曲率在流形学习等方面的 应用。
高维空间曲率研究
随着高维几何的发展,对高维空间中曲率的研究也日益重 要,未来可以进一步探讨高维空间中曲率的性质和计算方 法。
数值计算与模拟
随着计算机技术的发展,数值计算和模拟已经成为研究曲 率的重要手段,未来可以借助更先进的计算方法和模拟技 术,对曲率进行更精确和深入的研究。
03
曲率应用
曲率在几何学中的应用
曲率在几何学中有着广泛的应用,它描述了曲线在某一点的 弯曲程度。在平面几何中,曲率用于描述曲线在某一点的弯 曲程度,而在球面几何中,曲率则用于描述曲面在某一点的 弯曲程度。
在几何学中,曲率的概念可以帮助我们更好地理解空间中的 几何形状,以及它们之间的相互关系。例如,在研究行星运 动时,曲率的概念可以帮助我们理解行星轨道的形状和大小 。
3-7 曲率(高等数学)

§3.7 曲率教学内容:一.弧微分1.光滑曲线:设函数)(x f y =在区间(,)a b 内具有连续导数,则曲线)(x f y =在(,)a b 内的每点处有能连续转动的切线,称曲线)(x f y =为光滑曲线.2. 弧微分:函数()s x 关于x的微分d s x =,或者d s =.二.曲率1.定义:0lim →∆s s ∆∆α称为曲线在点M 处的曲率,即K =0lim →∆s s ∆∆α=d d sα.2. 计算公式:设曲线的方程为)(x y y =,且()y x 具有二阶导数,322d d (1')y K s y α''===+.三.曲率半径与曲率圆1. 曲率圆与曲率半径的定义:设曲线)(x f y =在点(,)M x y 处的曲率0K ≠(即0y ''≠),在点M 处作曲线的法线,法线指向曲线凹的一侧.在此侧的法线上取一点D ,使1MD Kρ==,以D 为圆心,ρ为半径作圆,称这个圆为曲线在点M 处的曲率圆,它的半径1Kρ=称为曲率半径,圆心D 称为曲率中心.图3.212.曲率圆与曲线在点M 处有相同的切线与曲率,且在点M 的邻近有相同的弯曲方向,从而曲率圆与曲线所对应的函数在点M 有相同的函数值、一阶导数值和二阶导数值.3.在工程设计中,一般可用曲率圆在点M 附近的一段弧来近似代替曲线弧.四.例题讲解例1.求直线b ax y +=的曲率.例2.求半径为R 的圆的曲率.例3.求曲线122--=x x y 在极小值点处的曲率.例4.在车床加工中,用圆柱形铣刀加工一弧长不大的椭圆形工件,该段弧的中点为椭圆长轴的顶点,其方程为222214050x y +=(单位:mm ),应选用多大直径的铣刀,可得较好的近似效果.。
高等数学上3.7平面曲线的曲率PPT

Q 70(千克力) 571.4(千克力),
641.5(千克力).
即:飞行员对座椅的压力为641.5千克力.
首页
上页
返回 第11页,共26页。
下页
结束
小结
运用微分学的理论,研究曲线和曲面的性质的数学分支—
—微分几何学.
1. 弧长微分 ds 1 y2 dx 或 ds (dx)2 (dy)2
3
要使 k最大, 必有 (4 5cos2 t )2 最小,
t , 3 此时 k最大,
22
首页
上页
返回 第13页,共26页。
下页
结束
补充:参数方程曲率公式
设
x y
(t ), (t ),
二阶可导,
dy dx
(t ) (t )
,
d2y dx 2
(t)
(t) (t) 3(t)
(t) .
高等数学上3.7平面曲线的曲率
首页
上页
返回 第1页,共26页。
下页
结束
一、 弧微分
设
在(a , b)内有连续导数, 其图形为 AB,
弧长 s AM s(x)
s M M M M x M M x
M M (x)2 (y)2
MM
x
y
y
f (x) M
B
A M y
x
oa x
bx
x x
M M 1 (y)2
的凹向一侧法线上取点 D 使
CR
T
M (x, y)
DM R 1
o
x
K
把以 D 为中心, R 为半径的圆叫做曲线在点 M 处的
曲率圆 ( 密切圆 ) , R 叫做曲率半径, D 叫做 曲率中心.
高等数学高数07第七节曲率

第七节 曲率在生产实践和工程技术中,常常需要研究曲线的弯曲程度,例如,设计铁路、高速公路的弯道时,就需要根据最高限速来确定弯道的弯曲程度. 为此,本节我们介绍曲率的概念及曲率的计算公式.分布图示★ 弧微分★ 曲率的定义 ★ 曲率的计算公式★ 直线与圆的曲率 ★ 例1 ★ 例2★ 曲率圆与曲率半径 ★ 例3★ 例4 ★ 例5 ★ 例6★ 内容小结 ★ 课堂练习★ 习题3-7 ★ 返回内容要点一、弧微分22)()(dy dx ds +=二、曲率及其计算公式.)1(232y y K '+''=三、曲率圆 曲率半径 曲率中心;例题选讲曲率的计算与应用例1 (E01) 抛物线c bx ax y ++=2上哪一点的曲率最大? 解 ,2b ax y +=',2a y =''∴.])2(1[|2|232b ax a K ++=显然,当abx 2-=时,K 最大. 又 ⎪⎪⎭⎫⎝⎛---a ac b a b 44,22为抛物线的顶点,故抛物线在顶点处的曲率最大.例2(E02) 在修筑铁路时,常需根据地形的特点和最高限速的要求来设计铁轨的圆弧弯道. 铁轨由直道转入圆弧弯道时, 若接头处的曲率突然改变, 容易发生事故, 为了行使平稳,往往在直道和圆弧弯道之间接入一段缓冲段A O(图3-7-7), 使轨道曲线的曲率由零连续地过渡到圆弧的曲率R 1, 其中R 为圆弧轨道的半径.证 根据分析,在缓冲段OA 上,,212x Rl y ='.1x Rly ='' 故在缓冲段始端0=x 处的曲率为.00=K )0,0(=''='y y 题意实际要求,0x l ≈,1⎪⎭⎫⎝⎛<<R l 故 0x x y ='Rl x 220=Rl l 22≈,2Rl =0x x y =''Rl x 0=Rl l ≈.1R= 故在终端A 的曲率为A K ()2321||x x y y ='+''=2322411⎪⎪⎭⎫ ⎝⎛+≈R l R ,1R≈).1(<<R l例3 (E03) 求曲线x y tan =在点)1,4(π处的曲率与曲率半径.解 ,sec 2x y ='x x y tan sec 22='',cos sin 23xx=曲率K 及曲率半径R 分别为 K ,)1(||2/32y y '+''=R K 1=.||)1(2/32y y '''+= 由24/='=πx y 及,44/=''=πx y 得点⎪⎭⎫⎝⎛1,4π处的曲率与曲率半径分别为 ,2554=K .455=R例4 求椭圆⎩⎨⎧==t b y ta x sin cos 在),0(b 点处的曲率及曲率半径.解 点),0(b 对应的参数,2π=t 由于,sin )(t a dtdxt -=='ϕ,cos )(t a t -=''ϕ ,cos )(t b dtdyt =='ψt b t sin )(-=''ψ 故将2π=t 代入得 ,2a dt dx -==⎪⎭⎫ ⎝⎛'πϕ,02=⎪⎭⎫ ⎝⎛''πϕ ,02==⎪⎭⎫ ⎝⎛'dtdy πψ,2b -=⎪⎭⎫ ⎝⎛''πψ由曲率公式, 有2/2/322)]()([|)()()()(|πψϕψϕψϕ='+''''-'''=t t t t t t t K 2a b =所求曲率半径为.2ba R =例5 (E04) 飞机沿抛物线4000/2x y =(单位为米)俯冲飞行, 在原点处速度为,/400秒米=v 飞行员体重70千克. 求俯冲到原点时,飞行员对座椅的压力.解 飞行员对座椅的压力(kg) ,P F Q += 其中飞行员的体重70=P (kg),离心力,2ρmv F =由40002x y =⇒0='x y 02000==x x ,0=0=''x y .20001=则曲线在原点处曲率为.20001=K 曲率半径为2000=ρ米. F ∴2000400702⨯=)(5600牛=),(4.571千克≈Q ∴)(4.571)(70千克力千克力+=).(4.641千克力=即:飞行员对座椅的压力为 641.4 千克力.例6 设)(x f y =为过原点的一条曲线, )0(),0(f f '''存在, 又知有一条抛物线)(x g y =与曲线)(x f y =在原点相切, 在该点处有相同的曲率, 且在该点附近此二曲线有相同的凹向, 求).(x g解 设.)(2c bx ax x g ++=依题可得),0()0(f g =),0()0(f g '=').0()0(f g ''='' 由0)0()0(==f g ⇒,0=c 由)0()0(f g '='⇒),0(f b '= 由)0()0(f g ''=''⇒),0(2f a ''=即),0(21f a ''= 因此所求函数为.)0()0(21)(2x f x f x g '+''=课堂练习1. 椭圆t x cos 2=, t y sin 3=上哪些点处曲率最大?。
高等数学 第3章 第九节 曲率
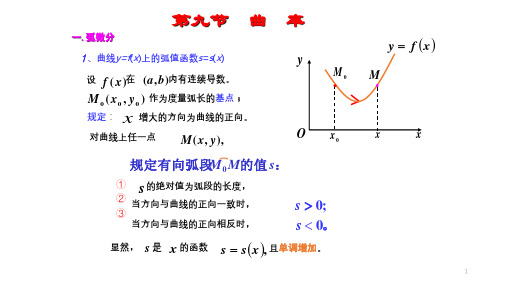
曲线的弯曲程度与下列两个量有关:
(1)切线转过的角度; (2)弧段的长度。 曲率:单位弧长上切线所转过的角度。
M1M2 N1N2
1 2
3
设 MM'的长度为
切线转过的角度为
平均曲率:
s , .
s
MM '的平均弯曲程度
K
s
y
M
•
s
M
M0
•
•
O
x
曲线在点M处的曲率:
K lim s0 s
x,
y
相应的有向弧段的值
s有增量 s,
s M 0 M M 0 M MM
s ?
x
y f x
M •
M0
y
• M•
x
s s MM MM MM o
x x x MM x
MM
MM
xs2与x2x总y是2 同号MM的MM
1 y 2 x
ds
lim
s
lim
MM
1
y
2
dx x0 x x0 MM
ds y
dx
3
1 y2 2
ds 1 y2 dx
d ?
dx
6
设曲线的参数方程为
x (t)
y
(t
)
't "t "t 't
K
'2 t '2 t 3/ 2
例1 计算 xy 1 在点 1,1 处的曲率。
解
y 1, x
y
1 x2
,
y
2 x3
.
y 1, y 2.
平均曲率的极限
若 lim 存在,则
高等数学曲率

yxddyxcRss2cin dd
1
R sin3
K
y
3
R
1 sin
3
3
(1 y2 )2 ( 1 cot 2 ) 2
1 csc 2
R
3
(csc 2 ) 2
1 . R
12
例3 抛物y线 ax2bxc上哪一点的曲 ? 率
解 y2a xb, y2a,
D
1
k
yf(x)
在凹的一侧取一点D,使
DM 1 , 以D为圆心, o
K
M
x
为半径作圆(如图),称此圆为曲线在点M处的曲率圆.
D曲率中 , 心 曲率半. 径
15
注意: 1.曲线上一点处的曲率半径与曲线在该点处的
曲率互为倒数.
即
1 K
,K
1
.
2.曲线上一点处的曲率半径越大,曲线在该点
复习
1.判定凹凸性的方法:
如果 f (x) 在 (a,b)内具有二阶导数,若在(a,b)内 (1) f(x)0,则曲线 f (x)在(a,b)内是凹的. (2) f(x)0,则曲线 f (x) 在 (a,b)内是凸的.
说明:拐点的横坐标可能是 y 0的根, 也可能是 y不存在的点.
弧微分公式
4
ds 1 y2dx
y
变形 ds
1
( dy)2 (d x)2
dx
(dx)2(dy)2
M
M0
ds
M
Tdy
R
dx
o
则有 (ds)2(dx)2(dy)2.
x0
x
xx x
弧微分的几何意义:ds 就是曲线 y f(x)上点M(x, y)
高等数学导数应用(三)曲率PPT课件

目录
• 曲率定义与计算 • 导数与曲率的关系 • 曲率在实际问题中的应用 • 曲率的应用案例分析 • 总结与展望
01
曲率定义与计算
曲率的定义
曲率是描述曲线在某一点弯曲程 度的量,定义为曲线在该点处切
线的斜率的变化率。
在二维平面上,曲线的曲率等于 其上任一点处切线的斜率的导数。
导数的性质
导数具有连续性、可导性、可积性等 性质,这些性质在研究函数的形态、 单调性、极值等问题中具有重要作用。
导数与曲率的关系
导数与曲率的关系
曲率是描述曲线在某一点弯曲程度的 量,与函数在该点的导数密切相关。 曲率等于函数在该点的导数的绝对值 。
导数与曲率的几何意义
在几何上,导数表示曲线在某一点的 切线斜率,而曲率表示该点附近曲线 的弯曲程度。因此,导数和曲率共同 决定了曲线在该点的形态。
在几何图形中,曲率的应用非常广泛,如圆、椭圆、 抛物线、双曲线等。
曲率决定了图形的形状和性质,如圆的曲率处处相等 且为常数,而抛物线的曲率只在顶点处为0。
在工程和科学研究中,曲率的应用也非常重要,如分 析机械零件的应力分布、研究光的传播路径等。
的定义
导数是函数在某一点的变化率,表示 函数在该点的切线斜率。
05
总结与展望
总结高等数学导数应用(三)曲率的主要内容
曲率的概念
曲率是描述曲线弯曲程度的量,对于二维平面上的曲 线,曲率等于切线方向的转动角速度。
导数与曲率的关系
曲率是函数二阶导数的几何意义,即曲率等于函数二 阶导数的值。
曲率的应用
曲率在几何、物理、工程等领域有着广泛的应用,如 分析机械零件的应力分布、预测股价波动等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y d 2. 曲率公式 K 3 2 ds (1 y ) 2 3. 曲率圆 2 32 1 (1 y ) 曲率半径 R y K 2 y (1 y ) x y 曲率中心 2 1 y y y
目录 上页 下页 返回 结束
思考与练习
K s
点 M 处的曲率
M
M s
d K lim s 0 s ds
注意: 直线上任意点处的曲率为 0 !
目录 上页 下页 返回 结束
例1. 求半径为R 的圆上任意点处的曲率 .
解: 如图所示 ,
s R
1 K lim s 0 s R
1) 2 2 x
3
O 1
x
2
显然 R
x 1
2 为最小值 .
利用 a 2 b 2 2 ab
目录 上页 下页 返回 结束
d K ds
d (arctan y) d x
又 故曲率计算公式为
K
y (1 y )
2 32
当 y 1 时 , 有曲率近似计算公式 K y
目录 上页 下页 返回 结束
说明:
x x(t ) 给出, 则 (1) 若曲线由参数方程 y y (t ) x y x y K 2 2 32 (x y )
目录 上页 下页 返回 结束
f (t ) (a 2 b 2 ) sin 2 t
三、 曲率圆与曲率半径
设 M 为曲线 C 上任一点 , 在点 M 处作曲线的切线和法线, 在曲线 的凹向一侧法线上取点 D 使
y
D( , )
C
R
M ( x, y )
T
1 x O DM R K 把以 D 为中心, R 为半径的圆叫做曲线在点 M 处的
由此可得曲率中心公式
2 y (1 y ) x y 1 y2 y y
y
D( , )
C
O
R
M ( x, y)
T
x
(注意 y 与 y 异号 )
当点 M (x , y) 沿曲线
移动时, 相应的曲率中心
的轨迹 G 称为曲线 C 的渐屈线 , 曲线 G 的渐伸线 . 满足方程组 ,C 称为曲线 2 2 2 ( M ( x , y ) 在曲率圆上 ) 曲率中心公式可看成渐 ( x ) ( y ) R x 屈线的参数方程 (参数为x). ( DM MT ) y y 点击图中任意点动画开始或暂停
第七节 平面曲线的曲率
曲线的弯 与切线的转角有关 曲程度 与曲线的弧长有关 主要内容: 一、 弧微分 二、 曲率及其计算公式 三、 曲率圆与曲率半径
目录 上页
第三章
M
M M
下页
返回
结束
一、 弧微分
设 在(a , b)内有连续导数, 其图形为 AB, 弧长 s AM s( x)
1 a (1 cos t ) 2
y(1 y2 ) x y 1 y2 y y
摆线
a ( sin ) a (1 cos )
( 仍为摆线 )
O
摆线 目录 上页 下页 返回 结束
内容小结
2 2 d s (d x ) (d y ) 1. 弧长微分 ds 1 y dx 或 2
目录 上页 下页 返回 结束
例4. 设一工件内表面的截痕为一椭圆, 现要用砂轮磨
削其内表面 , 问选择多大的砂轮比较合适? 解: 设椭圆方程为 由例3可知, 椭圆在 处曲率最大,
2 2
3
例3
y O
即曲率半径最小, 且为
x
(a sin t b cos t ) R ab
显然, 砂轮半径不超过
或有的地方磨不到的问题.
求此缓和曲线在其两个端点 解: 当 x [ 0 , l ] 时, 1 2 l 0 y x 2 Rl 2R 1 y x Rl 1 x K y Rl 1 显然 K x 0 0 ; K x l
处的曲率.
y
R B
O
l
1 3 y x 6 Rl
x
R
目录
上页
t
f (t )
0
b
2
π 2
π
2
3π 2
2π
b
2
a
b
2
a
2
设 0 b a , 则t 0 , π , 2 π时
y b
f (t ) 取最小值 , 从而 K 取最大值 .
这说明椭圆在点 ( a , 0 ) 处曲率
a
O
b
a x
最大.
K 最大
f (t ) a 2 sin 2 t b 2 cos 2 t 最小
1. 曲线在一点处的曲率圆与曲线有何密切关系?
答: 有公切线 ;
2. 求双曲线
凹向一致 ;
曲率相同.
的曲率半径 R , 并分析何处 R 最小? y 1 2 解: y 2 , y 3 , 则 x x 1
2
3 2
(1 y ) R y
(1
2
1) 2 x4
3
x3
1 ( x2 2
(2) 若曲线方程为 x ( y ) , 则
K
x ( 1 x )
2
3 2
K
y (1 y )
上页 下页 返回
2
3
2
目录
结束
1 3 x 作缓和曲线, 例2. 我国铁路常用立方抛物线 y 6 Rl 其中R是圆弧弯道的半径, l 是缓和曲线的长度, 且 l << R.
下页
返回
结束
例3. 求椭圆 解: x a sin t ;
在何处曲率最大?
y b cos t ;
故曲率为
x a cos t y b sin t
2
K
x y x y (x y )
2 2
3
ab
(a sin t b cos t )
y
s M M M M x M M x
M M (x) 2 (y ) 2 MM x MM y 2 1 ( ) MM x s s( x) lim 1 ( y) 2 x0 x
y f ( x) B M A M y x
求此缓和曲线在其两个端点 说明:
处的曲率.
铁路转弯时为保证行车 平稳安全, 离心力必须
连续变化 , 因此铁道的 曲率应连续变化 .
点击图片任意处播放\暂停
目录 上页 下页 返回 结束
1 3 x 作缓和曲线, 例2. 我国铁路常用立方抛物线 y 6 Rl 其中R是圆弧弯道的半径, l 是缓和曲线的长度, 且 l << R.
O a
x
x x
b x
MM lim 1 x0 M M
目录
上页
下页
返回
结束
2 2 或 d s (d x ) (d y ) ds 1 ( y) dx 2
x x(t ) 若曲线由参数方程表示: y y (t )
则弧长微分公式为
几何意义:
ds x 2 y 2 dt
2
2
2
t 0
才不会产生过量磨损 ,
目录
上页
下页
返回
结束
例5. 求摆线
的渐屈线方程 . 摆线
d ( y ) dt
sin t y , 解: y y x 1 cos t x 代入曲率中心公式, 得渐屈线方程 a (t sin t ) a (cos t 1)
x 表示对参 数 t 的导数
y
ds M T
dy sin dsΒιβλιοθήκη dx cos ; ds
d x O x x dx x
目录 上页 下页 返回 结束
M
T dy
二、曲率及其计算公式
在光滑弧上自点 M 开始取弧段, 其长为 s , 对应切线 转角为 , 定义 弧段 s 上的平均曲率
曲率圆 ( 密切圆 ) , R 叫做曲率半径, D 叫做 曲率中心. 在点M 处曲率圆与曲线有下列密切关系: (1) 有公切线; (2) 凹向一致; (3) 曲率相同 .
目录 上页 下页 返回 结束
设曲线方程为 曲率半径及曲率中心
且
求曲线上点M 处的 的坐标公式 .
设点M 处的曲率圆方程为
y
故曲率半径公式为
M s R M
可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ;
R 愈大, 则K 愈小 , 圆弧弯曲得愈小 .
目录
上页
下页
返回
结束
曲率K 的计算公式 设曲线弧 y f ( x) 二阶可导, 则由
得
π π tan y ( 设 ) 2 2 arctan y
2 1 (1 y ) R K y
3 2
D( , )
C
O
R
M ( x, y )
T
x
, 满足方程组
2 2 2 ( x ) ( y ) R x y y
( M ( x , y ) 在曲率圆上 )
( DM MT )
目录 上页 下页 返回 结束
2 2 2 2
3 2
K 最大
求驻点:
f (t ) a 2 sin 2 t b 2 cos 2 t 最小
f (t ) 2a 2 sin t cos t 2b2 cos t sin t (a 2 b 2 ) sin 2 t
