回归模型的建立与分析
建立回归模型五个步骤

建立回归模型五个步骤
1、确定变量:
明确定义了预测的具体目标,并确定了因变量。
例如某化学家想要了解多个预测变量是如何与棉布的抗皱性(因变量)相关联的。
因此,该化学家检测了在不同的凝固时间、凝固温度、甲醛浓度和催化剂比率(自变量)下生产的32片棉纤维素。
对每片棉布都记录了耐久压烫评级,即抗皱性的度量。
2、建立预测模型:
依据自变量和因变量的历史统计资料进行计算,在此基础上建立回归分析方程,即回归分析预测模型。
3、进行相关分析:
回归分析是因果因素(自变量)和预测因子(因变量)的数学统计分析。
只有当自变量和因变量之间存在某种关系时,建立的回归方程才有意义。
因此,作为自变量的因子是否与作为因变量的预测对象相关,程度的相关程度以及判断相关程度的程度是在回归分析中必须解决的问题。
相关分析通常需要相关性,并且相关度系数用于判断自变量和因变量之间的相关程度。
P<0.05的自变量,相关性显著
4、计算预测误差:
回归预测模型是否可用于实际预测取决于回归预测模型的测试和预测误差的计算。
回归方程只能通过回归方程作为预测模型来预测,只有当它通过各种测试且预测误差很小时才能预测。
该回归预测模型可以解释因变量73%的响应,是否可用视要求而定。
5、确定预测值:
利用回归预测模型计算预测值,并对预测值进行综合分析,确定最后的预测值。
回归分析中的主成分回归模型构建技巧(Ⅲ)

回归分析中的主成分回归模型构建技巧回归分析是统计学中一种常用的分析方法,用于研究自变量和因变量之间的关系。
主成分回归模型是回归分析的一种特殊形式,它将原始自变量通过主成分分析降维,然后再进行回归分析。
在实际应用中,构建主成分回归模型需要注意一些技巧,本文将对此进行探讨。
1. 数据准备首先,构建主成分回归模型需要准备一定数量的数据。
在收集数据时,需要确保数据的完整性和准确性,避免数据缺失或错误对模型构建造成影响。
此外,还需要考虑数据的分布情况,如果数据不服从正态分布,可能需要对数据进行变换处理,以满足模型建立的假设条件。
2. 主成分分析主成分回归模型的关键步骤是主成分分析,通过主成分分析可以将原始自变量降维,提取出最具代表性的主成分。
在进行主成分分析时,需要对数据进行标准化处理,使得各个变量具有相似的尺度,避免变量之间的量纲影响分析结果。
同时,还需要选择合适的主成分个数,通常可以通过累计方差贡献率达到一定阈值来确定主成分的个数,以保留足够的信息量。
3. 变量选择在构建主成分回归模型时,需要考虑哪些原始自变量可以纳入模型。
通常情况下,可以通过相关性分析、方差膨胀因子等方法来选择自变量。
此外,还可以考虑使用逐步回归或岭回归等方法来进一步筛选变量,以保证模型的简洁性和解释性。
4. 模型建立在进行主成分回归模型的建立时,需要将提取出的主成分作为自变量,以及可能的其他自变量一起纳入模型。
在建立模型时,需要注意多重共线性等问题,可以通过方差膨胀因子、特征值等方法来进行诊断。
同时,还需要考虑模型的拟合程度和预测能力,可以通过交叉验证等方法来评估模型的性能。
5. 结果解释最后,构建好主成分回归模型之后,需要对模型进行解释和评价。
可以通过系数的显著性检验、残差分析等方法来进行模型的解释和诊断。
同时,还可以利用模型进行预测和决策支持,为实际问题的解决提供参考。
总之,构建主成分回归模型是一项复杂而又重要的工作,需要综合运用数据处理、统计分析和模型建立等技能。
如何进行回归分析:步骤详解(四)

回归分析是统计学中一种重要的分析方法,用于研究两个或更多变量之间的关系。
它可以帮助我们了解变量之间的因果关系,预测未来的趋势,以及检验假设。
在实际应用中,回归分析被广泛用于经济学、社会学、医学等领域。
下面将详细介绍如何进行回归分析的步骤。
第一步:确定研究的目的和问题在进行回归分析之前,首先需要明确研究的目的和问题。
例如,我们想要了解某个因变量与几个自变量之间的关系,或者我们想要预测未来的趋势。
明确研究目的和问题可以帮助我们选择合适的回归模型和变量。
第二步:收集数据接下来,我们需要收集相关的数据。
数据可以是实验数据、调查数据或者是已有的数据集。
在收集数据的过程中,需要保证数据的质量和完整性,以及避免数据的缺失和错误。
同时,还需要考虑数据的样本量和代表性,以确保结果的可靠性和有效性。
第三步:选择合适的回归模型在确定了研究目的、问题和收集了相关数据之后,接下来需要选择合适的回归模型。
常见的回归模型包括线性回归模型、多元线性回归模型、逻辑回归模型等。
选择合适的回归模型需要考虑多个因素,包括变量之间的关系、数据类型、模型的假设和可解释性等。
第四步:建立回归模型在选择了合适的回归模型之后,接下来需要建立回归模型。
建立回归模型的过程包括确定因变量和自变量之间的关系、估计模型的参数、检验模型的拟合度等。
在建立回归模型的过程中,需要考虑模型的解释能力和预测能力,以及模型的稳健性和可靠性。
第五步:评估回归模型建立回归模型之后,需要对模型的拟合度进行评估。
常用的评估方法包括确定系数(R-squared)、残差分析、假设检验等。
评估回归模型的过程可以帮助我们了解模型的解释能力和预测能力,以及检验模型的假设和稳健性。
第六步:解释结果和做出推断最后,根据回归模型的结果,我们可以对变量之间的关系进行解释和推断。
通过对回归系数的解释和显著性检验,我们可以了解自变量与因变量之间的关系,以及变量对因变量的影响程度。
同时,还可以利用回归模型进行预测和假设检验,以支持决策和推断。
回归模型的工作原理及应用

回归模型的工作原理及应用一、回归模型的定义和背景回归模型是一种常见的统计分析方法,旨在通过建立一个数学模型,来探索自变量和因变量之间的关系,并预测未来的因变量值。
回归模型可应用于各种领域,如经济学、金融学、医学以及市场研究等。
二、回归模型的基本原理回归模型基于最小二乘法,通过最小化预测值与真实值之间的平方差,来确定自变量与因变量之间的关系。
以下是回归模型的工作原理及应用的基本步骤:1.收集数据:首先,我们需要收集关于自变量和因变量的数据。
这可以通过实验、调查或观察等方式获得。
2.选择特征:在建立回归模型之前,需要选择用于预测的自变量。
这些自变量应具有相关性,并且能够对因变量产生影响。
3.建立模型:在选择自变量后,我们使用这些自变量来建立回归模型。
回归模型可以是线性的,也可以是非线性的,取决于数据的分布和关系。
4.模型训练:模型训练是指通过使用已有数据,对回归模型的参数进行估计。
这可以通过最小化残差平方和来实现。
5.模型评估:在完成模型训练后,我们需要评估模型的性能。
这可以使用各种指标来衡量,如均方误差(MSE)、决定系数(R²)等。
三、回归模型的类型和应用案例回归模型可以分为线性回归、多项式回归、岭回归等不同类型。
以下是回归模型的一些常见应用案例:1.股票市场预测:回归模型可以用于分析历史股票数据并预测未来股价的走势。
通过考虑相关因素,如市场指数、公司盈利等,可以建立一个能够预测股价波动的回归模型。
2.销售预测:回归模型可以用于预测产品销售量与各种因素之间的关系。
例如,通过考虑广告支出、价格、竞争对手活动等因素,可以建立一个能够预测产品销售量的回归模型。
3.房价预测:回归模型可以用于预测房价与各种因素之间的关系。
例如,通过考虑房屋面积、地理位置、房龄等因素,可以建立一个能够预测房价的回归模型。
4.医学研究:回归模型可以用于医学研究中的预测和建模。
例如,通过考虑患者的年龄、性别、疾病历史等因素,可以建立一个能够预测疾病发展和治疗结果的回归模型。
总结:线性回归分析的基本步骤
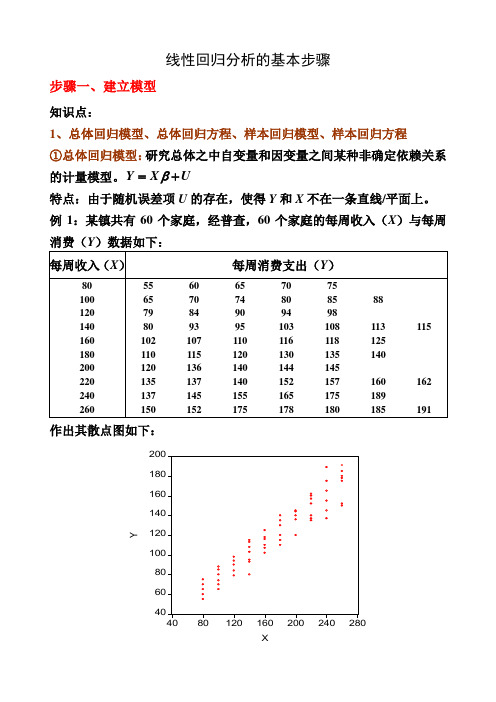
线性回归分析的基本步骤步骤一、建立模型知识点:1、总体回归模型、总体回归方程、样本回归模型、样本回归方程 ①总体回归模型:研究总体之中自变量和因变量之间某种非确定依赖关系的计量模型。
Y X U β=+特点:由于随机误差项U 的存在,使得Y 和X 不在一条直线/平面上。
例1:某镇共有60个家庭,经普查,60个家庭的每周收入(X )与每周消费(Y )数据如下:作出其散点图如下:②总体回归方程(线):由于假定0EU =,因此因变量的均值与自变量总处于一条直线上,这条直线()|E Y X X β=就称为总体回归线(方程)。
总体回归方程的求法:以例1的数据为例,求出E (Y |X 由于01|i i i E Y X X ββ=+,因此任意带入两个X i 和其对应的E (Y |X i )值,即可求出01ββ和,并进而得到总体回归方程。
如将()()222777100,|77200,|137X E Y X X E Y X ====和代入()01|i i i E Y X X ββ=+可得:01001177100171372000.6ββββββ=+=⎧⎧⇒⎨⎨=+=⎩⎩以上求出01ββ和反映了E (Y |X i )和X i 之间的真实关系,即所求的总体回归方程为:()|170.6i i i E Y X X =+,其图形为:③样本回归模型:总体通常难以得到,因此只能通过抽样得到样本数据。
如在例1中,通过抽样考察,我们得到了20个家庭的样本数据:那么描述样本数据中因变量Y 和自变量X 之间非确定依赖关系的模型ˆY X e β=+就称为样本回归模型。
④样本回归方程(线):通过样本数据估计出ˆβ,得到样本观测值的拟合值与解释变量之间的关系方程ˆˆY X β=称为样本回归方程。
如下图所示:⑤四者之间的关系:ⅰ:总体回归模型建立在总体数据之上,它描述的是因变量Y 和自变量X 之间的真实的非确定型依赖关系;样本回归模型建立在抽样数据基础之上,它描述的是因变量Y 和自变量X 之间的近似于真实的非确定型依赖关系。
线性回归模型的建模与分析方法

线性回归模型的建模与分析方法线性回归模型是一种常用的统计学方法,用于研究自变量与因变量之间的关系。
在本文中,我们将探讨线性回归模型的建模与分析方法,以及如何使用这些方法来解决实际问题。
一、线性回归模型的基本原理线性回归模型假设自变量与因变量之间存在线性关系,即因变量可以通过自变量的线性组合来预测。
其基本形式可以表示为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中,Y表示因变量,X1、X2、...、Xn表示自变量,β0、β1、β2、...、βn表示回归系数,ε表示误差项。
二、线性回归模型的建模步骤1. 收集数据:首先需要收集自变量和因变量的相关数据,确保数据的准确性和完整性。
2. 数据预处理:对数据进行清洗、缺失值处理、异常值处理等预处理步骤,以确保数据的可靠性。
3. 模型选择:根据实际问题和数据特点,选择适合的线性回归模型,如简单线性回归模型、多元线性回归模型等。
4. 模型拟合:使用最小二乘法等方法,拟合回归模型,得到回归系数的估计值。
5. 模型评估:通过统计指标如R方值、调整R方值、残差分析等,评估模型的拟合优度和预测能力。
6. 模型应用:利用已建立的模型进行预测、推断或决策,为实际问题提供解决方案。
三、线性回归模型的分析方法1. 回归系数的显著性检验:通过假设检验,判断回归系数是否显著不为零,进一步判断自变量对因变量的影响是否显著。
2. 多重共线性检验:通过计算自变量之间的相关系数矩阵,判断是否存在多重共线性问题。
若存在多重共线性,需要进行相应处理,如剔除相关性较高的自变量。
3. 残差分析:通过观察残差的分布情况,判断模型是否符合线性回归的基本假设,如误差项的独立性、正态性和方差齐性等。
4. 模型诊断:通过观察残差图、QQ图、杠杆值等,判断是否存在异常值、离群点或高杠杆观测点,并采取相应措施进行修正。
5. 模型优化:根据模型评估结果,对模型进行优化,如引入交互项、非线性变换等,以提高模型的拟合效果和预测准确性。
线性回归模型的构建与分析

线性回归模型的构建与分析线性回归是统计学中一种常见的建模方法,用于研究自变量与因变量之间的线性关系。
在实际应用中,线性回归模型被广泛用于预测、分析和建模。
本文将介绍线性回归模型的构建与分析过程,包括数据准备、模型建立、参数估计、模型评估等内容。
一、数据准备在构建线性回归模型之前,首先需要准备数据集。
数据集应包括自变量(特征)和因变量(目标变量),并且需要保证数据的质量和完整性。
通常情况下,我们会对数据进行清洗、缺失值处理、特征选择等操作,以确保数据的可靠性和有效性。
二、模型建立线性回归模型的数学表达形式为:$$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_nX_n +\varepsilon$$其中,$Y$为因变量,$\beta_0$为截距,$\beta_1, \beta_2, ...,\beta_n$为自变量的系数,$X_1, X_2, ..., X_n$为自变量,$\varepsilon$为误差项。
在建立模型时,需要根据实际问题选择合适的自变量,并利用最小二乘法等方法估计模型参数。
最小二乘法是一种常用的参数估计方法,通过最小化观测值与模型预测值之间的残差平方和来求解模型参数。
三、参数估计参数估计是线性回归模型中的关键步骤,它决定了模型的准确性和可靠性。
在参数估计过程中,我们需要计算各个自变量的系数$\beta_1, \beta_2, ..., \beta_n$,以及截距$\beta_0$。
这些参数的估计值将决定模型的形状和拟合程度。
通过最小二乘法可以求解出参数的闭式解,也可以利用梯度下降等迭代方法进行参数估计。
在实际应用中,通常会结合交叉验证等技术来选择最优的模型参数,以提高模型的泛化能力。
四、模型评估模型评估是判断线性回归模型好坏的重要标准。
常用的模型评估指标包括均方误差(Mean Squared Error,MSE)、决定系数(Coefficient of Determination,$R^2$)、残差分析等。
利用Excel进行回归分析和模型建立

利用Excel进行回归分析和模型建立回归分析是一种统计方法,用于研究因变量与一个或多个自变量之间的关系。
而Excel作为数据分析的重要工具,可以帮助我们进行回归分析和模型建立。
本文将为你介绍如何利用Excel进行回归分析和模型建立。
一、数据准备在进行回归分析前,首先需要准备好需要分析的数据。
打开Excel 并创建一个新的工作表。
将需要分析的数据按照表格的形式输入到工作表中。
确保每一列代表一个自变量,最后一列为因变量。
二、数据清理在进行回归分析前,有时候需要对数据进行清理和处理。
可以使用Excel提供的各种函数和工具来完成数据清理的任务。
例如,可以使用函数去除重复值、处理缺失值、转换数据类型等。
三、建立回归模型1. 打开Excel并在工作表中选择“数据”选项卡。
2. 点击“数据分析”按钮,在弹出的窗口中选择“回归”。
3. 在“回归”对话框中,将因变量和自变量的范围输入到对应的文本框中。
确保勾选上“标签”和“残差”选项。
4. 点击“确定”按钮,Excel会自动进行回归分析,并在工作表中生成回归结果的输出。
四、解读回归结果1. 回归输出的重要部分是回归方程。
它告诉我们因变量与自变量之间的关系。
回归方程通常以Y = a + bX的形式表示,其中Y是因变量,X是自变量,a是截距,b是斜率。
2. 另一个重要的输出是R方值,它反映了回归模型的拟合优度。
R方越接近1,说明模型拟合得越好。
3. 此外,还可以通过分析回归系数的显著性来判断自变量对因变量的影响。
一般情况下,显著性水平低于0.05被认为是统计显著的。
五、模型诊断在建立回归模型后,我们还需要对模型进行诊断,以确保模型的合理性和准确性。
1. 可以通过观察残差图来判断模型是否存在异方差性或数据点的异常值。
2. 可以使用Excel提供的其他统计函数和工具来进行正态性检验、多重共线性检验等。
六、模型优化如果回归模型存在问题,可以通过调整模型中的自变量或添加新的自变量来改善模型的拟合效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x 21 23 25 27 29 32 35 z 1.946 2.398 3.045 3.178 4.190 4.745 5.784
求得回归直线方程为^z =0.272x-3.849,
∴^y =e0.272x-3.849.
(8 分)
残差
yi
7
11
21
24
66
115 325
^yi 6.443 11.101 19.125 32.950 56.770 128.381 290.325
^ei 0.557 -0.101 1.875 -8.950 9.23 -13.381 34.675
(3)当x=40时,y=e0.272x-3.849≈1 131.
(10分) (12分)
小结 解决非线性回归问题的方法及步骤 (1)确定变量:确定解释变量为x,预报变量为y; (2)画散点图:通过观察散点图并与学过的函数(幂、指数、 对数函数、二次函数)作比较,选取拟合效果好的函数模型; (3)变量置换:通过变量置换把非线性问题转化为线性回归问 题; (4)分析拟合效果:通过计算相关指数等来判断拟合效果; (5)写出非线性回归方程.
[规范解答] (1)作出散点图如下图,从散点图可以看出x与y
不具有线性相关关系,根据已有知识可以发现样本点分布
在某一条指数函数曲线y=c1ec2x的周围,其中c1、c2为待
定的参数.
(4分)
(2)对两边取对数把指数关系变为线性关系,令z=ln y,则 有变换后的样本点应分布在直线z=bx+a,(a=ln c1,b= c2)的周围,这样就可以利用线性回归模型来建立y与x之间 的非线性回归方程了,数据可以转化为:
残差 图法
残差点比较均匀地落在水平的带状区域内,说明选 用的模型比较适合,这样的带状区域的宽度越窄, 说明模型拟合精度越高
残差平 方和
n
残差平方和为__i=_1__(y_i_-__^y_)2,残差平方和_越__小__,
模型拟合效果越好
相关指 数R2
n
yi-^yi2
i=1
R2 = 1 -
,R2 表示_解__释__变量对
i=1
i 1
iห้องสมุดไป่ตู้1
i=1
R2 1 3.1643 0.9999. 25553.3
即解释变量天数对预报变量繁殖细菌得个数解释了99.99%.
强化补清
完成教材全解相关内容
3.刻画回归效果的方式
数据点和它在回归直线上相应位置的差异(yi-y^i)是随
残差
机误差.称e^i=yi-y^i 为残差,e^i 称为相应于点(xi,yi)的
n
残差. (yi-y^i)2 称为残差平方和
i=1
残差 图
利用图形来分析残差特性,作图时纵坐标为__残__差_, 横坐标可以选为_样__本__编__号__,或_身__高__数__据__,或 _体__重__估__计__值__等,这样作出的图形称为残差图
x
1
2
3
4
5
6
Z 1.79 2.48 3.22 3.89 4.55 5.25
由计数器算得 Zˆ =0.69X 1.112 则有 yˆ=e0.69x1.112
(3) yˆ
6.06 12.09 24.09 48.04 95.77 190.9
y
6
12 25
49
95
190
n
n
n
n
eˆi2 ( yi yˆi )2 3.1643, ( yi y)2 yi2 ny2 25553.3.
独立自学
1.回归分析 回归分析是对具有_相__关__关__系__的两个变量进行统计分析的一 种常用方法.
2.线性回归模型 (1)由散点图易发现,样本点散布在某一条直线附近,而不 是一条直线上,不能用一次函数y=bx+a描述它们之间的 关系,因此用线性回归模型y=bx+a+e来表示,其中a、b 为未知参数,e为_随__机__误__差__ .
(4)按一定规则估计回归方程中的参数(如最小二乘法)。
(5)得出结果后分析残差图是否有异常(个别数据对应 残差过大,或残差呈现不随机的规律性,等等),过存在 异常,则检查数据是否有误,或模型是否合适等。
为了研究某种当细菌堂随诊时学间x变化,繁殖的个数,收
集数据如下:
天数x/ 1 2
天
繁殖个数 6 12
(1)作出散点图并求线性回归方程; (2)求出R2; (3)进行残差分析. [思路探索] 作残差分析时,一般从以下几个方面予以说 明:(1)散点图;(2)相关指数;(3)残差图中的异常点和样 本点的带状分布区域的宽窄.
[自主解答] (1)散点图如图
-x =16(5+10+15+20+25+30)=17.5, -y =16(7.25+8.12+8.95+9.90+10.9+11.8)≈9.487,
6
所以
6
(yi-^yi)2≈0.013 18,
(yi--y )2=14.678 4.
i=1
i=1
所以,R2=1-01.40.61378148≈0.999 1, 回归模型的拟合效果较好.
(3)由残差表中的数值可以看出第3个样本点的残差比较大, 需要确认在采集这个数据的时候是否有人为的错误,如果 有的话,需要纠正数据,重新建立回归模型;由表中数据 可以看出残差点比较均匀地落在不超过0.15的狭窄的水平 带状区域中,说明选用的线性回归模型的精度较高,由以 上分析可知,弹簧长度与拉力成线性关系. 规律方法 当资料点较少时,也可以利用残差表进行残差 分析,注意计算数据要认真细心,残差分析要全面.
n
yi--y 2
i=1
_预__报__变量变化的贡献率,R2 越接近于 1,表 示回归的效果越好
引导探究
【例1】 为研究重量x(单位:克)对弹簧长度y(单位:厘米)的影 响,对不同重量的6个物体进行测量,数据如下表所示:
x5
10 15 20 25 30
y 7.25 8.12 8.95 9.90 10.9 11.8
目标升华:
一般地,建立回归模型的基本步骤为:
(1)确定研究对象,明确哪个变量是解释变量,哪个变量 是预报变量。
(2)画出确定好的解释变量和预报变量的散点图,观察它 们之间的关系(如是否存在线性关系等)。
(3)由经验确定回归方程的类型(如我们观察到数据呈线 性关系,则选用线性回归方程y=bx+a).
6
6
x2i =2 275,xiyi=1 076.2
i=1
i=1
计算得,^b≈0.183,^a≈6.285, 所求回归直线方程为^y =0.183x+6.285. (2)列表如下: yi-^yi 0.05 0.005 -0.08 -0.045 0.04 0.025 yi--y -2.24 -1.37 -0.54 0.41 1.41 2.31
课题导入
前面我们已经初步学习了线性回归分析这节课我们继 续来对回归模型的建立和分析做一些探讨
本节课我们将介绍相关知识
目标引领
了解随机误差、残差、残差分析的概念; 会用残差分析判断线性回归模型的拟合效
果; 掌握建立回归模型的步骤; 通过对典型案例的探究,了解回归分析的
基本思想方法和初步应用.
y/个
3
4
25 49
56
95 190
(1)用天数作解释变量,繁殖个数作预报变量,作出这些
数据的散点图; (2) 描述解释变量与预报变量
繁殖个数
之间的关系;
(3) 计算残差、相关指数R2.
解:(1)散点图如右所示
天数
的周(围2,)于由是散令点Z图=l看n出y,样则本点分布在一条指数函数Cy=1eC2x
【例2】 下表为收集到的一组数据:
x 21 23 25 27 29 32 35 y 7 11 21 24 66 115 325
(1)作出x与y的散点图,并猜测x与y之间的关系; (2)建立x与y的关系,预报回归模型并计算残差; (3)利用所得模型,预报x=40时y的值. 审题指导 (1)画出散点图或进行相关性检验,确定两变 量x、y是否线性相关.由散点图得x、y之间的回归模型. (2)进行拟合,预报回归模型,求回归方程.
