初中数学九大几何模型-初中几何九大模型-初中九大几何模型
初中数学九大几何模型

初中数学九大几何模型、手拉手模型----旋转型全等(1)等边三角形【条件】:△ OAB^H A OCD均为等边三角形;DAED【结论】:①厶OA3A OBD②/ AEB=60 :③OE平分/【条件】:△ OAB^H A OCD均为等腰直角三角形;【结论】:①厶OA3A OBD②/ AEB=90 :③OE平分/ AEDED【结论】:①右图中△ OC3A OAB>n A OAS A OBD②延长AC交BD于点E,必有/ BECN BOA③ AC OD tan/OCD④BD±AC⑤连接AD BC,必有AD2 BC2 AB 2三、模型三、对角互补模型(1)全等型-90 °【条件】:①/ AOB=/ DCE=90 :②0C平分/ AOB【结论】:①CD=CE②OD+OE= 2 OC③S^DCESA OCDsCD :⑥ S^BCD证明提示:①作垂直,如图2,证明△ CDM^A CEN②过点C作CF丄OC 如图3,证明△FEC※当/ DCE的一边交AO的延长线于D时(如图4):以上三个结论:①CD=CE ② OE-OD=''2 OC③SA OCESA OCD(2) 全等型-120【条件】:①/ AOB=N DCE=120 :②。
平分/ AOB:3【结论】:① CD=CE ②OD+OE=OC ③ S^CES ^OCDS ^OCE— OC 2 4证明提示:①可参考“全等型 -90。
”证法一;②如右下图:在 OB 上取一点F ,使OF=OC 证明△ OCF 为等边三角形。
【条件】:①/ AOB=2i,/DCE=18O-2a;②CD=CE 【结论】:①OC 平分/ AOB ②OD+OE=2OCcos a; ③ S A DCESA OCDSA OCEOC sin a cos a※当/ DCE 的一边交AO 的延长线于 D 时(如右下图):原结论变成:① ______________________________________________________ ② ________________________________________________________ ; ③ ________________________________________________________ 。
初中数学九大几何模型-初中几何九大模型-初中九大几何模型
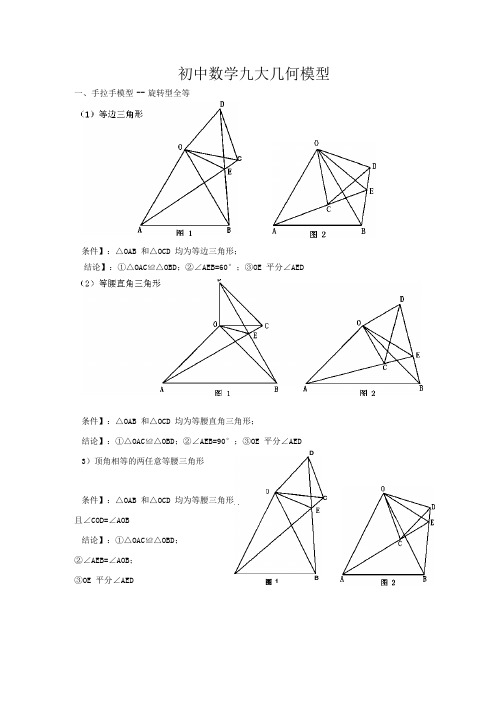
初中数学九大几何模型结论】:①△OAC≌△OBD;②∠AEB=60°;③OE 平分∠AED条件】:△OAB 和△OCD 均为等腰直角三角形;结论】:①△OAC≌△OBD;②∠AEB=90°;③OE 平分∠AED 3)顶角相等的两任意等腰三角形条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB结论】:①△OAC≌△OBD; ②∠AEB=∠AOB; ③OE 平分∠AEDC条件】:△OAB 和△OCD 均为等边三角形;一、手拉手模型 -- 旋转型全等B图 1DC二、模型二:手拉手模型--- 旋转型相似(1)一般情况【条件】:CD∥AB,将△OCD 旋转至右图的位置②延长 AC交 BD 于点E,必有∠BEC=∠BOA;③BD= OD= OB=tan∠OCD;④BD⊥AC;AC OC OA2⑤连接AD、BC,必有AD2+ BC2= AB2+CD2;⑥S三、模型三、对角互补模型1)全等型-90°结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;O O△BCD条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOBB2)全等型-120°条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB结论】:①CD=CE;②OD+OE=OC;③S△DCE = S△OCD + S△OCE = 3OC2证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB上取一点F,使OF=OC,证明△OCF为等边三角形。
3)全等型-任意角ɑ条件】:①∠AOB=2ɑ,∠DCE=180-2ɑ;②CD=CE;结论】:①OC 平分∠AOB;②OD+OE=2OC·cosɑ;③S△DCE = S△OCD + S△OCE =OC2sinαcosα※当∠DCE 的一边交 AO的延长线于 D 时(如右下图):原结论变成:①可参考上述第②种方法进行证明。
初中数学九大几何模型
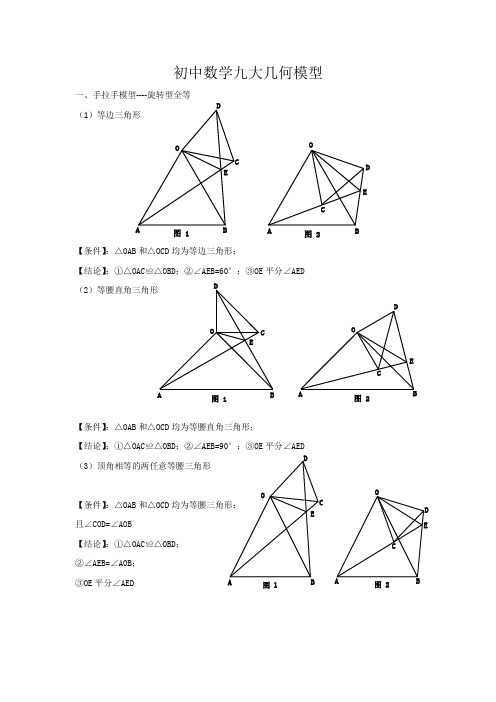
初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
(完整版)初中数学九大几何模型

初中数学九大几何模型OD ECABAED DOECBABOC ECAEDD图2图 2、手拉手模型 - 旋转型全等D E③OE 平分∠ AED图 2图 1 OABD OAO ②∠ AEB=∠AOB ; 且∠ COD=∠AOB1)等边三角形3)顶角相等的两任意等腰三角形 2)等腰直角三角形图 1图 1C结论】:①△ OAC ≌△ OBD ;C条件】:△ OAB 和△ OCD 均为等边三角形条件】:△ OAB 和△ OCD 均为等腰直角三角形条件】:△ OAB 和△ OCD 均为等腰三角形 结论】:①△ OAC ≌△ OBD ;②∠ AEB=60°;③ OE 平分∠ 结论】:①△ OAC ≌△ OBD ;②∠ AEB=90°;③ OE 平分∠、模型二:手拉手模型 -- 旋转型相似(1)一般情况 【条件】:CD ∥AB , 将△ OCD 旋转至右图的位置 O OD EA A结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ;②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOA2)特殊情况 条件】:CD ∥ AB ,∠ AOB=90°将△ OCD 旋转至右图的位置 A 结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ; ②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOA ; ③ A BD C O O C D O O A B tan ∠OCD ;④BD ⊥AC ; ⑤连接 AD 、BC ,必有 AD 2 BC 2 AB 2三、模型三、对角互补模型1)全等型 -90 ° 条件】:①∠ AOB=∠ DCE=90°;② OC 平分∠ AOB结论】:① CD=CE ;② OD+OE= 2 OC ;③ S △DCE CD ;⑥S△BCD证明提示: ①作垂直,如图 2,证明△ CDM ≌△ CEN ②过点 C 作 CF ⊥ OC , 如图 3,证明△ ODC ≌△ FEC ※当∠ DCE 的一边交 AO 的延长线于 D 时(如图 4): S△OCDS以上三个结论:① CD=CE ;② OE-OD= 2 OC ; ③ S △ OCE S △ OCD2)全等型 -120 °条件】:①∠ AOB=2∠ DCE=120°;② OC 平分∠ AOB32 结论】:① CD=CE ;② OD+OE=O ;C ③ S △DCES △OCDS △OCEOC 2 4证明提示:①可参考“全等型 -90 °”证法一;②如右下图:在 OB 上取一点 F ,使 OF=OC ,证明△ OCF 为等边三角形。
初中几何九大模型汇总

初中几何九大模型汇总1. 点(Point):点是几何中最基本的对象,它没有长度、宽度或高度,只有位置。
点通常用大写字母标记,例如A、B、C等。
2. 线段(Line Segment):线段是由两个点确定的,它是一条有限长度的直线。
线段通常用两个字母标记,如AB。
线段具有长度和方向。
3. 直线(Line):直线是无限延伸的线段,它由无数个点组成,没有起点和终点。
直线通常用一条小箭头标记,如AB。
直线上的任意两点可以确定一条直线。
4. 角(Angle):角是由两条射线共享一个起点而形成的,它是两边之间的夹角。
角可以分为锐角、直角和钝角。
角通常用大写字母标记,如∠ABC。
5. 三角形(Triangle):三角形是由三条线段组成的一个闭合图形。
三角形的内部有三个顶点和三条边。
三角形可以根据边长和角度分为不同的类型,如等边三角形、等腰三角形等。
6. 四边形(Quadrilateral):四边形是由四条线段组成的一个闭合图形。
四边形的内部有四个顶点和四条边。
四边形可以根据边长和角度分为不同的类型,如矩形、正方形、菱形等。
7. 五边形(Pentagon):五边形是由五条线段组成的一个闭合图形。
五边形的内部有五个顶点和五条边。
五边形可以分为凹五边形和凸五边形。
8. 六边形(Hexagon):六边形是由六条线段组成一个闭合图形。
六边形的内部有六个顶点和六条边。
六边形可以分为凹六边形和凸六边形。
9. 圆形(Circle):圆形是由一个中心点和一个半径确定的,它由无数个点组成的闭合曲线。
圆形的内部为圆的内部,外部为圆的外部。
通过研究这九大基本模型,我们可以深入了解几何形状的特征和性质。
学生们可通过观察和比较不同形状的特点,理解几何变换、相似性、对称性等概念。
此外,还可以通过实际生活中的例子,将几何知识应用于实际问题中,提高学生的应用能力。
总之,初中几何九大模型是学习几何必不可少的基础,通过对它们的认识和掌握,可以帮助学生更好地理解和应用几何知识。
初中数学九大几何模型
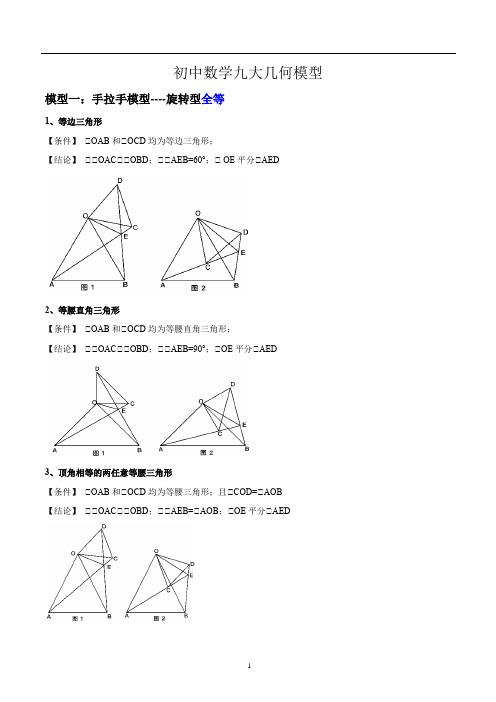
初中数学九大几何模型模型一:手拉手模型----旋转型全等1、等边三角形【条件】△OAB和△OCD均为等边三角形;【结论】△△OAC△△OBD;△△AEB=60°;△ OE平分△AED2、等腰直角三角形【条件】△OAB和△OCD均为等腰直角三角形;【结论】△△OAC△△OBD;△△AEB=90°;△OE平分△AED3、顶角相等的两任意等腰三角形【条件】△OAB和△OCD均为等腰三角形;且△COD=△AOB【结论】△△OAC△△OBD;△△AEB=△AOB;△OE平分△AED模型二:手拉手模型----旋转型相似1、一般情况【条件】 CD△AB ,将△OCD 旋转至右图的位置【结论】 △右图中△OCD△△OAB→→→△OAC△△OBD ;△延长AC 交BD 于点E ,必有△BEC=△BOA2、特殊情况【条件】 CD△AB ,△AOB=90° 将△OCD 旋转至右图的位置【结论】 △右图中△OCD△△OAB→→→△OAC△△OBD ; △延长AC 交BD 于点E ,必有△BEC =△BOA ; △BD AC=OD OC=OB OA=tan∠OCD ;△BD△AC ;△连接AD 、BC ,必有AD 2+BC 2=AB 2+CD 2 ; △BD AC S ABCD •=21模型三:对角互补模型1、全等型-90°【条件】 △△AOB=△DCE=90°;△OC 平分△AOB【结论】 △CD=CE ;△OD+OE=2OC ;△2ODCE OCD OCE 12S S S OC ∆∆=+= 证明提示:△作垂直,如图2,证明△CDM△△CEN△过点C 作CF△OC ,如图3,证明△ODC△△FEC ※当△DCE 的一边交AO 的延长线于D 时(如图4):以上三个结论:△CD=CE ;△OE -OD=2OC ;△2△OCD △OCE OC 21S S =-2、全等型-120°【条件】 △△AOB=2△FCE=120°;△OC 平分△AOB【结论】 △CF=CE ;△OF+OE=OC ;△2OFCE OCF OCE 4S S S ∆∆=+=证明提示:△可参考“全等型-90°”证法一;△如图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
初中数学九大几何模型-初中几何九大模型-初中九大几何模型之欧阳道创编
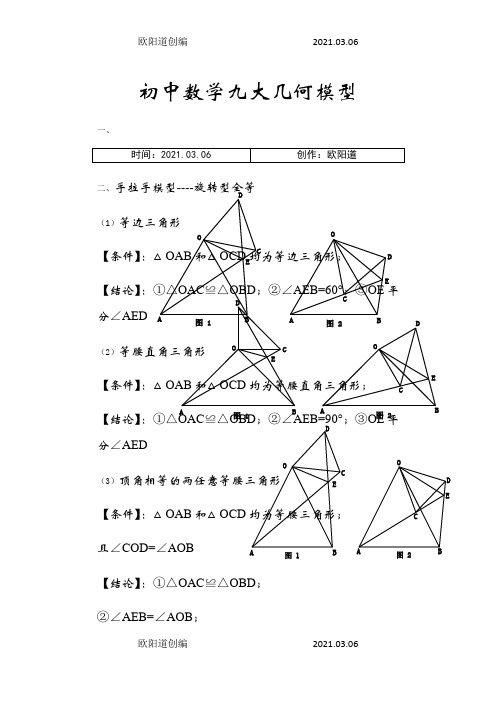
初中数学九大几何模型一、二、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED(2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED(3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ;OAB CDE 图 1OAB CD E图 2OABC DE图 1OBCDE图 2OABC DEOCD E图 1图 2③OE 平分∠AED二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB ,将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB→→→△OAC ∽△OBD ;②延长AC 交BD 于点E ,必有∠BEC=∠BOA(2)特殊情况【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB→→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD⨯= OA BCDOB CDEO BCDEOBCDACD三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB 【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE△OCD △DCEOC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ;③2△OCD △OCEOC 21S S =-(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCEOC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;A OBCDE M N 图 2A O BCDE F 图 3A OBCDEMN图 4②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
(完整版)初中数学九大几何模型

初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学九大几何模型之五兆芳芳创作一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED(2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED(3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED二、模型二:手拉手模型----旋转型相似OAB CDE 图 1OAB C D E图 2OABCDE图 1OACDE图 2OABC D EOCD E图 1图 2OCOCDE(1)一般情况【条件】:CD ∥AB ,将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB→→→△OAC∽△OBD ;②延长AC 交BD 于点E ,必有∠BEC=∠BOA(2)特殊情况【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB→→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD ACBDtan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB BC AD +=+;⑥BD AC 21S △BCD ⨯= 三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB 【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCEOC 21S S S =+= OAB CDEOBCDA OBCDE 图 1A OBCDE M N 图 2证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCEOC 21S S =-(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE;②OD+OE=OC ;③2△OCE △OCD △DCEOC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形.(3)全等型-任意角ɑ【条件】:①∠AOB=2ɑ,∠DCE=180-2ɑ;②CD=CE ;【结论】:①OC 平分∠AOB ;②OD+OE=2OC·cos ɑ; ③αcos αsin OC S S S 2△OCE △OCD △DCE⋅⋅=+=A O BCDE F 图 3A OBCDEMN图 4※当∠DCE 的一边交AO 的延长线于D 时(如右下图): 原结论酿成:①; ②; ③.可参考上述第②种办法进行证明.请思考初始条件的变更对模型的影响.对角互补模型总结:①罕有初始条件:四边形对角互补,注意两点:四点共圆有直角三角形斜边中线;②初始条件“角平分线”与“两边相等”的区别;③注意OC 平分∠AOB 时,∠CDE=∠CED=∠COA=∠COB 如何引导?四、模型四:角含半角模型90°(1)角含半角模型90°---1【条件】:①正方形ABCD ;②∠EAF=45°;【结论】:①EF=DF+BE ;②△CEF 的周长为正方形ABCD 周长的一半; 也可以这样:AOBEDCAO BCD E【条件】:①正方形ABCD ;②EF=DF+BE ;【结论】:①∠EAF=45°;(2)角含半角模型90°---2【条件】:①正方形ABCD ;②∠EAF=45°;【结论】:①EF=DF-BE ;(3)角含半角模型90°---3【条件】:①Rt △ABC ;②∠DAE=45°;【结论】:222DE CE BD =+(如图1)若∠DAE 旋转到△ABC 外部时,结论222DE CE BD =+仍然成立(如图2)(4)角含半角模型90°变形【条件】:①正方形ABCD ;②∠EAF=45°;【结论】:△AHE 为等腰直角三角形;证明:连接AC (办法不唯一) ∵∠DAC=∠EAF=45°,∴∠DAH=∠CAE ,又∵∠ACB=∠ADB=45°; ∴△DAH ∽△CAE ,∴AEACAHDA= ABCDFABDEFG ABC DEABCDE FABCD GHFEABCD GHFE∴△AHE ∽△ADC ,∴△AHE 为等腰直角三角形模型五:倍长中线类模型(1)倍长中线类模型---1【条件】:①矩形ABCD ;②BD=BE ;③DF=EF ; 【结论】:AF ⊥CF模型提取:①有平行线AD ∥BE ;②平行线间线段有中点DF=EF ;可以机关“8”字全等△ADF ≌△HEF.(2)倍长中线类模型---2【条件】:①平行四边形ABCD ;②BC=2AB ;③AM=DM ;④CE ⊥AB ;【结论】:∠EMD=3∠MEA帮助线:有平行AB ∥CD ,有中点AM=DM ,延长EM ,机关△AME ≌△DMF ,连接CM 机关等腰△EMC ,等腰△MCF.(通过机关8字全等线段数量及位置关系,角的大小转化)模型六:相似三角形360°旋转模型AB C E F DH ABFDHABCDME ABCDME F(1)相似三角形(等腰直角)360°旋转模型---倍长中线法 【条件】:①△ADE 、△ABC 均为等腰直角三角形;②EF=CF ; 【结论】:①DF=BF ;②DF ⊥BF帮助线:延长DF 到点G ,使FG=DF ,连接CG 、BG 、BD ,证明△BDG 为等腰直角三角形; 突破点:△ABD ≌△CBG ;难点:证明∠BAO=∠BCG (2)相似三角形(等腰直角)360°旋转模型---补全法【条件】:①△ADE 、△ABC 均为等腰直角三角形;②EF=CF ;【结论】:①DF=BF ;②DF ⊥BF帮助线:机关等腰直角△AEG 、△AHC ;帮助线思路:将DF 与BF 转化到CG 与EF.(3)任意相似直角三角形360°旋转模型---补全法【条件】:①△OAB ∽△ODC ;②∠OAB=∠ODC=90°;③BE=CE ;【结论】:①AE=DE ;②∠AED=2∠ABO帮助线:延长BA 到G ,使AG=AB ,延长CD 到点H 使DH=CD ,补全△OGB 、△OCH 机关旋转模型.转化AE 与DEA E BDFCA EBDFCHGA EBDFCABDFCGOADOADG H到CG 与BH ,难点在转化∠AED.(4)任意相似直角三角形360°旋转模型---倍长法【条件】:①△OAB ∽△ODC ;②∠OAB=∠ODC=90°;③BE=CE ;【结论】:①AE=DE ;②∠AED=2∠ABO帮助线:延长DE 至M ,使ME=DE ,将结论的两个条件转化为证明△AMD ∽△ABO ,此为难点,将△AMD ∽△ABC 持续转化为证明△ABM ∽△AOD ,使用两边成比例且夹角相等,此处难点在证明模型七:最短路程模型(1)最短路程模型一(将军饮马类)最后都转化到:“特点:①动点在直线上;②起点,终点固定(2)最短路程模型二(点到直线类1)【条件】:①OC 平分∠AOB ;②M 为OB 上一定点;③P 为OC 上一动点;④Q 为OB 上一动点;【问题】:求MP+PQ 最小时,P 、Q 的位置?OAB DCE帮助线:将作Q 关于OC 对称点Q’,转化PQ’=PQ ,过点M 作MH ⊥OA ,则MP+PQ=MP+PQ’≥MH(垂线段最短)(3)最短路程模型二(点到直线类2)【条件】:A(0,4),B(-2,0),P(0,n ) 【问题】:n 为何值时,PA 55PB +最小? 求解办法:①x 轴上取C(2,0),使sin ∠OAC=55;②过B作BD ⊥AC ,交y轴于点E ,即为所求;③tan ∠EBO=tan ∠(4)【条件】:①线段OA=4旋转;【问题】:AB 的最大值,最小值辨别为多少?【结论】:以点O 为圆心,OB 为半径作圆,如图所示,将问题转化为“三角形两边之和大于第三边,两边之差小于第三边”. 最大值:OA+OB ;最小值:OA-OBAPOQ MBQ'HPA OAB 最小值位置最大值位置【条件】:①线段OA=4,OB=2;②以点O 为圆心,OB ,OC 为半径作圆;③点P 是两圆所组成圆环内部(含鸿沟)一点;【结论】:若PA 的最大值为10,则为1,则OC= 3 ;若PA 的最小值为2,则PC【条件】:①Rt △OBC ,∠OBC=30°;②OC=2;③OA=1;④点P 为BC 上动点(可与端点重合); ⑤△OBC 绕点O旋转【结论】:PA 最大值为OA+OB=321+;PA 的最小值为13OA OB 21-==如下图,圆的最小半径为O 到BC 垂线段长.【条件】:在△∠C ;帮助线:以BC 的垂直平分线为对称轴,作点A 的对称点A’,连接AA’、BA’、CA’、则BA=AA’=CA’(注意这个结论)此种帮助线作法是二倍角三角形罕有的帮助线作法之一,不BCAB ABA'是唯一作法.模型九:相似三角形模型(1)相似三角形模型--根本型平行类:DE ∥BC ;A 字型 8字型 A 字型 结论:BCDEAC AE ABAD==(注意对应边要对应)(2)相似三角形模型---斜交型【条件】:如右图,∠AED=∠ACB=90°; 【结论】:AE×AB=AC×AD【条件】:如右图,∠ACE=∠ABC ; 【结论】:AC2=AE×AB第四个图还存在射影定理:AE×EC=BC×AC ;BC2=BE×BA ;CE2=AE×BE ;(3)相似三角形模型---一线三等角型【条件】:(1)图:∠ABC=∠ACE=∠CDE=90°;(2)图:∠ABC=∠ACE=∠CDE=60°;A B C DE图(1)(3)图:∠ABC=∠ACE=∠CDE=45°; 【结论】:①△ABC ∽△CDE ;②AB×DE=BC×CD ; 一线三等角模型也经经常使用来成立方程或函数关系.(4)相似三角形模型---圆幂定理型【条件】:(2)图:PA 为圆的切线;【结论】:(1)图:PA×PB=PC×PD (2)图:PA2=PC×PB; (3)图:PA×PB=PC×PD ;以上结论均可以通过相似三角形进行证明.ABCDE图(2)A图(1)。
