8-3-1逻辑推理.题库教师版
高考语文复习之逻辑推理题(教师版)

高考语文复习之逻辑推理题(教师版)考点探究2021年三套全国卷均在第21题设题考查了“语言表达准确”那个考点。
此题是从逻辑推理的角度设计的,要求对题中给出的各种结论(推断)进行评判,看是否符合客观实际,有无判定错误、推理偏颇以及说法绝对等逻辑问题。
2021年全国卷语用题要求:下面文字有三处推断存在问题,请参照①的方式,说明另外两处问题。
答题注意事项:1、推断(内容)★★★★★2、表述方式(形式)学会正确分析逻辑关系,提高解题能力典型例题下面文段有三处推断存在问题,请参照①的方式,说明另外两处问题。
(2021年全国卷Ⅱ第21题)云南的“思茅市”改成“普洱市”,四川的“南坪县”更名为“九寨沟县”后,都市的知名度都有了专门大提高,经济有了较快进展,可见,更名必定带来都市经济的进展。
我市的名字不够响亮,这严峻阻碍了我们的经济进展。
假如更名,就一定会带来我市的经济腾飞,因此,更名的事要尽快提到日程上来。
①更名并不一定能带来都市的进展。
②_________________________ 。
③_________________________。
②“都市名字不够响亮并不一定会严峻阻碍经济进展”③“更名并不一定会带来经济腾飞”实战演练1.下面文段有三处推断存在问题,请参考①的方式,说明另外两处问题。
(5分)手机是今天人类常使用的现代发明,能够满足生活中的所有需求,改变了人、社会,甚至世界。
作为工具的手机,几乎进化成人类躯体的一部分,手机里的信息,确实是一个人社会关系的全部。
没有手机的生活,会让人陷入惧怕的深潭。
①手机不一定能够满足生活中的所有需求。
②_____________________________。
③_____________________________。
手机里的信息不一定确实是一个人社会关系的全部没有手机的生活不一定会让人陷入惧怕的黑暗2.下面文段有三处推断存在问题,请参考①的方式,说明另外两处问题。
二年级上册简单逻辑推理题

二年级上册简单逻辑推理题
一、加法推理题
1. 2+2=4,3+3=6,那么4+3=?
2. 1+2+3=6,1+2+4=7,那么1+2+5=?
3. 2+3-4=1,3+4-5=2,那么4+5-6=?
二、减法推理题
1. 8-3=5,7-2=5,那么9-4=?
2. 10-6=4,9-5=4,那么8-7=?
3. 12-5=7,15-6=9,那么16-7=?
三、乘法推理题
1. 3*8=24,2*9=18,那么6*7=?
2. 7*7=49,6*8=48,那么8*8=?
3. 9*9+9=90,8*9+7=83,那么7*9+6=?
四、综合推理题
1. 小明有5个苹果,妈妈又给了他一些苹果,现在他一共有8个苹果。
请问妈妈给了他几个苹果?
2. 小华有5个本子,她把其中3个送给妹妹。
现在她还有几个本子?
3. 小明有3个玩具汽车,他给了弟弟一个玩具汽车。
现在他还有几个玩具汽车?
以上就是一些简单的逻辑推理题,适合二年级上册的学生进行思维训练和数学学习。
通过这些题目,可以锻炼学生的观察力、思考力和判断力,同时也可以帮助他们更好地理解和掌握数学知识。
河南省新乡市数学小学奥数系列8-3-1逻辑推理(二)

河南省新乡市数学小学奥数系列8-3-1逻辑推理(二)姓名:________ 班级:________ 成绩:________亲爱的同学,经过一段时间的学习,你们一定学到不少知识,今天就让我们大显身手吧!一、 (共37题;共163分)1. (1分) (2019六上·南康期末) 六年级1、2、3、4四个班举行拔河比赛,甲、乙、丙三个同学猜测四个班比赛的前三名名次.甲说:1班第三,3班第一;乙说:3班第二,2班第三;丙说:4班第二,1班第一.比赛结果,三个人都猜对了一半.那么,1班第________名,4班第________名.2. (5分)宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家”、“大作家”和“歌唱家”称呼他们,此外:⑴数学博士夸跳高冠军跳的高⑵跳高冠军和大作家常与宝宝一起看电影⑶短跑健将请小画家画贺年卡⑷数学博士和小画家关系很好⑸贝贝向大作家借过书⑹聪聪下象棋常赢贝贝和小画家问:宝宝、贝贝、聪聪各有哪两个外号吗?3. (1分)六年级四个班进行数学竞赛,小明猜想比赛的结果是:班第一名,班第二名,班第三名,班第四名.小华猜想比赛的结果是:班第一名,班第二名,班第三名,班第四名.结果只有小华猜到的班为第二名是正确的.那么这次竞赛的名次是________班第一名,________班第二名,________班第三名,________班第四名。
4. (5分)振华小学组织了一次投篮比赛,规定投进一球得分,投不进倒扣分.小亮投了个球,投进了个.那么,他应该得多少分?5. (5分)烟鬼甲每天抽50支烟,烟鬼乙每天抽10支烟。
5年后,烟鬼乙抽的烟比烟鬼甲抽的还多,为什么?6. (5分)架子上摆着大、中、小三种皮球,只知道小皮球每只20元,每层皮球的价钱同样多,每只中皮球和大皮球各需要多少元?7. (5分)给三个非常聪明的人各戴了一顶帽子.并且告诉他们,他们的帽子的颜色可能是红色的,也可能是蓝色的,没有其他颜色.且三人中至少有一个人的帽子是红色的.三人互相看了看,没有人能很快地说出自己戴的是什么颜色的帽子.三人又冥思苦想了一阵,几乎同时都猜到了自己戴了什么颜色的帽子.你知道他们三人各戴了什么颜色的帽子吗?请说明理由.8. (5分)甲、乙、丙、丁每人只会中、英、法、日四种语言中的两种,其中有一种语言只有一人会说.他们在一起交谈可有趣啦:⑴乙不会说英语,当甲与丙交谈时,却请他当翻译;⑵甲会日语,丁不会日语,但他们却能相互交谈;⑶乙、丙、丁找不到三人都会的语言;⑷没有人同时会日、法两种语言.请问:甲、乙、丙、丁各会哪两种语言?9. (5分)塑料袋里有六个橘子,如何均分给三个小孩,而塑料袋里仍有二个橘子?(不可以分开橘子)10. (5分)在下表中填入三人的名字。
一轮难题复习 推理与证明典型解答题 (教师版)
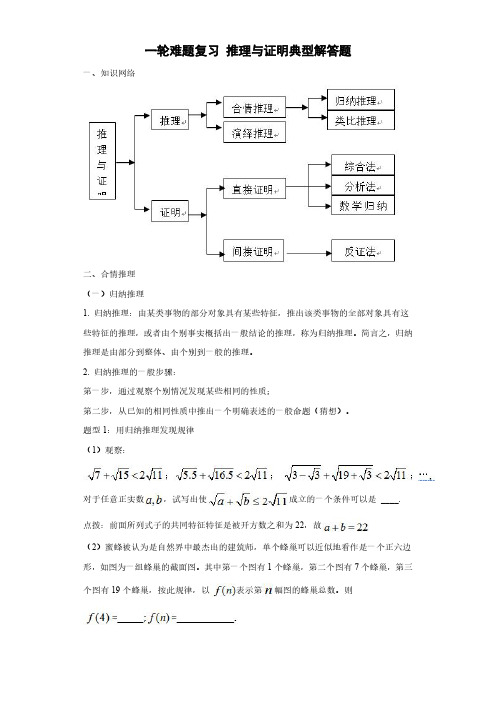
一轮难题复习推理与证明典型解答题一、知识网络二、合情推理(一)归纳推理1.归纳推理:由某类事物的部分对象具有某些特征,推出该类事物的全部对象具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理。
简言之,归纳推理是由部分到整体、由个别到一般的推理。
2.归纳推理的一般步骤:第一步,通过观察个别情况发现某些相同的性质;第二步,从已知的相同性质中推出一个明确表述的一般命题(猜想)。
题型1:用归纳推理发现规律(1)观察:对于任意正实数,试写出使成立的一个条件可以是____.点拨:前面所列式子的共同特征特征是被开方数之和为22,故(2)蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图。
其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以表示第幅图的蜂巢总数。
则【解题思路】找出的关系式[解析]总结:处理“递推型”问题的方法之一是寻找相邻两组数据的关系(二)类比推理1.类比推理:由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理。
简言之,类比推理是由特殊到特殊的推理。
2.类比推理的一般步骤:第一步:找出两类对象之间可以确切表述的相似特征;第二步:用一类对象的已知特征去推测另一类对象的特征,从而得出一个猜想.题型2:用类比推理猜想新的命题(1)已知正三角形内切圆的半径是高的,把这个结论推广到空间正四面体,类似的结论是______.【解题思路】从方法的类比入手[解析]原问题的解法为等面积法,即,类比问题的解法应为等体积法,即正四面体的内切球的半径是高总结:①不仅要注意形式的类比,还要注意方法的类比。
②类比推理常见的情形有:平面向空间类比;低维向高维类比;等差数列与等比数列类比;实数集的性质向复数集的性质类比;圆锥曲线间的类比等(三)合情推理1.定义:归纳推理和类比推理都有是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理。
11道经典逻辑推理题

11道经典的逻辑推理题(申请加精)猜帽子1有三顶红帽子和两顶蓝帽子。
将五顶中的三顶帽子分别戴在A、B、C三人头上。
这三人每人都只能看见其他两人头上的帽子,但看不见自己头上的帽子,并且也不知道剩余的两顶帽子的颜色。
问A:"你戴的是什么颜色的帽子?"A说:"不知道。
"问B:"你戴的是什么颜色的帽子?"B想了想之后,也说:"不知道。
"最后问C。
C回答说:"我知道我戴的帽子是什么颜色了。
"当然,C是在听了A、B的回答之后而作出推断的。
试问:C戴的是什么颜色的帽子?猜帽子2一群人开舞会,每人头上都戴着一顶帽子。
帽子只有黑白两种,黑的至少有一顶。
每个人都能看到其它人帽子的颜色,却看不到自己的。
主持人先让大家看看别人头上戴的是什幺帽子,然后关灯,如果有人认为自己戴的是黑帽子,就拍手。
第一次关灯,没有声音。
于是再开灯,大家再看一遍,关灯时仍然鸦雀无声。
一直到第三次关灯,才有劈劈啪啪打耳光的声音响起。
问有多少人戴着黑帽子?猜帽子3小明、小丰、小兰三位学生这学期在侦探推理竞赛中并列第一,但学校每年只会颁给一个人奖状,于是老师请他们放学后到办公室,决定谁拿这个奖状。
放学后,在办公室里老师让他们闭上眼,给他们每人戴了一顶帽子,再让他们挣开眼,然后说要看看他们的逻辑推理能力,并告诉他们帽子只有绿黄两种,请看到绿帽子的举手,谁先说出自己戴的帽子的颜色,就把奖状颁给谁。
三个人听后都举手了。
过了一会,小兰说:“我知道自己戴的是什么颜色的帽子了。
”请问小兰戴的是什么颜色的帽子?猜帽子4有3顶橙帽子,4顶青帽子,5顶紫帽子。
让10个人从矮到高站成一队,给他们每个人头上戴一顶帽子。
每个人都看不见自己戴的帽子颜色,只能看见站在前面比自己矮的人的帽子颜色。
所以最后一个人可以看见前面9个人头上帽子的颜色,而最前面那个人谁的帽子都看不见。
现在从最后那个人开始,问他是不是知道自己戴的帽子颜色,如果他回答说不知道,就继续问他前面那个人。
第七讲 逻辑推理(三) -教师版

(1)张教授的实验一共做了几个小时?
(2)他做完实验时,挂钟敲了多少下?
分析:由于挂钟只在整点报时,几点就报几下,共敲了39下,39要么是几个连续的小于13的正整数之和,要么是……。11,12,1,2……这样的几个正整数之和。只要知道报了几次时,也就知道了张教授的实验时间。
例1三名学生参加了若干科的考试,以考试名次积分,每科第一名得A分,第二名得B分,第三名得C分,且A>B>C>0,A,B,C都是整数。已知甲积分为22分,乙、丙积分都为9分,并且乙是英语第一名,问数学第二名是谁?
分析:甲、乙、丙三名学生参加了若干科的考试(至少2科),首先应估计到底是几科。依题意可列表如下:
若是第③、④种情况,乙都不可能得一个第一名且总分是9。
所以m不能是4。
(三)若m≥8,则A+B+C≤5,又A+B+C≥6,所以m≥8的情况不会出现。
(四)综上所述m只能是5。
解:设共有m科,m≥2,且m为整数。由题意可得m(A+B+C)=40=23×5,经分析可知m=5,A+B+C=8,由A,B,C是正整数,且C≥1可得下列2种情况:A=4,B=3,C=1或A=5,B=2,C=1。
若A=4,B=3,C=1,则乙不可能有一个第一名且总分是9。因此,A=5,B=2,C=1。
得分情况如下表:
说明:首先要把所有可能的得分情况逐一列举出来,有时,由于数据较多,还经常采用图表的办法帮助分析,使得分析过程清楚、简洁、一目了然,排除不合情理的情况,从而得出正确的结论。这是解决推理计算题目常用的排除法。
75道逻辑推理题及答案20道面试逻辑思维题目

75道逻辑推理题及答案20道面试逻辑思维题目【1】假设有一个池塘,里面有无穷多的水。
现有2个空水壶,容积分别为5升和6升。
问题是如何只用这2个水壶从池塘里取得3升的水。
由满6向空5倒,剩1升,把这1升倒5里,然后6剩满,倒5里面,由于5里面有1升水,因此6只能向5倒4升水,然后将6剩余的2升,倒入空的5里面,再灌满6向5里倒3升,剩余3升。
【2】周雯的妈妈就是豫林水泥厂的化验员。
一天,周雯走进化验室做作业。
略过后想要出去玩。
'等等,妈妈还要托福你一个题目,'她接着说道,'你看看这6只搞化验用的玻璃杯,前面3只盛满了水,后面3只是觑的。
你能够只移动1只玻璃杯,就便盛满水的杯子和空杯子间隔出来吗?'快乐动脑筋的周雯,就是学校里出名的'大机灵',她只想了一会儿就努力做到了。
恳请你想想看,'大机灵'就是怎样搞的?设杯子编号为abcdef,abc为满,def为空,把b中的水倒进e中即可。
【3】三个小伙子同时凤凰于飞了一个姑娘,为了同意他们谁能够嫁给这个姑娘,他们同意用枪展开一次对决。
小李的命中率就是30%,小黄比他好些,命中率就是50%,最差的枪手就是小林,他从不犯规,命中率就是%。
由于这个显而易见的事实,为公平确保安全,他们同意按这样的顺序:小李先开火,小黄第二,小林最后。
然后这样循环,直至他们只剩一个人。
那么这三个人中谁养下来的机会最小呢?他们都必须实行什么样的策略?小林在轮到自己且小黄没死的条件下必杀黄,再跟菜鸟李单挑。
所以黄在林活著的情况下必踢林,否则自己必死。
小李经过计算比较(过程略),会决定自己先打小林。
于是经排序,小李存有/≈33.6%的生机;小黄有/≈41.9%的生机;小林存有24.5%的生机。
哦,这样,那小李的第一枪会朝天开,以后当然是打敌人,谁活着打谁;小黄一如既往先踢林,小林还是先杀掉徐,冤家路窄啊!最后李,黄,林存活率约38:27:35;菜鸟活下来抱著得美人归的几率小。
逻辑思维题30题

逻辑思维题30题一、数字规律类1. 找规律:1,3,6,10,15,()- 解析:相邻两个数的差值依次为2、3、4、5,那么下一个差值应该是6。
15+6 = 21,所以括号里应填21。
2. 2,4,8,16,32,()- 解析:这组数字是后一个数为前一个数的2倍,32×2 = 64,所以括号里应填64。
3. 1,4,9,16,25,()- 解析:这些数依次是1²、2²、3²、4²、5²,那么下一个数就是6² = 36,括号里应填36。
二、逻辑推理类4. 甲、乙、丙三人中有一人是牧师,一人是骗子,一人是赌棍。
牧师只说真话,骗子只说假话,赌棍有时说真话有时说假话。
甲说:“丙是牧师。
”乙说:“甲是赌棍。
”丙说:“乙是骗子。
”那么甲、乙、丙分别是什么人?- 解析:假设甲是牧师,那么甲说“丙是牧师”就是假话,这与牧师说真话矛盾,所以甲不是牧师;假设丙是牧师,那么丙说“乙是骗子”是真话,此时甲就是赌棍,乙就是骗子,而甲说“丙是牧师”为真,不符合赌棍有时说真话有时说假话,所以丙不是牧师;所以乙是牧师,那么丙说的是假话,丙是骗子,甲就是赌棍。
5. 有四个孩子在一个房间里,他们分别是A、B、C、D。
A说:“B比C高。
”B说:“A比D高。
”C说:“我比D高。
”D说:“C比B高。
”如果他们之中只有一个人说的是真话,那么谁最高?- 解析:A说的“B比C高”和D说的“C比B高”相互矛盾,必然一真一假。
因为只有一个人说的是真话,所以B和C说的都是假话。
B说“ A比D高”为假,那么D比A高;C说“我比D高”为假,那么D比C高。
所以A说的是真话,B>C,又因为D>A,D>C,所以最高的是B。
6. 一个岛上住着两种人,一种是骑士,总是说真话;一种是无赖,总是说假话。
一天,你遇到岛上的两个人A和B。
A说:“或者我是无赖,或者B是骑士。
”根据这句话,你能判断出A和B分别是什么人吗?- 解析:假设A是无赖,那么他说的话就是假话。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-3逻辑推理教学目标1.掌握逻辑推理的解题思路与基本方法:列表、假设、对比分析、数论分析法等2.培养学生的逻辑推理能力,掌握解不同题型的突破口3.能够利用所学的数论等知识解复杂的逻辑推理题知识点拨逻辑推理作为数学思维中重要的一部分,经常出现在各种数学竞赛中,除此以外,逻辑推理还经常作为专项的容出现在各类选拔考试,甚至是面向成年人的考试当中。
对于学生学习数学来说,逻辑推理既有趣又可以开发智力,学生自主学习研究性比较高。
本讲我们主要从各个角度总结逻辑推理的解题方法。
一列表推理法逻辑推理问题的显著特点是层次多,条件纵横交错.如何从较繁杂的信息中选准突破口,层层剖析,一步步向结论靠近,是解决问题的关键.因此在推理过程中,我们也常常采用列表的方式,把错综复杂的约束条件用符号和图形表示出来,这样可以借助几何直观,把令人眼花缭乱的条件变得一目了然,答案也就容易找到了.二、假设推理用假设法解逻辑推理问题,就是根据题目的几种可能情况,逐一假设.如果推出矛盾,那么假设不成立;如果推不出矛盾,而是符合题意,那么假设成立.解题突破口:找题目所给的矛盾点进行假设三、体育比赛中的数学对于体育比赛形式的逻辑推理题,注意“一队的胜、负、平”必然对应着“另一队的负、胜、平”。
有时综合性的逻辑推理题需要将比赛情况用点以及连接这些点的线来表示,从整体考虑,通过数量比较、整数分解等方式寻找解题的突破口。
四、计算中的逻辑推理能够利用数论等知识通过计算解决逻辑推理题.例题精讲模块一、列表推理法【例 1】刚、马辉、强三个男孩各有一个妹妹,六个人进行乒乓球混合双打比赛.事先规定:兄妹二人不许搭伴.第一盘:刚和小丽对强和小英;第二盘:强和小红对刚和马辉的妹妹.问:三个男孩的妹妹分别是谁?【解析】因为兄妹二人不许搭伴,所以题目条件表明:刚与小丽、强与小英、强与小红都不是兄妹.由第二盘看出,小红不是马辉的妹妹.将这些关系画在左下表中,由左下表可得右下表.李强马辉刘刚小丽小红小英××××李强马辉刘刚小丽小红小英×√×××××√√刚与小红、马辉与小英、强与小丽分别是兄妹.【巩固】 王文、贝、丽分别是跳伞、田径、游泳运动员,现在知道:⑴贝从未上过天;⑵跳伞运动员已得过两块金牌;⑶丽还未得过第一名,她与田径运动员同年出生.请根据上述情况判断王文、贝、丽各是什么运动员?【解析】 为了能清楚地找到所给条件之间的关系,我们不妨运用列表法,列出下表,在表中“√”表示是,“×”表示不是,在任意一行或一列中,如果一格是“√”,可推出其它两格是“×”由⑴⑶可知贝、丽都不是跳伞运动员,可填出第一行,即王文是跳伞运动员;由⑶可知,丽也不是田径运动员,可填出第三列,即丽是游泳运动员,则贝是田径运动员.【巩固】 波、顾锋、英三位老师共同担负六年级某班的语文、数学、政治、体育、音乐和图画六门课的教学,每人教两门.现知道:⑴ 顾锋最年轻;⑵ ⑵波喜欢与体育老师、数学老师交谈;⑶ ⑶体育老师和图画老师都比政治老师年龄大;⑷ ⑷顾锋、音乐老师、语文老师经常一起去游泳;⑸ 英与语文老师是邻居.问:各人分别教哪两门课程?【解析】 波教语文、图画,顾锋教数学、政治,英教音乐、体育.由⑴⑶⑷推知顾锋教数学和政治;由⑵推知英教体育;由⑶⑸推知波教图画、语文.【巩固】 王平、宋丹、涛三个小学生都是少先队的干部,一个是大队长,一个是中队长,一个是小队长.一次数学测验,这三个人的成绩是:⑴涛比大队长的成绩好.⑵王平和中队长的成绩不相同.⑶中队长比宋丹的成绩差.请你根据这三个人的成绩,判断一下,谁是大队长呢?【解析】 根据条件⑵和⑶,王平和中队长的成绩不相同,中队长比宋丹的成绩差.,可以断定,王平不是中队长,宋丹也不是中队长,只有涛当中队长了.王平和宋丹两人谁是大队长呢?由⑴和⑶,涛比大队长的成绩好,中队长比宋丹的成绩差,可以推断出按成绩高低排列的话,宋丹的成绩比中队长(涛)的成绩好,涛的成绩比大队长的成绩好.这样,宋丹、涛就都不是大队长,那么,大队长肯定是王平.【例 2】 明、席辉和刚在、和天津工作,他们的职业是工人、农民和教师,已知:⑴明不在工作,席辉不在工作;⑵在工作的不是教师;⑶在工作的是工人;⑷席辉不是农民.问:这三人各住哪里?各是什么职业?【解析】 这道题的关系要复杂一些,要求我们通过推理,弄清人物、工作地点、职业三者之间的关系.三者的关系需要两两构造三个表,即人物与地点,人物与职业,地点与职业三个表.我们先将题目条件中所给出的关系用下面的表来表示,由条件⑴得到表1,由条件⑵、⑶得到表2,由条件⑷得到表3.因为各表中,每行每列只能有一个“√”,所以表2可填全为表5.由表5知农民在工作,又知席辉不是农民,所以席辉不在工作,可以将表1可填全完为表4由表4和表5知得到:明住在,是工人;席辉住在天津,是教师;刚住在,是农民.方法二:由题目条件可知:席辉不在工作,而在工作的是工人,所以席辉不是工人,又不是农民,那么席辉只能是教师,不在工作,就只能是在天津工作,那么明在工作,是工人。
刚在,是农民。
【巩固】甲、乙、丙三人,他们的籍贯分别是、广西、,他们的职业分别是教师、工人、演员.已知:⑴甲不是人,乙不是广西人;⑵人不是演员,广西人是教师;⑶乙不是工人.求这三人各自的籍贯和职业.【解析】由题意可画出下面三个表:将表3补全为表4.由表4知,工人是人,而乙不是工人,所以乙不是人,由此可将表1补全为表5.所以,甲是广西人,职业是教师;乙是人,职业是演员;丙是人,职业是工人.方法二:将能判断的条件先列入图表中,广西人是教师,但是乙不是广西人,所以乙不是教师,乙又不是工人,所以乙为演员。
在对应的地方打上“√”,对应的行列均打“×”。
但是人不是演员,所以乙不是人,乙就是人,所以甲是广西人,职业是教师;乙是人,职业是演员;丙是人,职业是工人。
【巩固】小明、小芳、小花各爱好游泳、羽毛球、乒乓球中的一项,并分别在一小、二小、三小中的一所小学上学。
现知道:(1)小明不在一小;(2)小芳不在二小(3)爱好乒乓球的不在三小;(4)爱好游泳的在一小;(5)爱好游泳的不是小芳。
问:三人上各爱好什么运动?各上哪所小学?【解析】这道题比上例复杂,因为要判断人、学校和爱好三个容。
先将题目条件中给出的关系用下面的表1、表2、表3表示:因为各表中,每行每列只能有一个“√”,所以表3可补全为表4。
由表4、表2知道,爱好游泳的在一小,小芳不爱游泳,所以小芳不在一小。
于是可将表1补全为表5。
对照表5和表4,得到:小明在二小上学,爱好打乒乓球;小芳在三小上学,爱好打羽毛球;小花在一小上学,爱好游泳。
【巩固】小王、小和小一位是工人,一位是农民,一位是教师,现在只知道:小比教师年龄大;小王与农民不同岁;农民比小年龄小。
问:谁是工人?谁是农民?谁是教师?【解析】这道题目并不难,聪明的小朋友思考一下就能得到答案,但是今天我们通过这道题目一起来学习一个十分有用的方法:列表分析法。
由题目条件可以知道:小不是教师,小王不是农民,小不是农民。
由此得到左下表。
表格中打“√”表示肯定,打“×”表示否定。
因为左上表中,任一行、任一列只能有一个“√”,其余是“×”,所以小是农民,于是得到右上表。
因为农民小比小年龄小,又小比教师年龄大,所以小比教师年龄大,即小不是教师。
因此得到左下表,从而得到右下表,即小是工人,小是农民,小王是教师。
例题中采用列表法,使得各种关系更明确。
为了讲解清楚,例题中画了几个表,实际解题时,不用画这么多表,只在一个表中先后画出各种关系即可。
需要注意的是:①第一步应将题目条件给出的关系画在表上,然后再依次将分析推理出的关系画在表上;②每行每列只能有一个“√”,如果出现了一个“√”,它所在的行和列的其余格中都应画“×”。
【例 3】甲、乙、丙、丁四个人的职业分别是教师、医生、律师、警察.已知:⑴教师不知道甲的职业;⑵医生曾给乙治过病;⑶律师是丙的法律顾问(经常见面);⑷丁不是律师;⑸乙和丙从未见过面.那么甲、乙、丙、丁的职业依次是:.【解析】律师、教师、警察.由⑶可以知道丙不是律师,但是他见过律师,再由⑸知乙不是律师,又由⑷可知甲是律师.于是由⑴和⑶知丙不是教师,由⑵和⑸知丙不是医生,从而丙是警察.再由⑵知乙是教师,丁是医生.列表如下(列表的好处在于直观明了,不会犯错误):【巩固】徐、王、、四位师傅分别是工厂的木工、车工、电工和钳工,他们都是象棋迷。
(1)电工只和车工下棋;(2)王、两位师傅经常与木工下棋;(3)徐师傅与电工下棋互有胜负;(4)师傅比钳工下得好。
问:徐、王、、四位师傅各从事什么工种?【解析】徐是车工,王是钳工,是木工,是电工。
【巩固】甲、乙、丙三个小学生都是少先队的干部,一个是大队长,一个是中队长,一个是小队长.一次数学测验,这三个人的成绩是:⑴丙比大队长的成绩好.⑵甲和中队长的成绩不相同.⑶中队长比乙的成绩差.请你根据这三个人的成绩,判断一下,谁是大队长呢?【解析】根据条件⑵和⑶,甲和中队长的成绩不相同,中队长比乙的成绩差,可以断定,甲不是中队长,乙也不是中队长,只有丙是中队长了(也可以列表确定中队长).甲和乙两人谁是大队长呢?由⑴和⑶,丙比大队长的成绩好,中队长比乙的成绩差,可以推断出按成绩高低排列的话,乙的成绩比中队长(丙)的成绩好,丙的成绩比大队长的成绩好.这样,乙、丙就都不是大队长,那么,大队长肯定是甲.【巩固】甲、乙、丙、丁在谈论他们及他们的同学何伟的居住地.甲说:“我和乙都住在,丙住在天津.”乙说:“我和丁都住在,丙住在天津.”丙说:“我和甲都不住在,何伟住在.”丁说:“甲和乙都住在,我住在.”假定他们每个人都说了两句真话,一句假话.问:不在场的何伟住在哪儿?【解析】 因为甲、乙都说“丙住在天津,”我们可以假设这句话是假话,那么甲、乙的前两句应当都是真话,推出乙既住在又住在,矛盾.所以假设不成立,即“丙住在天津”是真话.因为甲的前两句话中有一句假话,而甲、丁两人的前两句话相同,所以丁的第三句话“我住在”是真的.由此知乙的第二句话“丁住在”是假话,第一句“我住在”是真话;进而推知甲的第二句是假话,第一句“我住在”是真话;最后推知丙的第二句话是假话,第三句“何伟住在”是真话.所以,何伟住在.【巩固】 A ,B ,C ,D 分别是中国、日本、美国和法国人.已知:⑴A 和中国人是医生;⑵B 和法国人是教师;⑶C 和日本人职业不同;⑷D 不会看病.问:A ,B ,C ,D 各是哪国人,【解析】 有⑴⑵可知,A 、B 都不是中国人和法国人,再由⑴⑷知,D 也不是中国人,所以,C 是中国人,由⑶,日本人也是教师,从而推知,D 是法国人,得下表:最后由C 是中国人及⑴⑶,推知日本人是教师,再由⑵知B 是日本人.【巩固】 根据条件判断旅游团去了A 、B 、C 、D 、E 中的哪几个地方?⑴如果去A ,就必须去B ;⑵D 、E 两地至少去一地;⑶B 、C 两地只能去一地;⑷C 、E 两地要去都去,要不去都不去;⑸若去D ,则A 、E 两地必须去.【解析】 从⑶入手,分别假设去B 或C :⑶若去B 则不能去C ,⑷也不能去E ,⑵只能去D .⑸必须去A 、E ,与不能去E 矛盾.所以不能去B 假设去C :⑷必去E ,⑵需去D ,⑸必须去A 、E ,⑴去A 必须去B ,与⑶B 、C 不能同去矛盾,所以不能去D .综上只能去C 、E .【例 4】 甲、乙、丙、丁每人只会中、英、法、日四种语言中的两种,其中有一种语言只有一人会说.他们在一起交谈可有趣啦:⑴乙不会说英语,当甲与丙交谈时,却请他当翻译;⑵甲会日语,丁不会日语,但他们却能相互交谈;⑶乙、丙、丁找不到三人都会的语言;⑷没有人同时会日、法两种语言.请问:甲、乙、丙、丁各会哪两种语言?【解析】 由⑴⑵⑷可得下表,其中丙不会日语是因为甲会日语,且甲与丙交谈需要翻译.由下表看出,甲会的另一种语言不是中文就是英语.丁丙乙甲日法英中×××√× 先假设甲会说中文.由⑵知,丁也会中文;由⑴知丙不会中文,再由每人会两种语言,知丙会英、法语(见左下表:由⑴⑷推知乙会中文和法语;再由⑶及每人会两种语言,推知丁会英语(见右下表).结果符合题意.丁丙乙甲日法英中×√√√××××√√×√√√丁丙乙甲日法英中×√√√××××××√√×再假设甲会说英语.由⑵知,丁也会英语;由⑴知丙不会英语,再由每人会两种语言,知丙会中文和法语(见左下表);由⑴⑷推知,乙会中文和日语;再由⑶及每人会两种语言,推知丁会法语(见右下表).右下表与“有一种语言只有一人会说”矛盾.假设不成立.√丁丙乙甲日法英中×√√√××××√×√√√丁丙乙甲日法英中×√√√××××××√√×所以甲会中、日语,乙会中、法语,丙会英、法语,丁会中、英语.【巩固】宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家”、“大作家”和“歌唱家”称呼他们,此外:⑴数学博士夸跳高冠军跳的高⑵跳高冠军和大作家常与宝宝一起看电影⑶短跑健将请小画家画贺年卡⑷数学博士和小画家关系很好⑸贝贝向大作家借过书⑹聪聪下象棋常赢贝贝和小画家问:宝宝、贝贝、聪聪各有哪两个外号吗?【解析】由⑵知,宝宝不是跳高冠军和大作家;由⑸知,贝贝不是大作家;由⑹知,贝贝、聪聪都不是小画家,可以得到下表:因为宝宝是小画家,所以由⑶⑷知宝宝不是短跑健将和数学博士,推知宝宝是歌唱家,因为聪聪是大作家,所以由⑵知聪聪不是跳高冠军,推知贝贝是跳高冠军,因为贝贝是跳高冠军,所以由⑴知贝贝不是数学博士,将上面结论依次填入上表,得到下表:所以,宝宝是小画家和歌唱家,贝贝是短跑健将和跳高冠军,聪聪是数学博士和大作家.【例 5】(2007年省“创新杯”初赛)六年级四个班进行数学竞赛,小明猜想比赛的结果是:3班第一名,2班第二名,1班第三名,4班第四名.小华猜想比赛的结果是:2班第一名,4班第二名,3班第三名,1班第四名.结果只有小华猜到的4班为第二名是正确的.那么这次竞赛的名次是班第一名,班第二名,班第三名,班第四名。
