中考数学压轴题专项汇编专题角含半角模型
2024河南中考数学专题复习第三部分 题型二 微专题5 半角模型 课件

∴△AMN≌△AEN(SAS),∴∠AED=∠AMN, ∴∠AMB=∠AMN,∴MA平分∠BMH. ∵AB⊥BM,AH⊥MN,∴AB=AH. ∵AM=AM, ∴Rt△ABM≌Rt△AHM(HL),∴BM=MH=2, 同理可得NH=ND=3, 设BC=AB=x,则CM=x-2,CN=x-3, 在Rt△MCN中,由勾股定理得,(x-2)2+(x-3)2=52, 解得x1=6,x2=-1(舍去),∴AH=AB=6.
E
第1题图
2. 如图,在等边△ABC中,点P,Q分别在边AB,AC上,D为△ABC外
一点,且∠PDQ=60°,∠BDC=120°,BD=DC.
(1)如图①,若DP=DQ,请直接写出BP,QC,PQ之间的数量关系;
【解法提示】∵DP=DQ,∠PDQ=60°,∴△PDQ是等边三角形,
∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,
∴∠BAD+∠CAE=30°,∴∠CAF+∠CAE=30°,
第3题解图
即∠EAF=30°,∴∠EAF=∠EAD.
在△DAE和△FAE中,
AD AF EAD EAF , AE AE
∴△DAE≌△FAE(SAS),∴ED=EF.
第3题解图
∵∠ACB=∠ACF=60°,∴∠FCG=180°-∠ACB-∠ACF=60°.
则∠ABG=∠D=90°,
∠GAB=∠FAD,AG=AF,BG=DF.
G
∵∠ABE=90°,AB=AD,
∴∠ABE+∠ABG=180°,∴E,B,G三点共线.
第3题图①
∵∠BAD=60°,∠EAF=30°,
∴∠GAB+∠BAE=∠GAE=30°,
∴∠GAE=∠FAE.
在△EAG和△EAF中,
2025年中考数学总复习第二部分重难专题突破专题5“倍半角”模型解决旋转变换问题

∠BAD=∠EAF.∴ ∠EAG=∠EAF.又∵ AE=AE,∴
△AEG≌△AEF.∴ EG=EF.∵ EG=BE+BG,∴ EF
=BE+DF.
(3) 如图③,在四边形ABCD中,AD=AB,∠ABC与∠D互补,点E,
1
F分别在射线CB,DC上,且∠EAF= ∠BAD.当BC=4,CD=7,CF=1
的半角模型是90°含45°,120°含60°.
(1) 如图①,在正方形ABCD中,E,F分别是边AB,BC上的点,且
∠EDF=45°,探究线段EF,AE,FC之间的数量关系.
小明的探究思路如下:如图①,延长BC到点M,使CM=AE,连接
DM,先证明△ADE≌△CDM,再证明△DEF≌△DMF.小亮发现
2
时,△CEF的周长为 13 .
解:(3)解析:如图②,在DF上截取DM=BE,连接AM.
∵ ∠ABC与∠D互补,
∴ ∠D+∠ABC=∠ABE+∠ABC=180°.
∴ ∠D=∠ABE.∵ AD=AB,∴ △ADM≌△ABE.
∴ AM=AE,∠DAM=∠BAE.
∵ ∠EAF=∠BAE+∠BAF=∠DAM+∠BAF= ∠BAD,
∵ ∠EAF= ∠BAD,∴ ∠GAF=∠DAG+∠DAF=∠BAE+∠DAF
=∠BAD-∠EAF=∠EAF.∴ ∠EAF=∠GAF.
=,
在△AEF和△AGF中,ቐ∠=∠,
=,
∴ △AEF≌△AGF.∴ EF=GF.
∵ GF=DG+DF=BE+DF,∴ EF=BE+DF.
解:(2) EF=BE+DF.如图①,延长EB到点G,使
BG=DF,连接AG.∵ ∠ABC+∠D=180°,∠ABG+
2024中考数学全国真题分类卷 模型五 半角模型 强化训练(含答案)

2024中考数学全国真题分类卷模型五半角模型强化训练类型一正方形含半角1.综合与实践数学实践活动,是一种非常有效的学习方式.通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思维空间,丰富数学体验,让我们一起动手来折一折、转一转,体会活动带给我们的乐趣.折一折:将正方形纸片ABCD折叠,使边AB,AD都落在对角线AC上,展开得折痕AE,AF,连接EF,如图①.(1)∠EAF=________°,写出图中两个等腰三角形:________(不需要添加字母);转一转:将图①中的∠EAF绕点A旋转,使它的两边分别交边BC,CD于点P,Q,连接PQ,如图②.(2)线段BP,PQ,DQ之间的数量关系为_______________________________________;(3)连接正方形对角线BD,若图②中的∠PAQ的边AP,AQ分别交对角线BD于点M,点N,如图③,求CQBM的值.第1题图2.如图,△ABC是等腰直角三角形,AC=BC=4,∠C=90°,M,N分别是边AC,BC 上的点,以CM,CN为邻边作矩形PMCN,交AB于E,F.设CM=a,CN=b,若ab=8.(1)判断由线段AE,EF,BF组成的三角形的形状,并说明理由;(2)①当a=b时,求∠ECF的度数;②当a≠b时,①中的结论是否成立?并说明理由.3.如图①,在菱形ABCD中,∠ABC=60°,M,N分别是边BC,CD上的动点,∠MAN=60°,AM,AN分别交BD于点E,F.(1)求证:CM+CN=BC;(2)如图②,过点E作EG∥AN交DC的延长线于点G,求证:EG=EA;(3)如图③,若AB=1,∠AED=45°,求EF的长.第3题图参考答案与解析1.解:(1)45,△AEF ,△EFC ,(从△AEF ,△EFC ,△ABC ,△ADC 中任选两个即可);【解法提示】∵四边形ABCD 是正方形,∴AB =AD =BC =CD ,∠BAD =90°,∴△ABC ,△ADC 都是等腰三角形,∵∠BAE =∠CAE ,∠DAF =∠CAF ,∴∠EAF =12(∠BAC +∠DAC )=45°,∠BAE =∠DAF =22.5°,∵AB =AD ,∠B =∠D =90°,∴△BAE ≌△DAF (ASA),∴BE =DF ,AE =AF ,∵CB =CD ,∴CE =CF ,∴△AEF ,△CEF 都是等腰三角形.(2)PQ =BP +DQ ;【解法提示】如解图,延长CB 到点T ,使得BT =DQ ,连接AT .∵AD =AB ,∠ADQ =∠ABT =90°,DQ =BT ,∴△ADQ ≌△ABT (SAS),∴AT =AQ ,∠DAQ =∠BAT ,∵∠PAQ =45°,∴∠PAT =∠BAP +∠BAT =∠BAP +∠DAQ =45°,∴∠PAT =∠PAQ =45°,∵AP =AP ,∴△PAT ≌△PAQ (SAS),∴PQ =PT ,∵PT =PB +BT =PB +DQ ,∴PQ =BP +DQ .第1题解图(3)∵四边形ABCD 是正方形,∴∠ABM =∠ACQ =∠BAC =45°,AC =2AB ,∵∠BAC =∠PAQ =45°,∴∠BAM =∠CAQ ,∴△CAQ ∽△BAM ,∴CQ BM =AC AB =2.2.解:(1)由线段AE ,EF ,BF 组成的三角形是直角三角形.理由如下:∵AC =BC ,∠C =90°,∴∠A =∠B =45°.∵四边形PMCN 是矩形,∴∠CME =∠CNF =∠P =90°,AC ∥PN ,BC ∥PM ,∴∠AME =∠BNF =90°,∠A =∠PFE =45°,∠PEF =∠B =45°,∴△AME ,△PEF ,△BNF 都是等腰直角三角形,∴AM 2=12AE 2,PE 2=12EF 2,BN 2=12BF 2,∴S △AME =12AM ·ME =12AM 2=14AE 2,S △BNF =12BN ·NF =12BN 2=14BF 2,S △PEF =12PE ·PF =12PE 2=14EF 2.∵CM =a ,CN =b ,ab =8,∴S 矩形PMCN =8.∵AC =BC =4,∴S △ABC =12AC ·BC =8,∴S 矩形PMCN =S △ABC ,∴S △AME +S △BNF =S △PEF ,∴14AE 2+14BF 2=14EF 2,即AE 2+BF 2=EF 2,∴由线段AE ,EF ,BF 组成的三角形是直角三角形;(2)①如解图①,过点C 作CG ⊥AB 于点G ,∵AC =BC ,∠ACB =90°,∴G 为AB 的中点,∴CG =AG =BG =12AB .第2题解图①在Rt △ABC 中,AC =BC =4,根据勾股定理得AB =AC 2+BC 2=42,∴CG =AG =BG =22.∵ab =8,a =b ,∴a =b =22,即CM =CN =CG ,在Rt △CME 和Rt △CGE =CE =CG,∴Rt △CME ≌Rt △CGE (HL),∴∠MCE =∠ECG .同理可证Rt △CNF ≌Rt △CGF ,∴∠NCF =∠GCF ,∴∠ECF =∠ECG +∠GCF =12(∠MCG +∠NCG )=12∠MCN =45°;②成立.理由如下:当a ≠b 时,如解图②,将△BCF 绕点C 逆时针旋转90°得到△ACH ,连接EH ,第2题解图②∴∠HCF =90°,由旋转的性质可得△BCF ≌△ACH ,∴∠HAC =∠B =45°,AH =BF ,CH =CF ,∴∠HAC +∠BAC =∠HAE =90°,∴在Rt △AEH 中,根据勾股定理,得AH 2+AE 2=EH 2,即BF 2+AE 2=EH 2,由(1)知AE 2+BF 2=EF 2,∴EH =EF ,在△CEH 和△CEF =CF=EF =CE,∴△CEH ≌△CEF (SSS),∴∠ECF =∠ECH =12∠HCF =45°.3.(1)证明:如解图①,连接AC ,∵四边形ABCD 是菱形,∠ABC =60°,∴AB =BC ,AB ∥CD ,∴△ABC 是等边三角形,∴∠ABM =∠BAC =∠ACN =60°,∵∠BAC=∠MAN=60°,∴∠BAM+∠MAC=∠MAC+∠CAN,∴∠BAM=∠CAN,在△BAM和△CAN中,BAM=∠CAN,=ACABM=∠ACN∴△BAM≌△CAN(ASA),∴BM=CN,∴CM+CN=CM+BM=BC;第3题解图①(2)证明:如解图①,连接EC.在△ABE和△CBE中,=BC,ABE=∠CBE=BE∴△ABE≌△CBE(SAS),∴AE=CE,∠BAE=∠BCE,∵EG∥AN,∴∠G=∠AND,∵∠AND=∠CAN+∠ACN=∠CAN+60°,∠ECG=∠BCG+∠ECB=60°+∠ECB,∵∠ECB=∠BAE=∠CAN,∴∠ECG=∠AND=∠G,∴EC=EG,∵AE=EC,∴EG=EA;(3)解:如解图②,将△ABE 绕点A 逆时针旋转120°得到△ADQ ,连接FQ .第3题解图②∴AE =AQ ,∠BAE =∠DAQ ,∵∠MAN =60°,∴∠BAE +∠DAN =60°,∴∠DAQ +∠DAN =60°,即∠QAF =60°,∴∠EAF =∠QAF ,又∵AF =AF ,∴△AFE ≌△AFQ ,∴∠AQF =∠AEF =45°,∵∠AQD =∠AEB =135°,∴∠FQD =90°,∵∠QDF =∠ADQ +∠ADF =∠ABE +∠ADF =∠CDB +∠ADF =60°,设DQ =x ,则BE =x ,DF =2x ,EF =FQ =3x ,∵AB =AD =1,∠ABD =30°,∴BD =3,∵BE +EF +DF =BD ,即x +3x +2x =3,∴x =3-12,∴EF =3x =3-32.。
初中数学突破中考压轴题几何模型之正方形的半角模型教案

正方形角含半角模型提升例1.如图,折叠正方形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,使AD=2,求AG.例2.如图,P为正方形ABCD内一点,PA二PB=10,并且P点到CD边的距离也等于10,求正方形ABCD的面积?例3.如图,E、F分别为正方形ABCD的边BC、CD上的一点,AM丄EF,垂足为M,AM=AB,则有EF=BE+DF,为什么?例4.如图,在正方形ABCD的BC、CD边上取E、F两点,使Z EAF=45°,AG丄EF于G.求证:AG二AB BE例5.⑴如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,Z AOF=90。
.求证:BE=CF.⑵如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,Z FOH=90°,EF=4.求GH的长.【双基训练】1.如图6,点A在线段BG上,四边形ABCD与DEFG都是正方形,其边长分别为3cm和5cm,则ACDE的面积为cm2.2.你可以依次剪6张正方形纸片,拼成如图7所示图形.如果你所拼得的图形中正方形①的面积为1,且正方形⑥与正方形③的面积相等,那么正方形⑤的面积为.3•如图9,已知正方形ABCD的面积为35平方厘米,E、F分别为边AB、BC上的点.AF、CE相交于G,并且A ABF 的面积为14平方厘米,A BCE的面积为5平方厘米,那么四边形BEGF的面积是.4.如图,A、B、C三点在同一条直线上,AB=2BC。
分别以AB、BC为边作正方形ABEF和正方形BCMN,连接FN,EC。
求证:FN=EC。
13 EG 丄CD 5.如图,ABCD 是正方形.G 是BC 上的一点,DE 丄AG 于E ,BF 丄AG 于F .(1) 求证:△ABF =△DAE ;(2) 求证:DE =EF +FB .【纵向应用】6.在正方形ABCD 中,Z1=Z2.求证:OF =2BE&如图13,点E 为正方形ABCD 对角线BD 上一点,EF 丄BC ,求证:AE 丄FG7.在正方形ABCD 中,Z 1=Z 2.AE 丄DF ,求证:OG=扣 D G F D C边,在AABC 的外侧作正方形ACDE 和正方形CBFG,点P 是EF 半.9•已知:点E 、F 分别正方形ABCD 中AB 和BC 的中点,连接AF 和DE 相交于点G ,GH丄AD 于点H .(1) 求证:AF 丄DE ;(2) 如果AB =2,求GH 的长;(3) 求证:CG 二CD例1.已知:如图,P 是正方形ABCD 内点,ZPAD =Z PDA =15。
2024成都中考数学第一轮专题复习之第五章 微专题 半角模型 知识精练(含答案)

2024成都中考数学第一轮专题复习之第五章微专题半角模型知识精练1.问题提出:如图①,已知在△ABC中,∠BAC=45°,过点A作AD⊥BC于点D,AD=10,BD=4,求CD的长;第1题图①问题探究:如图②,已知在△ABC中,AB=AC,∠BAC=30°,AD⊥BC,探究AD与BC 的数量关系.第1题图②2.如图①,四边形ABCD是菱形,AC为对角线,点E,F分别在边BC,CD上,连接AE,AF,EF,已知∠ADC=∠EAF=60°.(1)判断△AEF的形状,并说明理由;(2)如图②,对角线BD分别交AE,AC,AF于点G,O,H,若该菱形的边长为6,DH=3.①求AH的长;②求△AGH的面积.图①图②第2题图参考答案与解析1.解:问题提出:如解图①,将△ADB ,△ADC 分别沿AB ,AC 折叠,得到△AD ′B ,△AC ′C ,延长D ′B ,C ′C 交于点E .∵∠BAC =45°,即∠BAD +∠CAD =45°,∴∠D ′AB +∠C ′AC =45°,∴∠D ′AC ′=90°.∵AD ⊥BC ,∴∠D ′=∠C ′=∠D ′AC ′=90°.∵AD ′=AC ′=AD =10,∴四边形AD ′EC ′为正方形.设CD =x ,则CE =10-x ,BE =10-4=6.在Rt △BCE 中,由勾股定理,得BE 2+CE 2=BC 2,即62+(10-x )2=(4+x )2,解得x =307.∴CD 的长为307;第1题解图①问题探究:如解图②,将△ADB ,△ADC 分别沿AB ,AC 折叠,得到△AD ′B ,△AC ′C ,延长D ′B ,C ′C 交于点E .∵∠BAC =30°,即∠BAD +∠CAD =30°,∴∠D ′AB +∠C ′AC =30°,∴∠D ′AC ′=60°,∴∠D ′EC ′=360°-90°-90°-60°=120°.∵AB=AC,∴∠ABC=∠ACB,∴∠ABD′=∠ABC,∠ACB=∠ACC′,∴∠DBE=∠DCE,∴BE=CE.∵AB=AC,AD⊥BC,BE=CE,∴A,D,E三点共线.在Rt△AD′E中,AD′=AD,则AE=AD′cos30°=23AD3,则DE=AE-AD=23AD3-AD,在Rt△BDE中,BD=DE·tan∠BED=(2-3)AD,则BC=2BD=(4-23)AD,∴BC=(4-23)AD.第1题解图②2.解:(1)△AEF是等边三角形,理由如下:∵四边形ABCD是菱形,∠ADC=60°,∴∠BAD=∠BCD=120°,∴∠DAC=∠ACD=∠ADC=∠ACB=60°,∴△ADC为等边三角形,∠DAF+∠FAC=60°,∴AC=AD.∵∠EAF=60°,∴∠FAC+∠CAE=60°,∴∠DAF=∠CAE.在△ADF和△ACE中,ADF =∠ACE ,=AC ,DAF =∠CAE ,∴△ADF ≌△ACE (ASA),∴AE =AF .∵∠EAF =60°,∴△AEF 是等边三角形;(2)①∵四边形ABCD 是菱形,∠ADC =60°,∴∠ADB =12∠ADC =30°.∵AD =6,∴OA =3,OD =33,∴OH =OD -DH =33-3=23.在Rt △AOH 中,AH =OA 2+OH 2=21;②如解图,将△AHG 沿直线AG 折叠,得到△AIG ,连接IB ,过点I 作IJ ⊥BD 于点J .第2题解图由题意可知,∠HAI =2∠HAG =120°,AD =6,∠ADB =∠ABD =30°,∴BD =2OD =63.∵∠HAI -∠HAB =∠DAB -∠HAB ,∴∠BAI =∠DAH .∵AB =AD,AH =AI ,∴△ADH ≌△ABI (SAS),∴IB =DH =3,∠ABI =∠ADH =30°,∴∠JBI =∠ABI +∠ABD =60°,∴BJ =IB ·cos ∠JBI =32,IJ =IB ·sin ∠JBI =32,∴GJ =DB -DH -HG -BJ =63-3-HG -32=923-HG .∵△AIG 是由△AHG 折叠得到,∴HG =IG ,在Rt △GJI 中,由勾股定理,得IG 2=IJ 2+GJ 2,∴HG 2=IJ 2+GJ 2,即HG 2=(32)2+(932-HG )2,解得HG =733,∴S △AHG =12HG ·OA =12×733×3=732.。
2024年中考数学总复习第一部分考点精讲第四单元三角形微专题半角模型

K
例1题图③
微专题 半角模型
∴△AHK≌△AHG(SAS),
∴HK=HG,
K
∵△ABD为等腰5°, ∴∠HDK=90°,
例1题图③
在Rt△HDK中,由勾股定理得HK2=DK2+HD2,
∴GH2=BG2+HD2.
微专题 半角模型
【方法二】翻折法 【方法二】证明:如图,将△ABG和△ADH分别沿AG和AH 翻折, ∵∠BAG+∠DAH=90°-∠GAH=45°, AB=AD, ∴AB,AD翻折后重合在AM上, ∴MG=BG,MH=DH,
∴G,B,C 三点共线,
∵∠BAD=120°,∠EAF=60°,
∴∠DAF+∠BAE=∠BAE+∠BAG
=120°-∠EAF=60°,
∴∠GAE=∠EAF,
G
例2题图
微专题 半角模型
在△AGE和△AFE中,
AG AF GAE FAE , AE AE
∴△AGE≌△AFE(SAS), ∴EF=GE=BE+BG=BE+DF.
G
例1题图②
微专题 半角模型
在△ANM和△AGM中,
AN AG MAN MAG , AM AM
∴△ANM≌△AGM(SAS),
∴MN=MG,
∵MG=BM+BG=BM+DN,
∴MN=MG=BM+DN;
G
例1题图②
微专题 半角模型
半角模型
半角模型.gsp
微专题 半角模型
半角模型
半角模型.gsp
M 例1题图③
微专题 半角模型
∵∠B=∠D=45°, ∴∠AMG=∠AMH=45°, ∴∠GMH=90°, ∴GM2+MH2=GH2, ∴GH2=BG2+HD2.
M 例1题图③
中考数学几何专题——半角模型(几何压轴)
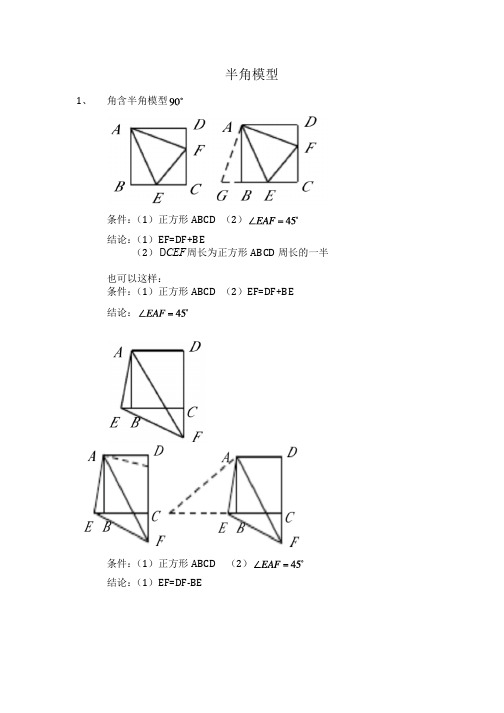
半角模型1、角含半角模型条件:(1)正方形ABCD (2)结论:(1)EF=DF+BE(2)D CEF周长为正方形ABCD周长的一半也可以这样:条件:(1)正方形ABCD (2)EF=DF+BE结论:条件:(1)正方形ABCD (2)结论:(1)EF=DF-BE条件:(1)结论:D AHE为等腰直角三角形证明:连接AC\ÐDAH=ÐCAE\D ADH相似于D ACE\DAAH=ACAE\D AHE相似于D ADC条件:(1)等腰直角D ABC(2)结论:BD2+CE2=DE2若ÐDAE旋转到D ABC外部时结论:BD2+CE2=DE2经典例题1.如图,正方形ABCD中,E、F分别在BC、DC上,且∠EAF=45°.求证:BE+DF=EF.2.如图,在正方形ABCD中,E和F分别是BC和CD上的点,AG⊥EF,∠EAF=45°,求证:AG=AD.3、已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)4、如图①△ABC是正三角形,△BDC是等腰三角形,BD=CD,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N,连接MN.(1)探究BM、MN、NC之间的关系,并说明理由.(2)若△ABC的边长为2,求△AMN的周长.(3)若点M、N分别是AB、CA延长线上的点,其它条件不变,在图②中画出图形,并说出BM、MN、NC之间的关系.5.(2014秋•安阳校级期中)在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC 上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.6.在△ABC中,∠BAC=90°,AB=AC,D、E在直线BC上,∠DAE=45°,(1)写出图中的相似三角形;(2)求证:BE•CD=2S△ABC,并探究BD、DE、CE之间的数量关系,给以证明.7.已知在△ABC中,AB=AC,点D、E在边BC上,将△ABD绕着点A旋转,得到△ACD′,接连D′E交AC于点O.(1)如图1,当△BAC=120°,△DAE=60°时,求证:DE=D′E;(2)如图2,当△DAE=45°,△BAC=90°,BD=DE时,在不舔加任何辅助线的情况下,请直接写出图2中的所有的全等三角形.8.(2014秋•通山县期中)如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D、E是BC 边上的任意两点,且∠DAE=45°.(1)将△ABD绕点A逆时针旋转90°,得到△ACF,请在图(1)中画出△ACF.(2)在(1)中,连接EF,探究线段BD,EC和DE之间有怎样的数量关系?写出猜想,并说明理由.(3)如图2,M、N分别是正方形ABCD的边BC、CD上一点,且BM+DN=MN,试求△MAN 的大小.9.△ABC的边BC在直线l上,点D,E是直线l上的两点,且BA=BD,CA=CE(1)如图1,若AB=AC,△BAC=90°,求△CAE的度数;(2)如图2,若△BAC=90°,求△CAE的度数;(3)如图3,设△BAC=α,△DAE=β,请直接写出α与β的关系式.10.(2011秋•朝阳区期末)已知,在△ABC中,∠BAC=90°,AB=AC,BC=,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.(1)请在图△中找出两对相似但不全等的三角形,写在横线上,;(2)设BE=m,CD=n,求m与n的函数关系式,并写出自变量n的取值范围;(3)如图△,当BE=CD时,求DE的长;(4)求证:无论BE与CD是否相等,都有DE2=BD2+CE2.11.(2014•平谷区一模)(1)如图1,点E、F分别是正方形ABCD的边BC、CD上的点,∠EAF=45°,连接EF,则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足MN2=BM2+DN2,请证明这个等量关系;(2)在△ABC中,AB=AC,点D、E分别为BC边上的两点.△如图2,当△BAC=60°,△DAE=30°时,BD、DE、EC应满足的等量关系是;△如图3,当△BAC=α,(0°<α<90°),△DAE=时,BD、DE、EC应满足的等量关系是.[参考:sin2α+cos2α=1]12.(2015•海宁市模拟)(1)探究:如图1和2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.△如图1,若△B、△ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,则能证得EF=BE+DF,请写出推理过程;△如图2,若△B、△D都不是直角,则当△B与△D满足数量关系时,仍有EF=BE+DF;(2)拓展:如图3,在△ABC中,△BAC=90°,AB=AC=2,点D、E均在边BC上,且△DAE=45°.若BD=1,求DE的长.13.(2015•滑县一模)(1)问题发现如图1,点E、F分别在正方形ABCD的边BC、CD上,△EAF=45°,连接EF、则EF=BE+DF,试说明理由;(2)类比引申如图2,在四边形ABCD中,AB=AD,△BAD=90°,点E、F分别在边BC、CD上,△EAF=45°,若△B,△D都不是直角,则当△B与△D满足等量关系时,仍有EF=BE+DF;(3)联想拓展如图3,在△ABC中,△BAC=90°,AB=AC,点D、E均在边BC上,且△DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程.14.(2014•山西校级模拟)已知△ABC中,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′,连结D′E.(1)如图1,当△BAC=120°,△DAE=60°时,求证:DE=D′E;(2)如图2,当DE=D′E时,△DAE与△BAC有怎样的数量关系?请写出,并说明理由.(3)如图3,在(2)的结论下,当△BAC=90°,BD与DE满足怎样的数量关系时,△D′EC 是等腰直角三角形?(直接写出结论,不必说明理由)。
中考数学复习满分突破(全国通用):专题12 半角模型(原卷版)

专题12半角模型半角模型的概述:当一个角包含着该角的半角,如90°角包含着45°角,120°角包含着60°角,270°角倍角关系,且这两个角共顶点,共顶点的两条边相等,则该模型为半角模型。
解包含着135°角,即出现12题方法为:1)过公共点作旋转,2)截长补短的方法构造全等解题。
基本模型:1)90°的半角模型(常考)已知正方形ABCD中,E,F分别是BC、CD上的点,∠EAF=45°,AE、AF分别与BD相交于点O、P,则:①EF=BE+DF②AE平分∠BEF,AF平分∠DFE③C∆CEF=2倍正方形边长④S∆ABE+S∆ADF=S∆AEF⑤AB=AG=AD(过点A作AG⊥EF,垂足为点G)⑥OP2=OB2+OD2⑦若点E为BC中点,则点F为CD三等分点⑧∆APO∽∆AEF∽∆DPF∽∆BEO∽∆DAO∽∆BPA⑨ABEP四点共圆、AOFD四点共圆、OECFP五点共圆⑩∆APE、∆AOF为等腰直角三角形(11)EF=2OP(12)S∆AEF=2S∆APO(13)AB2=BP×OD(14)CE•CF=2BE•DF(15)∆EPC为等腰三角形(16)PX=BX+DP(过点E作EX⊥BD,垂足为点X)证明:①思路:延长CD到点M,使DM=BE,连接AM先根据已知条件∆ABE≌∆ADM(SAS),由此可得AE=AM,∠BAE=∠DAM而∠BAE+∠FAD=45°,所以∠DAM+∠FAD=45°,可证明∆AEF≌∆AMF (SAS),由此可得EF=MF,而MF=DM+DF=BE+DF,因此EF=BE+DF②思路:∵∆AEF≌∆AMF(SAS)∴∠AFM=∠AFE,∠AMF=∠AEF∴AF平分∠DFE又∵∠AMF=∠AEB∴∠AEB=∠AEF∴AE平分∠BEF③思路:C∆CEF=EF+EC+FC=(BE+DF)+EC+FC=(BE+EC)+(DF+FC)=BC+DC=2BC④、⑤思路:过点A作AG⊥EF,垂足为点G根据②证明过程可知AFG=∠AFD,∠AEB=∠AEG因此可以证明:∆ABE≌∆AGE(AAS),∆AGF≌∆ADF(AAS)所以AB=AG=AD,S∆ABE=S∆AGE,S∆AGF=S∆ADF则S∆AEF=S∆AGE+S∆AGF=S∆ABE+S∆ADF⑥思路:绕点A将∆APD逆时针旋转90°得到∆ANB,使AD,AB重合因为∆APD≌∆ANB(AAS)所以AN=AP,BN=DP,∠NAB=∠PAD,∠ADP=∠ABN因为∠ADB=∠ABD=45°,所以∠NBO=90°因为∠BAE+∠PAD=45°所以∠NAB+∠BAE=45°则∆ANO≌∆APO(SAS)所以NO=OP在Rt∆NBO中,由勾股定理可知:ON2=OB2+NB2,则OP2=OB2+OD2⑦思路:已知tan∠EAB=BEAB =12,且∠EAB+∠FAD=45°∴tan∠FAD=13(“12345型”),∴DF:AD=1:3,即点F为CD的三等分点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题15 角含半角模型破题策略1. 等腰直角三角形角含半角如图,在△ABC 中,AB =AC ,∠BAC =90°,点D ,E 在BC 上且∠DAE =45° (1) △BAE ∽△ADE ∽△CDA(2)BD 2+CE 2=DE 2.45°EA BCD证明(1)易得∠ADC =∠B +∠BAD =∠EAB , 所以△BAE ∽△ADE ∽△CD A .(2)方法一(旋转法):如图1,将△ABD 绕点A 逆时针旋转90°得到△ACF ,连结EF .45°FEA BCD则∠EAF =∠EAD =45°,AF =AD , 所以△ADE ∽△FAE ( SAS ). 所以DE = EF .而CF =BD ,∠FCE =∠FCA +∠ACE =90°,所以BD 2+ CE 2=CF 2+CE 2=EF 2=DE 2.方法二(翻折法):如图2,作点B 关于AD 的对称点F ,连结AF ,DF ,EF .45°EA BCD因为∠BAD +∠EAC =∠DAF +∠EAF , 又因为∠BAD =∠DAF ,则∠FAE =∠CAE ,AF =AB =AC , 所以△FAE ∽△CAE (SAS ). 所以EF = E C .而DF =BD , ∠DFE =∠AFD + ∠AFE =90°,所以BD 2+ EC 2= FD 2+ EF 2= DE 2. 【拓展】①如图,在△ ABC 中,AB =AC ,∠BAC =90°,点D 在BC 上,点E 在BC 的延长线上,且∠DAE =45°,则BD 2+CE 2=DE 2.ED可以通过旋转、翻折的方法来证明,如图:EADFEAD②将等腰直角三角形变成任意的等腰三角形:如图,在△ABC 中,AB =AC ,点D ,E 在BC 上,且∠DAE =12∠BAC ,则以BD ,DE ,EC 为三边长的三角形有一个内角度数为180°-∠BA C .B可以通过旋转、翻折的方法将BD ,DE ,EC 转移到一个三角形中,如图:BCEBD2. 正方形角含半角如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,∠EAF =45°,连结EF ,则:45°图1ABCD E图2GF E A B 45°图3H F EABDC(1)EF =BE +DF;(2)如图2,过点A 作AG ⊥EF 于点G ,则AG =AD ;(3)如图3,连结BD 交AE 于点H ,连结FH . 则FH ⊥AE .(1)如图4,将△ABE 绕点A 逆时针旋转90°得到△ADI 证明.图4IEAB D则∠IAF =∠EAF =45°,AI =AE , 所以△AEF ∽△AIF (SAS ),所以EF =IF =DI +DF =BE +DF .(2)因为△AEF ∽△AIF ,AG ⊥EF ,AD ⊥IF , 所以AG =A D .(3)由∠HAF =∠HDF =45°可得A ,D ,F ,H 四点共圆, 从而∠AHF =180°-∠ADF =90°, 即FH ⊥AE .【拓展】①如图,在正方形ABCD 中,点E ,F 分别在边CB ,DC 的延长线上,∠EAF =45°,连结EF ,则EF =DF -BE .F BC E可以通过旋转的方法来证明.如图:EBA②如图,在一组邻边相等、对角互补的四边形ABCD 中,AB =AD ,∠BAD +∠C =180 °,点E ,F 分别在BC 、CD 上,∠EAF =12∠BAD ,连结EF ,则EF=BE+DF. ADCE可以通过旋转的方法来证明.如图:AFDCE G例题讲解例1 如图1,点E 、F 分别在正方形ABCD 的边BC 、CD 上,∠EAF =45°.(1) 试判断BE 、EF 、FD 之间的数量关系.(2) 如图2,在四边形ABCD 中,∠BAD ≠90°,AB =AD .∠B +∠D =180°,点E 、F 分别在BC 、CD 上,则当∠EAF 与∠BAD 满足 关系时,仍有EF =BE +FD .(3)如图3.在某公园的同一水平面上,四条通道围成四边形ABCD .已知AB =AD =80m ,∠B =60°,∠ADC =120°,∠BAD =150°,道路BC ,CD 上分别有景点 E ,F ,且AE ⊥AD .DF =40(3-1)m .现要在E 、F 之间修一条笔直的道路,求这条道路EF 的长.(结果取整数,参考数据:2=1.41,3=1.73)图1FA D CBE图2AD CF图3FCA EBD解: (1)由“正方形内含半角模型”可得EF =BE +FD . (2)∠BAD =2∠EAF ,理由如下:如图4,延长CD 至点G ,使得DG =BE .连结AG. 易证△ABE ≌△ADG (SAS ). 所以AE =AG ,即EF =BE +DF =DG +DF =GF . 从而证得△AEF ≌△AGF ( SSS ).所以∠EAF =∠GAF =12∠EAG =12∠BAD . 图4AD F图5HFCGA BED(3)如图5,将△ABE 绕点A 逆时针旋转1 50°至△ADG .连结AF .由题意可得∠BAE =60°所以△ABE 和△ADG 均为等腰直角三角形. 过点A 作 AH ⊥DG 于点H .则DH =12AD =40m ,AH =32 AD =3 m.而DF =4031)m. 所以∠EAF =∠GAF =45°.可得△EAF ≌△GAF (SAS ).所以EF =GF =80m+403l )m ≈109. 2m.例2如图,正方形ABCD 的边长为a ,BM 、DN 分别平分正方形的两个外角,且满足∠MA N =45°.连结MC 、NC 、MN .(1)与△ABM 相似的三角形是 ,BM g DN = (用含有a 的代数式表示); (2)求∠MCN 的度数;(3)请你猜想线段BM 、DN 和MN 之间的等量关系,并证明你的结论. NAC B解:(1)△NDA ,2a . (2)由(1)可得BM ABAD ND=, 所以BM DCBC DN=. 易证∠CBM =∠NDC =45°, 所以△BCM ∽△DNC . 则∠BCM =∠DNC ,所以∠MCN =360°一∠BCD 一∠BCM 一∠DCN =270°- (∠DNC +∠DCN ) =270°-(180°-∠DNC ) =135°.(3) 222BM DN MN +=,证明如下:如图,将△ADN 绕点A 顺时针旋转90°,得到△ABE ,连结EM. 易得AE =AN . ∠MAE =∠MAN =45°,∠EBM =90°, 所以△A ME ≌△AMN .(SAS ). 则ME =MN .在Rt △BME 中,222BM BE EM += 所以222BM DN EM +=.ENBC AM倒3 如图,在四边形ABCD 中,AD ∥BC ,∠BCD =90°,AB =BC +AD ,∠DAC =45°,E 为CD 上一点,且∠BAE =45°.若CD =4,求△ABE 的面积.图1BADCE解:如图1.过点A 作CB 的垂线,交CB 的延长线于点F .由∠DAC =45°,∠ADC =90°,可得AD =CD.所以四边形ADCF 为正方形. 从而AF = FC =4.令BC =m ,则AB =4+m ,BF =4-m .在Rt △AFB 中,有16+(4-m )2一(4+m )2所以AB =5,BF =3.如图2.将△ADE 绕点A 逆时针旋转90°至△AFG. 易证△AGH ≌△AEB .令DE =n ,则CE =4 -n ,BE =BG =3+n在Rt △BCE 中,有1+(4-n )2=(3+n )2,解得n =47. 所以BG =257. 从而15027ABE ABG S S AF BG ∆∆===g . 图2FADCEG进阶训练1.如图,等边△ABC 的边长为1,D 是△ABC 外一点且∠BDC =120°,BD =CD ,∠MDN =60°,求△AMN 的周长.NDABCM△AMN 的周长是2【提示】如图,延长AC 至点E ,使得CE =BM ,连结DE .先证△BMD ≌△CED ,再证△MDN ≌△EDN 即可.ENC BM2.如图,在正方形ABCD 中,连结BD ,E 、F 是边BC ,CD 上的点,△CEF 的周长是正方形ABCD 周长的一半,AE 、AF 分别与BD 交于M 、N ,试判断线段BM 、DN 和MN 之间的数量关系,并证明.NMCDFE BA解:BM 2+DN 2=MN 2.【提示】由△CEF 周长是正方形ABCD 周长的一半,想到“正方形角含半角”,从而旋转构造辅助线解决问题(如图1),证△AEF ≌△AGF ,得∠MAN =12∠BAD =4,然后,再由“等腰直角三角形含半角”(如图2)即可证得.H G G图2图1AFDM NNMDFA3.如图,在△ABC 中,∠ACB =90°,点D 在边AB 上,DE ⊥BC 于点E ,且DE =BC ,点F 在边AC 上,连结BF 交DE 于点G ,若∠DBF =45°,DG =275,BE =3,求CF 的长. G F EDCBA解:CF =125. 【提示】如图,将DE 向左平移至BH ,连结HD 并延长交AC 于点I ,则四边形HBCI 为正方形.将△BHD 绕点B 顺时针旋转90°至△BCJ ,则点J 在AC 的延长线上.连结DF ,由“正方形角含半角模型”可得DF =DH +CF ,∠DFB =∠JFB =∠DGF ,所以DF =DG ,从而求得CF 的长.JIHABC DEF G。
