仰角、俯角练习题
解直角三角函数仰角俯角专练家庭作业
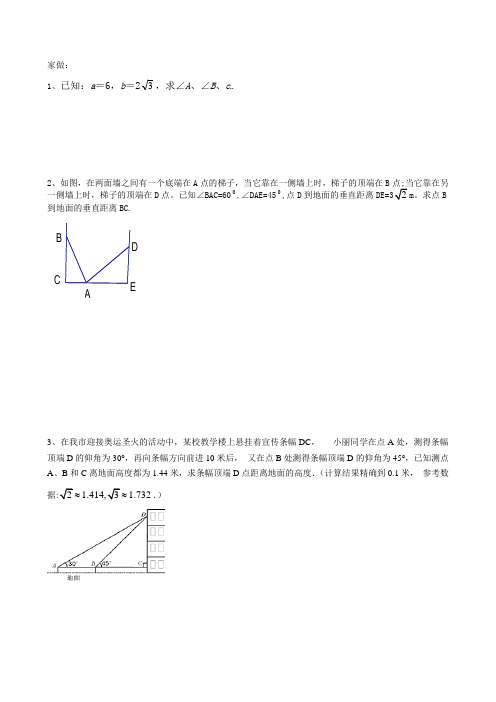
家做:1、已知:a =6,b =23,求∠A 、∠B 、c .2、如图,在两面墙之间有一个底端在A 点的梯子,当它靠在一侧墙上时,梯子的顶端在B一侧墙上时,梯子的顶端在D 点。
已知∠BAC=600,∠DAE=450,点D 到地面的垂直距离。
求点B到地面的垂直距离BC.3、在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC , 小丽同学在点A 处,测得条幅顶端D 的仰角为30°,再向条幅方向前进10米后, 又在点B 处测得条幅顶端D 的仰角为45°,已知测点A 、B 和C离地面高度都为1.44米,求条幅顶端D 点距离地面的高度.(计算结果精确到0.1米, 参考数据 1.732≈≈.)2sin 30cos 45tan 60-⋅+ 45tan 30cos 60sin -201()2sin 3032--+︒+-D E BCA30sin 2°13260tan 1)21(1+︒----—021)453tan 30-+︒-︒212cos 45()12-︒++ ︒-+-︒-30tan 3132)21(30sin 221—22)43()43(x x -=- 31022=-x x()()1211312-=-x x4、如图:矩形ABCD 的边BC 在x 轴上,E 是对角线AC 、BD 的交点,BC EF ⊥,垂足为F 。
函数x k y =在第一象限经过点A 、E 和点)21,8(,设EF 的长为m 。
(1)求函数xk y =的解析式;(2)求点A 的坐标(用m 表示),若︒=∠45AOB ,求EBF ∠tan 的值。
5、如图,小山上有一座铁塔AB,在D 处测得点A 的仰角为∠ADC=60°,点B 的仰角为∠BDC=45°;在E 处测得A 的仰角为∠E=30°,并测得DE=90米, 求小山高BC 和铁塔高AB6、如图,直线y= -x+b(b>o)与双曲线y= xk (x >0)交于A 、B 两点,连接OA 、OB ,AM ⊥y 轴于M ,BN ⊥x 轴于N ;有以下结论:①OA=OB ;②△AOM ≌△BON ;③若∠AOB =45°,则S △AoB=k ;④当AB=2时,ON -BN =1;其中结论正确的个数为 (写证明过程)7、如图,平行四边形AOBC 中,对角线交于点E ,双曲线k y x=(k>0)经过A 、E 两点,若平行四边形AOBC 的面积为18,求反比例函数的解析式。
备考2023年中考数学一轮复习-解直角三角形的应用﹣仰角俯角问题-综合题专训及答案

备考2023年中考数学一轮复习-解直角三角形的应用﹣仰角俯角问题-综合题专训及答案解直角三角形的应用﹣仰角俯角问题综合题专训1、(2018山西.中考真卷) 祥云桥位于省城太原南部,该桥塔主体由三根曲线塔柱组合而成,全桥共设13对直线型斜拉索,造型新颖,是“三晋大地”的一种象征.某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.项目内容课题测量斜拉索顶端到桥面的距离测量示意图说明:两侧最长斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内.测量数据∠A的度数∠B的度数AB的长度38°28°234米……(1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)(2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可).2、(2019石家庄.中考模拟) 如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在0B的位置时俯角∠FOB=60°,若OCLEF,点A比点B高7cm.(要求:本题中的计算结果均保留整数。
参考值:≈1.7;π≈3.1)求:(1)单摆的长度;【答案】解:解:设单摆的长度为x.过A作AM⊥OC于点M,过B作BN⊥OC于点N∵OC⊥EF.∴∠COE=∠COF=90°∴∠AOM=∠COE-∠AOE=90°-30°=60°∠BON=∠COF-∠BOF=90°-60°=30°在Rt△AOM中,OM=OA·cos60°= x在Rt△BON中,ON=OB·cos30°= x由题知:MN=7∴ON-OM= x- x=7解得:x=7 +7≈7×1.7+7≈19答:单摆的长度约19cm.(1)从点A摆动到点B经过的路径长.3、(2019丹东.中考模拟) 如图,为了测量小山顶的铁塔AB高度,王华和杨丽在平地上的C点处测得A点的仰角为45°,向前走了18m后到达D点,测得A点的仰角为60°,B点的仰角为30°(1)求证:AB=BD;(2)求证铁塔AB的高度.(结果精确到0.1米,其中≈1.41 )4、(2019海宁.中考模拟) 如图,小聪和小明在校园内测量钟楼MN的高度.小聪在A 处测得钟楼顶端N的仰角为45°,小明在B处测得钟楼顶端N的仰角为60°,并测得A,B两点之间的距离为27.3米,已知点A,M,B依次在同一直线上.(1)求钟楼MN的高度,(结果精确到0.1米)(2)因为要举办艺术节,学校在钟楼顶端N处拉了一条宣传竖幅,并固定在地面上的C处(点C在线段AM上).小聪测得点C处的仰角∠NCM等于75°,小明测得点C,M之间的距离约为5米,若小聪的仰角数据正确,问小明测得的数据“5米”是否正确?为什么?(参考数据: 1.41, 1.73)5、(2014绍兴.中考真卷) 九(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.(1)如图1,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数.(2)如图2,第二小组用皮尺量的EF为16米(E为护墙上的端点),EF的中点离地面FB的高度为1.9米,请你求出E点离地面FB的高度.(3)如图3,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰角为60°,求旗杆AE的高度(精确到0.1米).备用数据:tan60°=1.732,tan30°=0.577,=1.732,=1.414.6、(2018广州.中考模拟) 如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,巳知该山坡的坡度i(即tan∠ABC)为1:,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.(1)山坡坡角(即∠ABC)的度数等于度;(2)求A、B两点间的距离(结果精确到0.1米,参考数据:≈1.732).7、(2016盐田.中考模拟) 如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.(1)用α和β的三角函数表示CE;(2)当α=30°、β=60°时,求EF(结果精确到1m).(参考数据:≈1.414,≈1.732)8、(2019贵阳.中考模拟) 如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:的斜坡CD前进2 米到达点D,在点D 处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.(1)求点D的铅垂高度(结果保留根号);(2)求旗杆AB的高度(结果保留根号).9、(2019桂林.中考模拟) 如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:(沿斜坡从B到D时,其升高的高度与水平前进的距离之比),另一段斜坡AD的长400米,在斜坡BD的坡顶D处测得山顶A的仰角为45°(1)求斜坡BD的坡顶D到地面BC的高度是多少米?(2)求BC.(结果保留根号)10、(2017桂林.中考模拟) 如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6 米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.(1)求斜坡CD的高度DE;(2)求大楼AB的高度(结果保留根号).11、(2018海南.中考真卷) 如图,某数学兴趣小组为测量一棵古树BH和教学楼CG 的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G 的仰角∠GEF为60°,点A、B、C三点在同一水平线上.(1)计算古树 BH的高;(2)计算教学楼CG的高.(参考数据:≈14,≈1.7)12、(2018遵义.中考模拟) 为纪念遵义会议80周年献礼,遵义市政府对城市建设进行了整改,如图,已知斜坡AB长60 米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE 和一条新的斜坡BE(下面两个小题结果都保留根号).(1)若修建的斜坡BE的坡比为∶1,求休闲平台DE的长是多少米?(2)一座建筑物GH距离A点33米远(即AG=33米),小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H在同一个平面内,点C、A、G 在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?13、(2020铁岭.中考真卷) 如图,小明利用学到的数学知识测量大桥主架在水面以上的高度,在观测点处测得大桥主架顶端的仰角为30°,测得大桥主架与水面交汇点的俯角为14°,观测点与大桥主架的水平距离为60米,且垂直于桥面.(点在同一平面内)(参考数据)(1)求大桥主架在桥面以上的高度AM;(结果保留根号)(2)求大桥主架在水面以上的高度.(结果精确到1米)14、(2021八步.中考模拟) 如图,某中学数学课外学习小组想测量教学楼的高度,组员小方在处仰望教学楼顶端处,测得,小方接着向教学楼方向前进到处,测得,已知,,.(,)(1)求的值;(2)求教学楼的高度.(结果精确到)15、随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量翡翠湖某处东西岸边,两点之间的距离.如图所示,小星站在湖边的处遥控无人机,无人机在处距离地面的飞行高度是,此时从无人机测得岸边处的俯角为,他抬头仰视无人机时,仰角为,若小星的身高,(点,,,在同一平面内).(1)求仰角的正弦值;(2)求,两点之间的距离(结果精确到).(,,,,,)解直角三角形的应用﹣仰角俯角问题综合题答案1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:11.答案:12.答案:13.答案:14.答案:15.答案:。
备考2023年中考数学一轮复习-解直角三角形的应用﹣仰角俯角问题-填空题专训及答案

备考2023年中考数学一轮复习-解直角三角形的应用﹣仰角俯角问题-填空题专训及答案解直角三角形的应用﹣仰角俯角问题填空题专训1、(2012大连.中考真卷) 如图,为了测量电线杆AB的高度,小明将测量仪放在与电线杆的水平距离为9m的D处.若测角仪CD的高度为1.5m,在C处测得电线杆顶端A的仰角为36°,则电线杆AB的高度约为________m.(精确到0.1m).(参考数据sin36°≈0.59.cos36°≈0.81,tan36°≈0.73).2、(2015阜新.中考真卷) 如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为________m(结果保留根号).3、(2017庆云.中考模拟) 如图,从一艘船的点A处观测海岸上高为41m的灯塔BC (观测点A与灯塔底部C在一个水平面上),测得灯塔顶部B的仰角为35°,则观测点A到灯塔BC的距离为________.(精确到1m)【参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7】4、(2019苏州.中考模拟) 如图,在楼顶点处观察旗杆测得旗杆顶部的仰角为30°,旗杆底部的俯角为45°.已知楼高m,则旗杆的高度为________.(结果保留根号)5、(2014嘉兴.中考真卷) 如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为________ 米(用含α的代数式表示).6、(2016宁波.中考真卷) 如图,在一次数学课外实践活动中,小聪在距离旗杆10m 的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为________m(结果保留根号).7、(2018枣阳.中考模拟) 如图所示,小明在家里楼顶上的点A处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点C处的俯角为45°,两栋楼之间的距离为30m,则电梯楼的高BC为________米(精确到0.1).(参考数据:≈1.414,≈1.732).8、(2019孝感.中考真卷) 如图,在处利用测角仪测得某建筑物的顶端点的仰角为60°,点的仰角为45°,点到建筑物的距离为米,则________米.9、(2017黄石.中考真卷) 如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为________米.(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据:≈1.41,≈1.73)10、(2017番禺.中考模拟) 如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A,B,C在同一条直线上),则河的宽度AB约为________.11、(2019宝鸡.中考模拟) 如图,某飞机于空中探测某座山的高度,在点处飞机的飞行高度是米,从飞机上观测山顶目标的俯角是,飞机继续以相同的高度飞行米到地,此时观察目标的俯角是,则这座山的高度是________米(参考数据:,,)12、(2017.中考模拟) 如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC= ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为________米.13、(2020湖州.中考模拟) 如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°,热气球A的高度为270米,则这栋大楼的高度为________米.14、(2021浦东新.中考模拟) 如果从某一高处甲看低处乙的俯角为36度,那么从低处乙看高处甲的仰角是度.15、(2022汕尾.中考模拟) 如图,从楼顶处看楼下荷塘处的俯角为,看楼下荷塘处的俯角为,已知楼高为米,则荷塘的宽为米.(结果保留根号)16、(2021烟台.中考真卷) 数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为40米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,则旗杆的高度约为米.(结果精确到1米,参考数据:,)17、(2021百色.中考真卷) 数学活动小组为测量山顶电视塔的高度,在塔的椭圆平台遥控无人机.当无人机飞到点P处时,与平台中心O点的水平距离为15米,测得塔顶A点的仰角为30°,塔底B点的俯角为60°,则电视塔的高度为米.18、(2021赤峰.中考真卷) 某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C测一段水平雪道一端A处的俯角为50°,另一端B处的俯角为45°,若无人机镜头处的高度为米,点A,D,B在同一直线上,则通道AB的长度为米.(结果保留整数,参考数据,,)19、如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD 的长度为20m,DE的长为10m,则树AB的高度是m.20、如图,为了配合疫情工作,浦江某学校门口安装了体温监测仪器,体温检测有效识别区域AB长为6米,当身高为1.5米的学生进入识别区域时,在点B处测得摄像头M的仰角为,当学生刚好离开识别区域时,在点A处测得摄像头M的仰角为,则学校大门ME的高是米.解直角三角形的应用﹣仰角俯角问题填空题答案1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:11.答案:12.答案:13.答案:14.答案:15.答案:16.答案:17.答案:18.答案:19.答案:20.答案:。
第02课时 仰角、俯角、方位角

1.(5 分)如图,某地修建高速公路,要从 B 地向 C 地修一座隧道(B,
C 在同一水平面上),为了测量 B,C 两地之间的距离,某工程师乘坐热
气球从 C 地出发,垂直上升 100 m 到达 A 处,在 A 处观察 B 地俯角为
30°,则 B,C 两地之间的距离为( A )
A.100 3 m
B.50 2 m
一、选择题(每小题 6 分,共 12 分)
7.如图,从热气球 C 处测得地面 A,B 两点的俯角分别为 30°,45°,
如果此时热气球 C 处的高度 CD 为 100 米,点 A,D,B 在同一直线上,
则 A,B 两点的距离是( D )
A.200 米
B.200 3 米
C.220 3 米
D.100( 3+1)米
CED=60°,sin∠CED=CCDE ,∴CE= sinC6D0°= 2
3+1.5 3 =(4+
3)
2
≈5.7(米),答:拉线CE的长约为5.7米
11.(14分)(2014·黔东南州)黔东南州某校九年级某班开展数学活 动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B点测得 旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为 30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身 高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,
三、解答题(共42分) 10.(14分)(2014·钦州)如图,在电线杆CD上的C处引拉线CE,CF 固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米 的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30 °,求拉线CE的长.(结果保留小数点后一位,参考数据: 2 ≈ 1.414, 3≈1.732)
中考数学 中档题突破 专项训练三 解直角三角形的实际应用 类型一:仰角、俯角问题

0.81)
( B)
A.16.8 m
B.28.8 m
C.40.8 m
D.64.2 m
2.如图,运载火箭从地面O处发射,当火箭到达 点A时,地面D处的雷达站测得AD=4 000 m,仰角 为30°,3 s后,火箭直线上升到达点B处,此时 地面C处的雷达站测得B处的仰角为45°,点O,C,D 在同一直线上,已知C,D两处相距460 m,求火箭从A处到B处的平均 速度.(结果精确到个位,参考数据: 3≈1.732, 2≈1.414)
专项训练三 解直角三角 形的实际应用
类型一:仰角、俯角问题 1.★如图,一棵松树AB挺立在斜坡CB的顶端,斜坡CB长为52 m,
坡度为i=12:5,小张从与点C相距60 m的点D处向上爬 1ቤተ መጻሕፍቲ ባይዱ m到达观景 台DE的顶端点E,在此测得松树顶端点A的仰角为39°,则松树的高度
AB约为(参考数据:sin 39°≈0.63,cos 39°≈0.78,tan 39°≈
解:由题意,得AD=4 000 m,∠ADO=30°, CD=460 m,∠BCO=45°,在Rt△AOD中,∵AD=4 000 m, ∠ADO=30°,∴OA=12AD=2 000 m,OD= 23AD=2 000 3 m, 在Rt△BOC中,∠BCO=45°, ∴OB=OC=OD-CD=(2 000 3-460) m,∴AB=OB-OA≈1 004(m), ∴火箭的速度为1 004÷3≈335(m/s). 答:火箭从A处到B处的速度约为335 m/s.
解直角三角函数仰角俯角专题

11、如图,小明用一块有一个锐角为30 的直角三角板测量树高,已知小明离树的距离为4米,DE 为1.68米,那么这棵树大约有多高?(精确到0.1米)1.1如图,在高为h 的山顶上,测得一建筑物顶端与底部的俯角分别为30°和60°,用h 表示这个建筑物的高为 .1.2如图,塔AB 和楼CD 的水平距离为80m ,从楼顶C 处及楼底D 处测得塔顶A 的仰角分别为450和600,试求塔高和楼高。
2、如图,张华同学在学校某建筑物的C 点处测得旗杆顶部A 点的仰角为30 ,旗杆底部B 点的俯角45 .若旗杆底部B 点到建筑物的水平距离9B E 米,旗杆台阶高1米,则旗杆顶点A 离地面的高度为 米(结果保留根号).2.1如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为45,如果梯子的底端O 固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为60 ,求此保管室的宽度A B 的长.AB CD23、海中有一个小岛P ,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A 测得小岛P 在北偏东60°方向上,航行12海里到达B 点,这时测得小岛P 在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.4、如图,某中学九年级一班数学课外活动小组利用周末开展课外实践活动,他们要在某公园人工湖旁的小山AB 上,测量湖中两个小岛C 、D 间的距离.从山顶A 处测得湖中小岛C 的俯角为60°,测得湖中小岛D 的俯角为45°.已知小山AB 的高为180米,求小岛C 、D 间的距离.(计算过程和结果均不取近似值)5、汶川地震后,抢险队派一架直升飞机去A 、B 两个村庄抢险,飞机在距地面450米上空的P 点,测得A村的俯角为30︒,B 村的俯角为60︒(.如图7).求A 、B 两个村庄间的距离.(结果精确到米,参考数据1.414 1.732==)6、如图8,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45º降为30º,已知原滑滑板AB 的长为5米,点D 、B 、C 在同一水平地面上.(1)改善后滑滑板会加长多少?(精确到0.01)(2)若 滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?说明理由 (参考数据:2.449=== )Q B CP A45060︒30︒ AC B3。
俯角仰角练习题

俯角仰角练习题1. 某人站在一个高处俯视地面,他把抬头角度称为仰角。
某个点到此人的视线的角度称为俯角。
现假设此人距离地面10米,他的仰角为30度,则与此人眼睛的水平面相交的水平面上的物体A的俯角是多少度?解析:由题可知,此人的仰角为30度,即他的视线与水平面的夹角为30度。
物体A与此人眼睛的水平面相交,因此可以得知物体A的俯角也是30度。
2. 假设有一个物体B位于地面上,并且这个物体的高度为5米。
某人站在地面上,他抬头看着物体B,此时他的仰角为45度。
求此人与物体B视线的夹角,即俯角是多少度?解析:对于此题,我们需要找到与此人所站点与物体B确定的直线的垂直线。
由此可知,此垂直线与地面的夹角即为此人与物体B视线的夹角,即俯角。
根据三角形的性质可知,此垂直线与地面的夹角为45度。
因此,此人与物体B视线的夹角,即俯角为45度。
3. 在一个夜晚,某人站在一个高台上,观察附近的城市夜景。
此人站在一个高度为20米的位置,他的仰角为60度。
他发现城市中心的大楼C的俯角为30度。
请问大楼C的实际高度是多少?解析:根据此题可知,此人的仰角为60度。
由于大楼C的俯角为30度,即大楼C与此人视线的夹角为30度。
我们可以设大楼C的实际高度为H,根据三角形的性质可得:tan(30) = H/20解方程可得:H = 20 * tan(30) = 10√3 ≈ 17.32米因此,大楼C的实际高度约为17.32米。
4. 某人站在一座山上,他的高度为30米,他的仰角为45度。
他注意到山的脚下有一个湖泊D,他估计湖泊D的俯角为60度。
根据此情况,请计算湖泊D的实际宽度。
解析:根据此题可知,此人的仰角为45度。
湖泊D的俯角为60度,即湖泊D与此人视线的夹角为60度。
我们可以设湖泊D的实际宽度为W,根据三角形的性质可得:tan(45) = 30/W解方程可得:W = 30/tan(45) = 30 ≈ 30米因此,湖泊D的实际宽度约为30米。
28.2仰角俯角问题(包含答案)

28.2仰角俯角问题一.选择题(共8小题)1.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为()A.100m B.50m C.50m D.m2.如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=30°,则飞机A与指挥台B的距离为()A.1200m B.1200m C.1200m D.2400m3.如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是()A.200米B.200米C.220米D.100()米4.如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB 方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为()A.10米B.10米C.20米D.米5.兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得楼顶端A的仰角为60°,楼AB的高为()A.B.C.D.6.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为()A.米B.30sinα米C.30tanα米D.30cosα米7.小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高()A.600﹣250米B.600﹣250米C.350+350米D.500米8.如图,在水平地面上,由点A测得旗杆BC顶点C的仰角为60°,点A到旗杆的距离AB=12米,则旗杆的高度为()A.米B.6米 C.米 D.12米二.填空题(共5小题)9.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为米(结果保留整数,测角仪忽略不计,≈1.414,,1.732)10.如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,则乙楼的高度为米.11.如图,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=米.12.如图,线段AB、DC分别表示甲、乙两座楼房的高,AB⊥BC,DC⊥BC,两建筑物间距离BC=30米,若甲建筑物高AB=28米,在点A测得D点的仰角α=45°,则乙建筑物高DC=米.13.如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是m(结果保留根号)三.解答题(共5小题)14.如图,岸边的点A处距水面的高度AB为2.17米,桥墩顶部点C距水面的高度CD为12.17米.从点A处测得桥墩顶部点C的仰角为26°,求岸边的点A与桥墩顶部点C之间的距离.(结果精确到0.1米)(参考数据:sin26°=0.44,cos26°=0.90,tan26°=0.49)15.在数学课外实践活动中,要测量教学楼的高度AM.下面是两位同学的对话:请你根据两位同学的对话,结合图形计算教学楼的高度AM.(参考数据:sin20°≈,cos20°≈,tan20°≈)16.如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,≈1.7,≈1.4 )17.如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30°,再向旗杆的方向前进16米,到达点D 处(C、D、B三点在同一直线上),又测得旗杆顶端A的仰角为45°,请计算旗杆AB的高度(结果保留根号)18.小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.(结果保留整数)(参考数据:sin35°≈,cos35°≈,tan35°≈)28.2仰角俯角问题参考答案与试题解析一.选择题(共8小题)1.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为()A.100m B.50m C.50m D.m【解答】解:根据题意得:∠ABC=30°,AC⊥BC,AC=100m,在Rt△ABC中,BC===100(m).故选A.2.如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=30°,则飞机A与指挥台B的距离为()A.1200m B.1200m C.1200m D.2400m【解答】解:∵∠ABC=∠α=30°,∴AB==,即飞机A与指挥台B的距离为2400m.故选:D.3.如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是()A.200米B.200米C.220米D.100()米【解答】解:由已知,得∠A=30°,∠B=45°,CD=100,∵CD⊥AB于点D.∴在Rt△ACD中,∠CDA=90°,tanA=,∴AD===100在Rt△BCD中,∠CDB=90°,∠B=45°∴DB=CD=100米,∴AB=AD+DB=100+100=100(+1)米.故选D.4.如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB 方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为()A.10米B.10米C.20米D.米【解答】解:∵在直角三角形ADB中,∠D=30°,∴=tan30°∴BD==AB∵在直角三角形ABC中,∠ACB=60°,∴BC==AB∵CD=20∴CD=BD﹣BC=AB﹣AB=20解得:AB=10.故选A.5.兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得楼顶端A的仰角为60°,楼AB的高为()A.B.C.D.【解答】解:在Rt△AFG中,tan∠AFG=,∴FG==,在Rt△ACG中,tan∠ACG=,∴CG==AG.又∵CG﹣FG=30m,即AG﹣=30m,∴AG=15m,∴AB=(15+2)m.故选:D.6.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为()A.米B.30sinα米C.30tanα米D.30cosα米【解答】解:在Rt△ABO中,∵BO=30米,∠ABO为α,∴AO=BOtanα=30tanα(米).故选C.7.小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高()A.600﹣250米B.600﹣250米C.350+350米D.500米【解答】解:∵BE:AE=5:12,=13,∴BE:AE:AB=5:12:13,∵AB=1300米,∴AE=1200米,BE=500米,设EC=x米,∵∠DBF=60°,∴DF=x米.又∵∠DAC=30°,∴AC=CD.即:1200+x=(500+x),解得x=600﹣250.∴DF=x=600﹣750,∴CD=DF+CF=600﹣250(米).答:山高CD为(600﹣250)米.故选:B.8.如图,在水平地面上,由点A测得旗杆BC顶点C的仰角为60°,点A到旗杆的距离AB=12米,则旗杆的高度为()A.米B.6米 C.米 D.12米【解答】解:由于AB=12(米),仰角α=60°,则BC=AB•tan60°=12(米),故选C.二.填空题(共5小题)9.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为137米(结果保留整数,测角仪忽略不计,≈1.414,,1.732)【解答】解:如图,∠ABD=30°,∠ACD=45°,BC=100m,设AD=xm,在Rt△ACD中,∵tan∠ACD=,∴CD=AD=x,∴BD=BC+CD=x+100,在Rt△ABD中,∵tan∠ABD=,∴x=(x+100),∴x=50(+1)≈137,即山高AD为137米.故答案为137.10.如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,则乙楼的高度为(30+10)米.【解答】解:如图,过点A作AE⊥CD于点E,根据题意,∠CAE=45°,∠DAE=30°.∵AB⊥BD,CD⊥BD,∴四边形ABDE为矩形.∴BD=AE=30米.在Rt△ADE中,tan∠DAE=,∴DE=AE•tan∠DAE=30×=10米,在Rt△ACE中,由∠CAE=45°,得CE=AE=30米,∴CD=CE+DE=(30+10)米,故答案为(30+10).11.如图,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=100米.【解答】解:∵在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,∴船与观测者之间的水平距离BC=AC=100米.故答案为:100米.12.如图,线段AB、DC分别表示甲、乙两座楼房的高,AB⊥BC,DC⊥BC,两建筑物间距离BC=30米,若甲建筑物高AB=28米,在点A测得D点的仰角α=45°,则乙建筑物高DC=58米.【解答】解:过点A作AE⊥CD于点E.根据题意,得∠DAE=45°,AE=DE=BC=30.∴DC=DE+EC=DE+AB=30+28=58米.故答案为:58.13.如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是3+9m(结果保留根号)【解答】解:在Rt△ACD中,∵tan∠ACD=,∴tan30°=,∴=,∴AD=3m,在Rt△BCD中,∵∠BCD=45°,∴BD=CD=9m,∴AB=AD+BD=3+9(m).故答案为:3+9.三.解答题(共5小题)14.如图,岸边的点A处距水面的高度AB为2.17米,桥墩顶部点C距水面的高度CD为12.17米.从点A处测得桥墩顶部点C的仰角为26°,求岸边的点A与桥墩顶部点C之间的距离.(结果精确到0.1米)(参考数据:sin26°=0.44,cos26°=0.90,tan26°=0.49)【解答】解:由题意知,DE=AB=2.17,∴CE=CD﹣DE=12.17﹣2.17=10(m).在Rt△CAE中,∠CAE=26°,sin∠CAE=,∴AC===≈22.7(米).答:岸边的点A与桥墩顶部点C之间的距离约为22.7米.15.在数学课外实践活动中,要测量教学楼的高度AM.下面是两位同学的对话:请你根据两位同学的对话,结合图形计算教学楼的高度AM.(参考数据:sin20°≈,cos20°≈,tan20°≈)【解答】解:由题意得∠ABC=90°∵∠ACB=45°∴∠CAB=90°﹣∠ACB=90°﹣45°=45°∴AB=BC设AB=x,则BC=x,DB=20+x在Rt△ABD中∵tan∠ADB=∴tan20°=,∵tan20°≈,∴,x=11.25∵BM=CE=1.5∴AM=11.25+1.5=12.75答:教学楼的高AM是12.75米.方法二解:设BD为x,则BC=x﹣20∵∠ACB=45°,∠ABC=90°∴∠CAB=45°∴AB=BC=x﹣20在Rt△ABD中∵tan∠ADB=,∴tan20°=,∵tan20°=,∴,x=31.25∴BC=31.25﹣20=11.25∵BM=CE=1.5∴AM=11.25+1.5=12.75.答:教学楼的高AM约为12.75米.16.如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,≈1.7,≈1.4 )【解答】解:根据题意得:AB=18,DE=18,∠A=30°,∠EBC=60°,在R t△ADE中,AE===18∴BE=AE﹣AB=18﹣18,在R t△BCE中,CE=BE•tan60°=(18﹣18)=54﹣18,∴CD=CE﹣DE=54﹣18﹣18≈5米.17.如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30°,再向旗杆的方向前进16米,到达点D 处(C、D、B三点在同一直线上),又测得旗杆顶端A的仰角为45°,请计算旗杆AB的高度(结果保留根号)【解答】解:由题意可得,CD=16米,∵AB=CB•tan30°,AB=BD•tan45°,∴CB•tan30°=BD•tan45°,∴(CD+DB)×=BD×1,解得BD=8,∴AB=BD•tan45°=()米,即旗杆AB的高度是()米.18.小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.(结果保留整数)(参考数据:sin35°≈,cos35°≈,tan35°≈)【解答】解:作AD⊥BC交CB的延长线于D,设AD为x,由题意得,∠ABD=45°,∠ACD=35°,在Rt△ADB中,∠ABD=45°,∴DB=x,在Rt△ADC中,∠ACD=35°,∴tan∠ACD=,∴=,解得,x≈233m.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1•某地震救援队探测出某建筑物废墟下方点 C 处有生命迹象,已知废墟一侧地面上两探测点 A 、B 相距 3米,探测线与地面的夹角分别是
30°和60°(如图),试确定生命所在点 C 的深度. (结果精确到米,参考数据:
2 1.41, ,
3 1.73 )
5. 建于明洪武七年(1374年),高度33米的光岳楼是目前我国现存的最高大、最古老的楼阁之一(如图
①).喜爱数学实践活动的小伟,在 30米高的光岳楼顶楼 P 处,利用自制测角仪测得正南方向商店 A 点
的俯角为60,又测得其正前方的海源阁宾馆 B 点的俯角为30 (如图②)•求商店与海源阁宾馆之间的距
2•为了缓解酒泉市区内一些主要路段交通拥挤的现状, 交警队在一些主要路口设立了交通路况显示牌 (如 图)•已知立杆AB 高度是3m ,从侧面D 点测得显示牌顶端 C 点和底端B 点的仰角分别是60。
和45° •求
6.
汶川地震后,抢险队派一架直升飞机去 A 、B 两个村庄抢险,飞机在距地面
450米上空的P 点,测得
A 村的俯角为30°,
B 村的俯角为60° ,求A 、B 两个村庄间的距离.(结果精确到米,)
3.如图,为了测量某建筑物 CD 的高度,先在地面上用测角仪自 A 处测得建筑物顶部的仰角是 30°,然
后在水平地面上向建筑物前进了 100m ,此时自B 处测得建筑物顶部的仰角是 45°.已知测角仪的高度
7.
小明家所在居民楼的对面有一座大厦 AB , AB = 80米•为测量这座居
民楼与大厦之间的距离,小明从
自己家的窗户 C 处测得大厦顶部 A 的仰角为37°,大厦底部B 的俯角为48°・求小明家所在居民楼与
大厦的距离CD 的长度.(结果保留整数)(参考数据:)
3 3 7 11
sin37o -, tan37o -,sin 48°— , tan48o 一
5 4 10 10
.摩天轮是嘉峪关市的标志性景观之一•某校数学兴趣小组要测量摩天轮的高度•如图,他们在
C 处 测得摩天轮的最高点 A 的仰角为45°,再往摩天轮的方向前进 50 m 至
D 处,测得最高点 A 的仰角为
8.
如图所示,小明在
家里楼顶上的点 A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,
在点A
处看电梯楼顶部点 B 处的仰角为60°,在点A 处看这栋电梯楼底部点 C 处的俯角为45°,两栋楼之间 的距离为30m ,则电梯楼的高 BC 为多少米(精确到)•(参考数据:
2 1.414,.
3 1.732
)
离(结果保留根
号)
图①
路况显示牌BC 的高度.
参考数据.2 -,
3
1.732
是,请你计算出该建筑物的高度.
(取3 1.732,结果精确到1m )
E D
60° •求该兴趣小组测得的摩天轮的高度
AB o ( 3 1.732 ,结果保
留整数).
9•如图,一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,求海底黑匣13.在学习实践科学发展观的活动中,某单位在如图所示的办公楼迎街的墙面上垂挂一长为30米的宣传条幅AE,张明同学站在离办公楼的地面C处测得条幅顶端A的仰角为50°,测得条幅底端E的仰角为
10.如图,小刚同学在綦江南州广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6米到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E测得BE= 21米,请你帮小刚求出该屏幕上端与下端之间的距离CD.(结果保留根号)14.如图,从点A看一高台上的电线杆CD,顶端C的仰角为45°,向前走6米到B点,测得其顶端C和杆底D的仰角分别是600和30°,求电线杆CD的高(精确到米)
15.如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且CB=5米.
(1)求钢缆CD的长度;(精确到米)
子C点处距离海面的深度(精确到米,参考数据:
30。
.问张明同学是在离该单位办公楼水平距离多远的地方进行测量(精确到整数米)
(参考数据:sin50°~, cos50°~,tan50 °~, sin30° =, cos30°~,
tan30 °~)
11.如图,已知测速站P到公路L的距离PO为40米,一辆汽车在公路L上行驶,测得此车从点A行驶
到点B的所用时间为2秒,并测得/ APO=600,Z BPO=300,计算此车从A到B的平均速度,并判断此
车是否超过了每小时70千米的限制速
度。
(2)若AD=2米,灯的顶端E距离A处米,且/ EAB=120°,则灯的顶端
5
(参考数据:tan40 ° =, sin40° =, cos40° =—
4
12如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂
与底座构成的/ BAD=60° .使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C
到桌面的高度CE是多少cm (结果精确到0.1cm,参考数据:,3
16如图1,一架飞机在空中P处探测到某高山山顶D处的俯角为60°,此后飞机以300米/秒的速度沿平行于地面AB的方向匀速飞行,飞行10秒到山顶D的正上方C处,此时测得飞机距地平面的垂直高度为12千米,求这座山的高(精确到千米)。
