空气弹簧刚度计算
空气弹簧
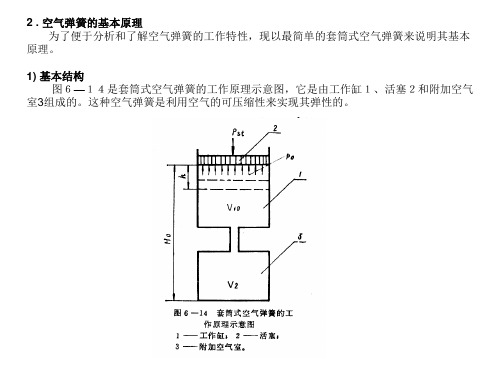
3) 套筒式空气弹簧的刚度 (1) 空气弹簧的刚度公式推导 当活塞由于振动而向下移动h时,工作缸容积减小了dV(V=V0一 dV,dV=Ah),根据气体状态方程有:
(6-31)
又V0=H0A, 故可将上式变为:
则
振动时,工作缸中的空气压力因压缩和拉伸而变化。振动时活塞上 的载荷P和位移h间的关系为:
也能得到足够低的刚度。
(4) 空重车自振频率基本不变 为了更清楚地看出刚度随载荷变化的情况,设静载荷Pst变P1,容积变为V1,内压力变为 p1,则刚度K1变为: (6-37) 自振频率为: (6-38) 于是,静载荷变化前后的刚度比为: (6-39) 因为空气弹簧悬挂装置通常都装有高度控制阀,所以,当静载荷变化时,工作缸内的容积不 变(V1=V0),于是静载荷变化前后的刚度比为: (6-40)
1) 载荷P和内压力p的关系
为了求出载荷P和内压力p的关系,作一平面A一A切于橡胶空气囊 的表面且垂直于气囊的轴线,如图6—16 (a)所示。由于胶囊是柔软的橡 胶薄膜,根据薄膜理论,这种气囊不能传递弯矩和横向力,因此,在通 过气囊切点处只传递平面A—A上的力。 由力的平衡条件得:
(6—42)
式中A1和R分别为橡胶空气囊的有效承压面积和有效半径。
由式(6—35)、(6—38)和(6—40)可知,静载荷变化前后的自振频率比为: (6-41) 由此可见,在采用高度控制阀的情况下,空重车的自振频率基本上保持不变。
(5) 空气弹簧的当量静挠度 通常把簧上载荷P与相应状态下的空气弹簧刚度K之比 P/K=fdst 称为空气弹簧的当量静挠度。
3 . 铁道车辆空气弹簧特点 铁道车辆上采用橡胶帘线式(简称橡胶式)空气弹簧, 它也具有上述套筒式 空气弹簧的基本特性,但又有其特点。 橡胶式空气弹簧的承压面积A1不是常数,而是随载荷变化的。 因为当载荷P 变化时,橡胶囊的形状也随着改变,因而承压面积A1和半径也随之改变。 图6—16表明橡胶式空气弹簧的工作原理,通常将任意状态下外载荷 P和囊内压力p之比P/p=A1称为有效承压面积,与之相应的橡胶囊半径R称 为有效半径。
弹簧刚度系数计算公式

弹簧刚度系数计算公式
弹簧刚度系数是弹簧的力学性质之一,它是指单位长度或单位位移所需要的力的大小。
弹簧刚度系数的计算公式为:
k = F/x
其中,k为弹簧刚度系数,单位为N/m或N/mm;F为弹簧所受的力,单位为N;x为弹簧的变形量,单位为m或mm。
在计算弹簧刚度系数时,需要注意以下几点:
1. 弹簧的变形量应该是弹簧长度的变化量,而不是弹簧的直径
或横截面积的变化量。
2. 弹簧刚度系数的值与弹簧的形状、材料、尺寸等因素有关,
因此在实际应用中需要根据具体情况进行计算。
3. 在弹簧所受力的范围内,弹簧的变形量与所受力成正比,因
此弹簧刚度系数应该是一个常数,但在弹簧所受力超过一定范围后,弹簧的变形量将不再与所受力成正比,此时弹簧刚度系数将发生变化。
综上所述,弹簧刚度系数是一个重要的弹簧力学参数,计算公式为k = F/x,可以根据实际情况进行计算,并需要注意弹簧的形状、材料、尺寸等因素。
- 1 -。
客车空气悬架刚度计算公式

客车空气悬架刚度计算公式引言。
客车空气悬架是一种通过空气压缩来调节车辆悬架刚度的技术,它可以根据路况和载重情况自动调节悬架的硬度,提高乘坐舒适性和稳定性。
在设计和调试客车空气悬架系统时,需要对悬架的刚度进行计算和分析,以确保其满足车辆的性能要求。
本文将介绍客车空气悬架刚度的计算公式及其应用。
客车空气悬架刚度的重要性。
客车空气悬架的刚度对车辆的悬架性能有着重要的影响。
合适的悬架刚度可以提高车辆的稳定性和操控性,减小车身的倾斜和颠簸感,提高乘坐舒适性。
此外,合适的悬架刚度还可以减小车辆在行驶过程中的振动和颠簸,延长车辆和悬架系统的使用寿命。
因此,客车空气悬架刚度的计算和调试是非常重要的。
客车空气悬架刚度的计算公式。
客车空气悬架刚度的计算公式可以通过以下步骤得出:第一步,确定悬架系统的参数。
首先,需要确定客车空气悬架系统的参数,包括空气弹簧的气压、气囊的体积和形状、悬架系统的几何结构等。
这些参数将直接影响悬架系统的刚度。
第二步,计算空气弹簧的刚度。
空气弹簧的刚度可以通过以下公式进行计算:K = P / Δ。
其中,K为空气弹簧的刚度,P为空气弹簧的气压,Δ为空气弹簧的变形量。
通过这个公式可以得到空气弹簧的刚度,从而确定悬架系统的刚度。
第三步,计算气囊的刚度。
气囊的刚度可以通过以下公式进行计算:K = P / Δ。
其中,K为气囊的刚度,P为气囊的气压,Δ为气囊的变形量。
通过这个公式可以得到气囊的刚度,从而确定悬架系统的刚度。
第四步,计算悬架系统的总刚度。
悬架系统的总刚度可以通过以下公式进行计算:K_total = K1 + K2 + ... + Kn。
其中,K_total为悬架系统的总刚度,K1、K2、...、Kn分别为悬架系统中各个部件的刚度。
将各个部件的刚度相加即可得到悬架系统的总刚度。
应用实例。
以某客车空气悬架系统为例,其空气弹簧的气压为0.6MPa,气囊的气压为0.5MPa,空气弹簧的变形量为10mm,气囊的变形量为8mm。
空气弹簧刚度计算公式

空气弹簧刚度计算公式1. 载荷与气压关系式:P (P P a )A----(1)式中:P 载荷P 气囊内绝对气压 A 气囊有效承压面积P a 标准大气压,其值与运算单位有关:采用 N 、mm 时,p a = 0.0981 V11N/mm 2采用 kgf 、cm 时,p a = 1 kgf/cm 2 采用 1b 、in 时,p a = 14.223 lb/in 2(psi)2. 气压与容积变化关系式 ------ 气体状态方程式p P 0(#)m式中:P 任一位置气囊内气体的绝对气压V 任一位置气囊内气体容积P 0静平衡位置气囊内气体的绝对气压 V 0静平衡位置气囊内气体容积m 多变指数,静态即等温过程 m =1;动态即绝热过程 m =1.4; 一般状态,可取 m =1.33。
刚度:弹性特性为弱非线性,取其导数,即式中: K 任一位置的刚度KdP dxP 载荷X气囊变形量即行程即:Kd[(p p a )A]dxV 0md[(P 0 歹 P a )A]dx (P oV o mv mdA dxAmp o V o mV^1dVdx当气囊处在平衡位置时, V = V o P= P o 即: K o (p op 厝 dxdV,dxA2mpov=-A ,在平衡位置时之偏频:n oP o mgA (P o p a )V o(Hz)----(3)----(4)式中:dA dx称为有效面积变化率;g 重力加速度。
可见, 降低 dAdx、增大V o ,可降低 n o ,提高平顺性P.S 有时采用相对气压 P 1来运算更为方便 p i = p - p a代入式(1)即P = p i A或:P o = P io P a----(5)代入式(3) 即:K oP io 譽 m(P iodx P a) A 2 V?n oi g dA 2 n A dxP io p a mgApioVo(Hz)----(6)----(7)又T An D 2 D 为有效直径,.dA nD dD dx 2 dx代入式(6)对囊式空气弹簧,一般dD =0.2--0.3 ,dx甚至有巴=-0.1 ,取决于活塞形状dx式中:dx 称为有效直径变化率。
空气弹簧刚度的精确仿真与解析计算研究

空气弹簧刚度的精确仿真与解析计算研究
空气弹簧刚度的精确仿真与解析计算研究是一个非常复杂的工程问题,涉及到材料力学、流体力学、热力学和控制系统等多个学科。
目前,随着计算机技术的发展,基于数值模拟和计算流体力学(CFD)的方法已经成为研究空气弹簧刚度的最佳选择。
在数值模拟方法中,通常使用有限元分析(FEA)或数值模拟(DNS)等方法来模拟空气弹簧的刚度。
有限元分析是一种基于有限个单元进行计算的方法,DNS则是一种基于时间域模拟的方法。
这两种方法都可以用来计算空气弹簧的刚度,但结果可能会有很大的差异。
在解析计算方法中,可以使用方程求解器来求解牛顿第二定律和流体力学方程,从而获得空气弹簧的刚度。
然而,这种方法需要对空气弹簧的结构非常熟悉,并且需要处理复杂的非线性方程,因此一般适合于对空气弹簧的结构和应用有很深入的了解的情况下使用。
对于空气弹簧刚度的精确仿真和解析计算,可以采用多种方法进行研究。
首先,需要确定空气弹簧的结构和材料,并使用适当的数值模拟和解析计算方法来模拟空气弹簧的性能和行为。
其次,需要对不同的数值模拟和解析计算方法进行比较和分析,以确定哪种方法更适合特定的研究问题和数据。
最后,需要对所得结果进行验证和测试,以验证方法和结果的可靠性和精度。
总之,空气弹簧刚度的精确仿真和解析计算研究是一个复杂的工程问题,需要综合运用多个学科的知识和方法,才能够获得可靠的结果和深入的理解。
弹簧刚度计算公式

弹簧刚度计算公式
弹簧刚度计算公式
建筑行业中,弹簧刚度是一个非常重要的参数。
从安全的角度来看,弹簧的刚度应该能够维持建筑物的均衡状态,使其不受受力改变时的破坏影响。
在计算建筑物的弹簧刚度时,有一个普遍的计算公式,即:
弹簧刚度 = 扭矩 (MM) / 弯曲半径 (MM)
该公式表明,弹簧刚度与扭矩和弯曲半径有关。
另外,它们之间也有一个显著的关联,即在恒定的角度下,随着力量的增加,弹簧刚度也会呈现递增特性。
在建筑物受受力改变时,弹簧刚度也会随之发生变化,在此过程中,弹簧刚度就起着重要的作用。
此外,在建筑物设计过程中,弹簧刚度还被应用于各种结构体系中,例如楼板唤动体、桥梁受力体等,用于确定这些体系的稳定性和受力安全性,确保这些结构的受力均衡性和可靠性。
因此,在建筑物的设计过程中,精确计算弹簧刚度是一项极其重要的任务,使用该计算公式可以有效的检测搭建的结构物体的刚度、受力平衡性。
空气弹簧刚度计算

空气弹簧刚度计算空气弹簧是一种常用的弹簧形式,由于其具有结构简单、体积小、自重轻、刚度可调等优点,被广泛应用于工业生产和科研实验中。
空气弹簧的刚度计算是评估其性能和设计的重要步骤。
本文将从空气弹簧的基本结构、弹簧刚度计算公式、刚度影响因素等方面进行介绍。
一、空气弹簧的基本结构空气弹簧是由柔性材料制成的空腔,常用的材料有橡胶、聚氨酯等。
弹簧通过气体充填或排放来调节其刚度。
空气弹簧一般由两个折皱的圆柱形膜片组成,通过螺纹连接器连接形成一个闭合的腔体。
当气体进入空气弹簧时,膜片会受到气体压力的作用而扩张,从而增大空气弹簧的刚度。
当气体被排放时,膜片会收缩,降低空气弹簧的刚度。
二、空气弹簧刚度计算公式k=(P1-P2)/Δh其中,k为空气弹簧的刚度,P1和P2分别为气体进入和排放时的压力,Δh为膜片变形的位移。
三、刚度影响因素1.压力差(P1-P2):气体充入或排放的压力差越大,弹簧的刚度越大。
2.膜片变形位移(Δh):膜片的变形位移越大,弹簧的刚度越大。
3.弹簧的结构参数:包括膜片的直径、厚度、材料等。
膜片直径越大,弹簧刚度越大;膜片厚度越大,弹簧刚度越小;膜片材料的刚度越大,弹簧刚度越大。
4.环境温度:环境温度的变化会影响气体的体积变化,从而影响弹簧的刚度。
一般来说,温度升高,空气弹簧的刚度会下降。
四、实际应用空气弹簧的刚度计算可以通过实验测量得出。
通常,可以通过加载不同的压力和测量弹簧变形来获得刚度值。
此外,还可以通过数值模拟方法进行计算。
数值模拟可以采用有限元方法,将空气弹簧模型建立为一个弹性体模型,通过施加不同的载荷和观察弹簧的变形来获得刚度。
在实际应用中,空气弹簧的刚度会影响到各种机械装置的性能。
例如,空气弹簧可以用于减震系统,通过调节空气弹簧的刚度来实现减震效果。
空气弹簧还可以用于振动隔离系统,通过调节刚度来减小振动的传递,从而减少机械设备的损坏。
总结:空气弹簧的刚度计算是评估其性能和设计的重要步骤。
动静刚度计算方法

2.2空气弹簧的支撑、弹性作用取决于空气弹簧内的压缩气体。
容积比、气体压缩系数基本上决定了理想空气弹簧的性能。
理想气体状态方程为绝对压力(Pa) 除以气体密度(kg/m3)等于气体常数(N•m/(kg•K) 乘以绝对温度(K)或者绝对压力(Pa) 乘以体积 = 气体质量 x 气体常数(N•m/(kg•K)) x绝对温度(K)不同的气体R值不同,空气的R=287N•m/(kg•K)当气体质量m为常数时:绝对压力(Pa)x体积的n次方=const(const为常数)式中,n----多变常数;当变速过程缓慢时,可将其视为等温过程,则n=1;当变速过程较快时,可视为绝热过程,不同的气体n值不同,空气n=1.4。
理想气体的微分方程为:绝热过程:体积的n次方x 绝对压力的导数 + n x 绝对压力 x 体积的(n-1)次方的导数=0等温过程难n=1时:体积x绝对压力的导数+绝对压力x体积的导数=0即绝对压力的导数除以绝对压力 = ―体积的导数除以体积空气弹簧的承载能力:F=变化压力x承载面积变化压力=绝对压力-原来的压力空气弹簧的理论刚度:空气弹簧的刚度是F对空气弹簧变形量(行程)s的导数,即k=承载能力对行程求导=初始压力x承载面积对s的导数+初始承载面积Ae0 x 压力对行程的导数由以上可知,空气弹簧刚度取决于两部分:式中右边第一项为弹簧的几何变化(有效承载面积的变化);第二项为空气弹簧内部压力的变化,而且刚度随弹簧的变形速度而变化。
注意到 Ae=体积对行程的导数当振动频率f﹥0.2 Hz时,可取n=K,此时其刚度可认为是动刚度,即Kd=初始压力x 有效面积对行程的导数+绝对温度x(初始压力+承载压力)x(有效承载面积的平方 除以 体积)当振动频率f﹤0.2 Hz时,可取n=1,此时的其刚度可认为是静刚度,即Kd=初始压力x 有效面积对行程的导数+(初始压力+承载压力)x(有效承载面积的平方 除以 体积)通过对空气弹簧力学公式的分析可知指数n的选取对空气弹簧刚度有重要影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空气弹簧刚度计算
1. 载荷与气压关系式:
)A p (p P a -= ----(1) 式中: P 载荷
p 气囊内绝对气压
A 气囊有效承压面积
a p 标准大气压,其值与运算单位有关: 采用N 、mm 时,a p =0.0981≈0.1N/mm 2 采用kgf 、cm 时,a p =1 kgf/cm 2
采用1b 、in 时,a p =14.223 lb/in 2(psi)
2. 气压与容积变化关系式―――气体状态方程式
m )V
V (p p 00= 式中: p 任一位置气囊内气体的绝对气压 V 任一位置气囊内气体容积 0p 静平衡位置气囊内气体的绝对气压 0V 静平衡位置气囊内气体容积
m 多变指数,静态即等温过程 m =1; 动态即绝热过程 m =1.4; 一般状态,可取 m =1.33。
3. 刚度:弹性特性为弱非线性,取其导数,即
dx
dP K = 式中: K 任一位置的刚度
P 载荷
x 气囊变形量即行程
即: dx
)A]p d[(p K a -= dx
)A]p V V d[(p a m m
00-= dx dV V V Amp dx dA )p V V (p 1m m 00a m m 00⋅--=+ ----(2)
当气囊处在平衡位置时,
V =0V , p =0p , dx
dV =-A , 即: 020a 00V A mp dx dA )p (p K +-= ----(3)
在平衡位置时之偏频:
0a 000)V p (p mgA p dx dA A g 2π1n -+⋅=
(Hz) ----(4)
式中:dx
dA 称为有效面积变化率; g 重力加速度。
可见,降低dx
dA 、增大0V ,可降低0n ,提高平顺性。
P.S.有时采用相对气压p 1来运算更为方便:
p 1 =p -a p ----(5) 代入式(1)即P = p 1
A
或:0p = a 10p p +
代入式(3) 即:02a 10100V A )p m(p dx dA p K ++= ----(6) 0
10a 100V mgA p p p dx dA A g 2π1n ⋅++⋅= (Hz) ----(7) 又∵2
D 4πA = D 为有效直径,
∴
dx
dD 2πD dx dA ⋅= 代入式(6) 0
2
a 10100V A )p m(p dx dD 2πDp K ++⋅= ----(8) 式中: dx
dD 称为有效直径变化率。
dx dD 或dx
dA 由空气弹簧制造商提供数据或曲线, 对囊式空气弹簧,一般dx
dD =0.2--0.3, 对膜式空气弹簧,一般dx
dD =0--0.2, 甚至有dx dD =-0.1,取决于活塞形状。
