安徽省舒城中学2020-2021学年高一上学期开学考试数学试题

合集下载

安徽省六安市舒城中学2019_2020学年高一数学上学期第四次统考试题

9.已知函数 y tan x 在 ( , ) 上是减函数，则( ) 22
A. 0 1 B. 1 0 C. 1
D. 1
10.若定义在实数集 R 上的 f (x) 满足： x (3,1) 时， f (x 1) ex ，对任意 x R ，都有
f (x 2) 1 成立，则 f (2019)= ( ) f (x)
20.解：（1）∵ f (x) 为奇函数， g(x) 为偶函数,∴ f (x) f (x), g(x) g(x) . 又 f (x) g(x) 2 log2 (1 x) ① 故 f (x) g(x) 2 log2 (1 x) ，即 f (x) g(x) 2 log2 (1 x) ②
.
5
16.
若函数
f
(x) cos( 3 2
x) ，且 Sn
f
(
)
7
f
( 2 ) 7
f
( n )(n N ) 7
，则
S1，S2，，S2020 中，正数的个数是
.
三、解答题：本大题共 6 小题，共 70 分。解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分 10 分)
已知角的终边上一点 P (a, 3a)(a 0) .
A. e2
B. e2
C. e
D.1
-2-
精品文档，欢迎下载！
11.已知函数 f (x) 2 sin x( 0) ，存在实数 x1, x2 ，对任意的 x R ，都有
f (x1)
f (x)
f (x2 ) 成立，且
x1 x2
的最小值为，则方程
2
f (x)
ln
x
0 的根的个数
为 ( )（注： e2 7.389 ）

安徽省六安市舒城中学2020学年高一数学上学期第三次统考(期中)试题(无答案)

舒城中学2020学年度第一学期期中考试高一数学（总分： 150分时间：120分钟）一、选择题1.已知集合{}54321，，，，=A ，{}0322≤--=x x x B ，则B A ⋂中的元素个数为（） A ．2B.3C ．4D ．52下列函数中，与函数x y =相同的函数是（）A.xx y 2= B.2x y = C.33x y = D.2)(x y =3.已知3)2()(2-++=x b ax x f 是定义在[31,]a a -上的偶函数，那么ab 的值是（）A .2- B.21-C.21D.24.函数)6(log 3)(2x x x f -++=的定义域是（）A ．()+∞,6B ．()6,3-C ．()+∞-,3D ．[)6,3-5.函数221)(x x f +=的值域是（）A ．⎪⎭⎫ ⎝⎛∞-21, B ． ⎥⎦⎤ ⎝⎛∞-21, C ．⎪⎭⎫ ⎝⎛21,0 D ．⎥⎦⎤ ⎝⎛21,06.方程7log 4=+x x 的解所在区间是（）A ．()2,1B ． ()4,3C ．()6,5D ．()7,6 7.已知函数()32221)(----=m mx m m x f 是幂函数，对任意的()+∞∈,0,21x x ，且21x x ≠，都有0)]()()[(2121<--x f x f x x ，则实数m =（）A ．2B ．1-C ． 4D ． 2或1-8.如果函数2)1(log ++=x y a （10≠>a a 且）的图像恒过定点A ，若A 也在b x f x+=2)(的图像上，则=b（）A ．0B ．1C ． 2D ．39.函数)10(≠>=a a a y x且与函数)(x f y =的图像关于直线x y =对称，则函数)(x f y =与二次函数x x a y --=2)1(在同一坐标系内的图像可能是（）A. B. C. D. 10.若10,0<<>>c b a ,则（）A. b a c c log log >B. c c b a log log >C. bac c > D. ccb a > 11.已知定义在R 上的函数)(x f 满足：对任意实数x 都有，)6()()(x f x f x f -==-，且[]0,3-∈x 时，)6(log )(21x x f +=，则)2018(f 的值为（）A. 3-B. 2-C. 2D. 3 12.已知函数⎩⎨⎧≥+-<-=0,460,)lg()(2x x x x x x f ，若关于x 的函数01)()(2=+-x bf x f 有8个不同的解，则实数b 的取值范围为（）A. ⎪⎭⎫ ⎝⎛4172，B. ⎥⎦⎤ ⎝⎛4172，C. ()82，D. ⎥⎦⎤⎢⎣⎡4172，二、填空题 13.若31=+-xx ，则=+-2121xx ．14.函数)23(log )(221+-=x x x f 的单调递增区间是．15.为了保证信息安全，传输必须使用加密方式，有一种方式其加密、解密原理如下：明文――→加密密文――→发送密文――→解密明文已知加密为2-=xa y (x 为明文，y 为密文)，如果明文“3”通过加密后得到密文为“6”，再发送，接受方通过解密得到明文“3”，若接受方接到密文为“14”，则原发的明文是． 16.设()f x 的定义域为D ，若()f x 满足条件：存在[],ab D ⊆，使得()f x 在[],a b 上的值域是,22a b ⎡⎤⎢⎥⎣⎦，则称()f x 为“半缩函数”．若函数()()ln x f x e t =+为“半缩函数”，则t 的取值范围是．三、解答题17.（本小题满分10分）已知集合{}12<-=x x A ，集合{}m x m x B -<<=12. （1）若B B A =⋃，求实数m 的取值范围. （2）若φ≠⋂B A ，求实数m 的取值范围.18. （本小题满分12分）已知)(x f 为二次函数，满足x x x f x f 82)1()1(2-=-++. （1）求)(x f 的表达式；（2）解关于x 的不等式4)3(-≥xf .19. （本小题满分12分）我们知道，人们对声音有不同的感觉，这与它的强度有关系. 声音的强度I 用瓦/平方米（2/W m ）表示. 但在实际测量中，常用声音的强度水平1L 表示，它们满足以下公式：1010lgIL I = （单位为分贝），10L ≥，其中120110I -=⨯，这是人们平均能听到的最小强度，是听觉的开端. 回答以下问题：（1）某学校发现，学生能够在晚自习期间安心学习，声音强度不能超过102110/W m -⨯，试问此声音强度产生的噪音为多少分贝？;（2）当下，广场舞流行于大街小巷，广场舞噪声扰民"伤不起"，尤其是学校周围，广场舞音箱声音太大，关上窗户也不行，学生学习受干扰，大人的心情也很烦燥。

3-2-1 单调性与最大(小)值(精练)(解析版)

3.2.1 单调性与最大（小）值（精练）【题组一定义法判断或证明函数的单调性】1．（2020·上海高一专题练习）证明幂函数12()f x x =在[)0,+∞上是增函数【答案】证明见解析【解析】设120x x ≤<，则11221212()()f x f x x x-=-121212x x x x x x -=-=+12x x <120x x ∴-<120x x ∴+>12()()0f x f x ∴-<即12()()f x f x <，此函数在[0,)+∞上是增函数.2．（2021·全国高一课时练习）已知函数f (x )=12x x ++，证明函数在(-2，+∞)上单调递增. 【答案】证明见解析.【解析】证明：∀x 1，x 2∈(-2，+∞)，且x 1>x 2>-2，f (x )=11122x x x +=-++ 则f (x 1)-f (x 2)=212x -+112x +=1212-(2)(2)x x x x ++，因为x 1>x 2>-2，所以x 1-x 2>0，x 1+2>0，x 2+2>0，所以1212-(2)(2)x x x x ++>0，所以f (x 1)>f (x 2)，所以f (x )在(-2，+∞)上单调递增.3．（2021·福建三明市·三明一中高一开学考试）已知函数()12x f x x -=+，[]3,5x ∈. （1）判断函数()f x 的单调性，并证明；（2）求函数()f x 的值域.【答案】（1）单调递增，证明见解析；（2）24,57⎡⎤⎢⎥⎣⎦【解析】（1）()12331222x x f x x x x -+-===-+++在区间[]3,5上单调递增，证明如下：任取[]12,3,5x x ∈且12x x <，()()1212213333112222f x f x x x x x ⎛⎫⎛⎫-=---=- ⎪ ⎪++++⎝⎭⎝⎭ ()()()()()()()12121212323232222x x x x x x x x +-+-==++++，因为1235x x ≤<≤，所以120x x -<，120x +>，220x +>，所以()()120f x f x -<，即()()12f x f x <，所以函数()f x 在区间[]3,5上单调递增.（2）由（1）知：()f x 在区间[]3,5上单调递增，所以()()min 3123325f x f -===+，()()max 5145527f x f -===+，所以函数()f x 的值域是24,57⎡⎤⎢⎥⎣⎦. 4．（2021·六安市裕安区新安中学高一期末）设函数1()f x x x=+，(1,)x ∈+∞.判断函数()f x 的单调性，并用定义证明；【答案】在(1,)+∞上为增函数，证明见解析. 【解析】任取12,(1,)x x ∈+∞且12x x <，()()12121211f x f x x x x x -=+-- ()()()()1212211212121212111x x x x x x x x x x x x x x x x --⎛⎫⎛⎫-=-+-=-+= ⎪ ⎪⎝⎭⎝⎭，因为121x x <<，所以120x x -<，1210x x ->，所以()()120f x f x -<，所以()()12f x f x <，所以()f x 在(1,)+∞上为增函数；【题组二性质法判断函数的单调性】1．（2020·巩义市第四高级中学高一月考）函数()2f x x=的单调递减区间为（） A ．(),-∞+∞ B ．()(),00,-∞⋃+∞ C ．()(),0,0,-∞+∞ D ．()0,∞+【答案】C 【解析】()2f x x=的定义域为()(),00,-∞⋃+∞，图象如图所示：所以()2f x x=的单调递减区间为()(),0,0,-∞+∞，故选：C2（2020·台州市黄岩中学高一月考）函数f (x )＝1－11x -（） A ．在(－1，＋∞)上单调递增 B ．在(1，＋∞)上单调递增 C ．在(－1，＋∞)上单调递减 D ．在(1，＋∞)上单调递减【答案】B【解析】f (x )图象可由y ＝－1x图象沿x 轴向右平移一个单位长度，再向上平移一个单位长度得到，如图所示．故选：B3．（2021·吉林长春市·长春外国语学校高一开学考试）以下函数在其定义域上为增函数的是（） A ．1(0)x yx xB ．2(0)y x x xC ．1y x =-D ．2yx【答案】B【解析】对于A 选项，111(0)x yx xx，由于反比例函数()10y x x=>为减函数，故1(0)x yx x为减函数，A 选项错误；对于B 选项，2(0)y x x x的对称轴为102x =-<，开口向上，故2(0)y x x x 为增函数，B选项正确；对于C 选项，由于()11y x x =-≤上是减函数，故由复合函数的单调性得1y x =-为定义域(],1-∞上的减函数，C 选项错误；对于D 选项，2y x 为减函数，故D 选项错误.故选：B.4．（2021·深圳市皇御苑学校高一期末）函数23y x x =+的单调递减区间为A ．3,2⎛⎤-∞- ⎥⎝⎦B ．3,2⎡⎫-+∞⎪⎢⎣⎭C ．[)0,+∞D ．(],3-∞-【答案】D【解析】由题意，230x x +≥，可得3x ≤-或0x ≥，函数23y x x =+的定义域为(][),30,-∞-⋃+∞，令23t x x =+，则外层函数y t =在[)0,+∞上单调递增，内层函数23t x x =+在上(],3-∞-单调递减，在[)0,+∞上单调递增，所以，函数23y x x =+的单调递减区间为(],3-∞-.故选：D.5．（2021·全国高一课时练习）下列函数中，在区间(1，+∞)上单调递增的是（） A ．y =-3x -1 B ．y =2xC ．y =x 2-4x +5 D ．y =|x -1|+2【答案】D【解析】由一次函数的性质可知，y =-3x -1在区间(1，+∞)上单调递减，故A 错误；由反比例函数的性质可知，y =2x在区间(1，+∞)上单调递减，故B 错误，由二次函数的性质可知，y =x 2-4x +5在(-∞，2)上单调递减，在(2，+∞)上单调递增，故C 错误；由一次函数的性质及图象的变换可知，y =|x -1|+2在(1，+∞)上单调递增. 故选：D.6．（2021·浙江高一期末）函数()254f x x x =-+的单调递减区间为________【答案】(],1-∞（或(),1-∞）【解析】对于函数()f x ，有2540x x -+≥，解得1x ≤或4x ≥. 所以，函数()f x 的定义域为(][),14,-∞+∞.内层函数254u x x =-+在区间(],1-∞上为减函数，在区间[)4,+∞上为增函数，外层函数y u =在[)0,+∞上为增函数，因此，函数()254f x x x =-+的单调递减区间为(],1-∞（或(),1-∞）.故答案为：(],1-∞（或(),1-∞）.7．（2021·贵溪市实验中学高二期末）函数2()26f x x x =+-的单调递增区间是____________；【答案】[)1,-+∞【解析】函数()226f x x x =+-的对称轴为1x =-，开口向上，所以函数()f x 的单调增区间为[)1,-+∞. 故答案为：[)1,-+∞8．（2020·和平区·天津市第二南开中学高一期中）函数243y x x =-++，[]0,3x ∈的单调递增区间是_____．【答案】[]0,2【解析】243y x x =-++的图象开口向下，又243y x x =-++的对称轴为42(1)2x =-=-⨯，()f x ∴的单调递增区间是[]0,2.故答案为：[]0,2.【题组三图像法判断函数的单调性】1．（2020·江苏）函数()||1f x x =-与()()2g x x x =-的单调递增区间分别为（） A ．[1，+∞)，[1，+∞) B ．(﹣∞，1]，[1，+∞) C ．(1，+∞)，(﹣∞，1] D ．(﹣∞，+∞)，[1，+∞)【答案】A 【解析】()1,111,1x x f x x x x -≥⎧=-=⎨-+<⎩，()f x ∴在[)1,+∞上单调递增，()()222()211g x x x x x x -=-==--，()g x ∴在[)1,+∞上单调递增，故选：A.2．（2020·太原市·山西实验中学高一月考）函数()2f x x x =-的单调减区间是（） A ．[]1,2 B ．[]1,0-C ．[]0,2D ．[2,)+∞【答案】A 【解析】()(2),2,(2),2,x x x f x x x x -⋅≥⎧=⎨-⋅<⎩∴直接通过解析式，结合二次函数图象得：(,1),(2,)-∞+∞递增，在[]1,2递减，故选：A.3．（2021·河南郑州市）函数f （x ）=|x 2﹣6x+8|的单调递增区间为（） A ．[3，+∞） B ．（﹣∞，2），（4，+∞） C ．（2，3），（4，+∞） D ．（﹣∞，2]，[3，4]【答案】C【解析】画出2()68f x x x =-+的图象如图：由图象可知，函数的增区间为(2,3),(4,+∞），故选C.4．（2020·福建省南安市侨光中学高一月考）函数()11g x x x =⋅-+的单调减区间为（） A ．12⎛⎤-∞ ⎥⎝⎦， B ．112⎡⎤⎢⎥⎣⎦，C ．[)1+∞， D ．][112⎛⎫-∞+∞ ⎪⎝⎭，，【答案】B【解析】()221,111=1,1x x x g x x x x x x ⎧-+≥=⋅-+⎨-++<⎩，画出函数图象，如图所示：根据图象知：函数的单调减区间为112⎡⎤⎢⎥⎣⎦，. 故选：B.5．（2021·银川市）函数2()68f x x x =-+的单调递增区间为（） A ．[3,)-+∞ B ．(,2),(4,)-∞+∞ C ．(2,3),(4,)+∞D ．(,2],[3,4]-∞-【答案】C【解析】2226824()686824x x x x f x x x x x x ⎧-+≤≥=-+=⎨-+-<<⎩或，所以()f x 递增区间是(2,3),(4,)+∞. 故选:C.6．（2021·重庆北碚区）函数()|2|f x x x =-的增区间是 A ．(,1]-∞ B ．[2,)+∞C ．(,1],[2,)-∞+∞D ．(,2)-∞【答案】C【解析】222,2()22,2x x x f x x x x x x ⎧-≥=-=⎨-+<⎩由二次函数的图象可知()f x 在(,1],[2,)-∞+∞上是增函数故选：C7．（2021·黑龙江哈尔滨市）已知函数()||2f x x x x =-，则有（） A ．()f x 是偶函数，递增区间为[0，)+∞ B ．()f x 是偶函数，递增区间为(-∞，1] C ．()f x 是奇函数，递减区间为[1-，1] D ．()f x 是奇函数，递增区间为(-∞，0] 【答案】C【解析】因为()||2f x x x x =-，所以()22()f x x x x x x x f x -=--+=-+=-，故()f x 为奇函数，因为222,0()2,0x x x f x x x x ⎧-=⎨--<⎩，结合二次函数性质可知，()f x 的单调递减区间为[1-，1]．故选：C ．8．（2020·龙岩市高级中学高一期中）（多选）函数2()68f x x x =-+在下列区间（）上单调递减． A ．(,2)-∞ B ．(,3)-∞C ．[]3,4D ．()2,3【答案】AC【解析】解：因为222268,4()6868,2468,2x x x f x x x x x x x x x ⎧-+≥⎪=-+=-+-<<⎨⎪-+≤⎩，函数图象如下所示：由图可知函数的单调递增区间为()2,3和()4,+∞，单调递减区间为(),2-∞和()3,4 故选：AC9．（2021·江苏扬州市）函数()|2|3f x x x =--的单调递增区间为______ 【答案】()(,1),2,-∞+∞【解析】由题意2x ≥时，22()(2)323(1)4f x x x x x x =--=--=--，在[2,)+∞是是增函数，2x <时，22()(2)323(1)2f x x x x x x =--=-+-=---，在(,1)-∞是递增，在(1,2)上递减．∴增区间为(,1)-∞，(2,)+∞．故答案为：(,1)-∞，(2,)+∞．10．（2021·江苏南京市）函数()21f x x =-的单调增区间为______.【答案】（-1，0）和（1，+ ∞）【解析】()21f x x =-可画出函数图象如下所示：由函数图象可知，函数在()1,0-和()1,+∞上单调递增. 故答案为：()1,0-和()1,+∞ 【题组四已知单调性求参数】1．（2021·新疆阿勒泰地区·高一期末）若函数f (x )＝(2a －1)x ＋b 在R 上是单调减函数，则有（）A ．a ≥12 B ．a ≤12 C ．a >12D ．a <12【答案】D【解析】函数f (x )＝(2a －1)x ＋b 在R 上是单调减函数，则2a －1<0，即a <12. 故选：D.2．（2021·全国）若函数()|2|f x x a =+的单调递减区间是(,3]-∞，则a 的值为 A ．3- B ．3C ．6-D ．6【答案】C 【解析】当2a x ≤-时，()2f x a x =-，()f x ∴单调递减区间为,2a ⎛⎤-∞- ⎥⎝⎦，32a∴-=，解得：6a =-.故选：C . 3．（2021·广西桂林市·高一期末）如果函数2()2(1)2f x x a x =--+在[3,)+∞上是增函数，那么实数a 的取值范围（） A ．3a ≤-B ．2a -C ．5a ≤D ．5a ≥【答案】B【解析】函数2()2(1)2f x x a x =--+为二次函数，对称轴为1x a =-，故函数在(),1a -∞-单调递减，(1+)a -∞，单调递增，因此：132a a -≤∴≥-.故选：B4．（2021·江西宜春市·高安中学高一期末（理））已知函数f (x )=221,143,1x x x x x ⎧-+<⎨-+≥⎩，在(0,3)a -上单调递减，则实数a 的取值范围是（） A ．[3，4] B ．[3，5]C ．(3，4]D ．(]3,5【答案】D【解析】函数221,1()43,1x x f x x x x ⎧-+<=⎨-+≥⎩，画出函数()f x 的大致图象，如图所示：函数()f x 在(0,3)a -上单调递减，∴由图象可知：032a <-≤，解得：35a <≤，故实数a 的取值范围是：(]3,5. 故选：D.5．（2021·四川省遂宁市第二中学校高一月考（文））已知函数()2f x ax =-在[0,2]上单调递减，则a的取值范围是（） A ．(0,1] B ．(0,1)C ．(0,2]D ．[2,)+∞【答案】A【解析】因为函数()2f x ax =-在[0,2]上单调递减，所以0220a a >⎧⎨-≥⎩ ，解得01a <≤，所以a 的取值范围是(0,1]，故选： A6．（2021·北京门头沟区·大峪中学高一期中）已知函数()2f x ax x =-,若对任意[)12,2,x x ∈+∞,且12x x ≠,不等式()()12120f x f x x x ->-恒成立,则实数a 的取值范围是A ．1,2⎛⎫+∞⎪⎝⎭B ．1,2⎡⎫+∞⎪⎢⎣⎭C ．1,4⎛⎫+∞⎪⎝⎭D ．1,4⎡⎫+∞⎪⎢⎣⎭【答案】D【解析】不妨设x 2＞x 1≥2，不等式()()1212f x f x x x --=22112212ax x ax x x x --+-=()()()12121212a x x x x x x x x -+---=a （x 1+x 2）﹣1，∵对任意x 1，x 2∈[2，+∞），且x 1≠x 2，不等式()()1212f x f x x x --＞0恒成立，∴x 2＞x 1≥2时，a （x 1+x 2）﹣1＞0，即a ＞121x x +恒成立∵x 2＞x 1≥2 ∴121x x +＜14∴a ≥14，即a 的取值范围为[14，+∞）；故选：D ．7．（2021·云南大理白族自治州·宾川四中高一开学考试）若()()31121a x a x f x ax x ⎧-+<=⎨-≥⎩，，是定义在(),-∞+∞上的减函数，则a 的取值范围是（） A ．11,63⎡⎫⎪⎢⎣⎭B ．11,63⎛⎤⎥⎝⎦C ．10,3⎛⎫ ⎪⎝⎭D ．1,3⎛⎤-∞ ⎥⎝⎦【答案】A【解析】因为()()31121a x a x f x ax x ⎧-+<=⎨-≥⎩，，是定义在(),-∞+∞上的减函数，所以(31)1231020a a aaa-⨯+≥-⎧⎪-<⎨⎪-<⎩，即1613aaa⎧≥⎪⎪⎪<⎨⎪>⎪⎪⎩，解得1163a≤<，故选：A8．（2021·应城市第一高级中学高一期末）（多选）函数()21x af xx-=+在区间()b+∞，上单调递增，则下列说法正确的是（）A．2a>-B．1b>-C．1b≥-D．2a<-【答案】AC【解析】()22211x a af xx x-+==-++，()f x在区间()b+∞，上单调递增，20a∴+>，2a>-∴，由()f x在区间()1+∞-，上单调递增，1b.故选：AC9．（2021·江苏高一）（多选）已知函数()25,1,1x ax xf x axx⎧---≤⎪=⎨>⎪⎩是R上的增函数，则实数a的取值可以是（）A．0B．2-C．1-D．3-【答案】BD【解析】由题意，函数25y x ax=---的图象开口朝下，对称轴为2ax=-，因为函数()25,1,1x ax xf x axx⎧---≤⎪=⎨>⎪⎩是R上的增函数，所以1215aaa a⎧-≥⎪⎪⎨<⎪⎪---≤⎩，解得32a--≤≤.所以实数a 的取值可以是2-，3-. 故选：BD.10.（2021·浙江高一期末）已知函数()()()()()24312121xa x f x x a x x ⎧-≤⎪=⎨+-+>⎪⎩在R 上是增函数，则实数a 的取值范围是_______．【答案】[)1,1-【解析】要使()f x 在R 上是增函数，则431114352a a a a ->⎧⎪-≤⎨⎪-≤-⎩，解得11a -≤<.故答案为：[)1,1-.11．（2021·青海西宁市·高一期末）函数2()21f x x kx k =-++在区间[1,3]-上不单调．．．，则实数k 的取值范围是_________．【答案】()4,12-【解析】二次函数2()21f x x kx k =-++在区间[1,3]-上不单调．．．则对称轴()1,34kx =∈-，即()4,12k ∈- 故答案为：()4,12-12．（2021·湖南高一期中）已知函数()()22212f x x k x k =+-++．（1）若不等式()0f x <的解集为{}3|1x x <<，求实数k 的值；（2）若函数()f x 在区间[]2,4上不单调，求实数k 的取值范围．【答案】（1）1k =-；（2）()3,1--.【解析】（1）由已知得方程()222120x k x k +-++=的两根为1和3，故由()()2241420k k ∆=--+>，解得12k <-，再由韦达定理有()22113213k k ⎧--=+⎨+=⨯⎩，得112k =-<-，符合要求，故实数k 的值为1k =-；（2）∵函数()f x 在区间[]2,4上不单调，二次函数对称轴为()1x k =--， ∴()214k <--<，解得31k -<<-，所以实数k 的取值范围为()3,1--．13．（2021·浙江高一期末）已知函数2()2(1)4f x x k x =+-+．（Ⅰ）若函数()f x 在区间[2,4]上具有单调性，求实数k 的取值范围；（Ⅱ）若()0f x >对任意的[1,2]x ∈恒成立，求实数k 的取值范围．【答案】（1）(,3][1,)-∞-⋃-+∞（2）()1,-+∞ 【解析】（1）由函数2()2(1)4f x x k x =+-+知，函数()f x 图象的对称轴为1x k =-. 因为函数()f x 在区间[]2,4上具有单调性，所以12k -≤或14k -≥，解得3k ≤-或1k ≥-，所以实数k 的取值范围为(,3][1,)-∞-⋃-+∞. （2）因为()0f x >对任意的[1,2]x ∈恒成立，所以可得42(1)k x x->--对任意的[1,2]x ∈恒成立，因为444()244y x x x x x=--=-+≤-⋅=-，当且仅当2x =时等号成立，即max 4y =-，所以只需2(1)4k ->-，解得1k -<，所以实数k 的取值范围为()1,-+∞. 【题组五利用单调性解不等】1．（2021·全国高一课时练习）已知y =f (x )是定义在区间(-2，2)上单调递减的函数，若f (m -1)>f (1-2m )，则m 的取值范围是_______.【答案】1223⎛⎫- ⎪⎝⎭，【解析】由题意得：-2-12-21-22-11-2m m m m <<⎧⎪<<⎨⎪<⎩，，，解得12-<m <23.故答案为：1223⎛⎫- ⎪⎝⎭，2（2021·全国高一课时练习）函数()y f x =满足：对任意的12,x x R ∈总有1212()()0f x f x x x ->-．则不等式2(1)(2)f m f m +>的解集为________．【答案】{|1}m m ≠【解析】因为对任意的12,x x R ∈总有1212()()0f x f x x x ->-所以函数()y f x =是R 上的单调增函数，从而由2(1)(2)f m f m +>得212m m +>，解得1m ≠．故答案为：{|1}m m ≠3．（2021·全国高一课时练习）已知f (x )是定义在(,0]-∞上的单调递增函数，且(2)3f -=，则满足(23)3f x -<的x 的取值范围是_______.【答案】x ＜12【解析】因为(2)3f -=，所以(23)3f x -<和化为(23)(2)f x f -<-，又因为f (x )是定义在(,0]-∞上的单调递增函数，所以232x -<-，解得12x <. 故答案为：12x <. 4（2021·江苏南通市·高一开学考试）设函数()f x 是定义在(),-∞+∞上的增函数，实数a 使得()()212f ax x f a --<-对于任意[]0,1x ∈都成立，则实数a 的取值范围是（）A ．(,1)-∞B ．[]2,0-C ．()222,222---+ D ．[]0,1【答案】A【解析】解：法一：由条件得1﹣ax ﹣x 2＜2﹣a 对于x ∈[0，1]恒成立令g （x ）＝x 2+ax ﹣a +1，只需g （x ）在[0，1]上的最小值大于0即可．g （x ）＝x 2+ax ﹣a +1＝（x 2a +）224a --a +1．①当2a-＜0，即a ＞0时，g （x ）min ＝g （0）＝1﹣a ＞0，∴a ＜1，故0＜a ＜1；②当02a ≤-≤1，即﹣2≤a ≤0时，g （x ）min ＝g （2a -）24a =--a +1＞0，∴﹣2﹣22＜a ＜﹣2+22，故﹣2≤a ≤0；③当2a ＞-1，即a ＜﹣2时，g （x ）min ＝g （1）＝2＞0，满足，故a ＜﹣2．综上a 的取值范围1a <，故选A.5．（2021·沂源县第二中学高一开学考试）若偶函数()f x 在(,0]-∞上是增函数，则下列关系式中成立的是（）A ．3(1)(2)2f f f ⎛⎫-<-< ⎪⎝⎭B ．3(1)(2)2f f f ⎛⎫-<-< ⎪⎝⎭C ．3(2)(1)2f f f ⎛⎫<-<- ⎪⎝⎭ D ．3(2)(1)2f f f ⎛⎫<-<- ⎪⎝⎭【答案】D【解析】因为()f x 为偶函数，所以(2)(2)f f =-，又因为()f x 在(,0]-∞上是增函数，且3212<--<-，所以3(2)(1)2f f f ⎛⎫-<-<- ⎪⎝⎭，即3(2)(1)2f f f ⎛⎫<-<- ⎪⎝⎭，故选：D.6．（2021·长宁区·上海市延安中学高一期末）设2,0()1,0x x f x x -⎧≤=⎨>⎩，则满足()()1 2f x f x +<的实数x的取值范围是__________. 【答案】(),0-∞【解析】作出函数2,0()1,0x x f x x -⎧≤=⎨>⎩的图像如图，满足(1)(2)f x f x +<2021x x x <⎧∴⎨<+⎩，解得0x <.故答案为：(),0-∞.7．（2021·全国高一课时练习）已知函数37().2x f x x +=+ （1）判断并证明函数()f x 在()2,-+∞的单调性；（2）若函数()f x 的定义域为()2,2-且满足2(23)()f m f m -+>，求m 的范围. 【答案】（1）证明见解析，(2,)x ∈-+∞时，函数37()2x f x x +=+为减函数；（2）()1,2. 【解析】（1）371()322x f x x x +==+++，()f x 在(2,)-+∞上是减函数，证明如下：设122x x >>-，则2112121211()()22(2)(2)x x f x f x x x x x --=-=++++， 122x x >>-，120x ∴+>，220x +>，210x x -<， 12()()f x f x ∴<，()f x ∴在(2,)-+∞上为减函数；（2）由（1）可知：当(2,2)x ∈-时，函数()f x 为减函数，∴由2(23)()f m f m -+>得，2222322223m m m m -<-+<⎧⎪-<<⎨⎪-+<⎩，解得12m <<，m ∴范围为(1,2)．【题组六利用单调性求最值】1．（2021·广东汕头市·高一期末）设函数2()1f x mx mx =--，若对于[1,3]x ∈，()>-f x m 恒成立，则实数m 的取值范围是（）A ．1,7⎛⎫-∞ ⎪⎝⎭B ．(1,)+∞C ．(,1)-∞D ．1,7⎛⎫+∞ ⎪⎝⎭【答案】B【解析】当0m =时，()1f x =-，由1m ->-，得1m ，不符合题意；当0m ≠时，函数()f x 的对称轴为12x =，当0m >时，函数()f x 在区间[1,3]上单调递增，此时函数min ()(1)1f x f ==-，要使[1,3]x ∈，()>-f x m 恒成立，只需1m ->-，解得1m ，所以1m ；当0m <时，函数()f x 在区间[1,3]上单调递减，此时函数min ()(3)61f x f m ==-，要使[1,3]x ∈，()>-f x m 恒成立，只需61m m ->-，解得17m >，不符合题意；综上：实数m 的取值范围是(1,)+∞. 故选：B2．（2021·广东广州市·高一期末）已知函数()()221f x x ax a R =+-∈，若()1,2x ∀∈，()0f x ≤，则a 的取值范围是_________. 【答案】7,2⎛⎤-∞- ⎥⎝⎦【解析】()1,2x ∀∈，()2021f x x ax =-≤+恒成立，即12,(1,2)a x x x≤-+∈恒成立，设1()2g x x x =-+在(1,2)单调递减，所以7()12g x -<<-，所以72a ≤-. 故答案为：7,2⎛⎤-∞- ⎥⎝⎦. 3．（2021·浙江高一期末）（多选）已知函数222y x x -=+的值域是[1，2]，则其定义域可能是（）A ．[0,1]B ．[ 1,2]C ．1,24⎡⎤⎢⎥⎣⎦D ．[1,1-]【答案】ABC【解析】因为函数222y x x -=+的值域是[1，2]，由2y =可得0x =或2x =，由1y =可得1x = 所以其定义域可以为A 、B 、C 中的集合故选：ABC4．（2021·全国高一课时练习）二次函数24y ax x a =++的最大值是3，则a =_______.【答案】1-【解析】根据题意，二次函数24y ax x a =++的最大值是3，则2041634a a a<⎧⎪⎨-=⎪⎩，解得1a =-.故答案为：1-.5．（2021·安徽省舒城中学高一开学考试）已知函数2()23f x x x =--在[]1m －，上的最大值为()f m ，则m 的取值范围是（）A ．(11]－， B ．(1,122]-+ C ．[122,)++∞ D ．(1,1][122,)-⋃++∞【答案】D【解析】()f x 的图象如下图：对称轴为1,(1)4x f ==，令2234x x --=，得122x =±. 因为(1)0f -=，所以数形结合可得11m -<或122m +.故选：D6（2021·云南文山壮族苗族自治州·砚山县第三高级中学高一期末）已知函数1()2f x x a =+，且1(2)5f =．（1）求a 的值；（2）试判断函数在(1,)+∞上的单调性，并给予证明；（3）求函数在[3,5]x ∈的最大值和最小值．【答案】（1）1a =，（2）减函数，证明见解析，（3）最大值17，最小值111 【解析】（1）因为1()2f x x a =+，且1(2)5f =，所以1145a =+，解得1a =，（2）函数1()21f x x =+在(1,)+∞上为减函数，证明如下：任取12,(1,)x x ∈+∞，且12x x <，则121211()()2121f x f x x x -=-++ 21122()(21)(21)x x x x -=++ 因为12,(1,)x x ∈+∞，且12x x <，所以210x x ->，12210,210x x +>+>，所以12())0(f x f x ->，即12()()f x f x >，所以函数1()21f x x =+在(1,)+∞上为减函数，（3）由（2）可知1()21f x x =+在[3,5]上为减函数，所以当3x =时，函数取得最大值，即max 11()2317f x ==⨯+，当5x =时，函数取得最小值，即min 11()25111f x ==⨯+ 7．（2020·重庆市万州南京中学高一期中）已知函数()1=+x f x x （1）用定义法判断()f x 在区间()1,-+∞上是增函数；（2）求函数()f x 在区间[]2,5上的最值.【答案】（1）证明见解析；（2）()()min max 25,36f x f x == 【解析】(1)证明：()1111111x x f x x x x +-===-+++ 任取()12,1,x x ∈-+∞，且12x x <()()1212111111f x f x x x ⎛⎫⎛⎫-=--- ⎪ ⎪++⎝⎭⎝⎭211111x x =-++()()()()12121111x x x x +-+=++121211x x x x 121x x -<<，12120,10,10x x x x ∴-<+>+>()()120f x f x ∴-<，即()()12f x f x <∴()f x 在()1,-+∞单调递增（2）由（1）知，()f x 在[]2,5单调递增，()()()()min max 252,536f x f f x f ∴==== 8．（2021·深圳第二外国语学校高一期末）已知函数1()2f x x x=+. （1）证明：证明函数()f x 在区间2,2⎛⎫+∞ ⎪ ⎪⎝⎭上单调递增；（2）若2()31f x a a ≥+-在[]1,3x ∈上恒成立，求实数a 的取值范围. 【答案】（1）证明见解析；（2）41a -≤≤.【解析】（1）任取1222x x <<，∴1212121122f x f x x x x x ()12121221x x x x x x -=-， ∵1222x x <<，∴120x x -<，12210x x ->，120x x >， ∴()()120f x f x -<，故函数()f x 在区间2,2⎛⎫+∞ ⎪ ⎪⎝⎭上单调递增；（2）2()31f x a a ≥+-在[]1,3x ∈上恒成立，等价于2min 31()a a f x +-≤，由（1）知()f x 在[]1,3x ∈单调递增，∴()min ()13f x f ==，∴2313a a +-≤，解得41a -≤≤.9．（2021·海南鑫源高级中学高一期末）一次函数()2(0)f x kx a =+≠且(1)5f =.（1）求k 的值；（2）证明()f x 在R 上单调递增.【答案】（1）3k =；（2）证明见解析.【解析】（1）一次函数()2(0)f x kx a =+≠且(1)5f =.则25k +=，则3k =.（2）证明：由（1）得()32f x x =+，在R 上任取1x ，2x ，令12x x <，则()1212()()3232f x f x x x -=+-+()123x x =- 12x x <，12()()0f x f x ∴-<，()f x ∴在R 上是单调递增函数．10．（2021·安徽高一开学考试）已知函数22()x f x x-=.（1）判断()f x 在(0,)+∞上的单调性，并用定义法证明；（2）已知()f x 在[]1,2上的最大值为m ，若正实数a ，b 满足ab m =，求11a b +最小值. 【答案】（1）()f x 在(0,)+∞上单调递增，证明见解析；（2）2.【解析】（1）函数()f x 在(0,+)∞上单调递增. 证明如下：令120x x >>，()()2212121212212222x x f x f x x x x x x x ---=-=-+- ()121221x x x x ⎛⎫=-+ ⎪⎝⎭. 因为120x x >>，所以120x x ->，120x x >，所以12122()(1)0x x x x -+>，所以()()120f x f x ->，即()()12f x f x >，所以函数()f x 在(0,)+∞上单调递增.（2）由（1）知函数()f x 在(0,)+∞上单调递增，所以函数()f x 在[]1,2上的最大值为222(2)12f -==，即1m =，所以1ab =，所以1122a b a b ab a b ab++==+≥=，当且仅当1a b ==时等号成立. 11．（2021·福建三明市·高一期末）已知函数21()1x f x x -=+．（1）判断()f x 在[)0,+∞上单调递增还是单调递减，并证明你的判断；（2）若[]1,x m ∈，()f x 的最大值与最小值的差为12，求m 的值．【答案】（1）()f x 在[)0,+∞上单调递增，证明见解析；（2）2m =.【解析】（1）()f x 在[)0,+∞上单调递增，证明如下：设任意的120x x ≤<，则()()()()121212121232121()1111x x x x f x f x x x x x ----=-=++++，因为120x x ≤<，故120x x -<，()()12110x x ++>，故()12()0f x f x -<即()12()f x f x <，故()f x 在[)0,+∞上单调递增.（2）由（1）可知()f x 在[]1,m 上为增函数，故()()()()min max 1211,,21m f x f f x f m m -====+ 所以2111122m m --=+，故2m =，此时1m 符合，故2m =.。

2020-2021学年安徽省六安市舒城县高一上学期期末数学试题(解析版)

故选：D
【点睛】在应用基本不等式求最值时，要把握不等式ቤተ መጻሕፍቲ ባይዱ立的三个条件，就是“一正——
各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，
就会出现错误．
12．设 m ， n 为正数，且 m n 2 ，则 1 1 的最小值为（） m1 n 2
3
A．
2
5
B．
3
7
C．
4
4
D．
f x 3 ln x 的零点所在的大致区间．
x
【详解】函数 f x 3 ln x 满足 f （2） 3 ln 2 0 ， f （3） 1 ln 3 0 ，
x
2
且函数 f x 是增函数
∴ f (2) f (3) 0
根据函数的零点的判定定理可得函数 f x 3 ln x 的零点所在的大致区间是 (2,3) ，
14．设函数 f x 的定义域为 R ， f x f x ， f x f 2 x ，当 x 0,1 时，
f
x
x3 ，则函数
g x
cos x
f
x
在区间
1 2
,
5 2
上的所有零点的和为（
）
A． 7
B． 6
C． 3
D． 2
【答案】A
【分析】推导出函数 f x 是周期为 2 的周期函数，作出函数 f x 与函数
的
图象，则下列说法不正确的是（）
A． g(x) 的最小正周期为
B．
g
(
x)
在区间
0,
2
上单调递减
C． x 不是函数 g x 图象的对称轴
12
D．
g
x
在

【精准解析】安徽省六安市舒城中学2019-2020学年高一上学期第四次统考数学试题

-1-
A. [ 3 , ] 44
[ , ] 22
【答案】A
【解析】
【分析】
B. [ , 0]
C. [ , 3 ]
D.
44
写出函数的单调增区间
2k
3 4
,
2k
4
，
k
Z
，然后取不同的
k
值，从而得到答案.
【详解】函数 y sin(x ) 4
2k x 2k ， k Z ，
【详解】由题,因为
sin tan
0 ,则
的终边落在第一象限或第四象限；
因为 cos tan 0 ,则的终边落在第三象限或第四象限；
综上, 的终边落在第四象限
故选 D
【点睛】本题考查象限角,考查三角函数值的符号的应用,属于基础题
3.函数 y sin(x ) 在闭区间（ 4
）上为增函数.
2
4
2
得 2k 3 x 2k ， k Z ，
4
4
所以函数
y
sin( x
) 的单调递增区间为
4
2k
3 4
, 2k
4
，
k
Z
，
当
k
0
，得到函数
y
sin( x
4
)
在
3 4
,
4
上单调递增.
故选：A.
【点睛】本题考查求正弦型函数的单调区间，属于简单题.
4.下列函数中，以π为周期的偶函数是（）
【解析】
【分析】
把
3
,
0
代入函数中，表述出
，然后选取不同的
k
值，从而得到答案.
-4-
【详解】因为函数

安徽省舒城中学2020学年高一数学上学期第一次统考试题(无答案)

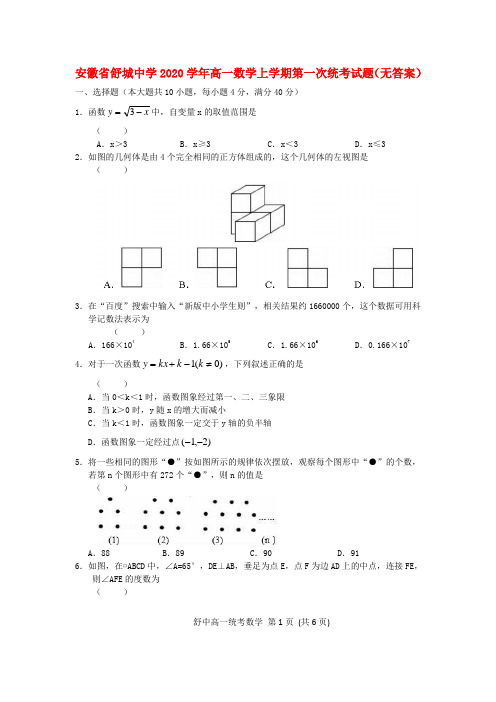
安徽省舒城中学2020学年高一数学上学期第一次统考试题（无答案）一、选择题（本大题共10小题，每小题4分，满分40分） 1．函数x y -=3中，自变量x 的取值范围是（）A ．x ＞3B ．x≥3C ．x ＜3D ．x≤3 2．如图的几何体是由4个完全相同的正方体组成的，这个几何体的左视图是（）3．在“百度”搜索中输入“新版中小学生则”，相关结果约1660000个，这个数据可用科学记数法表示为（）A ．166×104B ．1.66×105C ．1.66×106D ．0.166×107 4．对于一次函数)0(1≠-+=k k kx y ，下列叙述正确的是（）A ．当0＜k ＜1时，函数图象经过第一、二、三象限B ．当k ＞0时，y 随x 的增大而减小C ．当k ＜1时，函数图象一定交于y 轴的负半轴D ．函数图象一定经过点)2,1(--5．将一些相同的图形“●”按如图所示的规律依次摆放，观察每个图形中“●”的个数，若第n 个图形中有272个“●”，则n 的值是（）A ．88B ．89C ．90D ．916．如图，在▱ABCD 中，∠A=65°，DE⊥AB，垂足为点E ，点F 为边AD 上的中点，连接FE ，则∠AFE 的度数为（）舒中高一统考数学第1页 (共6页)A ．40°B ．50°C ．60°D ．70°7．如图，在Rt△ABC 中，∠C=90°，∠A=20°，BC=3，以点C 为圆心，BC 的长为半径的⊙C 交AB 于点D ，交AC 于点E ，则（劣弧）的长为（）A ．π32B ．π53C ．π31D ．π43 8．如图，若△ABC 和△DEF 的面积分别为S 1、S 2，则（）A ．S 1=21S 2B ．S 1=27S 2C ．S 1=S 2D ．S 1=58S 2 9．已知实数b a ,分别满足0462=+-a a ，0462=+-b b ，且b a ≠，则baa b +的值是A ．7B ．﹣7C ．11D ．﹣11（）10．函数c bx x y ++=2与x y =的图象如图所示，有以下结论：①b 2﹣4c ＞0；②b+c+1=0；③3b+c+6=0；④当1＜x ＜3时，x 2+（b ﹣1）x+c ＜0．其中正确的个数为（）A ．1B ．2C ．3D ．4二、填空题（本大题共4小题，每小题5分，满分20分） 11.分解因式：x xy 252-= ．12．如图，在平面直角坐标系中，点P 的坐标为（2，0），直线434+=xy 与x 轴、y 轴分别交于点A ，B ，点M 是直线AB 上的一个动点，则PM 的最小值为．13．如图，已知在Rt△OAC 中，O 为坐标原点，直角顶点C 在x 轴的正半轴上，反比例函数)0(≠=k xky 在第一象限的图象经过OA 的中点B ，交AC 于点D ，连接OD ．若△OCD∽△ACO，则直线OA 的解析式为．14．如图，O 为正方形ABCD 的重心，BE 平分∠DBC，交DC 于点E ，延长BC 到点F ，使CF=CE ，连接DF ，交BE 的延长线于点G ，连接OG 、OC ，OC 交BG 于点H ．下面四个结论：①△BCE≌△DCF；②OG∥AD；③BH=GH；④以BG 为直径的圆与DF 相切于点G ．其中正确的结论有．（把你认为正确结论的序号都填上）三、（本大题共2小题，每小题8分，满分16分）15．计算： 0260sin 2312127+--⎪⎭⎫ ⎝⎛-+- 16．先化简，再求值：121112-÷⎪⎭⎫⎝⎛--x x x ，其中3=x ．四、（本大题共2小题，每小题8分，满分16分）舒中高一统考数学第3页 (共6页)17．今年植树节，六安某中学组织师生开展植树造林活动，为了了解全校1200名学生的植树情况，随机抽样调查50名学生的植树情况，制成如下统计表和条形统计图（均不完整）．植树数量（棵）频数（人）频率3 5 0.14 20 0.456 10 0.2合计50 1（1）将统计表和条形统计图补充完整；（2）求抽样的50名学生植树数量的众数和中位数，并从描述数据集中趋势的量中选择一个恰当的量来估计该校1200名学生的植树数量．18．国家海洋局将中国钓鱼岛最高峰命名为“高华峰”，并对钓鱼岛进行常态化立体巡航．如图1，在一次巡航过程中，巡航飞机飞行高度为2001米，在点A测得高华峰顶F点的俯角为30°，保持方向不变前进1200米到达B点后测得F点俯角为45°，如图2．请据此计算钓鱼岛的最高海拔高度多少米．（结果保留整数，参考数值： =1.732， =1.414）五、（本大题共2小题，每小题10分，满分20分）19．如图，AB是⊙O的直径，AC是弦，CD是⊙O的切线，C为切点，AD⊥CD于点D．求证：（1）∠AOC=2∠ACD；（2）AC2=AB•AD．20．如图，在平面直角坐标系xOy 中，一次函数2-=kx y 的图象与x 、y 轴分别交于点A 、B ，与反比例函数)0(23<-=x x y 的图象交于点),23(n M - ．（1）求A 、B 两点的坐标；（2）设点P 是一次函数2-=kx y 图象上的一点，且满足△APO 的面积是△ABO 的面积的2倍，直接写出点P 的坐标．六．（本题满分12分）21．如图，在Rt△ABC 中，∠C=90°，BC=1，AC=2，把边长分别为x 1，x 2，x 3，…，x n 的n 个正方形依次放入△ABC 中，请回答下列问题：（1）按要求填表： n 1 2 3 x n （2）第n 个正方形的边长x n =；（3）若m ，n ，p ，q 是正整数，且x m •x n =x p •x q ，试判断m ，n ，p ，q 的关系．七．（本题满分12分）舒中高一统考数学第5页 (共6页)22．某工厂生产的A 种产品，它的成本是2元，售价是3元，年销量为100万件，为了获得更好的效益，厂家准备拿出一定的资金做广告；根据统计，每年投入的广告费是x （十万元），产品的年销量将是原销售量的y 倍，且y 是x 的二次函数，它们的关系如表： x （十万元）0 1 2 y11.51.8（1）求y 与x 的函数关系式；（2）如果把利润看成销售总额减去成本费和广告费，试写出年利润S （十万元）与广告费x （十万元的函数关系式）；（3）如果投入的年广告费为10万元～30万元，问广告费在什么范围内，工厂获得的利润最大？最大利润是多少？八．（本题满分14分）23．如图，抛物线a bx ax y 42-+=经过A （﹣1，0）、C （0，4）两点，与x 轴交于另一点B ．（1）求抛物线的解析式；（2）已知点D （m ，m+1）在第一象限的抛物线上，求点D 关于直线BC 对称的点的坐标；（3）在（2）的条件下，连接BD ，点P 为抛物线上一点，且∠DBP=45°，求点P 的坐标．。

2022-2023学年安徽省六安市舒城中学高一上学期开学考试数学试题(解析版)

2022-2023学年安徽省六安市舒城中学高一上学期开学考试数学试题一、单选题1．下列各角，与330°角的终边相同的角是（） A ．510° B ．150°C ．-150°D ．-390°【答案】D【分析】根据终边相同角的表示即可求解.【详解】与330°角的终边相同的角为330360,k k Z α=+∈，当2k =-时， 390α=-，故选：D2．315︒角的弧度数为（） A ．34πB ．74π C ．4π-D ．54π 【答案】B【分析】利用公式可求315︒角的弧度数. 【详解】315︒角对应的弧度数为3157ππ1804=，故选：B.3．将885-化为)()360Z,0,360k k αα⎡+⋅∈∈⎣的形式是（）A ．()1652360︒︒-+-⨯B ．()1953360︒︒+-⨯C ．()1952360︒︒+-⨯ D ．()1653360︒︒+-⨯【答案】B【分析】直接由终边相同的角的概念求解即可.【详解】由600,3α︒︒⎡⎤∈⎣⎦知()88519533195108060︒︒-+-⨯=-=.故选：B.4．半径为r ，圆心角是α(弧度)的扇形面积是（） A ．212r αB ．12r αC ．212r αD ．2212r α【答案】A【分析】由扇形的面积公式和弧长公式即可得答案. 【详解】解：因为扇形的半径为r ，圆心角是α(弧度)，所以扇形的弧长l r α=，又因为12S lr =，所以212S r α=.故选：A.5．给出下列四个命题: ①-75°是第四象限角； ②小于90的角是锐角； ③第二象限角比第一象限角大；④一条弦的长等于半径，这条弦所对的圆心角等于1弧度. 其中正确的命题有（） A ．1个 B ．2个 C ．3个 D ．4个【答案】A【分析】利用反例可判断②③的正误，根据1弧度的定义可判断④的正误，根据范围可判断①的正误.【详解】对于①，因为90750-︒<-︒<︒，故75-︒为第四象限角，对于②③，270210180-︒<-︒<-︒，故210-︒为第二象限角，但2103090-︒<︒<︒且30为第一象限角，故②③错误，对于④，因为1弧度的圆心角所对的弧长为半径，此时对应的弦长小于半径，故④错误，故选：A.6．00tan 300sin 450+的值为（）A ．1B ．1C ．1-D ．1-【答案】B【详解】()()00tan300sin450tan 36060sin 360901+=︒-︒+︒+︒=.故选B7．若()4sin ,5πα+=-且α是第二象限角，则cos α=（）A ．45-B ．35 C ．35D ．45【答案】B【分析】利用诱导公式求得sin α，再利用同角关系式即得. 【详解】由()4sin sin 5παα+=-=-，得4sin 5α，又由α为第二象限角，所以23cos 1sin 5αα=--=-．故选：B.8．在半径为1的单位圆中，一条弦AB 的长度为3，则弦AB 所对的圆心角α是（） A ．3α= B ．3πα=C ．6πα=D ．α=23π 【答案】D【分析】连接圆心与弦AB 的中点C ，解三角形求AOB ∠的大小. 【详解】连接圆心O 与弦AB 的中点C ，由圆的性质可得OC AB ⊥，在ACO △中，90ACO ∠=，1OA =，32AC =, 所以3sin 2AC AOC OA ∠==，又090AOC <∠<，所以60AOC ∠=，所以2120AOB AOC ∠=∠=, 所以23πα=，故选：D.9．已知5sin α，则44sin cos α-α=（） A ．35 B ．15-C ．15D ．35【答案】A【分析】先利用5sin α算出24cos 5α=，然后利用平方差公式对44sin cos αα-进行化简即可得到答案【详解】解：因为5sin α，且22sin +cos =1αα，所以24cos 5α=，所以()()44222222143sin cos sin cos sin cos sin cos 555αααααααα-=-+=-=-=-，故选：A10．已知tanα>0，且sinα+cosα>0，那么角α是 ( ) A ．第一象限角 B ．第二象限角 C ．第三象限角 D ．第四象限角【答案】A【详解】tan 0α>则角为第一或第三象限，而sin cos 0αα+>，故角为第一象限角.11．若[0,2)απ∈sin cos αα=-，则α的取值范围是（） A ．0,2π⎡⎤⎢⎥⎣⎦B ．,2ππ⎡⎤⎢⎥⎣⎦C ．3,2ππ⎡⎤⎢⎥⎣⎦D ．3,22ππ⎡⎫⎪⎢⎣⎭【答案】B【分析】根据同角三角函数关系，可得sin 0cos 0αα≥⎧⎨≤⎩，结合角α的范围，即可求得答案.【详解】sin cos sin cos αααα+=-，所以sin 0cos 0αα≥⎧⎨≤⎩，又[0,2)απ∈，所以,2παπ⎡⎤∈⎢⎥⎣⎦.故选：B二、填空题12．若角α的终边经过点()3,P b -，且3cos 5α=-，则b =__________.【答案】4±【分析】根据三角函数的定义，先计算r ，再利用余弦函数的定义求出b ．【详解】因为角α的终边经过点()3,P b -，所以OP ．因为3cos5α=-35=- ，所以4m =± ．故答案为：4±．【点睛】本题考查余弦函数的定义，解题的关键是正确运用定义，属于基础题． 13．已知sin cos 2sin cos αααα+=-，则tan α=_____【答案】3【分析】根据sin cos 2sin cos αααα+=-，分子分母同除以cos α，利用商数关系转化为关于tan α的方程求解..【详解】因为sin 1sin cos tan 1cos 2sin sin cos tan 11cos αααααααααα+++===---，解得tan 3α=. 故答案为：3【点睛】本题主要考查同角三角函数基本关系式，还考查了运算求解的能力，属于基础题.14．已知1cos 5α=，且α是第四象限的角，则cos 2πα⎛⎫+= ⎪⎝⎭_________. 【分析】由平方关系求得sin α，进而由诱导公式可求得结果. 【详解】1cos 5α=且α是第四象限角，sin α∴=故cos()sin 2παα+=-=. 15．已知2sin cos αα+=tan α=_________．【答案】2【分析】利用平方法，结合平方关系的同角三角函数关系式构造齐次式来求解. 【详解】因为2sin cos a a +=224sin cos 4sin cos 5a ααα++=，即22224sin cos 4sin cos 5sin cos a ααααα++=+，所以224tan 14tan 5tan 1a αα++=+，即()2tan 20α-=，所以tan 2α=. 故答案为：2.三、解答题16．（1）已知3sin 5α=-，求tan cos αα+的值（2()238sin tan 204033π⎛⎫---- ⎪⎝⎭【答案】（1）答案见解析；（2【分析】（1）由平方关系及商数关系分别求出cos ,tan αα即可求解；（2）由诱导公式结合特殊角的三角函数值即可求解.【详解】（1）由3sin 5α=-可得α为第三象限角或第四象限角，即4cos 5α==±，当α为第四象限角时，4cos 5α=，3tan 4α=-，则tan cos αα+3414520=-+=；当α为第三象限角时，4cos 5α=-，3tan 4α=，则tan cos αα+3414520=-=-；（2）()2cos 225cos 18045cos 452=+=-=-，8222sin sin 2sin sin 3333πππππ⎛⎫⎛⎫⎛⎫-=--=-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()()()tan 2040tan 6011180tan 60tan 603-=--⨯=-=-=-，()238sin tan 204033π⎛⎫---- ⎪⎝⎭(⎛⎛-= ⎝⎭⎝⎭17．化简 (1)222cos 112sin αα-- (2)()221tan cos αα+(3)2222tan sin tan sin αααα-- 【答案】(1)1； (2)1； (3)0.【分析】根据同角关系式化简即得.【详解】(1)222222222cos 12cos cos sin 12sin cos sin 2sin αααααααα---=-+- 2222cos sin 1cos sin αααα-==-； (2)()222222cos sin 1tan cos cos 1cos αααααα++=⋅=； (3)()2222222tan sin tan sin tan 1sin sin ααααααα--=--2222sin cos sin 0cos αααα=⋅-=. 18．已知α是第三象限角，且sin(π)cos(2π)tan(2π)tan(π)sin(3π)()f αααααα---+-+-=.(1)化简()f α；(2)若3sin 5α=-，求()f α；(3)若1860α︒=-，求()f α. 【答案】(1)cos α (2)45-(3)12【分析】（1）根据诱导公式化简求解.（2）利用同角三角函数的基本关系以及余弦在各象限的符号进行求解.（3）利用诱导公式进行大角化小角，负角化正角，再利用特殊角的余弦值进行求解. 【详解】(1)根据诱导公式有： sin(π)cos(2π)tan(2π)tan(π)sin(3π)()f αααααα---+-+-=sin cos tan()tan()sin ααααα--=cos α=(2)因为3sin 5α=-，α是第三象限角，所以4cos 5α=-所以4()cos 5f αα==-(3)因为1860α︒=-，所以()()()1860cos 1860cos1860f f α︒︒︒=-=-=()1cos 536060cos602=⨯+==. 19．是否存在实数k ，使得方程286210x kx k +++=的两个根是一个直角三角形的两个锐角的正弦值？若存在求出k 的值，若不存在请说明理由. 【答案】不存在，理由见解析【分析】设直角三角形的两个锐角为,αβ，利用韦达定理得到3sin cos 4k αα+=-，21sin cos 8k αα+=，再根据同角三角函数基本关系可求出k 的值，对k 的值进行检验可发现不满足条件，故假设不成立，k 的值不存在【详解】假设存在k 满足题意，则设直角三角形的两个锐角为,αβ，则sin ,sin αβ是方程286210x kx k +++=的两个实数根，因为90αβ︒+=，所以sin cos βα=，所以()236482103sin cos 421sin cos 8k k k k αααα⎧⎪∆=-⨯⨯+≥⎪⎪+=-⎨⎪+⎪=⎪⎩因为()222sin cos sin cos 2sin cos 12sin cos αααααααα+=++=+，所以23211248k k +⎛⎫-=+⨯ ⎪⎝⎭，解得2k =或109k =-，当2k =时，()23624822116∆=⨯-⨯⨯⨯+=-与0∆≥矛盾，故舍去；当109k =-时，1021119sin cos 0872αα⎛⎫⨯-+ ⎪⎝⎭==-<，与α为锐角矛盾，故舍去，综上所述，假设不成立，故不存在实数k ，使得方程286210x kx k +++=的两个根是一个直角三角形的两个锐角的正弦值。

2020-2021学年安徽省六安市舒城中学高一上学期期中数学试题(解析版)

2020-2021学年安徽省六安市舒城中学高一上学期期中数学试题一、单选题1．已知集合{|P x y ==，集合{|Q y y =，则P 与Q 的关系是（）A ．P Q =B ．P Q ⊆C ．P Q ⊇D ．PQ =∅【答案】C【分析】求函数定义域求得集合P ，求函数值域求得集合Q ，由此得出两个集合的关系.【详解】对于集合A ，由10x +≥解得1x ≥-.对于集合Q ，0y ≥.故集合P 包含集合Q ，所以本小题选C.【点睛】本小题主要考查集合与集合的关系，考查函数定义域和值域的求法，考查集合的研究对象，属于基础题.2．已知集合M 有3个真子集，集合N 有7个真子集，那么M N ⋃中的元素（）． A ．有5个 B ．至多有5个C ．至少有5个D ．至多有10个【答案】B【分析】先由题意，分别确定集合M 与集合N 中元素个数，再由并集的概念，即可得出结果.【详解】因为集合M 有3个真子集，所以M 中有2个元素．又集合N 有7个真子集，所以N 中有3个元素，因此M N ⋃中至多有5个元素．故选B【点睛】本题主要考查由真子集个数确定集合中元素的个数，以及并集中元素的个数问题，熟记集合并集的概念，以及真子集的概念即可，属于常考题型. 3．若0a <b <，则下列结论中不恒成立的是（） A ．a b > B ．11a b> C ．222a b ab +> D ．22ac bc <【答案】D【分析】利用不等式的性质逐一判断即可.【详解】因为0a <b <，所以a b >，11a b>，222a b ab +> 当0c时22ac bc <不成立故选：D【点睛】本题考查的是不等式的性质，较简单. 4．22530x x --<的一个必要不充分条件是A ．132x -<< B ．16x -<< C ．102x -<<D ．132x -<<【答案】B【分析】首先求解不等式，然后确定其必要不充分条件即可. 【详解】求解不等式22530x x --<可得132x -<<，结合所给的选项可知22530x x --<的一个必要不充分条件是16x -<<. 本题选择B 选项.【点睛】本题主要考查一元二次不等式的解法，充分条件与必要条件的理解等知识，意在考查学生的转化能力和计算求解能力.5．a ,b ,c ,d R +∈,设a b c dS a b c b c d c d a d a b=+++++++++++,则下列判断中正确的是( ) A ．01S << B ．12S <<C ．23S <<D ．34S <<【答案】B【详解】试题分析：a 、b 、c 、d ∈R ＋，a b c dS a b c b c d c d a a b d ∴=+++++++++++1a b c d a b c d a b c d a b c d a b c d>+++=++++++++++++ a b c dS a b c b c d c d a a b d =+++++++++++2a d a b c b c d a b c d a b c d a b c d a b c d++++<+++=++++++++++++ 12S ∴<<【解析】放缩法6．设0,0x y <<，且210x y ++=，则11x y+的最大值为A ．3--B ．6C ．6-D ．3+【分析】由已知得()(2)1x y -+-=，利用“1”的变换，先求[()()]11[()(2)]x y x y+--+--的最小值，即可求出结论. 【详解】0,0,0,0,()(2)1x y x y x y <<∴->->-+-=，1111([()(2]])[()())x x x y y y -+-+-+-=-323y xx y=++≥+312x y+≤--∴，当且仅当x =2,1x y ==.故选：A.【点睛】本题考查基本不等式求最值，要注意应用公式的条件“一正”“二定”“三等”缺一不可，属于中档题.7．已知函数2()1f x x mx =+-，若对于任意[,1]x m m ∈+，都有()0f x <成立，则实数m 的取值范围是（） A ．(1,0)- B ．(0,1)C．2⎛⎫- ⎪ ⎪⎝⎭D．【答案】C【分析】由题意根据二次函数图像的特征可得方程组22()210(1)(1)(1)10f m m f m m m m ⎧=-<⎨+=+++-<⎩，解不等式组即可得到答案. 【详解】因为函数2()1f x x mx =+-的图像是一条开口向上的抛物线，所以要使得对于任意[,1]x m m ∈+，都有()0f x <成立，则只需22()210(1)(1)(1)10f m m f m m m m ⎧=-<⎨+=+++-<⎩，解得：22302m m ⎧-<<⎪⎪⎨⎪-<<⎪⎩所以0m <<.【点睛】本题以二次函数为背景考察了恒成立问题，属基础题.8．已知[1,1]a ∈-时不等式2(4)420x a x a +-+->恒成立，则x 的取值范围为（）A ．(－∞，2)∪(3，＋∞)B ．(－∞，1)∪(2，＋∞)C ．(－∞，1)∪(3，＋∞)D ．(1，3)【答案】C【分析】根据题意，转化为关于a 的函数()2(2)44f a x a x x =-+-+，得出()0f a >对于任意[1,1]a ∈-恒成立，即可求解.【详解】由题意，因为[1,1]a ∈-时不等式2(4)420x a x a +-+->恒成立，可转化为关于a 的函数()2(2)44f a x a x x =-+-+，则()0f a >对于任意[1,1]a ∈-恒成立，则满足()()2215601320f x x f x x ⎧-=-+>⎪⎨=-+>⎪⎩，解得1x <或3x >，即x 的取值范围为(,1)(3,)-∞+∞.故选：C.【点睛】本题主要考查了不等式的恒成立问题，其中解答中根据条件转化为关于a 的函数，结合其图象特征，列出不等式组是解答的关键，着重考查转化思想，以及运算与求解能力.9．已知函数22()1x f x x =+，则(1)(2)(2019)(2020)f f f f +++++11112320192020f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭=（） A ．120162 B ．120172 C ．120182D ．120192【答案】D【分析】计算1()()f x f x+，根据特点使用倒序相加法可得结果.【详解】由222211()()1111x xf x fx xx⎛⎫⎪⎝⎭+=+=+⎛⎫+⎪⎝⎭所以()()()1112320201232020f f f f f f⎛⎫⎛⎫⎛⎫+=+==+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭则1111(2)(2019)(2020)20192320192020f f f f f f f⎛⎫⎛⎫⎛⎫⎛⎫++++++++=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭又1(1)2f=，则()11111 1(2)(2019)(2020)201923201920202 f f f f f f f f⎛⎫⎛⎫⎛⎫⎛⎫+++++++++=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭故选：D10．甲、乙两种商品在过去一段时间内的价格走势如图所示．假设某人持有资金120万元，他可以在t1至t4的任意时刻买卖这两种商品，且买卖能够立即成交（其他费用忽略不计）．如果他在t4时刻卖出所有商品，那么他将获得的最大利润是A．40万元B．60万元C．120万元D．140万元【答案】C【详解】试题分析：根据图象，在低价时买入，在高价时卖出能获得最大的利润．解：甲在6元时，全部买入，可以买120÷6=20（万）份，在t2时刻，全部卖出，此时获利20×2=40万，乙在4元时，买入，可以买（120+40）÷4=40（万）份，在t4时刻，全部卖出，此时获利40×2=80万，共获利40+80=120万，故选C【解析】函数模型的选择与应用；函数解析式的求解及常用方法． 11．已知Rt ABC 的斜边长为2.则下列关于ABC 的说法中，正确的是A ．周长的最大值为2+B ．周长的最小值为2+C ．面积的最大值为2D ．面积的最小值为1【答案】A【分析】因为Rt ABC ，由勾股定理可构建关系式，由基本不等式考查周长和面积的最值即可.【详解】设c 为斜边，所以2224a b c +==，由基本不等式的推论2a b +≤2a b +≤=，当且仅当a b ==据此可知a b +≤故△ABC 的周长2a b c ++≤，周长的最大值为2+，选项A 正确，B 错误，由基本不等式可知2242,2a b ab ab =+≥≤当且仅当a b ==由面积公式112S ab =≤，故面积的最大值为1，所以C ，D 选项错误；故选：A.【点睛】本题考查基本不等式在三角形的周长和面积上应用，属于中档题 12．设定义在R 上的函数()f x 满足()()21f x f x =+，且当[)1,0x ∈-时，()()1f x x x =-+.若对任意[),x λ∈+∞，不等式()34f x ≤恒成立，则实数λ的最小值是（） A ．178-B ．94-C ．114-D ．238-【答案】B【分析】当[)1,0x ∈-时，可得()()134f x x x +≤=-恒成立，再利用递推关系式()()21f x f x =+探讨[)21x ∈--，时适合，当[)32x ∈--，时，并不恒满足题意，画出函数草图，令()()34234x x -++=，解出x ，结合图形即可得结果. 【详解】由已知()()21f x f x =+，当[)1,0x ∈-时，()()2111324144f x x x x ⎛⎫=-++≤≤ ⎪⎝⎭=-+恒成立，可得当[)2,1x ∈--时，[)+11,0x ∈-，23113()2(1)2(1)[(1)1]]22224f x f x x x x ⎛⎫=+=-+++=-++≤≤ ⎪⎝⎭恒成立；当[)3,2x ∈--时，[)+21,0x ∈-，()()()()21423f x f x x x =+=-++.画出函数草图，令()()34234x x -++=，化简得21680990x x ++=，解得194x =-，2114x =-，由图可知，当94λ≥-时，不等式()34f x ≤恒成立.故选：B .【点睛】本题考查函数恒成立问题，考查等价转化思想与综合运算能力，考查逻辑思维能力与推理论证能力，属于难题.二、填空题13．已知函数21()(5)m f x m m x -=--是幂函数，且当(0,)x ∈+∞时，()f x 是增函数，则实数m 的值为__________．【答案】3【详解】函数()()215m f x m m x-=--是幂函数，所以251m m --=，解得3m =或2m =-，又当()0,x ∈+∞时，()f x 是增函数，所以10m ->，故3m =，填314．方程230x kx k -++=的两个根均大于2,则k 的取值范围是__________ 【答案】67k ≤<【分析】可将方程转化成函数，画出大致图像，再根据二次函数性质进行求解【详解】如图所示：必须同时满足以下三个条件： ①()24230f k k =-++> ②对称轴22kx => ③()2430k k =-+≥ 联立解得67k ≤<【点睛】方程与函数可进行等价转化，必要的时候可结合二次函数图像进行求解 15．已知实数0a ≠，函数2,1()2,1x a x f x x a x +<⎧=⎨--≥⎩，若(1)(1)f a f a -=+，则a 的值为________ 【答案】34-【分析】分当0a >时和当0a <时两种分别讨论求解方程，可得答案. 【详解】当0a >时，11,1+>1a a -<，所以(1)(1)f a f a -=+，()()211+2,a a a a -+=--解得302a =-<，不满足，舍去；当0a <时，1>1,1+1a a -<，所以()()1221,a a a a ---=++解得304a =-<，满足.故答案为：34-. 【点睛】本题考查解分段函数的方程，在分段函数求函数值的时候，要把自变量代入到所对应的解析式中是解本题的关键，属于基础题．16．已知函数()()22,03,0x x f x x x ⎧+≤⎪=⎨->⎪⎩，则关于x 的方程()()()()200,3f af x a x -=∈的所有实数根的和为_______. 【答案】3 【分析】由()()20fx af x -=可得出()0f x =和()()()0,3f x a a =∈，作出函数()y f x =的图象，由图象可得出方程()0f x =的根，将方程()()()0,3f x a a =∈的根视为直线y a =与函数()y f x =图象交点的横坐标，利用对称性可得出方程()()()0,3f x a a =∈的所有根之和，进而可求出原方程所有实根之和.【详解】()()()2003f x af x a -=<<，()0f x ∴=或()()03f x a a =<<.方程()()03f x a a =<<的根可视为直线y a =与函数()y f x =图象交点的横坐标，作出函数()y f x =和直线y a =的图象如下图：由图象可知，关于x 的方程()0f x =的实数根为2-、3.由于函数()22y x =+的图象关于直线2x =-对称，函数3y x =-的图象关于直线3x =对称，关于x 的方程()()03f x a a =<<存在四个实数根1x 、2x 、3x 、4x 如图所示，且1222+=-x x ，3432x x +=，1234462x x x x ∴+++=-+=，因此，所求方程的实数根的和为2323-++=. 故答案为：3.【点睛】本题考查方程的根之和，本质上就是求函数的零点之和，利用图象的对称性求解是解答的关键，考查数形结合思想的应用，属于中等题.三、解答题17．已知集合{}|{|023}Ax x B x a x a ≤≤≤≤＝，＝＋．（1）若()RA B R ＝，求a 的取值范围；（2）是否存在a 使()RA B R ＝且A B ∅＝∩？【答案】（1）10a -≤≤；（2）不存在【分析】（1）由A 以及全集R ，求出A 的补集，根据A 补集与B 的并集为R ，即可求出a 的范围；（2）根据题意列出关于a 的不等式组，求出不等式组的解集，即可求出a 的范围．【详解】（1）{}02|Ax x ≤≤＝，∴|0{RA x x <＝或2}x > ． ∵()RA B R ＝，∴032a a ≤⎧⎨+≥⎩∴10a -≤≤. （2）由（1）知()RA B R ＝时，10a -≤≤，所以233a ≤≤＋，所以A B ⊆，这与A B ∅＝∩矛盾．即这样的a 不存在．【点睛】此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键． 18．已知命题：“{}|11x x x ∃∈-<<，使等式20x x m --=成立”是真命题．（Ⅰ）求实数m 的取值集合M ；（Ⅱ）设不等式()(2)0x a x a -+-<的解集为N ，若x ∈N 是x M ∈的必要条件，求a 的取值范围．【答案】（1）（2）或.【详解】试题分析：（1）方程在有解，转化为函数在上的值域，实数m 的取值集合M 可求；（2）x N ∈是x M ∈的必要条件，分、、三种情况讨论即可求a 的取值范围．(1) 由题意知，方程20x x m --=在上有解，即m 的取值范围就为函数在上的值域，易得1|24M m m ⎧⎫=-≤<⎨⎬⎩⎭7分 (2) 因为x N ∈是x M ∈的必要条件，所以 8分当时，解集为空集，不满足题意 9分当时，，此时集合则，解得 12分当时，，此时集合则11{,4422a a a <-⇒<--≥ 15分综上9144a a ><-或 16分【解析】命题与逻辑、分类讨论思想.19．已知二次函数()f x 满足条件(0)1f =，及(1)()2f x f x x +-=.（1）求函数()f x 的解析式；（2）在区间[]1,1-上，函数()y f x =的图象恒在3y x m =+的图象上方，试确定实数m 的取值范围.【答案】（1）2()1f x x x =-+；（2）2m <-.【分析】（1）采用待定系数法，设出函数表达式，代入对应系数相等，列方程组即可求解.（2）由题意将问题化为不等式恒成立，然后采用分离参数法转化为求函数 2()41g x x x =-+最值，即可求解.【详解】（1）设2()(0)f x ax bx c a =++≠，∵(0)1f =，∴1c =.又(1)()2f x f x x +-=，得：22ax a b x ++=，∴220a a b =⎧⎨+=⎩，∴11a b =⎧⎨=-⎩，所以2()1f x x x =-+.（2）由题知：()3f x x m >+在[1,1]-上恒成立，即()3m f x x <-在[1,1]-上恒成立，令2()()341g x f x x x x =-=-+，所以原不等式min ()m g x ⇔<，又22()41(2)3g x x x x =-+=--，[1,1]x ∈-，所以min ()(1)2g x g ==-，所以2m <-.【点睛】本题考查待定系数法求函数表达式、不等式恒成立求参数的取值范围，属于中档题.20．定义在R 上的函数()f x 满足:①对于任意的实数m ，n 等式()f m n +=()()f m f n +恒成立；②当0x >时，()0f x <，且(1)2f =- （1）判断函数()f x 在R 上的奇偶性和单调性;（2）求函数()f x 在[4,4]-上的值域【答案】（1）()f x 在R 上是减函数，在R 上是奇函数；（2）[8,8]-【分析】（1）根据函数单调性的定义，作差，利用所给恒等式进行变形，判断()1f x 与()2f x 的大小，进而证明出()f x 的单调性；根据函数奇偶性的定义证明即可．（2）利用赋值先求出()2f ，再求出()4f 得值，根据函数为奇函数且为减函数，继而求出最值.【详解】（1）设1212,,x x R x x ∈<．在()()()f m n f m f n +=+中，令211,m x x n x =-=，则2112112121()()()()()()f x x x f x x f x f x f x f x x -+=-+⇒-=-．因为当0x >时，()0f x <，所以由210x x ->得，21()0f x x -<，即2121()()()0f x f x f x x -=-<，21()()f x f x <．因此()f x 在R 上是减函数．在()()()f m n f m f n +=+中，令0m n ==，得(0)0f =．再令m n =-得， (0)f =()()f m f m +-，()()f m f m -=-，因此()f x 在R 上是奇函数．（2）函数()f x 在[4,4]-上的最大值为(4)f -、最小值为(4)f ．在()()()f m n f m f n +=+中，令1m n ==得，(2)2(1)f f =；令2m n ==得，(4)2(2)4(1)8f f f ===-．故函数()f x 在[4,4]-上的值域是[8,8]-【点睛】本题给出抽象函数，验证函数的特殊性质并讨论了函数的单调性与奇偶性．着重考查了对弈的运算法则、函数的单调性与奇偶性等知识，利用“赋值法”使抽象函数问题具体化，是解决这类问题的关键所在，属于中档题．21．解关于x 的不等式11ax a x +≤+. 【答案】答案不唯一，具体见解析【分析】化简不等式为(1)(1)0ax x x--≤，对a 分类讨论，分0a =，0a ≠两大类，在0a ≠时，根据1a与0,1关系分三类，数轴穿根即可求解. 【详解】21(1)110ax a x ax a x x-+++≤+⇔≤ 即(1)(1)0ax x x--≤ 等价于(1)(1)00ax x x x --≤⎧⎨≠⎩1.0a =时，即()[)(1)0,01,0x x x x -≥⎧⇒∈-∞⋃+∞⎨≠⎩2.0a ≠时，三次不等式对应的方程的三个根分别为0，1和1a； ⑴0a <时，利用数轴标根法，大致图像为：[)1,01,x a ⎡⎫∴∈+∞⎪⎢⎣⎭；⑵0a >时，草图为：需要判断1a和1的大小①01a <<时，解集为()1,01,a ⎡⎤-∞⎢⎥⎣⎦； ②1a =时，解集为(){},01-∞； ③1a >时，解集为()1,0,1a ⎡⎤-∞⎢⎥⎣⎦. 综上：①0a <时，解集为[)1,01,a ⎡⎫+∞⎪⎢⎣⎭； ②0a =时，解集为()[),01,-∞+∞；③01a <<时，解集为()1,01,a ⎡⎤-∞⎢⎥⎣⎦； ④1a =时，解集为(){},01-∞； ⑤1a >时，解集为()1,0,1a ⎡⎤-∞⎢⎥⎣⎦. 【点睛】本题主要考查了含参不等式的解法，关键在于分类讨论思想方法，属于难题. 22．已知函数()2f x x bx c =++，且函数()1f x -是定义在R 上的偶函数. ⑴求实数b 的值.⑵若函数()()[]()2,1g x f x x =∈-的最小值为1，求函数()g x 的最大值.【答案】(1)2;(2)5【分析】(1)根据函数(1)f x -的对称轴以及图象变换可得()f x 的对称轴,从而可得b 的值;(2)由()g x 的最小值为1,可得()1g x ≥在[2,1]x ∈-上恒成立,解得c 的范围为2c ≥或4c ≤-,再分两种情况讨论,可求得()g x 的最大值.【详解】(1)因为函数(1)f x - 是定义在R 上的偶函数,所以(1)f x -的对称轴为0x =,所以()f x 的对称轴为1x =-, 所以12b -=-,解得2b = , (2)由(1)知,2()|()||2|g x f x x xc ==++([2,1]x ∈-),因为()g x 的最小值为1,所以2|2|1x x c ++≥ 在[2,1]x ∈-上恒成立,即221c x x ≤--- 或221c x x ≥--+ 在[2,1]x ∈-上恒成立,所以2min (21)4c x x ≤---=-或2max (21)2c x x ≥--+=,当4c ≤-时, 22()2(1)1410f x x x c x c c =++=++-≤+-< ()|()|()g x f x f x ==-=2(2)x x c -++2(1)1x c =-+-+,所以()g x =|()|f x 的最小值为(1)31f c -=--=,解得4c =-,此时()g x 的最大值为(1)|(1)|5g f -=-=.当2c ≥时,22()2(1)110f x x x c x c =++=++-≥>,所以()|()|()g x f x f x ===22x x c ++2(1)1x c =++-, 因为对称轴1[2,1]x =-∈-,所以min ()g x =(1)11g c -=-=,解得2c = ,符合. 此时()g x 的最大值为(1)122g =++=5,综上所述, 函数()g x 的最大值是5.【点睛】本题考查了二次函数的性质,二次函数在闭区间上的最值的求法以及分类讨论思想,根据最小值为1,即g (x )大于等于1,可以缩小c 的范围,可以减少讨论次数是解题关键.属难题.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

舒城中学2020级高一新生入学考试
数学试题
时间：120分钟分值：150分
一、选择题(本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要
求的) 1. 实数r q p 、、在数轴上的位置如图，化简()()()22
2
r q q p p r p ++
+-
-+的值为
（）
A .p r -2
B .q p 23--
C .p -
D .r p 23+- 2. 已知a 为实常数，则下列结论正确的是
（）
A .关于x 的方程a x a =的解是1±=x
B .关于x 的方程a x a =的解是1=x
C .关于x 的方程a x a =的解是1=x
D .关于x 的方程()
11+=+a x a 的解是1±=x
3. 观察下列数的规律： ,8,5,3,2,1,1，则第9个数是
（）
A . 21
B . 22
C . 33
D . 34
4. 抛物线)0(2
≠++=a c bx ax y 的对称轴为直线1-=x ，图象如图所示，给出以下结论：①ac b 42>；②0>abc ；③02=-b a ；④039>+-c b a ；错误的结论的个数为
（）
A . 0
B . 1
C . 2
D . 3
5. 一元二次不等式022>++bx ax 的解集是)3
1,21(-，则b a +的值是
（）
A ．10
B .—10
C .14
D .—14
6. 在两个袋内，分别装着写有1、2、3、4四个数字的4张卡片，今从每个袋中各任取一张卡片，则所取两卡片上数字之积为偶数的概率是
（）
A ．
2
1 B ．
165
C ．
167
D ．
4
3 7. 如图，矩形纸片ABCD 中，已知AD =8，折叠纸片使AB 边与对角线AC 重合，点B 落在点F 处，折痕为AE ，且EF =3，则AB 的长为（）
A . 6
B .4
C .
D . 3 8. 已知x 是正整数，则当函数290
1
--=x y 取得最小值时x 的值为
（）
A . 16
B . 17
C . 18
D . 19
9. 如图，正方形ABCD 的边长为4，P 为正方形边上一动点，运动路线是A →D →C →B →A ,设P 点经过的路程为x ，以点A 、P 、D 为顶点的三角形的面积是y .则下列图象能大致反映y 与x 的函数关系的是（）
10. 下列命题正确的是
（）
A ．若>a b ，则
11a b
<
B ．若>a b ，则22a b >
C ．若>a b ，c d <，则>a c b d --
D ．若>a b ，>c d ，则>ac bd
11. 若直角坐标系内两点P 、Q 满足条件①P 、Q 都在函数y 的图象上②P 、Q 关于原点对称，则称点对（P ，
Q ）是函数y 的一个“友好点对”（点对（P ，Q ）与（Q ，P ）看作同一个“友好点对”）。

已知函数
D
C
B
A
⎪⎩⎪
⎨⎧>≤++=021
014
22x x
x x x y ，，,则函数y 的“友好点对”有（）个 A ．0
B .1
C . 2
D .3
12.如图，在四边形ABCD 中，︒=∠135B ，︒=∠120C ，3=
AB ，61+=AD ，22=CD ，则BC
边的长为
（）
A ．
21
5-
B .22-
C ．2
3
D .
2
2
二、填空题(本题共4小题，每小题5分，共20分)
13.已知、、是互不相等的实数，是任意实数，化简：
14.已知012=++x x ，求++20062007x x ……+123+++x x x =_______.
15. 矩形ABCD 中，4=AB ,3=AD ，
将该矩形按照下图所示位置放置在直线AP 上，然后不滑动的转动，当它转动一周时（1A A →）叫做一次操作，则经过5次这样的操作，顶点A 经过的路线长等于；
16. 在ABC ∆中，5==AC AB ，5
4
cos =
B ，若以M 为圆心，17为半径的圆经过
C B 、两点，则线段AM 的长等于。

a b c x 222
()()()()()()()()()
x a x b x c a b a c c b a b c a c b ---++=------
三、解答题(本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17.（本小题满分10分）
（1）已知|a |<1，比较1
1＋a 与1－a 的大小
（2
）解不等式
18.（本小题满分12分）（1（2）先化简再求值：222524
1244
a a a a a a ⎛⎫-+-+÷ ⎪+++⎝⎭，其中2a =+
19.（本小题满分12分）已知函数⎪⎩⎪⎨⎧>-+-≤-=0
202
2
x k
x x x k
x y ，其中k 为实数.
（1）当0=k 时，在所给的网格内做出该函数图象的简图，并利用图象求0>x 时，函数的最大值；（2）当k 变化时，探究函数图象与x 轴的交点个数.
第19题图第20题图
1
32
x ≤+
20.（本小题满分12分）如图，抛物线14
17
452++-
=x x y 与y 轴交于A 点，过点A 的直线与抛物线交于另一点B ，过点B 作BC ⊥x 轴，垂足为点C (3，0). （1）求直线AB 的函数关系式；
（2）动点P 在线段OC 上从原点出发以每秒一个单位的速度向C 移动，过点P 作PN ⊥x 轴，交直线AB 于
点M ，交抛物线于点N 。

设点P 移动的时间为t 秒，MN 的长度为s 个单位，求s 与t 的函数关系式，并写出t 的取值范围； 21.（本小题满分12分）如图①，正方形ABCD 的边长为7， ADB ∠的角平分线DE 交AB 与点E . （1）求
AE
BE
的值；（2）若P 在线段BD 上运动，如图②，当BP 为何值时，AP EP +的值最小.
第21题图①
第21题图②
22.（本小题满分12分）在金融危机中,某钢材公司积压了部分圆钢,经清理知共有2009根.现将它们堆放在
一起. （1）若堆放成纵断面为正三角形(每一层的根数比上一层根数多1根),并使剩余的圆钢尽可能地少,则剩余了
多少根圆钢? （2）若堆成纵断面为等腰梯形(每一层的根数比上一层根数多1根),且不少于七层，
（Ⅰ）共有几种不同的方案?
（Ⅱ）已知每根圆钢的直径为10cm ，为考虑安全隐患，堆放高度不得高于4m ，则选择哪个方案，最
能节省堆放场地？。