高中数学《余弦定理》精品课件
合集下载
人教A版高中数学必修第二册《余弦定理》名师课件

=
+ , 所以 =
+ −
+ −
,得
所以 + − = , 所以 + =
所以△ABC是直角三角形.
= ,
.
方法归纳
判断三角形形状的思路
1、转化为三角形的边来判断
(1)△ABC为直角三角形⇔ 2 = b2 + c 2 或 b2 = 2 + c 2 或 c 2 = 2 + b2
△ 中的最大角与最小角的和为∘ .
=
典例讲授
例2、在△ABC中, = , = , =
,则
= ,sin A = .
解析
根据余弦定理,得
=
+
− =
+
得 = .由 = , − , = 及余弦定理的推论,得
变式训练
2.在△ 中,已知 = 3, = 2, ( + ) =
B.
A.4
C.3
1
,则
3
=( D )
D.
解析
由三角形内角和定理可知, = [ ° − ( + )] = −( + ) = − .
又由余弦定理,得
=
+
ቐ 2 = 2 + 2 − 2cos
2 = 2 + 2 − 2cos
2 + 2 − 2
cos =
2
2 + 2 − 2
cos =
2
余弦定理ppt课件

(1)求∠A(用角度制表示); (2)当 a= 3,△ABC 的面积 S= 23时,求 b 和∠B.
❖ 分析:(1)由平面向量共线定理可得出关于各 角的一个关系式,化简之后便可求出∠A;(2) 分别利用三角形面积公式及余弦定理列出关 于b,c的方程,求出b,c的值,进而求出∠B.
解析:(1)∵m∥n,
3
2 3
=12,
∴∠BAC=30°,所求角为 30°+45°=75°.
∴甲船应沿北偏东 75°方向航行.
答:甲船应沿北偏东 75°方向航行半小时后才能
与乙船相遇.
[例 5] 在△ABC 中,a、b、c 分别是∠A、∠B、∠C
的对边,若 m=(sin2B+2 C,1),n=(cos2A+72,4),且 m∥n.
即(281)2=9+y2-3y,整理得: (y-185)(y-98)=0, ∴y=185或 y=98(舍去),∴AD 的长为185.
❖ [例3] 在△ABC中,a·cosA=b·cosB,试确 定此三角形的外形.
解析:解法 1:由 a·cosA=b·cosB 以及余弦定理得 a·b2+2cb2c-a2=b·a2+2ca2c-b2, 得 a2(b2+c2-a2)=b2(a2+c2-b2), a2b2+a2c2-a4-a2b2-b2c2+b4=0,即(a2-b2)(c2-a2 -b2)=0. ∴a2=b2 或 c2=a2+b2, ∴a=b 或 c2=a2+b2.
❖ 二、余弦定理的运用
❖ 利用余弦定理可以处理两类斜三角形问题:
❖ 1.知三边,求⑪________. ❖ 2.知两边和它们的夹角,求⑫________
和⑬________.
❖ 友谊提示:了解运用余弦定理应留意以下 四点:
❖ (1)余弦定理提示了恣意三角形边角之间的 客观规律,是解三角形的重要工具;
❖ 分析:(1)由平面向量共线定理可得出关于各 角的一个关系式,化简之后便可求出∠A;(2) 分别利用三角形面积公式及余弦定理列出关 于b,c的方程,求出b,c的值,进而求出∠B.
解析:(1)∵m∥n,
3
2 3
=12,
∴∠BAC=30°,所求角为 30°+45°=75°.
∴甲船应沿北偏东 75°方向航行.
答:甲船应沿北偏东 75°方向航行半小时后才能
与乙船相遇.
[例 5] 在△ABC 中,a、b、c 分别是∠A、∠B、∠C
的对边,若 m=(sin2B+2 C,1),n=(cos2A+72,4),且 m∥n.
即(281)2=9+y2-3y,整理得: (y-185)(y-98)=0, ∴y=185或 y=98(舍去),∴AD 的长为185.
❖ [例3] 在△ABC中,a·cosA=b·cosB,试确 定此三角形的外形.
解析:解法 1:由 a·cosA=b·cosB 以及余弦定理得 a·b2+2cb2c-a2=b·a2+2ca2c-b2, 得 a2(b2+c2-a2)=b2(a2+c2-b2), a2b2+a2c2-a4-a2b2-b2c2+b4=0,即(a2-b2)(c2-a2 -b2)=0. ∴a2=b2 或 c2=a2+b2, ∴a=b 或 c2=a2+b2.
❖ 二、余弦定理的运用
❖ 利用余弦定理可以处理两类斜三角形问题:
❖ 1.知三边,求⑪________. ❖ 2.知两边和它们的夹角,求⑫________
和⑬________.
❖ 友谊提示:了解运用余弦定理应留意以下 四点:
❖ (1)余弦定理提示了恣意三角形边角之间的 客观规律,是解三角形的重要工具;
高中数学余弦定理PPT课件
sin2 A sin2 B sin2 C 2sinB sinC cos A
练习: 求sin2 700 sin2 500 sin 700 sin 500的值.
解:原式 sin2 700 sin2 500 2sin700 sin500 cos600
sin2 600 3
4 第14页/共45页
AC
得sin ABC AC sin BAC 0.5sin 75 0.4128,
BC
1.17
所以ABC 24.4 .
所以DAN DAB NAB ABC 15 9.4 .
答:渡船应按北偏西9.4 的方向,并以11.7km / h的速度航行.
P16练习1,2
25
第25页/共45页
例5 在ABC中,已知sin A 2sin B cos C, 试判断三角形的形状.
2
AB2 AC 2 2AM 2 1 BC 2 ,
练习:P177,13
2
因此, AM 1 2( AB2 AC 2 ) BC 2 . 2 第27页/共45页
27
作业:P17 2,8,11,12
28
第28页/共45页
29
第29页/共45页
提高性训练:
1、在△ABC中,求证: c=acosB+bcosA
第13页/共45页
剖析 剖 析 定 理
(4)能否把式子a2 b2 c2 2bccosA 转化为角的关系式?
分析: 由 正 弦 定 理: a b c 2R si nA si nB si nC
得 : a 2RsinA b 2R sin B c 2R sin C
代入a2 b2 c2 2bccosA并化简得:
b2+c2-a2 2bc
余弦定理(55张PPT)

2.在解三角形的过程中,求某一个角有时既可以用余 弦定理,也可以用正弦定理,两种方案有什么利弊呢?
提示:用余弦定理求角时,运算量较大,但角与余弦 值是一一对应的,无须讨论;而用正弦定理求角时,运算 量较小,但由于在区间(0,π)上角与正弦值不是一一对应 的,一般情况下一个正弦值可对应两个角,往往要依据角 的范围讨论解的情况.
新知初探
1.余弦定理 三角形中任何一边的平方等于其他两边的平方的和减 去这两边与它们的夹角的余弦的积的两倍.即
2.余弦定理的推论 余弦定理揭示了三角形中两边及其夹角与对边之间的 关系,它的另一种表达形式是 b2+c2-a2 cosA=_____________ , 2bc
a2+c2-b2 2ac cosB=_____________ , a2+b2-c2 2ab cosC=_____________.
类型二 [例2]
判断三角形的形状 在△ABC中,已知(a+b+c)(b+c-a)=3bc且
sinA=2sinBcosC,试确定△ABC的形状. [分析] 首先根据条件(a+b+c)(b+c-a)=3bc,利
用余弦定理求出一个角,再利用另一个条件,得到另外两 个角的关系,即可判断.
[解]
∵(a+b+c)(b+c-a)=3bc,
须知余弦定理是勾股定理的推广,勾股定理是余弦定
2 2 2 a > b + c 理的特例.角A为钝角⇔_____________,角A为直角⇔ 2 2 2 2 2 2 a = b + c a < b + c ____________,角A为锐角⇔____________.
3.利用余弦定理可解决的两类问题 余弦定理的每一个等式中都包含四个不同的量,它们 分别是三角形的三边和一个角,知道其中的三个量,代入 等式,便可求出第四个量来. 利用余弦定理可以解决以下两类解斜三角形的问题:
高中数学《余弦定理》课件

20
课前自主预习
课堂互动探究
随堂达标自测
课后课时精练
数学 ·必修5
解析 (1)由(b+c)∶(c+a)∶(a+b)=4∶5∶6,得 a∶ b∶c=7∶5∶3,∴边 a 最大.又 cosA=b2+2cb2c-a2=-12, ∴A=120°.
(2)由余弦定理的推论,得 cosA=AB22×+AABC×2-ABCC2=922+×892×-872=23,
29
课前自主预习
课堂互动探究
随堂达标自测
课后课时精练
数学 ·必修5
【跟踪训练 3】 在△ABC 中,若(a-ccosB)sinB=(b -ccosA)sinA,判断△ABC 的形状.
解 由正弦定理及余弦定理知,原等式可化为 a-c·a2+2ca2c-b2b=b-c·b2+2cb2c-a2a, 整理,得(b2-a2)(a2+b2-c2)=0, ∴a2+b2-c2=0 或 a2=b2, 故三角形为等腰三角形或直角三角形.
11
课前自主预习
课堂互动探究
随堂达标自测
课后课时精练
数学 ·必修5
拓展提升 已知两边及一角解三角形的两种情况
(1)三角形中已知两边和一边的对角,有两种解法.法 一利用余弦定理列出关于第三边的等量关系建立方程,运用 解方程的方法求出第三边的长,这样可免去判断取舍的麻 烦.法二直接运用正弦定理,先求角再求边.
19
课前自主预习
课堂互动探究
随堂达标自测
课后课时精练
数学 ·必修5
【跟踪训练 2】 (1)在△ABC 中,(b+c)∶(c+a)∶(a +b)=4∶5∶6,则此三角形的最大内角为__1_2_0_°___;
(2)在△ABC 中,已知 BC=7,AC=8,AB=9,试求 AC 边上的中线长.
余弦定理PPT课件

c
C
aB
探索探究
联系已经学过的知识和方法,可用 什么途径来解决这个问题?
即:如图,在△ABC中,
设BC=a, AC=b, AB=c.
A
已知a, b和∠C,求边c? b
c
C
aB
探索探究
联系已经学过的知识和方法,可用 什么途径来解决这个问题?
用向量来研究这问题. A
即:如图,在△C ABC中, B
设BC=a, AC=b, AB=c.
巩经典固例知题识 典型例题
例 在△ABC中,a = 6,b = 7,c = 10,求△ABC 中的 最大角和最小角(精确到1°).
解 由于a<b<c,所以C最大,A最小,由公式(1.12),有
cos C a2 b2 c2 62 72 102 0.1786,
2ab
267
所以 C ≈ 100°,
a2 b2 c2 2cbcos A. b2 a2 c2 2ac cos B,c2 a2 b2 2ab cosC.
可以证明,上述结论对于任意三角形都成立.于是得到余弦 定理.
思考2:
a2 b2 c2 2bc cos A b2 a2 c2 2ac cos B c2 a2 b2 2ab cos C
1.3.2余弦定理
复习引入
运用正弦定理能解怎样的三角形?
A C
B
复习引入
运用正弦定理能解怎样的三角形?
①已知三角形的任意两角及其一边;
②已知三角形的任意两边A 与其中一边
的对角.
C B
情境设置
问题1:
如果已知三角形的两边及其夹角, 根据三角形全等的判定方法,这个三
A
角形是大小、形状完全确定的三角形. C
高中数学《余弦定理》精品PPT课件

2R
2R
2R
sin A: sin B : sin C a : b : c
思考: 在△ABC中,已知CB=a,CA=b,CB
与CA 的夹角为∠C,
向量法
设
CB a,
求边c. CA b,
AB
c
c ab
c
2
c
c
(a
b)
(a
b)
a
a
2
a
b2
b
b
B. 2,3,4
C. 3,4,5
D. 4,5,6
分析: 要看哪一组符合要求,只需检验
哪一个选项中的最大角是钝角,即该角 的余弦值小于0。
9.在△ABC中,已知a=7,b=8,cosC= 求最大角的余弦值
13 14
,
分析:求最大角的余弦值,最主要的是判断
哪个角是最大角。由大边对大角,已知两边 可求出第三边,找到最大角。
练习
1. 在ABC中,已知a=2 ,c 6 2, B 1350,解此三角形
b 2 2, A 300,C 150
练习4.在△ABC中,已知a= 6 ,b=2,
c= 3 1 ,解三角形.
解:由余弦定理得
cos A b2 c2 a2 22 ( 3 1)2 ( 6)2 1
例1 在△ABC中,已知b=60cm,c=34cm,A=41o, 解该三角形(角度精确到1°,边长精确到1cm). 解:∵a²=b²+c²-2bccosA
=60²+34²-2×60×34×cos41o≈1676.82
∴a≈41(cm)
数学人教A版必修第二册6.4.3余弦定理课件

bsinC 2 abcosC 2
a2 b2 2abcosC
D
AD bsin C bsinC CD bcos C bcosC
BD a bcosC c2 AD2 BD2
bsinC 2 abcosC 2
a2 b2 2abcosC
高中数学
综上,我们得到:在ΔABC中,有
c2 a2 b2 2abcosC
高中数学
余弦定理:
三角形中任何一边的平方,等于其他两边平方和减去这两边与它们夹角 的余弦的积的两倍,即
a2 b2c22bccos A; b2 a2 c22accosB; c2 a2 b22abcosC.
推论:
cos Ab2 c2 a2 2bc
cosB a2 c2 b2 2ac
cosC a2 b2 c2 2ab
高中数学
分析讲授
思考1:在任意三角形中,三角形的边角之间有没有类似的 数量关系呢?
为了研究方便我们先作如下规定:
角 A 的对边是 a ,角B 的对边是b,角 C 的对边是 c .
高中数学
情况一:当C为直角时,
情况二:当C为锐角时,
情况三:当C为钝角时,
a2 b2 c2
D
AD bsinC CD bcosC,BD a bcosC c2 AD2 BD2
a2 b2c22bccos A; b2 a2 c2 2accosB; c2 a2 b2 2abcosC.
cos Ab2 c2 a2 2bc
cosB a2 c2 b2 2ac
cosC a2 b2 c2 2ab
高中数学
作业布置
练习册:完成P26-27
感谢您的观看
高中数学
知识应用
例1 在ΔABC中,已知 a4,b6 ,C 120 ,则边c=( )
a2 b2 2abcosC
D
AD bsin C bsinC CD bcos C bcosC
BD a bcosC c2 AD2 BD2
bsinC 2 abcosC 2
a2 b2 2abcosC
高中数学
综上,我们得到:在ΔABC中,有
c2 a2 b2 2abcosC
高中数学
余弦定理:
三角形中任何一边的平方,等于其他两边平方和减去这两边与它们夹角 的余弦的积的两倍,即
a2 b2c22bccos A; b2 a2 c22accosB; c2 a2 b22abcosC.
推论:
cos Ab2 c2 a2 2bc
cosB a2 c2 b2 2ac
cosC a2 b2 c2 2ab
高中数学
分析讲授
思考1:在任意三角形中,三角形的边角之间有没有类似的 数量关系呢?
为了研究方便我们先作如下规定:
角 A 的对边是 a ,角B 的对边是b,角 C 的对边是 c .
高中数学
情况一:当C为直角时,
情况二:当C为锐角时,
情况三:当C为钝角时,
a2 b2 c2
D
AD bsinC CD bcosC,BD a bcosC c2 AD2 BD2
a2 b2c22bccos A; b2 a2 c2 2accosB; c2 a2 b2 2abcosC.
cos Ab2 c2 a2 2bc
cosB a2 c2 b2 2ac
cosC a2 b2 c2 2ab
高中数学
作业布置
练习册:完成P26-27
感谢您的观看
高中数学
知识应用
例1 在ΔABC中,已知 a4,b6 ,C 120 ,则边c=( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5
2
2
2
归纳 A
余弦定理
a2=b2+c2-2bc· cosA
b
c B a
b2=c2+a2-2ca· cosB
c2=a2+b2-2ab· cosC
C
三角形任何一边的平方 等于其他两边平方的和减去 你能用文字说明吗? 这两边与它们夹角的余弦的 积的两倍。
6
讨论: 余弦定理指出了三角形三条边与其中一 个角之间的关系,应用余弦定理,我们 可以解决已知三角形的三边确定三角形 的角的问题,怎么确定呢?
16
1 在ABC中,a 3, c 8, B 60, 则ABC的周长 18 是___ 7___ 3 2 在ABC中,a=9,b=2 3, C 150, 则c
3 在ABC中,a 10, b 24, c 26, 则最大角的 余弦值为( 0 ) 2 / 3 4 在ABC中,已知a2 b2 bc c2 , 则角A为___
4
证明
向量法
c B a C
A
b
AB AB ( AC CB) ( AC CB)
AC AC 2 AC CB CB CB 2 2 2 ∴ AB = AC +2 AC CB cos(1800 -C)+ CB
∴ c = a + b - 2abcosC
A≈39°,
∴
B=180°-(A+C)=58°32′.
例题讲解
例 2:在ABC中,已知a=7,b=10,
c=6,解三角形.(精确到1 ° ) 解: ∵ ∴
c sin A b2+c2-a2 sin C 0.5954 cosA= =0.725, a 2bc C 36 或144 (舍) A≈44° a2+b2-c2 cosC= =0.807, 2ab C≈36°,
∵
∴ ∴B=180°-(A+Fra bibliotek)≈100°.
1 3
2 4
1 在ABC中,a 3, c 8, B 60, 则ABC的周长 18 是___ 7___ 3 2 在ABC中,a=9,b=2 3, C 150, 则c
3 在ABC中,a 10, b 24, c 26, 则最大角的 余弦值为( 0 ) /3 ___ 4 在ABC中,已知a2 b2 bc c2 , 则角A为2
15
1 在ABC中,a 3, c 8, B 60, 则ABC的周长 18 是___ 7___ 3 2 在ABC中,a=9,b=2 3, C 150, 则c
3 在ABC中,a 10, b 24, c 26, 则最大角的 余弦值为( 0 ) 2 / 3 4 在ABC中,已知a2 b2 bc c2 , 则角A为___
(1)已知三边求三个 角; (2)已知两边和它 们的夹角,求第三 边和其他两个角.
a 2 + b2 - c 2 cosC = 2ab
2 2 2 2 2
b2 + c2 - a 2 cosA = 2bc 2 a + c2 - b 2 cosB = 2ac
a =b +c-2bccosA
b =c +a-2accosB
沙河市第二中学 杨 蕾
1
复习
直角三角形中的边角关系:
A+B+C=180° A+B=C=90 ° c b 2、边的关系: a2+b2=c2 B a C 3、边角关系: a =cosB sinA= — c b = cosA sinB = — c
2
A 1、角的关系:
看一看想一想
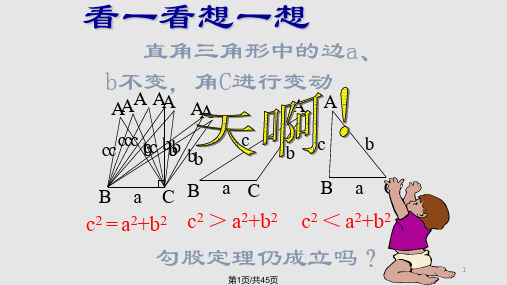
直角三角形中的边a、 b不变,角C进行变动
14
1 在ABC中,a 3, c 8, B 60, 则ABC的周长 18 是___ 7___ 3 2 在ABC中,a=9,b=2 3, C 150, 则c
3 在ABC中,a 10, b 24, c 26, 则最大角的 余弦值为( 0 ) /3 ___ 4 在ABC中,已知a2 b2 bc c2 , 则角A为2
a sin C sin A 0.6299 c 2 2 2 c =a +b -2abcosC, A 39 或141 c b a c≈4.297. b2+c2-a2 C B A cosA= ≈0.777, 2bc A C 82 28` A 39
A A A A A A A A A
c c c cb bb cc c b b b B a C B
c
a C
b
c
B a
b
C
c2 = a2+b2
c2 > a2+b2
c2 < a2+b2
3
勾股定理仍成立吗?
A c B a C b
c= ∣AB∣
c2=
AB= AC+ CB
= AB AB
AB AB= (AC+CB) (AC+CB)
归纳 A
变一变乐在其中
a2=b2+c2-2bc· cosA
b
c B a
b2=c2+a2-2ca· cosB
c2=a2+b2-2ab· cosC
b2+c2 - a2 cosA= 2bc c2+a2 - b2 cosB= 2ca a2+b2 - c2 cosC= 2ab
C
变形
8
余弦定理适用于任何三角形 余弦定理的作用
c =a +b-2abcosC
2 2 2
2
9
讨论:
勾股定理指出了直角三角形中三边平方 之间的关系,余弦定理则指出了一般三 角形中三边平方之间的关系,什么关系 时是直角?钝角?锐角?如何看这两个 定理之间的关系?
例题讲解
例 1:在ABC中,已知a=2.730,b=3.696, C=82°28′,解这个三角形. 解: 由 得 ∵ ∴
17
1 在ABC中,a 3, c 8, B 60, 则ABC的周长 18 是___ 7___ 3 2 在ABC中,a=9,b=2 3, C 150, 则c
3 在ABC中,a 10, b 24, c 26, 则最大角的 余弦值为( 0 ) /3 ___ 4 在ABC中,已知a2 b2 bc c2 , 则角A为2
2
2
2
归纳 A
余弦定理
a2=b2+c2-2bc· cosA
b
c B a
b2=c2+a2-2ca· cosB
c2=a2+b2-2ab· cosC
C
三角形任何一边的平方 等于其他两边平方的和减去 你能用文字说明吗? 这两边与它们夹角的余弦的 积的两倍。
6
讨论: 余弦定理指出了三角形三条边与其中一 个角之间的关系,应用余弦定理,我们 可以解决已知三角形的三边确定三角形 的角的问题,怎么确定呢?
16
1 在ABC中,a 3, c 8, B 60, 则ABC的周长 18 是___ 7___ 3 2 在ABC中,a=9,b=2 3, C 150, 则c
3 在ABC中,a 10, b 24, c 26, 则最大角的 余弦值为( 0 ) 2 / 3 4 在ABC中,已知a2 b2 bc c2 , 则角A为___
4
证明
向量法
c B a C
A
b
AB AB ( AC CB) ( AC CB)
AC AC 2 AC CB CB CB 2 2 2 ∴ AB = AC +2 AC CB cos(1800 -C)+ CB
∴ c = a + b - 2abcosC
A≈39°,
∴
B=180°-(A+C)=58°32′.
例题讲解
例 2:在ABC中,已知a=7,b=10,
c=6,解三角形.(精确到1 ° ) 解: ∵ ∴
c sin A b2+c2-a2 sin C 0.5954 cosA= =0.725, a 2bc C 36 或144 (舍) A≈44° a2+b2-c2 cosC= =0.807, 2ab C≈36°,
∵
∴ ∴B=180°-(A+Fra bibliotek)≈100°.
1 3
2 4
1 在ABC中,a 3, c 8, B 60, 则ABC的周长 18 是___ 7___ 3 2 在ABC中,a=9,b=2 3, C 150, 则c
3 在ABC中,a 10, b 24, c 26, 则最大角的 余弦值为( 0 ) /3 ___ 4 在ABC中,已知a2 b2 bc c2 , 则角A为2
15
1 在ABC中,a 3, c 8, B 60, 则ABC的周长 18 是___ 7___ 3 2 在ABC中,a=9,b=2 3, C 150, 则c
3 在ABC中,a 10, b 24, c 26, 则最大角的 余弦值为( 0 ) 2 / 3 4 在ABC中,已知a2 b2 bc c2 , 则角A为___
(1)已知三边求三个 角; (2)已知两边和它 们的夹角,求第三 边和其他两个角.
a 2 + b2 - c 2 cosC = 2ab
2 2 2 2 2
b2 + c2 - a 2 cosA = 2bc 2 a + c2 - b 2 cosB = 2ac
a =b +c-2bccosA
b =c +a-2accosB
沙河市第二中学 杨 蕾
1
复习
直角三角形中的边角关系:
A+B+C=180° A+B=C=90 ° c b 2、边的关系: a2+b2=c2 B a C 3、边角关系: a =cosB sinA= — c b = cosA sinB = — c
2
A 1、角的关系:
看一看想一想
直角三角形中的边a、 b不变,角C进行变动
14
1 在ABC中,a 3, c 8, B 60, 则ABC的周长 18 是___ 7___ 3 2 在ABC中,a=9,b=2 3, C 150, 则c
3 在ABC中,a 10, b 24, c 26, 则最大角的 余弦值为( 0 ) /3 ___ 4 在ABC中,已知a2 b2 bc c2 , 则角A为2
a sin C sin A 0.6299 c 2 2 2 c =a +b -2abcosC, A 39 或141 c b a c≈4.297. b2+c2-a2 C B A cosA= ≈0.777, 2bc A C 82 28` A 39
A A A A A A A A A
c c c cb bb cc c b b b B a C B
c
a C
b
c
B a
b
C
c2 = a2+b2
c2 > a2+b2
c2 < a2+b2
3
勾股定理仍成立吗?
A c B a C b
c= ∣AB∣
c2=
AB= AC+ CB
= AB AB
AB AB= (AC+CB) (AC+CB)
归纳 A
变一变乐在其中
a2=b2+c2-2bc· cosA
b
c B a
b2=c2+a2-2ca· cosB
c2=a2+b2-2ab· cosC
b2+c2 - a2 cosA= 2bc c2+a2 - b2 cosB= 2ca a2+b2 - c2 cosC= 2ab
C
变形
8
余弦定理适用于任何三角形 余弦定理的作用
c =a +b-2abcosC
2 2 2
2
9
讨论:
勾股定理指出了直角三角形中三边平方 之间的关系,余弦定理则指出了一般三 角形中三边平方之间的关系,什么关系 时是直角?钝角?锐角?如何看这两个 定理之间的关系?
例题讲解
例 1:在ABC中,已知a=2.730,b=3.696, C=82°28′,解这个三角形. 解: 由 得 ∵ ∴
17
1 在ABC中,a 3, c 8, B 60, 则ABC的周长 18 是___ 7___ 3 2 在ABC中,a=9,b=2 3, C 150, 则c
3 在ABC中,a 10, b 24, c 26, 则最大角的 余弦值为( 0 ) /3 ___ 4 在ABC中,已知a2 b2 bc c2 , 则角A为2
